Abstract
Information entropy, as a quantitative measure of complexity in nonlinear systems, has been widely researched in a variety of contexts. With the development of a nonlinear dynamic, the entropy is faced with severe challenges in dealing with those signals exhibiting extreme volatility. In order to address this problem of weighted permutation entropy, which may result in the inaccurate estimation of extreme volatility, we propose a rescaled range permutation entropy, which selects the ratio of range and standard deviation as the weight of different fragments in the time series, thereby effectively extracting the maximum volatility. By analyzing typical nonlinear systems, we investigate the sensitivities of four methods in chaotic time series where extreme volatility occurs. Compared with sample entropy, fuzzy entropy, and weighted permutation entropy, this rescaled range permutation entropy leads to a significant discernibility, which provides a new method for distinguishing the complexity of nonlinear systems with extreme volatility.
Export citation and abstract BibTeX RIS
Quantifying the complexity of natural systems has always been an important task in the field of nonlinear dynamics.[1–3] Various measures of complexity have been developed to compare time series, including the Lyapunov exponent,[4,5] entropy, Kolmogorov complexity,[6] and fractal dimensions.[7,8] As a measure of the average uncertainty of information, entropy enables a sufficient indication of nonlinear dynamics for complex chaotic systems. Since Shannon summarized previous studies and proposed the concept of information entropy in 1948, a variety of quantitative methods of characterizing system complexity have been proposed, such as approximate entropy,[9,10] sample entropy (SE),[11] multivariate sample entropy (MSE), permutation entropy,[12] multi-scale entropy,[13] and multivariate fuzzy entropy (MFE),[14] which have been widely employed in the fields of biological and pharmaceutical signal analysis.[15–19]
Permutation entropy (PE), proposed by Bandt and Pompe, has demonstrated greater robustness and more prominent classification capability than other entropies in terms of analyses of nonlinear signals.[20–22] However, PE ignores the amplitude information in the analysis of nonlinear time series. Bilal et al.[23] proposed the concept of weighted permutation entropy (WPE) for preserving the amplitude information of time series, which addressed the problems of weak resolution and robustness inherent in PE in respect of changes in sequence amplitude, and achieved good results in terms of practical application.[24–27] It was found, however, that adopting the variance as weight still experiences major limitations in terms of analyses of nonlinear signals with extreme volatility. Nonlinear systems with extreme volatility exist in a wide variety of fields, such as finance,[28,29] meteorology,[30–32] multiphase flow,[33,34] among others. Improving WPE has become an urgent problem to be solved.
In this Letter, we use the ratio of the range and the standard deviation of the sequence fragment as the weight, so as to obtain a rescaled range permutation entropy (RSPE). Signal resolution performances of MSE, MFE, RSPE and WPE are investigated and compared with the numerical analyses of typical nonlinear chaotic systems. The results suggest that RSPE demonstrates the potential capacity to characterize nonlinear systems with extreme volatility.
Firstly, we introduce the principles of the RSPE, and take n-variate time series defined as
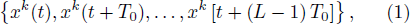
where L represents the length, T0 the sampling interval, and k the kth channel in the n-variate time series. Each channel is then decomposed into fragments of length m. A fragment of any channel can be expressed as
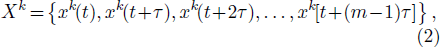
in which m is the embedding dimension, and τ denotes the delay time; n[L − (m − 1)τ] fragments are sorted from the original time series. Each fragment can be encoded according to the value of each element. An example is given as follows: When m equals 6, with τ = 1, if a fragment is expressed as {3,6,7,4,9,2}, it could be encoded as {2,4,5,3,6,1}. Code 1 therefore indicates that the signal amplitude in this position is the smallest of all elements in this fragment, code 2 indicates that the signal amplitude in this position is the second smallest of all elements in this fragment, and so on, until we arrive at code m, which contains the largest signal amplitude in this fragment. Each fragment has a code, which means that there should be m! codes at most. All fragments could be classified into m! permutations. It is possible to number each permutation as i and to express the number of the occurrence of fragments in each permutation as Ni. The probability of the occurrence of each permutation for all fragments can then be expressed as

In order to reflect information relating to amplitude in the signal, the weight of each permutation of the sequence is accumulated. One may introduce the probability of each permutation containing information of amplitude appearing in the fragments of all channels as
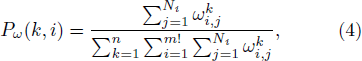
where
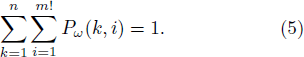
In formula (4),  represents the weight of the jth fragment on the ith permutation in the kth channel. The WPE for a certain permutation of the signal primarily considers the variance as the weight.[23] This variance mainly shows the average property of each element in each fragment on the same permutation, but the volatility will be weakened by the property of the variance. Therefore, for signals with extreme volatility, WPE cannot achieve sufficient resolution.
represents the weight of the jth fragment on the ith permutation in the kth channel. The WPE for a certain permutation of the signal primarily considers the variance as the weight.[23] This variance mainly shows the average property of each element in each fragment on the same permutation, but the volatility will be weakened by the property of the variance. Therefore, for signals with extreme volatility, WPE cannot achieve sufficient resolution.
In this study, we characterize the volatility of the fragments with the ratio of the range and standard deviation, rather than using variance as the weight in the WPE. Meanwhile, in order to perform unified processing for different fragments of the signal, the difference in the range is expected to be rescaled, i.e.:
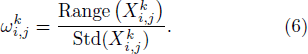
Range( ) is the range of the fragment
) is the range of the fragment  and Std(
and Std( ) denotes the standard deviation of the fragment
) denotes the standard deviation of the fragment  :
:
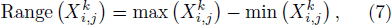
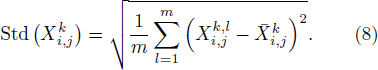
The length of the signal, L, should be large enough to ensure the accuracy of the calculation. The delay time τ and the embedding dimension m are two parameters to be determined, and are selected in accordance with the literature.[12]
The probability of each permutation containing amplitude information in the fragment can then be expressed as:

RSPE can then be defined as
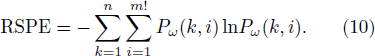
The multi-scale RSPE can be obtained by combining Eq. (10) with the coarse-grained method,[13] and the value of time series under different coarse-grained scales can be expressed as:
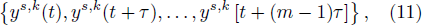
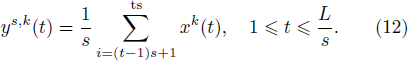
Substituting Eq. (12) into Eqs. (9) and (10) yields the multi-variate RSPE under scale s, as follows:
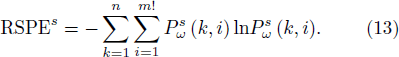
Next, we apply the above method to typical chaotic signals. In particular, we compute the MSE, MFE, WPE and RSPE of Schuster maps and Rössler maps, which exhibit extreme volatility.
We study Schuster maps, i.e., a class of maps generating fluctuant signals with chaotic bursts:
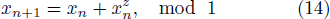
where the length of each time series is 213 points and the initial value is x0 = 0.05. Signals with different z values are shown in Fig. 1. In order to clearly show the details, Fig. 1 illustrates the volatility of the nine sequences, ranging from n = 0 to n = 1000.
Fig. 1. Schuster time series with different z values: (a) z = 1.1, (b) z = 1.2, (c) z = 1.3, (d) z = 1.4, (e) z = 1.5, (f) z = 1.6, (g) z = 1.7, (h) z = 1.8, (i) z = 1.9.
Download figure:
Standard imageThe sequence generated by the Schuster equation due to its different z values are taken as the signal source. The resolution of the complexity in different systems is analyzed using four entropies: MSE, MFE, WPE and RSPE, along with the coarse-grained method, as shown in Fig. 2.
Fig. 2. Four kinds of multi-scale entropy values obtained by processing nine types of Schuster sequence with different z values: (a) MSE, (b) MFE, (c) WPE, (d) RSPE (this study).
Download figure:
Standard imageThe Schuster sequences exhibit characteristics of extreme fluctuation, as shown in Fig. 1. The signal complexity decreases significantly with the increase of the z value. Figure 2 shows results for four types of multi-scale entropy (MSE, MFE, WPE and RSPE) in relation to nine Schuster sequences with different z values. Figures 2(a) and 2(b) show the results for MSE and MFE with the multi-scale method. While the classification in the low scale is good to some extent, there is still a confined space for classification, as the range of entropy values is between 0–2.5 for MSE and 0–1 for MFE. Moreover, when the scale increases, the different sequences in MSE and MFE exhibit poor resolution, and the curves start to tangle at low scale. Figure 2(c) shows the multi-scale entropy of the Schuster sequences obtained by WPE, which first increases and then decreases. The WPE entropy relating to the Schuster sequences is in the range 3.5–6.5, and the curves decrease hierarchically at low scales. When the scale exceeds 10, the difference between the different sequences is inconspicuous. Furthermore, the six sets of curves are entangled, and cannot be clearly distinguished. Figure 2(d) shows the results for multi-scale entropy of the Schuster sequence using RSPE. The entropy is in the range 1.5–6.5. This is clearly greater than MSE, MFE, and WPE, indicative of a larger space for classification. Between z = 1.1–1.5 and z = 1.6–1.9, differences appear in relation to the complexity of the sequences, which is the same rule as for the complexity of the original sequence changes with z in Fig. 1, i.e., in Figs. 1(e) and 1(f), the complexity of Schuster sequences decreases, and continuous low-amplitude points appear. There is a direct relation between the information structure and the complexity of the sequence. Therefore, RSPE demonstrates several advantages in terms of processing Schuster sequences, as regards the range, the direct reflection of sequence complexity, and the complexity differentiation.
Next, we study the Rössler maps, i.e., a class of maps which generate multi-variate signals with chaotic bursts. Here, we adopt a variety of different Rössler family[35] systems, having different parameters and initial values, so as to construct mutational multivariate sequences with different information structures:
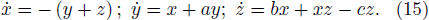
Sequence A1: the sequence generated by Eq. (15), where the parameters are configured as a = 0.36, b = 0.4, c = 4.5 with the initial value (x0,y0,z0) = (0,3,0).
Sequence A2: the sequence generated by Eq. (15), where the parameters are configured as a = 0.5, b = 0.4, c = 4.5 with the initial value (x0,y0,z0) = (0,3,0).
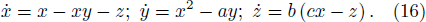
Sequence B: the sequence generated by Eq. (16), where the parameters are configured as a = 0.1, b = 0.08, c = 0.125 with the initial value (x0,y0,z0) = (0,0.2, − 10−6).
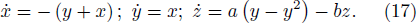
Sequence C1: the sequence generated by Eq. (17), where the parameters are configured as a = 0.2, b = 0 with the initial value (x0, y0, z0) = (0.3, 0, − 0.25).
Sequence C2: the sequence generated by Eq. (17), where the parameters are configured as a = 0.4, b = 0 with the initial value (x0, y0, z0) = (0.3, 0, − 0.25).
Sequence C3: the sequence generated by Eq. (17), where the parameters are configured as a = 0.386, b = 0.2 with the initial value (x0, y0, z0) = (0.4, − 0.4, − 0.7).
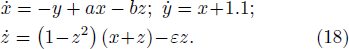
Sequence D: the sequence generated by Eq. (18), where the parameters are configured as: a = 0.2, b = 0, ε = 0.03 with the initial value (x0, y0, z0) = (0, 0, −1).
There are seven Rössler group systems with multi-variate sequences in this study. A1 and A2 are both generated by Eq. (15), but with different complexities. Similarly, C1, C2 and C3 are multi-variate chaotic sequences with different information structures, generated by Eq. (17), as shown in Fig. 3.
Fig. 3. Graph showing multiple sequences produced by Rössler systems in three dimensions: (a) series A1, (b) series A2, (c) series B, (d) series C1, (e) series C2, (f) series C3, (g) series D.
Download figure:
Standard imageThe multi-variate Rössler sequences of seven systems are combined with the multi-scale method to analyze the entropy (MSE, MFE, WPE and RSPE), as shown in Fig. 4.
Fig. 4. Four varieties of multivariate multi-scale entropy obtained by processing seven types of Rössler series: (a) MSE, (b) MFE, (c) WPE, (d) RSPE (this study).
Download figure:
Standard imageThe multi-variate sequences produced by Rössler systems have distinct characteristics of extreme volatility: In Figs. 3(a)–-3(g), sequences D and A2 are more complex than either sequences C3, C1, A1 or sequences C2, D. Figures 4(a) and 4(b) show the MSE and MFE methods of processing the different Rössler systems; the resolution of these two systems is poor compared to the RSPE method shown in Fig. 4(d), particularly in relation to the higher scales. Eventually the curves of MSE and MFE come across, making it difficult to show the complexity of the different systems. In Fig. 4(c), with an increase in scale, all the curves of WPE gradually increase with the scale. However, the WPE curves for the sequences A1, A2, B, C1, C2 and C3 show slope instability. From low to high scale, the trend of the curves changes repeatedly, leading to the sequences A1, C1, C3 being indistinguishable. Figure 4(d) shows the RSPE curves for each sequence. The slopes of the RSPE curves of sequences A1, B, C1, C2 and C3 are stable. With the increasing scale, the RSPE curves of sequences A1, C1 and C3 remain clearly separated. The slopes of sequences C2 and B are also preserved. The cross between the curves of sequences A2 and D in RSPE appears later than for the WPE curves. RSPE accurately reflects the complexity of the two sequences. In conclusion, the entropy resolution on multi-variate Rössler sequences of RSPE sequences performs far better than MSE, MFE or WPE.
In summary, the maximum volatility of the sequence is extracted using the ratio of range and standard deviation as the weight. RSPE can effectively improve on the capacity of WPE to identify and distinguish signals with extreme amplitude volatility. RSPE also improves the sensitivity of nonlinear complex recognition, and exhibits great adaptability to both single channel and multi-channel signals.
In the simulation experiments relating to typical chaotic time series with extreme fluctuations, RSPE shows excellent sensitivity: it can effectively classify the internal information structures of both Schuster and Rössler sequences. Its sensitivity is superior to MSE, MFE and WPE at both low scales and high scales. RSPE is compatible with WPE in terms of its capacity for recognition and discrimination of ordinary signal processing. It extends the adaptability of WPE in terms of volatility signals, and is of great significance in revealing the internal structure of information in dynamics systems which are nonlinear and exhibit extreme volatility.
Footnotes
Supported by the National Natural Science Foundation of China (Grant Nos. 51527805 and 11572220).




