The Astrophysical Journal Supplement Series, 148:195-211, 2003
© 2003. The American Astronomical Society. All rights reserved. Printed in U.S.A.

First-Year Wilkinson Microwave Anisotropy Probe (WMAP)¹ Observations: Parameter Estimation Methodology

L. Verde ,^2,3 H. V. Peiris ,² D. N. Spergel ,² M. R. Nolta ,⁴ C. L. Bennett ,⁵ M. Halpern ,⁶ G. Hinshaw ,⁵ N. Jarosik ,⁴ A. Kogut ,⁵ M. Limon ,^5,7 S. S. Meyer ,⁸ L. Page ,⁴ G. S. Tucker ,^5,7,9 E. Wollack ,⁵ and E. L. Wright ¹⁰

Received 2003 February 11; accepted 2003 May 30

ABSTRACT

We describe our methodology for comparing the Wilkinson Microwave Anisotropy Probe (WMAP) measurements of the cosmic microwave background (CMB) and other complementary data sets to theoretical models. The unprecedented quality of the WMAP data and the tight constraints on cosmological parameters that are derived require a rigorous analysis so that the approximations made in the modeling do not lead to significant biases. We describe our use of the likelihood function to characterize the statistical properties of the microwave background sky. We outline the use of the Monte Carlo Markov Chains to explore the likelihood of the data given a model to determine the best-fit cosmological parameters and their uncertainties. We add to the WMAP data the 700 Cosmic Background Imager (CBI) and Arcminute Cosmology Bolometer Array Receiver (ACBAR) measurements of the CMB, the galaxy power spectrum at z 0 obtained from the Two-Degree Field Galaxy Redshift Survey (2dFGRS), and the matter power spectrum at z 3 as measured with the Ly forest. These last two data sets complement the CMB measurements by probing the matter power spectrum of the nearby universe. Combining CMB and 2dFGRS requires that we include in our analysis a model for galaxy bias, redshift distortions, and the nonlinear growth of structure. We show how the statistical and systematic uncertainties in the model and the data are propagated through the full analysis.

1. INTRODUCTION

     Cosmic microwave background (CMB) experiments are powerful cosmological probes because the early universe is particularly simple and because the fluctuations over angular scales > 02 are described by linear theory (Peebles & Yu 1970; Bond & Efstathiou 1984; Zaldarriaga & Seljak 2000). Exploiting this simplicity to obtain precise constraints on cosmological parameters requires that we accurately characterize the performance of the instrument (Jarosik et al. 2003b; Page et al. 2003b; Barnes et al. 2003; Hinshaw et al. 2003a), the properties of the foregrounds (Bennett et al. 2003a), and the statistical properties of the microwave sky.

     The primary goal of this paper is to present our approach to extracting the cosmological parameters from the temperature-temperature angular power spectrum (TT) and the temperature-polarization angular cross-power spectrum (TE). In companion papers, we present the TT (Hinshaw et al. 2003a) and TE (Kogut et al. 2003) angular power spectra and show that the CMB fluctuations may be treated as Gaussian (Komatsu et al. 2003).

     Our basic approach is to constrain cosmological parameters with a likelihood analysis first of the Wilkinson Microwave Anisotropy Probe (WMAP) TT and TE spectra alone, then jointly with other CMB angular power spectrum determinations at higher angular resolution, and finally of all CMB power spectra data jointly with the power spectrum of the large-scale structure (LSS). In § 2 we describe the use of the likelihood function for the analysis of microwave background data. This builds on the Hinshaw et al. (2003b) methodology for determining the TT spectrum and its curvature matrix and Kogut et al. (2003), who describe our methodology for determining the TE spectrum. In § 3 we describe our use of Markov Chain Monte Carlo (MCMC) techniques to evaluate the likelihood function of model parameters. While WMAP's measurements are a powerful probe of cosmology, we can significantly enhance their scientific value by combining the WMAP data with other astronomical data sets. This paper also presents our approach for including external CMB data sets (§ 4), LSS data (§ 5), and Ly forest data (§ 6). When including external data sets, the reader should keep in mind that the physics and the instrumental effects involved in the interpretation of these external data sets (especially 2dFGRS and Ly) are much more complicated and less well understood than for WMAP data. Nevertheless, we aim to match the rigorous treatment of uncertainties in the WMAP angular power spectrum with the inclusion of known statistical and systematic effects (of the data and of the theory), in the complementary data sets.

2. LIKELIHOOD ANALYSIS OF WMAP ANGULAR POWER SPECTRA

     The first goal of our analysis program is to determine the values and confidence levels of the cosmological parameters that best describe the WMAP data for a given cosmological model. We also wish to discriminate between different classes of cosmological models, in other words, to assess whether a cosmological model is an acceptable fit to WMAP data.

     The ultimate goal of the likelihood analysis is to find a set of parameters that give an estimate of , the ensemble average of which the realization on our sky¹¹ is . The likelihood function, [|()], yields the probability of the data given a model and its parameters (). In our notation denotes our best estimator of (Hinshaw et al. 2003a) and is the theoretical prediction for angular power spectrum. From Bayes's theorem, we can split the expression for the probability of a model given the data as



where () describes our priors on cosmological parameters and we have neglected a normalization factor that does not depend on the parameters . Once the choice of the priors is specified, our estimator of is given by evaluated at the maximum of (|).

     ¹¹ Throughout this paper we use the convention that = ( + 1)C/(2).

2.1. Likelihood Function

     One of the generic predictions of inflationary models is that fluctuations in the gravitational potential have Gaussian random phases. Since the physics that governs the evolution of the temperature and metric fluctuations is linear, the temperature fluctuations are also Gaussian. If we ignore the effects of nonlinear physics at z < 10 and the effect of foregrounds, then all of the cosmological information in the microwave sky is encoded in the temperature and polarization power spectra. The leading-order low-redshift astrophysical effect is expected to be gravitational lensing of the CMB by foreground structures. We ignore this effect here as it generates a less than 1% covariance in the TT angular power spectrum on WMAP angular scales (Hu 2001; see also Spergel et al. 2003, § 3).

     There are several expected sources of noncosmological signal and of non-Gaussianity in the microwave sky. The most significant sources on the full sky are Galactic foreground emission, radio sources, and galaxy clusters. Bennett et al. (2003b) show that these contributions are greatly reduced if we restrict our analysis to a cut sky that masks bright sources and regions of bright Galactic emission. The residual contribution of these foregrounds is further reduced by the use of external templates to subtract foreground emission from the Q-, V-, and W-band maps. Komatsu et al. (2003) find no evidence for deviations from Gaussianity on this template-cleaned cut sky. While the sky cut greatly reduces foreground emission, it has the unfortunate effect of coupling multipole modes on the sky so that the power spectrum covariance matrix is no longer diagonal. The goal of this section is to include this covariance in the likelihood function.

     The likelihood function for the temperature fluctuations observed by a noiseless experiment with full-sky coverage has the form



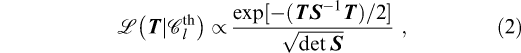
where denotes our temperature map and S_ij = (2 + 1)CP(_ij)/(4), where the P are the Legendre polynomials and _i is the pixel position on the map. If we expand the temperature map in spherical harmonics, T() = a_mY_m, then the likelihood function for each a_m has a simple form:



Since we assume that the universe is isotropic, the likelihood function is independent of m. Thus, we can sum over m and rewrite the likelihood function as



up to an irrelevant additive constant. Here, for a full-sky, noiseless experiment, we have identified 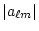² /(2 + 1) with . Note that the likelihood function depends only on the angular power spectrum. In this limit, the angular power spectrum encodes all of the cosmological information in the CMB.

     Characteristics of the instrument are also included in the likelihood analysis. Jarosik et al. (2003a) show that the detector noise is Gaussian (see their Fig. 6 and § 3.4); consequently, the pixel noise in the sky map is also Gaussian (Hinshaw et al. 2003b). The resolution of WMAP is quantified with a window function, w (Page et al. 2003a). Thus, the likelihood function for our CMB map has the same form as equation (2), but with replaced by = +, where is the nearly diagonal noise correlation matrix¹² and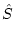 _ij = (2 + 1)CwP(_{i j})/(4).

     If foreground removal did not require a sky cut and if the noise were uniform and purely diagonal, then the likelihood function for the WMAP experiment would have the form (Bond, Jaffe, & Knox 2000)



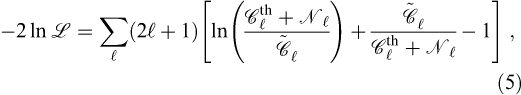
where the effective bias is related to the noise bias N as



Note that and appear together in equation (5) because the noise and cosmological fluctuations have the same statistical properties: they both are Gaussian random fields.

     Because of the foreground sky cut, different multipoles are correlated and only a fraction of the sky, f_sky, is used in the analysis. In this case, it becomes computationally prohibitive to compute the exact form of the likelihood function. There are several different approximations used in the CMB literature for the likelihood function. At large , equation (5) is often approximated as Gaussian:



where Q, the curvature matrix, is the inverse of the power spectrum covariance matrix.

     The power spectrum covariance encodes the uncertainties in the power spectrum due to cosmic variance, detector noise, point sources, the sky cut, and systematic errors. Hinshaw et al. (2003a) and § 2.2 describe the various terms that enter into the power spectrum covariance matrix.

     Since the likelihood function for the power spectrum is slightly non-Gaussian, equation (6) is a systematically biased estimator. Bond et al. (2000) suggest using a lognormal distribution, _LN (Bond et al. 2000; Sievers et al. 2002):



where z = ln( + ), = ln( + ), and is the local transformation of the curvature matrix Q to the lognormal variables z,



We find that, for the WMAP data, both equations (6) and (7) are biased estimators. We use an alternative approximation of the likelihood function for the values (eq. [11]) motivated by the following argument.

     We can expand the exact expression for the likelihood (eq. [4]) around its maximum by writing = (1 + ). Then, for a single multipole ,



We note that the Gaussian likelihood approximation is equivalent to the above expression truncated at ²:

     The Bond, Jaffe, & Knox (1998) expression for the lognormal likelihood for the equal variance approximation is



Thus, our approximation of the likelihood function is given by the form



where has the form of equation (7) apart from that is not given by equation (8) but by



We tested this form of the likelihood by making 100,000 full-sky realizations of the TT angular power spectrum . For each realization, the maximum likelihood amplitude of fluctuations in the underlying model was found and the mean value was computed. Since we kept all other model parameters fixed, this one-dimensional maximization was computationally trivial. The Gaussian approximation (eq. [6]) was found to systematically overestimate the amplitude of the fluctuations by 0.8%, while the lognormal approximation underestimates it by 0.2%. Equation (11) was found to be accurate to better than 0.1%.

     ¹² 1/f noise makes a nonrandom-phase contribution to the detector noise and leads to off-diagonal terms in the noise matrix. By making the noise N₀ a function of (denoted by N) we include this effect to leading order (Hinshaw et al. 2003b).

2.2. Curvature Matrix

     We obtain the curvature matrix in a form that can be used in the likelihood analysis from the power spectrum covariance matrix for computed in Hinshaw et al. (2003a). The matrix is composed of several terms of the following form:



where is the coupling introduced by the beam uncertainties and point-source subtraction ( = 0 if = ), ^K denotes the Kronecker delta function, and D denotes the diagonal terms,



The quantity r encodes the mode coupling due to the sky cut and is the dominant off-diagonal term (it is set to be 0 if = ). The mode-coupling coefficient, r, is most easily defined in terms of the curvature matrix, Q = D + r/ (see Hinshaw et al. 2003b).¹³

     The sky cut has two significant effects on the power spectrum covariance matrix. Because less data are used, the covariance matrix is increased by a factor of f_sky. An additional factor of f_sky arises from the coupling to nearby -modes. The additional term does not lead to a loss of information as nearby -modes are slightly anticorrelated.

     Hinshaw et al. (2003b) describe the beam uncertainty and point-source terms included in and . The beam and calibration uncertainties depend on the realization of the angular power spectrum on the sky , not on the theoretical angular power spectrum ; thus, they should not change as, in exploring the likelihood surface, we change in the expression for D. This differs from other approaches (e.g., Bridle et al. 2002). Rescaling all the contributions to the off-diagonal terms in the covariance matrix with is not correct and leads to a 2% bias in our estimator of , which propagates, for example, into a 2% error on the matter density parameter _m or 2% error on the spectral slope n_s.

     We find the curvature matrix by inverting equation (13):



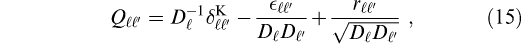
where we have assumed that the off-diagonal terms are small. For cosmological models that have very different from the best-fit , equation (15) does not yield the inverse of equation (13): in these cases the inversion of needs to be computed explicitly.

     We do not propagate the WMAP 0.5% calibration uncertainty in the covariance matrix as this uncertainty does not affect cosmological parameter determinations. This systematic only affects the power spectrum amplitude constraint at the 0.5% level, while the statistical error on this quantity is 10%.

2.2.1. Calibration with Monte Carlo Simulations

     The angular power spectrum is computed using three different weightings: uniform weighting in the signal-dominated regime ( < 200), an intermediate weighting scheme for 200 < < 450, and N_obs weighting (for the noise-dominated regime 450 < 900; Hinshaw et al. 2003b). Uniform weighting is a minimum variance weighting in the signal-dominated regime, and N_obs weighting is a minimum variance in the noise-dominated regime. However, in the intermediate regime the weighting schemes are not necessarily optimal and the analytic expression for the covariance matrix might thus underestimate the errors. To ensure that we have the appropriate errors, we calibrate the covariance matrix from 100,000 Monte Carlo realizations of the sky with the WMAP noise level, symmetrized beams, and the Kp2 sky cut. A good approximation of the curvature matrix can be obtained by using equations (13)(15), but substituting and f_sky with and f calibrated from the Monte Carlo simulations, as shown in Figures 1 and 2.

Fig. 1.   Ratio of the effective sky coverage to the actual sky coverage. This correction factor calibrates the expression for the Fisher matrix to the value obtained from the Monte Carlo approach. Here we show the ratio obtained from 100,000 simulations (jagged line); the smooth curve shows the fit we use, eq. (16). Note that, since we are switching between weighting schemes, the correction factors are not expected to smoothly interpolate between regimes.

Fig. 2.   Correction factor for the noise. The lines are as in Fig. 1. Note that, since we are switching between weighting schemes, the correction factors are not expected to smoothly interpolate between regimes.

     We find that for < 200 the weighting scheme is nearly optimal. The power spectrum covariance matrix (eq. [13]) gives a correct estimate of the error bars; thus, we do not need to calibrate or f_sky. We have computed an effective reduced ²,¹⁴ / -2 ln /, where is the number of degrees of freedom. The effective reduced ² from the Monte Carlo simulations in this range is consistent with unity.

     In the intermediate regime our Ansatz power spectrum covariance matrix (eq. [13]) slightly underestimates the errors. This can be corrected by computing the covariance matrix for an effective fraction of the sky f as shown in Figure 1. The jagged line is the ratio obtained from the Monte Carlo simulations, while the smooth curve shows the fit to f we adopt,



for 200 < < 450.

     For > 450, in the noise-dominated regime, the weighting is asymptotically optimal for . However, since we are using a smaller fraction of the sky, we need again to correct the f_sky factor. This numerical factor describes the reduction in effective sky coverage due to weighting the well-observed ecliptic poles more heavily than the ecliptic plane (see Fig. 3 of Bennett et al. 2003a). We fit this factor to the numerical simulations of the TT spectrum covariance matrix. Kogut et al. (2003) note that this same factor is also a good fit to the Monte Carlo simulations of the TE spectrum covariance matrix. For the noise-dominated regime, we define an effective sky fraction f = f_sky/1.14 and an effective noise given by



which can be obtained from the noise bias of the maps by a noise correction factor /. This is shown in Figure 2, where the smooth curve is the fit we adopt to this correction factor,



for > 450.

     This calibration of the covariance matrix from the Monte Carlo simulations allows us to use the effective reduced ² as a tool to assess goodness of fit. It can also be used to determine the relative likelihood of different models (e.g., Peiris et al. 2003).

     ¹⁴ This is not exactly the reduced ² because the likelihood is non-Gaussian especially at low .

2.3. Likelihood for the TE Angular Power Spectrum

     Since the TE signal is noise dominated, we adopt a Gaussian likelihood, where the curvature matrix is given by



The expression for D is given by equation (10) of Kogut et al. (2003), and the coupling coefficient due to the sky cut, r, is obtained from 100,000 Monte Carlo realizations of the sky with WMAP mask and noise level. The TE spectrum is computed with noise inverse weighting; in this regime r depends only on the difference = - and is set to be 0 at separations > 15. We use all multipoles 2 450, as comparison with the Monte Carlo realizations shows that in this regime equation (18) correctly estimates the TE uncertainties. We have also verified on the simulations that the Gaussian likelihood is an unbiased estimator and that the effective reduced ² is centered around 1.

     The amplitude of the covariance between TT and TE power spectra is 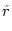/(1 + C/n), where 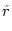is the correlation term (C)²(CC)^-1 0.2. Since C/n 0.25 for 1 yr data, we neglect this term, but we will include it in the 2+ yr analysis as it becomes increasingly important.

     We provide a subroutine¹⁵ that reads in a set of (TT, or TE, or both) and returns the likelihood for the WMAP data set, including all the effects described in this section.

3. MARKOV CHAIN MONTE CARLO LIKELIHOOD ANALYSIS

     The analysis described in Spergel et al. (2003) and Peiris et al. (2003) is numerically demanding. At each point in the six-dimensional (or more) parameter space a new model from CMBFAST¹⁶ (Seljak & Zaldarriaga 1996) is computed. Our version of the code incorporates a number of corrections and uses the RECFAST (Seager, Sasselov, & Scott 1999) recombination routine. Most of the likelihood calculations were done with four shared memory 32 CPU SGI Origin 300 with 600 MHz processors. With eight processors per calculation, each evaluation of CMBFAST for < 1500 for a flat reionized -dominated universe requires 3.6 s. (The scaling is not linear; with 32 processors each evaluation requires 1.62 s.)

     A grid-based likelihood analysis would have required prohibitive amounts of CPU time. For example, a coarse grid (20 grid points per dimension) with six parameters requires 6.4 × 10⁷ evaluations of the power spectra. At 1.6 s per evaluation, the calculation would take 1200 days. Christensen & Meyer (2000) proposed using MCMC to investigate the likelihood space. This approach has become the standard tool for CMB analyses (e.g., Christensen et al. 2001; Knox, Christensen, & Skordis 2001; Lewis & Bridle 2002; Kosowsky, Milosavljevic, & Jimenez 2002) and is the backbone of our analysis effort. For a flat reionized -dominated universe, we can evaluate the likelihood 120,000 times in less than 2 days using four sets of eight processors. As we explain below, this is adequate for finding the best-fit model and for reconstructing the 1 and 2 confidence levels for the cosmological parameters.

     We refer the reader to Gilks, Richardson, & Spiegelhalter (1996) for more information about MCMC. Here we only provide a brief introduction to the subject and concentrate on the issue of convergence.

3.1. Markov Chain Monte Carlo

     MCMC is a method to simulate posterior distributions. In particular, we simulate observations from the posterior distribution (|x), of a set of parameters given event x, obtained via Bayes's theorem,



where (x|) is the likelihood of event x given the model parameters and () is the prior probability density. For our application the WMAP denotes a set of cosmological parameters (e.g., for the standard, flat CDM model these could be the cold dark matter density parameter _c, the baryon density parameter _b, the spectral slope n_s, the Hubble constant [in units of 100 km s^-1 Mpc^-1] h, the optical depth , and the power spectrum amplitude A), and event x will be the set of observed .

     The MCMC generates random draws (i.e., simulations) from the posterior distribution that are a "fair" sample of the likelihood surface. From this sample, we can estimate all of the quantities of interest about the posterior distribution (mean, variance, confidence levels). The MCMC method scales approximately linearly with the number of parameters, thus allowing us to perform likelihood analysis in a reasonable amount of time.

     A properly derived and implemented MCMC draws from the joint posterior density (|x) once it has converged to the stationary distribution. The primary consideration in implementing MCMC is determining when the chain has converged. After an initial "burn-in"period, all further samples can be thought of as coming from the stationary distribution. In other words, the chain has no dependence on the starting location.

     Another fundamental problem of inference from Markov chains is that there are always areas of the target distribution that have not been covered by a finite chain. If the MCMC is run for a very long time, the ergodicity of the Markov chain guarantees that eventually the chain will cover all the target distribution, but in the short term the simulations cannot tell us about areas where they have not been. It is thus crucial that the chain achieves good "mixing." If the Markov chain does not move rapidly throughout the support of the target distribution because of poor mixing, it might take a prohibitive amount of time for the chain to fully explore the likelihood surface. Thus, it is important to have a convergence criterion and a mixing diagnostic. Plots of the sampled MCMC parameters or likelihood values versus iteration number are commonly used to provide such criteria (Fig. 3, left-hand panel). However, samples from a chain are typically serially correlated; very high autocorrelation leads to little movement of the chain and thus makes the chain "appear" to have converged. For a more detailed discussion see Gilks et al. (1996). Using an MCMC that has not fully explored the likelihood surface for determining cosmological parameters will yield wrong results. We describe below the method we use to ensure convergence and good mixing.

Fig. 3.   Unconverged Markov chains. The left-hand panel shows a trace plot of the likelihood values vs. iteration number for one MCMC (these are the first 3000 steps from one of our CDM model runs). Note the burn-in for the first 100 steps. In the right-hand panel, red dots are points of the chain in the (n, A)-plane after discarding the burn-in. Green dots are from another MCMC for the same data set and the same model. It is clear that, although the trace plot may appear to indicate that the chain has converged, it has not fully explored the likelihood surface. Using either of these two chains at this stage will give incorrect results for the best-fit cosmological parameters and their errors.

3.2. Convergence and Mixing

     We use the method proposed by Gelman & Rubin (1992) to test for convergence and mixing. They advocate comparing several sequences drawn from different starting points and checking to see that they are indistinguishable. This method not only tests convergence but can also diagnose poor mixing. For any analysis of the WMAP data, we strongly encourage the use of a convergence criterion.

     Let us consider M chains (the analyses in Spergel et al. 2003 and Peiris et al. 2003 use four chains unless otherwise stated) starting at well-separated points in parameter space; each has 2N elements, of which we consider only the last N: {y}, where i = 1, ,N and j = 1, ,M; i.e., y denotes a chain element (a point in parameter space), the index i runs over the elements in a chain, and the index j runs over the different chains. We define the mean of the chain



and the mean of the distribution



We then define the variance between chains as



and the variance within a chain as



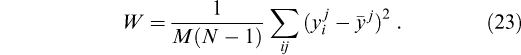
The quantity



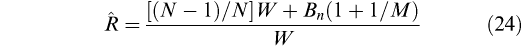
is the ratio of two estimates of the variance in the target distribution: the numerator is an estimate of the variance that is unbiased if the distribution is stationary, but it is otherwise an overestimate. The denominator is an underestimate of the variance of the target distribution if the individual sequences did not have time to converge.

     The convergence of the Markov chain is then monitored by recording the quantity for all the parameters and running the simulations until the values for are always less than 1.1. A. Gelman (Kaas et al. 1997) suggests to use values for < 1.2. Here we conservatively adopt the criterion < 1.1 as our definition of convergence. We have found that the four chains will sometimes go in and out of convergence as they explore the likelihood surface, especially if the number of points already in the chain is small. To avoid this, one could run many chains simultaneously or run one chain for a very long time (e.g., Panter, Heavens, & Jimenez 2002). Because of CPU-time constraints, we run four chains until they fulfill both of the following criteria: (1) they have reached convergence and (2) each chain contains at least 30,000 points. In addition to minimizing chance deviations from convergence, we find that this many points are needed to be able to robustly reconstruct the 1 and 2 levels of the marginalized likelihood for all the parameters. For most chains, the burn-in time is relatively rapid, so that we only discard the first 200 points in each chain; however, the results are not sensitive to this procedure.

3.3. Markov Chains in Practice

     In this section we explain the necessary steps to run an MCMC for the CMB temperature power spectrum. It is straightforward to generalize these instructions to include the temperature-polarization power spectrum and other data sets. The MCMC is essentially a random walk in parameter space, where the probability of being at any position in the space is proportional to the posterior probability.

     Here is our basic approach:

1. Start with a set of cosmological parameters {₁} and compute the and the likelihood ₁ = (|).

2. Take a random step in parameter space to obtain a new set of cosmological parameters {₂}. The probability distribution of the step is taken to be Gaussian in each direction i with rms given by _i. We will refer below to _i as the "step size." The choice of the step size is important to optimize the chain efficiency (see § 3.4.2).

3. Compute the for the new set of cosmological parameters and their likelihood ₂.

4. 4a. If ₂/₁ 1, "take the step," i.e., save the new set of cosmological parameters {₂} as part of the chain, then go to step 2 after the substitution {₁} {₂}.

5. 4b. If ₂/₁ < 1, draw a random number x from a uniform distribution from 0 to 1. If x ₂/₁, "do not take the step," i.e., save the parameter set {₁} as part of the chain and return to step 2. If x < ₂/₁, " take the step," i.e., do as in step 4a.

6. For each cosmological model run four chains starting at randomly chosen, well-separated points in parameter space. When the convergence criterion is satisfied and the chains have enough points to provide reasonable samples from the a posteriori distributions (i.e., enough points to be able to reconstruct the 1 and 2 levels of the marginalized likelihood for all the parameters), stop the chains.

3.4. Improving MCMC Efficiency

     The Markov chain efficiency can be improved in different ways. We have tuned our algorithm by reparameterization and optimization of the step size.

3.4.1. Reparameterization

     Degeneracies and poor parameter choices slow the rate of convergence and mixing of the Markov chain. There is one near-exact degeneracy (the geometric degeneracy) and several approximate degeneracies in the parameters describing the CMB power spectrum (Bond et al. 1994; Efstathiou & Bond 1999). The numerical effects of these degeneracies are reduced by finding a combination of cosmological parameters (e.g., _c, _b, h) that have essentially orthogonal effects on the angular power spectrum. The use of such parameter combinations removes or reduces degeneracies in the MCMC and hence speeds up convergence and improves mixing because the chain does not have to spend time exploring degeneracy directions. Kosowsky et al. (2002) introduced a set of reparameterizations to do just this. In addition, these new parameters reflect the underlying physical effects determining the form of the CMB power spectrum (we refer to these as physical parameters). This leads to particularly intuitive and transparent parameter dependencies of the CMB power spectrum.

     Following Kosowsky et al. (2002), we use a core set of six physical parameters. There are two parameters for the physical energy densities of cold dark matter, _{c c}h², and baryons, _{b b}h². There is a parameter for the characteristic angular scale of the acoustic peaks,



where a_dec is the scale factor at decoupling,



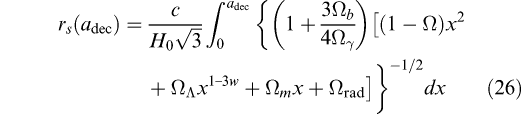
is the sound horizon at decoupling, and



is the angular diameter distance at decoupling, where H₀ denotes the Hubble constant and c is the speed of light. Here _m = _c + _b, denotes the dark energy density parameter, w is the equation of state of the dark energy component, = _m + , and the radiation density parameter _rad = + , where and are the photon and neutrino density parameters, respectively. For reionization we use the physical parameter exp(-2), where denotes the optical depth to the last scattering surface (not the decoupling surface). The remaining two core parameters are the spectral slope of the scalar primordial density perturbation power spectrum, n_s, and the overall amplitude of the primordial power spectrum, A. Both are normalized at k = 0.05 Mpc^-1 ( 700).

     For more complex models we add other parameters as described in Spergel et al. (2003) and Peiris et al. (2003) and in § 5. To investigate nonflat models, we use the vacuum energy, h². Other examples include the tensor index, n_t, the tensor-to-scalar ratio, r, and the running of the scalar spectral index, dn_s/d ln k.

     Here we relate the input parameter for the overall normalization, A, as in the CMBFAST code (ver. 4.1 with UNNORM option), to the amplitude of primordial comoving curvature perturbations , (k₀) (k³/2²)². We also relate our convention for the tensor perturbations to the one in the code. CMBFAST calculates



where is the Newtonian potential, g_T(k) is the radiation transfer function, and T₀ = 2.725 × 10⁶ is the CMB temperature in units of K. The tilde denotes that (k) is used in CMBFAST but differs from our convention, (k), where = /16. The comoving curvature perturbation, , is related to by = - ; thus, (k) = (25/9)(k). Note that this relation holds from radiation domination to matter domination with accuracy better than 0.5%.

     CMBFAST uses A to parameterize (k₀). The tensor perturbations are calculated accordingly. The relations are



Therefore, one obtains

     The amplitude A is normalized at k₁ = 0.05 Mpc^-1 and the tensor-to-scalar ratio r is evaluated at k₀ = 0.002 Mpc^-1, unless otherwise specified. To convert A(k₀) to A(k₁), we use

3.4.2. Step Size Optimization

     The choice of the step size in the Markov chain is crucial to improve the chain efficiency and speed up convergence. If the step size is too big, the acceptance rate will be very small; if the step size is too small, the acceptance rate will be high, but the chain will exhibit poor mixing. Both situations will lead to slow convergence. For our initial step sizes for each parameter we use the standard deviation for each parameter when all the other parameters are held fixed at the maximum likelihood value. These are easy to find once a preliminary chain has been run and the likelihood surface has been fitted, as explained in § 3.4.3. If a given parameter is roughly orthogonal to all the other parameters, it is not necessary to adjust the step size further; in the presence of severe degeneracies the step size estimate needs to be increased by a "banana correction" factor, which is approximately the ratio of the projection of the 1 error along the degeneracy to the projection perpendicular to the degeneracy.

     With these optimizations the convergence criterion is satisfied for the four chains after roughly 30,000 steps each (2N = 30,000) for a model with six parameters. On an Origin 300 machine this takes roughly 32 hr running each chain on eight processors. These numbers serve only as a rough indication: convergence speed depends on the model and on the data set. For a fixed number of parameters, convergence can be significantly slower if there are severe degeneracies among the parameters. Adding more data sets might slow down the evaluation of a single step in the chain but can also speed up convergence by breaking degeneracies.

3.4.3. Likelihood Surface Fitting

     The likelihood surface explored by the MCMC was found to be functionally well approximated by a quartic expansion of the cosmological parameters (for example, {_i} = {_b,_c,n,_A,,A}):



Here q are fit coefficients and _i are related to the cosmological parameters via _i = (_i - )/_i, where is the maximum likelihood value of the parameter. Lower order expansions were unable to reproduce the likelihood surface. With six parameters there are M_f = 210 fit coefficients. Writing equation (34) as y = , the minimum least-squares estimator for 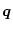is



where is the N × M_f matrix X_ij = x and N is the number of unique points in the chain.

     We run preliminary MCMC chains with "guesstimated" step sizes until there are 1000 unique points in total. Then we use equation (34) to cut through the likelihood surface at the maximum likelihood value to find the 1 level in each parameter direction (see § 3.4.2). This defines our "step size" for subsequent chains.

3.5. The Choice of Priors

     From Bayes's theorem (eq. [19]) we can infer (_i|x), the probability of the model parameters _i given the event x (i.e., our observation of the power spectra), from the likelihood function once the prior is specified. It is reasonable to take prior probabilities to be equal when nothing is known to the contrary (Bayes's postulate). Unless otherwise stated, we assume uniform priors on the parameters given in the following list:

1. 0 _c 1.

2. 0 _b 1.

3. 0.005 _A 0.1.

4. 0 0.3.

5. 0.5 A 2.5.

6. 0 n_s| 2.

7. 0 n_iso 2.

8. 0 f_iso 5000.

9. -0.5 dn/d ln k 0.5.

10. 0 r 2.5.

11. 0 1.

12. -3.2 (-1.2) w 0 (we will present two sets of results, one with the prior w -1.2 and the other with w -3.2).

13. 0 1.

     Except for the priors on and w (the equation of state of the dark energy component), the MCMCs never hit the imposed boundaries; thus, most of our choices for priors have no effect on the outcome. A detailed discussion about the prior on is presented in Spergel et al. (2003).

     We set a lower bound on w at -3.2 (-1.2), but we discard the region of parameter space where w < -3 (w < -1). This is necessary because our best-fit value for this parameter is close to the boundary. If we had instead set the prior to be w -3 (w -1), then the chains would fail to be a fair representation of the posterior distribution in the region of parameter space where the distance from the boundary is comparable to the step size.

3.6. MCMC Output Analysis

     We merge the four converged MCMCs (120,000 points) into one. From this we give the cosmological parameters that yield our best estimate of and the marginalized distribution of the parameters. We compute the marginalized distribution for one parameter and the joint distribution for two parameters, obtained marginalizing over all the other parameters. Since the MCMC passes objective tests for convergence and mixing, the density of points in parameter space is proportional to the posterior probability of the parameters.

     The marginalized distribution is obtained by projecting the MCMC points. For the marginalized parameter values , Spergel et al. (2003) quote the expectation value of the marginalized likelihood, _i d_i = 1/N _t,i. Here N is the number of points in the merged chain and _t,i denotes the value of parameter _i at the tth step of the chain. The last equality becomes clear if we consider that the MCMC gives to each point in parameter space a "weight" proportional to the number of steps the chain has spent at that particular location. The 100(1 - 2p)% confidence interval [c_p,c_1-p] for a parameter is estimated by setting c_p to the pth quantile of _t,i,t = 1, ,N and c_p-1 to the (1 - p)th quantile. The procedure is similar for multidimensional constraints: the density of points in the n-dimensional space is proportional to the likelihood, and multidimensional confidence levels can be found as illustrated in § 15.6 of Press et al. (1992).

     We note that the global maximum likelihood value for the parameters does not necessarily coincide with the expectation value of their marginalized distribution if the likelihood surface is not a multivariate Gaussian. We find that, for most of the parameters, the maximum likelihood values of the global joint fit are consistent with the expectation values of the marginalized distribution.

     A virtue of the MCMC method is that the addition of extra data sets in the joint analysis can efficiently be done with minimal computational effort from the MCMC output if the inclusion of extra data sets does not require the introduction of extra parameters or does not drive the param eters significantly away from the current best fit. For example, we add Ly power spectrum constraints to MCMC's outputs, but we cannot do this for the 2dFGRS, since this requires the introduction of two extra parameters ( and _p; see § 5.1 for more details).

     If the likelihood surface for a subset of parameters from an external (independent) data set is known, or if a prior needs to be added a posteriori, the joint likelihood surface can be obtained by multiplying the likelihood with the posterior distribution of the MCMC output. In Spergel et al. (2003) we follow this method to obtain the joint constraint of CMB with Type Ia supernova (Riess et al. 1998, 2001) data and CMB with Hubble Key Project Hubble constant (Freedman et al. 2001) determination.

     There is yet another advantage of the MCMC technique. The current version of CMBFAST with the nominal interpolation settings is accurate to 1%, but random numerical errors can sometimes exceed this. As the precision of the CMB measurements improves, these effects can become problematic for any approach that calculates derivatives as a function of parameters. Because MCMC calculations average over 100,000 CMB calculations, the MCMC technique is much less sensitive than either grid-based likelihood calculations or methods that numerically calculate the Fisher matrix.

4. EXTERNAL CMB DATA SETS

     The Cosmic Background Imager (CBI; Mason et al. 2002; Sievers et al. 2002; Pearson et al. 2002) and the Arcminute Cosmology Bolometer Array Receiver (ACBAR; Kuo et al. 2002) experiments complement WMAP by probing the amplitude of CMB temperature power spectrum at > 900. These observations probe the Silk damping tail and improve our analysis in two ways: (1) they improve our ability to constrain the baryon density, the amplitude of fluctuations, and the slope of the matter power spectrum, and (2) they improve convergence by preventing the chains from spending long periods of time in large, moderately low likelihood regions of parameter space.

     The CBI data set is described in Mason et al. (2002), in Pearson et al. (2002), and on their Web site.¹⁷ We use data from the CBI mosaic data set (Pearson et al. 2002) and do not include the deep data set as the two data sets are not independent. We use the three band powers from the even binning at central -values of 876, 1126, and 1301, thus ensuring that the chosen band power can be considered independent from the WMAP data. At 1500, the CBI experiment detected excess power. If the rms amplitude of mass fluctuations on scales of 8 h^-1 Mpc is ₈ 1, then this excess power can be interpreted as due to Sunayev-Zeldovich distortion from undetected galaxy clusters (Mason et al. 2002; Bond et al. 2002; Komatsu & Seljak 2002). We simplify our analyses by not using the CBI data on scales where this effect can be important. The correlations between different band powers are taken into account with the full covariance matrix; we use the lognormal form of the likelihood (as in Pearson et al 2002). In addition, we marginalize over a 10% calibration uncertainty (CBI beam uncertainties are negligible).

     The ACBAR data set is described in Kuo et al. (2002). We use the seven band powers at multipoles 842, 986, 1128, 1279, 1426, 1580, and 1716. As shown in Figure 4, these points do not overlap with the WMAP power spectrum except at 800, where WMAP is noise dominated. As shown in Figure 4, the ACBAR experiment is less sensitive to Sunyaev-Zeldovich contamination than CBI. We compute the likelihood analysis for cosmological parameters for the ACBAR data set following Goldstein et al. (2002) and using the error bars given on the ACBAR Web site.¹⁸ In addition, we marginalize over conservative beam and calibration uncertainties (B. Holzapfel 2002, private communication). In particular, we assume a calibration uncertainty of 20% (the double of the nominal value) and 5% beam uncertainty (60% larger than the nominal value).

Fig. 4.   CMB angular power spectrum (in K2) for our best-fit CDM model for > 800 and the Sunayev-Zeldovich contribution for 8 = 0.98 for CBI wavelengths (dotted line) and for ACBAR (dashed line). The vertical line shows the adopted cutoff for CBI and ACBAR.

     The ACBAR and CBI data are completely independent from each other (they map different regions of the sky) and from the WMAP data (the band powers we consider span different ranges). To perform the joint likelihood analysis, we simply multiply the individual likelihoods.

5. ANALYSIS OF LARGE-SCALE STRUCTURE DATA

     We can enhance the scientific value of the CMB data from z 1089 by combining it with measurements of the low-redshift universe. Galaxy redshift surveys allow us to measure the galaxy power spectrum at z 0, and observations of Ly absorption of about 50 quasar spectra (Ly forest) allow us to probe the dark matter power spectrum at redshift z 3.

     We use the Anglo-Australian Telescope Two-Degree Field Galaxy Redshift Survey (2dFGRS; Colless et al. 2001) as compiled in 2001 February. This survey probes the universe at redshift z_eff 0.1 and probes the power spectrum on scales corresponding to 0.022 < k < 0.2 (where k is in units of h Mpc^-1). The anticipated Sloan Digital Sky Survey (Gunn & Knapp 1993) power spectrum will be an important complement to 2dFGRS. We also use the linear matter power spectrum as recovered by Croft et al. (2002) from Ly forest observations. This power spectrum is reconstructed at an effective redshift z 2.72 and probes scales k > 0.2 h Mpc^-1. Together these data sets allow us to probe not only a wide range of physical scalesfrom k 1 × 10^-4 (30,000 Mpc h^-1) to k 1 (3 Mpc h^-1) (see Fig. 5)but also the evolution of a given scale with redshift.

Fig. 5.   Combined CMB and LSS data set. Top: CMB angular power spectrum in K2 as a function of k, where k is related to by = 0k (where 0 14,400 Mpc is the distance to the last scattering surface). Black points are the WMAP data, red points CBI, blue points ACBAR. Bottom: LSS data. Black points are the 2dFGRS measurements, and green points are the Ly measurements. Both LSS power spectra are in units of (Mpc h-1)3 and have been rescaled to z = 0. This plot only illustrates the scale coverage of all the data sets we consider. The various LSS power spectra as plotted here cannot be directly compared with the theory because of the effects outlined in § 5 (e.g., redshift-space distortions, nonlinearities, bias and window function effect).

     When including LSS data sets, one should keep in mind that the underlying physics for these data sets is much more complicated and less well understood than for WMAP data, and systematic and instrumental effects are much more important. We attempt here to include all the known (up-to-date) uncertainties and systematics in our analysis. In what follows, we illustrate our modeling of the "real-world" effects of LSS surveys and how we propagate systematic and statistical uncertainties into the parameter estimation. The goal of our modeling is to relate not just the shape but also the amplitude of the observed power spectrum to that of the linear matter power spectrum as constrained by CMB data. The reason for this will be clear in § 5.1.3; by using the information in the power spectrum amplitude, we can break some of the degeneracies among cosmological parameters.

5.1. The 2dFGRS Power Spectrum

     The 2dFGRS power spectrum, as released in 2002 June, has been calculated from the 2001 February catalog that includes 140,000 galaxies (Percival et al. 2001). The full survey is composed of 220,000 galaxies but is not yet available. The sample is magnitude limited at b_J = 19.45 and thus probes the universe at z_eff 0.1 and the power spectrum on scales corresponding to k > 0.015 h Mpc^-1. The input catalog is an extended version of the Automatic Plate Machine (APM) galaxy catalog (Maddox et al. 1990b; Maddox, Efstathiou, & Sutherland 1990a, 1996), which includes about 5 million galaxies to b_J = 20.5. The APM catalog was used previously to recover the three-dimensional power spectrum of galaxies by inverting the clustering properties of the two-dimensional galaxy distribution (Baugh & Efstathiou 1993; Efstathiou & Moody 2001). These techniques, however, are affected by sample variance and uncertainties in the photometry; a full three-dimensional analysis is thus more reliable.

     The power spectrum of the galaxy distribution as measured by LSS surveys, such as the 2dFGRS, cannot be directly compared to that of the initial density fluctuations, as predicted by theory, or recovered from WMAP or the combination of WMAP+CBI+ACBAR data sets. This is due to a number of intervening effects that can be broadly divided into two classes: effects due to the survey geometry (i.e., window function, selection function effects) and effects intrinsic to the galaxy distribution (e.g., redshift-space distortions, bias, nonlinearities).

5.1.1. Survey Geometry

     Galaxy surveys such as the 2dFGRS are magnitude limited rather than volume limited; thus, most nearby galaxies are included in the catalog while only the brighter of the more distant galaxies are selected. The selection function accounts for the fact that fewer galaxies are included in the survey as the distance (or the redshift) increases. An additional effect arises from the fact that the clustering properties of bright galaxies might be different from the average clustering properties of the galaxy population as a whole. The selection function does not take this into account (we return to this point in § 5.1.2).

     Moreover, the completeness across the sky is not constant, and the survey can only cover a fraction of the whole sky, sometimes with a very complicated geometry described by the window function. In particular, for the data we use, unobserved fields make the survey completeness a strongly varying function of position. The measured Fourier coefficients are therefore the true coefficients of the galaxy distribution convolved by the Fourier transform of the selection function (in the direction of the line of sight) and of the window function (on the plane of the sky). In this section we follow the standard notation used in LSS analyses and refer to all of these effects as window effects.

     The window not only modifies the measured power spectrum but also introduces spurious correlations between Fourier modes (see Percival et al. 2001 for more details). For the 2dFGRS these effects have been quantified by Monte Carlo simulations of mock catalogs of the survey.¹⁹ We include them in our analysis by convolving the theory power spectrum with the window "kernel" and by including off-diagonal terms in the covariance matrix.

     ¹⁹ For WMAP data, we deconvolve the raw measured by the effect of the window (the mask), thus leaving the effect of the window function and the mask only in the Fisher matrix. For LSS we will convolve the theory with the window, project the power spectrum into redshift space, and compare this to the observed power spectrum.

5.1.2. Effects Intrinsic to the Galaxy Distribution

     Linear gravitational evolution modifies the amplitude but not the shape of the underlying power spectrum. However, in the nonlinear regime (where the amplitude of fluctuations is / 1) this is no longer the case. Nonlinear gravitational evolution changes the shape of the power spectrum and introduces correlations between Fourier modes. This effect becomes important on scales k 0.1 h Mpc^-1, but the exact scale at which it appears and its detailed characteristic depend on cosmological parameters. Most of the clustering signal from galaxy surveys such as 2dFGRS comes from the regime where nonlinearities are nonnegligible because shot noise is the dominant source of error at k 0.5 h Mpc^-1 and the number density of modes scales as k³. These nonlinearities encode additional information about cosmology and motivate their inclusion in the present analysis. This approach is complicated by the fact that an accurate description of the fully nonlinear evolution of the galaxy power spectrum is complicated. In the literature, there are several different approaches to modeling the nonlinear evolution of the underlying dark matter power spectrum in real space: (1) linear (and extended) perturbation theory, (2) semianalytical modeling, and (3) numerical simulation. All of these approaches yield consistent results on the scales used in our analysis. We will use the semianalytical approach developed by Hamilton et al. (1991) and Peacock & Dodds (1996). In particular, we use the Ma et al. (1999) formulation of the nonlinear power spectrum. Figure 6 shows the effect of nonlinearities on the matter power spectrum on the scales of interest (compare solid and dashed lines).

Fig. 6.   Matter power spectrum in (Mpc h-1)3, linear in real space (solid line), nonlinear in real space (dashed line), and nonlinear in redshift space (dotted line). The error bars on the dotted line show the size of the statistical error bars per k bin of the 2dFGRS galaxy power spectrum. The power spectrum is in units of (Mpc h)3.

     Theory predicts the statistical properties of the continuous matter distribution, while observations are concerned with the galaxy distribution, which is discrete. Moreover, galaxies might not be faithful tracers of the mass distribution (i.e., the galaxy distribution might be biased). In the analysis of galaxy surveys it is assumed that galaxies form a Poisson sampling of an underlying continuous field that is related to the matter fluctuation field via the bias. It is possible to formally relate the discrete galaxy field and its continuous counterpart. For the power spectrum, this consists of the subtraction from the measured galaxy power spectrum of the shot-noise contribution. The published power spectra from galaxy surveys already have this contribution subtracted but are still biased with respect to the underlying mass power spectra.

     The idea that galaxies are biased tracers of the mass distribution even on large scales was introduced by Kaiser (1984) to explain the properties of Abell clusters. Nevertheless, the fact that galaxies of different morphologies have different clustering properties (hence different power spectra) was known much before (e.g., Hubble 1936; Dressler 1980; Postman & Geller 1984). Since the clustering properties of different types of galaxies are different, they cannot all be good tracers of the underlying mass distribution.²⁰

     In the simplest biasing model, the linear bias model, the mass and galaxy fractional overdensity fields and _g are related by _g() = b(). This implies that on all scales



This simple model (although justified by the Kaiser 1984 assumption that galaxies form on the highest peaks of the mass distribution) cannot be true in detail for two reasons. The first is that, on a fundamental level, the galaxy fluctuation field on small smoothing scales could become _g < -1, which corresponds to a negative galaxy density. The second is that, from an observational point of view, this scheme leaves the shape of the power spectrum unchanged while not all galaxy populations have the same observed power spectrum shape, although the differences are not large (e.g., Peacock & Dodds 1994; Norberg et al. 2001). Many different and more complicated biasing schemes have been introduced in the literature. For our purposes it is important to note that the bias of a sample of galaxies depends on the sample selection criteria and on the weighting scheme used in the analysis. Thus, different surveys will have different biases, and care must be taken when comparing the different galaxy power spectra.

     There are several indications that large-scale galaxy bias is scale independent on large scales (e.g., Hoekstra et al. 2002; Verde et al. 2002). This justifies adopting equation (36). For the 2dFGRS, the bias of galaxies has been measured by Verde et al. (2002), by using higher order correlations of the galaxy fluctuation field. They assume a generalization of the simple linear biasing scheme, _g = b₁ + b₂/2². They find no evidence for scale-dependent bias at least on linear and mildly nonlinear scales (i.e., k < 0.4 h Mpc^-1) and b₂ consistent with 0. This finding further supports the use of equation (36). In particular, they find b₁ = 1.06 ± 0.11. In our analysis we assume linear biasing.

     The Verde et al. (2002) bias measurement has to be interpreted with care. It applies to 2dFGRS galaxies weighted with a modification of the Feldman, Kaiser, & Peacock (1994) weighting scheme as described in Percival et al. (2001). It is important to note that, close to the observer, dim galaxies are included in the survey; the galaxy density is high, but a small volume of the sky is covered. On the other hand, far away from the observer, only very bright galaxies are included in the survey; a large volume is probed, but the galaxy density is low. As a consequence, clustering of dim galaxies in a small volume close to the observer contains most of the signal for the power spectrum at small scales. While rare, bright galaxies in a large volume enclose most of the information about the power spectrum on large scales. An "optimal" weighting scheme would thus weight dim galaxies on small scales and bright galaxies on large scales. This weighting scheme is, unfortunately, biased. Bright galaxies are more strongly clustered (i.e., more biased) than dim ones. This effect is known as "luminosity bias." The power spectrum recovered from such a weighting scheme will have optimal error bars but will exhibit scale-dependent bias. The weighting scheme used in Percival et al. (2001) is not optimal but is virtually unaffected by luminosity bias (Percival 2003). The power spectrum so obtained is that of two L_* galaxies on virtually all scales, and the effective redshift for the power spectrum is z_eff = 0.17, slightly larger than the effective redshift of the survey as defined by the selection function (Percival et al. 2001; Peacock et al. 2001).

     The final complication is that galaxy catalogs use the redshift as the third spatial coordinate. In a perfectly homogeneous Friedman universe, redshift would be an accurate distance indicator. Inhomogeneities, however, perturb the Hubble flow and introduce peculiar velocities. As Kaiser (1987) emphasized, the peculiar velocities distort the clustering pattern not only on small scales, where virialized objects produce "Fingers of God," but also on large scales, where coherent flows produce large-scale distortion components.

     On large (linear) scales the redshift-space effect on an individual Fourier component of the density fluctuation field can be modeled by



where the superscript s refers to the quantity in redshift space and is the cosine of the angle between the -vector and the line of sight. The Kaiser factor, , is the linear redshift-space distortion parameter. One defines = f/b, where f = d ln /d ln a, with = / and a = (1 + z)^-1; b is the linear bias parameter. The expression for f(z) is a known function of _m, , and z (Lahav et al. 1991),



where X = 1 + _mz + (a² - 1) and can be approximated by²¹ /b. The analysis of the 2dFGRS (Peacock et al. 2001; Percival et al. 2001) constrains f at the effective redshift of the survey. The effective redshift of the survey depends on the galaxy weighting scheme adopted to compute the power spectrum for the above work (z_eff 0.17). This peculiar velocity infall causes the overdensity to appear squashed along the line of sight. The net effect on the angle-averaged power spectrum in the small-angle approximation is



Thus, on large scales the redshift-space distortions boost the power spectrum if > 0.

     On smaller scales, virialized motions produce a radial smearing and the associated "Fingers of God" effect contaminates the wavelengths we are interested in. This is difficult to treat exactly, but as it is a smearing effect, it produces a mild damping of the power, acting in the opposite direction to the large-scale boosting by the Kaiser effect (see, e.g., Matsubara 1994). On these scales, the redshift-space correlation function is well modeled as a convolution of the real-space isotropic correlation function with some distribution function for the line-of-sight velocities (e.g., Davis & Peebles 1983; Cole, Fisher, & Weinberg 1994; Fisher 1995). Since the convolution in real space is equivalent to multiplication in Fourier space, the redshift-space power spectrum on small scales is multiplied by the square of the Fourier transform of the velocity distribution function (e.g., Peacock & Dodds 1994),



where _p denotes the line-of-sight pairwise velocity dispersion. If the pairwise velocity distribution is taken to be an exponential (e.g., Ballinger, Heavens, & Taylor 1995; Ballinger, Peacock, & Heavens 1996; Hatton & Cole 1998), which seems to be supported by simulations (e.g., Zurek et al. 1994) and observations (e.g., Marzke et al. 1995), then the damping factor is a Lorentzian (see also Kang et al. 2002),



We adopt this functional form as it is used by Peacock et al. (2001) in determining the redshift-space distortion parameters and _p from the 2dFGRS. The overall effect for the power spectrum in a thin shell in k-space is given by



obtained by averaging over in equation (40) with the damping factor given by equation (41). Figure 6 shows the effect of redshift-space distortions (eq. [42]) on the scales of interest.

     This model is simplistic for several reasons. The most important is that, because of the complicated geometry of the survey, the simple angle average operation performed to obtain equation (42) might not be strictly correct. In addition, equation (42) is obtained in the plane-parallel (also known as small-angle) approximation (i.e., as if the lines of sight to different galaxies on the sky were parallel).

     We have performed extensive testing of equation (42) using mock 2dFGRS catalogs obtained from the Hubble volume simulation. We find that the simulations' redshift-space power spectrum is consistent, given the errors, with equation (42), where P(k) is the simulations' real-space power spectrum up to k < 0.4 h Mpc^-1, even for the complicated geometry of the 2dFGRS. This means that up to k 0.4 the systematics introduced by equation (42) is smaller than the statistical errors; in the analysis we use only k 0.15. However, the value for in equation (42) needs to be calibrated on Monte Carlo realizations of the survey. We find that ^eff = 0.85. We have verified that our results for the cosmological parameters are insensitive to the exact choice of the correction factor. Peacock et al. (2001) measured the parameters and _p and their joint probability distribution from the survey, obtaining = 0.43 and _p = 385 km s^-1. This measurement has been obtained by using the full angular dependence of the power spectrum and therefore recovers directly and not ^eff. Hawkins et al. (2002) measured these parameters from a larger sample than the one from Peacock et al. (2001), obtaining a slightly different result. This is mostly due to a shift in the recovered value for _p. Since most of the galaxies in the Hawkins et al. (2002) sample are in the Peacock et al. (2001) sample, we conservatively extend our error bars on and by 10% and 30%, respectively, to include the new value within the 1 marginalized confidence contour and to include a possible error in the determination of ^eff. Figure 6 illustrates the importance of including all the above effects in our analysis.

     In our analysis we consider data in the k range 0.02 h Mpc^-1 < k < 0.2 h Mpc^-1. On large scales the limit is set by the accuracy of the window function model; on small scales the limit is set by where the covariance matrix has been extensively tested. In this regime we also have a weak dependence on the velocity dispersion parameter _p, the parameter with the largest systematic uncertainty.

     ²⁰ Galaxies are likely to be formed in the very high density regions of the matter fluctuation field; thus, they are formed very biased at z 0 (e.g., Lyman break galaxies), but then gravitational evolution should make the galaxy distribution less and less biased as time goes on (e.g., Fry 1996).

     ²¹ In our analysis we use the exact expression for as in eq. (38).

5.1.3. Motivation for this Modeling

     The motivation behind the complicated modeling of §§ 5.1.1 and 5.1.2 is to be able to infer the amplitude of the matter power spectrum from the observed galaxy clustering properties.

     Figures 7 and 8 illustrate how the modeling of §§ 5.1.1 and 5.1.2 helps in breaking degeneracies among cosmological parameters. For illustration, we consider two cases below: the degeneracy of the dark energy equation of state, w (Huey et al. 1999), with _b and n_s and the - h degeneracy, where = h².

Fig. 7.   Two cosmological models: b = 0.0235, m = 0.143, ns = 0.978, = 0.11, w = -0.426, h = 0.53 (solid line) and b = 0.0254, m = 0.137, ns = 1.024, = 0.08, w = -1, h = 0.77 (dotted line). The two models are indistinguishable within current error bars from the CMB angular power spectrum (left-hand panel; units for the power spectrum are K2). However, they can easily be distinguished if we can relate the observed power spectrum to the underlying matter power spectrum [right-hand panel; units for the power spectrum are (Mpc h-1)3]. The error bars on the solid line are examples of the size of the 2dFGRS and Ly power spectra statistical error bars for one data point at different scales. There are four error bars for 2dFGRS and four for Ly .

Fig. 8.   Two cosmological models: m = 0.26, b = 0.02319, = 0.12, ns = 0.953, = 0, h = 0.714 (solid line) and m = 0.26, b = 0.02319, = 0.12, ns = 0.953, = 0.02, h = 0.6 (dashed line). As before the two models are virtually indistinguishable from the CMB angular power spectrum (left-hand panel; units for the power spectrum are K2), but they can easily be distinguished if the matter power spectrum amplitude is known [right-hand panel; units for the power spectrum are (Mpc h-1)3]. The error bars on the solid line are examples of the size of the 2dFGRS and Ly power spectra statistical error bars for one data point. There are four error bars for 2dFGRS and four for Ly .

     Figure 7 shows two models that are virtually indistinguishable with CMB data, but which predict different amplitudes for the matter power spectra at z 0. This is because the linear growth factor and the shape parameter are different for the two cases. The two models differ in the values of _b, n_s, and w. The solid line is a model with w = -0.4, while the dotted line is a model with w = -1.

     In Figure 8 we show two sets of cosmological parameters that differ only in the values of the neutrino mass and the Hubble constant. These two models are virtually indistinguishable with CMB observations. However, the matter power spectrum in the two cases is different in shape and amplitude. Since redshift-space distortions and window function affect the power spectrum shape, extra information about cosmological parameters is encoded in its amplitude. By using this information, Spergel et al. (2003) obtain a cosmological upper bound on the neutrino mass that is 4 times better than current cosmological constraints (Elgarøy et al. 2002).

     For completeness, we have shown the power spectrum also for scales probed by the Ly forest (see § 6). The error bars in Figures 7 and 8 are examples of the size of the 2dFGRS and Ly power spectra statistical uncertainties in one data point, showing that the two models can be distinguished if the observed power spectrum can be related to the linear matter power spectrum without introducing large additional uncertainties.

5.1.4. Practical Approach

     The procedure we adopt in order to compare the observed galaxy power spectrum with the theory predictions is outlined below (the published 2dFGRS galaxy power spectrum has been already corrected for shot noise). For a given set of cosmological parameters and a pairwise velocity dispersion parameter we proceed as follows:

1. The MCMC selects a set of cosmological parameters and values for and _p. CMBFAST computes the theoretical linear matter power spectrum at z = 0.

2. We evolve the theoretical linear matter power spectrum to obtain the nonlinear matter power spectrum at the effective redshift of the survey, following the prescription of Ma et al. (1999).

3. We then obtain the redshift-space power spectrum for the mass by using equation (42) with ^eff calibrated from Monte Carlo realizations of the catalog.

4. The bias is computed from and _m using equation (38). The galaxy power spectrum is obtained by correcting for bias, equation (36).

5. The resulting power spectrum is convolved with the galaxy window function. We use the routine provided on the 2dFGRS Web site to perform this numerically. This is the power spectrum that can be compared with the quantity measured from a galaxy survey.

6. We can now evaluate the likelihood using the full covariance matrix as provided by the 2dFGRS team. We approximate the likelihood to be Gaussian as it was done by the team. In principle, this is not strictly correct since in the linear regime the power spectrum is an exponential distribution and in the nonlinear regime the distribution has contributions from higher orders correlations. However, because of the size of the survey we are considering, the central limit theorem ensures that the likelihood is well described by the Gaussian approximation (e.g., Scoccimarro, Zaldarriaga, & Hui 1999). Moreover, the covariance matrix for the 2dFGRS power spectrum has been computed by the 2dFGRS team under the assumption that the likelihood is Gaussian.

     We assume that the likelihood for the bias parameter is Gaussian, centered on b = 1.04 with dispersion _b = 0.11. This is a conservative overestimate of the error on the bias parameter, as noted in Verde et al. (2002). The determination of b is correlated with and _p, and the error quoted has already been marginalized over the uncertainties in these two parameters. In practice, for each step in the Markov chain we compute the likelihood according to items 16 above. The bias parameter is determined once , _p, and the other cosmological parameters are chosen. We then multiply the likelihood by the joint likelihood for and _p, as in Figure 4 of Peacock et al. (2001), and by the likelihood for the bias parameter. In effect, we use the determination of , _p, and b as priors. By multiplying the likelihood, we assume that the measurements of the redshift-space distortion parameters, bias, and the 2dFGRS power spectrum are independent. We justify this assumption below.

     The parameters needed to map the real-space nonlinear matter power spectrum onto the redshift-space galaxy spectrum are , _p, and b. These three parameters are not independent: not only is 1/b, but, more importantly, the three parameters are measured from the same catalog that we are using to constrain other cosmological parameters. However, the information we use to constrain cosmological parameters is all encoded in the shape and amplitude of the angle-averaged power spectrum. The information used to measure and _p is all encoded in the dependence of the Fourier coefficients (i.e., of the power spectrum) on the angle from the line of sight. Thus, we can treat the determinations of and _p as independent from the likelihood for cosmological parameters. The analysis of Verde et al. (2002) to measure the bias parameter from the 2dFGRS uses both information about the amplitude of the Fourier coefficients and their angular dependence. This dependence, however, is not that introduced by redshift-space distortions but is the configuration dependence of the bispectrum. Thus, in principle, we should not treat this measurement as completely independent. However, most of the signal for the bias measurement comes from the k range of 0.2 h Mpc^-1 < k < 0.4 h Mpc^-1, while the signal for the present analysis comes from k < 0.2 h Mpc^-1. Note that the configuration dependence of the bispectrum is largely independent of cosmology. This allows us to easily include a prior for the bias parameter in the analysis.

6. Ly FOREST DATA

     The Ly forest traces the fluctuations in the neutral gas density along the line of sight to distant quasars. Since most of this absorption is produced by low-density unshocked gas in the voids or in mildly overdense regions that are thought to be in ionization equilibrium, this gas is assumed to be an accurate tracer of the large-scale distribution of dark matter. In this epoch and on these scales the clustering of dark matter is still in the linear regime.

     Since the Ly forest observations are probing the distribution of matter at z 3, they are an important complement to the CMB data and the galaxy survey data. Because of their importance, there has been extensive numerical and observational work testing the notion that they trace the LSS. In our analyses, we find that the addition of Ly forest data appears to confirm trends seen in other data sets and tightens cosmological constraints. However, more observational and theoretical work is still needed to confirm the validity of the emerging consensus that the Ly forest data trace the LSS.

     Recent papers use two different approaches for analysis of the Ly forest power spectrum data. McDonald et al. (2000) and Zaldarriaga, Hui, & Tegmark (2001) directly compare the observed transmission spectra to the predictions from cosmological models. We follow the approach of Croft et al. (2002) and Gnedin & Hamilton (2002, hereafter GH), who use an analytical fitting function to recover the matter power spectrum from the transmission spectrum.²²

     GH factorize the linear power spectrum into four terms,



where P^fact(k) is a quantity that is independent of modeling and is almost directly measured. The other parameters convert this quantity into the linear matter power spectrum and encode the dependence on cosmology and the modeling of the intergalactic medium (IGM). In our treatment, we use the values of P^obs(k) (the estimator from Ly forest observations of P^fact) from GH and their parameterization in terms of equation (43) because it allows us to explicitly include the dependence of the recovered linear matter power spectrum on the cosmological parameters. Q encodes the dependence of the recovered linear power spectrum on the matter density parameter at z = 2.72. For Q we use the GH Ansatz of



Q_T = 20,000 K/T₀ (T₀ 20,000 K) parameterizes the dependence on the mean temperature of the IGM, and Q 1.11 parameterizes the dependence on the assumed mean optical depth. In addition to the statistical errors, GH quote a systematic uncertainty that we add to the statistical one. Finally, the uncertainties in Q, Q_T, and Q contribute to the overall normalization uncertainty. We use the Croft et al. (2002) prescription to parameterize this uncertainty as ln (A) = -1/2(A - 1)²/, where if A 1, then _Ly = 0.25, while if A > 1, _Ly = 0.29.

     N-body simulations are used to convert the flux power spectrum to the dark matter power spectrum and calibrate the form of equation (43). The two different groups, GH and Croft et al. (2002), have done this independently. The resulting power spectra agree well within the 1 errors for all data points except the last three. We thus increase the 1 uncertainties on the last three data points to make the two determinations of P_L(k) consistent and use this as a rough measure of the intrinsic systematic uncertainties in the Ly data.

     GH point out that the correlation in flux measured from the Ly forest samples power over a finite band of wavenumbers. The effective band-power windows are rather broad as a result of the peculiar velocities that smear power on scales comparable to the one-dimensional velocity dispersion. Thus, the recovered linear power spectrum is effectively smoothed with a window that becomes broader at smaller scales. In principle, the resulting covariance between estimates of power at different k needs to be taken into account to do a full likelihood analysis to extract cosmological parameters. However, the full covariance matrix is not available. Since the Ly data are such a powerful tool, we just perform a simple ² fit and caution the reader that interpreting the reduced ² as a measure of goodness of fit for this data set is not meaningful since the data are strongly correlated.

     To marginalize over the overall normalization uncertainty, we take advantage of the MCMC approach. In principle, we could marginalize over it analytically, as we do for the calibration uncertainty. Instead, at each step of the chain we compute the best-fit amplitude as done for point sources (Hinshaw et al. 2003b),



The likelihood for the Ly data for the model is given by ln _Ly = ln (P^obs|,P_L) + ln (). The marginalization is then automatically obtained from the MCMC output. In other words, the analytic marginalization computes (data|model)(A)dA, while we compute an estimator of this given by (data|model)()d.

     ²² After the present paper was submitted, a preprint appeared (Seljak et al. 2003) claiming that the treatment of GH and Croft et al. (2002) significantly underestimates the errors. Given the importance of this data set to tighten cosmological constraints, the Ly forest community should reach a consensus on the interpretation of these observations and on the level of systematic contamination.

7. CONCLUSIONS

     In this paper we have presented the basic formalism that we use for our likelihood analysis. This paper shows the final step on the path from time-ordered data to cosmological parameters. It provides the framework for the analysis of cosmological parameters and their implications for cosmology.

     The unprecedented quality of the WMAP data and the tight constraints on cosmological parameters that are derived require a rigorous analysis so that the approximations made in the modeling do not propagate into significant biases and systematic errors. We have derived an approximation to the exact likelihood function for the that is accurate to better than 0.1%, and we have carefully calibrated the temperature power spectrum covariance matrix with Monte Carlo simulations. This enables us to use the effective ² per degree of freedom as a tool to test whether or not a model is an acceptable fit to the data.

     We implement our likelihood analysis with the MCMC. We have concentrated on the issue of convergence and mixing, emphasizing how important these issues are in recovering cosmological parameter values and their confidence levels from the MCMC output.

     To the WMAP data sets (TT and TE angular power spectra) we have added the CBI and ACBAR measurement of the CMB on smaller angular scales, the 2dFGRS galaxy power spectrum at z 0, and the Ly forest matter power spectrum at z 3. These external data sets significantly enhance the scientific value of the WMAP measurement, by allowing us to break parameter degeneracies. While the underlying physics for these data sets is much more complicated and less well understood than for WMAP data, and systematic and instrumental effects are much more important, we feel we have made a significant step toward improving the rigor of the analysis of these data sets. We have included a detailed modeling of galaxy bias, redshift distortions, and the nonlinear growth of structure. We also include known (as to the present day) systematic and statistical uncertainties intrinsic to these other data sets.

     We thank Bill Holzapfel for invaluable discussions about the ACBAR data. We thank the 2dFGRS team for giving us access to the Monte Carlo realizations of the 2dFGRS. The mock catalogs of the 2dFGRS were constructed at the Institute for Computational Cosmology at Durham. We thank Will Percival for discussions and for providing us with the covariance matrix of the 2dFGRS power spectrum. L. V. is supported by NASA through Chandra Fellowship PF2-30022 issued by the Chandra X-Ray Observatory Center, which is operated by the Smithsonian Astrophysical Observatory and on behalf of NASA under contract NAS 8-39073. L. V. also acknowledges Rutgers University for support during the initial stages of this work. H. V. P. is supported by a Dodds Fellowship granted by Princeton University. The WMAP mission is made possible by the support of the Office of Space Sciences at NASA Headquarters and by the hard and capable work of scores of scientists, engineers, technicians, machinists, data analysts, budget analysts, managers, administrative staff, and reviewers.

REFERENCES

• Ballinger, W. E., Heavens, A. F., & Taylor, A. N. 1995, MNRAS, 276, L59 First citation in article | Crossref | ADS
• Ballinger, W. E., Peacock, J. A., & Heavens, A. F. 1996, MNRAS, 282, 877 First citation in article | Crossref | ADS
• Barnes, C., et al. 2003, ApJS, 148, 51 First citation in article | IOPscience | ADS
• Baugh, C. M., & Efstathiou, G. 1993, MNRAS, 265, 145 First citation in article | Crossref | ADS
• Bennett, C. L., et al. 2003a, ApJ, 583, 1 First citation in article | IOPscience | ADS
• . 2003b, ApJS, 148, 97 First citation in article | IOPscience | ADS
• Bond, J. R., Crittenden, R., Davis, R. L., Efstathiou, G., & Steinhardt, P. J. 1994, Phys. Rev. Lett., 72, 13 First citation in article | Crossref | ADS | PubMed
• Bond, J. R., & Efstathiou, G. 1984, ApJ, 285, L45 First citation in article | Crossref | ADS
• Bond, J. R., Jaffe, A. H., & Knox, L. 1998, Phys. Rev. D, 57, 2117 First citation in article | Crossref | ADS
• . 2000, ApJ, 533, 19 First citation in article | IOPscience | ADS
• Bond, J. R., et al. 2002, preprint (astro-ph/0205386) First citation in article | ADS | Preprint
• Bridle, S. L., Crittenden, R., Melchiorri, A., Hobson, M. P., Kneissl, R., & Lasenby, A. N. 2002, MNRAS, 335, 1193 First citation in article | Crossref | ADS
• Christensen, N., & Meyer, R. 2000, preprint (astr-ph/0006401) First citation in article | Preprint
• Christensen, N., Meyer, R., Knox, L., & Luey, B. 2001, Classical Quantum Gravity, 18, 2677 First citation in article | IOPscience | ADS
• Cole, S., Fisher, K. B., & Weinberg, D. H. 1994, MNRAS, 267, 785 First citation in article | Crossref | ADS
• Colless, M., et al. 2001, MNRAS, 328, 1039 First citation in article | Crossref | ADS
• Croft, R. A. C., Weinberg, D. H., Bolte, M., Burles, S., Hernquist, L., Katz, N., Kirkman, D., & Tytler, D. 2002, ApJ, 581, 20 First citation in article | IOPscience | ADS
• Davis, M., & Peebles, P. J. E. 1983, ApJ, 267, 465 First citation in article | Crossref | ADS
• Dressler, A. 1980, ApJ, 236, 351 First citation in article | Crossref | ADS
• Efstathiou, G., & Bond, J. R. 1999, MNRAS, 304, 75 First citation in article | Crossref | ADS
• Efstathiou, G., & Moody, S. J. 2001, MNRAS, 325, 1603 First citation in article | Crossref | ADS
• Elgarøy, Ø., et al. 2002, Phys. Rev. Lett., 89, 61301 First citation in article | Crossref | PubMed
• Feldman, H. A., Kaiser, N., & Peacock, J. A. 1994, ApJ, 426, 23 First citation in article | Crossref | ADS
• Fisher, K. B. 1995, ApJ, 448, 494 First citation in article | Crossref | ADS
• Freedman, W. L., et al. 2001, ApJ, 553, 47 First citation in article | IOPscience | ADS
• Fry, J. N. 1996, ApJ, 461, L65 First citation in article | IOPscience | ADS
• Gelman, A., & Rubin, D. 1992, Stat. Sci., 7, 457 First citation in article | Crossref
• Gilks, W. R., Richardson, S., & Spiegelhalter, D. J. 1996, Markov Chain Monte Carlo in Practice (London: Chapman and Hall) First citation in article | Crossref
• Gnedin, N. Y., & Hamilton, A. J. S. 2002, MNRAS, 334, 107 (GH) First citation in article | Crossref | ADS
• Goldstein, J. H., et al. 2002, ApJ, submitted First citation in article
• Gunn, J. E., & Knapp, G. R. 1993, in ASP Conf. Ser. 43, Sky Surveys: Protostars to Protogalaxies, ed. B. T. Soifer (San Francisco: ASP), 267 First citation in article | ADS
• Hamilton, A. J. S., Matthews, A., Kumar, P., & Lu, E. 1991, ApJ, 374, L1 First citation in article | Crossref | ADS
• Hatton, S., & Cole, S. 1998, MNRAS, 296, 10 First citation in article | Crossref | ADS
• Hawkins, E., et al. 2002, MNRAS, submitted First citation in article
• Hinshaw, G. F., et al. 2003a, ApJS, 148, 63 First citation in article | IOPscience | ADS
• . 2003b, ApJS, 148, 135 First citation in article | IOPscience | ADS
• Hoekstra, H., van Waerbeke, L., Gladders, M. D., Mellier, Y., & Yee, H. K. C. 2002, ApJ, 577, 604 First citation in article | IOPscience | ADS
• Hu, W. 2001, Phys. Rev. D, 64, 83005 First citation in article | Crossref | ADS
• Hubble, E. 1936, ApJ, 84, 517 First citation in article | Crossref | ADS
• Huey, G., Wang, L., Dave, R., Caldwell, R. R., & Steinhardt, P. J. 1999, Phys. Rev. D, 59, 63005 First citation in article | Crossref | ADS
• Jarosik, N., et al. 2003a, ApJS, 145, 413 First citation in article | IOPscience | ADS
• . 2003b, ApJS, 148, 29 First citation in article | IOPscience | ADS
• Kaiser, N. 1984, ApJ, 284, L9 First citation in article | Crossref | ADS
• . 1987, MNRAS, 227, 1 First citation in article | Crossref | ADS
• Kang, X., Jing, Y. P., Mo, H. J., & Börner, G. 2002, MNRAS, 336, 892 First citation in article | Crossref | ADS
• Kass, R. E., Carlin, B. P., Gelman, A., & Neal, R. M. 1997, J. Am. Stat. Assoc., 52, 93 First citation in article
• Knox, L., Christensen, N., & Skordis, C. 2001, ApJ, 563, L95 First citation in article | IOPscience | ADS
• Kogut, A., et al. 2003, ApJS, 148, 161 First citation in article | IOPscience | ADS
• Komatsu, E., & Seljak, U. 2002, MNRAS, 336, 1256 First citation in article | Crossref | ADS
• Komatsu, E., et al. 2003, ApJS, 148, 119 First citation in article | IOPscience | ADS
• Kosowsky, A., Milosavljevic, M., & Jimenez, R. 2002, Phys. Rev. D, 66, 63007 First citation in article | Crossref | ADS
• Kuo, C. L., et al. 2002, ApJ, submitted First citation in article
• Lahav, O., Rees, M. J., Lilje, P. B., & Primack, J. R. 1991, MNRAS, 251, 128 First citation in article | Crossref | ADS
• Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 First citation in article | Crossref | ADS
• Ma, C., Caldwell, R. R., Bode, P., & Wang, L. 1999, ApJ, 521, L1 First citation in article | IOPscience | ADS
• Maddox, S. J., Efstathiou, G., & Sutherland, W. J. 1990a, MNRAS, 246, 433 First citation in article | ADS
• . 1996, MNRAS, 283, 1227 First citation in article | Crossref | ADS
• Maddox, S. J., Efstathiou, G., Sutherland, W. J., & Loveday, J. 1990b, MNRAS, 243, 692 First citation in article | ADS
• Marzke, R. O., Geller, M. J., da Costa, L. N., & Huchra, J. P. 1995, AJ, 110, 477 First citation in article | Crossref | ADS
• Mason, B. S., et al. 2002, ApJ, submitted First citation in article
• Matsubara, T. 1994, ApJ, 424, 30 First citation in article | Crossref | ADS
• McDonald, P., Miralda-Escudé, J., Rauch, M., Sargent, W. L. W., Barlow, T. A., Cen, R., & Ostriker, J. P. 2000, ApJ, 543, 1 First citation in article | IOPscience | ADS
• Norberg, P., et al. 2001, MNRAS, 328, 64 First citation in article | Crossref | ADS
• Page, L., et al. 2003a, ApJ, 585, 566 First citation in article | IOPscience | ADS
• . 2003b, ApJS, 148, 39 First citation in article | IOPscience | ADS
• Panter, B., Heavens, A. F., & Jimenez, R. 2002, MNRAS, submitted First citation in article
• Peacock, J. A., & Dodds, S. J. 1994, MNRAS, 267, 1020 First citation in article | Crossref | ADS
• . 1996, MNRAS, 280, L19 First citation in article | Crossref | ADS
• Peacock, J. A., et al. 2001, Nature, 410, 169 First citation in article | Crossref | ADS | PubMed
• Pearson, T. J., et al. 2002, ApJ, submitted First citation in article
• Peebles, P. J. E., & Yu, J. T. 1970, ApJ, 162, 815 First citation in article | Crossref | ADS
• Peiris, H., et al. 2003, ApJS, 148, 213 First citation in article | IOPscience | ADS
• Percival, W. J. 2003, MNRAS, submitted First citation in article
• Percival, W. J., et al. 2001, MNRAS, 327, 1297 First citation in article | Crossref | ADS
• Postman, M., & Geller, M. J. 1984, ApJ, 281, 95 First citation in article | Crossref | ADS
• Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in C (2d ed.; Cambridge: Cambridge Univ. Press) First citation in article | ADS
• Riess, A. G., et al. 1998, AJ, 116, 1009 First citation in article | IOPscience | ADS
• . 2001, ApJ, 560, 49 First citation in article | IOPscience | ADS
• Scoccimarro, R., Zaldarriaga, M., & Hui, L. 1999, ApJ, 527, 1 First citation in article | IOPscience | ADS
• Seager, S., Sasselov, D. D., & Scott, D. 1999, ApJ, 523, L1 First citation in article | IOPscience | ADS
• Seljak, U., & Zaldarriaga, M. 1996, ApJ, 469, 437 First citation in article | Crossref | ADS
• Seljak, U., et al. 2003, preprint (astro-ph/0302571) First citation in article | ADS | Preprint
• Sievers, J. L., et al. 2002, preprint (astro-ph/0205387) First citation in article | ADS | Preprint
• Spergel, D. N., et al. 2003, ApJS, 148, 175 First citation in article | IOPscience | ADS
• Verde, L., et al. 2002, MNRAS, 335, 432 First citation in article | Crossref | ADS
• Zaldarriaga, M., Hui, L., & Tegmark, M. 2001, ApJ, 557, 519 First citation in article | IOPscience | ADS
• Zaldarriaga, M., & Seljak, U. 2000, ApJS, 129, 431 First citation in article | IOPscience | ADS
• Zurek, W. H., Quinn, P. J., Salmon, J. K., & Warren, M. S. 1994, ApJ, 431, 559 First citation in article | Crossref | ADS