THE ASTROPHYSICAL JOURNAL, 510:862–866, 1999 January 10
© 1999. The American Astronomical Society. All rights reserved. Printed in U.S.A.

Accretion Disk Blobs

HIDEYUKI KAMAYA 1

Department of Physics, Kyoto University, Sakyo-ku, Kyoto 606-8502, Japan; kamaya@tap.scphy.kyoto-u.ac.jp

Received 1998 June 9; accepted 1998 August 18


ABSTRACT

     Recent observations reveal a similar frequency dependence f-b in the X-rays from stellar black hole candidates and active galactic nuclei (AGNs). Several X-ray sources have a steeper decline of the power spectrum, b=1.5–1.7 at f>1.0 Hz. Data from EXOSAT have shown that AGNs have a universal slope of b∼1.55. These spectral dependencies give us information about the activity of accretion disks around compact gravity sources. To explain these power spectra and the activity of the accretion disks uniformly, several research groups hypothesize that many blobs exist on the disks and that the power spectra are explained by their activity. These accretion disk blobs are discussed in this paper. We show that accretion disk blobs cannot survive unless each of them is sustained by a tension that presumably originates from an external magnetic field.

     The diffusion mechanism of the magnetic field is also important, since the magnetic tension that sustains the blobs becomes ineffective when the strength of the magnetic field is smaller than a critical value. If we can determine this critical value, we will reveal something about the evolution of accretion disks.

Subject headings: accretion, accretion disks—black hole physics—hydrodynamics—stars: neutron—X-rays: stars

FOOTNOTES

     1 Research Fellow of JSPS.

§1. INTRODUCTION

     It is known that X-ray intensity largely and aperiodically varies on timescales of from several tens of seconds to milliseconds (e.g., Miyamoto et al. 1992). Moreover, there exist fluctuations with a frequency of f-b in X-rays from stellar black-hole candidates and active galactic nuclei (AGNs) (see Makishima 1988 for a review). It has been reported that at f≥1.0 Hz, b is 1.7 (Makishima 1988). Importantly, using the EXOSAT database, Lawrence & Papadakis (1993) have found a universal slope of b∼1.55 to be a more correct value for AGNs. Recent progress is discussed in Negoro (1996). Understanding the origin of f-b is one of the key issues for high-energy astronomy.

     To explain the observed rapid X-ray variability uniformly, it is essential that physical quantities in the accretion disk vary rapidly. Abramowicz et al. (1991, 1992) suggest a specific model for short-term variability. It is essential to their model that the rapid variability is due to the orbital motion of many bright spots. The bright spots rotate around the gravity source at nearly Kepler rotation speed. Here we have expected the lifetime of the blobs to be at least as long as the Kepler rotation timescale. This is because the blobs suddenly flare up during their circular motion. Mineshige et al. (1994a, 1994b) consider this picture of a black hole accretion disk in the framework of a simple cellular automata model (see also Takeuchi, Mineshige, & Negoro 1995). They call it the self-organized critical (SOC) model of the accretion disk. According to Mineshige's group, the SOC model also produces f-b-like fluctuations for any b.

     According to Takeuchi & Mineshige (1996), the SOC model suggests three points:

     1. Gas flow is two-dimensional. Also, the radial flow is important in the rotating disk.

     2. Physical quantities do not vary smoothly in accretion disks. Thus, many blobs are expected on a disk.

     3. For the critical state to obtain, there have to be mass reservoirs.

     

The first point suggests that the advection-dominant flow model is adequate (e.g., Abramowicz 1996; Narayan 1996). But although the other two points have been suggested by Abramowicz et al. (1991, 1992), the precise physics remains unclear. For example, we do not know how such blobs survive through the Kepler rotation timescale. If Takeuchi & Mineshige are correct, the blobs are created in the viscous timescale (see also Yonehara, Mineshige, & Welsh 1997). This is because the mass is reserved in the disk owing to the viscosity. That timescale is not shorter than the Kepler rotation timescale. Thus, if the destruction timescale is comparable to the Kepler rotation timescale, the blobs are never created in the viscous timescale.

     In § 2 we show, in the context of Takeuchi & Mineshige's second point, that the blobs could not survive through the timescales we are interested in if there were no surface tension on them. A specific model of the blobs is discussed in § 3. It is suggested in § 4 that magnetic fields may be important for the critical state noted in Takeuchi & Mineshige's third point. In this paper, we refer to this critical state as the SOC state. Adopting reasonable assumptions, some speculations are also presented in this section. The final section is devoted to summary and discussion of advection-dominated accretion flow.

§2. ON THE WEBER NUMBER

     The Weber number, We, is one of the fundamental indexes of hydrodynamics. Its definition is



where ρb is the density of the blob on the accretion disk, ub is the velocity of the blob, L is the size of the blob, and σ is the surface tension on the blob.

     For example, the surface tension on a spherical blob is defined as



Here the pressure jumps across the interface, Δp. If the pressure in the blob is larger (smaller) than that in the ambient flow, Δp is always positive (negative).

     The physical meaning of We is the following:



Since the blobs are affected by the Coriolis force, the tidal force, and anisotropic turbulent pressure, they are significantly deformed if We is much larger than unity. The inequality We≫1 means that the applied forces exceed the restoring forces because of the surface tension. If there were no surface tension, blobs would easily be destroyed and thus would never exist on disks.

     Some might think that there is some mechanism that sustains the blobs against the disturbances mentioned. In the stellar compact object or massive black hole, the self-gravity in the blobs may be neglected, since the size of the blobs is much smaller than the so-called Jeans length. Thus, first of all, we consider pressures. Each blob may have gas pressure, pbg, turbulent pressure, pbt, and magnetic pressure, pbm. Since the effect of the magnetic field is discussed in the subsequent section, we omit it here. We should note that the accretion disk has strong turbulence (see, e.g., Kato 1996). In this section, we pay attention to the turbulence inside the blobs. We regard the anisotropic component of the turbulent pressure as the main internal disturbance affecting the blobs. We let pbt denote only the isotropic component of the turbulent pressure. For simplicity, all of the pressures in the blobs are regarded as isotropic. Further, we define the external pressure as pe. The blob expands if p$\mathstrut{_{e}}$<p$\mathstrut{_{{\rm {\rm bg}}}}$+p$\mathstrut{_{{\rm {\rm bt}}}}$ and shrinks if p$\mathstrut{_{e}}$>p$\mathstrut{_{{\rm {\rm bg}}}}$+p$\mathstrut{_{{\rm {\rm bt}}}}$, restoring its spherical form. Isotropic pressure likes the sphere.

     The deformation of a blob is restored only by an imbalance on its surface between the pbg and pbt. The equality We∼1 is expected whenever the form of the blobs is restored. But when We∼1, Δp must be a significantly large value, since Δp∼σ/L. Given that the Weber number is on the order of the unity, We∼1, we expect



from equation (2.1). If we consider the motion of the blob around, for example, a black hole, the last term in equation (2.3) is significantly large. Indeed, we estimate Δp to be



Before the blobs flare up, the temperature in them may be lower than that in the disk (e.g. Yonehara et al. 1997). Therefore, the Mach number for the blobs, M$\mathstrut{^{2}_{b}}$=u$\mathstrut{^{2}_{b}}$ρ$\mathstrut{_{b}}$/(p$\mathstrut{_{{\rm {\rm bg}}}}$+p$\mathstrut{_{{\rm {\rm bt}}}}$), is generally much larger than unity in the accretion disk, inasmuch as the blobs rotate around the central gravity source in the Kepler rotation timescale. It should be noted that ub is not the relative velocity of the blobs and the disk gas; it is the speed of the blobs and is nearly the Kepler rotation speed (e.g., Abramowicz et al. 1991). Thus, significantly large Δp must emerge when we let only isotropic pressures sustain the form of the blobs. As a result, inasmuch as Δp≠0, all the blobs expand suddenly or collapse, since |Δp|&Gt;p$\mathstrut{_{{\rm bg}}}$+p$\mathstrut{_{{\rm {\rm bt}}}}$.

     Even if Δp∼0, the blobs are easily destroyed by fluid dynamical instabilities, since We&Gt;1 (Simpkins & Bales 1972). Fluid dynamical instabilities are expected whenever a blob's inertial motion is not suppressed. We should note that the blobs are accelerated by the central gravity source. This acceleration can trigger, for example, a buoyancy-driven instability. Thus, in this section, we show that the blobs on a disk are not maintained by the isotropic pressures. This is our main conclusion, and some might think it too evident. But as far as the author is aware, this is the first quantitative proof that has been presented. The timescale for the destruction is discussed below.

     First, the former case, Δp≠0, is discussed. The estimate in equation (2.4) means that the blobs must collapse or explode in the dynamical timescale, since We∼1. This is because the Weber number is approximately interpreted as



The expansion or collapse timescale is the sound-crossing timescale. But from We∼1, the sound-crossing timescale is comparable to the destruction timescale. The destruction timescale is nearly the Kepler rotation timescale. This is because the destruction is triggered by the inertia motion of the blobs. The inertia motion originates from the rotation around a compact object, say, a black hole. The timescale for the rotation is nearly the Kepler rotation timescale. Thus, we can regard the destruction timescale as the Kepler rotation timescale. Therefore, when We∼1, all the blobs will collapse or explode within the Kepler rotation timescale.

     When We&Gt;1 (or when Δp=0), the destruction timescale is much shorter than the restoring timescale. This destruction is caused by the inertia of the blobs themselves. In other words, the destruction timescale is comparable to the dynamical timescale in the disk, i.e., the Kepler rotation timescale. Thus, the blobs are easily destroyed during a single rotation around the gravity source.

     A mechanism that possibly sustains the blobs is discussed in § 4.

§3. A SPECIFIC MODEL

     In the previous section, a general discussion of the blobs on accretion disks is presented. Here, for readers' convenience, we present a specific model of blobs on accretion disks, applying the previous theory to specific conditions. We assume an equilibrium state of blobs (as clumps) with hot plasma (∼109 K). This is similar to the condition adopted by Krolik (1998), but whereas he finds an equilibrium state for accretion disks with clumps, we consider its dynamics. In short, we are concerned with the dynamical stability of a gas mixture that is composed of dense clumps and hot (coronal) gas. It should be noted that in order to reach a clear conclusion, we do not consider magnetic fields in this section.

     First we assume that the collision frequency between clumps is smaller than the orbital frequency. In this case, Thomson optical depth is measured from the midplane to the surface (see, e.g. Krolik 1998):



Here αcl is an effective viscous parameter originating from the clumps, αH is a Shakura & Sunyaev—type viscous parameter (Shakura & Sunyaev 1973), $\mathstrut{{\ucpmathaccent{m}{"7016}}}$/m$\mathstrut{_{e}}$ is the ratio of the mean mass per particle to the electron mass, $\mathstrut{{\ucpmathaccent{m}{"705F}}}$ is the accretion rate in Eddington units (for unit efficiency), Θ is the hot phase temperature in units of m$\mathstrut{_{e}}$c$\mathstrut{^{2}}$/k, &Mscr; is the velocity dispersion of the clumps in units of the hot phase sound speed, x=rc$\mathstrut{^{2}}$/GM, and RT is the relativistic correction factor to the integrated stress (Novikov & Thorne 1973). Note that at x=10, R$\mathstrut{_{{\rm T}}}$&sime;0.1–0.5, depending on the black hole spin.

     Next we consider energy conservation in the hot phase. Several heating mechanisms may act, all having roughly constant rate per unit volume. For example, adjacent hot gases are pulled by the clump, and the energy of their random motions is eventually dissipated into the heat of the hot gas. The hot phase is cooled by inverse Compton scattering. Pietrini & Krolik (1998) showed that when τ$\mathstrut{_{h}}$∼1, the thermal balance of a plasma cooled by inverse Compton scattering may be described approximately by an expression that in this context becomes



Here τh is the half-Compton optical depth of the hot phase, and C is a covering fraction of clumps along a vertical line of sight.

     The clumps are heated both by dissipative collisions and by absorbing X-rays radiated by the hot phase. If they reradiate thermally and C<1, their outer surface temperature is



where m=M/M$\mathstrut{_{{\odot}}}$ and RR is the relativistic correction factor for the dissipation rate per unit area (Novikov & Thorne 1973). If, as is likely, α$\mathstrut{_{{\rm cl}}}$/C>α$\mathstrut{_{H}}$, so that most of the dissipation associated with αcl occurs deep inside the clumps, the temperature at their centers is larger than Ts by a factor ∼(1+τcl)1/4, where τcl is the Rosseland mean optical depth through a clump.

     The gas pressure in the hot phase is generally somewhat greater than the radiation pressure. Approximate pressure balance with the clumps thus implies a gas density in the clumps,



where Rz is the relativistic correction factor for the vertical gravity (Abramowicz, Lanza, & Percival 1997). At such high densities, the approximation of thermal radiation (eq. [3.3]) should be reasonably valid, even when (as in AGNs) m∼10$\mathstrut{^{8}}$.

     Thus, indeed, we find a dynamical equilibrium state for accretion disks with many clumps. Pressure equilibrium (Δp∼0) is possible, because the size of the clumps is much smaller than that of the accretion disk itself and the sound crossing time over the clumps is significantly short. It is therefore reasonable, as a first step, to assume pressure equilibrium between the hot gas and the clumps. Such a condition is observationally reasonable for AGNs and black hole candidates (Krolik 1998). However, when pressure equilibrium (Δp∼0) is established, the Weber number becomes significantly larger, as shown in the previous section (i.e., the clumps are dynamically unstable). Thus, we need a stabilizing mechanism for the clumps. In the next section, we propose a scenario for stable clumps or blobs and stress the importance of the magnetic field in the accretion disks. We again note, as stated in § 1, that if the number or volume fraction of the blobs is kept over the diffusion timescale, the accretion-disk-with-blobs model (Takeuchi & Mineshige 1996) does not explain some of the observational evidence (although their strategy is partly supported by Manmoto et al. 1996).

§4. MAGNETIC FIELD

     It is at least clear from the above that the blobs must have surface tension if they are to survive over the Kepler rotation timescale. We believe the origin of this surface tension to be a magnetic field. Some might think that the magnetic fields in blobs could not produce such surface tension. However, the blobs could be sustained by an external global magnetic field of the disk. The accretion disk is composed of plasma, and such plasma usually has a magnetic field. Moreover, external magnetic tension is never isotropic. Deformation of the blobs is restored not only by magnetic pressure but also by magnetic tension. In this section, therefore, we consider whether the surface tension of the blobs effectively originates from a global magnetic field of the accretion disk (e.g., Mineshige, Kusunose, & Matsumoto 1995).

     A magnetic field is easily strengthened by the dynamo mechanism, since strong velocity shear is expected in the accretion disk. We may estimate the strength of the field as B$\mathstrut{^{2}}$∼ρ$\mathstrut{_{b}}$u$\mathstrut{^{2}_{b}}$. Effective magnetic pressure is estimated as B2. Effective surface tension will be estimated as σ∼B$\mathstrut{^{2}}$L. Thus, the Weber number is nearly unity:



Only when a strong magnetic field exists will a low Weber number (We) be realized. Note that although this discussion is not supported by observations, it does not require any strange physical assumptions.

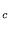
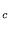
     If the origin of the surface tension is magnetic tension, the following mechanism is possible. We assume that a blob has critical surface tension σc. This critical tension denotes that the blob is destroyed by its inertia motion when σ$\mathstrut{_{c}}$&Gt;σ but is sustained by the magnetic tension when σ$\mathstrut{_{c}}$&Lt;σ. 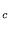That is to say, to determine a critical tension, σc, is to find that We=1.0∼ρ$\mathstrut{_{b}}$u$\mathstrut{^{2}_{b}}$L/σ$\mathstrut{_{c}}$ for a given accretion disk model (i.e., given ρb and ub). Thus, we determine the critical magnetic field,



from equation (4.1). Once the accretion disk model is determined, we can examine whether the model has a SOC state. When the magnetic field becomes smaller than Bc, blobs (and the SOC state) do not exist on the disk. But if the magnetic field is above Bc, many blobs exist on the disk.

     Thus this discussion supports the suggestions made by Mineshige et al. (1995) with respect to low-β and high-β disks.. Here β∼p$\mathstrut{_{{\rm gas}}}$/B$\mathstrut{^{2}}$ and pgas is mean pressure in the accretion disk. According to Mineshige et al., high-β disks do not have explicit blobs, while the low-β disk can have many blobs, which are threaded by the toroidal magnetic field. In other words, the blobs in high-β disks are destroyed because they are not sustained by magnetic tension, whereas those in low-β disks are sustained by magnetic fields. That is to say, the magnetic field is larger than Bc in low-β disks and smaller than Bc in high-β disks.

     Mineshige et al. (1995) state that magnetic dissipation is required to explain bimodal spectral states (Miyamoto et al. 1993). When a low-β disk transforms into a high-β disk, the magnetic field must dissipate. At the same time, the blobs on the disk break or evaporate. This magnetic dissipation may be ohmic dissipation or the Parker instability (Parker 1966). Formation of blobs also will be triggered by the Parker instability (see Shibata 1996 for a review). Thus, for the accretion disk with a SOC state, the Parker instability is adequate. Some might think that the magnetic field easily escapes from the disk to the corona above it. The magnetic flux may be lost by means of the Parker instability before the low-β disk is realized. In the author's opinion, the escape of the flux tube may be suppressed by the corona. This is because the growth rate of the Parker instability is reduced by the effect of the corona (e.g., Kamaya et al. 1997). When the blobs flare up (Abramowicz et al. 1991, 1992), magnetic reconnection may be triggered (Haardt & Maraschi 1991). Thus, the magnetic fields in the disk and in the corona above it (e.g., Haardt & Maraschi 1991) may be significant for understanding the variability in X-rays (e.g., Wallinder et al. 1992).

§5. SUMMARY AND DISCUSSION

     In this paper, we show that the blobs on an accretion disk around a compact object (for example, a black hole) are not sustained by isotropic pressures. It is suggested that a magnetic field always must be included in the accretion disk to explain the variability in X-rays. Mineshige et al. (1995) have partly done this, and the author argues that their approach should be extended. At least, whenever geometrically thin disks with blobs are expected, we need magnetic fields to explain how the blobs on the disk are sustained.

     Haardt & Maraschi (1991) discussed a two-phase model for the X-ray emission from AGNs to explain the variability in X-rays. According to their paper, gravitational power is dissipated via buoyancy and reconnection of the magnetic field in a hot tenuous corona (hot phase) that surrounds the main body of an accretion disk (cold phase). The main cooling mechanism of the hot layer is Comptonization of soft photons, thermally produced in the underlying cold phase. Hard Comptonized photons are backscattered into the thick phase, where they are in part reprocessed into soft blackbody power and in part reflected. Coupled thermal balance equations for the two phases yield the temperature of the hot phase and the slope of the Comptonized component self-consistently as a function of the substantial fraction of the gravitational power and the optical depth of the hot phase. In the author's opinion, if we can combine the theories of Mineshige et al. (1995) and Haardt & Maraschi (1991), a more realistic picture of the accretion disks around compact objects will be obtained.

     A key point in this paper is that M$\mathstrut{_{b}}$&Gt;1. But if advection-dominant flow (Ichimaru 1976, 1977) is permitted, the condition M$\mathstrut{_{b}}$≥1 is possible even when We∼1. This means that the destruction timescale is the sound crossing timescale, since the magnitude of the pressure disturbance is nearly the same as the ambient pressure (see eq. [2.4]). However, even when the flow around the central gravity source is advection-dominant, the destruction timescale is comparable to the Kepler rotation timescale, since We∼1 (tension case). In other words, the destruction timescale by the pressure disturbance is comparable to the Kepler rotation timescale. If We&Gt;1 (nontension case), the destruction timescale becomes much shorter than the restoring timescale. At this time, the blobs are destroyed by the mechanism with the shortest timescale. Even in the case of advection-dominant flow, such blobs will be destroyed in the Kepler rotation timescale.

     For the advection flow, however, the blobs can fall into the gravity source in the Kepler rotation timescale. Thus, we would think that any advection flow model must keep the blobs. But it should be remembered that many blobs are needed in the disk (see point [2] in this paper). The blobs are created in viscous timescales (e.g., Yonehara et al. 1997), and since the viscous timescale is longer than the Kepler rotation timescale, all of the blobs fall into the gravity source before new blobs are generated. Thus, the advection flow model does not perfectly explain the observed rapid variability, and we need some mechanism to keep the blobs on the accretion disk. Moreover, it is not clear that the advection-dominant flow is steady, and thus the intermittency reviewed in § 1 (Takeuchi & Mineshige 1996) cannot be explained by the advection model. The advection model, therefore, should be modified along the lines begun by Mineshige el al. (1995) to explain the intermittency of accretion disks with many blobs.

ACKNOWLEDGMENTS

     I am grateful for discussions with S. Mineshige, whose critical comments were very useful. I also acknowledge an anonymous referee for encouraging comments and useful suggestions about the references. I am thankful to H. Sato, N. Sugiyama, and R. Nishi for their continuous encouragement. This work is financially supported by JSPS.

REFERENCES