876, 1998 May 10 We compare the p-mode oscillation spectra of solar models, constructed under the assumption that the universal gravitation constant G varied monotonically over the course of the solar lifetime, to the most recent solar p-mode frequency observations from the Global Oscillation Network Group (GONG) instrument and Birmingham Solar Oscillation Network (BiSON). The GONG instrument consists of six telescopes spread over different longitude around the Earth, each recording, once every minute, Doppler shift images of the Sun's surface. BiSON also consists of a network of six telescopes specifically designed to observe low-l p-modes. We find that only those solar models constructed with (1/G)dG/dt 
1.6 × 10-12 yr-1 are consistent with the observations. This constraint not only probes G over cosmic time, it is stronger by almost one order of magnitude than constraints on the current maximum time variation coming from radar ranging and binary pulsar timing measurements.
Subject headings: gravitation
Sun: evolutionSun: oscillations
Since Dirac's Large Numbers Hypothesis (Dirac 1938) the notion that at least some fundamental parameters have evolved over cosmological time has remained of interest. Of course, until there existed realistic models for early universe cosmology, based on plausible microphysics, Dirac's suggestion remained essentially numerological. Nevertheless, during the intervening years, the extremely small relative strength of gravity compared to all the other known fundamental forces in nature has led many to suspect that this ratio might be explainable dynamically. With the advent of inflation, and more recently, superstring-inspired models, it is now clear that this idea may have some meat to it. In particular, theories in which, in addition to the Einstein metric tensor, an extra scalar field is introduced, the value of which determines the magnitude of the gravitational coupling constant, G, arise naturally in several contexts. Scalar-tensor theories (Brans & Dicke 1961; Bergmann 1968; Wagoner 1970; Nordtvedt 1970) have recently been proposed, for example, to overcome several cosmological difficulties associated with a graceful exit from inflation (La & Steinhardt 1989; Weinberg 1989; Steinhardt & Accetta 1990; Liddle & Wands 1992). In addition, such theories often arise in the low-energy limit of superstring theories, involving so-called dilaton fields (Green, Schwarz, & Witten 1988).
With this motivation, it is clear that an empirical investigation into possible time variation of the gravitational constant is warranted. While it is most natural that any rapid variation in this quantity would have occurred very early in the history of the universe, some residual small variation on cosmological timescales might be expected.
Currently the strongest constraint on G variation extending back to early times comes from models of big bang nucleosynthesis (BBN) which predict the primordial abundances of the light elements. By comparing these abundance predictions to currently observed abundances adjusted to compensate for the nuclear processing that occurs after the big bang, Accetta, Krauss, & Romanelli (1990) found | 
(t) | 10-12 yr-1, where (t) 
(1/G0)(dG/dt), assuming a monotonic variation in G. Of course this constraint is subject to the assumption not only of monotonicity, but also to the known systematic uncertainties arising when comparing primordial predicted abundances with inferred primordial abundances based on present day observations (see for example, Copi, Schramm, & Turner 1995; Deliyannis, Boesgaard, & King 1995; Krauss & Kernan 1995).
Constraints on the time variation of G today have so far been, however, approximately one order of magnitude less restrictive. Determinations based on celestial mechanics, such as laser ranging of the Moon (Müller et al. 1991) and radar ranging of Mars (Shapiro 1990) provide the strongest present day constraints on the variation of G, i.e., | (t) | 10 × 10-12 yr-1. Other methods, such as those utilizing neutron star masses (Thorsett 1996), globular cluster ages (Degl'Innocenti et al. 1995), and binary pulsar timings (Damour & Gundlach 1991) and helioseismology Demarque et al. (1994, hereafter DKGN) have yielded similar constraints. We should note that although Guenther et al. (1995) showed that solar g-modes could provide a much tighter present day constraint on G variation, to date no one, despite repeated attempts, has been able to verify the g-mode observations of Hill & Gu (1990), who remain the sole group claiming to have seen g-modes. Until there is verification of Hill's observations, we cannot attach any confidence to the contraints on G variation set by them.
There is reason to investigate improvements in the helioseismology constraint in particular. Like the BBN constraint, it probes the variation of G over cosmic time. While it does not have the lever arm of the BBN limit, it is less subject to uncertainties associated with the physics of the early universe. In particular, recent, albeit fine-tuned, scalar-tensor models have been proposed whose particular time variation during BBN is designed to produce results consistent with current constraints from light element abundances in the oldest stars (Deliyannis et al. 1995), and whose time variation goes to zero today (Alimi & Serna 1997). Clearly it is useful to have a post-BBN probe of such ideas. Moreover, recent developments, both in measurements of solar p-modes, and in modeling of the Sun suggest a new stronger constraint could in principle be derived, as we briefly outline below.
The idea of using stellar evolution to constrain possible variations in G comes to us originally from Teller (1948) who showed (see also appendix in Degl'Innocenti et al. 1995) that the luminosity L of a star depends on G according to L 
G7. Several attempts to directly check for G variation utilizing the G dependence on luminosity have been made using globular cluster H-R diagrams (Prather 1976; Degl'Innocenti et al. 1995) but have not yet yielded any stronger constraints than those relying on celestial mechanics.
If G were to vary on a nuclear timescale (billions of years), then the rates of nuclear burning of hydrogen into helium on the main-sequence would also vary. This in turn would affect the current central abundances of hydrogen and helium. Because helioseismology enables us to probe the structure of the solar interior, we can use the observed p-mode oscillation frequencies to constrain the rate of G variation. Specifically, from helioseismology we can determine the run of sound speed in the core of the Sun, which, with the aid of an accurate equation of state, can be used to determine the central densities and abundances of hydrogen and helium.
In 1994 Demarque et al. (DKGN) used helioseismology to constrain the rate of variation of the universal gravitational constant G averaged over the lifetime of the Sun. Taking G(t) t-
, they showed that the p-mode frequencies of only those solar models with | | 0.10 [equivalent to | (t) | 10 × 10-12 yr-1] match, within the error bars, the observed solar p-mode frequency spectrum. At the time they used the best available solar p-mode oscillation data summarized by Libbrecht, Woodward, & Kaufman (1990) and the best solar model physics. Since then improvements have been made to both the solar p-mode data and the solar model. The GONG (Global Oscillation Network Group; Harvey et al. 1996; Christensen-Dalsgaard et al. 1996) instrument and the BiSON (Birmingham Solar Oscillation Network; Chaplin et al. 1996) are both providing us with almost one order of magnitude more accurate low-l p-mode frequencies. The physics of the solar model now includes both helium and heavy element diffusion and the equation of state calculation now uses tables derived from the detailed atomic physics calculations of the OPAL group at Lawrence Livermore Laboratories. As a consequence, we are now able to provide a tenfold tighter constraint on the variation in G than in DKGN.
In this paper we briefly review the current state of the solar model and our implementation of G(t) in the solar model calculation. We introduce the use of the p-mode small spacing and explain how we use it to probe the deep interior of the Sun. We then compare the p-mode small spacings of our models to the GONG and the BiSON derived small spacings and determine the rate of variation of G. From previous solar model calculations (Guenther & Demarque 1997, hereafter GD) we know that the uncertainty in the current age of the Sun introduces the largest uncertainty in our model calculations with regad to the deep interior, we therefore use this uncertainty to estimate the uncertainty in our determination of G variations.
Our solar models are derived from a numerical calculation of the evolution of a 1 M
star from the zero age main sequence, where nuclear burning just begins to provide the dominant source of power, to the present age of the Sun, 4.53 ± 0.04 Gyr, determined from the ages of the oldest meteorites (GD). Although the basic equations of stellar evolution remain unchanged since Schwarzschild (1958), the modeling of the constitutive physics, such as the nuclear reaction network, the opacities, and the equation of state, have changed because of our ability to solve more of the detailed atomic physics. These improvements have gone hand in hand with the development of helioseismology which demanded better solar models, that is solar models that more accurately reproduce the observed oscillation spectrum.
Specific features of the solar model today are primarily characterized by the stellar evolution code used, the source of the constitutive physics, the values used to constrain the model, and supplemental physics that have not in the past been included. The sources of errors in the models, especially those affecting the core, are discussed in GD and Morel, Provost, & Berthomieu (1997). Here, all models were calculated using the "Yale" stellar evolution code (YREC) (Guenther et al. 1992). Our solar models use the nuclear cross sections from Bahcall & Pinsonneault (1992). The interior opacity is determined from OPAL tables (Iglesias & Rogers 1996) and the near surface and atmosphere opacity is determined from the tables of Alexander & Ferguson (1994). The thermodynamic properties of the matter are obtained from the OPAL equation of state tables (Rogers 1986; Rogers, Swenson, & Iglesias 1996).
We have supplemented the standard physics by including the effects of gravitational settling of helium and heavy elements. Elements heavier than hydrogen are predicted to diffuse downward out of the surface convection zone into the radiative region below. Because the amounts are small, diffusion does not directly affect the run of density, but it does affect the run of opacity which in turn affects the structure. We use the formulation described in Bahcall, Pinsonneault, & Wasserburg (1995) to model the effects of helium and heavy element diffusion. Note that all models listed in Table 1 satisfy, within the uncertainties, the observational constraint that (Z/X) = 0.0244 ± 0.001 (Grevesse, Noels, & Sauval 1996).
We note that the models calculated here differ from the models calculated in DKGN by the inclusion of helium and heavy element diffusion and by the use of the OPAL equation of state tables (GD). Since numerical solutions of the detailed atomic physics are now available in table form (Rogers 1986; Rogers et al. 1996) from the OPAL group at Lawrence Livermore Laboratories we have replaced the crude analytical approximations previously used in our stellar evolutionary calculations. These physics have improved the agreement between the model and the observed p-mode spectrum by more than a factor of two (GD) (±0.1% difference in the frequency range 12003000 
Hz) compared to the solar models used in DKGN and have, for the first time, enabled us to place serious constraints on the structure of the core.
The helium abundance, for which no direct observational value exists, and the mixing length parameter, a free parameter for the mixing length theory used to model the convective energy transport and adjust the model radius, were treated as adjustable parameters of the model. They were adjusted to produce models that have identical radii (R = 6.9598 × 1010 cm) to one part in 105 and identical luminosities. (L = 3.8515 × 1033 ergs s-1) to one part in 105 at an age of 4.55 Gyr. As a consequence, identically constrained solar models with different variations in G will have different values of the mixing length parameter, which affects the depth of the convection zone, and they will have different helium abundances, which affects the run of density in the model. At the same time, by producing identically constrained models at an age of 4.55 Gyr, the residual uncertainty associated with the solar age (±0.04 Gyr) can be used to establish the uncertainty associated with the model itself in our results.
We choose the same power law form to represent the time variation in G as in DKGN. That is, we replaced the constant G with the following function:
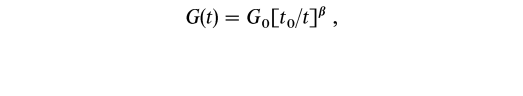
where t0 is the present-day age of the universe, and G0 is the present-day value of the gravitational constant (Cohen & Taylor 1986). Assuming a value of t0 of 12 Gyr therefore yields (t0) = (1/G0)(dG/dt) = (-83 × 10-12 yr-1).
Table 1 lists some of the characteristics of the resultant models calculated. From left to right Table 1 lists , the surface hydrogen mass fraction, the surface heavy element mass fraction, the age, the mixing length parameter, the initial hydrogen mass fraction, the initial heavy element mass fraction, the convective envelope mass, the radius fraction of the base of the convective envelope, the base ten logarithm of the central pressure, the base ten logarithm of the central temperature, the base ten logarithm of the central density, the central mass fraction of hydrogen, the central mass fraction of heavy elements, the 37Cl SNU flux, and the 71Ga SNU flux. In addition to the runs with different values of we also calculated models evolved to different ages. From GD we know that the uncertainty in the Sun's age is the most important factor with regard to fixing the central structure from the oscillations modes. To obtain an estimate of the uncertainty associated with the solar age, we bracket the age of the Sun, 4.53 ± 0.04 Gyr (GD), with solar models with ages 4.50, 4.55, and 4.60 Gyr, and adopt 4.55 Gyr as our reference age.
The resultant solar models, calculated to a numerical resolution of 1800 shells, were input into Guenther's nonradial, nonadiabatic stellar pulsation program (Guenther 1994). The pulsation program uses the Henyey relaxation method to solve the linearized pulsation equations. Radiative energy gains and losses are accounted for in the Eddington approximation. The nonadiabatic coupling of convection and the oscillations is not taken into account, but based on the results of a thorough investigation by Balmforth (1992a, 1992b, and 1992c) we expect that the perturbation by convection on the p-mode frequencies will be small of similar order to the perturbation due to radiative effects. Regardless, because the nonadiabatic effects are confined to the surface layers they do not affect the second-order spacing parameter.
Because the largest changes to the structure due to variations in G appear in the dense central regions we calculated the p-mode frequencies of the deepest penetrating modes, the l = 0, 1, 2, and 3. Furthermore, we used the small frequency spacings to cancel out most of the surface effects on the frequencies where p-modes are maximally sensitive and where we know our solar model physics to be crudest. Known from asymptotic theory (Tassoul 1980), the small spacing, defined as 
(n, l) 
(n, l) - (n - 1, l + 2), where l is the azimuthal order and n is the radial order of the mode, is very sensitive to the sound speed in the central regions of the star. Indeed, its sensitivity to the interior structure dominates its sensitivity to the surface layers for the lowest l-values.
In Figure 1 we plot the radial variation component of the eigenfunctions of several low-l p-modes. The order and degree of the p-modes are (n = 17, l = 0), (n = 16, l = 2), and (n = 15, l = 4). The plots show, by example, that the small spacing combination of p-modes involves modes whose eigenfunctions are nearly identical throughout all but the most central regions. Notice that the match between (n = 17, l = 0), (n = 16, l = 2), which defines the small spacing (n = 17, l = 0) is better than the match between (n = 16, l = 2), (n = 15, l = 4) which defines (n = 14, l = 2). The match worsens as one goes to higher l-values. Because the combination defined by the small spacing involves p-modes with nearly identical eigenfunctions, except in the deep interior, one expects that the frequencies of the modes will be similar, with the frequency differences depending primarily on the structure near the core. This is not completely true because the amplitudes of the p-modes are several orders of magnitude greater near the surface, so that even small differences between the eigenfunctions in this region can have a measurable effect on the frequencies. Regardless, for the lowest l-value small spacings, this contamination is small enough that the small spacings can be used as an effective probe of the solar core. We do note that as higher l-values are considered, the known errors in the structure of the near surface layers of the solar model, introduce a systematic offset in the frequency differences, noticeable already, in the l = 1 small spacings (see GD for more details and examples).
Fig. 1
We first compare the small spacings in our models to the most recent p-mode frequency averages obtained from the GONG instrument (Harvey et al. 1996). Specifically we use the merged multimonth averaged data set, mrnx951120v1, which contains averaged data from 1995 August 23 to 1996 February 18. Again, because we are interested only in the core, where variations in G have their maximum effect, we focus our attention on only the l = 0, 1, 2, and 3 p-modes for our comparisons. We also compare the small spacings in our models to recent results from BiSON (Chaplin et al. 1996). The BiSON instrument currently provides the most accurate low-l low-frequency p-mode data.
To provide continuity with the p-mode comparisons in DKGN we show in Figure 2 the p-mode frequency differences, model minus observed (from GONG), for selected modes between l = 0100. This plot is provided to illustrate the improvements in the solar model and the p-mode data but will not be used to constrain G variations. Lines connect common l-valued modes. If our solar models were near perfect then, of course, the bundle of lines would tightly lie along a horizontal line passing through 0 Hz on the y-axis. The nonzero slope is known to be a consequence of errors in the surface layers of the solar model due to, among other possibilities, the imperfect mixing length approximation used to model convective energy transport (Demarque, Guenther, & Kim 1997). That the differences between the model and observed frequencies increases as the mode frequency increases is a consequence of the fact that the sensitivity to the outermost layers increases with the frequency of the mode. The tightness of the bundle of lines corresponds to the quality of the fit of the model's interior structure to the Sun. Note that the observational error bars are approximately ±0.1 Hz for p-mode frequencies from 15003000 Hz, hence, are not resolvable on the scale of this plot. In Figure 2a we show the p-mode frequency differences for the 4.55 Gyr reference model calculated for this paper and in Figure 2b we show the p-mode frequency differences for the = 0.0 reference model in DKGN.
Fig. 2
In Figures 3 and 4 we plot small spacing differences, model minus observed, for l = 0 and 1 p-modes. In Figure 3 we have used the GONG data, and in Figure 4 we have used the BiSON data. All the varying G models calculated are shown. The horizontal row of data points with error bars correspond to the sum of the uncertainty in frequency of the two p-modes used to calculate the observed small spacing. Here the high sensitivity of the small spacing to interior structure changes is revealed. The small spacing easily distinguishes the varying G models. We note that for most of the frequency range the up and down fluctuations in the small spacing differences are comparable in magnitude to the errors quoted for the observations. Although the BiSON data are not as extensive as the GONG data, they are more accurate in the frequency region covered. The error bars for the two lowest l = 0 p-modes for GONG (Fig. 3) are probably underestimated. This is suggested not only by the larger disagreement between the model and observations, but also by the very good agreement between the model and the BiSON observations in the same frequency region (Fig. 4). We will ignore the two lowest l = 0 p-modes from GONG in our interpretation of the results.
Fig. 3 
Fig. 4
Taking the observational uncertainties at face value (and ignoring the two lowest l = 0 p-modes from GONG), models with power law variations for G(t) with | | 
0.02 appear inconsistent with the BiSON and GONG data. This corresponds to limiting the time rate of change of G(t) during the past 4.5 Gyr to | (t0) | 1.6 × 10-12 yr-1. Note that because it is clear from the graphs that observational uncertainties still seem to dominate the fit between the models and the data, we have chosen to constrain by utilizing a visual discrimination rather than choosing to do a 
2 analysis or other more sophisticated statistical estimator, which seemed inappropriate at the present time.
Not counting nonstandard assumptions like core mixing, the uncertainty in model p-mode frequencies as a result of uncertainties in the core of the solar model is dominated, as we earlier indicated, by our uncertainty in the solar age as determined from the ages of the oldest meteorites, given as 4.53 ± 0.04 Gyr (GD). In Figures 5a and 5b we plot the small spacing differences, model minus GONG data, for solar models with ages 4.50, 4.55, and 4.60 Gyr (note that all the varying G solar models were evolved to an age of 4.55 Gyr), which comfortably bracket the meteoritic age of the Sun. Clearly, the age uncertainty introduces a variance in the predictions that is less than the current observational uncertainty for GONG data. The age uncertainty is comparable to the observational uncertainty for BiSON data. We therefore suspect that most of the up and down fluctuations in the small spacing differences for GONG are associated with the observational error, especially the two l = 0 p-modes at the lowest frequencies. The small spacing differences for the 4.55 Gyr nonvarying G model, as shown in Figure 4, are within the observational error bar estimates for the BiSON data.
Fig. 5
Over the lifetime of the Sun, the average monotonic variation of G is constrained to (t0) = 0.0 ± 1.6 × 10-12 yr-1, where the error is based on the stated uncertainties associated with the GONG and BiSON data, the uncertainty in the age of the Sun, and the assumption that the uncertainty in the standard solar model core is subdominant. The latter assumption depends primarily on the notion that there is nothing unusual taking place in the core of the present day Sun. While our limit is applied to only monotonic variations, the 30 Myr thermal relaxation timescale of the solar interior probably precludes the possibility of using seismology to test for oscillatory G variations that occur on shorter timescales, as their effect on the interior structure would be smoothed out.
While it is always possible that unknown new physics associated wth the solar core might mask the effect of possible time variation of G, it is unlikely that these effects would conspire to cancel them exactly at a level much larger than the variation associated with the current known uncertainties in the solar model, without introducing disagreement in other ways. Indeed, the great agreement between the current solar model predictions and the data suggest that we cannot be that far off track. In any case, as both data, and solar models improve, the limits derived here should continue to tighten.
We are grateful for the tremendous effort of the GONG and the BiSON group in producing high-quality oscillation data. D. B. G. would like to thank NSERC for their support, and graduate student R. Tanaja for his assistance in carrying out some of the model calculations. L. M. K. would like to thank the DOE for support, and CERN for hospitality while this work was completed.
. 1992b, MNRAS, 255, 632 First citation in article | Crossref | ADS. 1992c, MNRAS, 255, 639 First citation in article | Crossref | ADS
Full image (30kb) | Discussion in textRadial variation r of three different p-modes are plotted as a function of radius fraction x. The radial variation is normalized to 1.0 at the surface (x = 1.0). Because the eigenfunctions of these three p-modes are nearly identical in shape in all but the central regions of the Sun, the differences in their frequencies, which defines the small spacing, depends sensitively on the structure in the deep interior. By analyzing the frequency differences between similar combinations of p-modes one can probe the deepest layers in the Sun. See formal discussion in text.
Full image (31kb) | Discussion in textThe p-mode frequency differences, solar model minus observed (GONG), for a sample of p-modes (l = 0, 2, 3, 10, 20, 30, 40, 50, 60, 80, 100) are plotted opposite the observed frequencies. Lines connect common l-values. The model p-mode frequencies used in (a) were calculated from the reference 4.55 Gyr solar model described in this paper. The model p-mode frequencies used in (b) were calculated from the = 0.0 model used in DKGN. The improved agreement between the model and the observed p-mode frequencies for the circa 1997 solar model compared to the circa 1994 solar model is a direct consequence of the improved equation of state and the inclusion of helium and heavy element diffusion in the 1997 solar model.
Full image (41kb) | Discussion in textThe l = 0 (a) and the l = 1 (b), small spacing differences, solar model minus observed, calculated from the varying G solar models are plotted opposite the observed frequency. The observational data are from GONG. The value of the variation exponent used in the solar model annotates, on the right, the corresponding small spacing differences. The error bars through the row of horizontal data points define the observational error. The heavy solid black line corresponds to the reference, = 0.0, 4.55 Gyr solar model.
Full image (27kb) | Discussion in textSimilar to Fig. 3 except BiSON data are used. Although BiSON data do not cover as extended a frequency range as the low-l GONG data, the error bar estimates for BiSON data are more than a factor of 2 smaller than for GONG.
Full image (30kb) | Discussion in textTo illustrate the error associated with the solar model calculation itself, we show the l = 0 (a) and the l = 1 (b), small spacing differences, solar model minus observed (GONG), for solar models of three different ages, 4.50, 4.55, and 4.60 Gyr (all have = 0.0). The effect on the small spacings of the uncertainty in the age of the Sun is everywhere less than the observational uncertainty in the p-mode frequencies.
|
Xsurf | Zsurf | Age a |  |
X0 | Z0 | CZ (M ) |
CZ (x) |
log Pc | log Tc | log  c |
Xc | Zc |  (37Cl) |
(71Ga) |
| -0.10... | 0.72902 | 0.01814 | 4.55 | 2.012 | 0.69802 | 0.020 | 0.0224 | 0.717 | 17.361 | 7.195 | 2.168 | 0.35933 | 0.02102 | 7.730 | 130 |
| -0.04... | 0.73435 | 0.01807 | 4.55 | 2.056 | 0.70284 | 0.020 | 0.0236 | 0.714 | 17.369 | 7.196 | 2.180 | 0.34554 | 0.02104 | 8.130 | 132 |
| -0.02... | 0.73614 | 0.01804 | 4.55 | 2.072 | 0.70450 | 0.020 | 0.0238 | 0.714 | 17.371 | 7.197 | 2.184 | 0.34065 | 0.02105 | 8.280 | 133 |
| 0.00... | 0.73752 | 0.01803 | 4.50 | 2.079 | 0.70576 | 0.020 | 0.0242 | 0.712 | 17.373 | 7.197 | 2.187 | 0.33781 | 0.02105 | 8.350 | 133 |
| 0.00... | 0.73796 | 0.01802 | 4.55 | 2.088 | 0.70620 | 0.020 | 0.0245 | 0.712 | 17.374 | 7.198 | 2.188 | 0.33563 | 0.02106 | 8.440 | 134 |
| 0.00... | 0.73858 | 0.01801 | 4.60 | 2.096 | 0.70671 | 0.020 | 0.0244 | 0.712 | 17.375 | 7.198 | 2.191 | 0.33302 | 0.02107 | 8.540 | 134 |
| 0.02... | 0.73974 | 0.01799 | 4.55 | 2.104 | 0.70791 | 0.020 | 0.0250 | 0.711 | 17.377 | 7.198 | 2.193 | 0.33042 | 0.02107 | 8.600 | 134 |
| 0.04... | 0.74146 | 0.01796 | 4.55 | 2.120 | 0.70966 | 0.020 | 0.0255 | 0.709 | 17.379 | 7.199 | 2.198 | 0.32507 | 0.02108 | 8.770 | 135 |
| 0.10... | 0.74657 | 0.01796 | 4.55 | 2.170 | 0.71508 | 0.020 | 0.0268 | 0.707 | 17.389 | 7.201 | 2.213 | 0.30808 | 0.02111 | 9.330 | 138 |