THE ASTROPHYSICAL JOURNAL, 482:420–432, 1997 June 10
© 1997. The American Astronomical Society. All rights reserved. Printed in U.S.A.

The End of the Main Sequence

GREGORY LAUGHLIN, 1 PETER BODENHEIMER, 2 AND FRED C. ADAMS 1

Received 1996 August 26; accepted 1996 December 13


ABSTRACT

     We present stellar evolution calculations for the lowest mass stars, i.e., those stars with masses in the range 0.08 M&sun; ≤ M* ≤ 0.25 M&sun;. Our particular emphasis is on the post–main-sequence evolution of these objects. We establish a hydrogen-burning timescale of τH ∼ 1.0 × 1013 years for the minimum-mass main-sequence star. This timescale determines the duration over which the light of our Galaxy is dominated by a conventional stellar contribution. We find that for masses M* < 0.25 M&sun;, stars remain fully convective for a significant fraction of the duration of their evolution. The maintenance of full convection precludes the development of large composition gradients and allows the entire star to build up a large helium mass fraction. We find that stars with masses M < 0.20 M&sun; will never evolve through a red giant stage. After becoming gradually brighter and bluer for trillions of years, these late M dwarfs of today will develop radiative-conductive cores and mild nuclear shell sources; these stars then end their lives as helium white dwarfs. Our work has significant bearing on the general question of why stars become red giants. The fact that the lowest mass stars grow neither red nor giant as they evolve provides an important insight into this problem. Through both analytical and numerical arguments, we have determined that the development of low-mass red giants requires a combination of (1) increasing core luminosity, (2) the existence of molecular weight gradients between the core and the envelope, and (3) the presence of an atmospheric opacity which is an increasing function of temperature. Finally, we discuss the implications of our results with regards to the long-term fate and evolution of the Galaxy.

Subject headings: stars: evolution—stars: interiors—stars: late-type—stars: low-mass, brown dwarfs

FOOTNOTES

     1 Physics Department, University of Michigan, Ann Arbor, MI 48109.

     2 University of California Observatories/Lick Observatory and Board of Studies in Astronomy and Astrophysics, University of California, Santa Cruz, CA 95064.

§1. INTRODUCTION

     The red dwarf stars are a model of persistence. A very large number of Hubble times will come and go before the faintest stars even begin to show outward signs of evolution. As a result, almost no attention has been paid to their less than imminent demise.

     Nevertheless, an investigation into the fate of the M dwarfs does hold a certain intrinsic value. The faintest stars are clearly the most numerous (see, e.g., Henry, Kirkpatrick, & Simons 1994). One can hardly argue that the theory of stellar evolution has a balanced emphasis when the future development of the majority of stars is largely unknown. The lowest mass stars also play an important role in the theory of the future (Islam 1977; Dyson 1979; Adams & Laughlin 1996). Furthermore, and from a more practical standpoint, evolving M stars provide useful insights into stellar evolution in general. In particular, they can help to clarify the still controversial question of why higher mass stars evolve into red giants (e.g., Whitworth 1989; Renzini et al. 1992; Faulkner 1997). If one wishes to understand why heavier stars develop red giant structures, it is helpful to take a careful look at why the lowest mass stars do not.

     Considerable effort has gone into refining both the observations and the theoretical models of M dwarfs on the main sequence. For a recent review of the observational status, see Burrows & Liebert (1994). Starting with the efforts of Kumar (1963), successive authors have sought to improve the theoretical main-sequence models, with an eye toward providing agreement with the observed properties. Realistic M dwarf models still present a difficult problem. The physics required to an accurate treatment is quite complex, and at times somewhat uncertain. Thirty years ago, when the classical field of numerical stellar evolution was being established (for a revew, see Iben 1967, 1974), the physical uncertainties were simply too large to say much about the evolution of M stars with any degree of confidence. The situation is quite different now. The present degree of knowledge is secure to the degree that the general trend of evolution which we discuss, and even many of the specific points, should be on solid ground.

     The organization of this paper is as follows. In the next section, § 2, we outline the basic physics and assumptions employed in our stellar evolution code. In § 3, we describe our main-sequence model and make comparisons with the recent low-mass stellar models in the literature (Burrows et al. 1993). We then go on to provide a detailed description of the entire course of evolution of a model 0.1 M&sun; star. Next we describe the change in character of evolution for models spanning the mass range 0.06 M&sun; ≤ M* ≤ 0.25 M&sun;. The results obtained from these calculations are then used to motivate a discussion in § 4 regarding the gradual transition to red giant structures that occurs in evolving stars over the mass range 0.16 M&sun; ≤ M* ≤ 0.20 M&sun;. In the last section, § 5, we put our results in a broader perspective and review our main conclusions.

§2. ASSUMPTIONS AND MODEL PHYSICS

§2.1. The Stellar Evolution Code

     Many papers have considered the pre–main-sequence and main-sequence structure of M stars. A partial list might include the efforts of Kumar (1963), Copeland, Jensen & Jorgensen (1970), and Grossman & Graboske (1971), as well as more recent studies with updated physics, such as those by Burrows, Hubbard, & Lunine (1989), Burrows et al. (1993), Laughlin & Bodenheimer (1993, hereafter LB93), D'Antona & Mazzitelli (1985, 1986, 1994, and Baraffe et al. (1995).

     In this investigation, we have used a set of input physics similar to that employed by other workers studying low-mass stars. Specifically, our code incorporates the Lagrangian Henyey scheme (Henyey, Forbes, & Gould 1964) to evolve the equations of stellar structure. The overall computational routine is an updated version of the program employed in LB93. The initial chemical composition is solar.

     The equation of state in the nonideal partially degenerate regime is computed from a mass-weighted average of the hydrogen and helium tables published by Saumon, Chabrier, & Van Horn (1995). Low-mass main-sequence stars and brown dwarfs tend to be convective throughout the bulk of their structure. Where convection is present, we assume that the adiabatic gradient is capable of transporting the entire flux of energy. At an outer fitting point, the interior solution is matched to a radiative/convective model atmosphere, which defines the photospheric structure. Nonadiabatic convection in the atmospheric layers is treated with a mixing-length prescription. Radiative opacities for the high-temperature interior are taken from the Weiss, Keady, & Magee (1990) formulations of the Los Alamos opacities, with linear interpolation between the hydrogen-rich King IVa table and the helium-rich Ross-Aller 2 table. These opacities were employed because they are tabulated for higher densities than the more recent OPAL tables. In the deep interiors of low-mass stars, at late evolutionary stages, electron conduction becomes increasingly capable of transporting appreciable amounts of energy. We account for this process by employing the Hubbard & Lampe (1969) tables for hydrogen- and helium-rich mixtures.

     Low-temperature opacities represent a decisive factor in the overall structure of stars at the bottom of the main sequence. At temperatures below 5000 K, hardy molecules such as CO begin to provide opacity, and as temperatures decline, a bewildering variety of molecular species contribute, notably H2O. Opacities drop rapidly in the temperature range 5000–2000 K, then rise very rapidly with decreasing T as refractory grains begin to contribute. Our molecular opacity tables for the solar composition are taken from Alexander, Johnson, & Rypma (1983) and supplemented in the low-temperature region by the grain and ice tabulations of Pollack, McKay, & Christofferson (1985).

     Nuclear reaction cross sections and energy generation rates are implemented using the prescriptions of Bahcall (1989). For interior temperatures less than Tc &ap; 8 × 106 K, the PPI chain does not reach equilibrium on timescales of interest, and the reaction rates of the p + p reaction and of 3He + 3He → 4He + 2p are therefore taken separately into account. As a result, in the temperature range (3–5) × 106 K, the mass fraction of 3He tends to increase with time. At temperatures higher than 8 × 106 K, the PPI chain is assumed to be in equilibrium. When the interior temperatures exceed 15 × 106 K, the PPII and PPIII reaction chains begin to make a significant contribution to the overall energy budget. The branching ratios are taken into account using the prescription of Parker, Bahcall, & Fowler (1964). In our set of calculations, these corrections come into play only in highly evolved central mixtures that are almost entirely helium. At still higher temperatures (T > 2 × 107 K) the CNO cycle is relevant and is taken into account.

     Ion screening contributes to increased reaction rates in the relatively low-temperature, high-density cores of low-mass main-sequence stars. Weak and intermediate screening are accounted for in the PPI chain using the prescription of Graboske et al. (1973).

§2.2. Major Uncertainties

     It is important to point out that our calculations encompass a number of uncertainties, some of which are endemic to the main-sequence models and others that come into play as the M stars evolve. The first major source of inaccuracy and uncertainty is associated with the gray model atmosphere and the use of Rosseland mean rather than frequency-dependent opacities. The spectra of M stars bear only a rather faint resemblance to blackbodies, and are fraught with thick molecular absorption lines, back-warming, and other serious complications. Significant progress with nongray model atmospheres for M dwarfs is now being made (e.g., Allard & Hauschildt 1995), but fresh problems arise when one considers the gradual transition to the helium-rich atmospheres which today's red dwarfs will eventually acquire.

     The problem of frequency-dependent radiative transfer in the atmosphere brings out a second shortcoming in our models, namely the lack of molecular and grain opacity tables for mixtures with depleted hydrogen fractions. One expects that within a given star, the future scarcity of hydrogen will lead to increased transparency at a given temperature and density because of the nonreactivity of helium and the absence of absorbing molecules such as water and methane. We account in an ad hoc fashion for this general decrease by using an opacity function of the form



which is invoked at temperatures lower than the minimum temperatures tabulated by Weiss et al. (1990) for their helium-rich mixture, that is, in the atmospheric layers only. We have experimented with various other prescriptions, and have found only quantitative rather than qualitative differences in the timescale and future course of evolution.

     A third source of uncertainty is the question of long-term mass loss, a phenomenon which our evolutionary models do not consider. Low-mass stars are known to produce significant coronal activity, as exhibited by numerous X-ray flares. Stellar winds almost certainly result from this activity, but the amount of mass that they carry away is unknown. The depletion associated with such winds may be important for evolution that encompasses many Hubble times. Salpeter (1982) has considered the issue of mass loss from M dwarfs, and although he was not able to reach a firm conclusion, he proffered the opinion that the smallest stars will not be significantly depleted during the course of hydrogen burning. Salpeter also pointed out that in order to constrain the possible mass loss from these stars, one can use limits on the observed abundance of 3He in the interstellar medium. If low-mass stars experience large amounts of mass loss, they will significantly enrich the interstellar medium with 3He.

     Expressed as a mass fraction, the observed abundance of 3He in the interstellar medium is X3 &ap; 4 × 10-5 (see the recent measurements from the Ulysses satellite; Gloeckler & Geiss 1996). The current predictions of big bang nucleosynthesis (e.g., Walker et al. 1991; Kolb & Turner 1990; Yang et al. 1984) can be made consistent with this abundance for some part of the allowed range of baryon-to-photon ratios η (Steigman & Tosi 1995). As a result, no enrichment of 3He need have come from the low-mass stars; in particular, the abundance [D + 3He] seems to be constant over the age of the solar system (see Turner et al. 1996). We can work the problem the other way by assuming that all of the observed 3He is the result of mass-loss from red dwarfs. Constructing an argument analogous to that of Salpeter (1982), we can find a limit on the mass fraction g ejected by a typical low-mass star during a Hubble time (which we take to be 1010 yr). Assuming that most stars are about half the age of the galaxy and that the fraction of the mass of a star processed into 3He during a Hubble time is f = 0.003, we find the limit.



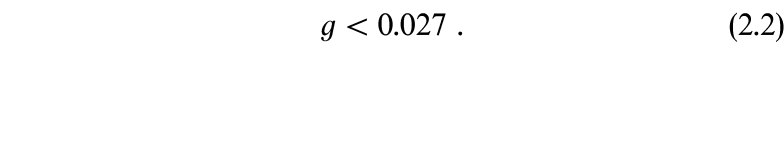
     This limit is quite conservative; the true constraint will be much tighter than that obtained above. Red giants belch significant quantities of 3He into the interstellar medium. In addition, no 3He enrichment is actually observed. Thus, although some uncertainties remain, the rough argument given here clearly indicates that the M dwarfs are not a transient population in the midst of furiously boiling away.

§3. THE EVOLUTION OF M STARS

     Given the basic stellar evolution model described above, it is possible to determine the long-term fate and evolution of low-mass stars. The main focus of our discussion concerns the post–main-sequence evolution of these objects (see § 3.2 and § 3.3), although we briefly remark on the main-sequence properties (§ 3.1).

§3.1. Main-Sequence Properties

     Because a number of groups (including our own) have extensively studied the pre–main-sequence and main-sequence properties of M dwarfs and brown dwarfs, we have not made this task a priority in the current paper. The properties of our main-sequence model are similar in all respects to the main-sequence model B discussed in LB93. In particular, the position of the present model on the Hertzsprung-Russell and mass-luminosity diagrams is essentially the same as that of the LB93 model. The only major difference in input physics at the main-sequence stage between the present model and the LB93 model B is the inclusion of new equations of state for hydrogen and helium (from Saumon et al. 1995). An interesting result of the inclusion of this new, more sophisticated equation of state is that it reproduces, in a physically justifiable manner, the effects of the ad hoc softening in the non-ideal regime carried out by LB93 on the older equation of state calculations by Fontaine, Graboske, & Van Horn (1977).

     Likewise, none of LB93's conclusions regarding the mass and luminosity functions of low-mass stars would be materially changed if they were recomputed with the present model. The main-sequence model in the current calculations is compared with that of Burrows et al. (1993) in Table 1.

     As discussed in LB93, the previously computed model B and (by extension) the model of this paper compare quite favorably with observed M stars plotted on the Hertzsprung-Russell diagram. For instance, Leggett, Harris, & Dahn (1994) found that the LB93 model B provides a considerably better fit to their aggregate of low-mass Hyads than does the Burrows et al. (1993) model. Of course, such fits require the applications of bolometric corrections in order to translate observed photometric properties into luminosities and effective temperatures. In the case of the M dwarfs, these corrections are notoriously difficult (see Kirkpatrick et al. 1993). Different corrections can change the quality of the fits. Furthermore, our main-sequence model does not fit the observed mass-luminosity diagram as well as the model of Burrows et al. (1993). Our stars tend to be somewhat underluminous at a given mass. For a further evaluation of these issues, the reader is referred to the discussion in LB93. In any case, our main-sequence model is adequate for our present purposes. We are primarily concerned with the general trend of post–main-sequence evolution. Further improvements in the agreement between M dwarf main-sequence models and observations are now being made largely through the incorporation of sophisticated frequency-dependent model atmospheres into the evolutionary sequences. See for example, Baraffe et al. (1995), and Chabrier, Baraffe, & Plez (1996).

§3.2. Post–Main-Sequence Evolution

     Figure 1 charts the more than 6 × 1012 yr life of a 0.1 M&sun; star in the Hertzsprung-Russell diagram. After condensing out of a molecular cloud core, the star descends the convective Hayashi track and arrives on the zero-age main sequence, defined as the point where nuclear reactions first contribute 100% of the star's radiated luminosity. Primordial deuterium burning and the “deuterium main sequence” phase have been neglected. At the zero-age main sequence point, which occurs after 2 Gyr of contraction, the star has a photospheric temperature of T* = 2228 K and a luminosity of log10 [L*/L&sun;] = -3.38.

Fig. 1

     Upon reaching the main sequence, the evolutionary timescale slows dramatically, and the star suffers only extraordinarily slow and gradual signs of aging. For the first trillion years, the mass fraction contained in 3He increases steadily. The mass fraction of hydrogen and the two helium isotopes are displayed in the inset chart in Figure 1, which plots core composition as a function of time. Because the 0.10 M&sun; star is completely convective, 3He produced in the core is mixed throughout the entire structure. The star thus maintains a homogeneous composition while increasing its average molecular weight, and consequently grows steadily hotter and more luminous. After 1.38 × 1012 yr, the star has a mass fraction in 3He of 9.95%, which constitutes a maximum value. At this moment, the central temperature is 4.8 × 106 K. At later times, the 3He is consumed faster than it is produced and the mass fraction declines.

     The buildup of 3He has an interesting effect on the star. As 3He accumulates, the nuclear energy generation rate at a particular temperature and density increases. The core is therefore able to expand and steadily reduce its density, even in the face of a slowly increasing total luminosity. As the hydrogen mass fraction of the star drops from its initial value of XH = 0.7 to XH = 0.5, the central density decreases from 309 to 204 gm cm-3. The temperature in the core during this epoch rises slowly from 4.4 to 5.1 million kelvins.

     Between 1.5 and 4 Gyr, the mass fraction of 3He declines steadily, eventually reaching the structurally negligible values associated with equilibrium PPI burning. During this broad main-sequence phase, the star is methodically turning itself into 4He. After 3.05 Gyr, 4He comes to dominate the mass fraction. At this point the photosphere has heated to a temperature of T* = 2500 K and the luminosity is just less than 0.1% of the current solar value.

     As the amount of available hydrogen per gram diminishes, the energy generation rate at a particular temperature and density declines. The central regions are compelled to grow denser and hotter in order to satisfy the energy demands of the star. After 5.74 Gyr, the star contains only 16% hydrogen by mass, the surface temperature is T* = 3450 K, and the luminosity is log10 [L*/L&sun;] = -2.54. This point represents a critical juncture in the evolution of the star. The increasing helium fraction lowers the opacity to the point where radiative transport is capable of transmitting the energy flux, and convection ceases in the center. This development of a radiative core, which soon spreads through the nuclear burning region, almost immediately fixes the composition of the envelope. The unchanging envelope composition in turn allows for the development of a mild composition inhomogeneity, as the remaining hydrogen in the radiative core is rapidly converted into helium. The development of the radiative core causes the entire star to contract slightly and produces a mild but sudden decline in luminosity. This behavior can be seen on the evolutionary track in the Hertzsprung-Russell diagram.

     Once the radiative core has developed, the near-eternal youth of the star draws to a close, and the evolutionary timescale accelerates. The central regions become isothermal as hydrogen is exhausted, and the core steadily increases in mass as a modest nuclear shell source works its way outward through the star. The shell-burning source is located within the radiative region of the star, and so the envelope composition continues to remain fixed. The evolution of the star in the H-R diagram during this phase is toward rapidly higher temperatures. The unassuming 0.10 M&sun; red dwarf stars of today will eventually grow hotter than the current Sun, although they will never be more than ∼1% as bright. Evolution to higher temperatures occurs because the whole star contracts in order to keep the nuclear energy generation going at a sufficient rate. In a certain respect, the evolution during this period resembles the Henyey radiative contraction phase that our own Sun experienced during its final stage of pre–main-sequence evolution.

     When the core temperature reaches 12 million kelvins, the center of the star derives the majority of its support from degeneracy pressure, and conductive transport begins to dominate. In this degenerate regime, further contraction does not lead to higher temperatures, and both the overall luminosity of the star and the central temperature begin to decline. The star continues to be driven to higher surface temperatures over the next several billion years as it continues to contract, but eventually the surface temperature also reaches a maximum (T* = 5807 K). After this point, the star “turns the corner” in the Hertzsprung-Russell diagram, i.e., it begins to evolve toward lower luminosity and lower surface temperature.

     Interestingly, the shell source is still active at this point, and nuclear reactions are able to provide nearly all of the steadily declining luminosity during a protracted phase of further contraction. Slowly, the shell source is extinguished, and the star ends its life as a cooling, low-mass helium white dwarf with a moderately enriched (15.5%) hydrogen envelope. The envelope composition masks the incredible overall efficiency of the low-mass stars; the overall final hydrogen mass fraction is just more than 1%. It is interesting to point out that similar low-mass helium degenerates actually exist today. They can result from particularly rapacious binary evolution processes in systems containing much more massive stars. Our calculations follow the helium white dwarf along its cooling curve to a luminosity of log10 [L*/L&sun;] = -5.287 and a surface temperature of T* = 1651 K, conditions which prevail 540 billion years after the star first develops its radiative core. The total nuclear burning lifetime of the star is somewhat more than 6 trillion years.

     The foregoing life story of a 0.1 M&sun; red dwarf illustrates that the future evolution of low-mass M stars seems quite securely determined (within the model-dependent assumptions). The major uncertainties inherent in red giant mass loss which hamper deterministic calculations for higher mass stars are avoided. The smallest stars will ultimately be very efficient at turning their allotment of hydrogen into helium. Over the long term, they will make much better use of their initial resources than the evolving stars of today.

     The future course of evolution for a 0.1 M&sun; star is placed in perspective by Figure 2, which is a Hertzsprung-Russell diagram showing the evolution of stars ranging from 0.06 to 0.25 M&sun;. The 0.06 M&sun; object lies beneath the threshold for equilibrium hydrogen burning, and thus rapidly cools and fades away along the hydrogen brown dwarf branch. The figure shows that the general trend of evolution for stars with masses between 0.08 M&sun; and 0.16 M&sun; is quite similar to the 0.10 M&sun; case described above. The models are mainly delineated by increasingly dramatic blueward excursions following the first appearance of a radiative core. Furthermore, as the masses of the stars increase, radiative cores appear at progressively earlier times in the evolution, endowing the final dwarfs with progressively richer concentrations of unburned hydrogen in their outer layers. This point will be taken up in more detail below.

Fig. 2

     The mass range in the vicinity of 0.16 ≤ M*/M&sun; ≤ 0.20 is an important transition in the theory of stellar structure. Upon achieving core degeneracy, these stars continue to increase their core temperatures. Rising core temperatures are associated with increasing luminosity generation in the overlying shell sources, and hence a mounting luminosity for the entire star as the shell source burns its way outwards. It is this rising luminosity which ultimately fuels the ascent of higher mass stars up the red giant branch. The core temperature trend is delineated in Figure 3, which plots central temperature versus the central density for a range of models under discussion.

Fig. 3

     In connection with their increased luminosity output, the transitional stars in the 0.16 ≤ M*/M&sun; ≤ 0.20 mass range are able to produce increasingly larger expansions of the overall stellar radius after the radiative hydrogen-exhausted core has developed. This growing ability to swell is illustrated in Figure 4, which charts stellar radius as a function of time for evolutionary sequences of eight different masses. The factor of expansion relative to the radius of the star at the point where the radiative-conductive core first appears is also logged in Table 2, which correlates the maximum expansion factor with the final hydrogen fraction present in the envelope.

Fig. 4

     Our M* = 0.25 M&sun; model develops a radiative core before its hydrogen fraction has dropped below XH = 0.5. A one-quarter solar mass star will increase its radius by more than a factor of ten, and its track in the Hertzsprung-Russell diagram (see Fig. 2) is very reminiscent of a classic ascent up the giant branch. Indeed, when confronted with the later evolution of the 0.25 M&sun; model the Henyey code was plagued with a drastically decreasing time step which put a stop to further computational progress. This particular obstacle is one which methods such as the Eggleton (1971) scheme were designed to circumvent. We therefore declare that the lowest mass red giant has a mass of M* &ap; 0.25 M&sun;. This cutoff is of course slightly arbitrary. Figure 2 shows that the transition between low-mass stars that do not become red giants and the somewhat higher mass stars that do is not completely sharp (see also the discussion of § 4).

§3.3. Additional Features of Post–Main-Sequence Evolution

     Within the computed collective fate of the low-mass stars there are some interesting features of evolution. For instance, it is clear from the Hertzsprung-Russell diagram (Fig. 2) that the 0.14 and 0.16 M&sun; stars experience protracted periods during which their luminosity is relatively constant in the face of slow increases in the temperature. For example, as the hydrogen burning nuclear shell source methodically consumes the 30% hydrogen envelope, the 0.16 M&sun; star will take a leisurely 5.5 Gyr to increase its luminosity from L* = 0.10 to 0.27 L&sun;. Given the example of the Earth, it seems quite possible that these phases would allow ample time for life to evolve on any appropriately situated terrestrial planets. Before this epoch, these planets would have languished in cold storage as their primary stars churned through trillions of years of fully convective main-sequence evolution.

     Another curious aspect of evolution is seen in the central temperature versus central density diagram (Fig. 3). For stars in the transitional mass range 0.16 M&sun; ≤ M* ≤ 0.25 M&sun;, the arrival on the main sequence is characterized by a temporary maximum in both central temperature and central density. As 3He builds up in the core, the efficiency of nuclear energy generation per gram of material increases. In order to maintain equilibrium, we find numerically that the stars respond to this fuel enrichment by slowly expanding and cooling their cores.

§4. RED GIANTS

     Although it is widely known that many stars become red giants during their post–main-sequence evolution, the nature of the exact physical mechanism which drives the development of red giants is the subject of lively, and occasionally heated, debate. Many detailed studies of the problem have been made (see, e.g., Iben & Renzini 1984; Whitworth 1989; Eggleton & Cannon 1991; Renzini et al. 1992), but a simple physical explanation of the phenomenon is still lacking (see, e.g., Hansen & Kawaler 1994 and Kippenhahn & Weigert 1990 for further discussion of this issue). In this work, we obtain a fresh perspective on the problem by considering stars of very low mass. The limiting case of stellar evolution is vital to understanding red giants, because stars of sufficiently low mass grow neither red nor giant. The faintest stars evolve by becoming increasingly hotter while remaining small, i.e., they become “blue dwarfs”. Here, within the context of general arguments, simple analytic models, and numerical experiments, we argue that the lowest mass red giants arise from a combination of (1) a rapidly rising core luminosity, (2) a compositional gradient between the core and the envelope, and (3) the existence of a photospheric opacity which increases with temperature.

§4.1. Rising Luminosity

     At the most basic level, the development of red giants is linked to the fact that increasingly massive stars will produce progressively larger luminosity increases. During the course of evolution, a 0.08 M&sun; star will increase in luminosity by only a factor of ∼15. A 0.16 M&sun; star produces a 140-fold luminosity increase, whereas a 0.25 M&sun; star will increase in brightness by a factor of close to a thousand (see Fig. 2). The large luminosity increases in the heavier stars are due to the fact that they can produce more massive helium cores as evolution proceeds. Because of degeneracy, the more massive cores are denser and physically smaller. These properties lead inexorably to an increase in core temperature with increasing mass (see Fig. 3), and hence to larger luminosities from the active nuclear shell sources. These luminosities are intrinsic to the masses of the helium cores, and are largely independent of the overlying envelope composition.

§4.2. Compositional Gradients

     One significant result of our stellar evolutionary calculations is the discovery that the nuclear burning regions of the late M stars will all eventually switch from being convective to being radiative.

     The eventual appearance of radiative cores in all low-mass stars capable of burning hydrogen means that all stars eventually develop the most basic property inherent to red giants, namely an isothermal helium core surrounded by an actively burning hydrogen shell source. As one progresses to higher and higher masses, stars are able to burn relatively less of their hydrogen during the fully convective phase; as a result, the molecular weight discontinuity across the shell sources becomes steadily larger. As emphasized by Whitworth (1989) and Faulkner (1997), inhomogeneous core/envelope configurations provide structural conditions that predispose stars toward giant-like configurations. Indeed, as indicated by both Figure 4 and Table 1, the increasing hydrogen fraction of the envelope is correlated with the increasing ability to expand the envelope.

     The role of composition, in particular the molecular weight gradient, in determining the envelope expansion can be illustrated by an alternative sequence of stellar models. We have taken two additional M* = 0.20 M&sun; stars, and increased their initial helium fraction well beyond the standard abundance from big bang nucleosynthesis. The first alternate star has an initial hydrogen fraction of 20%, and the second alternate star has an initial hydrogen fraction of only 10%. These models are to be compared with our standard M* = 0.20 M&sun; model, which has worked itself down to 37% hydrogen at the point when the radiative core first appears.

     Because of their high helium content, the two alternate stars experience radiative energy transport in the center from the start. They exhaust their central reserve of hydrogen and soon develop degenerate isothermal helium cores. The three 0.20 M&sun; stars thus form a sequence of envelope/core models with decreasing molecular weight gradients, and hence provide a framework for testing the dependence of both radial expansion and luminosity on envelope composition. Figure 5 plots the stellar radius versus the luminosity for these three models. The general trend of evolution is from left to right, i.e., from lower luminosity to higher luminosity. The depleted hydrogen models start their evolution at considerably larger luminosities, but all three stars show comparable luminosities for a given core mass. Nevertheless, the depleted models experience much smaller increases in radius. This behavior indicates that the overall luminosity of the stars is determined by the contracting core, and has relatively little to do with the composition gradient between the core and the envelope. Larger compositional gradients appear to be a vital element in determining the relative ability of the star to expand.

Fig. 5

§4.3. Photospheric Opacity

     In equilibrium, the internal luminosity L* of the star is radiated into space. The surface properties of the star obey the usual relation



where R* is the stellar radius, T* is the effective surface temperature, and σB is the Stefan-Boltzmann constant. Faced with the increasing luminosity described above, a star in equilibrium must either increase its radius or increase its temperature (or both). Numerically we find that very low mass stars, M* ∼ 0.1 M&sun;, become blue dwarfs, i.e., they increase their temperatures. On the other hand, higher mass stars M&sun; ∼ 0.25 M&sun;, tend to increase their radius and keep the temperature roughly constant. The star could also depart from equilibrium; this point is taken up below.

     Near the stellar surface, convection must become superadiabatic, and hence increasingly ineffective. Stars have no choice but to radiate from their photospheres. The consequences of this requirement are shown in Figure 6, where we plot the evolution of the M* = 0.06, 0.08, 0.10, 0.12, 0.16, and 0.25 M&sun; models as a function of their photospheric densities and temperatures. The size of a point corresponding to a converged model is in direct proportion to the stellar radius. The expansion of the M* = 0.25 M&sun; model as it becomes a red giant is dramatically visible. The hydrogen-rich opacity table has been plotted as a gray-scale backdrop to the diagram; darker regions correspond to larger opacities. The general increase in opacity toward the top of the diagram is due to H- and hydrogen ionization, whereas the opaque region below log10T &ap; 3.3 is due to molecules and grains. This figure demonstrates that in order to achieve efficient radiation, there is a general overall tendency for evolving stars to adjust their envelope structure so as to occupy more transparent regions in the photospheric ρ-T diagram.

Fig. 6

     If the opacity in the stellar photosphere is a sharply increasing function of temperature, then the requirement that the star is in equilibrium as well as radiating from its photosphere implies an effective upper bound



for the photosphere. Once the star is in a configuration where the photospheric temperature is approaching Tmax, the star has no choice but to increase its radius rather than increase its temperature. In this manner the opacity controls, in part, when a star becomes a red giant.

     The maximum temperature Tmax is determined by the opacity, which, in evolving low-mass stars, is strongly dependent on the relative hydrogen fraction in the atmosphere. Our evolutionary calculations show that as the overall stellar mass increases, radiative cores appear earlier and earlier in the course of stellar evolution and lock in progressively larger hydrogen fractions in the stellar envelope. The net effect is that the higher mass stars end up with increasingly hydrogen-rich atmospheres, and hence see large photospheric increases in opacity as the temperature rises from 3000 to 104 K, sufficient to enhance the development of red giant structures once the stellar mass is on the order of 0.25 M&sun;.

     The foregoing argument focuses on the role of photospheric opacity and does not take into account the possibilities of departures from thermal equilibrium. In the present context, departures from equilibrium imply that the star is generating more energy than it can radiate away from its surface. This state of affairs implies that the thermal energy of the star must increase; this increase, in turn, will tend to make the star larger.

     Indeed, Renzini et al. (1992) have identified the very rapid inflation of high-mass stars from main-sequence to red giant dimensions with a broadly similar opacity-driven departure from thermal equilibrium. In their picture, rising core luminosity leads to expansion and increasing opacity in the lower radiative envelope. The larger opacity spurs local departures from thermal equilibrium, resulting in the rapid expansion of the star in the context of a thermal runaway. (In a further broad similarity with our low-mass stars, the opacity-driven effect is not the entire story: a 15 M&sun; evolutionary sequence by Weiss [1989] with constant opacity throughout the star is observed to evolve into a red giant. However, the constant opacity star is less inclined to become a giant in the sense that at a given luminosity, a realistic 15 M&sun; model has a much larger radius than Weiss's [1989] constant opacity star.)

     In the descriptive picture given above, we have identified the importance of a photospheric opacity “wall” in prompting the development of red giants. The overall effect of the opacity “wall” can also be obtained from the usual equations of stellar structure. In the outermost part of the star, we consider the final transfer of energy outward to be described by the radiation conduction approximation for stellar structure, i.e.,



where the temperature T, the opacity κ, and the density ρ have their photospheric values. Following Renzini et al. (1992), we remove the dependence on the temperature gradient by using the equation of hydrostatic equilibrium, which can be written in the form



where n is an effective polytropic index which characterizes the physical structure of the star (see also Schwarzschild 1958). As a rough approximation, we consider the index n to be nearly constant in time for a given star (an assumption also made by Renzini et al. 1992). Here Rg is the gas constant and μ is the mean molecular weight of the gas in the stellar envelope.

     Combining the above two equations, we obtain an expression for the stellar luminosity,



In this simple model, we assume that this expression applies at the stellar photosphere, so that all quantities are to be evaluated at the surface of the star. Notice also that we have grouped the factors in a particular manner. The first group contains numerical constants, the second contains physical constants. The third group contains physical quantities that are (nearly) constant for a given star, whereas the final group contains those quantities which change as the star expands and/or contracts.

     It will be useful to assume that the opacity κ can be written in the simple power-law form



where C is a constant. Notice that we have written the opacity as an increasing function of temperature T; this dependence is valid for the regime of interest (see Fig. 6). In addition, we are interested in the stellar radius R* rather than the photospheric density ρ. For a uniform-density sphere, these quantities are simply related &parl0;ρ∝M$\mathstrut{_{*}}$/R$\mathstrut{^{3}_{*}}$&parr0;; here we take into account possible departures from this simple law by using the more general relation



     Using the form (4.6) for the opacity and the ansatz (4.7), we can expand expression (4.5) for the luminosity in the form



Similarly, using the photospheric boundary condition (4.1), we obtain a second second expression of the form



After a bit of rearrangement, we can solve these two equations to obtain



and



     These results suggest that as the luminosity increases, both the surface temperature and the stellar radius tend to increase (and the photospheric density tends to decrease). This predicted behavior is consistent with that shown in the photospheric ρ-T diagram for the numerical models (see Fig. 5). In the limit that the opacity is a very strongly increasing function of temperature (i.e., the “opacity wall” concept), the index ω → ∞. In this limit, the above expressions (4.10) and (4.11) imply that ΔT*/T* → 0 and ΔR*/R* → γ-1(ΔL*/L*). In other words, in this limit, as the luminosity increases, the stellar radius must increase, and the surface temperature cannot increase. These conditions describe the ascent of a star up the red giant branch.

     The idea that the photospheric opacity can effectively enforce a maximum surface temperature in evolving low-mass stars can be verified by an illustrative numerical experiment: we employ a stellar model with mass M* = 0.25 M&sun; and we approximate the opacity with a very steeply increasing function of temperature for sufficiently high temperatures. In particular, for T > TI, we replace the true photospheric opacity (from our opacity tables) with a simple function of the form



where the temperature scale TW determines the rate at which opacity increases with temperature. The transition temperature TI is taken to be 3500 K, corresponding roughly to the minimum of the opacity function plotted in Figure 5. As the scale TW decreases, the stellar photosphere experiences an increasingly harder opacity “wall”, in which in turn enforces a maximum photospheric temperature.

     As argued above, the existence of a rapidly increasing photospheric opacity as a function of temperature should be necessary for an ascent up the red giant branch. The result of this experiment is shown in the H-R diagram of Figure 7, where we plot the evolutionary tracks of a 0.25 M&sun; star for various values of the scale TW. For large values of the scale TW, the opacity is considerably less than what will be found in a realistic star, and is indeed insufficient to enforce a maximum temperature. For the case with TW = 8000, the photospheric opacity is very nearly constant. The star evolves steadily to higher surface temperatures and thus becomes a blue dwarf. In the opposite limit, for small values of the scale TW, the opacity wall becomes very hard and thus strongly enforces a maximum temperature; the star responds by evolving upward in the H-R diagram and becoming a red giant. The behavior of the tracks shown in Figure 7 is fully consistent with both the general argument and the simple analytic model presented above.

Fig. 7

§5. DISCUSSION

     Although the study of evolving M dwarfs involves timescales much longer than the current age of the universe, there are several compelling reasons for examining the future of these low-mass stars. Because the low-mass stars are the most numerous, one can argue that the theory of stellar evolution is incomplete until the long-term evolution of the majority of stars has been calculated. The future of the galaxy will also be determined by the properties of these low-mass stars. In a more practical vein, evolving M stars clarify the process by which stars make the transition to red giant structures.

§5.1. Summary of Results

     The main results of this paper can be summarized as follows.

     1. This paper calculates for the first time the long-term fate and evolution of the lowest mass stars, i.e., those stars with masses in the range 0.08 M&sun; ≤ M* ≤ 0.25 M&sun; (see Figs. 1 and 2).

     2. We have established evolutionary timescale estimates for the M stars. With our set of input physics, the lowest mass star, M* = 0.08 M&sun;, has a main-sequence lifetime of τMS ∼ 1 × 1013 yr. This timescale decreases to τMS &ap; 1012 yr for a star with mass M* = 0.20 M&sun;.

     3. This paper shows that stars of sufficiently low mass, M* < 0.16 M&sun;, will never become red giants. Stars in the mass range 0.16 M&sun; ≤ M* ≤ 0.25 M&sun; represent a transitional class which display some red giant-like properties, but abort their ascent up the red giant branch before becoming either very red or very large. On the other hand, stars with masses M* > 0.25 M&sun;, but less than a yet to be determined mass scale near 0.50 M&sun; (determined by the red giant mass-loss rate) evolve to become red giants, but do not reach the tip of the red giant branch.

     4. This paper also sheds light on the physical mechanisms which cause low-mass stars to become red giants (see Figs. 4–7). Red giant structures arise through a combination of the increasing luminosity produced by the stellar interior and increasing compositional gradients across the boundary of the core-envelope structure. The luminosity is generally an increasing function of time and tends to cause both the surface temperature and the stellar radius to increase. Increasing composition inhomogeneities appear to predispose heavier evolved stars (those with mass M > 0.16 M&sun;) toward expansion. When the photospheric opacity is a sufficiently steeply increasing function of temperature, an effective maximum temperature is enforced on the stellar surface. When this maximum occurs, the star increases its radius (at essentially constant or declining temperature) and thereby becomes a red giant.

§5.2. Implications for the Future of the Galaxy

     The evolution of the low-mass stars has important ramifications for the evolution of the galaxy on timescales that greatly exceed the current age of the universe. The overall luminosity of the galaxy is determined by two competing effects. The first is that the luminosity of main-sequence stars is an increasing function of time. As discussed above, this feature of stellar evolution is an important part of the process by which stars become red giants. The second effect is that the star formation rate, and hence the total number of stars, is expected to be a decreasing function of time over the long timescales considered in this section (see. e.g., Kennicutt, Tamblyn, & Congdon 1995). These two effects tend to cancel and the luminosity of the galaxy will remain very roughly comparable to its present-day value over the time range τ < 1013 yr. After that time, when the lowest mass stars have completed their post–main-sequence evolution and have begun their descent as helium white dwarfs, the luminosity of the galaxy will plummet precipitously.

     The luminosity of the dying stars, which will be in the form of white dwarfs, need not fall to zero. The capture and subsequent annihilation of halo dark matter will keep these stars much hotter than they would be otherwise (see Adams & Laughlin 1996). The white dwarfs produced in stellar evolution will maintain an effective luminosity of L* ∼ 10-12 L&sun; and a surface temperature of T* ∼ 63 K for a timescale up to τ ∼ 1025 yr. As a result, an entire galaxy of such stars will have a total combined luminosity roughly comparable to that of today's Sun.

§5.3. Future Work

     Although this paper gives an overall view of very low mass stellar evolution down to the end of the main sequence, several higher order issues remain to be studied. First, it will be interesting to examine the post–main-sequence evolution of stars in the 0.25–0.50 M&sun; range. Such an investigation will set the minimum star mass required to evolve to helium burning, and will also determine in more detail the manner by which low-mass red giants abort their ascent and head for the blue.

     Our work has focused on starting states that have nearly solar composition. In the future of the galaxy, when the role of these low-mass stars become increasingly important, the metallicity is expected to increase. As a result, opacities at higher metallicities must be computed and then used to study the future evolution of high metallicity stars. Another important issue is the question of mass loss, both for very low mass stars and for somewhat larger stars like the Sun. As discussed in § 2.2, even relatively small outflow rates can affect stellar evolution over the very long timescales appropriate for low-mass stars.

     Finally, further work should still be done to refine our understanding of exactly why the smallest stars are unable to develop into red giants. The work presented in this paper (see § 4) has focused in detail on the role played by photospheric opacity in helping to produce red giant structures. However, the opacity can only drive a star to become a red giant when the photospheric conditions are in a regime where the opacity is a sharply increasing function of temperature; further work must be done to clarify more precisely why the modest core-envelope structures of the smallest stars are incapable of providing those conditions.

     This work has been conducted in part under the auspices of a NASA Astrophysics Theory Program that supports a joint Center for Star Formation Studies at the NASA Ames Research Center, UC Berkeley, and UC Santa Cruz. This work was also supported by an NSF Young Investigator Award, NASA grant NAG 5-2869, and by funds from the Physics Department at the University of Michigan. The authors would like to thank the referee, I. Baraffe, for providing useful criticism of the manuscript.

REFERENCES

FIGURES


Full image (56kb) | Discussion in text
     FIG. 1.—Evolution in the Hertzsprung-Russell diagram for a star of mass M* = 0.10 M&sun;. Each small filled circle delineating the evolutionary track represents a separate converged model. The star begins its evolution on a pre–main-sequence Hayashi track and ends up as a helium white dwarf, cooling into obscurity. The inset diagram shows the chemical composition of the star over the course of its evolution; the mass fractions in H, 3He, and 4He are plotted as functions of time.

Full image (122kb) | Discussion in text
     FIG. 2.—Evolution in the Hertzsprung-Russell diagram for stars with masses in the range 0.06 M&sun; ≤ M* ≤ 0.25 M&sun;. The inset diagram shows the corresponding main-sequence lifetimes as a function of stellar mass.

Full image (45kb) | Discussion in text
     FIG. 3.—Evolution in the central temperature vs. central density plane for stellar models with masses in the range 0.06 M&sun; ≤ M* ≤ 0.25 M&sun;

Full image (89kb) | Discussion in text
     FIG. 4.—Radius vs. time diagram for stellar models with mass ranging from 0.08 M&sun; to 0.25 M&sun;. In each sequence of models (except for the 0.25 M&sun; model) a maximum radius is reached, and at the very latest times plotted, the radius is shrinking.

Full image (81kb) | Discussion in text
     FIG. 5.—Radius vs. luminosity as a function of helium enrichment for the alternate sequence of stellar models with mass M* = 0.20 M&sun;. The models with depleted hydrogen (helium enrichment) start their evolution at considerably larger luminosities and show much smaller increases in radii.

Full image (270kb) | Discussion in text
     FIG. 6.—Photospheric evolution in the density-temperature plane. The evolutionary sequences are plotted on top of the hydrogen-rich opacity table. Darker shades of gray represent higher opacities. The size of the open circle representing a converged model is in proportion to the actual radius of the star. The stars begin their evolution on the Hayashi track, clustered fairly close together near the point log10T &ap; 3.3, log10ρ &ap; -5.5. Notice that the M* = 0.08 model slides all the way along the grain opacity boundary to a photospheric density log10ρ &ap; -5.5 before reaching the main sequence.

Full image (93kb) | Discussion in text
     FIG. 7.—Evolution of stars in the H-R diagram for varying treatments of opacity. All stars have mass M* = 0.25 M&sun;. The collection of evolutionary tracks corresponds to different opacity laws with increasing sensitivity at high temperatures, i.e., different values of TW (as labeled). As the opacity law becomes a more steeply rising function of temperature (as TW decreases), the stars more readily attain red giant-like configurations in general accordance with the theoretical arguments of § 4.

TABLES

TABLE 1
COMPARISON OF STELLAR MODELS
Model M*(M&sun;) log10Te log10L* R*
(109 cm)		 TC
(106 K)		 log10ρc
LBA 0.08 3.24 -3.96 8.02 3.520 2.60
BHSL 0.08 3.33 -3.83 6.12 2.796 2.94
LBA 0.15 3.42 -2.814 12.94 5.533 2.26
BHSL 0.15 3.50 -2.503 12.60 5.344 2.29
LBA 0.20 3.46 -2.498 15.92 6.340 2.13
BHSL 0.20 3.52 -2.248 15.70 6.041 2.13

     NOTES.— LBA: models of this paper. BHSL: model X of Burrows et al. (1993). For each model of mass M*, the table gives the effective temperature Te (K), the stellar luminosity L* (L&sun;), the stellar radius R* (109 cm), the central temperature TC (106 K), and the central density ρC (g cm-3).

Image of typeset table | Discussion in text
TABLE 2
STELLAR PARAMETERS AT THE EPOCH OF MAXIMUM RADIAL EXTENT
M* XH R*/RC
0.08 0.1135 1.0
0.09 0.1521 1.0
0.10 0.1840 1.0
0.12 0.2420 1.0
0.13 0.2585 1.011
0.14 0.2796 1.153
0.16 0.3154 1.631
0.18 0.3869 3.045
0.20 0.4387 5.100
0.25 0.5107 >10

     NOTES.— For stars of mass M*, the table shows the hydrogen mass fraction XH in the stellar envelope (a quantity that is fixed at the moment when a radiative core develops) and the ratio R*/RC of the radius of the star at its maximum size to the radius it had at the moment when the radiative core first appeared.

Image of typeset table | Discussion in text