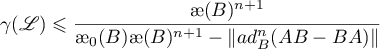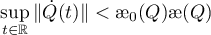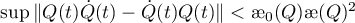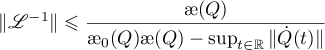Abstract
By applying Lyapunov's equation, the method of similar operators, and the methods of harmonic analysis, we obtain estimates for the parameters of exponential dichotomy and for the Green's function constructed for a hyperbolic operator semigroup and a hyperbolic linear relation. Estimates are obtained using quantities which are determined by the resolvent of the infinitesimal operator of the operator semigroup and of the linear relation.
Bibliography: 51 titles.
Export citation and abstract BibTeX RIS
§ 1. Introduction. Basic concepts and results
Let  be a complex Hilbert space, and
be a complex Hilbert space, and 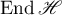 the Banach algebra of linear bounded operators acting in
the Banach algebra of linear bounded operators acting in  . We consider a strongly continuous operator semigroup (semigroup of class
. We consider a strongly continuous operator semigroup (semigroup of class  )
)
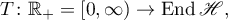
and let 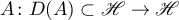 be its infinitesimal operator (see [1]).
be its infinitesimal operator (see [1]).
We consider the linear differential equation
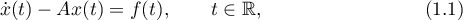
where the function  belongs to one of the following Banach function spaces. Let
belongs to one of the following Banach function spaces. Let  denote the Banach space of bounded continuous functions defined on
denote the Banach space of bounded continuous functions defined on 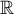 with values in
with values in  with the norm
with the norm 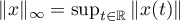 . The symbol
. The symbol  ,
, ![$p \in [1, \infty]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn10.gif) , is used for denoting the Banach space of (classes of) Bochner measurable functions
, is used for denoting the Banach space of (classes of) Bochner measurable functions 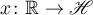 for which the following quantity is finite:
for which the following quantity is finite:
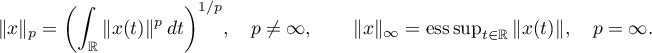
If 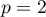 , then
, then 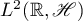 is a Hilbert space with the inner product
is a Hilbert space with the inner product 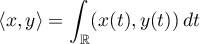 ,
, 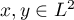 . We use the symbol
. We use the symbol  to denote one of the spaces
to denote one of the spaces 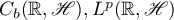 ,
, ![$p \in [1,\infty]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn18.gif) .
.
A weak bounded solution of equation (1.1), where  , is defined to be a function
, is defined to be a function  such that the equations
such that the equations
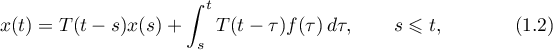
hold for all 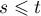 in
in  .
.
The following problem is important: find necessary and sufficient conditions on the operator  that ensure the existence and uniqueness of a (weak) solution
that ensure the existence and uniqueness of a (weak) solution  for any function
for any function  . This problem is equivalent to the differential operator
. This problem is equivalent to the differential operator
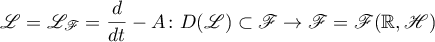
being continuously invertible. This is defined as follows. A function  is considered to belong to the domain of definition
is considered to belong to the domain of definition 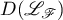 of the operator if there exists a function
of the operator if there exists a function  such that
such that  is a weak solution of the differential equation (1.1), that is, equations (1.2) hold. The operator
is a weak solution of the differential equation (1.1), that is, equations (1.2) hold. The operator  is said to be continuously invertible if its kernel
is said to be continuously invertible if its kernel  is zero and the image
is zero and the image  coincides with
coincides with  . Consequently,
. Consequently,  .
.
Definition 1. An operator semigroup  is said to be hyperbolic or admitting exponential dichotomy if the spectrum
is said to be hyperbolic or admitting exponential dichotomy if the spectrum 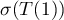 of the operator
of the operator 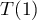 has the property
has the property

where  is the unit circle.
is the unit circle.
The following result is contained in [2]–[5].
Theorem 1. For the operator 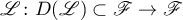 to be continuously invertible it is necessary and sufficient that the semigroup
to be continuously invertible it is necessary and sufficient that the semigroup  be hyperbolic.
be hyperbolic.
Theorem 2, which follows, was proved by Prüss (see [6], [7]) for operator semigroups of class  (see also [8] and [9] for degenerate operator semigroups, where the role of the operator
(see also [8] and [9] for degenerate operator semigroups, where the role of the operator  is taken by a linear relation [9]).
is taken by a linear relation [9]).
Theorem 2. For a (strongly continuous) operator semigroup  to be hyperbolic, it is necessary and sufficient that the following two conditions hold:
to be hyperbolic, it is necessary and sufficient that the following two conditions hold:


where  is the resolvent of the operator
is the resolvent of the operator  and
and 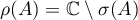 is its resolvent set.
is its resolvent set.
When an operator semigroup 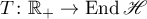 is hyperbolic, this gives rise to the decomposition
is hyperbolic, this gives rise to the decomposition

where  and
and 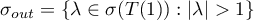 . We consider the Riesz projector (see [1]–[3])
. We consider the Riesz projector (see [1]–[3])
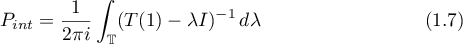
constructed with respect to the set  and put
and put 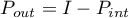 , where
, where  is the identity operator in the algebra
is the identity operator in the algebra  . Then the Hilbert space
. Then the Hilbert space  can be represented as the direct sum of the closed linear subspace
can be represented as the direct sum of the closed linear subspace 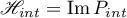 that is the image of the projector
that is the image of the projector 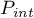 and the subspace
and the subspace 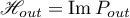 :
:
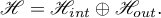
It follows from (1.7) that the projectors 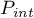 ,
,  commute with the operators
commute with the operators  ,
, 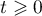 , and, consequently, the subspaces
, and, consequently, the subspaces 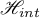 ,
,  are invariant under the operators
are invariant under the operators  ,
, 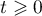 . Furthermore, we note that these subspaces are nonzero if
. Furthermore, we note that these subspaces are nonzero if 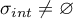 ,
, 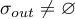 simultaneously for the sets in the decomposition (1.6). We consider (for more details see [4] and [10]) the operator semigroup
simultaneously for the sets in the decomposition (1.6). We consider (for more details see [4] and [10]) the operator semigroup
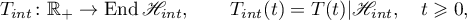
and the operator group 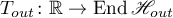 defined by the equations
defined by the equations
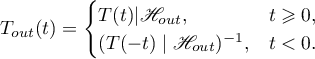
Theorem 3. (see [2]–[4]) If the semigroup  is hyperbolic, then the operator
is hyperbolic, then the operator 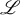 is continuously invertible and the inverse operator
is continuously invertible and the inverse operator  is defined by the formula
is defined by the formula
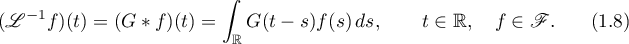
The Green's function 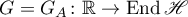 has the form
has the form
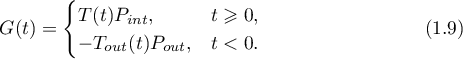
For a hyperbolic semigroup  it is possible to derive the existence of constants
it is possible to derive the existence of constants 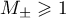 ,
, 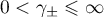 , such that the Green's function
, such that the Green's function 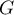 admits estimates of the form
admits estimates of the form
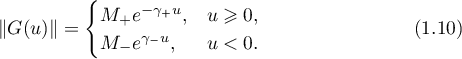
(See [2] and [4] for more details.)
Note that we set  if the semigroup
if the semigroup  is exponentially stable, that is,
is exponentially stable, that is,
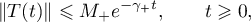
which is equivalent to the condition  (correspondingly we set
(correspondingly we set  if
if  ).
).
The numbers  ,
,  in (1.10) are called the exponents of exponential dichotomy of the function
in (1.10) are called the exponents of exponential dichotomy of the function  , and the two ordered pairs of numbers
, and the two ordered pairs of numbers 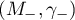 ,
, 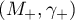 are called the parameters of exponential dichotomy. If the semigroup
are called the parameters of exponential dichotomy. If the semigroup  is exponentially stable, then we call the pair of numbers
is exponentially stable, then we call the pair of numbers 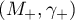 the parameters of exponential stability of the semigroup
the parameters of exponential stability of the semigroup  .
.
The representation (1.8) of the inverse operator of 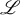 (under the condition (1.3) that the semigroup
(under the condition (1.3) that the semigroup  is hyperbolic or under the conditions (1.4), (1.5)) implies that the norm of the operator
is hyperbolic or under the conditions (1.4), (1.5)) implies that the norm of the operator 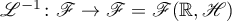 admits estimates of the form
admits estimates of the form
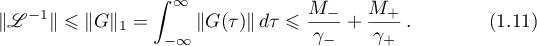
The estimates (1.11) allows us to obtain a condition for the solvability in the space 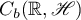 of a nonlinear equation of the form
of a nonlinear equation of the form

where 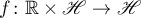 is a continuous function (in the first argument) and is uniformly continuous with respect to the second argument in any ball in
is a continuous function (in the first argument) and is uniformly continuous with respect to the second argument in any ball in  and satisfies a Lipschitz condition in the second variable:
and satisfies a Lipschitz condition in the second variable:
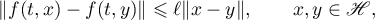
where 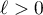 is some constant. Then the following theorem holds.
is some constant. Then the following theorem holds.
Theorem 4. Equation (1.12) has a weak solution 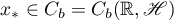 if the condition
if the condition  holds. Furthermore,
holds. Furthermore,
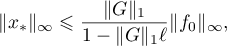
where 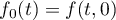 ,
, 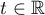 .
.
Proof. The proof of an analogue of Theorem 4 can be found in [11]; a definition of a weak solution of a nonlinear equation can also be found there. This proof is based on an application of the contraction mapping principle [12] to the integral equation
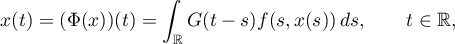
where 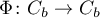 is a contraction map with contraction constant
is a contraction map with contraction constant  .
.
Thus, Theorem 4 shows that it is important to obtain an estimate for 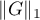 . In this paper we use the following quantities for our estimates (see also the formulae in Theorem 8):
. In this paper we use the following quantities for our estimates (see also the formulae in Theorem 8):


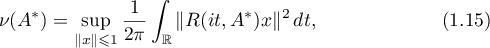
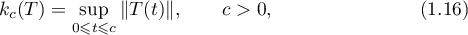

where  is the numerical range of the operator
is the numerical range of the operator  (see [13]). Thus, in the estimates (1.13)–(1.15) we use quantities constructed from the resolvent of the operator
(see [13]). Thus, in the estimates (1.13)–(1.15) we use quantities constructed from the resolvent of the operator  .
.
That 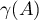 is finite follows from Theorem 2. Its importance is that it gives the equality
is finite follows from Theorem 2. Its importance is that it gives the equality 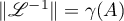 for the norm of the inverse operator of the differential operator
for the norm of the inverse operator of the differential operator 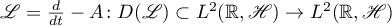 . This equality was proved in Lemma 4 of [4] using Parseval's equation. The quantity
. This equality was proved in Lemma 4 of [4] using Parseval's equation. The quantity 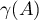 was used in [14], [4], [15] to estimate the norms of the inverse operators of differential operators. In [16] this quantity was called the frequency characteristic of the operator
was used in [14], [4], [15] to estimate the norms of the inverse operators of differential operators. In [16] this quantity was called the frequency characteristic of the operator  .
.
The quantity  was used in [14] for
was used in [14] for  , where
, where  is a finite- dimensional space. It was called the integral criterion of the quality of dichotomy. The estimate
is a finite- dimensional space. It was called the integral criterion of the quality of dichotomy. The estimate  was established in [10].
was established in [10].
We also point out (without proof) the estimate 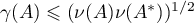 .
.
The quantity 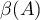 defined by equation (1.17) with respect to the numerical range
defined by equation (1.17) with respect to the numerical range  of the operator
of the operator  is important in connection with the following theorem (see [17], Theorem I.4.2 and §I.4.4).
is important in connection with the following theorem (see [17], Theorem I.4.2 and §I.4.4).
Theorem 5. For an operator 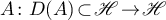 with domain of definition
with domain of definition 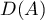 , which is dense in
, which is dense in  , to be the infinitesimal operator of an operator semigroup
, to be the infinitesimal operator of an operator semigroup  satisfying the estimate
satisfying the estimate

where  , it is necessary and sufficient that the following conditions hold:
, it is necessary and sufficient that the following conditions hold:
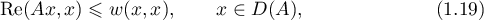
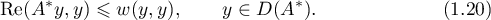
Thus, if (1.18) holds, this is equivalent to both the conditions 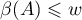 and
and 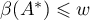 holding, that is, the numerical ranges
holding, that is, the numerical ranges  and
and 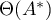 of the operators
of the operators  and
and 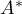 are contained in the half-plane
are contained in the half-plane  (conditions (1.19), (1.20) hold). But a
(conditions (1.19), (1.20) hold). But a  such that the estimate (1.18) is true does not exist for every semigroup
such that the estimate (1.18) is true does not exist for every semigroup 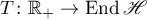 . In §4 we present an example of an operator semigroup whose infinitesimal operator and its adjoint operator have numerical ranges that coincide with the entire complex plane.
. In §4 we present an example of an operator semigroup whose infinitesimal operator and its adjoint operator have numerical ranges that coincide with the entire complex plane.
The next assumption on the infinitesimal operator  of an operator group
of an operator group  is used in the hypotheses of the following theorem.
is used in the hypotheses of the following theorem.
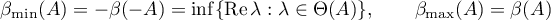
are finite, and  ,
,  .
.
Remark 1. The conditions of Assumption 1 hold for an operator

if  and the operator
and the operator  admits a bounded extension to
admits a bounded extension to  to a (selfadjoint) operator
to a (selfadjoint) operator  , whose spectrum
, whose spectrum 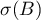 satisfies the conditions
satisfies the conditions 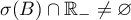 and
and 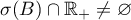 , where
, where ![${\mathbb{R}_{-}=(-\infty,0]}$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn110.gif) . In particular, these conditions are satisfied by the operator
. In particular, these conditions are satisfied by the operator  , where
, where 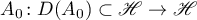 is a selfadjoint operator and the spectrum of
is a selfadjoint operator and the spectrum of  satisfies
satisfies 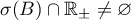 .
.
Theorem 6. Let 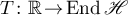 be a hyperbolic operator group satisfying Assumption 1. Then the Green's function
be a hyperbolic operator group satisfying Assumption 1. Then the Green's function 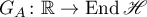 admits an estimate of the form
admits an estimate of the form
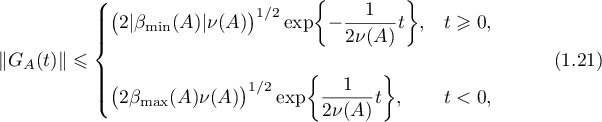

Corollary 1. Under the conditions of Theorem 2 the norms of the projectors 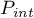 ,
,  occurring in the definition of the Green's function (formula (1.9)) admit the estimate
occurring in the definition of the Green's function (formula (1.9)) admit the estimate
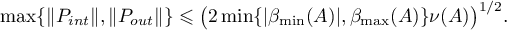
In proving Theorem 6 we make essential use of Theorem 6 in [10], in which a necessary and sufficient condition for operator groups to be hyperbolic was obtained. It was based on using Lyapunov's equation (see also [3], Theorem 4.40). The proof of Theorem 6 depends on constructing the indefinite metric defined by a selfadjoint operator  in the Hilbert space
in the Hilbert space  ; with respect to this the solution of the corresponding differential equation decays exponentially as
; with respect to this the solution of the corresponding differential equation decays exponentially as  . In [10] an example was constructed of a hyperbolic semigroup of compact operators for which the operator
. In [10] an example was constructed of a hyperbolic semigroup of compact operators for which the operator  defined from Lyapunov's equation is not invertible, that is, it does not seem possible to obtain analogues of Theorem 6 for operator semigroups in this way. For a finite-dimensional space
defined from Lyapunov's equation is not invertible, that is, it does not seem possible to obtain analogues of Theorem 6 for operator semigroups in this way. For a finite-dimensional space  , analogues of Theorem 6 were obtained in [14], [18]–[22].
, analogues of Theorem 6 were obtained in [14], [18]–[22].
Suppose that  is an exponentially stable operator semigroup. Then (see [3], [10], and [23]) Lyapunov's equation
is an exponentially stable operator semigroup. Then (see [3], [10], and [23]) Lyapunov's equation

has a solution 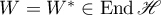 which is defined by the formula
which is defined by the formula
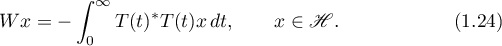
Thus,  and
and  ,
, 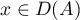 . Furthermore, the operator
. Furthermore, the operator 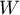 is negative-definite but not is necessarily continuously invertible.
is negative-definite but not is necessarily continuously invertible.
Theorem 7. Suppose that  is an exponentially stable operator semigroup and the operator
is an exponentially stable operator semigroup and the operator 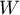 is continuously invertible. Then the following estimates hold:
is continuously invertible. Then the following estimates hold:
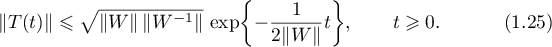
Note that for an exponentially stable operator group 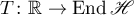 the operator
the operator 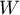 is invertible (see [10] and Theorem 17). It follows from Remark 2 (see §2) that
is invertible (see [10] and Theorem 17). It follows from Remark 2 (see §2) that  .
.
In the case of a finite-dimensional space  the estimate (1.25) was given in [14], §9.3.
the estimate (1.25) was given in [14], §9.3.
In §3 we describe a different method for obtaining an estimate for the Green's function based on using the methods of harmonic analysis.
Along with the quantities defined by formulae (1.13)–(1.17), new quantities  ,
, 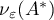 are introduced into consideration in Theorem 8. They are defined for an arbitrary linear operator
are introduced into consideration in Theorem 8. They are defined for an arbitrary linear operator 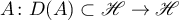 that has non-empty resolvent set
that has non-empty resolvent set 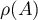 and for which the following quantities are finite:
and for which the following quantities are finite:
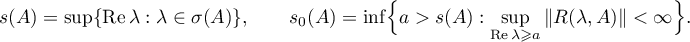
The quantity  is called the spectral bound of the operator
is called the spectral bound of the operator  (see [7], [23]), and the quantity
(see [7], [23]), and the quantity 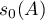 the abscissa of uniform boundedness of the resolvent of the operator
the abscissa of uniform boundedness of the resolvent of the operator  .
.
For an arbitrary (strongly continuous) operator semigroup  , the quantity
, the quantity

is called the type of the semigroup  or the growth constant of the semigroup
or the growth constant of the semigroup  (see [7], [23]).
(see [7], [23]).
Note that  for the infinitesimal operator
for the infinitesimal operator  of the semigroup
of the semigroup  . Furthermore,
. Furthermore, 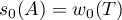 by Theorem 2. For operator semigroups in a Banach space these quantities may be different [7].
by Theorem 2. For operator semigroups in a Banach space these quantities may be different [7].
Theorem 8. An operator 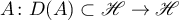 with
with 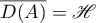 is the infinitesimal operator of an exponentially stable operator semigroup
is the infinitesimal operator of an exponentially stable operator semigroup  if and only if for some
if and only if for some  the following conditions hold:
the following conditions hold:
- 1)

- 2)
 ;
; - 3)
 .
.
When these conditions hold, the semigroup  admits the estimate
admits the estimate

Furthermore, conditions 1)– 3) hold for any  .
.
Theorem 8 is essential to the proof of Theorem 18 in §3, where estimates of the Green's function for sectorial operators are obtained.
In view of the difficulty of obtaining estimates for  and
and 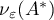 , the quantities
, the quantities 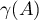 ,
,  ,
,  ,
, 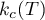 defined by formulae (1.13)–(1.16) are used in the following theorems.
defined by formulae (1.13)–(1.16) are used in the following theorems.
The estimates presented below in Theorems 9–11 are obtained for a hyperbolic operator semigroup  with infinitesimal operator
with infinitesimal operator  .
.
Theorem 9. The Green's function 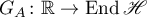 admits estimates of the form
admits estimates of the form
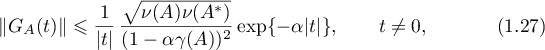
for any number 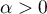 satisfying the condition
satisfying the condition  . In particular (for
. In particular (for 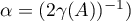 , the following estimates hold:
, the following estimates hold:
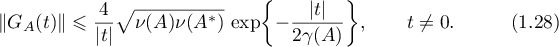
Corollary 2. Suppose that  is an exponentially stable operator semigroup. Then
is an exponentially stable operator semigroup. Then 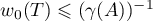 .
.
The next two theorems follows from Theorem 9.
Theorem 10. Let  be an exponentially stable operator semigroup. Then it admits estimates of the form
be an exponentially stable operator semigroup. Then it admits estimates of the form
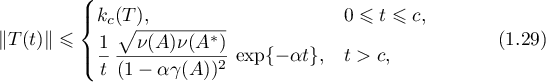
for any number 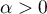 satisfying the condition
satisfying the condition 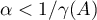 and for any
and for any 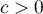 .
.
In the following theorem, the quantity 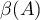 defined by equation (1.17) is used in estimating the quantity
defined by equation (1.17) is used in estimating the quantity 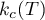 . Furthermore, Theorem 5 is used.
. Furthermore, Theorem 5 is used.
Theorem 11. If 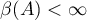 and
and  is an exponentially stable operator semigroup, then
is an exponentially stable operator semigroup, then
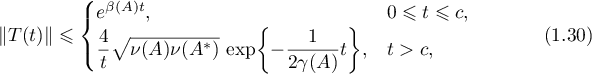
for any number 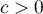 . Furthermore,
. Furthermore,
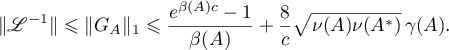
Suppose that
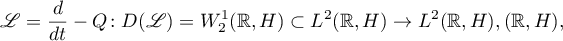
where 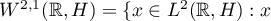 is absolutely continuous and
is absolutely continuous and 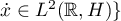 is a Sobolev space and
is a Sobolev space and  , is a continuously invertible operator. It was proved in [15] that the operator
, is a continuously invertible operator. It was proved in [15] that the operator 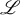 is continuously invertible in
is continuously invertible in  and that
and that
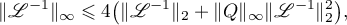
where  and
and  are the norms of the operator
are the norms of the operator 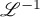 in
in 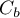 and
and  , respectively. In the proof in [15], completely different methods were used (these were later used in the theory of wavelets [24]).
, respectively. In the proof in [15], completely different methods were used (these were later used in the theory of wavelets [24]).
The results in §5 are connected with estimates for the Green's function constructed for a hyperbolic linear relation. We present the basic ideas in the theory of linear relations we use here; these are described in detail in [9], [25]–[27] (also see [28] and [29]).
Let  be a complex Banach space. Any linear subspace
be a complex Banach space. Any linear subspace  in the Cartesian product
in the Cartesian product 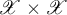 is called a linear relation on the Banach space
is called a linear relation on the Banach space  . In what follows, any linear operator
. In what follows, any linear operator 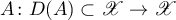 is identified with the linear relation
is identified with the linear relation
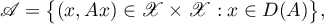
which is the graph of the operator  . Thus, we have the inclusion
. Thus, we have the inclusion
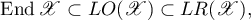
where 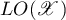 is the set of linear operators acting in
is the set of linear operators acting in  and
and 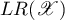 is the set of linear relations on
is the set of linear relations on  . The set of linear relations that are closed in
. The set of linear relations that are closed in 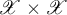 is denoted by
is denoted by  .
.
The subspace
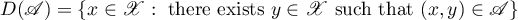
is called the domain of definition of the relation 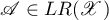 . Let
. Let  , where
, where  , denote the set
, denote the set 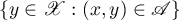 . The subspaces
. The subspaces  and
and  are called the kernel and image of
are called the kernel and image of 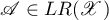 , respectively.
, respectively.
The sum of two relations 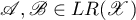 is defined to be a linear subspace of
is defined to be a linear subspace of 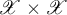 of the form
of the form
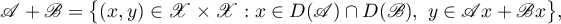
where  is the algebraic sum of two subsets
is the algebraic sum of two subsets  ,
, 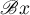 . The product of linear relations
. The product of linear relations 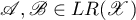 is defined to be a linear subspace of
is defined to be a linear subspace of 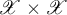 of the form
of the form
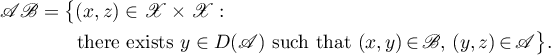
If 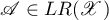 , then the inverse relation
, then the inverse relation  is defined by the equation
is defined by the equation 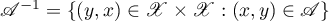 . Clearly,
. Clearly, 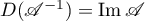 and
and  .
.
A relation  in
in  is said to be continuously invertible if
is said to be continuously invertible if 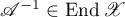 , that is,
, that is,  (
( is injective) and
is injective) and 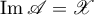 (
( is surjective). The resolvent set of a relation
is surjective). The resolvent set of a relation  is defined to be the set
is defined to be the set  of all
of all  such that
such that 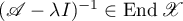 , that is, the relation
, that is, the relation  is continuously invertible. The spectrum of
is continuously invertible. The spectrum of  is defined to be the set
is defined to be the set 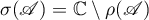 .
.
It should be noted that the set  is open, and the spectrum
is open, and the spectrum  of
of 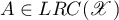 is closed. The function
is closed. The function
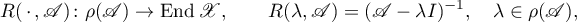
is called the resolvent of 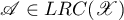 .
.
A closed linear subspace 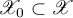 is said to be invariant for a relation
is said to be invariant for a relation 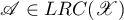 with non-empty
with non-empty  if it is invariant under all the operators
if it is invariant under all the operators  ,
, 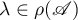 . The restriction of a relation
. The restriction of a relation  to a subspace
to a subspace 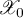 is defined to be the relation
is defined to be the relation 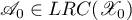 the resolvent of which is the restriction
the resolvent of which is the restriction  ,
, 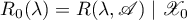 ,
, 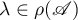 , of the resolvent
, of the resolvent  to the subspace
to the subspace 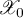 ; it is denoted by
; it is denoted by 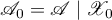 .
.
If 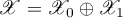 is a direct sum of subspaces invariant under
is a direct sum of subspaces invariant under 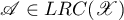 and
and 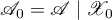 ,
, 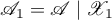 , then we say that
, then we say that  is the direct sum of the relations
is the direct sum of the relations  and
and 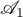 and write
and write 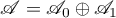 . An operator
. An operator  is said to commute with a relation
is said to commute with a relation  if
if 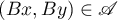 for any
for any  .
.
Definition 2. A relation  is said to be hyperbolic (with respect to the circle
is said to be hyperbolic (with respect to the circle 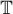 ) if
) if

If (1.31) holds for  then we have the representation
then we have the representation

where 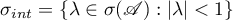 and
and 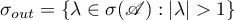 . The following result follows from [25] (see also Theorem 4.2 in [26] and Theorem 5.2.10 in [27]).
. The following result follows from [25] (see also Theorem 4.2 in [26] and Theorem 5.2.10 in [27]).
Theorem 12. Let  be a hyperbolic linear relation on a space
be a hyperbolic linear relation on a space  . Then the space
. Then the space  admits a representation in the form
admits a representation in the form

of the direct sum of closed subspaces 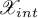 ,
,  invariant under the linear relation
invariant under the linear relation  , and
, and 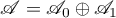 , where
, where 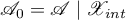 and
and 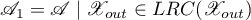 have the following properties:
have the following properties:
- 1)
 ,
,  ;
; - 2)
 ,
,  ,
,  .
.
We obtain the decomposition (1.33) of the space  by the means of Riesz projector
by the means of Riesz projector
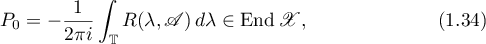
which commutes with the relation  . Furthermore,
. Furthermore, 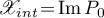 and
and 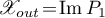 , where
, where  is the complementary projector to
is the complementary projector to  .
.
Let 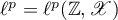 , where
, where ![$p \in [1,\infty]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn18.gif) , denote the Banach space of two-sided sequences
, denote the Banach space of two-sided sequences  such that the quantity
such that the quantity
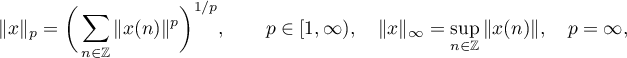
is finite; this is defined to be the norm in the space 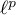 .
.
We consider the difference inclusion

where 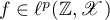 and
and  . By a solution of this inclusion we mean a two-sided sequence
. By a solution of this inclusion we mean a two-sided sequence 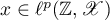 satisfying (1.35) for every
satisfying (1.35) for every 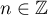 , that is,
, that is,  ,
, 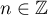 . We construct a linear relation
. We construct a linear relation  on the Banach space
on the Banach space  . This relation consists of pairs
. This relation consists of pairs 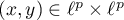 such that
such that
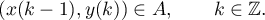
We point out that the closedness of  implies the closedness of
implies the closedness of  . Based on Theorem 12 and the results in [30] (where the case
. Based on Theorem 12 and the results in [30] (where the case 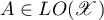 was considered), Bichegkuev [31] obtained the following result.
was considered), Bichegkuev [31] obtained the following result.
Theorem 13. The following conditions are equivalent:
- 1)
- 2)the relation
 is hyperbolic;
is hyperbolic; - 3)the relation
 is continuously invertible.
is continuously invertible.
If one of these conditions holds, then the operator  admits a representation of the form
admits a representation of the form
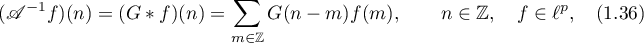
where the function  , which is called the Green's function for the difference inclusion (1.35), has the form
, which is called the Green's function for the difference inclusion (1.35), has the form
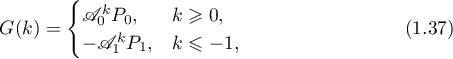
where  ,
, 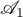 ,
,  ,
, 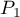 are defined in Theorem 12.
are defined in Theorem 12.
To estimate the Green's function 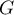 , we use the quantity
, we use the quantity
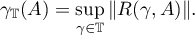
It follows from formula (1.36) that the norm of the operator  admits the estimate
admits the estimate
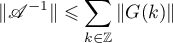
in any of the Banach spaces  ,
, ![$p\in [1,\infty]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn247.gif) .
.
Theorem 14. Suppose that  is a hyperbolic relation. Then the following estimate holds:
is a hyperbolic relation. Then the following estimate holds:
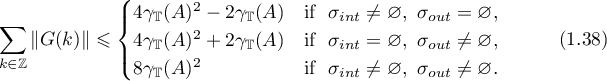
Estimate (1.38) can be used in questions concerning the solvability in  of the nonlinear difference inclusion
of the nonlinear difference inclusion
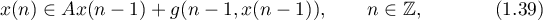
where  is a hyperbolic linear relation on
is a hyperbolic linear relation on  and
and  is a map with the following properties:
is a map with the following properties:
- 1)
 for any
for any  ,
, - 2)
 ,
,  , for some
, for some  .
.
Theorem 15. The difference inclusion (1.39) is solvable in the space  if
if
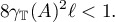
In §6 we present examples of hyperbolic operator semigroups. The examples and results presented here are closely connected with the results in [32]–[37]. In §7 we discuss some of the results obtained.
§ 2. Estimates for the parameters of exponential dichotomy and the Green's function in the case of an operator group
Throughout this section,  is a strongly continuous operator semigroup. If it is hyperbolic, then we use the notation introduced in §1.
is a strongly continuous operator semigroup. If it is hyperbolic, then we use the notation introduced in §1.
Let  be the infinitesimal operator of the hyperbolic operator semigroup
be the infinitesimal operator of the hyperbolic operator semigroup  . In the Banach algebra
. In the Banach algebra  we consider Lyapunov's equation
we consider Lyapunov's equation
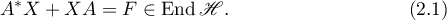
With the left-hand side of this equation we associate the transformer (following M. Krein's terminology)
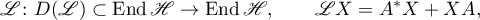
with domain of definition
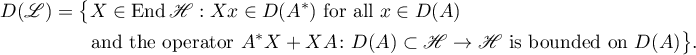
If 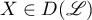 , then, since
, then, since 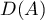 is dense in
is dense in  , the extension of the operator
, the extension of the operator 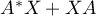 to the space
to the space  is well defined and is denoted by the same symbol
is well defined and is denoted by the same symbol 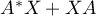 .
.
We introduce into consideration closed subspaces in the algebra  of the form
of the form
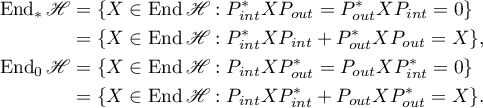
The following two theorems were obtained in [3] and [10]. They are essential to the proofs of Theorems 6 and 7.
Theorem 16. (see [3]) Suppose that the semigroup  is hyperbolic. Then equation (2.1) is solvable for any operator
is hyperbolic. Then equation (2.1) is solvable for any operator  in the subspace
in the subspace 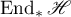 , and there exists a unique solution
, and there exists a unique solution 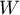 belonging to the subspace
belonging to the subspace 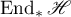 . This solution can be represented by the formula
. This solution can be represented by the formula
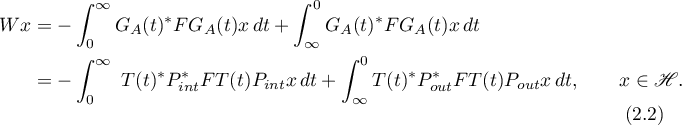
In particular, if 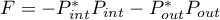 , then the operator
, then the operator 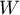 has the form
has the form
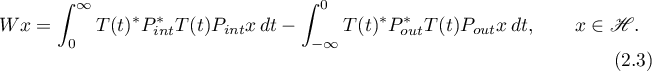
Theorem 17. (see [10]) For a (strongly continuous) operator group  to be hyperbolic, it is necessary and sufficient that there exist uniformly negative- definite operators
to be hyperbolic, it is necessary and sufficient that there exist uniformly negative- definite operators  ,
, 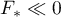 in the algebra
in the algebra  such that the equations (2.1) and
such that the equations (2.1) and

have continuously invertible selfadjoint solutions 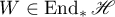 and
and  , respectively. The solution
, respectively. The solution 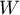 is defined by (2.2), and the operator
is defined by (2.2), and the operator  has the form
has the form
Remark 2. It was established in [10] that the Fourier transform 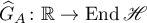 of the Green's function of the hyperbolic operator semigroup
of the Green's function of the hyperbolic operator semigroup  coincides with the restriction of the resolvent of the operator
coincides with the restriction of the resolvent of the operator  to the imaginary axis
to the imaginary axis 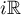 , that is, the equations
, that is, the equations

hold. Therefore it follows from formulae (2.2)–(2.5) (using Plancherel's identity) that the equations
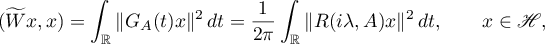
hold if  and
and 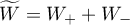 , where
, where
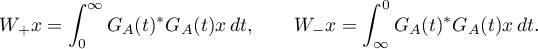
Consequently,
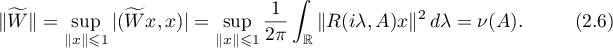
Let  be a (strongly continuous) operator group. Along with the group
be a (strongly continuous) operator group. Along with the group  , we consider the operator group
, we consider the operator group 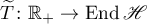 ,
, 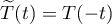 ,
, 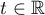 . Its infinitesimal operator is the operator
. Its infinitesimal operator is the operator  .
.
In proving Theorem 6 we use the following lemma.
Lemma 1. The following estimates hold:
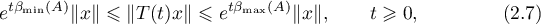
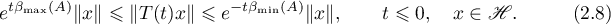
Proof. In (2.7) the right-hand inequalities follow from Theorem 5, where  . Since
. Since 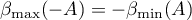 , we have
, we have
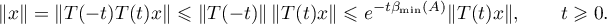
Consequently, the left-hand side of (2.7) also holds. The estimates (2.8) follow from (2.7) applied to the operator semigroup  . Furthermore, we need to take the equation
. Furthermore, we need to take the equation 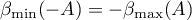 into account. The lemma is proved.
into account. The lemma is proved.
Proof of Theorem 6 We consider the operators  ,
, 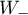 ,
, 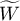 in Remark 2 and take account of the fact that
in Remark 2 and take account of the fact that  (see (2.6)). Since the operators
(see (2.6)). Since the operators  ,
, 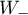 are uniformly positive, we have
are uniformly positive, we have
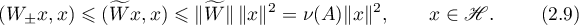
Lemma 1 implies the estimates
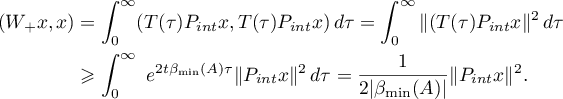
Consequently, we have the estimates
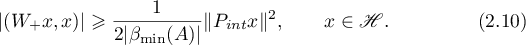
Let 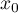 be an arbitrary vector in
be an arbitrary vector in 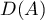 . Consider the function
. Consider the function  ,
,  ,
, 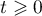 . For
. For 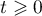 we obtain the equations
we obtain the equations
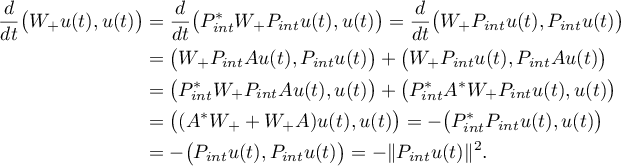
Using (2.9) with  we deduce that
we deduce that
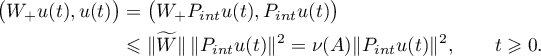
Thus,
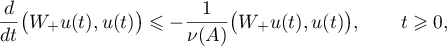
and, consequently,
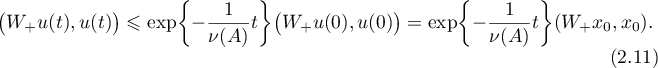
Using the estimates (2.9), (2.10) and (2.11) we obtain
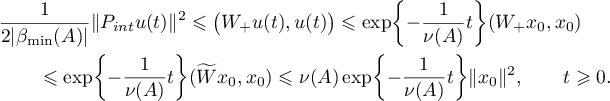
Since 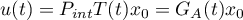 ,
, 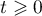 , and
, and 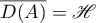 , it follows that
, it follows that
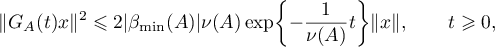
for any vector 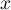 in
in  . Thus,
. Thus,
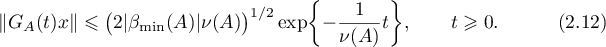
The estimate for  for
for 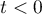 is obtained from the preceding one if we consider the operator group
is obtained from the preceding one if we consider the operator group 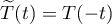 ,
, 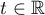 , for
, for 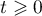 . Since the operator
. Since the operator  is a generator, it follows that
is a generator, it follows that  for
for  . Since
. Since 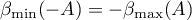 , for
, for 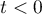 we obtain that
we obtain that
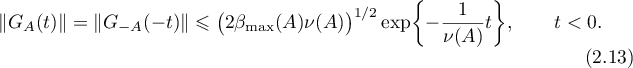
The estimates (2.12), (2.13) obtained above imply the estimates (1.21) and (1.22) that were to be proved. Theorem 6 is proved.
Proof of Theorem 7 Let  be the operator defined by (1.24) and satisfying Lyapunov's equation (1.23), let
be the operator defined by (1.24) and satisfying Lyapunov's equation (1.23), let  be an arbitrary vector in
be an arbitrary vector in  , and let
, and let 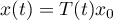 ,
, 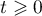 . Then
. Then
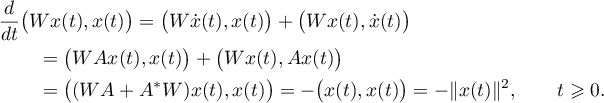
It follows from the inequalities
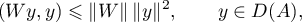
that
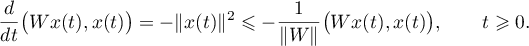
Therefore,
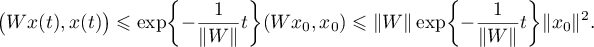
Since
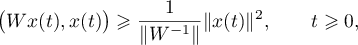
we have
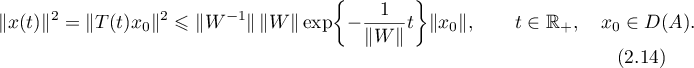
Since the operator semigroup  is bounded on any finite interval
is bounded on any finite interval ![$[0,r]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn293.gif) ,
, 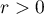 , and
, and 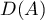 is dense in the space
is dense in the space  , it follows from (2.14) that
, it follows from (2.14) that
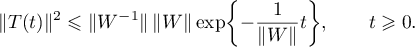
This inequality gives (1.25). The theorem is proved.
§ 3. Estimates of the Green's function constructed for a hyperbolic operator semigroup; proofs of Theorems 8–11
Proof of Theorem 8 Necessity. Let  be a (strongly continuous) bounded operator semigroup with infinitesimal operator
be a (strongly continuous) bounded operator semigroup with infinitesimal operator  . Then
. Then  .
.
For any number  the operator semigroup
the operator semigroup 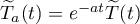 ,
, 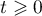 , is an exponentially stable operator semigroup with infinitesimal operator
, is an exponentially stable operator semigroup with infinitesimal operator 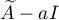 . Then equation (2.5) implies that
. Then equation (2.5) implies that

From this representation for any 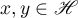 we obtain the estimates
we obtain the estimates
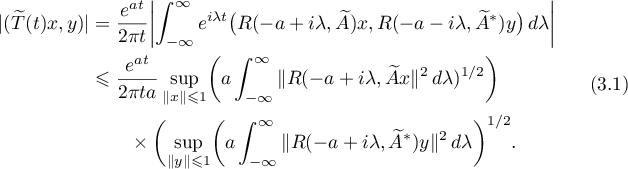
For any number  the operator semigroup
the operator semigroup
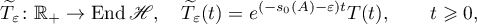
is bounded. Its infinitesimal operator is the operator  . Applying (3.1) to the operator semigroup
. Applying (3.1) to the operator semigroup 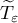 , we find that for any
, we find that for any 
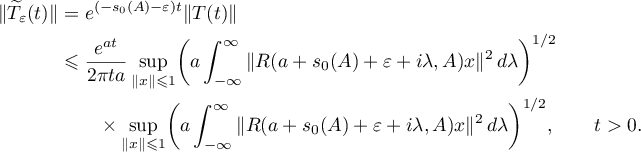
Using these estimates with 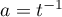 we obtain
we obtain
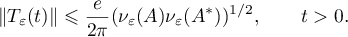
Consequently,
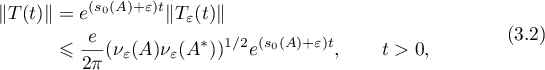
for any  . Thus, (1.26) follows from (3.2).
. Thus, (1.26) follows from (3.2).
The sufficiency of the conditions in the theorem follows from Gomilko's theorem applied to the operator semigroup  (see [38]). Namely, if conditions 1)–3) of Theorem 8 hold, then the semigroup
(see [38]). Namely, if conditions 1)–3) of Theorem 8 hold, then the semigroup  is bounded for any
is bounded for any  . Therefore the semigroup
. Therefore the semigroup  ,
,  , is exponentially stable if we set
, is exponentially stable if we set 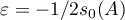 . Theorem 8 is proved.
. Theorem 8 is proved.
Theorem 8 can be used to estimate the parameter of exponential stability of analytic operator semigroups. Their infinitesimal operators are sectorial operators (see [7], [39]).
An operator 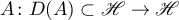 is said to be sectorial with angle
is said to be sectorial with angle  if for some
if for some  the sector
the sector
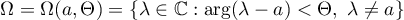
is contained in the resolvent set 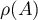 of the operator
of the operator  and for every
and for every  there exists a number
there exists a number 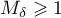 such that
such that
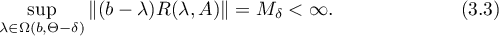
Let 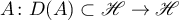 be a sectorial operator whose spectrum is contained in the half-plane
be a sectorial operator whose spectrum is contained in the half-plane  . It follows from the properties of sectorial operators (see [7], [39]) that the operator
. It follows from the properties of sectorial operators (see [7], [39]) that the operator  is the infinitesimal operator of some analytic operator semigroup
is the infinitesimal operator of some analytic operator semigroup  , and the equations
, and the equations
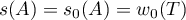
hold.
We point out straight away that an operator  being sectorial does not ensure that conditions (1.19), (1.20) in Theorem 5 hold. Moreover, in §4 we construct an example of a sectorial operator whose spectrum is negative. The operator has compact resolvent and its numerical range fills
being sectorial does not ensure that conditions (1.19), (1.20) in Theorem 5 hold. Moreover, in §4 we construct an example of a sectorial operator whose spectrum is negative. The operator has compact resolvent and its numerical range fills  .
.
Since 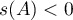 , the operator semigroup
, the operator semigroup  is exponentially stable. It follows from (3.3) that we can assume that
is exponentially stable. It follows from (3.3) that we can assume that 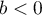 in (3.3). Moreover, there exists a constant
in (3.3). Moreover, there exists a constant  such that
such that
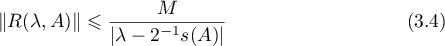
for all  contained in the half-plane
contained in the half-plane
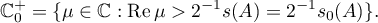
Theorem 18. Let 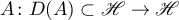 be a sectorial operator such that
be a sectorial operator such that 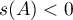 whose resolvent satisfies the estimate (3.4) in the half-plane
whose resolvent satisfies the estimate (3.4) in the half-plane 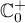 . Then a semigroup
. Then a semigroup  whose infinitesimal operator is the operator
whose infinitesimal operator is the operator  admits the estimate
admits the estimate
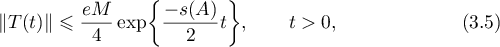
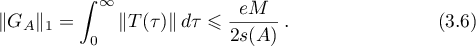
Proof. To obtain the estimates we use Theorem 8, setting 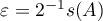 . For this
. For this 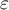 we obtain the following estimates for the quantities
we obtain the following estimates for the quantities  and
and 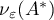 :
:
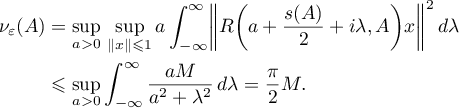
Since

the same constant 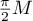 estimates the quantity
estimates the quantity 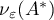 . The estimate (3.5) now follows from (1.26), and the estimate (3.6) from (3.5). The theorem is proved.
. The estimate (3.5) now follows from (1.26), and the estimate (3.6) from (3.5). The theorem is proved.
Proof of Theorem 9 Using the representation of the function  in the form (2.5), the equations
in the form (2.5), the equations  ,
, 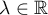 , and the properties of the Fourier transform, we obtain the estimates
, and the properties of the Fourier transform, we obtain the estimates
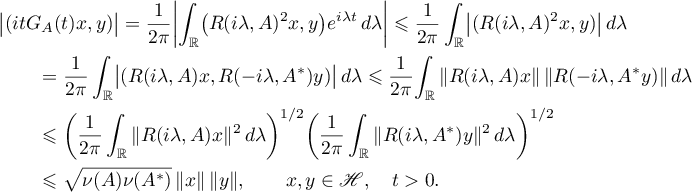
Now, the vectors 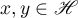 are arbitrary, so we set
are arbitrary, so we set 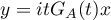 . Then
. Then

Consequently, the estimates (1.27), (1.28) hold. The theorem is proved.
Theorem 10 (the estimates (1.29)) immediately follows from Theorem 9.
Theorem 11 (the estimates (1.30)) follows from Theorems 5 and 9.
§ 4. On the numerical range of the infinitesimal operator of an operator semigroup
In connection with Theorem 6, the question of estimating the quantities 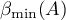 ,
, 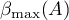 for the infinitesimal operator
for the infinitesimal operator  of an operator semigroup
of an operator semigroup 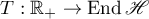 plays an important role. These quantities can be infinite, and, moreover, here we construct an example of an operator semigroup whose infinitesimal operator has compact resolvent and linear combinations of whose eigenvectors are dense in the entire space. In this example the numerical range of the infinitesimal operator fills the entire complex plane
plays an important role. These quantities can be infinite, and, moreover, here we construct an example of an operator semigroup whose infinitesimal operator has compact resolvent and linear combinations of whose eigenvectors are dense in the entire space. In this example the numerical range of the infinitesimal operator fills the entire complex plane  .
.
Example 1. An operator semigroup  , where
, where 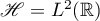 , of the form
, of the form
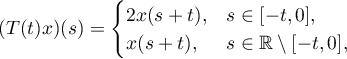
is such that 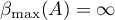 for its infinitesimal operator
for its infinitesimal operator  . This fact follows from the equations
. This fact follows from the equations 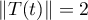 ,
, 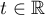 , and Theorem 5.
, and Theorem 5.
Example 2. We consider the Hilbert space  of sequences
of sequences  , where
, where  ,
, 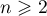 , with the inner product
, with the inner product 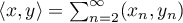 ,
, 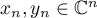 . We define a sequence
. We define a sequence  ,
, 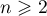 , of nilpotent operators by the equations
, of nilpotent operators by the equations
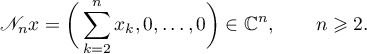
The nilpotency index of every operator 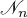 is equal to two, that is,
is equal to two, that is,  . We consider the family of vectors
. We consider the family of vectors 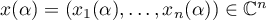 ,
,  , where
, where
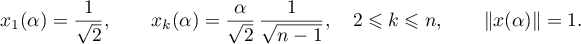
The numerical range 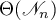 of the nilpotent operator
of the nilpotent operator 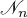 contains the set of complex numbers of the form
contains the set of complex numbers of the form
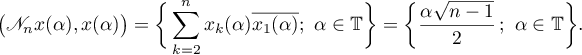
Thus,
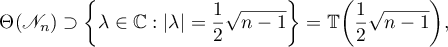
where the right-hand side is the circle of radius  . By Hausdorff's theorem [13] the set
. By Hausdorff's theorem [13] the set 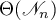 is convex and therefore contains the disc
is convex and therefore contains the disc
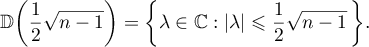
We further consider the operators
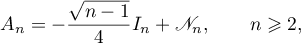
where 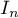 is the identity operator in
is the identity operator in 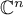 . From these operators we construct an operator semigroup
. From these operators we construct an operator semigroup 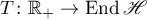 by the formula
by the formula
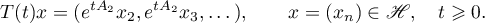
Since
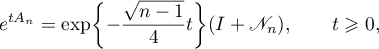
it follows that
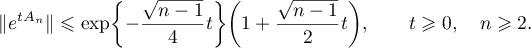
Since
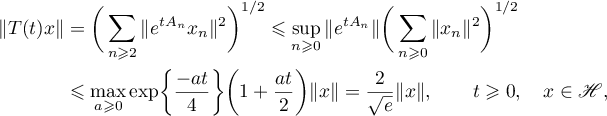
it follows that the operator semigroup  is bounded, and
is bounded, and
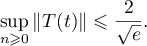
It is easy to see that 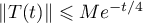 ,
, 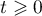 , that is, the semigroup constructed above is exponentially stable. In view of the fact that the semigroup
, that is, the semigroup constructed above is exponentially stable. In view of the fact that the semigroup  is continuous on every finite-dimensional subspace
is continuous on every finite-dimensional subspace  ,
, 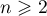 , and this system of subspaces is dense in
, and this system of subspaces is dense in  , the boundedness of the operator semigroup
, the boundedness of the operator semigroup  implies that it is strongly continuous on
implies that it is strongly continuous on  .
.
Let  be the infinitesimal operator of the operator semigroup
be the infinitesimal operator of the operator semigroup  constructed above. Since the subspaces
constructed above. Since the subspaces 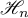 ,
, 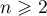 , are invariant for
, are invariant for  , the numerical range
, the numerical range 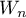 of the restriction
of the restriction 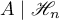 of the operator
of the operator  to
to 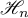 is contained in the numerical range
is contained in the numerical range  of the operator
of the operator  . Since
. Since
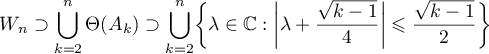
(we have used the equation  ) and since the set
) and since the set
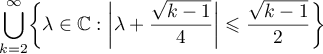
coincides with  , it follows that
, it follows that 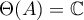 . It follows from the definition of the operator
. It follows from the definition of the operator  that the eigenvectors and generalized eigenvectors of this operator generate the space
that the eigenvectors and generalized eigenvectors of this operator generate the space  , and the operator
, and the operator  has compact resolvent.
has compact resolvent.
We now consider the sequence of operators 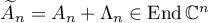 ,
, 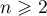 , where
, where  ,
,  . We extend the definition of the operator semigroup
. We extend the definition of the operator semigroup  by the equations
by the equations

Its infinitesimal operator is the operator  , where
, where  ,
, 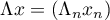 ,
,  . This operator semigroup is strongly continuous (since
. This operator semigroup is strongly continuous (since  is a bounded perturbation of the operator
is a bounded perturbation of the operator  ), the numerical range
), the numerical range 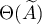 of
of  coincides with
coincides with  , the resolvent of
, the resolvent of  is compact, and the linear hull of the eigenvectors of
is compact, and the linear hull of the eigenvectors of  is dense in the space
is dense in the space  (
( has no generalized eigenvectors).
has no generalized eigenvectors).
§ 5. Proofs of Theorems 14, 15
Let  be a hyperbolic relation on a Banach space
be a hyperbolic relation on a Banach space  , that is, condition (1.31) holds. Then the spectrum
, that is, condition (1.31) holds. Then the spectrum 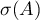 of
of  can be represented in the form (1.32). We consider the quantities
can be represented in the form (1.32). We consider the quantities  and
and 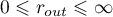 setting
setting  if
if  , and
, and  if
if 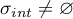 . We set
. We set  if
if  , and
, and 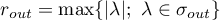 if
if 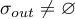 .
.
The resolvent 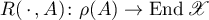 of the relation
of the relation  is a pseudoresolvent (see [1]), which by condition (1.31) of Theorem 14 is holomorphic on the open set
is a pseudoresolvent (see [1]), which by condition (1.31) of Theorem 14 is holomorphic on the open set 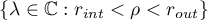 . Therefore, using the functional calculus for linear relations [25] or Theorem 5.9.3 in [1] for pseudoresolvents (see also the proof of Theorem 6.1 in [27]), we obtain the representation
. Therefore, using the functional calculus for linear relations [25] or Theorem 5.9.3 in [1] for pseudoresolvents (see also the proof of Theorem 6.1 in [27]), we obtain the representation
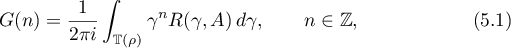
where  is the circle of radius
is the circle of radius 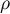 satisfying
satisfying  .
.
For 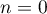 we obtain the formula (see also formula (1.34))
we obtain the formula (see also formula (1.34))

for the Riesz projector 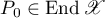 constructed with respect to the spectral set
constructed with respect to the spectral set  .
.
First we suppose that 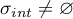 and estimate the norms
and estimate the norms 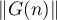 of the operators
of the operators  ,
, 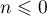 .
.
It follows from the representation (1.37) of the Green's function 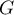 that
that
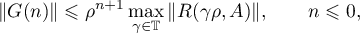
where 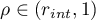 . We express the relation
. We express the relation  , where
, where 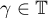 ,
, 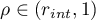 , in the following form:
, in the following form:
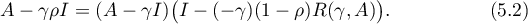
Since the operator
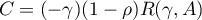
satisfies  ,
, 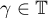 , it follows that
, it follows that  for
for 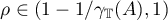 . Since the spectral radius of a bounded operator does not exceed its norm, we have the inequality
. Since the spectral radius of a bounded operator does not exceed its norm, we have the inequality
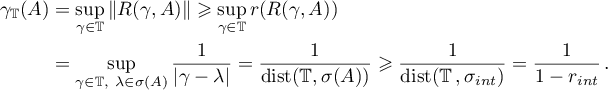
Here we have used the equation
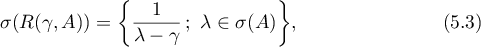
which follows from Theorem 2.4 in [25]. Consequently,  and
and 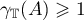 .
.
Then it follows from equation (5.2) that the relation  is continuously invertible,
is continuously invertible,  , and the estimate
, and the estimate
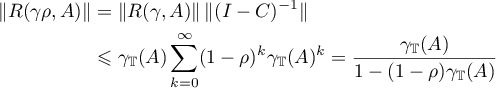
holds for all 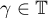 and
and 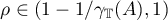 . Therefore,
. Therefore,
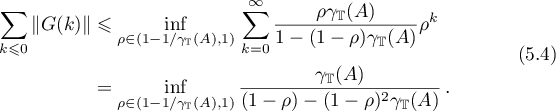
The infimum is attained at the point 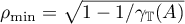 . In order to avoid a cumbersome expression for the estimate, we set
. In order to avoid a cumbersome expression for the estimate, we set  on the right-hand side of (5.4). Then we have the estimate
on the right-hand side of (5.4). Then we have the estimate
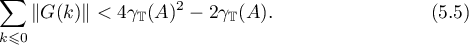
Now suppose that 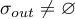 . It follows from (5.3), where
. It follows from (5.3), where 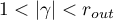 , that
, that
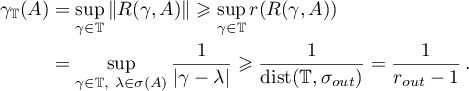
Therefore,  . We write the relation
. We write the relation  in the form
in the form
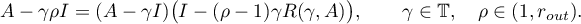
Since
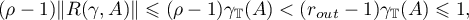
the relation  is continuously invertible for all
is continuously invertible for all 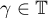 ,
,  and
and
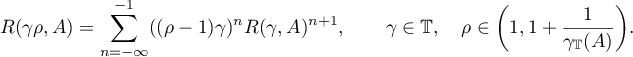
Consequently,
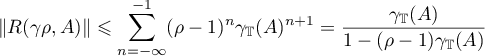
for all 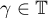 and
and  . Therefore we obtain the estimate
. Therefore we obtain the estimate
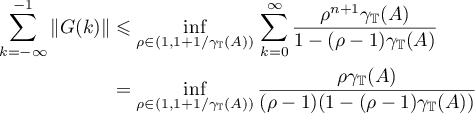
from formula (5.1). We set 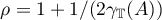 ; then
; then
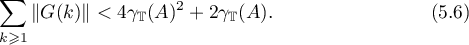
The estimates (5.5) and (5.6) obtained above yield the estimates in the theorem that are to be proved. Theorem 14 is proved.
Proof of Theorem 15 Since the relation 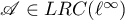 is continuously invertible, every solution
is continuously invertible, every solution 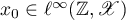 of the nonlinear difference inclusion (1.39) is a solution of the difference equation
of the nonlinear difference inclusion (1.39) is a solution of the difference equation
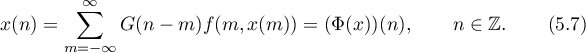
The converse is also true. The map 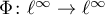 defined by the right-hand side of this equation satisfies a Lipschitz condition with constant
defined by the right-hand side of this equation satisfies a Lipschitz condition with constant
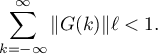
Consequently, equation (5.7) is solvable by the contraction mapping principle, and its solution is a solution of the difference inclusion (1.39). The theorem is proved.
§ 6. Hyperbolicity conditions for some classes of operator semigroups. Examples
We consider an operator of the form
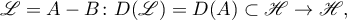
where 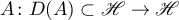 is an antiselfadjoint operator (that is,
is an antiselfadjoint operator (that is, 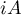 is selfadjoint) with domain of definition
is selfadjoint) with domain of definition 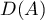 and
and 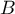 is an invertible selfadjoint operator in the algebra
is an invertible selfadjoint operator in the algebra  . By Stone's theorem (see [1], Theorem 22.4.3) the operator
. By Stone's theorem (see [1], Theorem 22.4.3) the operator  is the infinitesimal operator of some strongly continuous group of isometry operators
is the infinitesimal operator of some strongly continuous group of isometry operators 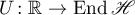 . Consequently, the operator
. Consequently, the operator 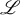 is the infinitesimal operator of some operator group
is the infinitesimal operator of some operator group 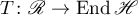 of class
of class  (see [1], Theorem 13.2.1).
(see [1], Theorem 13.2.1).
If  and
and 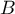 commute, then the operator
commute, then the operator 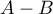 is a normal operator, and therefore its spectrum
is a normal operator, and therefore its spectrum 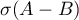 is contained in the set
is contained in the set
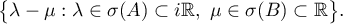
Consequently,  and
and 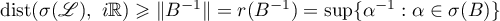 . Therefore,
. Therefore, 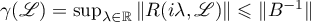 . Thus, by Theorem 2 (conditions (1.4) and (1.5) hold) the operator semigroup
. Thus, by Theorem 2 (conditions (1.4) and (1.5) hold) the operator semigroup  is hyperbolic. If the operators
is hyperbolic. If the operators  and
and 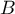 do not commute, then this result, generally speaking, is not true.
do not commute, then this result, generally speaking, is not true.
We introduce some quantities and concepts in terms of which we shall state the result on hyperbolicity conditions for the operator semigroup  under consideration.
under consideration.
We consider the two sets

and the two quantities

where

that is, 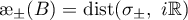 and
and 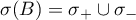 . In what follows we assume that both
. In what follows we assume that both  and
and  are non-empty sets.
are non-empty sets.
Let 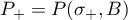 and
and 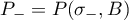 denote the Riesz projectors constructed with respect to the sets
denote the Riesz projectors constructed with respect to the sets  and
and  , respectively. Since the operator
, respectively. Since the operator 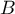 is selfadjoint, these projectors are orthogonal.
is selfadjoint, these projectors are orthogonal.
Along with the operator  we consider the transformer (operator in the space of operators)
we consider the transformer (operator in the space of operators)  with domain of definition
with domain of definition 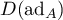 consisting of operators
consisting of operators 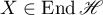 that take the domain of definition
that take the domain of definition 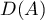 into the domain of definition
into the domain of definition 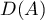 ; furthermore, the operator
; furthermore, the operator 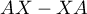 admits an extension with domain of definition
admits an extension with domain of definition 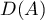 to some operator
to some operator  in
in  , which we denote by the same symbol
, which we denote by the same symbol 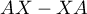 or
or ![$[A,X]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn424.gif) . Furthermore, we set
. Furthermore, we set  .
.
Theorem 19. (see [32]) Suppose that an invertible operator 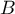 belongs to the domain of definition
belongs to the domain of definition 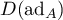 of the transformer
of the transformer 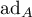 and one of the following conditions holds:
and one of the following conditions holds:
- 1)
 ,
, - 2)
![$\|[B, AB-BA]\| < {\unicode{230}}_{0}(B){\unicode{230}}(B)^{2}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) ,
, - 3)
 ,
,  ,
,
where 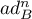 is the
is the 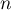 th power of the bounded transformer
th power of the bounded transformer  defined by the formula
defined by the formula 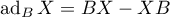 ,
, 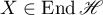 . Then the semigroup
. Then the semigroup  (whose infinitesimal operator is the operator
(whose infinitesimal operator is the operator 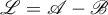 ) is hyperbolic and the following estimates hold (corresponding to each of the conditions of the theorem):
) is hyperbolic and the following estimates hold (corresponding to each of the conditions of the theorem):
- 1')
 ,
, - 2')
![$\gamma(\mathscr{L}) \leqslant \dfrac{{\unicode{230}}(B)^{2}}{{\unicode{230}}_{0}(B){\unicode{230}}(B)^{2}-\|[B,AB-BA]\|}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) ,
, - 3')
 ,
,  ,
,
where  .
.
It is important to note that since  is antiselfadjoint and the operator
is antiselfadjoint and the operator 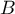 is selfadjoint we have
is selfadjoint we have  ,
,  . Therefore,
. Therefore,
We consider a concrete example of a differential operator satisfying the conditions of Theorem 19.
Example 3. Let  be the differentiation operator acting in the Hilbert space
be the differentiation operator acting in the Hilbert space 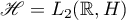 of square-integrable functions defined on
of square-integrable functions defined on 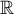 with values in a complex Hilbert space
with values in a complex Hilbert space  . Recall that
. Recall that 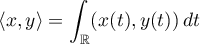 ,
, 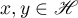 , is the inner product in
, is the inner product in  if
if  is the inner product in
is the inner product in  . Its domain of definition is the Sobolev space
. Its domain of definition is the Sobolev space 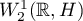 contained in
contained in 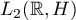 . The operator
. The operator  is the infinitesimal operator of the group of (isometry) operators of shifts of functions in
is the infinitesimal operator of the group of (isometry) operators of shifts of functions in 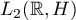 and therefore is antiselfadjoint.
and therefore is antiselfadjoint.
If 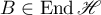 is the operator of multiplication by a bounded continuous function
is the operator of multiplication by a bounded continuous function  , that is,
, that is, 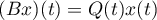 ,
,  ,
, 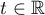 , then
, then 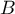 belongs to
belongs to 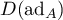 if
if 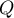 is continuously differentiable and its derivative
is continuously differentiable and its derivative  is bounded on
is bounded on 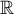 . In this case,
. In this case, 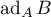 is the operator of multiplication by the derivative
is the operator of multiplication by the derivative 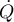 of
of 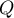 , that is,
, that is,
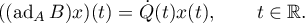
Theorem 19 immediately implies the following theorem.
Theorem 20. Suppose that 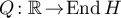 is a continuously differentiable bounded function with bounded derivative
is a continuously differentiable bounded function with bounded derivative 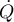 whose values are selfadjoint invertible operators, and suppose that one of the following conditions holds:
whose values are selfadjoint invertible operators, and suppose that one of the following conditions holds:
- 1)
 ,
, - 2)
 ,
,
where
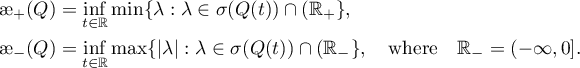
Then the differential operator  is invertible and the inverse operator admits the estimate corresponding to conditions 1), 2):
is invertible and the inverse operator admits the estimate corresponding to conditions 1), 2):
 ,
,  .
.
We point out that it follows from [2] that the differential operator 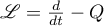 under consideration is the infinitesimal operator of the strongly continuous operator group
under consideration is the infinitesimal operator of the strongly continuous operator group 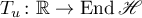 defined by the equations
defined by the equations
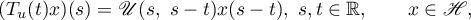
where 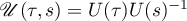 ,
,  , and
, and 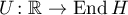 is the Cauchy operator function, that is,
is the Cauchy operator function, that is,  ,
, 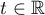 ,
, 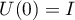 (see [40], Ch. III). Under the hypotheses of Theorem 14 the operator semigroup
(see [40], Ch. III). Under the hypotheses of Theorem 14 the operator semigroup 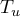 is hyperbolic.
is hyperbolic.
The next theorem follows directly from Theorem 20 and the remark made after the statement of Theorem 11.
Theorem 21. Suppose that a function 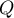 is bounded, continuously differentiable,
is bounded, continuously differentiable,  , and condition 2) of Theorem 20 holds. Then the operator
, and condition 2) of Theorem 20 holds. Then the operator
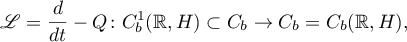
where  , is continuously invertible and its norm
, is continuously invertible and its norm  admits the estimate
admits the estimate
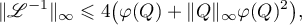
where ![$\varphi(Q)={\unicode{230}}(Q)^{2}\bigl({\unicode{230}}_{0}(Q){\unicode{230}}(Q)^{2}- \|[Q,\dot{Q}]\|_{\infty}\bigr)$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn477.gif) and
and ![$\|[Q,\dot{Q}]\|_{\infty}$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn478.gif) is the norm of the function
is the norm of the function ![$Q\dot{Q}-\dot{Q}Q=[Q, \dot{Q}]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn479.gif) in
in  .
.
To estimate the quantities defined by formulae (1.13)–(1.17) and used in Theorems 6, 7, 9–11, 18, 21, we can apply the method of similar operators described in [34]–[37]. Note that this method can be applied to a wider class of operators than those considered here.
Suppose that  is a selfadjoint operator, semibounded above, with compact resolvent and that its spectrum
is a selfadjoint operator, semibounded above, with compact resolvent and that its spectrum 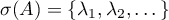 has the properties
has the properties
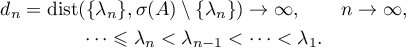
As  is semibounded above, the quantity
is semibounded above, the quantity 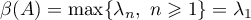 is finite. Let
is finite. Let  ,
, 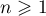 , be the Riesz projectors (these are orthoprojectors) constructed with respect to the one-point sets
, be the Riesz projectors (these are orthoprojectors) constructed with respect to the one-point sets  ,
, 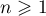 . Then
. Then  ,
, 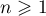 , and
, and 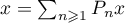 ,
,  . The operator
. The operator  is sectorial, and, moreover, it is the infinitesimal operator of the operator semigroup
is sectorial, and, moreover, it is the infinitesimal operator of the operator semigroup
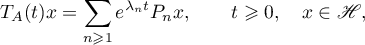
for which 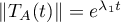 ,
, 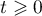 . The operator
. The operator 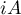 is antiselfadjoint and therefore is the infinitesimal operator of the isometry group
is antiselfadjoint and therefore is the infinitesimal operator of the isometry group
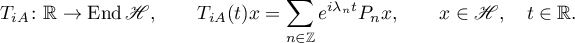
For any positive integer 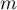 , we define two transformers in the algebra
, we define two transformers in the algebra 

The transformer 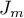 (the operator of block diagonalization) is defined by the formula
(the operator of block diagonalization) is defined by the formula
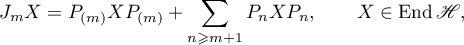
where the convergence of the series is understood in the strong operator topology and the projector 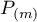 has the form
has the form 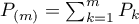 . It is easy to show that
. It is easy to show that 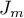 is a projector and
is a projector and 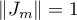 (see [36], [37]); furthermore, the series in the definition of
(see [36], [37]); furthermore, the series in the definition of  is unconditionally strongly convergent. If the image
is unconditionally strongly convergent. If the image  of every projector
of every projector  ,
, 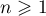 , is one-dimensional, then
, is one-dimensional, then  ,
, 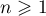 , where
, where 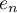 is an eigenvector of the operator
is an eigenvector of the operator  corresponding to the eigenvalue
corresponding to the eigenvalue  . In this case, the matrix of the operator
. In this case, the matrix of the operator 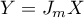 with respect to the orthonormal basis
with respect to the orthonormal basis 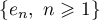 has the form
has the form  , where
, where 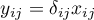 and
and  is the Kronecker delta for
is the Kronecker delta for 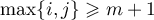 , and
, and 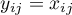 if
if 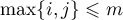 . Here,
. Here, 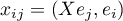 ,
, 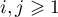 , is the matrix of an operator
, is the matrix of an operator 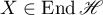 .
.
We define the transformer  using the transformer
using the transformer  ,
,
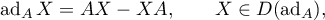
with domain of definition 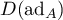 consisting of operators
consisting of operators 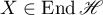 that have the following properties:
that have the following properties:
- 1)
 ,
, - 2)the operator
 admits a bounded extension
admits a bounded extension  to the space
to the space  (and we set
(and we set  .
.
The transformer  is defined on every operator
is defined on every operator 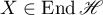 as the (unique) solution
as the (unique) solution 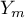 of the equation
of the equation
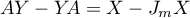
satisfying the condition 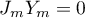 . Thus,
. Thus,  for any operator
for any operator 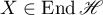 . The transformer
. The transformer  is a bounded operator, and the estimate
is a bounded operator, and the estimate
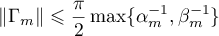
holds (see [34], [36]), where 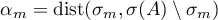 and
and 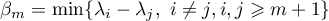 . Consequently,
. Consequently,  . In addition we point out that the operator
. In addition we point out that the operator 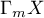 , where
, where 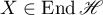 , is completely determined by operators of the form (operator blocks)
, is completely determined by operators of the form (operator blocks)
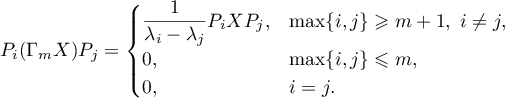
Consequently, if 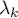 ,
,  , are simple eigenvalues of the operator
, are simple eigenvalues of the operator  , then the matrix
, then the matrix  of the operator
of the operator  has the form
has the form
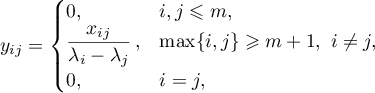
where 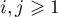 and
and  ,
, 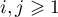 , is the matrix of the operator
, is the matrix of the operator 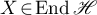 .
.
Definition 3. Two linear operators 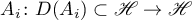 ,
, 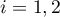 , are said to be similar if there exists a continuously invertible operator
, are said to be similar if there exists a continuously invertible operator  such that
such that  and
and  ,
, 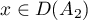 . The operator
. The operator  is called the operator of transformation of
is called the operator of transformation of 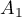 into the operator
into the operator 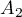 .
.
Similar operators have a number of coinciding spectral properties. We have the following lemma, which follows immediately from Definition 3.
Lemma 2. Suppose that  ,
, 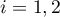 , are two similar operators and
, are two similar operators and  is an operator of transformation of
is an operator of transformation of 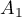 into
into 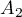 . Then the following hold:
. Then the following hold:
1)  ,
,  ,
,  ,
,  , where
, where  ,
,  ,
, 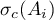 ,
, 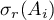 ,
, 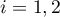 , are the spectrum, the discrete, continuous, and residual spectra of the operators
, are the spectrum, the discrete, continuous, and residual spectra of the operators  ,
, 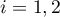 , respectively;
, respectively;
2) if the operator 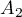 admits a decomposition
admits a decomposition 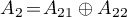 , where
, where 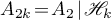 ,
,  , is the restriction of
, is the restriction of 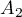 to
to  with respect to the direct sum
with respect to the direct sum 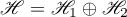 of subspaces
of subspaces 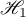 ,
, 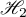 that are invariant under
that are invariant under 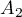 , then the subspaces
, then the subspaces 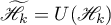 ,
,  , are invariant under the operator
, are invariant under the operator 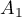 and
and  , where
, where  ,
,  , with respect to the decomposition
, with respect to the decomposition  ; furthermore, if
; furthermore, if 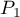 is the projector effecting the decomposition
is the projector effecting the decomposition 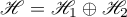 (that is,
(that is, 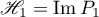 is the image of the projector
is the image of the projector 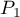 and
and  , where
, where 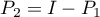 is the complementary projector of
is the complementary projector of 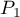 ), then the projector
), then the projector  effecting the decomposition
effecting the decomposition  , is defined by the formula
, is defined by the formula
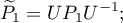
3) if 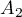 is the infinitesimal operator of a strongly continuous operator semigroup
is the infinitesimal operator of a strongly continuous operator semigroup 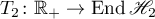 , then the operator
, then the operator 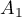 is the infinitesimal operator of the strongly continuous operator semigroup
is the infinitesimal operator of the strongly continuous operator semigroup
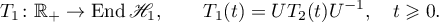
The following result (see [34]–[37]) is the main result where the method of similar operators is used in problems concerning obtaining estimates for the parameters of exponential dichotomy and the Green's function of a perturbed selfadjoint operator  with the properties listed above.
with the properties listed above.
Theorem 22. Suppose that  and a positive integer
and a positive integer 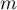 is chosen in such a way that the condition
is chosen in such a way that the condition
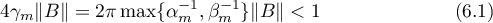
holds. Then the operator 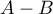 is similar to the operator
is similar to the operator 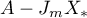 , where the operator
, where the operator  is a solution of the (nonlinear) equation
is a solution of the (nonlinear) equation
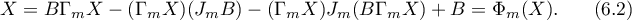
This solution can be found using the method of simple iterations by setting 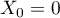 ,
,  (the operator
(the operator 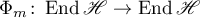 is a contraction in the ball
is a contraction in the ball  , and the operator
, and the operator 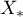 is contained in this ball). A similarity transformation of the operator
is contained in this ball). A similarity transformation of the operator 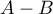 into the operator
into the operator  is effected by the operator
is effected by the operator  , that is,
, that is,
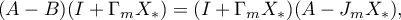
Furthermore, 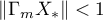 .
.
Theorem 18 and Lemma 2 imply the following.
Theorem 23. Suppose that  and a positive integer
and a positive integer 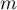 satisfies (6.1). The operator
satisfies (6.1). The operator 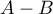 and the similar operator
and the similar operator  (by Theorem 18) are the infinitesimal operators of the analytic operator semigroups
(by Theorem 18) are the infinitesimal operators of the analytic operator semigroups  ,
, 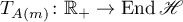 , respectively, and the equations
, respectively, and the equations
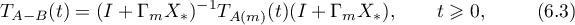
hold, where 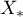 is a solution of the nonlinear equation (6.2) satisfying the condition
is a solution of the nonlinear equation (6.2) satisfying the condition  . If the operator semigroup
. If the operator semigroup  is hyperbolic, then the operator semigroup
is hyperbolic, then the operator semigroup  is also hyperbolic and the Green's functions
is also hyperbolic and the Green's functions  ,
, 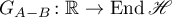 constructed for them are connected by the similarity relation
constructed for them are connected by the similarity relation
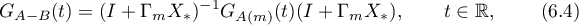
and
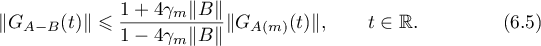
Thus, because of (6.3) and (6.4), the method of similar operators makes it possible to reduce studying the operator semigroup  to studying the operator semigroup
to studying the operator semigroup  and to obtain estimates for the Green's function
and to obtain estimates for the Green's function 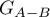 by using estimates of the Green's function
by using estimates of the Green's function  under the condition that the operator semigroup
under the condition that the operator semigroup  is hyperbolic.
is hyperbolic.
It follows from the form of the operator  that it commutes with all the projectors
that it commutes with all the projectors 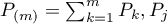 ,
,  . Consequently, the subspaces
. Consequently, the subspaces 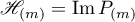 ,
, 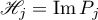 ,
, 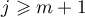 , are invariant under the operator
, are invariant under the operator 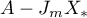 . These subspaces also have the same invariance property for the operators
. These subspaces also have the same invariance property for the operators 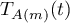 ,
, 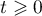 .
.
The Hilbert space  can be represented in the form
can be represented in the form
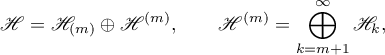
which is an orthogonal direct sum of the subspaces 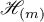 ,
,  ,
,  . Therefore the operator semigroup
. Therefore the operator semigroup  and the Green's function
and the Green's function  (under the condition that
(under the condition that  is hyperbolic) admit decompositions of the form
is hyperbolic) admit decompositions of the form
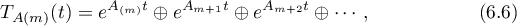
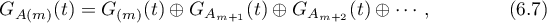
where 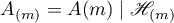 ,
, 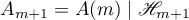 ,
, 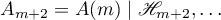 , the Green's function
, the Green's function 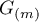 is constructed for the operator
is constructed for the operator 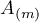 ,
,  is constructed for the operator
is constructed for the operator  , and so on. Note that the operators
, and so on. Note that the operators  act in the finite-dimensional spaces
act in the finite-dimensional spaces  , respectively; furthermore, it follows from Theorem 18 (from equation (6.2)) that these operators are determined by the equations
, respectively; furthermore, it follows from Theorem 18 (from equation (6.2)) that these operators are determined by the equations
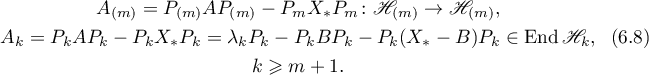
Equation (6.2), whose solution is the operator 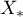 , and the definition of the transformers
, and the definition of the transformers  ,
, 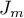 imply the equations
imply the equations
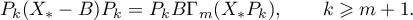
Since (we use the equations 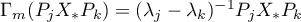 ,
, 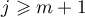 ,
, 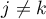 )
)
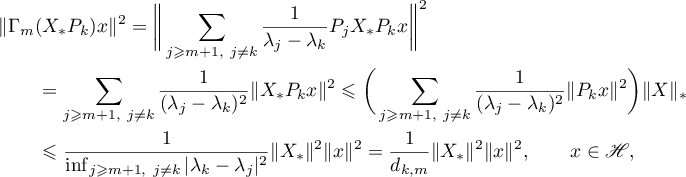
it follows that  ,
,  , and therefore,
, and therefore,
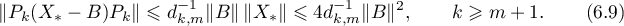
It follows from the representation (6.7) of the Green's function  of the operator
of the operator  that
that
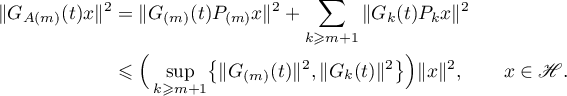
Therefore we have the estimates (see (6.5))
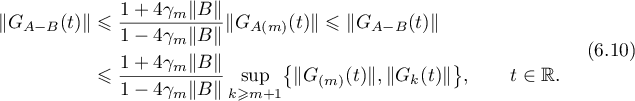
Thus, due to the method of similar operators it is possible to `split' the operator  and reduce estimating the Green's function
and reduce estimating the Green's function  to estimating the Green's functions
to estimating the Green's functions 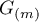 ,
,  ,
,  , which are constructed for operators acting in finite-dimensional spaces. It follows from (6.8), which gives a representation of the operators
, which are constructed for operators acting in finite-dimensional spaces. It follows from (6.8), which gives a representation of the operators 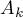 ,
,  , that
, that

where 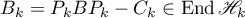 ,
,  ,
,  , and the estimate (6.9) implies that
, and the estimate (6.9) implies that 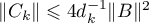 . Consequently
. Consequently 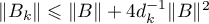 . Therefore there exists a positive integer
. Therefore there exists a positive integer 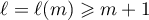 such that
such that
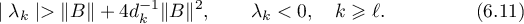
It follows from these estimates and (6.6) that the operator exponential  decays exponentially and, consequently,
decays exponentially and, consequently,  ;
; 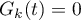 ,
, 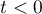 ,
, 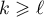 . Therefore the question of whether the operator semigroup
. Therefore the question of whether the operator semigroup  is hyperbolic has been reduced to the question of whether the operator group
is hyperbolic has been reduced to the question of whether the operator group  ,
,  ,
,  , is hyperbolic. Thus, we have established the following.
, is hyperbolic. Thus, we have established the following.
Theorem 24. The operator semigroup  is hyperbolic if and only if the following conditions hold:
is hyperbolic if and only if the following conditions hold:
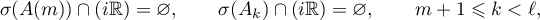
where the number  is such that (6.11) holds. When these conditions hold, the Green's function
is such that (6.11) holds. When these conditions hold, the Green's function 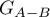 admits the estimate (6.10).
admits the estimate (6.10).
We point out that if the number 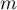 is chosen to be sufficiently big (satisfying the estimate (6.11), where
is chosen to be sufficiently big (satisfying the estimate (6.11), where 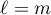 , along with condition (6.1)), then the condition that the semigroup
, along with condition (6.1)), then the condition that the semigroup  be hyperbolic is equivalent to the validity of the condition
be hyperbolic is equivalent to the validity of the condition  . It is also important to note that the operator
. It is also important to note that the operator  can be represented in the form
can be represented in the form
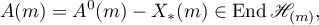
where
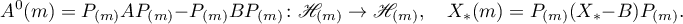
Furthermore,  .
.
Let ![$\mathscr{H}=L^{2}[0,1]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn625.gif) be the Hilbert space of square-integrable complex-valued functions defined on the interval
be the Hilbert space of square-integrable complex-valued functions defined on the interval ![$[0,1]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn626.gif) with the inner product
with the inner product 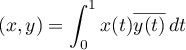 ,
, 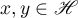 . An example of an operator satisfying the conditions listed above is given by the differential operator
. An example of an operator satisfying the conditions listed above is given by the differential operator
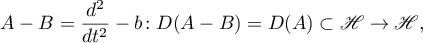
where 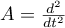 ,
,  is the operator of multiplication by an essentially bounded function
is the operator of multiplication by an essentially bounded function ![$b\colon [0,1] \to \mathbb{C}$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn629.gif) (in what follows,
(in what follows, ![$\|b\|_{\infty}=\operatorname{ess}\,\sup_{t \in [0,1]}|b(t)|$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn630.gif) ), and
), and ![$D(A)=\{x \in \mathscr{H}: x \ \text{is absolutely continuous and} \ \dot{x} \in L^{2} [0,1]\}$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn631.gif) .
.
The operator  is a selfadjoint operator with compact resolvent. Its spectrum coincides with the set
is a selfadjoint operator with compact resolvent. Its spectrum coincides with the set  , the eigenfunctions
, the eigenfunctions  ,
, ![$t\in [0,1]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn634.gif) ,
, 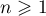 , form an orthonormal basis in
, form an orthonormal basis in ![$\mathscr{H}=L^{2}[0,1]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn625.gif) , and
, and  ,
, 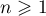 . The operator
. The operator 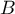 is bounded and
is bounded and  . The Riesz projector
. The Riesz projector  constructed with respect to the one-point set
constructed with respect to the one-point set  has the form
has the form  ,
, 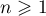 , and
, and  . In this case the quantities used in Theorem 20 have the form
. In this case the quantities used in Theorem 20 have the form
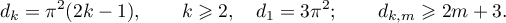
§ 7. Comments on the results obtained and some additional assertions
To estimate the parameters of exponential stability of a strongly continuous operator semigroup  , one can use the Hille-Phillips-Yosida theorem (see [1]). The following holds.
, one can use the Hille-Phillips-Yosida theorem (see [1]). The following holds.
Theorem 25. For numbers  , where
, where  ,
,  , to be the parameters of exponential stability of a semigroup
, to be the parameters of exponential stability of a semigroup  with infinitesimal operator
with infinitesimal operator  it is necessary and sufficient that for all
it is necessary and sufficient that for all 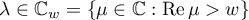 and
and 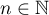 the following estimates hold:
the following estimates hold:

Condition (7.1) is difficult to verify because of the need to estimate the norms of powers of the operators  ,
,  .
.
If  is a finite-dimensional space and an operator
is a finite-dimensional space and an operator  has spectrum
has spectrum 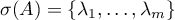 with
with 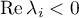 ,
, 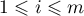 , then the exponential stability of the operator-valued function
, then the exponential stability of the operator-valued function 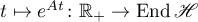 follows from the following Gel'fand-Shilov estimate (see [41], Ch. II, §6, and [40], Ch. I, Exercise 16):
follows from the following Gel'fand-Shilov estimate (see [41], Ch. II, §6, and [40], Ch. I, Exercise 16):

where 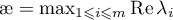 and
and 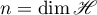 . This estimate can be used to estimate the parameters of exponential stability of the operator semigroup
. This estimate can be used to estimate the parameters of exponential stability of the operator semigroup  in §6. Namely, after a similarity transformation, estimating the Green's function
in §6. Namely, after a similarity transformation, estimating the Green's function 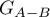 reduces to estimating the Green's function
reduces to estimating the Green's function  constructed for the operator
constructed for the operator  . Using the estimates (7.2), an estimate for the Green's function under the condition
. Using the estimates (7.2), an estimate for the Green's function under the condition  makes it possible to obtain a sufficient condition for the exponential decay of the operator semigroup
makes it possible to obtain a sufficient condition for the exponential decay of the operator semigroup  and the corresponding estimates on the parameters of exponential stability.
and the corresponding estimates on the parameters of exponential stability.
The exponential decay of an operator semigroup  satisfying the condition
satisfying the condition  ,
,  , was established by Pazy (see [42], [43]). The principle of uniform boundedness for operators (see [1]) implies that
, was established by Pazy (see [42], [43]). The principle of uniform boundedness for operators (see [1]) implies that
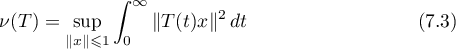
is finite. Since the semigroup  is decaying exponentially, it follows that
is decaying exponentially, it follows that 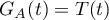 ,
,  , and therefore it follows from equation (7.3) that
, and therefore it follows from equation (7.3) that 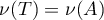 . Consequently, we can apply Theorem 7 to estimate this type of operator semigroup. Thus, the following holds.
. Consequently, we can apply Theorem 7 to estimate this type of operator semigroup. Thus, the following holds.
Theorem 26. Suppose that an operator semigroup  satisfies the Pazy condition (the quantity (7.3) is finite). Then
satisfies the Pazy condition (the quantity (7.3) is finite). Then  is an exponentially stable operator semigroup and the estimate
is an exponentially stable operator semigroup and the estimate
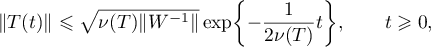
holds for this semigroup under the condition that the solution  of Lyapunov's equation (1.23), defined by formula (1.24), is continuously invertible.
of Lyapunov's equation (1.23), defined by formula (1.24), is continuously invertible.
Under the condition that the operator 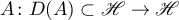 can be represented in the form
can be represented in the form 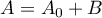 , where
, where 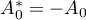 ,
,  , this operator is the infinitesimal operator (see [1]) of a strongly continuous operator group
, this operator is the infinitesimal operator (see [1]) of a strongly continuous operator group  with numerical range for which
with numerical range for which 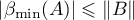 and
and 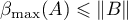 . Therefore Assumption 1 in §2 holds and, consequently, the assertion of Theorem 6 is true for these operators; also the quantities
. Therefore Assumption 1 in §2 holds and, consequently, the assertion of Theorem 6 is true for these operators; also the quantities 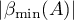 and
and 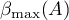 (in the estimates (1.21) and (1.22)) can be replaced by the number
(in the estimates (1.21) and (1.22)) can be replaced by the number 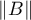 .
.
Commenting on the results of §6 we point out that if a linear relation 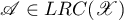 is a closed linear operator, then it was established in [30] that the operator
is a closed linear operator, then it was established in [30] that the operator  is invertible simultaneously in all the spaces
is invertible simultaneously in all the spaces 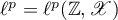 ,
, ![$p \in [1,\infty]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn18.gif) , and the following estimates were obtained for the Green's function
, and the following estimates were obtained for the Green's function  :
:
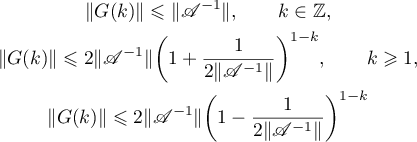
if  ,
, 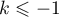 , and
, and 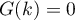 if
if 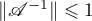 (if
(if  is a Hilbert space, then in all these estimates the quantity
is a Hilbert space, then in all these estimates the quantity  can be replaced by the quantity
can be replaced by the quantity 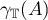 ). Furthermore, the estimate
). Furthermore, the estimate
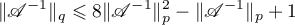
is true, where the symbols 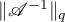 and
and 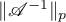 denote the norm of
denote the norm of 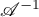 in the spaces
in the spaces  and
and 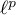 , respectively. In particular, if
, respectively. In particular, if 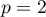 and
and  is a Hilbert space, then
is a Hilbert space, then  and therefore,
and therefore,
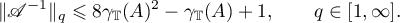
If the operator  belongs to the algebra
belongs to the algebra  , then
, then  ,
, ![$p \in [1,\infty]$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn18.gif) , and we can use the results in [43]–[47] about estimates for elements of inverse matrices for bounded operators (see also [48]) to estimate the Green's function
, and we can use the results in [43]–[47] about estimates for elements of inverse matrices for bounded operators (see also [48]) to estimate the Green's function 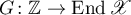 . For example, Theorem 3 in [43], in particular, gives the estimate
. For example, Theorem 3 in [43], in particular, gives the estimate 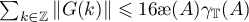 , where
, where 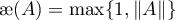 , under the assumption that
, under the assumption that  is a Hilbert space.
is a Hilbert space.
For an operator  ,
,  , such that
, such that 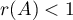 , estimates for the norms of powers of the operator
, estimates for the norms of powers of the operator  of the form
of the form
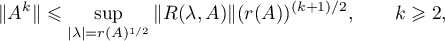
were obtained in the monograph [14], §8.5. Such estimates are also true for  in the case of an arbitrary Banach space
in the case of an arbitrary Banach space  if
if  .
.
Suppose that  and
and  with
with  . To estimate
. To estimate  ,
, 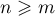 , we can use the Gel'fand-Shilov method, above, which they applied to obtain the estimate (7.2) for the operator exponential. First suppose that the eigenvalues of the operator
, we can use the Gel'fand-Shilov method, above, which they applied to obtain the estimate (7.2) for the operator exponential. First suppose that the eigenvalues of the operator  are simple, and let
are simple, and let 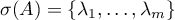 . Then, in accordance with the Gel'fand-Shilov method based on using the interpolation polynomial in the Newton form, for any
. Then, in accordance with the Gel'fand-Shilov method based on using the interpolation polynomial in the Newton form, for any 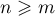 we represent the operator
we represent the operator  in the form
in the form

where the numbers  ,
, 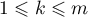 , admit estimates of the form
, admit estimates of the form
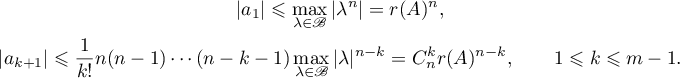
Here the symbol  denotes the convex hull in
denotes the convex hull in  of the eigenvalues
of the eigenvalues  of the operator
of the operator  . If the eigenvalues are not simple, then we have to consider a sequence of operators
. If the eigenvalues are not simple, then we have to consider a sequence of operators  in
in  converging to
converging to  in which every operator has simple eigenvalues.
in which every operator has simple eigenvalues.
The estimates given above imply the following.
Theorem 27. The following estimates hold
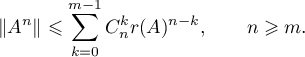
Gil' [49] developed a method for estimating the norms of powers of an operator  (as well as
(as well as  ) using the quantity
) using the quantity
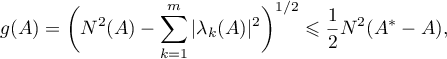
where 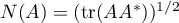 is the Hilbert-Schmidt norm of
is the Hilbert-Schmidt norm of  . Namely, the estimates
. Namely, the estimates
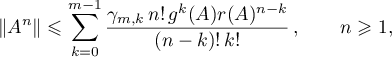
hold, where
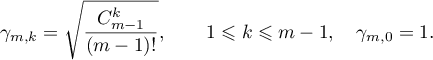
We point out that in Theorems 3–5 in [50] estimates of solutions of differential equations with periodic coefficients were obtained based on using Lyapunov's differential matrix equation. A detailed proof of Theorem 13 is given in [51].




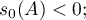
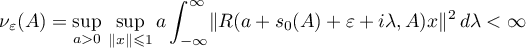
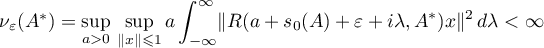
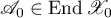
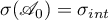

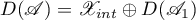
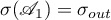




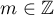
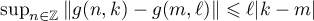
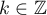
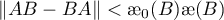
![$\|[B, AB-BA]\| < {\unicode{230}}_{0}(B){\unicode{230}}(B)^{2}$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn428.gif)
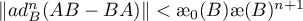
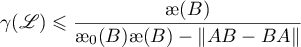
![$\gamma(\mathscr{L}) \leqslant \dfrac{{\unicode{230}}(B)^{2}}{{\unicode{230}}_{0}(B){\unicode{230}}(B)^{2}-\|[B,AB-BA]\|}$](https://content.cld.iop.org/journals/1064-5616/206/8/1049/revision1/MSB_206_8_1049ieqn438.gif)