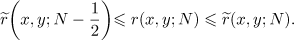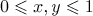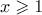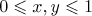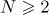Abstract
New results related to number theoretic model of spin chains are proved. We solve Arnold's problem on the Gauss-Kuz'min statistics for quadratic irrationals.
Bibliography: 24 titles.
Export citation and abstract BibTeX RIS
§1. Introduction
In [1], a number-theoretic model for spin chains was presented; this model uses Farey series (for the subsequent results, see [2]–[4]). In this model, to a finite chain of spins each of which can be directed upwards ( ) or downwards (
) or downwards (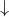 ), a product of the matrices
), a product of the matrices
is assigned, according to the rule  and
and  . For example,
. For example,
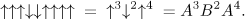
By the energy of a given configuration we mean the quantity

Let 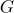 be the free multiplicative monoid generated by the matrices
be the free multiplicative monoid generated by the matrices  and
and  . From a physical viewpoint, the asymptotic behaviour of the number of configurations with a given energy,
. From a physical viewpoint, the asymptotic behaviour of the number of configurations with a given energy,
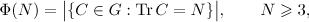
and the number of configurations in which the energy does not exceed a given quantity,

are of interest. The conjecture that

was presented in [1] and, at the same time, the asymptotic formula
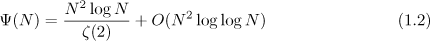
was proved in [3].
The conjecture (1.1) was disproved in [4]. It turns out that the arithmetic function 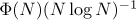 has a smooth limit distribution. In [5], the two-term asymptotic formula
has a smooth limit distribution. In [5], the two-term asymptotic formula

was obtained for the quantity 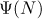 , where
, where
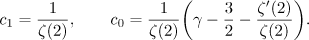
Problems concerning the asymptotic behaviour of 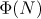 and
and 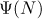 are closely related to the distribution of quadratic irrationals and the closed geodesics corresponding to these irrationals on the modular surface (see [6] and [5]). For a reduced quadratic irrational
are closely related to the distribution of quadratic irrationals and the closed geodesics corresponding to these irrationals on the modular surface (see [6] and [5]). For a reduced quadratic irrational 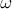 (which has a purely periodic representation in the form of a continued fraction) we let
(which has a purely periodic representation in the form of a continued fraction) we let 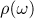 denote the length which is defined as the length of the corresponding closed geodesic. As was proved in [6],
denote the length which is defined as the length of the corresponding closed geodesic. As was proved in [6],

The relationship between reduced quadratic irrationals and finite products of the matrices 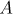 and
and  (see [3]) was used in [5] to obtain an asymptotic formula with an explicit estimate for the remainder term,
(see [3]) was used in [5] to obtain an asymptotic formula with an explicit estimate for the remainder term,
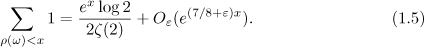
In this paper, we prove the asymptotic formula

which refines equation (1.3), and a formula refining (1.5), namely,
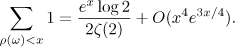
Equation (1.6) is a special case of a more general result concerning the Gauss-Kuz'min statistics for spin chains (see Theorems 1 and 2). Another consequence of this result gives a solution to Arnold's problem (see [7], Problem 1993–11) on the statistical properties of the partial quotients of quadratic irrationals. Let ![$x,y\in [0,1]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn16.gif) be real numbers and
be real numbers and
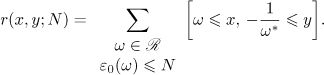
Here  is the set of reduced quadratic irrationals,
is the set of reduced quadratic irrationals, 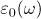 is the fundamental solution of Pell's equation
is the fundamental solution of Pell's equation

 , where
, where  is the minimal polynomial of
is the minimal polynomial of  , and
, and  stands for the number conjugate to
stands for the number conjugate to  ; moreover,
; moreover, ![$[A]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn24.gif) stands for
stands for  if the statement
if the statement  is true and for
is true and for 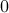 otherwise. Then (see Theorem 3)
otherwise. Then (see Theorem 3)

that is, Gauss-Kuz'min statistics for the quadratic irrationals are described by the same distribution function  and the same corresponding density
and the same corresponding density

as occur in the Gauss-Kuz'min statistics for the rationals and for almost all reals.
The proofs of the theorems use the approach suggested in [5].
The author thanks the referee for pointing out the inaccuracies in the original version of the paper.
§2. Application of bounds for the Kloosterman sums
The main tool for solving problems which can be reduced to the distribution of solutions of the congruence 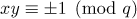 is the following lemma.
is the following lemma.
Lemma 1. Let 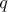 be a positive integer and
be a positive integer and  . Then
. Then

where 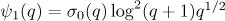 .
.
For a proof see, for example, [8].
In the next lemma, an asymptotic formula for the number of solutions of the congruence  under the graph of the simplest linear function can be proved in a similar way.
under the graph of the simplest linear function can be proved in a similar way.
Lemma 2. Let 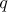 be a positive integer, let
be a positive integer, let  , let
, let  be an integer, and let
be an integer, and let  be a linear function for which
be a linear function for which 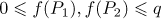 . Then the sum
. Then the sum
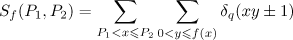
admits the following asymptotic formula (for any choice of sign in the symbol 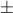 ):
):
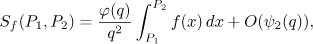
where 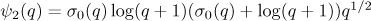 .
.
Proof. Assume that  . The case of
. The case of 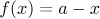 can be proved similarly. Expand the function
can be proved similarly. Expand the function
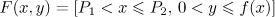
in a finite Fourier series,
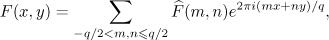
with the Fourier coefficients

Then the given sum can be represented in the form
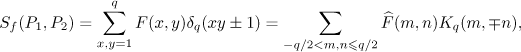
where
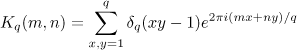
are Kloosterman sums. Distinguishing the term with 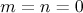 , we obtain the equation
, we obtain the equation
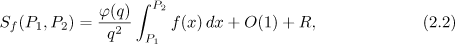
where
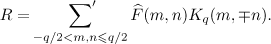
Here and below, a dash  on the summation sign means that the term for which all variables of summation vanish is omitted.
on the summation sign means that the term for which all variables of summation vanish is omitted.
Using the bound
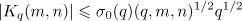
for the Kloosterman sums (see [9]), we obtain the following inequalities for the remainder  :
:

where
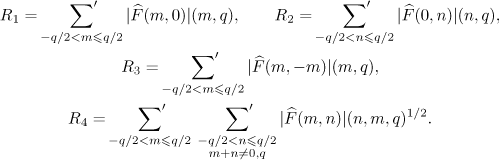
We will estimate the Fourier coefficients of the function  . If
. If  , then
, then

If  , then
, then
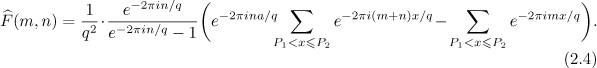
Therefore, for  we have
we have

and the remainder  can be estimated in just the same way as the remainder
can be estimated in just the same way as the remainder 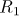 ,
,

If  and
and 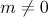 , then, by (2.4),
, then, by (2.4),
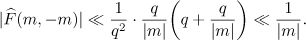
Hence, the same bound is obtained for the remainder  ,
,
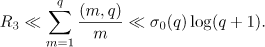
In the remaining cases ( ,
,  ,
,  ), by (2.4) we have
), by (2.4) we have

In particular, if 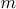 and
and  have different signs, then
have different signs, then
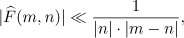
and, if the signs are the same, then

Therefore,  , where
, where

Introducing the variables 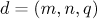 ,
, 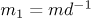 , and
, and 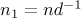 , we obtain the following bound for the first sum:
, we obtain the following bound for the first sum:
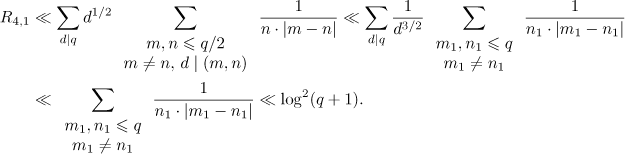
The second sum can be estimated similarly to the first,
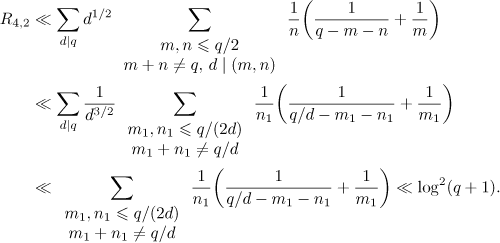
Thus, 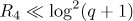 .
.
Substituting the above bounds for the remainders  ,
, 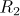 ,
,  , and
, and  into (2.3), we arrive at the relation
into (2.3), we arrive at the relation
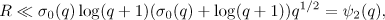
and, taking account of equation (2.2), this leads to the statement of the lemma.
§3. Spin chains and continued fractions
We let 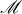 denote the set of all integer matrices
denote the set of all integer matrices

with determinant  for which
for which
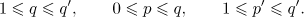
This set is partitioned into two disjoint sets 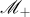 and
and 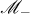 , which consist of matrices with determinants
, which consist of matrices with determinants 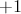 and
and  , respectively. The elements of the set
, respectively. The elements of the set  form a multiplicative semigroup and are in a one-to-one correspondence with the (non-empty) families of positive integers constructed using the rule (see [10])
form a multiplicative semigroup and are in a one-to-one correspondence with the (non-empty) families of positive integers constructed using the rule (see [10])
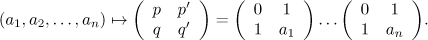
The inverse map is constructed using the equations

As in [5] and [3], to evaluate the function  , we consider the products of the matrices
, we consider the products of the matrices 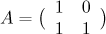 and
and  of even and odd length separately. To be definite, we assume that the products begin with the matrix
of even and odd length separately. To be definite, we assume that the products begin with the matrix 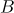 . Following the notation in [5], we introduce the sets
. Following the notation in [5], we introduce the sets  and
and  as follows:
as follows:

We set the family of positive integers  in correspondence with the continued fraction
in correspondence with the continued fraction ![$[0;a_1,\dots ,a_n]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn83.gif) and the sequence of approximants
and the sequence of approximants ![$p_k/q_k=[0;a_1,\dots ,a_k]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn84.gif) ,
,  . The properties of the continued fractions imply that
. The properties of the continued fractions imply that

where 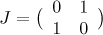 . Therefore, the quantities
. Therefore, the quantities

can also be defined by the equalities
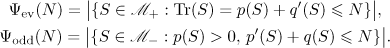
By hypothesis all the products under consideration begin with the matrix  , and so
, and so

To describe the behaviour of the partial quotients in the continued fractions for real numbers, it is convenient to use the measure (see [11])

Let a real number ![$\alpha \in [0,1]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn88.gif) be given by an infinite continued fraction
be given by an infinite continued fraction ![$\alpha =[0;a_1,a_2,\dots, a_n , \dots]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn89.gif) and let
and let ![$p_n(\alpha )/q_n(\alpha )=[0;a_1,\dots ,a_n]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn92.gif) and
and ![$r_n(\alpha )=[0;a_{n+1},a_{n+2},\dots ]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn93.gif) . Then
. Then ![$\alpha =[0;a_1,\dots ,a_n+r_n(\alpha )]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn94.gif) ,
, ![$q_{n-1}(\alpha )/q_{n}(\alpha )=[0;a_n,\dots ,a_1]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn95.gif) , and the behaviour of the elements of the continued fraction near the index
, and the behaviour of the elements of the continued fraction near the index  is described in the mean by the function (the Gauss-Kuz'min statistics treated in a generalized sense)
is described in the mean by the function (the Gauss-Kuz'min statistics treated in a generalized sense)

Here
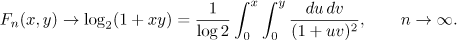
In particular, for  we deal with the Gauss measure
we deal with the Gauss measure

and the corresponding distribution function  .
.
The spin chains model under consideration is closely connected with continued fractions. Therefore, to describe the properties of generic configurations, it is natural to introduce characteristics similar to the Gauss-Kuz'min statistics. The object we introduce characterizes local properties of spin configurations.
For real ![$x,y\in [0,1]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn99.gif) we write
we write
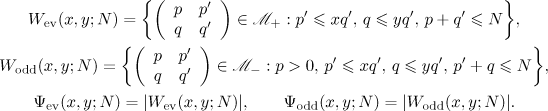
In particular,  and
and 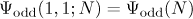 .
.
Arnold conjectured (see [7], Problem 1993–11) that the partial quotients of rationals and quadratic irrationals behave in the mean in just the same way as those for almost all reals. This statement was proved by Lochs (see [12]) for the rationals, in the simplest case when the averaging is carried out over the fractions  ,
, 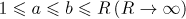 . For the case when the averaging is carried out over the points in a sector
. For the case when the averaging is carried out over the points in a sector  ,
,  , as was suggested in the original setting of the problem, the conjecture was proved by Avdeeva and Bykovskii (see [13] and [14], and also [15] and [8]). The known Gauss-Kuz'min statistics for finite continued fractions enabled us to solve the Sinaǐ problem on the statistical properties of trajectories of particles in two-dimensional crystal lattices (see [16]), to obtain new results on the behaviour in the mean of various versions of the Euclidean algorithm (see [17], [18]), and to find the distribution density of the normalized Frobenius numbers with three arguments (see [19]).
, as was suggested in the original setting of the problem, the conjecture was proved by Avdeeva and Bykovskii (see [13] and [14], and also [15] and [8]). The known Gauss-Kuz'min statistics for finite continued fractions enabled us to solve the Sinaǐ problem on the statistical properties of trajectories of particles in two-dimensional crystal lattices (see [16]), to obtain new results on the behaviour in the mean of various versions of the Euclidean algorithm (see [17], [18]), and to find the distribution density of the normalized Frobenius numbers with three arguments (see [19]).
It turns out that the quantities  an
an 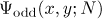 , viewed as functions of
, viewed as functions of 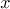 and
and 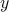 , exhibit fundamentally different behaviour. The even chains satisfy the Gauss-Kuz'min law (as do the rational numbers in the Arnold problem), whereas the odd ones do not.
, exhibit fundamentally different behaviour. The even chains satisfy the Gauss-Kuz'min law (as do the rational numbers in the Arnold problem), whereas the odd ones do not.
The relationship between the behaviour of the function  and the distribution of quadratic irrationals, which was noted in [5] and [3], helps to prove Arnold's conjecture for the quadratic irrationals and to refine the asymptotic formula (1.5).
and the distribution of quadratic irrationals, which was noted in [5] and [3], helps to prove Arnold's conjecture for the quadratic irrationals and to refine the asymptotic formula (1.5).
§4. Spin chains and the Gauss-Kuz'min statistics
Theorem 1. Let  and
and 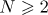 . Then the following asymptotic formula holds:
. Then the following asymptotic formula holds:

with an absolute constant in the remainder term.
Proof. We transform the given quantity,
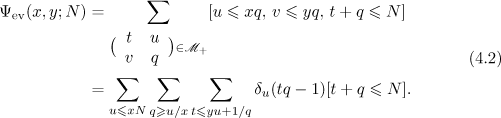
There is at most one value of the variable 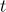 lying in the interval
lying in the interval 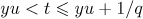 . Therefore,
. Therefore,

for 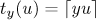 . Thus,
. Thus,

It follows from the equation
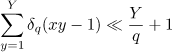
that the quantity 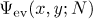 admits the bound
admits the bound
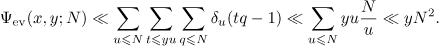
Since 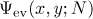 is symmetric with respect to
is symmetric with respect to  and
and 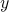 , the bound
, the bound
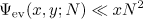
also holds. Therefore,

for 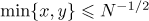 , and formula (4.1) holds. Thus, it is sufficient to prove that (4.1) holds under the assumption that
, and formula (4.1) holds. Thus, it is sufficient to prove that (4.1) holds under the assumption that  . In formula (4.3), Lemmas 1 and 2 can be applied to the inner double sum. Taking the formula (see [20], Ch. II, Problem 19)
. In formula (4.3), Lemmas 1 and 2 can be applied to the inner double sum. Taking the formula (see [20], Ch. II, Problem 19)
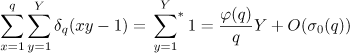
into account (here and below, an asterisk  means that the variable of summation ranges over the reduced system of residues), we obtain the equation
means that the variable of summation ranges over the reduced system of residues), we obtain the equation
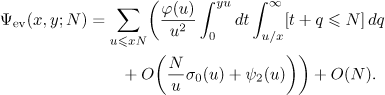
It follows from the standard bounds
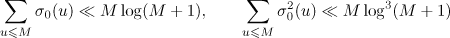
that
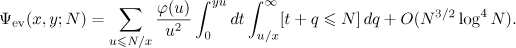
Applying the identity (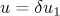 )
)
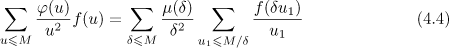
and introducing the variables  and
and  , we arrive at the asymptotic formula
, we arrive at the asymptotic formula
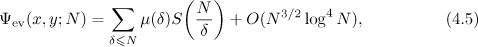
where
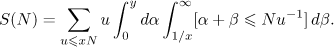
We represent the sum  in the form
in the form

where

After evaluating the integrals
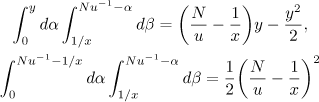
we arrive at the asymptotic formulae
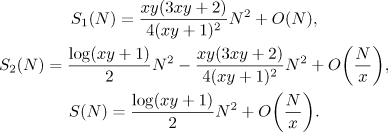
By assumption, 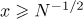 . Hence,
. Hence, 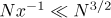 . Therefore, substituting the asymptotic formula for the sum
. Therefore, substituting the asymptotic formula for the sum  into (4.5), we obtain the desired equation for
into (4.5), we obtain the desired equation for 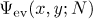 .
.
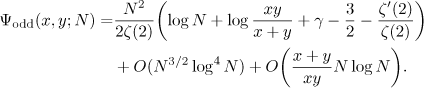
Proof. Repeating the arguments in the proof of Theorem 1, we arrive at the equations
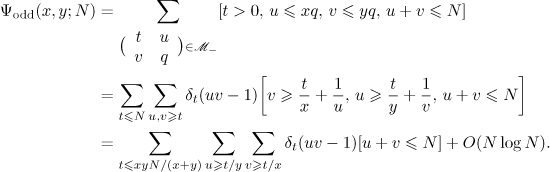
The boundary of the domain in which 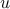 and
and  vary intersects at most
vary intersects at most  squares of the form
squares of the form ![$[at,(a+1)t]\times [bt,(b+1)t]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn138.gif) . Therefore, applying Lemmas 1 and 2, we obtain the equations
. Therefore, applying Lemmas 1 and 2, we obtain the equations

Using (4.4) again and changing to the variables  and
and 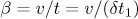 , we see that
, we see that
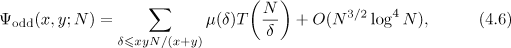
where

Substituting the asymptotic formula for  into (4.6) and applying the formula
into (4.6) and applying the formula
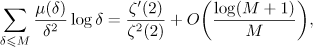
we obtain the statement of the theorem.

Remark. Comparing the results of Theorems 1 and 2, we can conclude that the even and odd spin chains have a fundamentally different structure in the mean. It seems that these cases should be separated and studied independently. In contrast to the leading term in Theorem 1, the leading term in Theorem 2 does not depend on 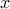 and
and  , because it is obtained by summing matrices of the form
, because it is obtained by summing matrices of the form  in which
in which 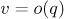 and
and 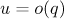 .
.
§5. Gauss-Kuz'min statistics for quadratic irrationals
Let ![$AX^2+BX+C\in \mathbb {Z}[X]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn148.gif)
 be the minimal polynomial of a quadratic irrational
be the minimal polynomial of a quadratic irrational  and let
and let  . We denote the number conjugate to
. We denote the number conjugate to 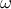 by
by 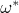 . In the field
. In the field  , the number
, the number 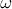 has trace
has trace 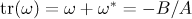 and norm
and norm  . A quadratic irrational
. A quadratic irrational  is said to be reduced if it can be decomposed into a purely periodic continued fraction,
is said to be reduced if it can be decomposed into a purely periodic continued fraction,

of period 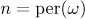 . Here, by the Galois theorem (see [21]),
. Here, by the Galois theorem (see [21]),
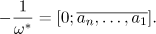
We denote the set of all reduced quadratic irrationals by  . The length of a number
. The length of a number 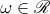 is the quantity
is the quantity 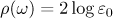 , where
, where  is the fundamental solution of Pell's equation
is the fundamental solution of Pell's equation
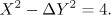
The term 'length' is used because, on the modular surface 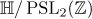 , where
, where 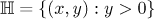 stands for the upper half-plane, there is a closed geodesic corresponding to a pair of quadratic irrationals
stands for the upper half-plane, there is a closed geodesic corresponding to a pair of quadratic irrationals  and
and 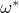 (the projection of the geodesic joining
(the projection of the geodesic joining  and
and 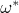 ) whose length in the classical metric
) whose length in the classical metric  is precisely equal to
is precisely equal to  (see [6] and [22]).
(see [6] and [22]).
For a reduced quadratic irrational ![$\omega =[0;\overline{a_1,\dots ,a_n}]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn173.gif) we write
we write
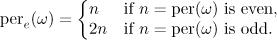
In this case, the fundamental unit can be found using Smith's formula (see [23] and [24], § 2.4),
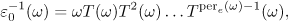
where 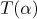 stands for the Gauss map
stands for the Gauss map  .
.
For the manipulations below, we need the following properties of the reduced quadratic irrationals and their corresponding fundamental units (see [3], Propositions 2.1 and 4.1).
 For every positive integer
For every positive integer 
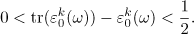
 If
If ![$\omega =[0;\overline{a_1,\dots ,a_{2m}}]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn179.gif) ,
,  ,
,  , then
, then
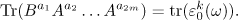
Let
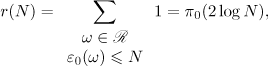
where  stands for the number of reduced quadratic irrationals whose length does not exceed
stands for the number of reduced quadratic irrationals whose length does not exceed  . The next statement can be extracted from the proofs of Propositions 4.3 and 4.5 in [3] (see also [5]).
. The next statement can be extracted from the proofs of Propositions 4.3 and 4.5 in [3] (see also [5]).
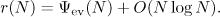
Proof. We first assume that 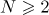 is a real number. By property
is a real number. By property 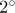 , the map
, the map
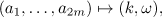
which assigns the quadratic irrational ![$\omega =[0;\overline{a_1,\dots ,a_{n}}]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn187.gif) and the number
and the number  to a family of positive integers
to a family of positive integers  , is a bijection between the set
, is a bijection between the set 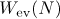 and the set of pairs
and the set of pairs 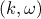 , where
, where  ,
, 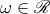 and
and  . Hence,
. Hence,

where

We can impose the condition  because the inequality
because the inequality
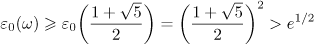
holds for every  .
.
It follows from (5.2) that  . By property
. By property 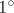 ,
,
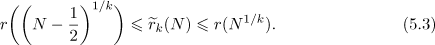
Therefore, 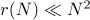 ,
, 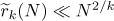 , and
, and

It follows from (5.3) that

Thus,
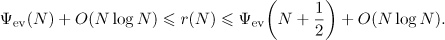
However, the equation 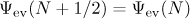 holds for integer
holds for integer  , and therefore the statement of the lemma follows from the estimates for
, and therefore the statement of the lemma follows from the estimates for  obtained above.
obtained above.
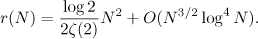
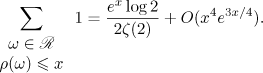
To evaluate the Gauss-Kuz'min statistics for the reduced quadratic irrationals, we introduce the quantity  for the reals
for the reals ![$x,y\in [0,1]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn207.gif) and for
and for  (we assume that the sequence of partial quotients is extended to the negative indices by periodicity) as follows:
(we assume that the sequence of partial quotients is extended to the negative indices by periodicity) as follows:
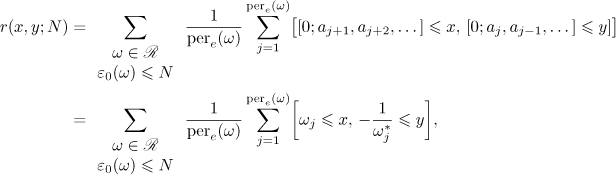
where ![$\omega _j=T^{j}(\omega )=[0;a_{j+1},a_{j+2},\dots ]$](https://content.cld.iop.org/journals/1064-5616/204/5/762/revision1/msb_204_5_762ieqn209.gif) . In particular,
. In particular,  . For all equivalent numbers
. For all equivalent numbers 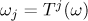 we count the Gauss-Kuz'min statistics only once, and the sum
we count the Gauss-Kuz'min statistics only once, and the sum  can also be represented in the form
can also be represented in the form
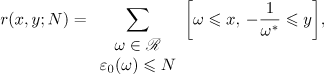
that is, the sum 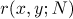 describes the behaviour in the mean of the closed geodesics on the modular surface.
describes the behaviour in the mean of the closed geodesics on the modular surface.
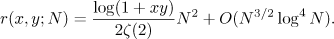

By definition, 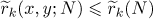 . Thus, it follows from (5.4) that
. Thus, it follows from (5.4) that
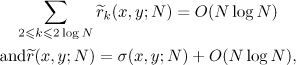
where
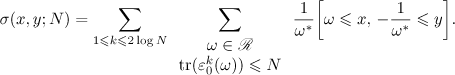
By property  the sum which has arisen can be represented in the form
the sum which has arisen can be represented in the form
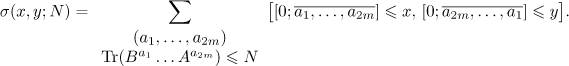
A pair of positive integers 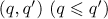 can be completed to a matrix
can be completed to a matrix  in two ways at most. Therefore, the number of matrices
in two ways at most. Therefore, the number of matrices
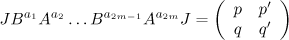
for which  can be estimated by
can be estimated by  . For the families
. For the families  to which a matrix with
to which a matrix with  corresponds we have
corresponds we have

Hence, on the one hand,

On the other hand,

that is,

If 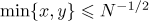 , then Theorem 3 follows from Theorem 1 and from the bound (5.5). If
, then Theorem 3 follows from Theorem 1 and from the bound (5.5). If  , then, by Theorem 1,
, then, by Theorem 1,
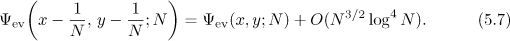
Combining the above relations (5.6) and (5.7), we obtain the asymptotic formula  . Thus, by Theorem 1,
. Thus, by Theorem 1,
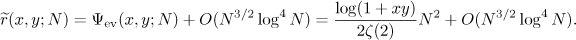
To complete the proof of the theorem, it remains to note that, by property  , the desired function
, the desired function  is connected with
is connected with  by the inequalities
by the inequalities