Abstract
Generalizations and refinements are given for results of Kozlov and Treschev on non-uniform averagings in the ergodic theorem in the case of operator semigroups on spaces of integrable functions and semigroups of measure-preserving transformations. Conditions on the averaging measures are studied under which the averages converge for broad classes of integrable functions.
Bibliography: 96 items.
Export citation and abstract BibTeX RIS
| This research was supported by the Russian Foundation for Basic Research (grants nos. 18-31-20008 and 20-01-00432), Moscow Center of Fundamental and Applied Mathematics, and the Foundation for the Advancement of Theoretical Physics and Mathematics BASIS (grant no. 18-1-6-83-1). |
§ 1. Introduction
This paper is devoted to generalizations and refinements of several results of Kozlov and Treschev in [58]–[60], [56] connected with the study of convergence of non-uniform averagings in the situation of the individual ergodic theorem and its extensions. In its original setting their problem was concerned with classical dynamical systems on manifolds (see [55], [61], and [57]), but both the formulations of the results and the methods of proofs could be carried over directly to a considerably more general context of measure spaces, measurable transformations of them, and functions on them. Moreover, in this more general situation the formulations and proofs turned out to be even slightly simpler. Therefore, our discussion below follows this generality. The cited papers have attracted the attention of other researchers and have been further developed (see [15], [20], [21], [53], [54], and also the recent paper [67] in physics). Below we give a survey of this research along with some new results.
The aforementioned non-uniform averaging is defined by the formula
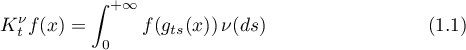
for integrable functions  on a probability space
on a probability space  on which a semigroup of measurable transformations
on which a semigroup of measurable transformations  ,
,  , acts with preservation of the measure
, acts with preservation of the measure  , that is,
, that is,  ,
,  , and the map
, and the map  is measurable, where
is measurable, where  is a Borel probability measure on
is a Borel probability measure on  . A more general problem deals with the integrals
. A more general problem deals with the integrals
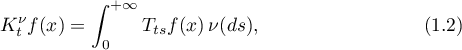
where  is a semigroup of bounded linear operators on the space
is a semigroup of bounded linear operators on the space  . The question is posed of the existence of the limit of the function
. The question is posed of the existence of the limit of the function  almost everywhere or in the mean as
almost everywhere or in the mean as  . In addition, in this situation there arises an interesting dynamics of measures on the space
. In addition, in this situation there arises an interesting dynamics of measures on the space  (see §5).
(see §5).
If  is Lebesgue measure on the interval
is Lebesgue measure on the interval ![$[0,1]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn16.gif) , then after the change of variable
, then after the change of variable  we arrive at the classical averages
we arrive at the classical averages
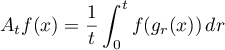
or, in the operator case,
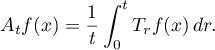
For the former integral the Birkhoff–Khinchin theorem (see [15], [64], [75], [31], and [34]) gives convergence almost everywhere for any integrable function  , to the function
, to the function  equal to the conditional expectation of
equal to the conditional expectation of  with respect to the
with respect to the  -algebra
-algebra  generated by all measurable functions invariant with respect to all the transformations
generated by all measurable functions invariant with respect to all the transformations  . This conditional expectation is also the projection
. This conditional expectation is also the projection  of
of  on the subspace of functions invariant with respect to all the transformations
on the subspace of functions invariant with respect to all the transformations  . For the latter integral a number of convergence results are also known, which we present in §3. The Kozlov–Treschev theorem gives convergence of
. For the latter integral a number of convergence results are also known, which we present in §3. The Kozlov–Treschev theorem gives convergence of  to the same limit for bounded measurable functions
to the same limit for bounded measurable functions  and absolutely continuous measures
and absolutely continuous measures  .
.
There is a vast literature on individual ergodic theorems for operator semigroups (not necessarily generated by transformations of measure spaces, as in the first ergodic theorems) on spaces of integrable functions, beginning with the classical works [33] and [34] by Dunford and Schwartz, the main results in which will be recalled below. We note the survey [3], the papers [12], [5], [40], [90], [91], [51], [65], [44], [94], [95] investigating convergence of the ratios  , which reduce to
, which reduce to  for
for  and
and  but are more natural in other situations, the papers [35], [77], [80], [38], [39], [36], and [37] on convergence of resolvent averages of the form
but are more natural in other situations, the papers [35], [77], [80], [38], [39], [36], and [37] on convergence of resolvent averages of the form
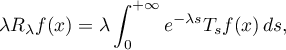
which corresponds to the weight  and
and  (such averages were considered as early as [33] and [34]), the paper [1] on averaging with monotone weights, and also the papers [78], [79], [81], [82], [71], [13], and [96] on classical averaging or averaging with other special weights. However, it should be noted that the author of [12] already considered non-uniform averages of the form
(such averages were considered as early as [33] and [34]), the paper [1] on averaging with monotone weights, and also the papers [78], [79], [81], [82], [71], [13], and [96] on classical averaging or averaging with other special weights. However, it should be noted that the author of [12] already considered non-uniform averages of the form

where  is an increasing function of bounded variation satisfying the equation
is an increasing function of bounded variation satisfying the equation  with some probability measure
with some probability measure  . In this setting the existence of a limit was proved for the ratio
. In this setting the existence of a limit was proved for the ratio  , where
, where  and
and  is a probability density with respect to
is a probability density with respect to  . If
. If  , then this case is similar to the classical situation with division of an integral by
, then this case is similar to the classical situation with division of an integral by  ; the only difference is that the integral over
; the only difference is that the integral over ![$[0,t]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn37.gif) is taken not with respect to Lebesgue measure, but with respect to
is taken not with respect to Lebesgue measure, but with respect to  . In addition, [28] and [29] dealt with non-uniform averages exactly of the form (1.1) with densities
. In addition, [28] and [29] dealt with non-uniform averages exactly of the form (1.1) with densities  having bounded supports, which has some specific features (results in these papers are mentioned below). In [6], sequences of non-uniform averages defined by sequences of different weights were studied. Many works have been devoted to non-uniform discrete averages for single transformations or operators (see [64], [11], [69], and the literature therein). Certain non-uniform averages of a different kind connected with ergodic group actions were considered in [87]–[89], [7], [70], and [42], where there are also additional references. There is an even more extensive literature on convergence of averages in the mean, but here we hardly touch upon this question.
having bounded supports, which has some specific features (results in these papers are mentioned below). In [6], sequences of non-uniform averages defined by sequences of different weights were studied. Many works have been devoted to non-uniform discrete averages for single transformations or operators (see [64], [11], [69], and the literature therein). Certain non-uniform averages of a different kind connected with ergodic group actions were considered in [87]–[89], [7], [70], and [42], where there are also additional references. There is an even more extensive literature on convergence of averages in the mean, but here we hardly touch upon this question.
In §3 we discuss convergence of non-uniform averages for unbounded functions  mostly in the second, more general, case of semigroups. In §4, non-uniform averaging of stochastic systems is considered. In §5, weak convergence of measures generated by the averaging measure is discussed.
mostly in the second, more general, case of semigroups. In §4, non-uniform averaging of stochastic systems is considered. In §5, weak convergence of measures generated by the averaging measure is discussed.
§ 2. Notation, terminology and auxiliary results
Throughout, we use the basic standard notions and facts connected with the Lebesgue integral, the spaces  with their classical norms
with their classical norms  , and linear operators. In some constructions and results we use certain more special concepts introduced below.
, and linear operators. In some constructions and results we use certain more special concepts introduced below.
In particular, we shall use the Orlicz classes of integrable functions generated by convex functions (see [62] and [76]). An increasing convex function  on
on  is called an
is called an  -function if
-function if
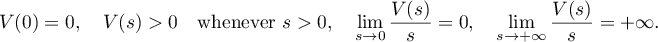
In other words,
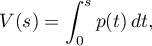
where  is a non-decreasing function on
is a non-decreasing function on  such that
such that
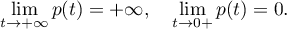
An  -function
-function  is said to satisfy the
is said to satisfy the  -condition for large values if, for some
-condition for large values if, for some  and
and  , we have
, we have
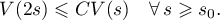
For every  this implies the estimate
this implies the estimate

with some  . If this condition holds for
. If this condition holds for  , then
, then  is said to satisfy the global
is said to satisfy the global  -condition.
-condition.
For such a function we obtain
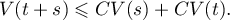
To satisfy the  -condition for large values it suffices to have the estimate
-condition for large values it suffices to have the estimate
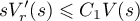
for the right-hand derivative  of the function
of the function  outside some interval (see [62], Chap. 1, §4).
outside some interval (see [62], Chap. 1, §4).
Typical examples of  -functions
-functions  satisfying the global
satisfying the global  -condition are
-condition are  with
with  (but not with
(but not with  ) and also
) and also  .
.
Below we use the known fact (see [62], §8 and Lemma 5.1 in §5) that, for every integrable function  , there exists an
, there exists an  -function
-function  satisfying the global
satisfying the global  -condition for which the function
-condition for which the function  is integrable.
is integrable.
For an  -function
-function  on
on  the complementary (or complex conjugate) function
the complementary (or complex conjugate) function  is defined by
is defined by
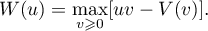
Hence Young's inequality  holds. The complementary function is also convex and increasing (and is an
holds. The complementary function is also convex and increasing (and is an  -function). For example, if
-function). For example, if  , where
, where  , then
, then  , where
, where  .
.
The Orlicz class  generated by a given
generated by a given  -function
-function  consists of the equivalence classes of
consists of the equivalence classes of  -measurable functions
-measurable functions  for which
for which  . One has
. One has  . It is known that the Orlicz class
. It is known that the Orlicz class  is a convex set, but for an atomless measure
is a convex set, but for an atomless measure  it becomes a linear space precisely when the function
it becomes a linear space precisely when the function  satisfies the
satisfies the  -condition for large values. Even if
-condition for large values. Even if  does not satisfy this condition, one can introduce the Banach space
does not satisfy this condition, one can introduce the Banach space  of equivalence classes of measurable functions with finite Orlicz norm
of equivalence classes of measurable functions with finite Orlicz norm
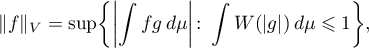
where  is the complementary function for
is the complementary function for  . Then
. Then  , and if the
, and if the  -condition holds for large values, then the two sets are equal (in the general case
-condition holds for large values, then the two sets are equal (in the general case  coincides with the linear span of the class
coincides with the linear span of the class  ). In addition, in the general case
). In addition, in the general case

for  and
and  . The Orlicz norm is equivalent to the Luxemburg norm defined without the complementary function by the equality
. The Orlicz norm is equivalent to the Luxemburg norm defined without the complementary function by the equality
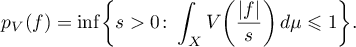
One has  . If the
. If the  -condition holds for large values, then convergence of a sequence
-condition holds for large values, then convergence of a sequence  to zero in one of these norms is equivalent to convergence to zero of the integrals of
to zero in one of these norms is equivalent to convergence to zero of the integrals of  (see [62], Theorem 9.4).
(see [62], Theorem 9.4).
A linear operator  on the space
on the space  is said to be non-negative if
is said to be non-negative if  for all
for all  .
.
The norm of an operator  on
on  will be denoted by
will be denoted by  , and the norm of an operator
, and the norm of an operator  between Banach spaces
between Banach spaces  and
and  is denoted by
is denoted by  .
.
If  is a probability space and
is a probability space and  is a sub-
is a sub- -algebra of
-algebra of  , then the conditional expectation of a
, then the conditional expectation of a  -integrable function
-integrable function  is the
is the  -integrable function
-integrable function  which is measurable with respect to
which is measurable with respect to  and such that
and such that
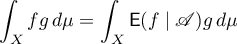
for all bounded  -measurable functions
-measurable functions  . One can also say that this is the projection of
. One can also say that this is the projection of  with some special properties on the subspace of
with some special properties on the subspace of  -measurable functions (for functions in
-measurable functions (for functions in  this is the usual orthogonal projection).
this is the usual orthogonal projection).
Below we need the following Jensen inequality for operators, which can be extracted from the results in [43] but which for the reader's convenience we derive here from the usual Jensen inequality (we even give two derivations).
Lemma 2.1. Let  be a probability space and let
be a probability space and let  be a non-negative operator with
be a non-negative operator with  . Suppose that
. Suppose that  is an increasing convex function on
is an increasing convex function on  with
with  . Then
. Then
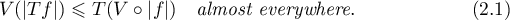
If  extends to a continuous operator from
extends to a continuous operator from  to
to  and
and  is such that
is such that  , then this estimate remains valid.
, then this estimate remains valid.
Proof. Since  by the non-negativity of
by the non-negativity of  , we can assume that
, we can assume that  . Moreover, it suffices to prove the assertion for bounded
. Moreover, it suffices to prove the assertion for bounded  . Fix some
. Fix some  -measurable bounded versions of the functions
-measurable bounded versions of the functions  and
and  .
.
For every  , we can find measurable sets
, we can find measurable sets  such that for
such that for  -almost all
-almost all  we get that
we get that  for all
for all  and
and
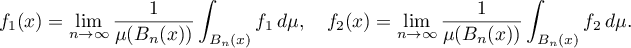
For example, one can take the sets
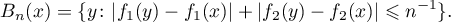
Then for a fixed  we cover
we cover  by the measurable disjoint sets
by the measurable disjoint sets
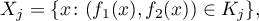
where a finite collection of disjoint Borel sets  of diameter less than
of diameter less than  covers a square containing the values of the map
covers a square containing the values of the map  , and we take only those sets
, and we take only those sets  which have positive
which have positive  -measure. For every point
-measure. For every point  in such a set
in such a set  we have
we have  , hence
, hence  . Moreover,
. Moreover,
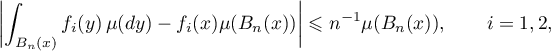
which gives the indicated relations.
Now fix a point  such that
such that  for all
for all  and let
and let  and
and  be the indicated limits. Consider the non-negative measure
be the indicated limits. Consider the non-negative measure
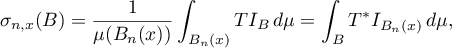
where  is the bounded operator on
is the bounded operator on  adjoint to the operator
adjoint to the operator  on
on  . Thus, the measure
. Thus, the measure  is given by the density
is given by the density  with respect to the measure
with respect to the measure  . The integral of a bounded measurable function
. The integral of a bounded measurable function  with respect to the measure
with respect to the measure  is given by
is given by

It is clear that  , since
, since  .
.
By the condition  and the convexity of
and the convexity of  , for the subprobability measure
, for the subprobability measure  we have Jensen's inequality
we have Jensen's inequality
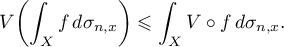
By our choice of  and the continuity of
and the continuity of  we obtain
we obtain  on the left-hand side and
on the left-hand side and  on the right-hand side as
on the right-hand side as  .
.
Let us consider another justification for the case of  . We recall (for example, see [27], §11.6) that the Gelfand transform
. We recall (for example, see [27], §11.6) that the Gelfand transform  defines a linear isometry of the complex Banach algebra
defines a linear isometry of the complex Banach algebra  and the space
and the space  of continuous complex functions on the compact space
of continuous complex functions on the compact space  of maximal ideals of this Banach algebra; moreover,
of maximal ideals of this Banach algebra; moreover,  is a homomorphism of algebras and preserves the non-negativity of elements. Hence, the non-negative operator
is a homomorphism of algebras and preserves the non-negativity of elements. Hence, the non-negative operator  on
on  generates a non-negative operator
generates a non-negative operator  on
on  by the formula
by the formula  . By the Riesz theorem, for every
. By the Riesz theorem, for every  there exists a Radon measure
there exists a Radon measure  on
on  for which
for which
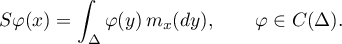
This measure is non-negative because  for
for  . In addition,
. In addition,  since
since  , as follows from the estimate
, as follows from the estimate  and the equality
and the equality  . By the usual Jensen's inequality for subprobability measures we get that
. By the usual Jensen's inequality for subprobability measures we get that  for
for  . Now it remains to observe that
. Now it remains to observe that  for all non-negative
for all non-negative  , since for every continuous function
, since for every continuous function  on the real line we have
on the real line we have  , because this is true for all polynomials
, because this is true for all polynomials  and remains true for their uniform limits on a closed interval containing the values of
and remains true for their uniform limits on a closed interval containing the values of  . Finally, it is worth noting that in most applications the operators with the stated properties are given in integral form by means of families of measures, so for them the assertion follows directly from Jensen's inequality.
. Finally, it is worth noting that in most applications the operators with the stated properties are given in integral form by means of families of measures, so for them the assertion follows directly from Jensen's inequality. 
Remark 2.2. If instead of the condition  we impose the weaker condition
we impose the weaker condition  , where
, where  , and the function
, and the function  is required to satisfy the global
is required to satisfy the global  -condition, then from (2.1) we obtain the estimate
-condition, then from (2.1) we obtain the estimate
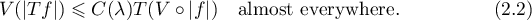
Remark 2.3. (i) It is known (see [64], §4.1, Theorem 1.3, for example) that for every bounded operator  on
on  there exists a non-negative operator
there exists a non-negative operator  with the same norm and defined on non-negative functions by
with the same norm and defined on non-negative functions by
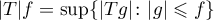
such that for all functions in 

For a contraction  this gives the estimate
this gives the estimate
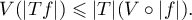
(ii) For every bounded operator  on
on  there also exists a non-negative operator
there also exists a non-negative operator  on
on  with the same norm (and defined by the same formula) for which (2.3) is true. If the operator
with the same norm (and defined by the same formula) for which (2.3) is true. If the operator  is a contraction on
is a contraction on  , then so is
, then so is  . This was proved by Kantorovich [49] for more general lattices, and was later rediscovered by several authors in studying operators on
. This was proved by Kantorovich [49] for more general lattices, and was later rediscovered by several authors in studying operators on  (see [33], [30], and also the comments in [64], §4.1). Thus, any operator
(see [33], [30], and also the comments in [64], §4.1). Thus, any operator  with finite norms on
with finite norms on  and
and  is majorized by a non-negative operator
is majorized by a non-negative operator  with preservation of both norms. For a semigroup of operators
with preservation of both norms. For a semigroup of operators  , the operators
, the operators  constructed by the indicated formula do not always form a semigroup, but it was proved in [51] and [65] (see also [64], §7.2, Theorem 2.7) that if
constructed by the indicated formula do not always form a semigroup, but it was proved in [51] and [65] (see also [64], §7.2, Theorem 2.7) that if  is a contractive operator semigroup on
is a contractive operator semigroup on  , then there exists a contractive semigroup
, then there exists a contractive semigroup  of non-negative operators for which
of non-negative operators for which  , and moreover,
, and moreover,  for every contractive semigroup of non-negative operators
for every contractive semigroup of non-negative operators  with the property that
with the property that  . Unlike the case of a single operator, it is important here that the semigroup be contractive (see [51]). If the maps
. Unlike the case of a single operator, it is important here that the semigroup be contractive (see [51]). If the maps  are continuous on
are continuous on  for all
for all  , then this property is inherited by the semigroup
, then this property is inherited by the semigroup  . Finally, it follows from the proofs given in these works that if
. Finally, it follows from the proofs given in these works that if  for all
for all  , then
, then  .
.
The following technical lemma will be useful below.
Lemma 2.4. Let  and
and  . Then the function
. Then the function
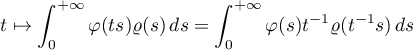
is continuous on  . The same is true if
. The same is true if  and
and  , where
, where  and
and  , or if the function
, or if the function  is concentrated on a bounded interval and there is an
is concentrated on a bounded interval and there is an  -function
-function  such that
such that  and
and  are integrable, where
are integrable, where  is the complementary function for
is the complementary function for  .
.
If  is an arbitrary non-negative measurable function on
is an arbitrary non-negative measurable function on  , then
, then
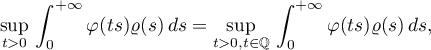
where infinite values of integrals and suprema are allowed.
Proof. It is well known that for every measurable function  on
on  the functions
the functions  converge to
converge to  in measure on every compact interval as
in measure on every compact interval as  in
in  . This implies the continuity of the map
. This implies the continuity of the map  from
from  to the space
to the space  and also to the space
and also to the space  or the Orlicz space
or the Orlicz space  provided that
provided that  belongs to this space. Hence, the integral of a product with the function
belongs to this space. Hence, the integral of a product with the function  is continuous in
is continuous in  .
.
The last assertion of the lemma is valid for bounded functions  by the continuity in
by the continuity in  of the corresponding integrals, which increase pointwise to the (possibly, infinite) integral containing
of the corresponding integrals, which increase pointwise to the (possibly, infinite) integral containing  . Then the suprema for
. Then the suprema for  increase to the supremum for
increase to the supremum for  .
. 
We recall that bounded countably additive measures on the Borel  -algebra
-algebra  of a topological space
of a topological space  are called Borel measures. A non-negative Borel measure
are called Borel measures. A non-negative Borel measure  is called a Radon measure if for any Borel set
is called a Radon measure if for any Borel set  and any
and any  , there exists a compact set
, there exists a compact set  such that
such that  . A signed Borel measure
. A signed Borel measure  is said to be Radon if its total variation
is said to be Radon if its total variation  defined by
defined by  is Radon, where
is Radon, where  and
and  are the positive and negative parts of
are the positive and negative parts of  , respectively (information about measures can be found in [15]).
, respectively (information about measures can be found in [15]).
We also recall that a Hausdorff topological space said to be Souslin if it is the image of some complete separable metric space under a continuous map. On Souslin spaces all Borel measures are Radon.
A sequence of Borel measures  on a topological space
on a topological space  is said to be weakly convergent to a Borel measure
is said to be weakly convergent to a Borel measure  if for every bounded continuous function
if for every bounded continuous function  on
on 
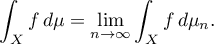
This convergence is weaker than the convergence  for every Borel set. However, in the case of Radon probability measures on completely regular spaces weak convergence is equivalent to convergence on all Borel sets
for every Borel set. However, in the case of Radon probability measures on completely regular spaces weak convergence is equivalent to convergence on all Borel sets  such that the topological boundary of
such that the topological boundary of  (the difference between the closure and the interior) has zero
(the difference between the closure and the interior) has zero  -measure. About weak convergence of measures see [15] and [19].
-measure. About weak convergence of measures see [15] and [19].
§ 3. Non-uniform Kozlov–Treschev averagings and the ergodic theorem
We have already stated the classical ergodic theorem on convergence of averages almost everywhere, that is, the so-called individual ergodic theorem (which differs from ergodic theorems on convergence in some norm). This theorem has interesting and non-trivial generalizations (proved by other means) to the case of a semigroup of bounded linear operators  on
on  . We shall present several such generalizations. First we recall that a semigroup
. We shall present several such generalizations. First we recall that a semigroup  of bounded linear operators on a Banach space
of bounded linear operators on a Banach space  is said to be strongly measurable if for every
is said to be strongly measurable if for every  the map
the map  with values in
with values in  is Lebesgue measurable. Such a semigroup is said to be strongly integrable on compact intervals if the indicated maps are Bochner integrable on every compact interval. Strong measurability implies the continuity of the map
is Lebesgue measurable. Such a semigroup is said to be strongly integrable on compact intervals if the indicated maps are Bochner integrable on every compact interval. Strong measurability implies the continuity of the map  for
for  , but it does not imply the strong continuity of the semigroup, which is continuity of the map
, but it does not imply the strong continuity of the semigroup, which is continuity of the map  also at zero (see [4]). It is known (see [34], Theorem III.11.17) that for any Bochner integrable map
also at zero (see [4]). It is known (see [34], Theorem III.11.17) that for any Bochner integrable map ![$\psi\colon [a,b]\to L^1(\mu)$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn177.gif) there exists a real function
there exists a real function  on
on ![$[a,b]\times X$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn179.gif) which is integrable with respect to the product of Lebesgue measure and
which is integrable with respect to the product of Lebesgue measure and  (and which is measurable with respect to the product of the corresponding
(and which is measurable with respect to the product of the corresponding  -algebras) such that for almost every
-algebras) such that for almost every  the function
the function  is a representative of the equivalence class of the element
is a representative of the equivalence class of the element  . In [23] (Exercise 1.8.14) a simple construction is described that, in the case of a separable measure
. In [23] (Exercise 1.8.14) a simple construction is described that, in the case of a separable measure  (that is, a measure with separable
(that is, a measure with separable  ) and a family of
) and a family of  -integrable functions
-integrable functions  with
with  and
and  a measurable space such that the integrals of the functions
a measurable space such that the integrals of the functions  over sets in
over sets in  are measurable in
are measurable in  , enables one to construct an
, enables one to construct an  -measurable function
-measurable function  with
with  almost everywhere for every fixed
almost everywhere for every fixed  . In place of separability of the measure
. In place of separability of the measure  it suffices to have separability of the subspace generated by all the
it suffices to have separability of the subspace generated by all the  , so this construction applies to any continuous map
, so this construction applies to any continuous map  from
from  to
to  . With the aid of the indicated version of
. With the aid of the indicated version of  one can give meaning to the integral of
one can give meaning to the integral of  with respect to
with respect to  for any fixed
for any fixed  . The situation is similar for general Borel measures on
. The situation is similar for general Borel measures on  instead of Lebesgue measure. Throughout, in integrals we mean such versions. It is useful to note that if a function on
instead of Lebesgue measure. Throughout, in integrals we mean such versions. It is useful to note that if a function on  is continuous in the first argument and
is continuous in the first argument and  -measurable in the second argument, then it is
-measurable in the second argument, then it is  -measurable (see [15], Lemma 6.4.6). In addition, Lemma 2.4 enables us, under the conditions we are considering, to compute the maximal functions introduced below by using rational
-measurable (see [15], Lemma 6.4.6). In addition, Lemma 2.4 enables us, under the conditions we are considering, to compute the maximal functions introduced below by using rational  .
.
The following result was proved in the paper [33] by Dunford and Schwartz (which they included in §11 of Chap. IV and §7 of Chap. VIII of their well-known monograph [34]).
Theorem 3.1. Let  be a strongly measurable operator semigroup on
be a strongly measurable operator semigroup on  such that
such that
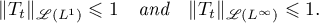
Then for every function  the averages
the averages
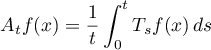
converge  -almost everywhere as
-almost everywhere as  .
.
The limit function  is some projection of the function
is some projection of the function  onto the closed subspace of all functions in
onto the closed subspace of all functions in  that are invariant with respect to the operators
that are invariant with respect to the operators  . However, one should bear in mind that, unlike the Hilbert space
. However, one should bear in mind that, unlike the Hilbert space  , a projection onto a closed subspace in
, a projection onto a closed subspace in  need not exist or may be non-unique. If the
need not exist or may be non-unique. If the  are Markov operators, which means that
are Markov operators, which means that  for
for  and
and  , and the measure
, and the measure  is invariant with respect to them, that is,
is invariant with respect to them, that is,
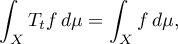
which also gives the equality  , then
, then  coincides with the conditional expectation of
coincides with the conditional expectation of  with respect to the
with respect to the  -algebra
-algebra  generated by all functions in
generated by all functions in  that are invariant with respect to the
that are invariant with respect to the  . If only constants have this property, then the limit in the theorem equals the integral of
. If only constants have this property, then the limit in the theorem equals the integral of  . For general semigroups the limit function
. For general semigroups the limit function  can differ from the conditional expectation. For example, if
can differ from the conditional expectation. For example, if  , then the limit is zero.
, then the limit is zero.
The same authors (see [34], Theorem VIII.7.7) obtained the following useful estimate. It employs the following convention. It is known (see [15], Theorem 4.7.1) that, given a family  of
of  - measurable functions for which there exists a
- measurable functions for which there exists a  -measurable function
-measurable function  with the property that for each
with the property that for each  we have
we have  almost everywhere (such a function
almost everywhere (such a function  is called a lattice upper bound of the given family), there exists an at most countable set of indices
is called a lattice upper bound of the given family), there exists an at most countable set of indices  such that for each
such that for each  we have
we have  almost everywhere. Any other lattice upper bound of the given family is
almost everywhere. Any other lattice upper bound of the given family is  almost everywhere. This enables one to define the lattice least upper bound (lattice supremum)
almost everywhere. This enables one to define the lattice least upper bound (lattice supremum)  as a measurable function by taking the supremum over a countable subset. Of course, with this convention one can obtain a function that is smaller than the usual
as a measurable function by taking the supremum over a countable subset. Of course, with this convention one can obtain a function that is smaller than the usual  , and moreover, the usual supremum can give a non-measurable function. Nevertheless, if
, and moreover, the usual supremum can give a non-measurable function. Nevertheless, if  and the function
and the function  is measurable in both arguments, then the usual supremum with respect to
is measurable in both arguments, then the usual supremum with respect to  will also give a
will also give a  -measurable function (see [15], Corollary 2.12.8 and Exercise 6.10.42), but it is not always the lattice supremum (for example, if
-measurable function (see [15], Corollary 2.12.8 and Exercise 6.10.42), but it is not always the lattice supremum (for example, if  for
for  and
and  for
for  on an interval with Lebesgue measure, then the usual supremum equals
on an interval with Lebesgue measure, then the usual supremum equals  while the lattice supremum is
while the lattice supremum is  ).
).
Theorem 3.2. Suppose that in the situation of the previous theorem  , where
, where  , is a family of functions such that there exists a function
, is a family of functions such that there exists a function  with
with  for all
for all  . Let
. Let
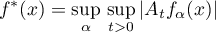
(in the sense of the lattice supremum). Then in the case 
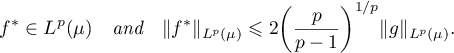
In the case  , and under the additional assumption that
, and under the additional assumption that  ,
,
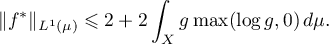
Note that in the case of a single function  (which is our interest here), to compute
(which is our interest here), to compute  we can take the supremum over rational
we can take the supremum over rational  by the continuity of
by the continuity of  in
in  , and for this we do not need the general remark made above.
, and for this we do not need the general remark made above.
It is known that the estimates  and
and  imply the inequality
imply the inequality  for all
for all  . It was noted in [37] (see also [2]) that in the case of non-negative operators the last inequality gives the estimate
. It was noted in [37] (see also [2]) that in the case of non-negative operators the last inequality gives the estimate  .
.
In [41] estimates for  were studied in the weighted space
were studied in the weighted space  for a strongly continuous semigroup of non-negative operators
for a strongly continuous semigroup of non-negative operators  on
on  , and it was shown that the boundedness of
, and it was shown that the boundedness of  in
in  is equivalent to the uniform boundedness of the norms of the operators
is equivalent to the uniform boundedness of the norms of the operators  themselves on
themselves on  .
.
In the study of convergence almost everywhere the following theorem of Banach [8] (see also [9]) has proved useful. In this theorem  is the space of equivalence classes of
is the space of equivalence classes of  -measurable functions equipped with the topology of convergence in measure, which is generated by the metric
-measurable functions equipped with the topology of convergence in measure, which is generated by the metric
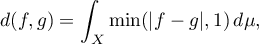
making  a complete metric topological vector space.
a complete metric topological vector space.
Theorem 3.3. Let  be a Banach space and let
be a Banach space and let  be a sequence of continuous linear operators such that for every
be a sequence of continuous linear operators such that for every  in some dense set the limit
in some dense set the limit  exists for
exists for  -almost all
-almost all  . Suppose also that for every
. Suppose also that for every 
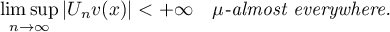
Then for every  the limit
the limit
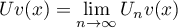
exists almost everywhere, and  is a continuous linear operator.
is a continuous linear operator.
In addition, an analogous assertion is true for a family of continuous linear operators  ,
,  , with
, with  replaced by
replaced by  , under the additional condition of the uniform continuity of
, under the additional condition of the uniform continuity of  in measure on compact intervals, that is, under the condition that for every
in measure on compact intervals, that is, under the condition that for every  and every pair of numbers
and every pair of numbers  and
and  there exists a
there exists a  such that for every vector
such that for every vector  with
with  one has the estimate
one has the estimate  for all
for all  .
.
The last condition of uniform continuity in measure is satisfied in all the situations of interest for us, because for this condition to hold it suffices that the norm  be bounded by some number
be bounded by some number  on the interval
on the interval ![$[0,L]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn245.gif) , since by the Chebyshev inequality this gives us that
, since by the Chebyshev inequality this gives us that
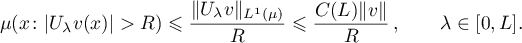
If in this theorem of Banach one takes everywhere finite versions of the measurable functions  , then
, then  can be replaced by
can be replaced by  .
.
In [32], [33], and [34], Theorem IV.11.3, the reader can find the following generalization of Banach's result.
Theorem 3.4. Let  be countable sets. Suppose that for every
be countable sets. Suppose that for every  a continuous linear operator
a continuous linear operator  from a Banach space
from a Banach space  to
to  is given such that for every
is given such that for every 

Suppose also that for every  in some dense subset of
in some dense subset of  ,
,
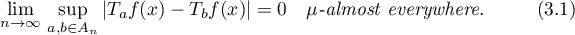
Then (3.1) is true for all  .
.
In our situation this can be applied to the countable set of times  and its subsets
and its subsets  .
.
Below we consider applications of these theorems to generalizations of the Kozlov–Treschev theorem, but we note at once that even without these rather subtle facts one can easily obtain the assertion (i) from the next proposition. The assertion (ii) follows from the Banach theorem (it is easy to verify that its hypotheses are satisfied).
Proposition 3.5. (i) Let  be a Banach space continuously embedded in
be a Banach space continuously embedded in  , let
, let  be a Banach space continuously embedded in
be a Banach space continuously embedded in  , and let
, and let  be a family of continuous linear operators from
be a family of continuous linear operators from  to
to  such that the functions
such that the functions  belong to
belong to  for
for  -almost all
-almost all  when
when  ,
,  , and
, and  . Suppose that for every pair
. Suppose that for every pair  and
and  with
with  the estimate
the estimate
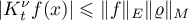
holds for all  and almost all
and almost all  . If the limit
. If the limit  exists almost everywhere for elements
exists almost everywhere for elements  and
and  of sets dense in
of sets dense in  and
and  , respectively, then this is true for all
, respectively, then this is true for all  and
and  .
.
(ii) This assertion remains valid if the estimate above is replaced by the weaker estimate
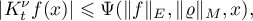
where  is a non-negative function on
is a non-negative function on  that is continuous in
that is continuous in  and measurable in
and measurable in  .
.
Example 3.6. The Kozlov–Treschev theorem follows from this proposition by the classical ergodic theorem if we take  and
and  , since
, since  contains a dense subset of step functions with bounded support, that is, finite linear combinations of the indicator functions of intervals, and for the indicator function of an interval
contains a dense subset of step functions with bounded support, that is, finite linear combinations of the indicator functions of intervals, and for the indicator function of an interval ![$[a,b]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn264.gif) the assertion is true by the classical ergodic theorem (since it is true for the indicator functions of
the assertion is true by the classical ergodic theorem (since it is true for the indicator functions of ![$[0,b]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn265.gif) and
and ![$[0,a]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn266.gif) , which can be verified by a change of variable, as in the case of the interval
, which can be verified by a change of variable, as in the case of the interval ![$[0,1]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn16.gif) ). Moreover, it is obvious that
). Moreover, it is obvious that
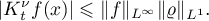
This observation clearly remains in force in the more general situation of Theorem 3.1. Actually, we only need here to have the conclusion of Theorem 3.1 for bounded functions  together with the estimate
together with the estimate  .
.
For  and
and  one can take suitable Orlicz spaces, provided that we have managed to estimate the maximal function
one can take suitable Orlicz spaces, provided that we have managed to estimate the maximal function  .
.
We note straightaway that convergence of  in
in  is not a problem, because if we have the estimate
is not a problem, because if we have the estimate  for some probability measure
for some probability measure  , then we get the estimate
, then we get the estimate
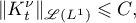
which implies the convergence of  in
in  for all
for all  provided there is convergence for all elements
provided there is convergence for all elements  in some dense set, say, for bounded functions or functions with finitely many values. Therefore, for every sequence of points
in some dense set, say, for bounded functions or functions with finitely many values. Therefore, for every sequence of points  tending to infinity there is a subsequence
tending to infinity there is a subsequence  for which the functions
for which the functions  converge
converge  -almost everywhere. If
-almost everywhere. If  and
and  , then the same estimate implies convergence in
, then the same estimate implies convergence in  .
.
Here we are interested not in methods for giving an independent proof of the existence of a pointwise limit for non-uniform averages (although we will say something about such methods), but rather in ways to derive it from the case of the usual averaging. One such way was already pointed out by Dunford and Schwartz [33], who observed that for a monotonically decreasing positive integrable function  on
on  ,
,
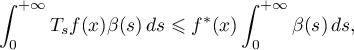
where the classical maximal function generated by  is defined by
is defined by
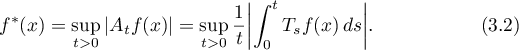
In our situation we have the same inequality:
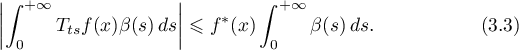
It follows from the case  using the change of variable
using the change of variable  . We explain the justification in this case. For a continuously differentiable function
. We explain the justification in this case. For a continuously differentiable function  , we get by integrating by parts that
, we get by integrating by parts that
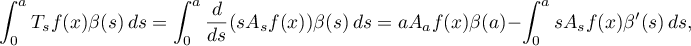
which can be estimated from above by the quantity
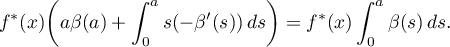
Letting  , we obtain the desired estimate for a continuously differentiable decreasing function
, we obtain the desired estimate for a continuously differentiable decreasing function  , and the general case is deduced by means of approximations (though in the previous calculations we could use the Lebesgue–Stieltjes integral for a general monotone function
, and the general case is deduced by means of approximations (though in the previous calculations we could use the Lebesgue–Stieltjes integral for a general monotone function  ). The inequality for
). The inequality for  gives (3.3) with the absolute value.
gives (3.3) with the absolute value.
Thus, the result of Banach stated above implies the following assertion.
Theorem 3.7. Suppose that for a strongly measurable semigroup  of operators on
of operators on  the classical theorem on the existence of limits of the functions
the classical theorem on the existence of limits of the functions  almost everywhere holds for all
almost everywhere holds for all  . If the density
. If the density  of the measure
of the measure  is estimated from above by an integrable monotonically decreasing function,
is estimated from above by an integrable monotonically decreasing function,  , and for each
, and for each  the function
the function  is integrable on
is integrable on  , then for every function
, then for every function 

almost everywhere. If the measure  is invariant with respect to the operators
is invariant with respect to the operators  and there are no non-constant functions which are invariant with respect to the semigroup
and there are no non-constant functions which are invariant with respect to the semigroup  , then
, then
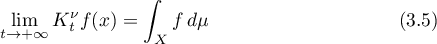
for  -almost all
-almost all  .
.
Proof. The integrability of  ensures the existence of
ensures the existence of  for almost all
for almost all  , since the integral of
, since the integral of  with respect to the measure
with respect to the measure  turns out to be finite. The inequality (3.3) ensures that
turns out to be finite. The inequality (3.3) ensures that  almost everywhere for all
almost everywhere for all  . In order to apply Banach's theorem, we have to verify that the assertion of the theorem is true for bounded
. In order to apply Banach's theorem, we have to verify that the assertion of the theorem is true for bounded  . This follows from Proposition 3.5 applied to
. This follows from Proposition 3.5 applied to  and
and  , where as a dense subset one should take the set of step functions
, where as a dense subset one should take the set of step functions  with bounded support (for them convergence is ensured by the classical theorem, the validity of which for the given semigroup is assumed in our hypotheses).
with bounded support (for them convergence is ensured by the classical theorem, the validity of which for the given semigroup is assumed in our hypotheses). 
Corollary 3.8. Let  be a strongly measurable semigroup of operators on
be a strongly measurable semigroup of operators on  such that
such that  and
and  . If the density
. If the density  of the measure
of the measure  is estimated from above by an integrable monotonically decreasing function, then the conclusion of the previous theorem holds for every function
is estimated from above by an integrable monotonically decreasing function, then the conclusion of the previous theorem holds for every function  .
.
Remark 3.9. The Banach theorem cited above leads to the following somewhat more general conclusion: if under the conditions on the semigroup indicated in Theorem 3.7 the equality (3.4) holds for all  for some density
for some density  , then it remains valid for every density
, then it remains valid for every density  , where
, where  is a constant. Note also that one can combine different conditions on the density
is a constant. Note also that one can combine different conditions on the density  by writing it as a sum or by partitioning the half-line.
by writing it as a sum or by partitioning the half-line.
Unlike the case of the classical averaging, where the convergence is for all integrable functions  , in the Kozlov–Treschev construction it is necessary to impose certain restrictions on
, in the Kozlov–Treschev construction it is necessary to impose certain restrictions on  or on the connection between
or on the connection between  and
and  . Let us consider a modification of the example in [20].
. Let us consider a modification of the example in [20].
Example 3.10. Let  be the unit circle with normalized Lebesgue measure
be the unit circle with normalized Lebesgue measure  , and let the transformation
, and let the transformation  be rotation by the angle
be rotation by the angle  , that is, let
, that is, let  for
for  , where
, where  . Also, let
. Also, let
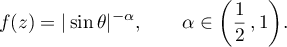
There is an absolutely continuous probability measure  with support in
with support in ![$[0,1]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn16.gif) such that
such that  for all
for all  . Moreover, the density
. Moreover, the density  of
of  can be taken in
can be taken in ![$L^r[0,1]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn293.gif) with some
with some  , and the function
, and the function  belongs to
belongs to  with
with  .
.
Indeed, let  and
and  . We take the probability measure
. We take the probability measure  with density
with density  concentrated on the set
concentrated on the set
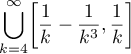
by specifying
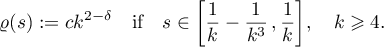
At all other points in ![$[0,1]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn16.gif) we set
we set  , and the constant
, and the constant  is taken so that
is taken so that  is a probability measure. Then
is a probability measure. Then
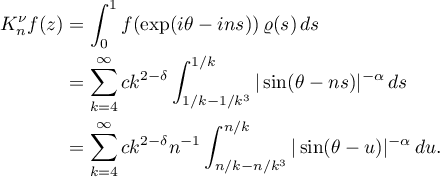
It is known (see [50], §8) that for every  there exists an infinite set of pairs of natural numbers
there exists an infinite set of pairs of natural numbers  and
and  such that
such that
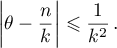
For such triples  ,
,  ,
,  we find that
we find that
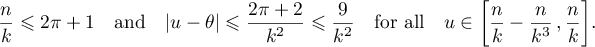
Therefore, by the equality  we have
we have
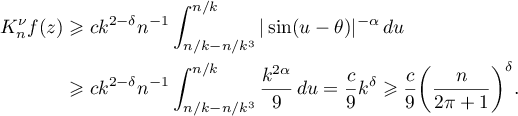
Hence  . Note that
. Note that ![$\varrho\in L^r[0,1]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn304.gif) for
for  .
.
Remark 3.11. The following result of Stein ([86], p. 73) is well known. Let  be a strongly continuous operator semigroup on
be a strongly continuous operator semigroup on  such that
such that  and
and  and such that these operators are self-adjoint on
and such that these operators are self-adjoint on  . Then the maximal function
. Then the maximal function
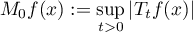
has the property that for every  there exists a number
there exists a number  such that for all
such that for all 
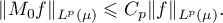
In our situation we obtain from this estimate the inequalities
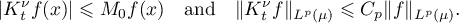
Thus, for every absolutely continuous measure  and every function
and every function  with
with  one has convergence of
one has convergence of  almost everywhere. This follows from the Banach theorem (for which one only needs the estimate
almost everywhere. This follows from the Banach theorem (for which one only needs the estimate  almost everywhere), but is easily verified directly. However, the operators
almost everywhere), but is easily verified directly. However, the operators  generated by transformations
generated by transformations  of the space
of the space  are usually not symmetric on
are usually not symmetric on  . On the contrary, general operator semigroups arising in applications are frequently symmetric. For example, the Ornstein–Uhlenbeck semigroup (see [18], [14], [16], and [17]) is defined by the formula
. On the contrary, general operator semigroups arising in applications are frequently symmetric. For example, the Ornstein–Uhlenbeck semigroup (see [18], [14], [16], and [17]) is defined by the formula
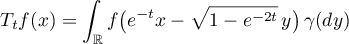
on the space  with respect to the standard Gaussian measure with density
with respect to the standard Gaussian measure with density  on the real line. The Ornstein–Uhlenbeck semigroup is non-negative and symmetric on the space
on the real line. The Ornstein–Uhlenbeck semigroup is non-negative and symmetric on the space  , and moreover, it is contractive on all the spaces
, and moreover, it is contractive on all the spaces  . The generator of this semigroup on
. The generator of this semigroup on  is the Ornstein–Uhlenbeck operator given by
is the Ornstein–Uhlenbeck operator given by  on the space
on the space  of Sobolev functions with respect to
of Sobolev functions with respect to  . The measure
. The measure  is invariant with respect to this semigroup, that is,
is invariant with respect to this semigroup, that is,
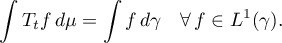
Note that in the results presented here we do not assume that the measure  is invariant with respect to the operators
is invariant with respect to the operators  (of course, for the operators generated by measure-preserving transformations
(of course, for the operators generated by measure-preserving transformations  this will be automatically the case), but if
this will be automatically the case), but if  is nevertheless invariant for non-negative operators
is nevertheless invariant for non-negative operators  , then
, then  . If, in addition,
. If, in addition,  (that is, the operators are Markov), then
(that is, the operators are Markov), then  .
.
The case of a measure  with bounded support has some features making it possible to apply the classical ergodic theorem. Suppose that for a
with bounded support has some features making it possible to apply the classical ergodic theorem. Suppose that for a  -integrable function
-integrable function  we choose some
we choose some  -function
-function  on
on  satisfying the global
satisfying the global  -condition and such that the function
-condition and such that the function  is also integrable. Such a choice is always possible, as explained in §2. Suppose in addition that the following condition holds for a strongly measurable semigroup
is also integrable. Such a choice is always possible, as explained in §2. Suppose in addition that the following condition holds for a strongly measurable semigroup  of bounded operators on
of bounded operators on  : for some
: for some 
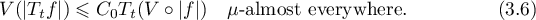
This condition holds with  by Lemma 2.1 if the operators
by Lemma 2.1 if the operators  are continuous and non-negative on
are continuous and non-negative on  and are contractions on
and are contractions on  . It holds with some
. It holds with some  if the operators
if the operators  are continuous and non-negative on
are continuous and non-negative on  and their norms on
and their norms on  are bounded by
are bounded by  .
.
Lemma 3.12. Suppose that the condition (3.6) is satisfied and the operators  are non-negative. Let
are non-negative. Let  be the complementary function for
be the complementary function for  . If the density
. If the density  on the interval
on the interval ![$[0,\tau]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn322.gif) is such that the function
is such that the function  is integrable on
is integrable on ![$[0,\tau]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn322.gif) , then
, then  -almost everywhere
-almost everywhere
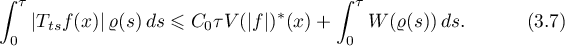
Moreover, this inequality holds if  and
and  .
.
Proof. By Young's inequality, for every 
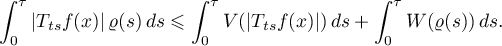
The first integral on the right-hand side does not exceed
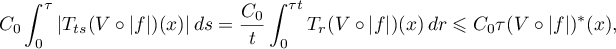
which gives the desired estimate. In the case of a contractive semigroup on  and
and  we can take the dominating semigroup of non-negative operators
we can take the dominating semigroup of non-negative operators  indicated in Remark 2.3. These are contractions on
indicated in Remark 2.3. These are contractions on  and on
and on  , and hence they satisfy (3.6), so the inequality (3.7) holds for them, and then it holds also for the original semigroup.
, and hence they satisfy (3.6), so the inequality (3.7) holds for them, and then it holds also for the original semigroup. 
The Banach theorem stated above and the convergence of the classical averages for bounded functions  imply the following assertion in view of Lemma 3.12.
imply the following assertion in view of Lemma 3.12.
Theorem 3.13. Let  be a strongly measurable operator semigroup on
be a strongly measurable operator semigroup on  such that
such that
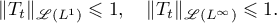
Suppose that the density  is concentrated on the interval
is concentrated on the interval ![$[0,\tau]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn322.gif) and the function
and the function  is integrable on
is integrable on ![$[0,\tau]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn322.gif) , where
, where  is the complementary function for
is the complementary function for  . Then the equality (3.4) holds for
. Then the equality (3.4) holds for  -almost all
-almost all  .
.
Below we will consider the maximal function also for non-uniform averagings.
Example 3.14. Let  be a strongly measurable operator semigroup on
be a strongly measurable operator semigroup on  such that
such that
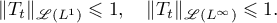
Suppose that  for some
for some  , and the density
, and the density ![$\varrho\in L^q[a,b]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn327.gif) is concentrated on the interval
is concentrated on the interval ![$[a,b]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn264.gif) , where
, where  . Then (3.4) holds for
. Then (3.4) holds for  -almost all
-almost all  .
.
This assertion is contained in [53], where the condition (3.6) was used without justification in the proof, but according to Lemma 2.1 this is legitimate (yet another inaccuracy in the proof in [53] is that it employs the estimate (3.8) below, for which the condition  is needed, but according to what we proved above the result is true for
is needed, but according to what we proved above the result is true for  as well).
as well).
It was shown above that the condition (3.6) enables us to obtain an estimate that can then be combined with the Banach theorem. However, the convergence we are interested in can be proved directly on the basis of (3.6), without using the maximal function (see below). For semigroups generated by transformations of the space  Theorem 3.13 was proved in [20] (as noted above, it also follows from results in [28] and [29]).
Theorem 3.13 was proved in [20] (as noted above, it also follows from results in [28] and [29]).
Remark 3.15. (i) Suppose that the operators  are Markov and the measure
are Markov and the measure  is invariant for them. We observe that in the proof of convergence the general case reduces to the case
is invariant for them. We observe that in the proof of convergence the general case reduces to the case  . Indeed, for
. Indeed, for  convergence is trivial, since
convergence is trivial, since  by the invariance of
by the invariance of  -measurable integrable functions with respect to
-measurable integrable functions with respect to  . Moreover, we have
. Moreover, we have  .
.
When we use a convex function  satisfying the global
satisfying the global  -condition and such that the function
-condition and such that the function  is integrable, we find that once
is integrable, we find that once  is replaced by the difference
is replaced by the difference  the function
the function  will also be integrable, because
will also be integrable, because

by the  -condition, and the function
-condition, and the function  is estimated from above by the integrable function
is estimated from above by the integrable function  according to Jensen's inequality (see [15], Proposition 10.1.9).
according to Jensen's inequality (see [15], Proposition 10.1.9).
(ii) Let us see how Theorem 3.13 can be proved directly in this situation without using the Banach theorem. Recall that the chosen function  satisfies the
satisfies the  -condition. As indicated in (i), it suffices to consider the case where
-condition. As indicated in (i), it suffices to consider the case where  . For each
. For each  we introduce the bounded cut-off functions
we introduce the bounded cut-off functions
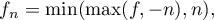
which converge to  pointwise and in
pointwise and in  , and moreover, the compositions
, and moreover, the compositions  converge to
converge to  in the same way. We write
in the same way. We write  as
as

The functions  converge pointwise to zero and do not exceed
converge pointwise to zero and do not exceed  in absolute value. Hence, the integrals of the functions
in absolute value. Hence, the integrals of the functions  converge to zero. Therefore, the integrals of the conditional expectations
converge to zero. Therefore, the integrals of the conditional expectations  also converge to zero. Passing to a subsequence, we can assume that
also converge to zero. Passing to a subsequence, we can assume that  almost everywhere. The functions
almost everywhere. The functions  converge in
converge in  to
to  , that is, to zero in our situation. Passing to a subsequence once again, we can assume that
, that is, to zero in our situation. Passing to a subsequence once again, we can assume that  almost everywhere.
almost everywhere.
For any  the bounded function
the bounded function  is such that
is such that  almost everywhere as
almost everywhere as  . Let us take a set
. Let us take a set  of unit measure for all of whose points
of unit measure for all of whose points  there is such convergence for each
there is such convergence for each  and also the convergence
and also the convergence  and the convergence
and the convergence  .
.
We show that  for all
for all  . Let
. Let  . By the
. By the  -condition there exists a
-condition there exists a  such that
such that  if the integral of
if the integral of  is less than
is less than  (see [62], Theorem 9.4). Fix
(see [62], Theorem 9.4). Fix  such that
such that

Next we take  such that
such that
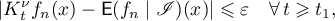
which is possible by the boundedness of  . Hence
. Hence
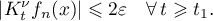
Further, we have the estimate
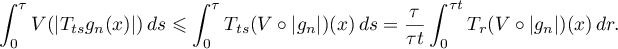
As  , the right-hand side tends to
, the right-hand side tends to  . Hence, there exists a
. Hence, there exists a  such that the left-hand side is less than
such that the left-hand side is less than  for all
for all  . Therefore, for such
. Therefore, for such  the function
the function  satisfies
satisfies  . We finally obtain
. We finally obtain
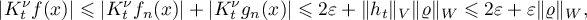
which completes the proof.
In [53] there is a proof of the following assertion giving convergence for families of functions in the case of a measurable semiflow  of measure-preserving transformations of the space
of measure-preserving transformations of the space  .
.
Theorem 3.16. Let  be some set of
be some set of  -measurable functions on the space
-measurable functions on the space  such that
such that  . Also, suppose that the function
. Also, suppose that the function  is measurable with respect to
is measurable with respect to  , the density
, the density  has support in an interval
has support in an interval ![$[a,b]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn264.gif) ,
, ![$\varrho\in L^q[a,b]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn327.gif) , where
, where ![$p\in [1,+\infty]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn369.gif) and
and  , and
, and  for
for  . Let
. Let  be a positive function on
be a positive function on  such that
such that  and
and  . If
. If  almost everywhere as
almost everywhere as  , then
, then
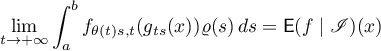
for  -almost all
-almost all  .
.
We mention a result in [53] for maximal functions generated by a weight (it was assumed there that the operators are non-negative, but according to Remark 2.3 the estimate remains valid even without this assumption). We return to these functions below.
Theorem 3.17. Let  be a strongly measurable operator semigroup on
be a strongly measurable operator semigroup on  such that
such that

In addition, suppose that  , where
, where ![$q\in (1,+\infty]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn377.gif) , and that there exists a decreasing function
, and that there exists a decreasing function  such that for some
such that for some 
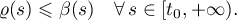
Then for any function  with
with 
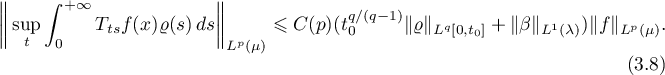
Note that  by a condition of the theorem, and hence the weight
by a condition of the theorem, and hence the weight  need not belong to
need not belong to  .
.
According to what we said above, the supremum on the left-hand side of (3.8) can be taken over a countable dense set.
Now it is appropriate to mention a number of results in the papers [28] and [29] involving convergence of averages of the form
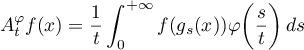
defined by a probability density  with bounded support on the half-line in the case of a semiflow of transformations
with bounded support on the half-line in the case of a semiflow of transformations  preserving the measure
preserving the measure  , and also convergence of more general averages of the form
, and also convergence of more general averages of the form
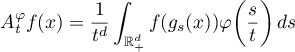
for transformations  preserving the measure
preserving the measure  and indexed by points
and indexed by points  such that
such that  and
and  .
.
In the cited papers convergence of such averages was investigated using the Lorentz class  defined for any probability density
defined for any probability density  on
on ![$[0,1]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn16.gif) and consisting of equivalence classes of
and consisting of equivalence classes of  -measurable functions
-measurable functions  with finite quantity
with finite quantity
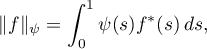
where  is the decreasing equimeasurable rearrangement of the function
is the decreasing equimeasurable rearrangement of the function  , that is, the decreasing right-continuous function on
, that is, the decreasing right-continuous function on  for which
for which
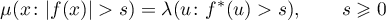
(where  is Lebesgue measure). On Lorentz classes of the indicated form see [72] and [63], Chap. II, §5. In the case where the function
is Lebesgue measure). On Lorentz classes of the indicated form see [72] and [63], Chap. II, §5. In the case where the function  is decreasing (and only in this case), the Lorentz class
is decreasing (and only in this case), the Lorentz class  is a normed space with the norm
is a normed space with the norm  (the fact that this is indeed a norm is not obvious and needs verification). Then this space is a Banach space.
(the fact that this is indeed a norm is not obvious and needs verification). Then this space is a Banach space.
The following results were proved in [28].
Theorem 3.18. Let  be a probability density on the cube
be a probability density on the cube ![$[0,1]^d$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn389.gif) with Lebesgue measure, let
with Lebesgue measure, let  be its decreasing equimeasurable rearrangement on
be its decreasing equimeasurable rearrangement on  , and let
, and let  . Then
. Then  exists
exists  -almost everywhere.
-almost everywhere.
The justification employs some estimates for the maximal function

(the same as in Theorem 3.17).
Theorem 3.19. There is a number  depending only on
depending only on  , with
, with  , such that for all non-negative functions
, such that for all non-negative functions  and all
and all 
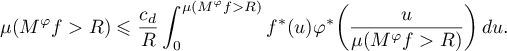
In place of the unit cube in  one can use any cube with normalized Lebesgue measure, and this also lets us use the function
one can use any cube with normalized Lebesgue measure, and this also lets us use the function  . It is interesting to consider the case of a weight
. It is interesting to consider the case of a weight  with non-compact support (there are also Lorentz classes for such weights; see [72] and [63], Chap. II, §5).
with non-compact support (there are also Lorentz classes for such weights; see [72] and [63], Chap. II, §5).
In addition, it was shown in [28] that if  and
and  is an increasing weight on
is an increasing weight on  , then for the existence of the limit the inclusion
, then for the existence of the limit the inclusion  is necessary in the following sense: if
is necessary in the following sense: if  and
and  , where
, where  is Lebesgue measure, then there exists a function
is Lebesgue measure, then there exists a function  on
on  which is equimeasurable with
which is equimeasurable with  and such that, for the flow of shifts by
and such that, for the flow of shifts by  (mod
(mod  ), convergence of
), convergence of  fails for every
fails for every  .
.
It would be interesting to obtain analogues of these results for operator semigroups on  . It is clear that Theorem 3.18 implies Theorem 3.13 in the case of the semigroup
. It is clear that Theorem 3.18 implies Theorem 3.13 in the case of the semigroup  generated by the transformations
generated by the transformations  , because in the situation of Theorem 3.13 the integral of
, because in the situation of Theorem 3.13 the integral of  is estimated by the sum of the integrals of
is estimated by the sum of the integrals of  and
and  over the interval
over the interval ![$[0,1]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn16.gif) , where the integral of
, where the integral of  over
over ![$[0,1]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn16.gif) with respect to Lebesgue measure equals the integral of
with respect to Lebesgue measure equals the integral of  with respect to the measure
with respect to the measure  . One can derive Theorem 3.18 from Theorem 3.19 by means of the Banach theorem. Indeed, the estimate for the maximal function shows that the measure of the set of points
. One can derive Theorem 3.18 from Theorem 3.19 by means of the Banach theorem. Indeed, the estimate for the maximal function shows that the measure of the set of points  with
with  is zero, for if it is equal to a number
is zero, for if it is equal to a number  , then the integral on the right-hand side is not less than
, then the integral on the right-hand side is not less than  , but this integral is not greater than the integral of
, but this integral is not greater than the integral of  because
because  is decreasing, and
is decreasing, and  is integrable since
is integrable since  , all of which leads to a contradiction as
, all of which leads to a contradiction as  . Thus, the function
. Thus, the function  is bounded with respect to
is bounded with respect to  for almost all
for almost all  , and the bounded functions (for which the limit exists, as we know) are dense in the Banach space
, and the bounded functions (for which the limit exists, as we know) are dense in the Banach space  (see [63], Chap. II, §5). It would be interesting to continue the study of the maximal function (3.9), which is more naturally connected with the summation method for general densities. This is also important for obtaining conditions for convergence without using the classical averaging, which undoubtedly should lead to more general and sharper results.
(see [63], Chap. II, §5). It would be interesting to continue the study of the maximal function (3.9), which is more naturally connected with the summation method for general densities. This is also important for obtaining conditions for convergence without using the classical averaging, which undoubtedly should lead to more general and sharper results.
The next assertion gives conditions enabling us to get rid of boundedness of the support or monotonicity of  by requiring some estimates at infinity which admit arbitrarily high peaks (see [20] for the proof).
by requiring some estimates at infinity which admit arbitrarily high peaks (see [20] for the proof).
Theorem 3.20. Suppose that the semigroup  is generated by a semigroup of measure-preserving transformations
is generated by a semigroup of measure-preserving transformations  of the space
of the space  . Suppose also that the density
. Suppose also that the density  of the measure
of the measure  satisfies the following condition: there exist positive numbers
satisfies the following condition: there exist positive numbers  such that
such that  for
for  ,
,  , and
, and  . Let
. Let  be a
be a  -integrable function. Then the equality
-integrable function. Then the equality
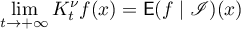
holds for  -almost all
-almost all  , and if the semiflow
, and if the semiflow  is ergodic, then (3.5) holds.
is ergodic, then (3.5) holds.
Is it possible to omit the absolute continuity of the averaging measure  ? It is readily seen that in many cases the presence of atoms of the measure
? It is readily seen that in many cases the presence of atoms of the measure  excludes convergence of
excludes convergence of  . For example, if
. For example, if  is just the Dirac measure at the point
is just the Dirac measure at the point  , then
, then  . For the group of rotations
. For the group of rotations  of the circle by the angle
of the circle by the angle  there is no limit of
there is no limit of  as
as  , so it is easy to find even a continuous function
, so it is easy to find even a continuous function  for which
for which  has no limit for any
has no limit for any  . The case of an atomless measure is more interesting, but also here the limit can fail to exist even for bounded continuous functions in the same example of the group of rotations
. The case of an atomless measure is more interesting, but also here the limit can fail to exist even for bounded continuous functions in the same example of the group of rotations  by the angle
by the angle  on the circle with Lebesgue measure
on the circle with Lebesgue measure  . Indeed, it is known (see [73], §2.2) that there exists an atomless singular Borel probability measure
. Indeed, it is known (see [73], §2.2) that there exists an atomless singular Borel probability measure  on
on ![$[0,1]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn16.gif) such that its Fourier transform
such that its Fourier transform  has no limit at infinity. Then for the simplest function
has no limit at infinity. Then for the simplest function  we get that
we get that  has no limit as
has no limit as  for any
for any  . However, it is not clear whether there exists a singular probability measure
. However, it is not clear whether there exists a singular probability measure  on
on ![$[0,1]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn16.gif) such that for the group of rotations under consideration the limit of
such that for the group of rotations under consideration the limit of  exists
exists  -almost everywhere as
-almost everywhere as  for every bounded Borel function
for every bounded Borel function  (or every function
(or every function  ). If we admit only continuous functions
). If we admit only continuous functions  in this setting, then the answer is affirmative. Indeed, then it suffices to have a limit for all polynomials in
in this setting, then the answer is affirmative. Indeed, then it suffices to have a limit for all polynomials in  and
and  , that is, it suffices that the Fourier transform of the measure
, that is, it suffices that the Fourier transform of the measure  have zero limit at infinity. It is well known that there exist singular measures
have zero limit at infinity. It is well known that there exist singular measures  with this property (see §2.2 in [73]). In this situation the existence of the limit of
with this property (see §2.2 in [73]). In this situation the existence of the limit of  for all
for all  turns out to be equivalent to the property that the maximal function
turns out to be equivalent to the property that the maximal function  is finite
is finite  -almost everywhere for such
-almost everywhere for such  . The case of continuous
. The case of continuous  is discussed in the next section. Of course, convergence of
is discussed in the next section. Of course, convergence of  to
to  in
in  can hold for singular measures
can hold for singular measures  too. For example, this is the case for the group of rotations of the circle with Lebesgue measure and every measure
too. For example, this is the case for the group of rotations of the circle with Lebesgue measure and every measure  whose Fourier transform tends to zero at infinity. This is clear from the convergence already noted on continuous functions along with the estimate
whose Fourier transform tends to zero at infinity. This is clear from the convergence already noted on continuous functions along with the estimate  , which holds for all probability measures
, which holds for all probability measures  .
.
Korolev [54] obtained an analogue of the well-known Wiener–Wintner theorem for the case of non-uniform averaging. The latter theorem [93] asserts the following for the usual averages: for any ergodic semigroup  of measure-preserving transformations and every integrable function
of measure-preserving transformations and every integrable function  , there exists a set
, there exists a set  with
with  such that for all
such that for all  and
and  the averages
the averages
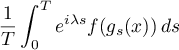
have a limit as  , and if the semigroup
, and if the semigroup  is weakly mixing and
is weakly mixing and  , then this limit is
, then this limit is  .
.
We recall that a semigroup  of measure-preserving transformations of the space
of measure-preserving transformations of the space  is said to be weakly mixing (see [31], Chap. 1, §6) if for every two functions
is said to be weakly mixing (see [31], Chap. 1, §6) if for every two functions 
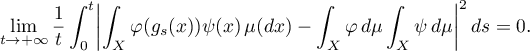
This property implies ergodicity. An analogous property is introduced for operator semigroups.
Consider the non-uniform averages
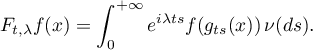
Korolev [54] proved the following assertion.
Theorem 3.21. Let  be a weakly mixing semigroup. Then for every function
be a weakly mixing semigroup. Then for every function  and every probability density
and every probability density  on
on  with bounded support, where
with bounded support, where  and
and ![$p,q\in [1,+\infty]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn438.gif) , there exists a set
, there exists a set  such that
such that  and for all
and for all  and
and 
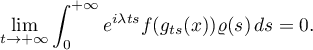
In connection with the Wiener–Wintner theorem we mention the papers [83] and [10], and also [68] and [74], where singular averagings were considered. It would be interesting to extend these results to the case of operator semigroups. It is also of interest to study the rate of convergence of non-uniform averages, which has already been investigated for the usual averages (see [47], [48]). Finally, the question arises of possible analogues of results in [45] and [46] in the situation under consideration.
§ 4. Non-uniform averagings for stochastic systems
In [21] non-uniform averagings were considered for stochastic equations. The main distinction of the stochastic case from the deterministic case is the absence of the semigroup property with respect to the time.
Let  be a continuous map on
be a continuous map on  with values in the space of linear operators on
with values in the space of linear operators on  , let
, let  be a Borel vector field on
be a Borel vector field on  , and let
, and let  ,
,  , be a
, be a  -dimensional Wiener process. We shall assume that
-dimensional Wiener process. We shall assume that  ,
,  , is the coordinate process on
, is the coordinate process on  , where
, where  is the space of all continuous trajectories on the half-line with the topology of uniform convergence on compact sets,
is the space of all continuous trajectories on the half-line with the topology of uniform convergence on compact sets,  is the Borel
is the Borel  -algebra, and
-algebra, and  is the Wiener measure.
is the Wiener measure.
We consider the stochastic differential equation

The formal generator of the diffusion defined by this equation has the form
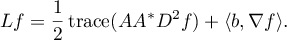
Suppose that the following conditions are satisfied:
(i)  , where
, where  is the local Sobolev class of functions in
is the local Sobolev class of functions in  with first-order generalized derivatives in
with first-order generalized derivatives in  , and moreover,
, and moreover,  ,
,  , where
, where  is a positive constant, and
is a positive constant, and  is a locally bounded map;
is a locally bounded map;
(ii) there exists a function  such that the sets
such that the sets  are compact and
are compact and
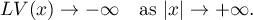
With the aid of results in [92] one can show that there exists a strong solution  of the indicated equation. It is also known (see [23] and [22]) that the process obtained has a unique invariant probability measure
of the indicated equation. It is also known (see [23] and [22]) that the process obtained has a unique invariant probability measure  with a positive continuous density of class
with a positive continuous density of class  with respect to Lebesgue measure, and the strongly continuous semigroup
with respect to Lebesgue measure, and the strongly continuous semigroup  on
on  generated by the process
generated by the process  is strongly Feller, that is, it takes functions in
is strongly Feller, that is, it takes functions in  to continuous functions, and the measure
to continuous functions, and the measure  is ergodic with respect to this semigroup, that is, if
is ergodic with respect to this semigroup, that is, if  for all
for all  , then the function
, then the function  coincides with a constant almost everywhere. For what follows, only the listed properties of the process and its transition semigroup will be essential.
coincides with a constant almost everywhere. For what follows, only the listed properties of the process and its transition semigroup will be essential.
We denote by  the image of the Wiener measure under the map
the image of the Wiener measure under the map  defined by
defined by  . It is readily seen that the measures
. It is readily seen that the measures  are weakly continuous in
are weakly continuous in  , and hence the map
, and hence the map  is measurable for every set
is measurable for every set  . We define a probability measure
. We define a probability measure  on the space
on the space  by
by
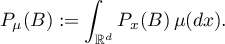
On the path space  the semigroup of shifts
the semigroup of shifts  acts by the formula
acts by the formula  . It is known (see [85], Chap. 1, §1.2) that the measure
. It is known (see [85], Chap. 1, §1.2) that the measure  on
on  is ergodic if and only if
is ergodic if and only if  is ergodic, and this holds under our assumptions.
is ergodic, and this holds under our assumptions.
Let  , where
, where  . It follows from the Birkhoff–Khinchin ergodic theorem that for
. It follows from the Birkhoff–Khinchin ergodic theorem that for  -almost all
-almost all 
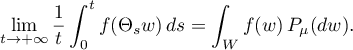
Let  be the class of all
be the class of all  -invariant sets. The ergodicity of
-invariant sets. The ergodicity of  implies that the sets in
implies that the sets in  have
have  -measure
-measure  or
or  .
.
The following ergodic theorem with the usual averaging holds (variants of this theorem can be found in [85], Chap. 1, §1.2, Theorem 7, and [66], §1.3, and [21] contains a short proof in precisely the given formulation).
Theorem 4.1. Let the conditions (i) and (ii) hold. Then for every Borel function  in
in 
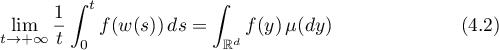
for  -almost all
-almost all  and for every
and for every  .
.
Since  , the previous theorem gives the following assertion.
, the previous theorem gives the following assertion.
Corollary 4.2. Let the conditions (i) and (ii) hold. Then for any Borel function  in
in  and any
and any 
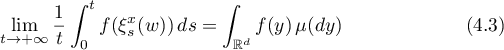
for  -almost all
-almost all  .
.
We proceed to Kozlov–Treschev type averaging in the stochastic case. Let  be an absolutely continuous probability measure on
be an absolutely continuous probability measure on  with density
with density  with respect to Lebesgue measure. For every function
with respect to Lebesgue measure. For every function  the averages
the averages
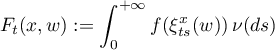
are defined for  -almost all
-almost all  , where
, where  is the Wiener measure. For these averages
is the Wiener measure. For these averages  we obtain the following assertion.
we obtain the following assertion.
Corollary 4.3. Let the conditions (i) and (ii) hold. Then for every bounded Borel function  on
on  and for every
and for every 
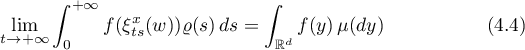
for  -almost all
-almost all  .
.
For functions  in
in  the following assertion is valid.
the following assertion is valid.
Theorem 4.4. Let the conditions (i) and (ii) hold and let  and
and  , where
, where  is a probability density and
is a probability density and  . Assume one of the conditions
. Assume one of the conditions
(i) the density  has bounded support in the interval
has bounded support in the interval ![$[a,b]$](https://content.cld.iop.org/journals/0036-0279/75/3/393/revision1/RMS_75_3_393ieqn264.gif) ,
,
(ii)  and there exists a non-decreasing function
and there exists a non-decreasing function  on
on  such that
such that  ,
,  , and
, and  on
on  for some
for some  .
.
Then for any  and for
and for  -almost all
-almost all 
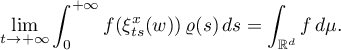
Besides non-uniform averages of stochastic systems, it would be interesting to apply analogous ideas to convergence of solutions of non-linear parabolic equations to stationary distributions (see [24]–[26], [84]), and also to analysis of attractors (see [52]).
§ 5. Dynamics of measures
Non-uniform Kozlov–Treschev averagings generated by transformations  of
of  preserving the measure
preserving the measure  motivate the consideration of a family of probability measures
motivate the consideration of a family of probability measures  on
on  defined in the following way: the measure
defined in the following way: the measure  is the image of the measure
is the image of the measure  under the map
under the map

By the definition of the image of a measure, the integral of a  -measurable bounded function
-measurable bounded function  with respect to the measure
with respect to the measure  is given by the formula
is given by the formula
Here we discuss the character of convergence of the measures  to the measure
to the measure  . In the case of an ergodic system the result due to Kozlov and Treschev has some similarity to convergence of the measures
. In the case of an ergodic system the result due to Kozlov and Treschev has some similarity to convergence of the measures  to
to  in the topology of convergence on every set. However, this convergence can fail literally, because convergence for almost all
in the topology of convergence on every set. However, this convergence can fail literally, because convergence for almost all  appears only after the integration of every fixed function
appears only after the integration of every fixed function  , and therefore the corresponding measure-zero set can depend on
, and therefore the corresponding measure-zero set can depend on  . For example, consider the ergodic group
. For example, consider the ergodic group  of shifts along trajectories of the differential equation
of shifts along trajectories of the differential equation
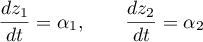
(with incommensurable  and
and  ) on the two-dimensional torus
) on the two-dimensional torus  with the normalized Lebesgue measure
with the normalized Lebesgue measure  , which is invariant with respect to
, which is invariant with respect to  . For every Borel probability measure
. For every Borel probability measure  on
on  , all the measures
, all the measures  are singular with respect to
are singular with respect to  , since every measure
, since every measure  is concentrated on a curve of
is concentrated on a curve of  -measure zero. Hence for no
-measure zero. Hence for no  can one have convergence of these measures to
can one have convergence of these measures to  on every set (although for an absolutely continuous measure
on every set (although for an absolutely continuous measure  one has weak convergence, as we shall see below). In this circle of questions it turns out to be natural to employ the topological structure of the space
one has weak convergence, as we shall see below). In this circle of questions it turns out to be natural to employ the topological structure of the space  , because we shall be discussing weak convergence of measures with respect to the duality with the space of bounded continuous functions (see §2). As above, we assume the joint measurability of
, because we shall be discussing weak convergence of measures with respect to the duality with the space of bounded continuous functions (see §2). As above, we assume the joint measurability of  with respect to
with respect to  .
.
The next results were proved in [20].
Theorem 5.1. Let  be a Radon probability measure on a completely regular topological space
be a Radon probability measure on a completely regular topological space  such that all compact sets in
such that all compact sets in  are metrizable (for example,
are metrizable (for example,  is itself metrizable or is a Souslin space). Suppose that the semiflow
is itself metrizable or is a Souslin space). Suppose that the semiflow  is ergodic. Let the measure
is ergodic. Let the measure  be absolutely continuous with respect to Lebesgue measure on
be absolutely continuous with respect to Lebesgue measure on  . Then for
. Then for  -almost all
-almost all  the measures
the measures  converge weakly to
converge weakly to  as
as  .
.
We recall that a family  of Radon measures on a space
of Radon measures on a space  is said to be uniformly tight if for any
is said to be uniformly tight if for any  there exists a compact set
there exists a compact set  such that
such that
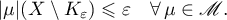
According to the Prohorov theorem, every weakly convergent sequence of Borel measures on a complete separable metric space is uniformly tight. It is also known that every uniformly tight family of Radon measures that is bounded in variation on a completely regular space  has a compact closure in the weak topology (see [15] or [19]). If the space
has a compact closure in the weak topology (see [15] or [19]). If the space  is Souslin, then every sequence of measures in such a family contains a weakly convergent subsequence.
is Souslin, then every sequence of measures in such a family contains a weakly convergent subsequence.
Theorem 5.2. Suppose that  is a Souslin (or metric) space and
is a Souslin (or metric) space and  is a Radon probability measure such that the semiflow
is a Radon probability measure such that the semiflow  is ergodic. Let the measure
is ergodic. Let the measure  be absolutely continuous. Then for any
be absolutely continuous. Then for any  there exists a compact set
there exists a compact set  such that
such that  and the family of measures
and the family of measures  with
with  and
and  is uniformly tight.
is uniformly tight.
Since  is the Dirac measure at the point
is the Dirac measure at the point  , in the case of a non-compact space
, in the case of a non-compact space  one cannot manage without removing some part of the space and making an indentation from zero with respect to
one cannot manage without removing some part of the space and making an indentation from zero with respect to  . However, it is not clear whether it is enough just to remove some part of the space.
. However, it is not clear whether it is enough just to remove some part of the space.
We now discuss analogous questions for singular atomless measures  on
on  with Fourier transform
with Fourier transform  given by
given by
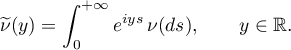
Example 5.3. Let  be the unit circle with the normalized Lebesgue measure
be the unit circle with the normalized Lebesgue measure  and let the transformation
and let the transformation  be rotation by the angle
be rotation by the angle  . If the Fourier transform of
. If the Fourier transform of  tends to zero at infinity, then the measures
tends to zero at infinity, then the measures  converge weakly to
converge weakly to  for all
for all  as
as  .
.
Conversely, if one has weak convergence for some  , then the Fourier transform of
, then the Fourier transform of  tends to zero at infinity.
tends to zero at infinity.
Indeed, for the function  or
or  on
on  we have, respectively,
we have, respectively,
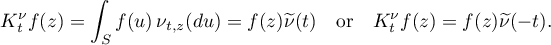
If for some  we have weak convergence of the measures
we have weak convergence of the measures  , then
, then  has some limits
has some limits  and
and  at
at  and
and  . We show that both limits are zero. It is known (see [73], Theorem 3.2.3) that the limit
. We show that both limits are zero. It is known (see [73], Theorem 3.2.3) that the limit
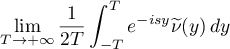
equals the size of the jump at the point  of the distribution function of the probability measure
of the distribution function of the probability measure  , which equals zero in our case due to the absence of atoms of
, which equals zero in our case due to the absence of atoms of  . Taking
. Taking  , we see that this is possible only in the case when
, we see that this is possible only in the case when  . The convolution
. The convolution  has no atom at zero either, so for its Fourier transform
has no atom at zero either, so for its Fourier transform  the indicated limit at
the indicated limit at  also equals zero. Hence
also equals zero. Hence  , and thus
, and thus  .
.
If we are given that  as
as  , then for the functions
, then for the functions  of the form
of the form  with non-zero integer
with non-zero integer  the integrals with respect to the measures
the integrals with respect to the measures  tend to zero. The integral of
tend to zero. The integral of  equals
equals  . Then convergence holds for finite linear combinations of such functions, but they uniformly approximate all continuous functions on the circle.
. Then convergence holds for finite linear combinations of such functions, but they uniformly approximate all continuous functions on the circle.
In the stochastic case considered in §4, as in the case of the deterministic semigroup, there arise the measures  on
on  defined as the images of the measure
defined as the images of the measure  under the maps
under the maps
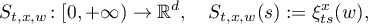
that is, the integral of a bounded Borel function  with respect to the measure
with respect to the measure  is given by the formula
is given by the formula
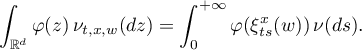
We mention two results obtained in [21]. As in §4, we assume that the probability space for our system is the path space  with the Wiener measure
with the Wiener measure  .
.
Theorem 5.4. Suppose that the conditions (i) and (ii) after (4.1) hold,  is the solution of (4.1), and
is the solution of (4.1), and  is the corresponding invariant probability measure for the process. Let
is the corresponding invariant probability measure for the process. Let  be an absolutely continuous Borel probability measure on
be an absolutely continuous Borel probability measure on  . Then for any
. Then for any  and for
and for  -almost all
-almost all  the measures
the measures  converge weakly to the measure
converge weakly to the measure  as
as  .
.
There is also an analogue of the theorem on uniform tightness.
Theorem 5.5. Under the hypotheses of the previous theorem, for any  there exists a compact set
there exists a compact set  such that
such that  and the family of measures
and the family of measures

is uniformly tight.
The author thanks F.-Y. Wang and S. V. Shaposhnikov for useful discussions.


