Interference effects in the high-order harmonic amplification process in the active medium of a plasma-based X-ray laser modulated by an optical field

The control of the electromagnetic radiation − matter interaction on a sub-optical-cycle time scale is one of the most topical problems of modern optics. In addition to the deep fundamental significance, these studies open up the possibility of extremely fast (three orders of magnitude faster than the microwave electronics allows) electronic current control in various media. In addition, the study of strongly nonlinear interaction of electromagnetic radiation with matter often requires the development of new theoretical approaches, the appearance of which, in turn, stimulates the search for new regimes of interaction between radiation and matter.

Over the past decade, the interaction of noble gas atoms with the radiation of high-order harmonics of an optical laser field (usually a sequence of attosecond pulses or a single attosecond pulse) combined with optical radiation of the fundamental frequency (a replica of the field used to generate the harmonics) has been actively studied [1 − 8] (see also review [9]). In these studies, the frequency of one of the harmonics is close to the frequency of a transition from the ground state to one of the low-lying excited energy levels [2 − 5, 7, 8] or to an autoionisation state of the atoms [1, 6]. The intensity of the optical field is insufficient for ionisation or multiphoton excitation of the atoms from the ground state, but is large enough to substantially couple ('dress') the excited states. The excitation and ionisation of the atoms occurs with the participation of harmonics of various orders and with the absorption of a different number of photons of the optical field. In this case, the probabilities of ionisation and population of excited atomic states, as well as the probability of absorbing radiation of a certain harmonic, turn out to be periodic functions (generally anharmonic) depending on the delay of the harmonic signal relative to the optical field of fundamental frequency with a period equal to the half-period of optical radiation. This periodicity is due to the interference of the excitation and ionisation paths of atoms (or absorption of harmonics of a given order) involving a different number of optical field photons, which is constructive or destructive depending on the ratio of the phase difference between harmonics of adjacent orders and the phase of the optical field. A shift and broadening of the excited energy levels of gas atoms following the oscillations of the optical field strength were also observed [5].

In later experiments [10, 11], the generation of high-order harmonics of the optical field was studied under similar conditions [when both a moderate-intensity laser field of fundamental frequency and seed radiation of harmonics of the vacuum ultraviolet (VUV) range are initially present]. It was shown that the interference of the paths of ionisation of atoms and the generation of electronic wave packets in free space leads to a periodic dependence of the intensity of the newly generated harmonics on the delay between the VUV radiation of the seed and the optical field of fundamental frequency. An analysis of the properties of harmonics of various orders makes it possible to study the subfemtosecond dynamics of atoms in a combined VUV and optical fields.

In addition, in recent years, the possibility of controlling the conductivity of dielectrics and semiconductors on a time scale of the order of an optical cycle fractions has attracted considerable interest [12 – 16]. For this purpose, a solid-state sample is irradiated with an intense and extremely short (with a few-cycle duration) optical pulse, which transfers electrons to the conduction band and creates holes in the valence band, and also causes intraband transitions over a time of a fraction of a femtosecond. Additionally, the sample is irradiated by a single attosecond VUV pulse, which allows measuring the parameters (for example, the absorption coefficient for the VUV radiation) of the medium depending on the delay between the probing harmonics and the optical field. In particular, it was shown that in a certain range of laser field intensities, the process of electron excitation is reversible, and after the end of the optical pulse, the population of the conduction band quickly (with a subfemtosecond delay) returns to its original value.

In this paper, we study the role of interference in the process of amplifying high-order harmonics of optical radiation in the active medium of a plasma-based X-ray laser, additionally irradiated by the laser field at the fundamental frequency. This work deals with the same group of problems as the previous studies of interference effects in a strong laser field combined with the radiation of its high-order harmonics. However, it differs by two fundamentally new features. First, we consider an active medium, where energy is transferred from matter to field, and not vice versa. Second, the medium is a plasma of multiply charged ions, which makes it necessary to take into account the propagation effects associated with the difference in the phase velocities of the optical and VUV fields due to plasma dispersion.

For the first time, the possibility of amplifying sets of high-order optical harmonics and sequences of attosecond pulses in a modulated active medium of a plasma-based X-ray laser was demonstrated in Ref. [17]. However, in [17] the plasma was assumed dense for the modulating optical field, so that the mutual influence of harmonics on each other in the process of amplification was suppressed. On the contrary, the present work considers the case of a relatively weak plasma dispersion at the frequency of the modulating field. We show that in this case each harmonic not only is amplified in the medium, but also generates a multi-frequency coherently scattered field at the frequencies of other harmonics. A change in the initial phases of the amplified harmonics and the modulating field, as well as a change in the medium thickness, leads to a change in the nature of the interference between the harmonic radiation and the set of coherently scattered fields. This, in turn, allows controlling the energy characteristics of harmonics, namely, the total energy density and relative amplitudes of the harmonics at the output of the modulated active medium.

Let us consider a hydrogen-like active medium of a plasma-based X-ray laser, simultaneously irradiated by an optical field with a fundamental frequency Ω and radiation of its three neighbouring high-order harmonics. One of them (the central one, we number it as 0) is tuned to resonance with the active medium transition (with taking into account the time-average shift of the energy levels of resonant ions under the action of the optical field). The other two harmonics (we number them as +1 and −1) are detuned from the resonance by ±2 frequencies of the modulating field. In the considered case of the three harmonics, it turns out to be possible to obtain a simple analytical solution for their amplitudes, which includes all the interference effects of interest.

Thus, the resonant component of the incident field is a combination of three linearly polarised high-order harmonics with the same amplitudes (amplitude moduli) E₀, the central frequencies of which are separated by 2Ω:

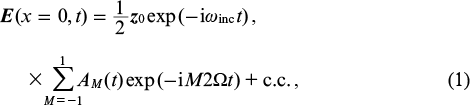
where z₀ is the unit vector of polarisation of the harmonic radiation; A_M(τ) = E₀ exp(iφ_M)θ(τ) is the slowly varying complex amplitude of the Mth harmonic at the input to the medium; φ_M is the phase of the Mth harmonic; and θ(τ) is the Heaviside function. Similarly to Refs [17 – 19], as an active medium, we consider a plasma of hydrogen-like ions initially populating the excited energy level with n = 2 (where n is the principal quantum number). We assume that the frequency of the central harmonic, ω_inc, is equal to the frequency of the transition between energy levels with n = 1 and n = 2, and that ω_inc ≫ 2Ω.

At the same time, the active plasma medium is irradiated by a replica of the laser field at the fundamental frequency Ω with linear polarisation coinciding with the polarisation of harmonics (1) and amplitude E_las, whose magnitude is below the ionisation threshold of the medium:

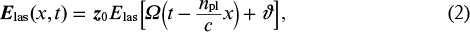
where ϑ is the initial phase of the laser field at the front edge of the plasma layer; c is the speed of light in vacuum; 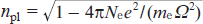is the plasma refractive index at the optical field frequency; N_e is the concentration of free electrons; and m_e and e are the electron mass and charge, respectively. Under the influence of the optical field (2), due to the Stark effect, the degenerate energy level with n = 2 is split into three sublevels. The energies of two of them, corresponding to the eigenstates of the Hamiltonian of hydrogen-like ions in the parabolic coordinate system and 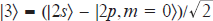, where m characterises the projection of the orbital angular momentum of ions on the z axis, trace the local value of the electric field (2) in space and time due to the linear Stark effect. They also experience constant shift due to the quadratic Stark effect

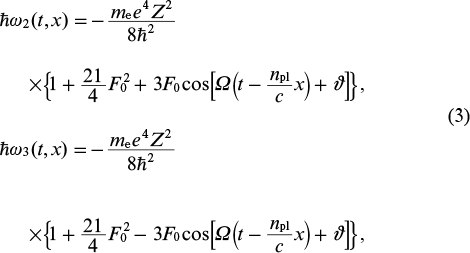
where F₀ = (2/Z)³E_las/E_a is the normalised amplitude of the laser field; E_a ≈ 5.14 × 10⁹ V cm⁻¹ is the atomic unit of the electric field strength; ħ is the Planck constant; and Z is the charge number of resonant ions. Thus, the energies of the states |2⟩ and |3⟩ turn out to be modulated by the laser field (2). Due to this fact, below we will call field (2) a modulating field. The third energy level is doubly degenerate and corresponds to the eigenstates |4⟩ = |2p, m = 1⟩ and |5⟩ = |2p, m = −1⟩. The energies of these states under the action of a modulating field experience only a constant shift due to the quadratic Stark effect: . Note that the ground state |1⟩ = |1s⟩ also experiences a slight shift due to the quadratic Stark effect: .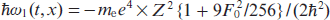

Note that the dipole moments of the transitions |2⟩ → |1⟩, |3⟩ → |1⟩ are oriented along the polarisation direction of the modulating field, i.e., along the z axis. Accordingly, these transitions are resonantly excited by the radiation of harmonics (1), which leads to the appearance of resonant polarisation of the medium:

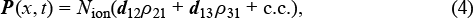
where d₁₂ = z₀d_tr; d₁₃ = − z₀d_tr; d_tr = (2⁷/3⁵)ea₀/Z; α₀ is the Bohr radius; ρ_ij are elements of the density matrix of the medium; and N_ion is the concentration of resonant ions. The dipole moments of the transitions |4⟩ → |1⟩ and |5⟩ → |1⟩ are oriented perpendicular to the z axis; d₁₄ = d₁₅ = iy₀d_tr. These transitions give rise to the generation of amplified spontaneous radiation polarised along the y axis, as well as to a decrease in the population difference, and hence gain reduction, at the transitions |2⟩ → |1⟩ and |3⟩ → |1⟩ (due to populating the ground state of ions). However, as shown in Refs [17, 19], at a sufficiently high seeding radiation intensity (1), the influence of amplified spontaneous emission can be neglected. Below, in order to obtain a sufficiently simple analytical solution, we will consider this condition to be fulfilled and exclude the states |4⟩ and |5⟩ from consideration (in Section 4, we present the results of calculations taking these states into account).

In addition, in order to derive an analytical solution, we will assume that the interaction between the electric field of harmonics (1) and the medium is linear and the change in the population difference at the resonance transitions can be neglected (below we present the calculation results taking into account the nonlinearity of the medium). We also assume that the central frequency of the harmonics radiation is tuned to exact resonance with the transitions |2⟩ → |1⟩ and |3⟩ → |1⟩, i.e. 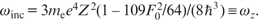. Then, in the approximation of slowly varying amplitudes for the resonant field E(x, τ) and polarisation of the medium P(x, τ), as well as in the resonant (rotating wave) approximation for the density matrix elements, the system of equations describing the transformation of field (1) in the modulated active hydrogen-like plasma medium will have the form:

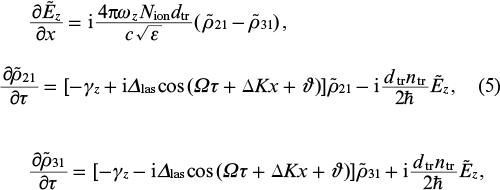
where 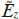and 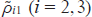are the slowly varying amplitudes of the harmonic fields and the amplitudes of quantum coherences of the medium; Δ_las = 3m_e e⁴Z²F₀/(8ħ³) is the modulation depth of the frequencies of transitions |2⟩ → |1⟩ and |3⟩ → |1⟩ due to the linear Stark effect; 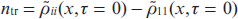is the initial population difference at these transitions (i = 2, 3); 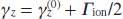is the relaxation rate of the resonant polarisation of the medium; 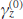is the relaxation rate of resonant polarisation in the absence of a modulating field;

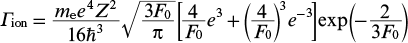
is the rate of tunnel ionisation from the excited states |2⟩ and |3⟩ under the action of the modulating field; ΔK = Ω (1 − n_pl)/c is the contribution to the wave number of the modulating optical field due to plasma dispersion; 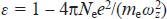is the plasma permittivity at the central frequency of the radiation of harmonics (1); and τ = τ − x/c is the local time. Below we take into account that the relaxation rate of the resonant polarisation is much lower than the frequency of the optical field, Ω/γ_z ≫ 1.

We seek a solution for the slowly varying harmonic field amplitude 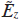in the form

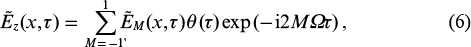
where are functions of time slowly varying on the scale of the optical field cycle at the fundamental frequency. The solution to the second equation of system (5) is sought in the form

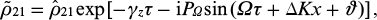
where P_Ω = Δ_las/Ω is the modulation index (a ratio between the amplitude of the shift of the excited energy levels due to linear Stark effect and the frequency of the modulating field). Then, taking into account Eqn (6), the second equation in (5) takes the form:

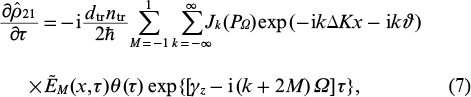
where J_k(P_Ω) is the Bessel function of the first kind of the kth order. For brevity, we omit the argument of the Bessel function: J_k(P_Ω) ≡ J_k. Integrating Eqn (7) in the approximation 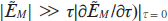, which corresponds to the initial stage of field amplification in the medium, and also taking into account that Ω/γ_z ≫ 1, we obtain a solution for the coherence 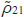in the form

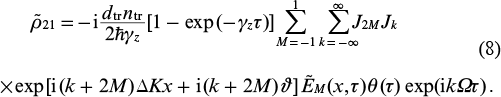
Similarly, we obtain a solution for the coherence :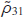

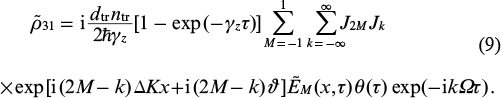
Now substituting Eqns (6), (8) and (9) into the first equation of system (5), we obtain equations which describe the transformation of the amplitude of each harmonic of the incident field during their propagation through the modulated active medium:

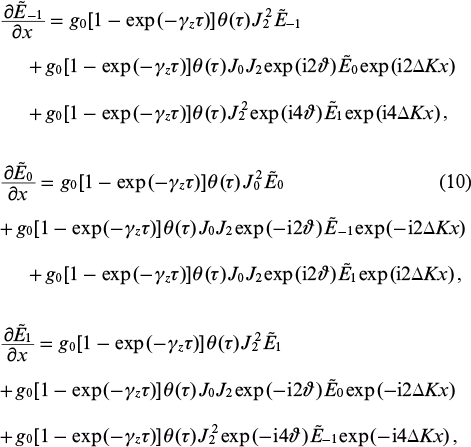
where is the gain of the active medium in the absence of modulation. Formally, system (10) can be rewritten in the integral form:

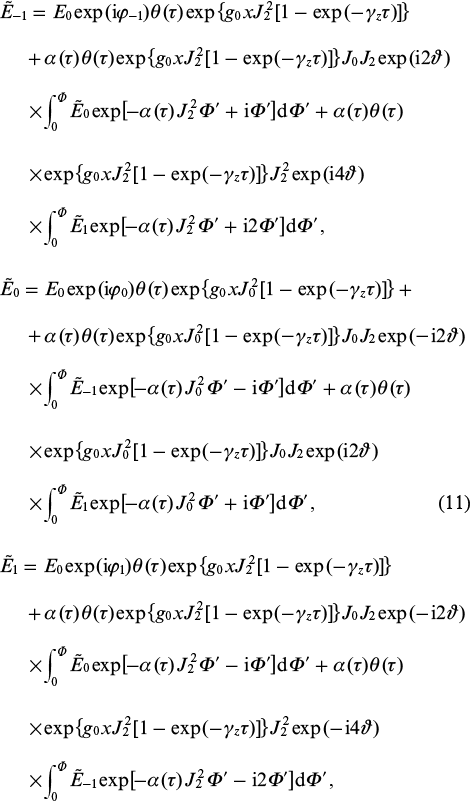
where Φ = 2ΔKx is the normalised coordinate characterising the phase shift of the modulating field during its propagation in plasma; α(τ) = g₀[1 − exp(−γ_zτ)]/(2ΔK) is the ratio of gain coefficient for the resonant radiation to the the contribution to the wave number of the modulating optical field due to plasma dispersion. It is seen that the first term in each of Eqns (11) describes the gain of each harmonic propagating independently of the others through the medium with the effective gain 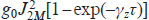, where M = 0, ±1 is the number of the appropriate harmonic [Eqns (11) account for the fact that J₋₂ = J₂]. This gain is time-dependent, since a finite time of ∼1/γ_z is required to induce the polarisation response of the medium to an incident resonant field with a sharp leading edge. It also depends of the frequency and intensity of the modulating field via the modulation index P_Ω. The remaining terms in Eqns (11) characterise the impact of the rest harmonics on the amplitude of the Mth harmonic.

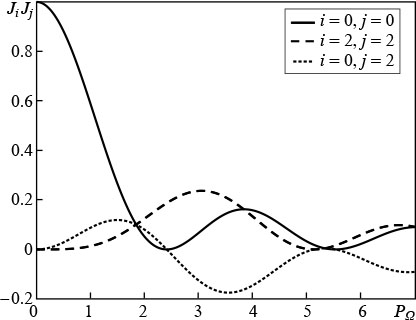
As shown in Ref. [17], if the plasma is dense, so that the phase velocity of the modulating laser field in the medium is significantly different from the velocity of light in vacuum, and g₀/(2ΔK) ≪ 1, then each harmonic in the spectrum of the incident resonant radiation is amplified independently of the rest ones. In this case, the effect of the terms in (11) containing the integrals can be neglected and the relative phases of the harmonics do not change during amplification. If, in addition, the modulation index P_Ω is chosen such that the squares of Bessel functions of different orders are approximately equal to each other (in the case of three harmonics , see Fig. 1), then all harmonics of the incident radiation are equally amplified, and at the output from the medium, the time profile of the harmonic signal does not change.

Zoom In Zoom Out Reset image size

On the other hand, if , then the harmonic gain coefficients are different (Fig. 1), which allows controlling the relative amplitudes of the zero and ±1st harmonics at the output of the modulated active medium. At the same time, the ±1st harmonics have the same gain at any modulation indices (since 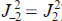), and therefore, in the process of amplification in a dense plasma, their amplitudes remain equal.

Now we consider the case of a lower-density plasma, when the phase velocity of the optical field is close to the speed of light in vacuum. In this case, as shown in Refs [18, 19], when a medium is irradiated with a single resonant harmonic, its radiation is effectively scattered by a modulation wave travelling with the phase velocity of the optical field in the medium. Due to this fact, the harmonic generates in the medium a combination of spectral components separated from each other by twice the frequency of the modulating field. Under certain conditions, namely, at the optimum modulation index and at the optimal thickness of the medium, which is determined by the plasma density and the frequency of the modulating field, the spectral components of the coherently scattered field have the greatest amplitude and are in phase with the amplified radiation of the incident (resonant) harmonic.

If such a low-density active plasma medium is irradiated by a set of harmonics, each of which is resonant to the corresponding induced spectral line of the gain [17], then the field of each harmonic will not only be amplified, but also efficiently generate coherently scattered radiation at the frequencies of the other harmonics. This scattering is described by the integral terms in equations (11).

Let us consider, for example, the second term in the first equation (11). It characterises the effect of scattering of zero-harmonic radiation with a complex amplitude 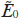on the amplitude of the minus first harmonic 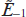. The efficiency of such scattering is characterised by the product α(τ)J₀J₂ ≈ J₀J₂/Λ (see Fig. 1), which depends on the amplitude E_las and frequency Ω or, equivalently, on the wavelength Λ = 2πc/Ω of the modulating field. For efficient scattering, it is necessary to select the values of these parameters optimally. It should be borne in mind that, on the one hand, the use of too strong a modulating field is unacceptable because of the fast ionisation from the excited states of the active medium. On the other hand, increasing the wavelength of the modulating field is also undesirable, because it reduces the efficiency of scattering of the harmonics into each other due to enhanced plasma dispersion at the frequency of the modulating field, i.e., a decrease in the parameter α(τ).

In addition, the amplitude of the coherently scattered field generated by the zero harmonic at the frequency of the minus first harmonic substantially depends on the thickness of the medium. This is because this field is a sum of partial waves generated in previous layers of the medium due to scattering of zero-harmonic radiation by a modulation wave moving with the phase velocity of the optical field. Since this velocity is different from the propagation velocity of harmonics, each partial wave is delayed, which is described by the factors exp(iΦ) in the right-hand sides of Eqns (11). As a result, in a sufficiently thin layer of the medium, if amplification can be neglected, the resulting amplitude of the coherently scattered field from the zero harmonic at the frequency of the minus first harmonic will be proportional to sin(Φ/2). Thus, at a thickness of the medium corresponding to Φ = π, the amplitude of the coherently scattered field will be maximal, and at a thickness of the medium corresponding to Φ = 2π, it will be minimal.

It is also seen from Eqns (11) that the resulting amplitude of the Mth harmonic substantially depends on the relative phases of the harmonics at the input to the medium φ_M and on the initial phase of the modulating field ϑ. If the relation between φ_M, ϑ, and Φ is such that all terms in Eqns (11) are in phase, then due to the constructive interference of coherently scattered fields with the radiation of harmonics, the gain of the harmonics increases significantly compared to their independent gain in a dense plasma [17]. We call this effect interference amplification of harmonics. At the same time, it is possible to choose a phase relationship between φ_M, ϑ, and Φ such that coherently scattered fields are in antiphase with the radiation of harmonics, and this will lead to a decrease in amplitudes and the total energy of harmonics, compared with the case of their independent amplification. We call this effect interference suppression of harmonic amplification. Below, we will illustrate both of these cases, both based on an analytical solution and by numerical solution of a more general nonlinear system of equations for harmonic amplitudes.

Thus, in a low-density plasma active medium, where the phase velocity of the optical field is close to the speed of light in vacuum, the spectral characteristics of amplified harmonics substantially (in the general case, nonmonotonically) depend not only on the modulation index P_Ω, but also on the phase of the modulating field, relative phases of harmonics, and the thickness of the medium. As a result, the coherent control becomes possible (i) of the transfer of energy from the medium to the field and (ii) of the spectral characteristics of the amplified radiation via constructive or destructive interference between the amplified incident field and coherently scattered fields.

This section provides simple analytical estimates that show the possibility of interference control of the spectral characteristics of the radiation of three harmonics at the output of the modulated active plasma medium. To simplify the analysis, we consider the modulation index P_Ω ≈ 1.84. In this case, J₀(1.84) = J₂ (1.84) ≡ J (Fig. 1), and in a dense plasma the harmonics of the incident radiation (1) will be amplified uniformly with the gain g₀J². At the same time, in a less dense plasma, taking into account coherent scattering of the harmonics into each other, their complex amplitudes will have the following form:

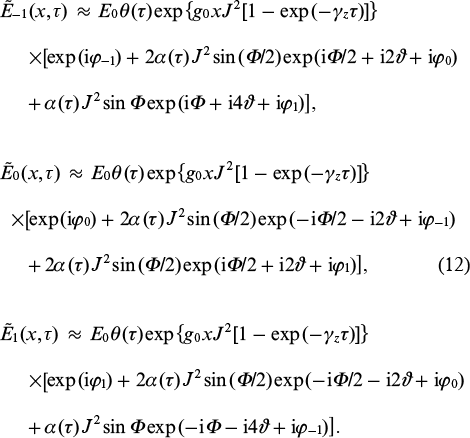
These expressions are derived from Eqns (11) using the first-order perturbation theory with α(τ) J² as a small parameter. The energy densities of the considered harmonics in the approximation α(τ) J² ≪ 1 are written as

where 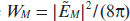is the energy density of the Mth harmonic (M = 0, ±1), while is the energy density of an individual harmonic (any of the three) propagating independently in a dense plasma. In Eqns (13), we use the notations

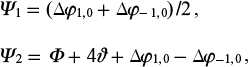
where Δφ_{1, 0} = φ₁ − φ₀ is the difference between the initial phases of the first and zero harmonics, and Δφ_{−1, 0} = φ₋₁ − φ₀ is the difference between the initial phases of the minus first and zero harmonics. Note that the intensity of the Mth harmonic differs from its energy density only by a constant factor equal to the speed of light in vacuum, i.e., I_M = cW_M. Correspondingly, Eqns (13) also characterise the phase dependences of the intensities of the harmonics.

Let us analyse the impact of coherent scattering on the characteristics of amplified harmonics. For this purpose, we introduce the efficiency of interference amplification

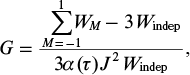
which characterises the contribution to the energy density of harmonics from coherently scattered fields, as well as the quantities characterising the asymmetry of harmonic amplification (normalised differences of the energy densities of the harmonics of different orders):

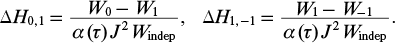
Substituting expressions (13) into these definitions, we obtain

It is seen from Eqn (14) that the quantities G, ΔH_{0, 1}, and ΔH_{1, −1} depend on the relations between the phases of the harmonics and the initial phase of the modulating field via parameters Ψ₁ and Ψ₂. The last of them also depends on the thickness of the medium via the phase incursion Φ of the modulating field in the plasma. Below, we will assume that 0 ⩽ Ψ₁ < 2π, since the harmonic phase difference multiple of 2π does not introduce new physical sense, and Ψ₂ can have any value, since the thickness of the medium, generally speaking, is not limited by anything.

From Eqn (14), in particular, it follows that for Ψ₁ = π/2 and Ψ₂ = π/2, the mutual gain efficiency G of harmonics will be zero. This means that the total energy of harmonics will be the same as in the case of their independent amplification in a dense plasma. In this case, however, the spectrum of harmonics becomes asymmetric, which is directly seen from the values of the parameters 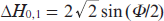and 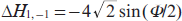. Thus, for a thickness of the medium satisfying the condition 2πk < Φ/2 < (2k + 1)π (k = 0, 1, 2,...,), W₁ < W₀ < W₋₁, while for (2k + 1)π < Φ/2 < (2k + 2)π, the opposite case is realised: W₁ > W₀ > W₋₁. If the thickness of the medium satisfies the condition Φ/2 = πk, then the amplitudes of the harmonics will be equal to each other (as in the case of their independent amplification), while the amplitudes of the coherently scattered fields are equal to zero.

Next, we find the conditions under which the efficiency of interference amplification of harmonics will be maximised or minimised. For this purpose, we differentiate G with respect to Ψ₁, Ψ₂ and equate the derivatives to zero. Thus, we obtain a system of two equations with respect to Ψ₁, Ψ₂:

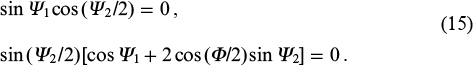
Let us consider the solutions of the system of Eqns (15). If Ψ₁ = 0, Ψ₂ = 4πk or Ψ₁ = π, Ψ₂ = 2 (2k + 1)π (k is an integer), then the efficiency of mutual amplification of harmonics is

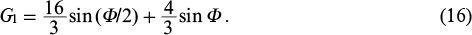
By using Eqn (12), it can be shown that this solution corresponds to the case when coherently scattered fields are in phase with the radiation of harmonics, while the harmonics themselves are in phase with each other. In this case, the effect of interference amplification of harmonics is realised. Note that, according to the definition of Ψ₂, such phase matching can be realised only for a certain initial phase of the modulating field ϑ and only for a certain thickness of the medium Φ, which are related as ϑ = −Φ/4 + Δφ_−1,0/2, where the phase shift multiple of 2π is omitted, and Δφ_−1,0 = −Δφ_1,0.

If Ψ₁ = 0 and Ψ₂ = 2(2k + 1)π or Ψ₁ = π and Ψ₂ = 4πk, then

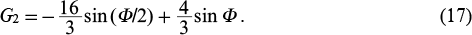
In this case, the total coherently scattered field generated by a set of harmonics of different orders appears to be in antiphase with the radiation of harmonics themselves (which are still in phase with each other), which leads to a lower radiation energy than in the case of independent amplification of harmonics in a dense plasma. In this case, the relationship between ϑ and Φ is as follows: ϑ = −π/2 − Φ/4 + Δφ_{−1, 0}/2. Thus, a change in the initial phase of the modulating field by π/2 relative to case (16) or, similarly, a delay of the harmonic signal by a quarter of the period of the optical field at the fundamental frequency leads to a transition from maximum interference amplification to interference suppression of harmonics amplification.

The remaining solutions of system (15) correspond to the intermediate efficiency of interference amplification of harmonics. Thus, if Ψ₁ = π/2, 3π/2 and Ψ₂ = (2k + 1)π, which corresponds to Δφ_{1, 0} = −Δφ_{−1, 0} + π and ϑ = −Φ/4 + Δφ_{−1, 0}/2, then

If Ψ₁ = 0 and Ψ₂ satisfies the relation cos(Ψ₂/2) = − 0.5 × [cos(Φ/2)]⁻¹, which is realised only when |cos(Φ/2)| > 1/2, the interference gain efficiency is

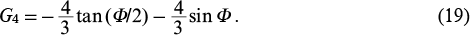
And if Ψ₁ = π and the condition cos(Ψ₂/2) = 0.5/cos(Φ/2) is fulfilled, which again is possible with |cos(Φ/2)| > 1/2, then

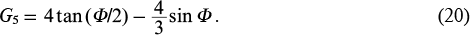
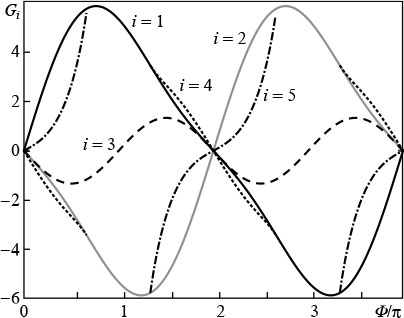
The dependences of the gain efficiency of harmonics on the thickness of the medium in the found 'ultimate' interference amplification regimes (16) − (20) are shown in Fig. 2. It is worth noting that each point on the curves corresponds to certain (and, generally, different) values of the initial phase of the modulating field and the phases of harmonics at the input to the medium, which are interrelated by the appropriate values of Ψ₁ and Ψ₂ (16) − (20). It is seen that during the propagation of harmonics through the modulated active medium, the effect of their mutual amplification is periodically replaced by the effect of interference suppression of amplification. At the same time, it should be noted that for any possible (including negative) value of the coefficient G, the energy is transferred from matter to field, i.e., the radiation of harmonic is amplified as it propagates through the medium. The coefficient G characterises the difference in the spatial dependence of the total energy density of harmonics from the exponential function. The minimum thickness of the medium at which the mutual amplification of the three harmonics is greatest corresponds to Φ_opt ≈ 0.76π, with G₁(Φ_opt) ≈ 5.87, G₂(Φ_opt) ≈ − 4.12, and G₃(Φ_opt) ≈ − 0.91, while G₄ and G₅ are not determined.

Zoom In Zoom Out Reset image size

The efficiency of interference amplification of harmonics, as well as the asymmetry of their spectrum [see Eqn (14)], substantially depend on the initial phase of the modulating field ϑ (or, which is the same, on the delay between the modulating field and the radiation of harmonics). For two 'ultimate' combinations of the initial phases of harmonics, i.e. all three harmonics are in-phase, and the first (or minus first) harmonic is in antiphase to the in-phase zero and minus first (or zero and first) harmonics, and for the optimal value Φ = Φ_opt, these dependences are plotted in Fig. 3. It can be seen from Fig. 3,a that if the incident harmonics are in phase with each other, then during amplification the harmonic spectrum remains symmetric, i.e., the amplitudes of the ±1st harmonics are equal to each other for any value of the parameter ϑ. At the same time, depending on the value of ϑ, the amplitude of the central component is either greater or smaller than the amplitudes of the ±1st harmonics. Thus, in the case of the most efficient interference amplification of harmonics, which is realised at ϑ = − 0.19π, Ψ₁ = Ψ₂ = 0 and Δφ_{−1, 0} = Δφ_{1, 0} = 0, we have ΔH_{0, 1}(Φ_opt) ≈ 2.35 and ΔH_{1, −1}(Φ_opt) = 0, i.e., W₀ > W₁ = W₋₁. When the initial phase of the modulating field changes by π/2 namely, at ϑ = 0.31π, the opposite case is realised, i.e., the interference suppression of amplification. In this case, ΔH_{0, 1}(Φ_opt) ≈ −5.09 and ΔH_{1, −1}(Φ_opt) = 0, i.e., W₀ < W₁ = W₋₁. If one of the side harmonics of the incident radiation (1) is in antiphase with respect to other harmonics, for example, Δφ_{1, 0} = π and Δφ_{−1, 0} = 0 (Ψ₁ = π/2, Fig. 3b), then the dependence of harmonics spectrum asymmetry upon the initial phase of the modulating field is more complex. For example, if ϑ = − 0.19π (Ψ₂ = π), then ΔH_{0, 1}(Φ_opt) ≈ 5.09 and ΔH_{1, −1}(Φ_opt) = −7.44, i.e., W₋₁ > W₀ > W₁; if ϑ = 0.31π (Ψ₂ = 3π), then ΔH_{0, 1}(Φ_opt) ≈ −2.35 and ΔH_{1, −1}(Φ_opt) = 7.44, i.e., W₋₁ < W₀ < W₁. Correspondingly, in this case, a change in the initial phase of the modulating field by π/2 leads to a mirror reflection of the harmonic spectrum with respect to the zero component. Thus, if the incident field of harmonics (1) is not in-phase, interference gain or suppression of amplification of harmonics is accompanied by a violation of the symmetry of their spectrum. This asymmetry can be of applied significance, since it allows correcting the amplitude distortion of the spectrum of harmonics in the process of their amplification.

Zoom In Zoom Out Reset image size

To conclude this section, we note once again that the best conditions for the mutual amplification of three harmonics at a modulation index P_Ω ≈ 1.84 are achieved when coherently scattered fields constructively interfere with harmonics. This is realised when Δφ_{−1, 0} = − Δφ_{1, 0} and ϑ = −Φ/4 + Δφ_{−1, 0}/2 (Ψ₁ = Ψ₂ = 0), and when the amplitudes of the coherently scattered fields are maximised, which corresponds to Φ_opt ≈ 0.76π (the phase shift by 2π is omitted here). In this case, according to Eqn (14), in the regime of the most efficient interference amplification, the amplitude of the zero harmonic will be greater than the amplitudes of ±1st harmonics. If the initial phase of the modulating field ϑ is shifted by π/2 (or, what is the same, the harmonic signal is delayed by a quarter of the period of the modulating field), then coherently scattered fields will destructively interfere with the radiation of amplified harmonics, leading to a decrease in the resulting field energy at the output of the medium. Moreover, in the regime of interference suppression of amplification at the thickness of the medium corresponding to Φ_opt ≈ 0.76π, the amplitude of the zero component will be smaller than the amplitudes of ±1st harmonics.

In Section 4, the results of the analytical theory are compared with the results of numerical modelling, taking into account the nonlinearity of the active medium, as well as the generation of amplified spontaneous emission from noise.

Here we analyse the possibilities of interference control of the amplification of high-order harmonics of optical radiation based on the numerical solution of Maxwell − Bloch equations for the active medium of a plasma-based X-ray laser with inversion at the transition n = 1 → n = 2 in hydrogen-like ions Li²⁺ [20]. For correct description of the amplification of high-order harmonics in a real active medium, it is necessary to take into account the nonlinear effects arising from changes in the populations of the ground and excited states of resonant ions. It is also necessary to consider the generation of amplified spontaneous radiation of orthogonal polarisation, which can overlap in time and space with amplified radiation of harmonics and decrease the efficiency of their amplification due to an increase in the population of the ground state of ions. Both of these factors are taken into account in the five-level model of the active medium used below. The model is described in detail in Refs [17 – 19] and will not be presented here.

We consider the active medium of a recombination plasma-based X-ray laser based on hydrogen-like Li²⁺ ions with a wavelength of oscillation and gain in the vicinity of 13.5 nm (in the vacuum ultraviolet range). We assume that the plasma consists only of resonant ions with a concentration of N_ion = 1.5 × 10¹⁷ cm⁻³ and free electrons with a concentration of N_e = 3 × 10¹⁷ cm⁻³. We assume the characteristic temperature to be 1 eV for ions, and 2 eV for electrons, which corresponds to the conditions of the experiment [20] (see also [21]). In this case, the characteristic times of collisional and radiative relaxation of coherence at the inverted transition of the ions are 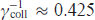ps and 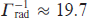ps, respectively. Similar to Refs [17 – 19], we assume that at the initial moment of time all resonant ions are equally likely to be in one of the excited states with n = 2 with equal probability. In this case, the initial population differences between the excited and ground state (the difference of the corresponding diagonal elements of the density matrix of the active medium) is equal to 1/4: 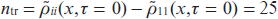, i = 2, 3, 4, 5.

Next, we choose the intensity of the modulating field just below the tunnelling ionisation threshold from the resonant excited states of the ions (so that ionisation does not have a significant effect on the amplification of the harmonics signal), namely: I_las = 4 × 10¹⁴ W cm⁻². In this case, the characteristic time of tunnel ionisation from the excited states of ions is 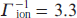ps. Taking into account all the relaxation mechanisms, the characteristic lifetime of the coherences at the resonant transitions |2⟩ → |1⟩ and |3⟩ → |1⟩, or, what is the same, the build-up time of the resonant polarisation of the medium appears to be approximately equal to 395 fs. For the considered modulating field intensity, the modulation index is P_Ω ≈ 1.84, if the wavelength of the modulating field is Λ = 2πc/Ω ≈ 0.78 μm.

For the above parameters of the plasma and the modulating field, the optimal value of the parameter Φ ≈ 0.76π found in Section 3 corresponds to the thickness of the medium L ≈ 1.8 mm. The radius of the plasma channel R is assumed to be 50 μm.

We accepted that the radiation intensity of a single harmonic at the entrance to the medium is 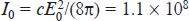W cm⁻²; this corresponds to the field energy density of an individual harmonic 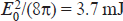cm⁻³. In this case, at the considered thicknesses of the medium (up to 3 mm), the amplified spontaneous emission turns out to be much weaker than the total radiation of the three harmonics, and the gain saturation effect at the initial time moments (γ_zτ < 1) can be neglected.

Figure 4 shows the results of numerical calculations of the total energy density of the three harmonics W_total(x, τ) = W₋₁ + W₀ + W₁ depending on the thickness of the medium x at time τ = 200 fs, satisfying the condition γ_zτ < 1 (Fig. 4a) and depending on the time τ at the optimal medium thickness x = 1.8 mm (Fig. 4b) for different combinations of the initial phases of the harmonics and the modulating field. The solid curves correspond to the interference amplification of harmonics: Ψ₁ = Ψ₂ = 0. The initial phase of the modulating field is determined up to phase difference between the zero and minus first harmonics, so that setting Δφ_{−1, 0} = Δφ_{1, 0} = 0 we obtain the optimal value ϑ = −Φ_opt/4 ≈ −0.19π. In the case under consideration, the total energy of harmonics turns out to be significantly higher than in the case of their independent amplification in a dense plasma (the corresponding solutions in Fig. 4 are shown by dotted curves) in full agreement with the analytical solution obtained in Section 3. At the same time, the dashed curves in Fig. 4 correspond to the conditions of the interference suppression of amplification: Ψ₁ = 0, Ψ₂ = 2π (for Δφ_{−1, 0} = Δφ_{1, 0} = 0 the corresponding initial phase of the modulating field is ϑ = −π/2 − Φ_opt/4 ≈ − 0.69π). In this case, the energy of harmonics is significantly lower than in the case of their independent amplification in a dense plasma.

Zoom In Zoom Out Reset image size

Note that for simulating a dense plasma we increased the electron concentration by a factor of 10, assuming that nonresonant ions (e.g., hydrogen ions [22]) are present in the plasma. As it is easy to see from Fig. 4a, the dependence of the harmonics energy on the thickness of the medium (dashed curve) approaches an exponential function with insignificant oscillations due to the mutual influence of harmonics [in this case, it is weak because the parameter α(τ) is small]. We assumed Δφ_{−1, 0} = Δφ_{1, 0} = ϑ = 0 (in a dense plasma, the values of these parameters do not play a significant role). Note that the characteristic scale of spatial energy oscillations ('steps') in Fig. 4a corresponds to a change in the parameter Φ by 2π. Moreover, the higher the electron concentration, the proportionally shorter the period of spatial oscillations of the harmonics energy. Thus, in the case of a dense plasma (dotted line in Fig. 4a), the concentration of electrons is 3 × 10¹⁸ cm⁻³, and the spatial period of the energy oscillations is approximately 0.5 mm. For other solutions, this scale is of the order of 5 mm, and the corresponding oscillations are shown in Fig. 4a only partially (since the maximum considered thickness of the medium is 3 mm). Note that the scale of spatial energy oscillations can be used to determine the concentration of free electrons in the plasma.

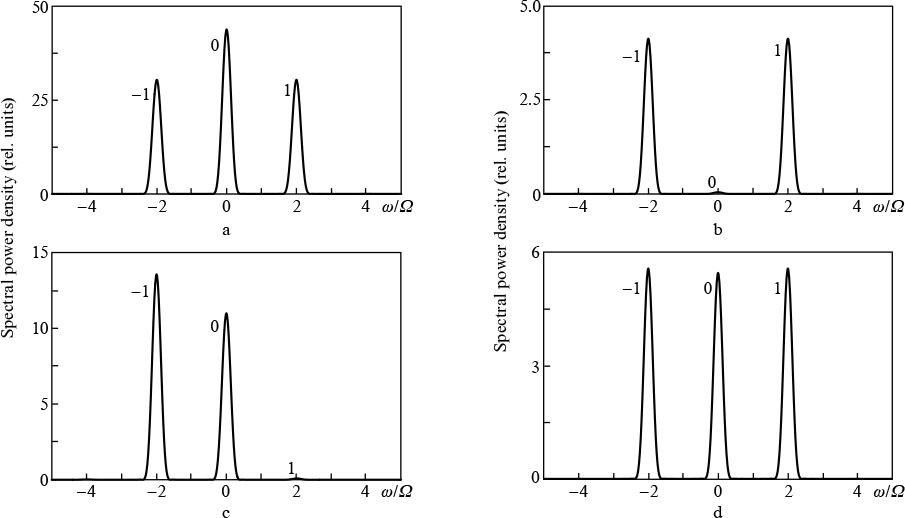
Figure 5 shows the spectra of harmonics in the medium having the optimal thickness x = 1.8 mm at the time near τ = 200 fs. They clearly show the possibility of interference control of the relative amplitudes of harmonics in the process of amplification by changing the initial phase of the modulating field and/or the initial phases of harmonics at the input to the medium. Thus, under conditions of maximum interference amplification of harmonics at Δφ_{−1, 0} = Δφ_{1, 0} = 0 and ϑ = −Φ_opt/4 ≈ −0.19π (Fig. 5a) the zero harmonic acquires the largest amplitude, while the amplitudes of ±1st harmonics are equal to each other: W₀ > W₁ = W₋₁. At the same time, in the case of interference suppression of harmonic amplification at Δφ_{−1, 0} = Δφ_{1, 0} = 0 and ϑ = −π/2 − Φ_opt/4 ≈ −0.69π (Fig. 5b) the situation turns out to be opposite: the amplitude of the zero harmonic is significantly smaller than the amplitudes of ±1st harmonics, W₀ < W₁ = W₋₁. It is also possible to minimise the amplitude of the first or minus first harmonic. Thus, if Δφ_{−1, 0} = 0, Δφ_{1, 0} = π and ϑ = −Φ_opt/4 ≈ −0.19π (Fig. 5c), the amplitude of the first harmonic is smaller than the amplitude of zero harmonic, which is in turn smaller than the amplitude of the minus first harmonic: W₋₁ > W₀ > W₁. And if Δφ_{−1, 0} = π, Δφ_{1, 0} = 0, and ϑ = −Φ_opt/4 ≈ −0.19π, the opposite result is achieved, i.e., W₋₁ < W₀ < W₁, and the ratios of amplitudes of the most intense harmonic, which experienced average amplification, and the weakest harmonic will remain unchanged. Figure 5d shows the spectrum of harmonics in the case of their amplification in a dense plasma (when the electron concentration is 10 times higher than in Figs 5a − 5c). As expected, in this case all harmonics are amplified uniformly. Note that the dependence of the asymmetry of the amplified harmonics spectrum on the distribution of their initial phases can be used not only to control the amplitudes of harmonics (in particular, to compensate for initial spectrum asymmetry), but also to determine the relative input phases of harmonics from their output amplitudes.

Zoom In Zoom Out Reset image size

To observe the interference effects discussed in the paper experimentally, it is, first of all, necessary to ensure the uniformity and invariance of the concentration of free electrons, the amplitude and initial phase of the modulating field, and the initial phases of harmonics, since these parameters primarily affect the interference of multifrequency coherently scattered fields with the radiation of harmonics. However, the change in the role of interference effects (shift of interference maxima and minima, changes in the spectral and energy characteristics of harmonics), due to the dependence of these parameters on time and longitudinal coordinate, can be described in terms of Eqns (5) with variable parameters. In this case, of course, the solution of these equations will have a more complex form than (12). As for the transverse inhomogeneities of the concentration of free electrons, the amplitude and the initial phase of the modulating field and the initial phases of harmonics, they will lead to a change in the interference characteristics in the cross section of the harmonics beam. These effects can be theoretically simulated using a spatially non-one-dimensional model and investigated experimentally by measurements with transverse resolution. Nevertheless, under optimal experimental conditions it is desirable to reduce the role of these effects by using a sufficiently short pulse of harmonics radiation and a sufficiently long pulse of the modulating field (to minimise the influence of time dependences of the characteristics of the medium and the modulating field). The harmonics should be focused into a spot of small diameter (to improve transverse uniformity of electron concentration and amplitude of the modulating field) and the sample should be sufficiently short compared to the Rayleigh length of the optical and VUV fields, and located at their focus (to ensure longitudinal uniformity of the field characteristics).

Thus, we have investigated the interference effects arising in the process of amplification of a set of three neighbouring high-order harmonics of optical radiation in the active medium of a plasma-based X-ray laser, simultaneously irradiated with a replica of the optical field of fundamental frequency. It is shown that in a medium with not too strong plasma dispersion at the frequency of the optical field, each of the harmonics during amplification generates a coherently scattered field at frequencies of other harmonics. The interference of coherently scattered fields with the radiation of harmonics significantly affects the efficiency of energy transfer from the active medium to resonant radiation, as well as the energy distribution between harmonics of different orders. In particular, under certain conditions, the effect of interference amplification of harmonics is realised, and due to constructive interference of the radiation of harmonics with coherently scattered fields, the total energy of the amplified radiation appears to be greater than in the case of independent amplification of each harmonic in a dense plasma. It is also possible to realise the opposite effect, i.e., interference suppression of gain. In this case, coherently scattered fields interfere destructively with radiation of harmonics, and the total energy of resonant radiation decreases, as compared to the case of independent amplification of harmonics in a dense plasma. The considered interference effects substantially depend on the relative phases of harmonics at the input to the medium and on the initial phase of the optical field of fundamental frequency (equivalent to a delay of the harmonics with respect to the optical field by a fraction of its period). In particular, the phases of input harmonics determine the degree of asymmetry of the spectrum of amplified output harmonics, which can be used both to control the spectrum of harmonics during amplification and to determine the initial phases of amplified harmonics. In addition, the role of interference effects periodically changes with the thickness of the medium, which is due to a change in the phase difference between the modulating optical field and the radiation of harmonics due to plasma dispersion at the optical frequency. In particular, the growth of the total energy of harmonics is accompanied by its periodic oscillations in space, the scale of which allows assessing the concentration of free electrons in the active medium. This work is the first study of the interference effects arising from the optical (on the scale of an optical field cycle) modulation of the parameters of the active medium of a plasma X-ray laser in a strong laser field. The results can be used both to control the characteristics of high-harmonic radiation in the process of amplification, and for diagnostics of the parameters of amplified radiation and active medium.

This work was supported by the Russian Science Foundation (Grant No. 19-72-00140).