ABSTRACT
The Schulhof family, a tight cluster of small asteroids around the central main belt body (2384) Schulhof, belongs to a so far rare class of very young families (estimated ages less than 1 Myr). Characterization of these asteroid clusters may provide important insights into the physics of the catastrophic disruption of their parent body. The case of the Schulhof family has been up to now complicated by the existence of two proposed epochs of its origin. In this paper, we first use our own photometric observations, as well as archival data, to determine the rotation rate and spin axis orientation of the largest fragment (2384) Schulhof. Our data also allow us to better constrain the absolute magnitude of this asteroid, and thus also improve the determination of its geometric albedo. Next, using the up-to-date catalog of asteroid orbits, we perform a new search of smaller members in the Schulhof family, increasing their number by 50%. Finally, the available data are used to access Schulhof's family age anew. We now find that the younger of the previously proposed two ages of this family is not correct, resulting from a large orbital uncertainty of single-opposition members. Our new runs reveal a single age solution of about 800 kyr with a realistic uncertainty of 200 kyr.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Analysis of asteroid families, clusters of fragments born in the disruption of a common progenitor, offers a unique possibility to study outcomes from extremely energetic collisions in space. This is because computer models of these events could only be constrained and justified with the data from asteroid families. It has been recognized (e.g., Nesvorný et al. 2015, and references therein) that the configuration of large and old families is changed over a Gyr timescale by both gravitational and non-gravitational perturbations. Thus the compact and young families, in which the abovementioned effects did not have enough time to build significant perturbations, provide the least biased sample for collisional outcome studies. The first family in the sub-Myr age class has been discovered only recently around the largest fragment (1270) Datura (Nesvorný et al. 2006). A few more examples followed (e.g., Nesvorný & Vokrouhlický 2006; Pravec & Vokrouhlický 2009), but the field is still in the early days of its development. We need more young families to be discovered, and those that are presently known need to be better characterized using astronomical observations.
In this paper, we analyze a peculiar case of a young family around the main belt asteroid (2384) Schulhof. Part of this family was discovered by Pravec & Vokrouhlický (2009), who reported a cluster of objects about (81337) 2000 GP36. However, Vokrouhlický & Nesvorný (2011) later recognized that this was just a substructure of a more extended family related to the largest member (2384) Schulhof, thus the Schulhof family. They also found that the cluster around (81337) 2000 GP36 has a curious disconnect from (2384) Schulhof, manifested mainly in a ∼5° difference in secular angles Ω and ϖ. Yet the bodies showed a perfect past orbital convergence to (2384) Schulhof some 780 ± 100 kyr ago. Vokrouhlický & Nesvorný (2011) were mainly struck by their finding that the small asteroids in the immediate vicinity of (2384) Schulhof, clearly members of its family, indicated a preference to a <100 kyr age, as inferred from their past convergence to (2384) Schulhof. This suggested age was different from that determined by orbital evolution of the remaining members. They suggested the possibility of two formation events in the Schulhof family within the past Myr. While it is not impossible, or perhaps even not uncommon, that a cascade of collisions exists in asteroid families,10 here the available time is very short. Vokrouhlický & Nesvorný (2011) estimated that a second collisional event in the Schulhof family in the past 100 kyr is very unlikely. Rather, they speculated about the possibility that the family formation event some 780 kyr ago left the largest fragment (2384) Schulhof near the state of fission instability that manifested itself recently and led to the formation of the cluster of kilometer-size members in its vicinity. If so, this would have been a first example of such a colorful evolution. However, a third possibility was that the estimated very young ages of some members in the Schulhof family were incorrect, perhaps due to their poorly known orbits. This situation motivated us to revisit the Schulhof family with a principal goal to resolve its age puzzle.
In Section 2 we first report our photometric observations of the largest member (2384) Schulhof. They allowed us to improve the estimate of the absolute magnitude of this asteroid, which, when combined with the WISE measurements, has implications on the value of its geometric albedo. We use this corrected albedo value in order to estimate the sizes of other members in the family. Second, the data allowed us to use inverse methods to resolve rotation parameters of (2384) Schulhof, namely the sidereal rotation period and pole orientation. The latter also feeds an interesting constraint into our backward orbital integrations with the goal of estimating the family age. In Section 3 we update the list of Schulhof family members. We find that the number of family members significantly increased over the past few years through discoveries of small, kilometer-size objects. Even more importantly, orbits of previously known objects improved with new astrometric data from the past few years. With this new information, we revisit the problem of Schulhof family age using orbital convergence of its currently known members (Section 4).
2. (2384) SCHULHOF
Basic information about this S-type main belt asteroid, located at the outskirts of the Eunomia family, can be found in Section 2.1 of Vokrouhlický & Nesvorný (2011). Spectral observations and broadband photometry from the Sloan Digital Sky Survey mentioned in that reference were later complemented by WISE observations in near- and mid-thermal bands. Based on these data, Masiero et al. (2011) derived Schulhof's size D = 11.72 ± 0.14 km and geometric albedo  (both formal values of uncertainty). Their solution assumed an absolute magnitude value H = 11.7 given by the Minor Planet Center catalog, which was based on astrometric survey observations. Our photometric observations allowed us to determine Schulhof's absolute magnitude more accurately, and thus apply methodology as in Pravec et al. (2012) to correct the estimated geometric albedo value (Section 2.1).
(both formal values of uncertainty). Their solution assumed an absolute magnitude value H = 11.7 given by the Minor Planet Center catalog, which was based on astrometric survey observations. Our photometric observations allowed us to determine Schulhof's absolute magnitude more accurately, and thus apply methodology as in Pravec et al. (2012) to correct the estimated geometric albedo value (Section 2.1).
Additionally, preliminary results of Schulhof's rotation state have been obtained by Hanuš et al. (2013), who used 121 sparse photometry observations of the Catalina Sky Survey and a priori information of the short rotation period from Ditteon et al. (2002). Their model revealed a retrograde rotation with two nominal pole orientations (λ, β) = (172°, −76°) and 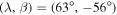 for the ecliptic longitude λ and latitude β. Given the very limited data set, the uncertainty in both coordinates may be ≃10°–15°. The sidereal rotation period was P = 3.29367 hr. Here, we use a combination of sparse and dense photometric observations to improve the solution. The traditional dense light curves were both archival from Ditteon et al. (2002) and from our own new observations (Section 2.1).
for the ecliptic longitude λ and latitude β. Given the very limited data set, the uncertainty in both coordinates may be ≃10°–15°. The sidereal rotation period was P = 3.29367 hr. Here, we use a combination of sparse and dense photometric observations to improve the solution. The traditional dense light curves were both archival from Ditteon et al. (2002) and from our own new observations (Section 2.1).
2.1. Observations
The data set consisted of about 20 light curves (dense photometry) observed during four apparitions and sparse-in-time photometry from the Catalina Sky Survey in the R and V filters that we downloaded from the AstDyS site.11 Table 1 summarizes the available data. Observations in the 2012 apparition were numerous and they extended over several lunations before and after the opposition. This allowed us to unambiguously phase-link the observations from other apparitions and thus obtain an unambiguous solution of the sidereal rotation period for this asteroid.
Table 1. Aspect Data for the Photometric Observations of (2384) Schulhof
| Date | r | Δ | α | λ | β | Observer |
|---|---|---|---|---|---|---|
| (AU) | (AU) | (deg) | (deg) | (deg) | ||
| Dense Photometry | ||||||
| 2002 03 23.1 | 2.345 | 1.358 | 4.4 | 173.1 | 4.6 | Ditteon et al. (2002) |
| 2002 04 05.1 | 2.336 | 1.391 | 10.5 | 170.2 | 3.0 | Ditteon et al. (2002) |
| 2002 04 10.2 | 2.332 | 1.415 | 12.7 | 169.3 | 2.4 | Ditteon et al. (2002) |
| 2002 04 11.2 | 2.331 | 1.420 | 13.2 | 169.2 | 2.3 | Ditteon et al. (2002) |
| 2012 09 09.9 | 2.880 | 1.947 | 9.2 | 14.6 | −0.9 | Skalnaté Pleso |
| 2012 09 10.3 | 2.880 | 1.945 | 9.0 | 14.5 | −0.9 | Sugarloaf Mountain |
| 2012 09 11.3 | 2.880 | 1.939 | 8.7 | 14.3 | −0.9 | Sugarloaf Mountain |
| 2012 10 04.9 | 2.894 | 1.894 | 1.0 | 9.0 | 0.7 | Ondřejov |
| 2012 12 01.7 | 2.916 | 2.393 | 18.2 | 2.3 | 3.6 | Ondřejov |
| 2012 12 03.7 | 2.917 | 2.421 | 18.4 | 2.4 | 3.7 | Abastumani |
| 2012 12 03.8 | 2.917 | 2.421 | 18.4 | 2.4 | 3.7 | Ondřejov |
| 2012 12 05.8 | 2.918 | 2.449 | 18.7 | 2.6 | 3.8 | Ondřejov |
| 2012 12 06.7 | 2.918 | 2.462 | 18.8 | 2.6 | 3.8 | Abastumani |
| 2012 12 07.8 | 2.918 | 2.477 | 18.9 | 2.7 | 3.8 | Ondřejov |
| 2012 12 08.7 | 2.918 | 2.490 | 18.9 | 2.8 | 3.8 | Ondřejov |
| 2012 12 09.7 | 2.919 | 2.504 | 19.0 | 2.9 | 3.9 | Abastumani |
| 2013 01 02.7 | 2.923 | 2.850 | 19.6 | 6.7 | 4.4 | Abastumani |
| 2013 12 23.1 | 2.728 | 1.790 | 7.7 | 97.4 | 20.9 | Abastumani |
| 2013 12 24.1 | 2.727 | 1.787 | 7.6 | 97.1 | 20.9 | Ondřejov |
| 2014 02 02.8 | 2.679 | 1.915 | 15.8 | 88.9 | 19.0 | Abastumani |
| 2015 03 22.3 | 2.299 | 1.557 | 20.2 | 233.6 | −8.7 | PROMPT |
| Sparse Photometry | ||||||
| 1999–2005 | CSS, R filter (24 points) | |||||
| 2005–2010 | CSS, V filter (97 points) | |||||
Note. The observations are given sequentially in time, starting with dense photometry data and followed with sparse photometry data. For each light curve observation we provide the asteroid's distance from the Sun r and from the Earth Δ, the solar phase angle α, the geocentric ecliptic coordinates (λ, β), and the observatory or source: Skalnaté Pleso is a 0.61 m telescope located at the Astronomical Institute of the Slovak Academy od Sciences, Sugarloaf Mountain is a 0.5 m telescope located in South Deerfield, Massachusetts, Ondřejov is a 0.65 m telescope located at the Astronomical Institute of the Czech Academy od Sciences, Abastumani is a 0.7 m Maksutov camera located at the Abastumani Astrophysical Observatory, Georgia, PROMPT is a 0.41 m robotic telescope of the University of North Carolina at Chapel Hill located at Cerro Tololo, and CSS is the Catalina Sky Survey where we used data from the 0.8 m Catalina telescope (observatory code 703).
Download table as: ASCIITypeset image
We took photometric observations of (2384) Schulhof with the 0.65 m telescope in Ondřejov over six nights in 2012 and one night in 2013. The observations were taken with the Bessell R filter and they were calibrated in the Cousins R photometric system using Landolt (1992) standard stars with absolute errors of 0.01 mag. Integration times were 180 s and the telescope was tracked at the half-apparent rate of the asteroid. The observations were reduced using procedures described in Pravec et al. (2006).
Observations at Sugarloaf Mountain Observatory were made using a 0.5 m, f/4.0 reflector. The imaging CCD was a SBIG ST-10XME cooled to −15 C. Images with integration times of 110 seconds were taken through a clear filter. Absolute magnitudes were estimated using a method inherent in the analysis software, which was MPO Canopus. This calibration method is based on referencing a hybrid star catalog consisting mostly of 2MASS stars in the V band. The accuracy is estimated to be 0.07 mag.
The photometric observation of (2384) Schulhof was also obtained on 2012 September 9 with the 0.61 m f/4.3 reflector at the Skalnaté Pleso Observatory through the Cousins R filter and SBIG ST-10XME with 3 × 3 binning with resolution of 1.6 arcsec px−1. 240 s CCD frames were reduced in the standard way using bias, dark, and flat field frames.
We also observed (2384) Schulhof at Abastumani Observatory using the 0.7 m Maksutov telescope over four nights during the 2012–2013 opposition and two nights during the 2013–2014 opposition. Images were taken through a clear filter and reduced using techniques explained in Krugly et al. (2002). The photometric measurements were performed with ASTPHOT software (Mottola et al. 1995). The estimated uncertainty of the photometric points was better than 0.02 mag.
Finally, observations of (2384) Schulhof were also made with the 0.41 m PROMPT-1 telescope at Cerro Tololo on one night in 2015. The observations were taken with a LUM (IR Block) filter with an exposure time of 180 s. The observations were reduced with standard aperture photometry procedures using the photometry program MIRA.
Our well-calibrated observations covered a large enough interval of phase angles to determine Schulhof's absolute magnitude H. From the Ondřejov observations, we derived the mean absolute magnitude in the Cousins R band HR = 11.64 ± 0.03 and slope factor G = 0.24 ± 0.02. Considering the mean  value for S-type asteroids (e.g., Pravec et al. 2012) and recalling that (2384) Schulhof has measured SDSS colors matching those spectral classifications, we obtain H = 12.13 ± 0.06. This is significantly different from the value of 11.7 quoted above and used by the WISE team to determine Schulhof's size D and geometric albedo pV.12
Using the method presented in Section 4 of Pravec et al. (2012), we can improve the WISE solution of D and pV. In particular, we obtained D = 11.57 ± 0.14 km and
value for S-type asteroids (e.g., Pravec et al. 2012) and recalling that (2384) Schulhof has measured SDSS colors matching those spectral classifications, we obtain H = 12.13 ± 0.06. This is significantly different from the value of 11.7 quoted above and used by the WISE team to determine Schulhof's size D and geometric albedo pV.12
Using the method presented in Section 4 of Pravec et al. (2012), we can improve the WISE solution of D and pV. In particular, we obtained D = 11.57 ± 0.14 km and 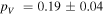 . As explained in Pravec et al. (2012; see also Harris & Harris 1997), a more significant correction concerns the geometric albedo value. We note that both uncertainties are formal. Their realistic values may be somewhat larger (especially as far as the size is concerned).
. As explained in Pravec et al. (2012; see also Harris & Harris 1997), a more significant correction concerns the geometric albedo value. We note that both uncertainties are formal. Their realistic values may be somewhat larger (especially as far as the size is concerned).
The size of (2384) Schulhof allows us to estimate two important quantitative parameters needed for the analysis of past convergence of Schulhof family members (Section 4): (i) the escape velocity from this body ≃7 m s−1 and (ii) the Hill radius of its gravitational influence ≃2800 km (both assume 2 g cm−3 bulk density). Their values for the parent body of the Schulhof family were only slightly larger. Since we do not have enough information about the smaller family members yet, we shall assume ≃7 m s−1 and ≃3000 km for the parent object escape velocity and Hill radius.
2.2. Rotation State and Shape Solution
To reconstruct the physical model of Schulhof, we applied the light curve inversion method of Kaasalainen et al. (2001) to the photometric data listed in Table 1; see Figure 1 for the match between the sample of the observations and the model. We found a unique solution for the sidereal rotation period of 3.293677 ± 0.000002 hr for which the pole direction converged to two local minima of the χ2 function at ecliptic longitude and latitude (λ, β) = (173°, −81°) (pole P1) and (λ, β) = (65°, −54°) (pole P2). To estimate the uncertainties of these pole directions (Figure 2), we mapped the χ2 function for all pole directions on the sky and set the boundary of acceptable solutions in accord with the method described in Vokrouhlický et al. (2011). For both pole values, the region of acceptable solutions was more elongated along the β coordinate, which means that the longitude was determined better than the latitude. Because the available data set is still not very large and the number of adjusted parameters is significant, the uncertainty zone does not have an ellipsoidal shape. Rather, it is irregular and in the case of the P1 pole not centered at the formal best solution. Nevertheless, we note that the maximum southern latitude statistically compatible with the data is ≃ −40°. This corresponds to a minimum obliquity value of ≃135°. The shape model corresponding to the P1 pole is shown in Figure 3. The P2 shape model has a similar pole-on silhouette but is less flattened in the rotation-axis direction. Both shape models, as well as the complete set of dense light curve data used in our analysis, are available at the DAMIT website.13
Figure 1. Examples of light curve data of (2384) Schulhof (symbols; see Table 1) fitted with synthetic light curves (solid curves) produced by the model in Figures 2 and 3 (nominal P1 solution). The abscissa is a rotation phase for a sidereal period of 3.293677 hr with an arbitrary origin, and the ordinate is the relative intensity with an arbitrary zero point (for non-calibrated data). The viewing and illumination geometry is given by the aspect angle θ, the solar aspect angle θ0, and the solar phase angle α.
Download figure:
Standard image High-resolution imageFigure 2. Quality of fit between the data and the model represented using a sinusoidal projection of the sky in ecliptic coordinates: color-coded is the reduced χ2 value (see the sidebar for numeric values). The two local minima P1 and P2 (yellow circles) are the formal best-fit solutions. The estimated uncertainty of the poles is shown as two solid boundaries around P1 and P2.
Download figure:
Standard image High-resolution imageFigure 3. Shape model for (2384) Schulhof reconstructed from the available photometic data for the pole P1 solution. The left and middle panels yield two perpendicular equatorial views, and the right panel shows a view from the rotation pole.
Download figure:
Standard image High-resolution image3. THE SCHULHOF FAMILY: MEMBERSHIP AS OF 2015 JUNE
In order to obtain a current, updated census of Schulhof family members, we searched small asteroids in the vicinity of the (2384) Schulhof orbit in the five-dimensional space of osculating orbital elements (excluding the mean anomaly). Instead of using a specific metric function such as in Vokrouhlický & Nesvorný (2011) to set the search limit, we used a simpler but more robust procedure. Taking the nominal osculating orbit of (2384) Schulhof as of epoch MJD 57200, we searched in the MPCORB catalog for all asteroid orbits whose osculating orbital elements satisfy the following conditions: (i) a difference in semimajor axis a smaller than 0.01 AU, (ii) a difference in eccentricity e smaller than 0.005, (iii) a difference in inclination I smaller than 0 25, and (iv) differences in the longitude of node Ω and perihelion ϖ both smaller than 20°. Given the metric coefficients adopted in Vokrouhlický & Nesvorný (2011), the maximum orbital difference would correspond to a distance d ≃ 240 m s−1, dominated by contributions from the eccentricity, inclination, and semimajor axis differences. The liberal constraint on secular angles, much larger than for the previously known Schulhof family members, presumably allowed us to also find smaller objects that drifted farther from the family center via the Yarkovsky effect, and have thus differentially precessed away from the orbit of (2384) Schulhof.
25, and (iv) differences in the longitude of node Ω and perihelion ϖ both smaller than 20°. Given the metric coefficients adopted in Vokrouhlický & Nesvorný (2011), the maximum orbital difference would correspond to a distance d ≃ 240 m s−1, dominated by contributions from the eccentricity, inclination, and semimajor axis differences. The liberal constraint on secular angles, much larger than for the previously known Schulhof family members, presumably allowed us to also find smaller objects that drifted farther from the family center via the Yarkovsky effect, and have thus differentially precessed away from the orbit of (2384) Schulhof.
With the above outlined procedure we found 15 objects in Schulhof's vicinity. This sample contained all eight formerly known members discussed in Vokrouhlický & Nesvorný (2011), but also additional asteroids that could potentially enlarge the population of small members in this family. We numerically integrated nominal orbits of these objects for 2 Myr backward in time with only gravitational effects of the Sun and planets included. While only approximate, the results from this initial simulation were able to guide us further about potential membership in the family. In particular, we were able to identify interlopers whose orbits diverged from (2384) Schulhof in secular angles. At this stage we excluded single-opposition asteroids 2013 GV46 and 2015 HT102, whose orbits were too uncertain,14 and a multi-opposition object (134979) 2001 FF53. Indeed, its distance from (2384) Schulhof in the space of proper orbital elements, using the standard metric and proper elements available at the AstDyS site, is ≥250 m s−1, incompatible with membership in the Schulhof family. The remaining objects, listed in Table 2, were considered potential members in the Schulhof family and their orbital convergence to (2384) Schulhof was further studied in Section 4.
Table 2. Osculating Equinoctical Orbital Elements, their Uncertainties, and other Parameters of Members of the Schulhof Family
| Asteroid | a | h | k | p | q | λ | H | |
|---|---|---|---|---|---|---|---|---|
| (AU) | (deg) | (mag) | ||||||
| 2384 | Schulhof | 2.61073976 | −0.06558297 | −0.09964829 | 0.01634335 | 0.11750505 | 236.456789 | 12.13 |
| 81337 | 2000 GP36 | 2.60746049 | −0.06082211 | −0.10600342 | 0.02140639 | 0.11782906 | 48.503356 | 14.8 |
| 271044 | 2003 FK6 | 2.61118723 | −0.05573209 | −0.10349324 | 0.02469900 | 0.11726167 | 162.563612 | 16.2 |
| 286239 | 2001 UR193 | 2.60845331 | −0.06012707 | −0.10499199 | 0.01973692 | 0.11780724 | 105.196017 | 15.8 |
| 2007 EV68 | 2.61162493 | −0.06457354 | −0.10094959 | 0.01654135 | 0.11758211 | 174.872037 | 17.4 | |
| 2008 EK72 | 2.60863545 | −0.07384363 | −0.10213992 | 0.01017344 | 0.11761195 | 80.729751 | 17.3 | |
| 2008 RA126 | 2.61077522 | −0.06482315 | −0.09967222 | 0.01752765 | 0.11749122 | 229.598461 | 17.0 | |
| 2009 EL11 | 2.60940710 | −0.06835457 | −0.10236857 | 0.01641037 | 0.11767508 | 346.085711 | 17.0 | |
| 2008 GW33 | 2.60895415 | −0.05826216 | −0.10488603 | 0.02719196 | 0.11740821 | 93.583869 | 18.1 | |
| 2012 FM46 | 2.60920074 | −0.06697867 | −0.10327702 | 0.01384413 | 0.11780422 | 107.257212 | 17.5 | |
| 2015 FN344 | 2.61023729 | −0.05942008 | −0.10131130 | 0.02000528 | 0.11750266 | 220.192182 | 17.3 | |
| 2015 GH4 | 2.61069318 | −0.06434578 | −0.09993936 | 0.01705728 | 0.11752486 | 219.946974 | 17.4 | |
Uncertainty ( ) ) |
||||||||
| 2384 | Schulhof | 1.3e-8 | 5.6e-8 | 6.7e-8 | 5.1e-8 | 6.5e-8 | 6.2e-6 | ... |
| 81337 | 2000 GP36 | 3.0e-8 | 8.0e-8 | 1.1e-7 | 6.4e-8 | 1.1e-7 | 1.4e-5 | ... |
| 271044 | 2003 FK6 | 1.4e-7 | 1.8e-7 | 4.8e-7 | 1.0e-7 | 1.1e-7 | 4.9e-5 | ... |
| 286239 | 2001 UR193 | 6.4e-8 | 1.4e-7 | 2.1e-7 | 9.2e-8 | 1.7e-7 | 2.2e-5 | ... |
| 2007 EV68 | 1.4e-6 | 5.2e-6 | 5.6e-6 | 1.4e-7 | 3.8e-7 | 7.4e-4 | ... | |
| 2008 EK72 | 2.8e-7 | 2.5e-7 | 1.0e-6 | 1.5e-7 | 2.6e-7 | 1.2e-4 | ... | |
| 2008 RA126 | 4.4e-7 | 7.1e-7 | 2.9e-6 | 1.8e-7 | 4.1e-7 | 1.2e-4 | ... | |
| 2009 EL11 | 2.2e-6 | 4.0e-6 | 7.9e-6 | 1.9e-7 | 7.7e-7 | 7.3e-4 | ... | |
| 2008 GW33 | 1.0e-3 | 4.8e-4 | 4.0e-4 | 4.7e-5 | 2.1e-4 | 3.2e-1 | ... | |
| 2012 FM46 | 2.7e-4 | 6.1e-5 | 4.8e-5 | 2.5e-6 | 4.4e-5 | 4.2e-2 | ... | |
| 2015 FN344 | 6.1e-5 | 2.4e-5 | 7.7e-6 | 1.0e-6 | 3.2e-6 | 2.2e-3 | ... | |
| 2015 GH4 | 9.6e-5 | 1.5e-4 | 2.0e-5 | 6.8e-6 | 2.5e-5 | 1.7e-2 | ... | |
Note. Osculating orbital elements and their uncertainty for epoch MJD 57200 as calculated by the OrbFit9 software (http://adams.dm.unipi.it/∼orbmaint/orbfit/). The uncertainties are simply given by the square root of the corresponding diagonal terms of the covariance matrix; our method of clone generation also takes into account correlation effects expressed by the off-diagonal terms. We use a heliocentric equinoctical system of non-singular elements: a is the semimajor axis, 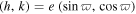 where e is the eccentricity and ϖ is the longitude of perihelion,
where e is the eccentricity and ϖ is the longitude of perihelion, 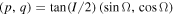 where I is the inclination and Ω is the longitude of node, and
where I is the inclination and Ω is the longitude of node, and  is the mean longitude in orbit (M is the mean anomaly). The default reference system is that of the mean ecliptic of J2000. The absolute magnitude values H were taken from the AstDyS site, except for (2384) Schulhof, for which we use our derived value. Note that the uncertainty in H may be as large as 1 mag, especially for single-opposition objects 2008 GW33, 2012 FM46, 2015 FN344, and 2015 GH4. The exception is again (2384) Schulhof whose H value is tighly constrained to ±0.06 mag. Vereš et al. (2015) provide ∼16.6 mag for 286239 from the data analysis of Pan STARRS PS1 observations.
is the mean longitude in orbit (M is the mean anomaly). The default reference system is that of the mean ecliptic of J2000. The absolute magnitude values H were taken from the AstDyS site, except for (2384) Schulhof, for which we use our derived value. Note that the uncertainty in H may be as large as 1 mag, especially for single-opposition objects 2008 GW33, 2012 FM46, 2015 FN344, and 2015 GH4. The exception is again (2384) Schulhof whose H value is tighly constrained to ±0.06 mag. Vereš et al. (2015) provide ∼16.6 mag for 286239 from the data analysis of Pan STARRS PS1 observations.
Download table as: ASCIITypeset image
In order to make sure that we did not miss any additional member candidates, we also extended the region of search in the osculating orbital space around (2384) Schulhof to 0.02 AU distance in the semimajor axis, 0.015 distance in the eccentricity, 0 4 distance in the inclination, and 30° in the longitude of node and perihelion. We found 30 asteroids in this zone. None of the 15 new objects showed past orbital convergence to (2384) Schulhof, so we consider them as background bodies. This result did not motivate a further search for Schulhof members in a still larger surrounding zone.
4 distance in the inclination, and 30° in the longitude of node and perihelion. We found 30 asteroids in this zone. None of the 15 new objects showed past orbital convergence to (2384) Schulhof, so we consider them as background bodies. This result did not motivate a further search for Schulhof members in a still larger surrounding zone.
The novelty in Schulhof family membership, especially in regard to its age estimate studied in the next section, is basically twofold:
- 1.the number of family members increased by 50%, from 8 in Vokrouhlický & Nesvorný (2011; their Tables 1 and 2) to 12 listed in Table 2; this is both by including small asteroids discovered after 2011, but also by realizing that the multi-opposition asteroid 2008 EK72 was mistakenly considered to be an interloper by Vokrouhlický & Nesvorný (2011);
- 2.orbits of several previously known members have significantly improved since 2011 by adding new astrometric data to their orbital solution; this is especially important for 2007 EV68 and 2008 RA126, which were recovered and are now multi-opposition instead of single-opposition objects.
With this much improved data set we may analyze the Schulhof family in a more detail and eventually revisit the issue of its age.
3.1. The Schulhof Family: A Proper Element Portrait
In order to assess the structure of the Schulhof family in the space of orbital elements, we computed synthetic proper values for semimajor axis, eccentricity, and sine of inclination. While our method is closely related to the concept introduced by Knežević et al. (2002), we slightly modified the procedure to suit our task. This is because we also want to provide proper elements for less accurate orbits, including some of the single-opposition members in Table 2 (note the AstDyS group computes synthetic proper elements for the numbered and multi-opposition asteroids only). Our procedure is as follows.
For each of the asteroids in Table 2, except for 2008 GW33 whose orbit is the least accurate, we first created 100 clone versions in the six-dimensional space of equinoctical elements 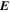 at the initial epoch MJD 57200. We obtained them using the probability distribution
at the initial epoch MJD 57200. We obtained them using the probability distribution  ∝
∝  , where (i) Δ
, where (i) Δ =
=  −
−  is the difference with respect to the best-fit orbital values
is the difference with respect to the best-fit orbital values  ⋆ (Table 2) and (ii) Σ is the covariance matrix of the orbital solution downloaded from the AstDyS Web site. For each of the orbital representations (clones) we also stored its weight given by the
⋆ (Table 2) and (ii) Σ is the covariance matrix of the orbital solution downloaded from the AstDyS Web site. For each of the orbital representations (clones) we also stored its weight given by the  value. Planetary state vectors and velocities for the same epoch were obtained from the JPL DE 405 ephemerides file. Each of the 100 orbital realizations for all asteroids were numerically integrated, together with planets, using a well documented and tested package swift.15
The integration time step was 5 days and the force model contained gravitational effects from the Sun and planets only. We tracked all orbits for 20 Myr with an output density of 50 years. The output data were then split into five 6.6 Myr long segments uniformly distributed over the integrated time interval (such that the initial time of the first segment was 0 Myr and the last time of the last segment was 20 Myr). The length of the segments was chosen to accommodate 217 output points and to be long enough to allow good resolution of the lowest planetary frequencies g8 and s8. At each of the segments we (i) computed the mean value of the semimajor axis and (ii) determined the Fourier representation of the non-singular orbital elements
value. Planetary state vectors and velocities for the same epoch were obtained from the JPL DE 405 ephemerides file. Each of the 100 orbital realizations for all asteroids were numerically integrated, together with planets, using a well documented and tested package swift.15
The integration time step was 5 days and the force model contained gravitational effects from the Sun and planets only. We tracked all orbits for 20 Myr with an output density of 50 years. The output data were then split into five 6.6 Myr long segments uniformly distributed over the integrated time interval (such that the initial time of the first segment was 0 Myr and the last time of the last segment was 20 Myr). The length of the segments was chosen to accommodate 217 output points and to be long enough to allow good resolution of the lowest planetary frequencies g8 and s8. At each of the segments we (i) computed the mean value of the semimajor axis and (ii) determined the Fourier representation of the non-singular orbital elements 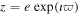 and
and 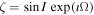 , where e is the eccentricity, ϖ the longitude of pericenter, I the inclination, and Ω the longitude of the node. For (ii) we used the frequency modified Fourier transform by Šidlichovský & Nesvorný (1996). We identified planetary terms and the proper term, and computed the amplitude of the latter. For a given asteroid, we performed this computation for each of its clones and each of the five segments in time. We then combined the results using the clone statistical weights given by its
, where e is the eccentricity, ϖ the longitude of pericenter, I the inclination, and Ω the longitude of the node. For (ii) we used the frequency modified Fourier transform by Šidlichovský & Nesvorný (1996). We identified planetary terms and the proper term, and computed the amplitude of the latter. For a given asteroid, we performed this computation for each of its clones and each of the five segments in time. We then combined the results using the clone statistical weights given by its 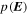 value. This way we obtained mean values of the proper elements aP, eP, and sin IP. Individual values of each clone at each of its segments served to estimate statistical variance that we report as the uncertainty of each of the proper values. We note that typically the uncertainty in aP is dominated by the uncertainty of the initial osculating semimajor axis, especially for the less constrained orbits, while the uncertainties in eP and sin IP are mainly given by the variance in their computation at different time segments.
value. This way we obtained mean values of the proper elements aP, eP, and sin IP. Individual values of each clone at each of its segments served to estimate statistical variance that we report as the uncertainty of each of the proper values. We note that typically the uncertainty in aP is dominated by the uncertainty of the initial osculating semimajor axis, especially for the less constrained orbits, while the uncertainties in eP and sin IP are mainly given by the variance in their computation at different time segments.
Figure 4 summarizes the results. We divided the family zone into three zones/boxes A, B, and C. Asteroids in A have orbits very similar to (2384) Schulhof, both in proper and osculating orbital elements. They constitute the immediate vicinity of this largest member in the family and contain multi-opposition objects 2007 EV68, 2008 RA126, 2009 EL11, and a single-opposition member 2015 GH4. Group B is what Pravec & Vokrouhlický (2009) thought to be family around (81337) 2000 GP36. It is composed of a compact cluster of numbered members 81337, 271044, and 286239 and a single-opposition object 2015 FN344. As of today, group B contains the second to fourth largest members in the family (Table 2), though we cannot exclude that other members of a comparable size are yet to be discovered. One of the features that puzzled Vokrouhlický & Nesvorný (2011) was the division of the family into the A and B zones. No objects were known in region C at that time. At this moment, however, we start to detect some Schulhof members even in this zone: a multi-opposition asteroid 2008 EK72 and a single-opposition asteroid 2012 FM46. It is important that 2008 EK72 exhibits the same convergence pattern to (2384) Schulhof as all numbered asteroids in box B (Section 4.1).
Figure 4. Proper elements, and their uncertainty intervals, of the Schulhof family members computed with the methods described in Section 3.1: semimajor axis vs. sine of inclination (top) and semimajor axis vs. eccentricity (bottom). The family is divided into three zones: A, B, and C. Multi-opposition asteroids are represented by black symbols and single-opposition asteroids are represented by gray symbols. Box A contains the largest fragment (2384) Schulhof (diamond symbol) and objects with very similar orbits (including the single-opposition asteroid 2015 GH4). Box B is occupied by the remaining numbered asteroids around (81337) 2000 GP36 and the single-opposition asteroid 2015 FN344. Box C contains 2008 EK72, a formerly unrecognized member in the family, and a single-opposition asteroid 2012 FM46. The orbit of single-opposition asteroid 2008 GW33 was not included in this plot because its uncertainty is too large. The dashed line shows orbits at a formal 3 m s−1 distance from (2384) Schulhof in the displayed elements using a standard metric in the proper element space (e.g., Zappalà et al. 1990): it assumes an isotropic velocity field, ω + v = 60° at the top panel and v = 130° at the bottom panel, with ω and v being the argument of perihelion and the true anomaly. In the three-dimensional distance in proper element space, using the standard metric, the distance to (2384) Schulhof is slightly larger; for instance, (81337) 2000 GP36 is at about 3.6 m s−1 and 2008 EK72 at 6.7 m s−1. The adjusted choice of ω and v, as in this figure, could bring them even closer.
Download figure:
Standard image High-resolution imageAs for the convergence results reported in the next section, it is interesting to note that asteroids in boxes B and C have opposite initial differences in secular angles with respect to (2384) Schulhof: those in box B have δΩ > 1° and  , while those in box C have δΩ < −1° and δ ϖ > 1°. As mentioned above, asteroids in box A have orbits that are very similar to (2384) Schulhof, including the osculating values of the secular angles. In fact, this correlation between the secular angles and position in the family is an indication of their common origin.
, while those in box C have δΩ < −1° and δ ϖ > 1°. As mentioned above, asteroids in box A have orbits that are very similar to (2384) Schulhof, including the osculating values of the secular angles. In fact, this correlation between the secular angles and position in the family is an indication of their common origin.
4. THE SCHULHOF FAMILY: A REVISED AGE ESTIMATE
We used numerical integration of heliocentric orbits backward in time to identify the epoch of common origin for members of the Schulhof family. Ideally, this manifests through convergence of all asteroids to the same location in space with a small relative dispersion in velocity, conditions that are expected at their mutual separation when the family formed. However, several effects imply that we should be satisfied with only an approximation in a real life. First, observations do not allow us to determine the current orbits of the Schulhof members with infinite accuracy. Second, our propagation model may not be complete or sufficiently accurate, and orbital motion is known to be chaotic in the presence of planetary gravitational perturbations. These issues need to be remembered when interpreting our results.
The outline of our approach has been presented in several previous publications (e.g., Nesvorný & Vokrouhlický 2006; Vokrouhlický & Nesvorný 2011). We shall not repeat technical details here, since an interested reader may consult the abovementioned papers. We only recall the main points and comment when advances in our knowledge of physical parameters allow us to tighten the range of their admissible values.
We follow the methodology in Vokrouhlický & Nesvorný (2011) by first considering past convergence of smaller objects in the Schulhof family to its largest member (2384) Schulhof. This is justified by the dominant size of this largest fragment in the family, but we are mainly led to this by the previously stated possibility of different convergence epochs for different members. In each of the 11 jobs performed we thus included (2384) Schulhof and one of the smaller objects listed in Table 2. Each of the bodies was represented by a certain number of geometric and Yarkovsky clones. The former sampled the uncertainty hyper-ellipsoid in the six-dimensional space of equinoctic heliocentric orbital elements. They were constructed using the same procedure as the clones used in Section 3.1 to compute proper elements, i.e., we generated them in accord with the probability density function p(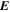 ). The more accurate orbit of (2384) Schulhof was represented by 31 clones, the less accurate orbits of smaller members by 61 clones. Each of the geometric clones itself was represented by a certain number of Yarkovsky clones to which different thermal acceleration strengths were given. Since we know that (2384) Schulhof has a retrograde rotation (Section 2.2), we can restrict the range of possible drift-rate values da/dt in the semimajor axis for this body: because da/dt < 0 with dt positive, our backward integrations must in fact include fictitious positive da/dt values.16
We use 21 Yarkovsky clones that sample the interval from 0 to the [da/dt]max value estimated for its mean heliocentric distance and size (see Vokrouhlický 1999; Bottke et al. 2006). In the case of other Schulhof members, we have no information about their rotation states. Therefore, we must assign all possible negative and positive values of the semimajor axis drift of their Yarkovsky clones in the interval
). The more accurate orbit of (2384) Schulhof was represented by 31 clones, the less accurate orbits of smaller members by 61 clones. Each of the geometric clones itself was represented by a certain number of Yarkovsky clones to which different thermal acceleration strengths were given. Since we know that (2384) Schulhof has a retrograde rotation (Section 2.2), we can restrict the range of possible drift-rate values da/dt in the semimajor axis for this body: because da/dt < 0 with dt positive, our backward integrations must in fact include fictitious positive da/dt values.16
We use 21 Yarkovsky clones that sample the interval from 0 to the [da/dt]max value estimated for its mean heliocentric distance and size (see Vokrouhlický 1999; Bottke et al. 2006). In the case of other Schulhof members, we have no information about their rotation states. Therefore, we must assign all possible negative and positive values of the semimajor axis drift of their Yarkovsky clones in the interval ![$(-{[{da}/{dt}]}_{{\rm{max}}},{[{da}/{dt}]}_{{\rm{max}}})$](https://content.cld.iop.org/journals/1538-3881/151/3/56/revision1/aj521901ieqn22.gif) , with the maximum values adjusted to their smaller size. In this case we use 71 Yarkovsky clones. Altogether we thus always use 651 clone variants for (2384) Schulhof and 4331 clone variants for other Schulhof family members. To estimate their size, we use the pV = 0.19 geometric albedo derived above for (2384) Schulhof and assume the absolute magnitude values from Table 2.
, with the maximum values adjusted to their smaller size. In this case we use 71 Yarkovsky clones. Altogether we thus always use 651 clone variants for (2384) Schulhof and 4331 clone variants for other Schulhof family members. To estimate their size, we use the pV = 0.19 geometric albedo derived above for (2384) Schulhof and assume the absolute magnitude values from Table 2.
We use the swift package, extended to account for the Yarkovsky effect as explained in Nesvorný & Vokrouhlický (2006), for our numerical runs. Gravitational effects due to all planets, including Mercury, were taken into account. The initial epoch was MJD 57200, for which planetary state vectors were obtained from the JPL ephemerides file. We used a propagation time step of 5 days, output state vectors of all simulated clones every 5 years, and we followed the orbits to 1.5 Myr backward in time. Outputs from each of the runs were analyzed using two techniques.
First, we monitored the convergence of the secular angles Ω and ϖ of each of the small members toward (2384) Schulhof. At every output time step we randomly selected two million identifications of pairs consisting of one clone variant of each integrated asteroid and evaluated differences δΩ and δϖ of their nodes and perihelia. Instead of using these two values separately, we combined them into a velocity metric function

where na ≈ 18.5 km s−1 is the orbital speed of asteroids in the cluster. As discussed in Nesvorný & Vokrouhlický (2006), (1) is based on Gauss equations of the perturbation theory and connects δΩ and δϖ to an estimate of a characteristic instant change in orbital velocity δV (with a random direction in space). For reference, we may mention that  is equivalent to about δV ≃ 10 m s−1. We compared δV with the expected escape velocity of ≃7 m s−1 from the parent body of the Schulhof family (Section 2.1), such that only pair combinations with δV ≤ 7 m s−1 would be considered successful. Obviously, this is the weakest convergence condition, because it does not take into account the behavior of other orbital elements.
is equivalent to about δV ≃ 10 m s−1. We compared δV with the expected escape velocity of ≃7 m s−1 from the parent body of the Schulhof family (Section 2.1), such that only pair combinations with δV ≤ 7 m s−1 would be considered successful. Obviously, this is the weakest convergence condition, because it does not take into account the behavior of other orbital elements.
Stronger convergence criteria were used in our second method. In this case, primarily used to track the history of asteroid pairs (e.g., Vokrouhlický & Nesvorný 2008), we monitored the true convergence of Schulhof family members toward (2384) Schulhof in Cartesian space. For each of the two million pair trials at every output step, we then computed their distance d and relative velocity v. Satisfactory convergence occurred when d was smaller than the estimated Hill sphere of influence of the family's parent body and v was smaller than its escape velocity. In quantitative terms we used d ≤ 3000 km and v ≤ 7 m s−1 estimated in Section 2.1. However, since our integrations are not perfect for various reasons mentioned at the beginning of Section 4, we also tested the d ≤ 4500 km and d ≤ 6000 km thresholds and considered them as rather satisfactory cases. We verified that the pair configurations that satisfied this second convergence criterion generally also satisfied the first criterion using just the secular angles.
4.1. Numbered Members and 2008 EK72
We start discussing our results by first considering the case of the most accurately determined orbits, namely numbered asteroids 81337, 271044, and 286239 from zone B and 2008 EK72 from zone C (see Figure 4 and Table 2). All of these objects have a very good convergence to (2384) Schulhof at about the same time, some 800 kyr ago. An example for 81337 is shown in Figures 5 and 6, while the cases for other three asteroids are very similar. This is shown in a less detailed way in the left column of Figures 7 and 8.
Figure 5. Convergence of secular angles of (81337) 2000 GP36 and (2384) Schulhof; the abscissa is the time in the past in kiloyears. Top: number of trials for which δV < 5 m s−1 (gray histogram) and δV < 2 m s−1 (black histogram). Data were binned into 10 kyr intervals and normalized to the maximum of the gray distribution. Bottom: example of a convergence at ∼750 kyr. The difference in longitude of the node is black and the difference in argument of the pericenter is gray (both relative to Schulhof's orbit).
Download figure:
Standard image High-resolution imageFigure 6. Convergence of the Cartesian space distance and relative velocity of clones for (81337) 2000 GP36 and (2384) Schulhof. Top: number of trials for which the clone distance was <1.5 times the Hill radius of Schulhof (gray histogram) and <1 Hill radius (black histogram) and the relative velocity of the encounter was <7 m s−1. Data were binned into 20 kyr intervals and normalized to the maximum of the gray distribution. Middle: minimum distance between the trial clones at 5 year intervals (gray symbols). The black solid line is the mean value over a 5 kyr running window and the dashed horizontal line is the estimated Hill radius for (2384) Schulhof (∼3000 km). Bottom: relative encounter velocity between the trial clones that have minimum separation (middle panel). The dashed horizontal line is the estimated escape speed from (2384) Schulhof (∼7 m s−1).
Download figure:
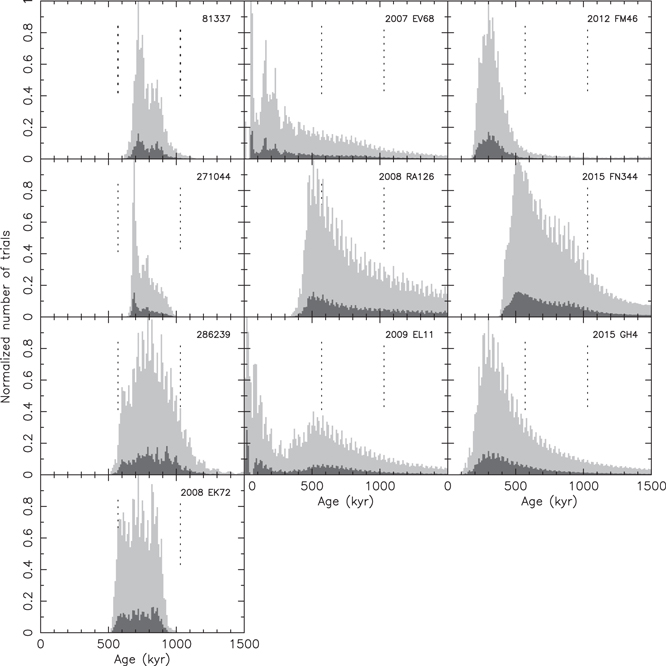
Standard image High-resolution imageFigure 7. Convergence of secular angles of Schulhof family members and (2384) Schulhof as in the top panel of Figure 5. The histograms show the number of successful trials for which δV < 5 m s−1 (gray histogram) and δV < 2 m s−1 (black histogram). The left column is for the members with currently the most accurate orbits (Section 4.1; asteroid identification by the label in the top right corner). The middle column is for members with less accurate but still multi-opposition orbits. The right column is for members with the least accurate single-opposition orbits. The dashed vertical lines delimit 10% and 90% limits of the age obtained from the cumulative version of the gray histograms and obtained from the most accurate orbits in the left column.
Download figure:
Standard image High-resolution imageFigure 8. Same as in Figure 7 but now for successful convergence in the Cartesian space (see also the top panel in Figure 6). The gray histogram is for convergence to distance at 1.5 Hill radii of the Schulhof parent body (≃4500 km) and the black histogram is for convergence to distance at 1 Hill radius of the Schulhof parent body (≃3000 km); in both cases the velocity is smaller than 7 m s−1. The dashed vertical lines delimit 10% and 90% limits of the age obtained from the cumulative version of the gray histograms and obtained from the most accurate orbits in the left column.
Download figure:
Standard image High-resolution imageFocusing first on our initial method, convergence of secular angles, we constructed a cumulative distribution of successful convergent trials with δV ≤ 5 m s−1, and determined time instants at 10%, 50% (median), and 90% levels. We obtained the following estimates for convergence to (2384) Schulhof: (i) (81337) 2000 GP36 at  kyr, (ii) (271044) 2003 FK6 at
kyr, (ii) (271044) 2003 FK6 at 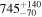 kyr, (iii) (286239) 2001 UR193 at
kyr, (iii) (286239) 2001 UR193 at  kyr, and (iv) 2008 EK72 at
kyr, and (iv) 2008 EK72 at  kyr. These intervals largely overlap. In order to adopt a conservative approach to combine these estimates, we evaluate the mean value of the medians but keep the extreme minimum age for the 10% level and extreme maximum age for the 90% level over all cases. This provides an age estimate of
kyr. These intervals largely overlap. In order to adopt a conservative approach to combine these estimates, we evaluate the mean value of the medians but keep the extreme minimum age for the 10% level and extreme maximum age for the 90% level over all cases. This provides an age estimate of  kyr, in agreement with findings in Vokrouhlický & Nesvorný (2011).
kyr, in agreement with findings in Vokrouhlický & Nesvorný (2011).
Next, we examined our second method, the stronger convergence criterion, namely, the true encounter of the clone variants in physical space at a very low relative speed. Figure 6 shows the exemplary case of (81337) 2000 GP36's affinity to (2384) Schulhof. It is important to find that the two bodies have a possibility of very close encounters and that they occur within the well-defined interval of time previously hinted at by the secular angle convergence. While the minimum v of the order of 0.5 m s−1 or less is frequently met, d reaches below the Hill radius only occasionally. This could be because of a slight incompleteness of our force model, the 5 year output frequency (in fact longer than the orbital period of Schulhof members), or a small number of clone variants used. Using conservative criteria d ≤ 4500 km (i.e., 1.5 times the Hill radius) and v ≤ 7 m s−1, we collect a number of successful trials (top panel of Figure 6). Turning the distribution to a cumulative form and determining the 10%, 50% (median), and 90% levels as above, we obtain  kyr. Similar results are also obtained for other asteroids in this class with ages of (i) (271044) 2003 FK6 at
kyr. Similar results are also obtained for other asteroids in this class with ages of (i) (271044) 2003 FK6 at  kyr, (ii) (286239) 2001 UR193 at
kyr, (ii) (286239) 2001 UR193 at 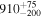 kyr, and (iii) 2008 EK72 at
kyr, and (iii) 2008 EK72 at  kyr. We again collected these results into a conservative estimate of the family's age:
kyr. We again collected these results into a conservative estimate of the family's age:  kyr.
kyr.
Additionally, we probed a simultaneous convergence of the secular angles of all asteroids with well-determined orbits considered in this section. Note that this was the original tool used by Nesvorný et al. (2006) and Nesvorný & Vokrouhlický (2006) to estimate the ages of their discovered young clusters. In this simulation, we used 11 geometric and 21 Yarkovsky clones for (2384) Schulhof, still employing the obliquity constraint from our solution in Section 2. All other smaller members were represented by 21 geometric and 41 Yarkovsky clones, this time allowing both positive and negative drift values in semimajor axis by the thermal accelerations. We probed their orbital evolution to 1.5 Myr ago, storing their state vectors every 5 years. At each of the output epochs we considered 25 million trial identifications between the clones of each of the five asteroids and computed the node and pericenter dispersal δΩ and  using the formula given in Nesvorný & Vokrouhlický (2006). These were inserted into the velocity dispersal estimate by Equation (1). We required δV ≤ 5 m s−1 to record a successful convergence. Figure 9 shows a normalized statistical distribution of these converging solutions binned into 25 kyr intervals of time. As expected, the resulting distribution roughly represents a combined intersection of converging distributions shown in the left column of Figure 7. The median, 10%, and 90% of the distribution provide yet another age estimate for the cluster of
using the formula given in Nesvorný & Vokrouhlický (2006). These were inserted into the velocity dispersal estimate by Equation (1). We required δV ≤ 5 m s−1 to record a successful convergence. Figure 9 shows a normalized statistical distribution of these converging solutions binned into 25 kyr intervals of time. As expected, the resulting distribution roughly represents a combined intersection of converging distributions shown in the left column of Figure 7. The median, 10%, and 90% of the distribution provide yet another age estimate for the cluster of 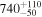 kyr.
kyr.
Figure 9. Convergence of secular angles of Schulhof family members with the most accurately determined orbits—(2384) Schulhof, (81337) 2000 GP36, (271044) 2003 FK6, (286239) 2001 UR193, and 2008 EK72—using the criterion in Equation (1). Here, δΩ and δϖ are the node and pericenter dispersal of all five objects. The histogram shows a normalized number of converging solutions with a threshold δV ≤ 5 m s−1.
Download figure:
Standard image High-resolution imageFinally, we comment on the Yarkovsky drift values da/dt for secondary components that exhibit successful convergence to (2384) Schulhof. In an ideal case, their distribution would be single-valued, or indicate a strong preference for a small interval of da/dt values. In that case, our results would also predict the sense of rotation of these smaller members in the family. Unfortunately, we find that the da/dt values are flat (randomly distributed). In other words, the secondary clones with different da/dt values have the possibility to converge at different time instants in the past, thus prohibiting us from constraining their rotation parameters. The same conclusion also applies to our runs in the next paragraphs.
4.2. Remaining Multi-opposition Members
We now turn to the case of slightly less accurate, but still reliable, multi-opposition orbits that were not considered in the previous section. These are 2007 EV68, 2008 RA126, and 2009 EL11, all located in box A in Figure 4. This means that all have initial orbits very similar to (2384) Schulhof. We note that the cases of 2007 EV68 and 2009 EL11 were already analyzed by Vokrouhlický & Nesvorný (2011), by then single-opposition asteroids, and they seemed to indicate preferential early convergence to (2384) Schulhof (age <100 kyr).
Results from our first method are shown in the middle column of Figure 7. Both 2007 EV68 and 2009 EL11 still offer young solutions. However, we note that this is very likely a bias of the convergence method that uses just the proximity of secular angles. In fact, their initial values provide an already quite low δV, and their short-period oscillations promptly result in fulfillment of the δV ≤ 7 m s−1 condition. So these early solutions are not fully diagnostic. In this respect, we point to the rising "hump feature" in the number of convergent solutions of 2009 EL11 around 660 kyr (and also to a lesser degree in the case of 2007 EV68). Apparently, the orbit of 2008 RA126 is slightly farther from (2384) Schulhof, and the short-period oscillations of the secular angles do not permit these early solutions. Instead, only solutions from ∼500 kyr appear possible, with many in the formal interval of solutions determined from analysis of the accurate orbits in Section 4.1.
Our conclusions are neatly confirmed when using the second method, thus there is complete convergence in the Cartesian space. In this case both 2007 EV68 and 2009 EL11 show clear preference to ages >500 kyr, with most in the interval derived from the accurate orbits in Section 4.1. This is also confirmed by the solution for 2008 RA126.
We may thus conclude that all multi-opposition asteroids present a consistent picture of the Schulhof family age.
4.3. Single-opposition Members
Finally, we consider the least accurate orbits, namely, single-opposition ones. Incidentally, we take one example from each of the boxes A, B, and C from Figure 4 (gray symbols): 2012 FM46 (box C), 2015 FN344 (box B), and 2015 GH4 (box A).
Figure 7 (last column) shows the results of our first method based on the behavior of the secular angles. As expected, the orbits starting from boxes B and C do not exhibit early age solutions. This is because their initial orbits, despite being quite uncertain, are distant enough from (2384) Schulhof that some period of time is needed to build enough changes in Ω and ϖ to approach the values for the largest member in the family. Interestingly, even the nearby (box A) single-opposition orbit of 2015 GH4 currently indicates the same pattern, and the statistical distribution of its successful solutions in time is similar to 2008 RA126. Slightly anomalous to the group is the case of 2012 FM46, which has an earlier peak and a more strongly damped tail than the distribution of successful solutions.
Results from the second convergence method are shown in Figure 8 (last column). The solution for the best constrained orbit in this class, 2015 FN344, fits well the age determined from the best orbits in box B. Data from 2015 GH4 are shifted to a slightly younger age, but this feature is possible to attribute to its currently poor orbital solution. This is because, by taking a constant number of clones for both objects, the method contains a bias toward detecting younger ages as the cloud of clones is quickly dispersing in time. This produces a characteristic  tail in the number of successful solutions (e.g., J. Žižka et al. 2016, in preparation). While not dwelling on this issue in more detail, we consider solution for 2015 GH4 consistent with a ≃(700–800) kyr age of the family. On the contrary, results from 2012 FM46 remain somewhat anomalous. The formal solution is
tail in the number of successful solutions (e.g., J. Žižka et al. 2016, in preparation). While not dwelling on this issue in more detail, we consider solution for 2015 GH4 consistent with a ≃(700–800) kyr age of the family. On the contrary, results from 2012 FM46 remain somewhat anomalous. The formal solution is  kyr and they decay faster than
kyr and they decay faster than  toward older age solutions. Only 5% of cases are convergent beyond 700 kyr ago. Given the experience with the previous study and the possibly misleading information from the analysis of the single-opposition objects (note that 2012 FM46 is the least accurate orbit in its class; Table 2), we refrain from drawing bold conclusions from this single case. More details will be obtained if the body is recovered during its next opposition in 2016 February or March.
toward older age solutions. Only 5% of cases are convergent beyond 700 kyr ago. Given the experience with the previous study and the possibly misleading information from the analysis of the single-opposition objects (note that 2012 FM46 is the least accurate orbit in its class; Table 2), we refrain from drawing bold conclusions from this single case. More details will be obtained if the body is recovered during its next opposition in 2016 February or March.
5. CONCLUSIONS
With (2384) Schulhof's rotation state determined in this paper, we continue our survey of the largest fragments in young asteroid families (the first being (1270) Datura in Vokrouhlický et al. 2009). More results on other families will follow in a separate publication. Here, we used the information about Schulhof's obliquity to constrain the parameter space of admissible thermal accelerations of this asteroid in sampling its possible past orbital evolution. We also used our observations to improve the formal solution of Schulhof's geometric albedo by the WISE mission. The same value has also been used to estimate sizes of smaller family members, needed for our orbital integrations.
We found that all members with reliable enough orbits converge to the largest fragment (2384) Schulhof at approximately 800 kyr ago. As various methods provide slightly different, but statistically compatible, age values (Section 4.1), we prefer to report a realistic result of 800 kyr with a 200 kyr uncertainty. Further astrometric and physical observations, including recoveries of currently single-opposition members, will allow us to tighten the uncertainties in the initial orbits and the space of free parameters required for modeling the thermal forces. This will in turn lead to a better age estimate of this family. Asteroids with poorly determined orbits that result in off-track age solutions may require special attention (currently the case of 2012 FM46). However, experience from our previous work indicates that these results should not be overstated. The same conclusion certainly also applies to the case of other young families and efforts to determine their age.
Our work also confirms that the Schulhof family remains an interesting case for models of output from catastrophic disruption or large cratering events.17 One of the challenging features that has already been noted by Vokrouhlický & Nesvorný (2011) and remains valid in our study is the polarized distribution of its largest members. This is best seen in Figure 4, where the largest fragment (2384) Schulhof is in box A, approximately in the center of the family, while the next three largest fragments (81337) 2000 GP36, (271044) 2003 FK6, and (286239) 2001 UR193 are all located in box B, asymmetrically shifted toward smaller values of the proper semimajor axis. This means that they were all ejected approximately opposite from the direction along the track with respect to (2384) Schulhof in the initial collisional event that formed the family. Note that we assume approximate completeness of the family at absolute magnitude values of ≃(16–16.5) (see, e.g., Denneau et al. 2015). Indeed, no object belonging to the family of this size category has been found since 2003 and there is only a limited number of single-opposition asteroids with absolute magnitudes between 14 and 16 with the semimajor axis ranging from 2.55 to 2.65 AU. That said, however, we currently cannot exclude that one or two H ≤ 16 Schulhof family members are yet to be discovered.
We thank Joe Masiero for valuable comments on the submitted version of this paper. This work was supported by the Czech Science Foundation (grants P209-12-0229 and GA13-01308S). M.H. thanks VEGA—the Slovak Grant Agency for Science (grant 2/0032/14) and project ITMS No. 26220120009, based on the supporting operational research and development program financed from the European Regional Development Fund. The observations and data reduction at Abasumani were supported by the Shota Rustaveli National Science Foundation, grant FR/379/6-300/14.
Footnotes
- 10
For instance, asteroid Schulhof itself is nominally a member of an old Eunomia family (e.g., Nesvorný HCM Asteroid Families at the PDS website, http://sbn.psi.edu/pds/resource/nesvornyfam.html). As another example recall also the case of a Gyr-old Koronis family that contains results from more recent disruptions such as the Karin family (e.g., Nesvorný et al. 2015 and references therein).
- 11
- 12
We note that the outlined procecedure is only approximate, but in our case provides a satisfactorily accurate result. In principle one would need to iteratively rerun the thermal model used by WISE with the new H magnitude (J. Masiero 2015, private communication). However, this is less critical for main belt asteroids, where the thermal modeling is basically constrained by W3 and W4 bands, than for near-Earth asteroids, where W2 can be a significant constraint on thermal emission (and thus diameter; see, e.g., Masiero et al. 2014).
- 13
- 14
We remark that future recovery of these orbits may help our understanding of whether these objects are Schulhof family members.
- 15
- 16
This is because we use dt positive for backward integrations too, but reverse the initial velocities.
- 17
Note that a simple compound of known small members in the Schulhof family has a volume of ∼4% of (2384) Schulhof. This would place the impact event well within the realm of a cratering event, even though no effort is currently being put toward removing the bias against the discovery of kilometer-sized and smaller members.