Abstract
We probe the diffusive motion of particles in slowly sheared three-dimensional granular suspensions. For sufficiently large strains, the particle dynamics exhibits diffusive Gaussian statistics, with the diffusivity proportional to the local strain rate —consistent with a local, quasi-static picture. Surprisingly, the diffusivity is also inversely proportional to the depth of the particles below the granular surface —at their free surface, the diffusivity thus appears to diverge and is ill defined. We find that the crossover to Gaussian displacement statistics is governed by the same depth dependence, evidencing a non-trivial strain scale in three-dimensional granular flows.
Export citation and abstract BibTeX RIS
Flowing soft disordered solids, such as colloidal glasses and gels [1–3], foams and emulsions [4–6] or granular media [7–13], exhibit rich particle dynamics and complex rheology. In the last decade, major progress has been made in the understanding of the rheology of granular media and suspensions. Important developments include the description of rapid, "inertial" dry granular flows [7, 8], and the observation of connections between this inertial rheology and the classical rheology of density-matched suspensions [14]. The most challenging regime is that of very slow flows, where the stresses become (approximately) rate independent [15] and non-local effects play an important role [16–18]. Little is known about the fluctuations of the microscopic grain motion, i.e., self-diffusion, in such flows. A recurring problem is that granular media are opaque, so only motion in two-dimensional (2D) model systems [9], near transparant walls [10, 19] or at a free surface can be observed [11]. Walls lead to layering [20] and other artifacts [21], while at the free surface, the particles experience a different local geometry than in the bulk. Measurements in the bulk of a granular flow are thus essential.
Recently, we have shown [13] that for sufficiently slow flows, dry granular media and non–density-matched, but optically matched suspensions exhibit identical flow patterns and rheology, opening up the possibility to probe 3D microscopic particle dynamics within slow granular flows. Here we experimentally probe the full 3D particle trajectories of a sheared granular suspension in a split bottom cell (fig. 1). We focus on sufficiently slow strain rates so that viscous effects are negligible: as detailed below, typical Reynolds and Stokes numbers are of order 10−4 and 10, respectively, implying that we are in the so-called free fall regime, relevant for dry granular flows [13, 22].
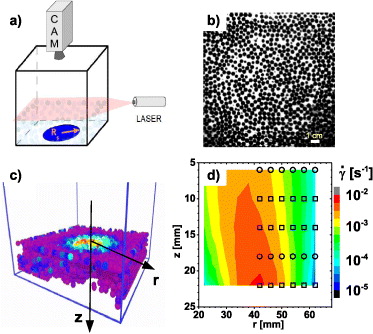
Fig. 1: (a) Setup: a slowly rotating disk at the bottom of a cubic container drives a slow granular flow. In this experiment, we probe driving rates Ω from 0.005 to 0.05 rpm. The container is filled with non–density-matched suspension consisting of PMMA beads, index matched fluid and fluorescent dye. The motion of the particles in this granular suspension are captured in 3D by vertical scanning of a lasersheet. (b) Example of image obtained by illuminating a single slice and capturing the image with a CCD camera. The scale bar represents 1 cm. (c) After particle tracking, the motion of the particles can be resolved in 3D —in this rendered image, the color of the particles represents their instantaneous velocity. (d) Strain rate field (for the case Ω = 0.05 rpm), where the color code denotes the strain rate 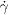 . Symbols indicate the region in which we will probe local strain rates and fluctuations (circles: data used in fig. 2(a), (b), (c); squares: additional data used in fig. 2(d)).
. Symbols indicate the region in which we will probe local strain rates and fluctuations (circles: data used in fig. 2(a), (b), (c); squares: additional data used in fig. 2(d)).
Download figure:
Standard imageIn a quasi-static picture, the mean squared displacements should only depend on the strain, or equivalently, the diffusion coefficient should be proportional to the strain rate, as seen already in [9, 23]. By extracting the particle diffusivity and local strain rates from our particle trajectories, we confirm that this is true in 3D also.
The crucial point is that our 3D geometry allows us to probe the depth dependence of the diffusivity. In the simplest picture, one might expect the diffusion to the independent of depth. However, our main result is showing that the diffusion is inverse proportional to the depth, and thus diverges near the free surface: at the free surface, diffusivity is ill defined. To answer whether this depth dependence stems from a depth dependence of the mean squared displacements or of the characteristic strain, both of which can lead to a depth dependent diffusivity, we probe the displacement distributions. These evolve from very wide distributions at short time with (reduced) kurtosis exceeding 40, to Gaussian distributions at late times. We find that, for a given depth, the kurtosis scales as a power law with strain, and that we can collapse kurtosis data taken at different depths by introducing a depth dependent characteristic strain scale —the same depth dependent characteristic strain scale governs the diffusivity. Taken together, the granular fluctuations provide strong evidence for a non-trivial, depth dependent strain scale which governs slow granular flows.
Setup
We probe the particle trajectories in the bulk of a gravitational (non–density-matched) granular suspension sheared in the split-bottom geometry [12, 13, 24]. This geometry produces smooth and reproducible flow profiles, is well studied and allows to investigate a wide range of shear rates within a single experiment. This allows us to probe the relation between particle displacements,  , and distance to the free surface.
, and distance to the free surface.
We use an identical geometry as the one used in [13] (see fig. 1(a)). A cubic container (width 150 mm), at the bottom of which a disk of radius Rs = 45 mm rotates at an angular velocity Ω ranging from 0.005 to 0.05 rpm, driven by a microstepping motor.
Imaging of the suspension is performed using an index-matching technique, as introduced in [13, 25–28]. The granular suspension consists of monodisperse PMMA spheres (Engineering Labs, diameter 4.6 mm ±0.1 mm placed in a mixture of Triton X-100, fluorescent dye (Nile Blue) and a few droplets of a 37% HCl solution to tune the absorption spectrum of the dye. The fluid is prepared to closely match the refractive index of particles. The difference in density between the fluid and the particles is Δρ = 110 ± 5 kg/m3. The fluids viscosity is 0.30 ± 0.05 Pa s. The split-bottom cell is filled with grains up to a fixed height H = 25 ± 2 mm; there is always a layer of fluid above the grains, so that the fluids surface tension does not play a role for the particle dynamics. The suspension is illuminated with a laser sheet (λ = 635 nm, power 30 mW) parallel to the bottom of the box (fig. 1(a)) and mounted on a z-stage which allows the illumination of slices of the suspension at different heights (every 500 μm, starting 3 mm from the bottom of the box). The thickness of the laser sheet is ≈200 μm.
Image acquisition is done with a triggered 8 bit CCD camera operating at 10 Hz. Both the camera and laser sheet are mounted on vertical stages and can be translated synchronously (velocity ∼5 mm/s) so that the probed slice of the suspension always stays in focus. Since the fluid is fluorescent but the particles are not, a single slice shows a collection of black disks (cross-sections) on a white background (see fig. 1(b)). The contrast is sufficient to image the entire box, but best on the half closest to the laser, where we focus our analysis. We determine the particle trajectories using 3D tracking techniques developed for confocal images of colloidal suspensions [29]. We follow the particles up to 1000 consecutive scans. We estimate the tracking error, obtained by tracking particles in a stationary packing, to be 1/30 of the diameter in the plane of the sheet and 1/10 in the vertical direction.
Flow profiles and local strain rates
From the 3D particle tracking, we obtain a time sequence (maximum 1000 steps) of particles positions  , where i denotes the label of the approximately 5000 particle trajectories which can be reconstructed. Since the shear-rate is not homogeneous in the split-bottom geometry, we divide the measurement area into bins. Given the azimuthal symmetry of the problem, these bins are chosen as squared tori (axis of revolution the vertical axis z) of size dR = dZ = 4 mm (≈0.85 d). We determine the average velocity
, where i denotes the label of the approximately 5000 particle trajectories which can be reconstructed. Since the shear-rate is not homogeneous in the split-bottom geometry, we divide the measurement area into bins. Given the azimuthal symmetry of the problem, these bins are chosen as squared tori (axis of revolution the vertical axis z) of size dR = dZ = 4 mm (≈0.85 d). We determine the average velocity  within each bin. The flow is orthoradial, as the transverse components vr and vz are negligible compared to vθ = rω(r,z).
within each bin. The flow is orthoradial, as the transverse components vr and vz are negligible compared to vθ = rω(r,z).
The normalized average angular velocity field ω(r,z)/Ω is independent of Ω in the range used here [13]. As expected for this value of the ratio H/Rs [12, 13, 24], the flow has a "trumpet like" shape, with shear bands arising from the edge of the rotating disc and propagating within the bulk of the suspension. We successfully fit ω(r,Z0)/Ω for different Z0 using error functions [12, 13, 24] (not shown). We use these fits to get an accurate estimate for the local strain rate within each bin, assuming that the velocity gradient tensor has an unique non-zero component

The resulting local strain rate is plotted in fig. 1(d). For r less than 20 mm, the average steady flow overwhelms the fluctuations, and Taylor dispersion may become important —similarly, for r > 62 mm the particle motion becomes so small that tracking noise overwhelms our data. Staying in the intermediate spatial range, indicated in fig. 1(d), and varying the disk rotation speed from Ω = 0.005 rpm to 0.05 rpm, we access local strain rates from 10−5 up to 10−2 s−1.
Diffusivity
We have investigated the time evolution of the non-affine part of the trajectory: Δsμ(Δt), where μ denotes the component r, θ or z. In general, this entails getting rid of the affine component; in the simplest setting, one could simply subtract  , where Δxμ(Δt) = xμ(t + Δt) − xμ(t) —a more subtle approach subtracts the integral of vμ [30]. In the longitudinal (θ) direction, the mean flow dominates, Taylor dispersion plays an important role, and reliable data for the non-affine fluctuations are hard to obtain. We have thus focused on the z and r components of the fluctuations for large r, where the mean flow is absent, and where no corrections are needed. While all our data for the z-diffusion is consistent with the trends seen for the
r-diffusion, the spatial resolution in z is less, so we focus our presentation on the radial diffusion.
, where Δxμ(Δt) = xμ(t + Δt) − xμ(t) —a more subtle approach subtracts the integral of vμ [30]. In the longitudinal (θ) direction, the mean flow dominates, Taylor dispersion plays an important role, and reliable data for the non-affine fluctuations are hard to obtain. We have thus focused on the z and r components of the fluctuations for large r, where the mean flow is absent, and where no corrections are needed. While all our data for the z-diffusion is consistent with the trends seen for the
r-diffusion, the spatial resolution in z is less, so we focus our presentation on the radial diffusion.
The normalized mean square displacements 〈Δsr(Δt)2〉/d2 are plotted as a function of Δt in fig. 2(a), for two values of z, six values of r and a concomitant range of local strain rates which spans roughly two decades. At late times, the observed behavior is diffusive, and the mean squared displacement increases linearly with the time lag. We thus define a diffusion coefficient D as the limit for large Δt of the ratio 〈Δsr(Δt)2〉/(Δt). For the cases shown in fig. 2(a), this diffusion coefficient varies by two orders of magnitude.
Fig. 2: (a) Examples of non-dimensional mean squared displacements 〈Δs2r〉/d2 as a function of the time interval Δt. Ω is fixed at 0.05 rpm, and we only plot data at z = 7 mm and z = 19 mm, for several values of r as indicated (see fig. 1(d)) —for these values, the local strain rate 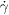 varies over 2.5 decades. At late times, the curves all show a simple linear growth including diffusive behavior, with a diffusivity which clearly grows with the local strain rate. (b) When plotted as a function of the local strain
varies over 2.5 decades. At late times, the curves all show a simple linear growth including diffusive behavior, with a diffusivity which clearly grows with the local strain rate. (b) When plotted as a function of the local strain 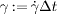 , mean squared displacements for the same value of z collapse, indicating that the dynamics are quasi-static. Families of collapsed curves are surprisingly distinct for different z. At late times, the curves all show a simple linear growth with strain, allowing the unambiguous definition of a dimensionless diffusion coefficient as D: = 〈Δs2r〉/d2/γ. (c) By rescaling the local strain with the inverse of the dimensionless layer number z/d, the mean squared displacements for z = 7 mm and z = 19 mm can be scaled on top of each other. (d) Similarly, the values of D for all values of z and r (see fig. 1(d)) vary linearly with the inverse of the depth. The solid line is the prediction from eq. (4). Inset: D as a function of
, mean squared displacements for the same value of z collapse, indicating that the dynamics are quasi-static. Families of collapsed curves are surprisingly distinct for different z. At late times, the curves all show a simple linear growth with strain, allowing the unambiguous definition of a dimensionless diffusion coefficient as D: = 〈Δs2r〉/d2/γ. (c) By rescaling the local strain with the inverse of the dimensionless layer number z/d, the mean squared displacements for z = 7 mm and z = 19 mm can be scaled on top of each other. (d) Similarly, the values of D for all values of z and r (see fig. 1(d)) vary linearly with the inverse of the depth. The solid line is the prediction from eq. (4). Inset: D as a function of 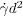 , from which the pressure effect on diffusion is explicit.
, from which the pressure effect on diffusion is explicit.
Download figure:
Standard imageIn the simple local, quasi-static picture, the mean square displacements would be determined by the local accumulated strain, 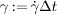 . Hence, one expects that these curves would collapse when plotted as a function of the strain. Surprisingly, plotting 〈Δsr(Δt)2〉/d2 as a function of
. Hence, one expects that these curves would collapse when plotted as a function of the strain. Surprisingly, plotting 〈Δsr(Δt)2〉/d2 as a function of 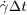 does not achieve to collapse the data into a single curve, but rather we find two distinct curves, corresponding to data taken at the two different z positions (see fig. 2(b)). The diffusivity thus depends both on the strain rate and the vertical position in the sample.
does not achieve to collapse the data into a single curve, but rather we find two distinct curves, corresponding to data taken at the two different z positions (see fig. 2(b)). The diffusivity thus depends both on the strain rate and the vertical position in the sample.
An alternative perspective on diffusivity starts from assuming a Stokes-Einstein relation: D = kT/(3πηd) where D, η and d are diffusion constant, effective viscosity and particle diameter, and kT refers to an effective temperature [31, 32]. For slow granular flows, shear stresses τ are set by friction: τ = μP, where μ is the friction coefficient. As a consequence, the ratio of shear stress and strain rate (the effective viscosity), scales as  , and substituting this into the Stokes-Einstein relation, one obtains that
, and substituting this into the Stokes-Einstein relation, one obtains that

so that the diffusion would be inverse proportional to the local granular pressure, which is set by the depth of the granular bed z (eq. (2)).
As a non-dimensional characteristic of the depth of the granular bed we take z/d —an integer that counts the number of grain layers to the free surface. To obtain data collapse consistent with the prediction D ∼ P−1, we can either multiply the mean squared displacements 〈Δsr(Δt)2〉 with z/d, or multiply the local strain with d/z; as we explain below, we believe the latter captures the physics best. In fig. 2(c) we show that all the mean squared displacements show good data collapse when plotted as a function of 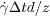 .
.
In fig. 2(d) we combine our measured radial diffusivities for six values of r, five values of z and three global driving rates, and find that in good approximation:

with a proportionality constant of order one. If the diffusion coefficient is plotted as a function of the strain rate only, the diffusivities show a clear trend with z (see inset of fig. 2(d)).
Whereas there is mounting evidence for the non-local nature of slow granular flows [4, 16–18]; it appears that local plastic events affect the viscosity in regions further away. One might have expected that such non-local rheology would go hand in hand with a non-local picture for diffusion, where the local diffusion constant is governed by the strain rate in a finite region around the point where the diffusion is probed. The good scaling collapse obtained with purely local metrics suggests that non-local effects in particle diffusion are weak or absent.
Displacement distributions
The rescaling of the diffusion constant with inverse pressure leaves open one question: is it fundamentally the strain scale or the displacement scale that is affected by the pressure? To answer this question, we have probed the probability distribution function (PDF) of the radial particle displacements over a range of lag times Δt, depths z/d and local strain rates 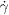 .
.
While for late lag times the distributions become Gaussian, for small Δt we see appreciable deviations, with very wide PDFs for the shortest lag times we can probe (see fig. 3(a)).
Fig. 3: (a) PDF of radial displacements, for different values of the reduced kurtosis γ2, showing the range of displacement distributions that we observe. The corresponding values of (r,z,Δt) are, respectively, from high to low kurtosis: (62,18,9); (62,18,72); (62,18,180); (62,18,378); (42,18,9); (42,18,180) in [mm,mm,s]. (b) The radially averaged kurtosis decays with the γ. (c) The radially averaged kurtosis collapses when plotted as a function of the renormalized strain γd/z, and decays as a non-trivial power law.
Download figure:
Standard imageWe characterize the non-Gaussianity of the PDFs by the reduced kurtosis γ2 = 〈Δs4r〉/〈Δs2r〉2 − 3, and determine the radial averages of the kurtosis, which thus only depends on z and γ. In fig. 3(b) and (c) we compare plots of the kurtosis γ2(z) for z = 6,10,14,18 and 22 mm, as a function of strain γ and rescaled strain γd/z. Clearly, the rescaled strain performs a better rescaling of the kurtosis, even though the curve for z = 22, i.e. close to the bottom, appears to deviate from the other curves. Together with our rescaling of D, this provides strong evidence for a pressure dependent characteristic strain  .
.
We finally note that on short time scales, the particle displacement distributions appear to have fat tails. We note that the kurtosis shows clear power law scaling with the rescaled strain, with an exponent of approximately −0.7. Such power law decay of the kurtosis may happen when the underlying stochastic process is heavy-tailed [33], and is a signature that the distribution of individual jumps is of power law form.
Discussion
Our results show that particle displacements in sheared granular flow are diffusive on long time scales, with a diffusivity proportional to the shear rate [1, 9] and a surprisingly inverse proportionality to depth.
A natural question concerns the microscopic origin of the diffusion scale in slow granular flows. In a Langevin equation type of approach, the order of magnitude of the diffusion coefficient is  , where F0 is the stochastic force acting on the particles and
, where F0 is the stochastic force acting on the particles and 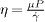 , the effective drag coefficient.
, the effective drag coefficient.
Considering the forces (gravitation, viscous, friction, inertial) and the velocity scales (say U < RsΩ) in the present study, we see that the viscous forces
Fv ∼ 3πηfdU (where ηf is the fluid viscosity) and inertial forces 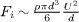 are negligible with respect to gravitational
are negligible with respect to gravitational 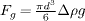 and frictional forces Ff ∼ μPd2. In other words, the Reynolds number is very small Re = Fi/Fv ∼ 10−4 and the Stokes number is large St = Fg/Fv ∼ 10. We are in the "free fall" regime described by Courrech du Pont et al. in [22] —indeed, we expect our data to be relevant for slow dry flows also.
and frictional forces Ff ∼ μPd2. In other words, the Reynolds number is very small Re = Fi/Fv ∼ 10−4 and the Stokes number is large St = Fg/Fv ∼ 10. We are in the "free fall" regime described by Courrech du Pont et al. in [22] —indeed, we expect our data to be relevant for slow dry flows also.
This leaves frictional and gravitational forces as scales that set the diffusion. Clearly, friction sets the drag, but it is not obvious whether friction or gravity provides the dominant stochastic force. If friction would dominate, both the driving and damping would be set by it, and we would expect that the diffusion coefficient would be independent of depth. In contrast, the combination of a gravitational drive and frictional damping gives the observed depth dependence of the diffusion as we show now. Assuming that gravity sets the driving force for diffusion, we find that

since p ≈ Δρgz and μ ≈ 0.5 [13]. This expression is plotted as a solid line in fig. 2(d). The agreement is reasonable, supporting the idea of gravity as a driving force for granular diffusion in slow flows. A self-diffusion coefficient dependent on the depth within the flow was reported earlier by Hsiau et al. in [34]. However, their study concern much faster flows (strain rates are two order of magnitude higher than in our work) and the diffusivity was obtained from particles moving close to a wall, not in bulk flow. To our knowledge, this work reports for the first time a 1/z dependence of the diffusivity in slow granular bulk flows.
Acknowledgments
The authors thank Jeroen Mesman for outstanding technical support in the conception and construction of our 3D scanner, Kinga Lörincz for her help in the image analysis, and Bob Behringer, Daniel Bonn and Guillaume Ovarlez for fruitful discussion. This work is part of the research programme of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organisation for Scientific Research (NWO).