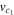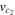We analyse the long-time large-distance asymptotics of the longitudinal correlation functions of the Heisenberg-Ising chain in the easy-axis regime. We show that in this regime the leading asymptotics of the dynamical two-point functions is entirely determined by the two-spinon contribution to their form factor expansion. Its explicit form is obtained from a saddle-point analysis of the corresponding double integral. It describes the propagation of a wave front with velocity which is found to be the maximal possible group velocity. Like in wave propagation in dispersive media the wave front is preceded by a precursor running ahead with velocity . As a special case we obtain the explicit form of the asymptotics of the auto-correlation function.


Purpose-led Publishing is a coalition of three not-for-profit publishers in the field of physical sciences: AIP Publishing, the American Physical Society and IOP Publishing.
Together, as publishers that will always put purpose above profit, we have defined a set of industry standards that underpin high-quality, ethical scholarly communications.
We are proudly declaring that science is our only shareholder.
Highlights of 2016
The Journal of Physics A: Mathematical and Theoretical collection of highlights showcases some of the excellent papers we published in 2016.
We would like to thank all of our authors for choosing to submit their high-quality work to the journal and thank our referees and board members for providing constructive peer review and maintaining the quality standards of the journal.
All journal articles are free to read until the end of December 2017.
We hope that you will find this collection of articles interesting and that you will consider Journal of Physics A for your next paper. We look forward to working with you throughout 2017, during which we will be celebrating the 50th anniversary of the journal.
Rebecca Gillan, Executive Editor
Journal of Physics A: Mathematical and Theoretical
Letters
Show article list
Maxime Dugave et al 2016 J. Phys. A: Math. Theor. 49 07LT01
Dorje C Brody 2016 J. Phys. A: Math. Theor. 49 10LT03
In recent reports, suggestions have been put forward to the effect that parity and time-reversal (PT) symmetry in quantum mechanics is incompatible with causality. It is shown here, in contrast, that PT-symmetric quantum mechanics is fully consistent with standard quantum mechanics. This follows from the surprising fact that the much-discussed metric operator on Hilbert space is not physically observable. In particular, for closed quantum systems in finite dimensions there is no statistical test that one can perform on the outcomes of measurements to determine whether the Hamiltonian is Hermitian in the conventional sense, or PT-symmetric—the two theories are indistinguishable. Nontrivial physical effects arising as a consequence of PT symmetry are expected to be observed, nevertheless, for open quantum systems with balanced gain and loss.
C Cedzich et al 2016 J. Phys. A: Math. Theor. 49 21LT01
We outline a theory of symmetry protected topological phases of one-dimensional quantum walks. We assume spectral gaps around the symmetry-distinguished points +1 and −1, in which only discrete eigenvalues are allowed. The phase classification by integer or binary indices extends the classification known for translation invariant systems in terms of their band structure. However, our theory requires no translation invariance whatsoever, and the indices we define in this general setting are invariant under arbitrary symmetric local perturbations, even those that cannot be continuously contracted to the identity. More precisely we define two indices for every walk, characterizing the behavior far to the right and far to the left, respectively. Their sum is a lower bound on the number of eigenstates at +1 and −1. For a translation invariant system the indices add up to zero, so one of them already characterizes the phase. By joining two bulk phases with different indices we get a walk in which the right and left indices no longer cancel, so the theory predicts bound states at +1 or −1. This is a rigorous statement of bulk-edge correspondence. The results also apply to the Hamiltonian case with a single gap at zero.
Paul Fendley 2016 J. Phys. A: Math. Theor. 49 30LT01
I explicitly construct a strong zero mode in the XYZ chain or, equivalently, Majorana wires coupled via a four-fermion interaction. The strong zero mode is an operator that pairs states in different symmetry sectors, resulting in identical spectra up to exponentially small finite-size corrections. Such pairing occurs in the Ising/Majorana fermion chain and possibly in strongly disordered many-body localized phases. The proof here shows that the strong zero mode occurs in a clean interacting system, and that it possesses some remarkable structure—despite being a rather elaborate operator, it squares to the identity. Eigenstate phase transitions separate regions with different strong zero modes.
Patrick Pietzonka et al 2016 J. Phys. A: Math. Theor. 49 34LT01
We provide a proof of a recently conjectured universal bound on current fluctuations in Markovian processes. This bound establishes a link between the fluctuations of an individual observable current, the cycle affinities driving the system into a non-equilibrium steady state, and the topology of the network. The proof is based on a decomposition of the network into independent cycles with both positive affinity and positive stationary cycle current. This formalism allows for a refinement of the bound for systems in equilibrium or with locally vanishing affinities.
 SYM theory at finite coupling
SYM theory at finite coupling
Benjamin Basso et al 2016 J. Phys. A: Math. Theor. 49 41LT01
We report on the complete OPE series for the 6-gluon MHV and NMHV amplitudes in planar 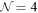 SYM theory. Namely, we provide a finite coupling prediction for all the terms in the expansion of these amplitudes around the collinear limit. These furnish a non-perturbative representation of the full amplitudes.
SYM theory. Namely, we provide a finite coupling prediction for all the terms in the expansion of these amplitudes around the collinear limit. These furnish a non-perturbative representation of the full amplitudes.
Riccardo Borsato et al 2016 J. Phys. A: Math. Theor. 49 41LT03
We analyze the spectrum of perturbative closed strings on 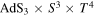 with Ramond–Ramond flux using integrable methods. By solving the crossing equations we determine the massless and mixed-mass dressing factors of the worldsheet S matrix and derive the Bethe equations. Using these, we construct the underlying integrable spin chain and show that it reproduces the reducible spin chain conjectured at weak coupling in Olof Ohlsson S, Bogdan S Jr and Torrielli A 2013 (arXiv:1211.1952). We find that the string-theory massless modes are described by gapless excitations of the spin chain. The resulting degeneracy of vacua matches precisely the protected supergravity spectrum found by de Boer.
with Ramond–Ramond flux using integrable methods. By solving the crossing equations we determine the massless and mixed-mass dressing factors of the worldsheet S matrix and derive the Bethe equations. Using these, we construct the underlying integrable spin chain and show that it reproduces the reducible spin chain conjectured at weak coupling in Olof Ohlsson S, Bogdan S Jr and Torrielli A 2013 (arXiv:1211.1952). We find that the string-theory massless modes are described by gapless excitations of the spin chain. The resulting degeneracy of vacua matches precisely the protected supergravity spectrum found by de Boer.
Malte Henkel 2016 J. Phys. A: Math. Theor. 49 49LT02
The non-stationary relaxation and physical ageing in the diffusion-limited erosion process (dle) is studied through the exact solution of its Langevin equation, in d spatial dimensions. The dynamical exponent z = 1, the growth exponent  and the ageing exponents
and the ageing exponents  and
and  are found. In d = 1 spatial dimension, a new representation of the meta-conformal Lie algebra, isomorphic to
are found. In d = 1 spatial dimension, a new representation of the meta-conformal Lie algebra, isomorphic to  , acts as a dynamical symmetry of the noise-averaged dle Langevin equation. Its infinitesimal generators are non-local in space. The exact form of the full time-space dependence of the two-time response function of dle is reproduced for d = 1 from this symmetry. The relationship to the terrace-step-kink model of vicinal surfaces is discussed.
, acts as a dynamical symmetry of the noise-averaged dle Langevin equation. Its infinitesimal generators are non-local in space. The exact form of the full time-space dependence of the two-time response function of dle is reproduced for d = 1 from this symmetry. The relationship to the terrace-step-kink model of vicinal surfaces is discussed.
Statistical physics: nonequilibrium systems, computational methods and modern equilibrium theory
Show article list
J Cividini et al 2016 J. Phys. A: Math. Theor. 49 085002
We study the statistics of the gaps in the random average process on a ring with particles hopping symmetrically, except one tracer particle which could be driven. These particles hop either to the left or to the right by a random fraction η of the space available till next particle in the respective directions. The random fraction  is chosen from a distribution
is chosen from a distribution 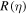 . For a non-driven tracer, when
. For a non-driven tracer, when 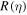 satisfies a necessary and sufficient condition, the stationary joint distribution of the gaps between successive particles takes a universal form that is factorized except for a global constraint. Some interesting explicit forms of
satisfies a necessary and sufficient condition, the stationary joint distribution of the gaps between successive particles takes a universal form that is factorized except for a global constraint. Some interesting explicit forms of 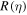 are found which satisfy this condition. In the case of a driven tracer, the system reaches a current-carrying steady state where such factorization does not hold. Analytical progress has been made in the thermodynamic limit, where we computed the single site distribution inside the bulk. We have also computed the two point gap–gap correlation exactly in that limit. Numerical simulations support our analytical results.
are found which satisfy this condition. In the case of a driven tracer, the system reaches a current-carrying steady state where such factorization does not hold. Analytical progress has been made in the thermodynamic limit, where we computed the single site distribution inside the bulk. We have also computed the two point gap–gap correlation exactly in that limit. Numerical simulations support our analytical results.
Alexandre Rosas et al 2016 J. Phys. A: Math. Theor. 49 095001
We consider arrays of the simplest two-state (on–off) stochastic units. The units are Markovian, that is, the transitions between the two states occur at a given rate. We construct arrays of N globally coupled binary units, and observe a remarkable richness of behavior as the control parameter that measures the coupling strength is increased. In the mean field limit as  we consider the four simplest polynomial forms of coupling that lead to bifurcations, and characterize the associated phase transitions of the arrays. When N is finite there are fluctuations about the well-defined steady states of the infinite arrays. We study the nature of these fluctuations and their effects on the bifurcations in all cases by constructing the appropriate Langevin equations and the associated Fokker–Planck equations.
we consider the four simplest polynomial forms of coupling that lead to bifurcations, and characterize the associated phase transitions of the arrays. When N is finite there are fluctuations about the well-defined steady states of the infinite arrays. We study the nature of these fluctuations and their effects on the bifurcations in all cases by constructing the appropriate Langevin equations and the associated Fokker–Planck equations.

Spyros Sotiriadis and Gabriele Martelloni 2016 J. Phys. A: Math. Theor. 49 095002
Ground states ofinteracting QFTs are non-Gaussian states, i.e. their connected n-point correlation functions do not vanish for 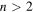 , in contrast to the free QFT case. We show that, when the ground state of an interacting QFT evolves under a free massive QFT for a long time (a scenario that can be realised by a quantum quench), the connected correlation functions decay and all local physical observables equilibrate to values that are given by a Gaussian density matrix that retains memory only of the two-point initial correlation function. The argument hinges upon the fundamental physical principle of cluster decomposition, which is valid for the ground state of a general QFT. An analogous result was already known to be valid in the case of d = 1 spatial dimensions, where it is a special case of the so-called generalised Gibbs ensemble (GGE) hypothesis, and we now generalise it to higher dimensions. Moreover, in the case of massless free evolution, despite the fact that the evolution may lead not to equilibration but instead to unbounded increase of correlations with time, the GGE gives correctly the leading-order asymptotic behaviour of correlation functions in the thermodynamic and large time limit. The demonstration is performed in the context of a bosonic relativistic QFT, but the arguments apply more generally.
, in contrast to the free QFT case. We show that, when the ground state of an interacting QFT evolves under a free massive QFT for a long time (a scenario that can be realised by a quantum quench), the connected correlation functions decay and all local physical observables equilibrate to values that are given by a Gaussian density matrix that retains memory only of the two-point initial correlation function. The argument hinges upon the fundamental physical principle of cluster decomposition, which is valid for the ground state of a general QFT. An analogous result was already known to be valid in the case of d = 1 spatial dimensions, where it is a special case of the so-called generalised Gibbs ensemble (GGE) hypothesis, and we now generalise it to higher dimensions. Moreover, in the case of massless free evolution, despite the fact that the evolution may lead not to equilibration but instead to unbounded increase of correlations with time, the GGE gives correctly the leading-order asymptotic behaviour of correlation functions in the thermodynamic and large time limit. The demonstration is performed in the context of a bosonic relativistic QFT, but the arguments apply more generally.
Igor M Sokolov 2016 J. Phys. A: Math. Theor. 49 095003
The Alexander–Orbach (AO) relation dw = 2df/ds connecting the fractal dimension of a random walk's (RW) trajectory dw or the exponent of anomalous diffusion α = 2/dw on a fractal structure with the fractal and spectral dimension of the structure itself plays a key role in discussion of dynamical properties of complex systems including living cells and single biomolecules. This relation however does not hold universally and breaks down for some structures like diffusion limited aggregates and Eden trees. We show that the alternative to the AO relation is the explicit dependence of the coefficient of the anomalous diffusion on the system's size, i.e. the absence of its thermodynamical limit. The prerequisite for its breakdown is the dependence of the local structure of possible steps of the RW on the system's size. The discussion is illustrated by the examples of diffusion on a Koch curve (AO-conform) and on a Cantor dust (violating AO relation).
Christian R Scullard and Jesper Lykke Jacobsen 2016 J. Phys. A: Math. Theor. 49 125003
We compute critical polynomials for the q-state Potts model on the Archimedean lattices, using a parallel implementation of the algorithm of Jacobsen (2014 J. Phys. A: Math. Theor 47 135001) that gives us access to larger sizes than previously possible. The exact polynomials are computed for bases of size 6 × 6 unit cells, and the root in the temperature variable 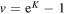 is determined numerically at q = 1 for bases of size 8 × 8. This leads to improved results for bond percolation thresholds, and for the Potts-model critical manifolds in the real (q, v) plane. In the two most favourable cases, we find now the kagome-lattice threshold to eleven digits and that of the
is determined numerically at q = 1 for bases of size 8 × 8. This leads to improved results for bond percolation thresholds, and for the Potts-model critical manifolds in the real (q, v) plane. In the two most favourable cases, we find now the kagome-lattice threshold to eleven digits and that of the  lattice to thirteen. Our critical manifolds reveal many interesting features in the antiferromagnetic region of the Potts model, and determine accurately the extent of the Berker–Kadanoff phase for the lattices studied.
lattice to thirteen. Our critical manifolds reveal many interesting features in the antiferromagnetic region of the Potts model, and determine accurately the extent of the Berker–Kadanoff phase for the lattices studied.
Silvio Franz and Giorgio Parisi 2016 J. Phys. A: Math. Theor. 49 145001
We study a well known neural network model—the perceptron—as a simple statistical physics model of jamming of hard objects. We exhibit two regimes: (1) a convex optimization regime where jamming is hypostatic and non-critical; (2) a non-convex optimization regime where jamming is isostatic and critical. We characterize the critical jamming phase through exponents describing the distribution laws of forces and gaps. Surprisingly we find that these exponents coincide with the corresponding ones recently computed in high dimensional hard spheres. In addition, modifying the perceptron to a random linear programming problem, we show that isostaticity is not a sufficient condition for singular force and gap distributions. For that, fragmentation of the space of solutions (replica symmetry breaking) appears to be a crucial ingredient. We hypothesize universality for a large class of non-convex constrained satisfaction problems with continuous variables.
O Cohen and D Mukamel 2016 J. Phys. A: Math. Theor. 49 155002
We study the effect of a one-dimensional driving field on the interface between two coexisting phases in a two dimensional model. This is done by considering an Ising model on a cylinder with Glauber dynamics in all sites and additional biased Kawasaki dynamics in the central ring. Based on the exact solution of the two-dimensional Ising model, we are able to compute the phase diagram of the driven model within a special limit of fast drive and slow spin flips in the central ring. The model is found to exhibit two phases where the interface is pinned to the central ring: one in which it fluctuates symmetrically around the central ring and another where it fluctuates asymmetrically. In addition, we find a phase where the interface is centered in the bulk of the system, either below or above the central ring of the cylinder. In the latter case, the symmetry breaking is 'stronger' than that found in equilibrium when considering a repulsive potential on the central ring. This equilibrium model is analyzed here by using a restricted solid-on-solid model.
Esteban Guevara Hidalgo and Vivien Lecomte 2016 J. Phys. A: Math. Theor. 49 205002
We analyse numerically the effects of small population size in the initial transient regime of a simple example population dynamics. These effects play an important role for the numerical determination of large deviation functions of additive observables for stochastic processes. A method commonly used in order to determine such functions is the so-called cloning algorithm which in its non-constant population version essentially reduces to the determination of the growth rate of a population, averaged over many realizations of the dynamics. However, the averaging of populations is highly dependent not only on the number of realizations of the population dynamics, and on the initial population size but also on the cut-off time (or population) considered to stop their numerical evolution. This may result in an over-influence of discreteness effects at initial times, caused by small population size. We overcome these effects by introducing a (realization-dependent) time delay in the evolution of populations, additional to the discarding of the initial transient regime of the population growth where these discreteness effects are strong. We show that the improvement in the estimation of the large deviation function comes precisely from these two main contributions.
Cécile Monthus 2016 J. Phys. A: Math. Theor. 49 305002
The iterative methods to diagonalize matrices and many-body Hamiltonians can be reformulated as flows of Hamiltonians towards diagonalization driven by unitary transformations that preserve the spectrum. After a comparative overview of the various types of discrete flows (Jacobi, QR-algorithm) and differential flows (Toda, Wegner, White) that have been introduced in the past, we focus on the random XXZ chain with random fields in order to determine the best closed flow within a given subspace of running Hamiltonians. For the special case of the free-fermion random XX chain with random fields, the flow coincides with the Toda differential flow for tridiagonal matrices which is related to the classical integrable Toda chain and which can be seen as the continuous analog of the discrete QR-algorithm. For the random XXZ chain with random fields that displays a many-body-localization transition, the present differential flow should be an interesting alternative to compare with the discrete flow that has been proposed recently to study the many-body-localization properties in a model of interacting fermions (Rademaker and Ortuno 2016 Phys. Rev. Lett. 116, 010404).
Olivier Bénichou et al 2016 J. Phys. A: Math. Theor. 49 335002
We analyze the joint distributions and temporal correlations between the partial maximum m and the global maximum M achieved by a Brownian bridge on the subinterval ![$[0,{t}_{1}]$](https://content.cld.iop.org/journals/1751-8121/49/33/335002/revision1/jpaaa2f96ieqn1.gif) and on the entire interval
and on the entire interval ![$[0,t]$](https://content.cld.iop.org/journals/1751-8121/49/33/335002/revision1/jpaaa2f96ieqn2.gif) , respectively. We determine three probability distribution functions: the joint distribution
, respectively. We determine three probability distribution functions: the joint distribution 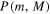 of both maxima; the distribution P(m) of the partial maximum; and the distribution
of both maxima; the distribution P(m) of the partial maximum; and the distribution 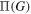 of the gap between the maxima,
of the gap between the maxima, 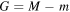 . We present exact results for the moments of these distributions and quantify the temporal correlations between m and M by calculating the Pearson correlation coefficient.
. We present exact results for the moments of these distributions and quantify the temporal correlations between m and M by calculating the Pearson correlation coefficient.
Michele Campisi and Rosario Fazio 2016 J. Phys. A: Math. Theor. 49 345002
By modelling heat engines as driven multi-partite system we show that their dissipation can be expressed in terms of the lag (relative entropy) between the perturbed state of each partition and their equilibrium state, and the correlations that build up among the partitions. We show that the non-negativity of the overall dissipation implies Carnot formulation of the second law. We illustrate the rich interplay between correlations and lags with a two-qubit device driven by a quantum gate.
Chaotic and complex systems
Show article list
M I Sena-Junior and A M S Macêdo 2016 J. Phys. A: Math. Theor. 49 045101
Quantum transport through devices coupled to electron reservoirs can be described in terms of the full counting statistics (FCS) of charge transfer. Transport observables, such as conductance and shot-noise power are just cumulants of FCS and can be obtained from the sample's average density of transmission eigenvalues, which in turn can be obtained from a finite element representation of the saddle-point equation of the Keldysh (or supersymmetric) nonlinear sigma model, known as quantum circuit theory. Normal universal metallic behavior in the semiclassical regime is controlled by the presence of a Fabry–Pérot singularity in the average density of transmission eigenvalues. We present general conditions for the suppression of Fabry–Pérot modes in the semiclassical regime in a sample of arbitrary shape, a disordered conductor or a network of ballistic quantum dots, which leads to an anomalous metallic phase. Through a double-scaling limit, we derive a scaling equation for anomalous metallic transport, in the form of a nonlinear differential equation, which generalizes the ballistic-diffusive scaling equation of a normal metal. The two-parameter stationary solution of our scaling equation generalizes Dorokhov's universal single-parameter distribution of transmission eigenvalues. We provide a simple interpretation of the stationary solution using a thermodynamic analogy with a spin-glass system. As an application, we consider a system formed by a diffusive wire coupled via a barrier to normal-superconductor reservoirs. We observe anomalous reflectionless tunneling, when all perfectly transmitting channels are suppressed, which cannot be explained by the usual mechanism of disorder-induced opening of tunneling channels.
Sara Munday and Georgie Knight 2016 J. Phys. A: Math. Theor. 49 085101
We investigate the scaling of the escape rate from piecewise linear dynamical systems displaying intermittency due to the presence of an indifferent fixed point. Strong intermittent behaviour in the dynamics can result in the system preserving an infinite measure. We define a neighbourhood of the indifferent fixed point to be a hole through which points escape and investigate the scaling of the rate of this escape as the length of the hole decreases, both in the finite measure preserving case and infinite measure preserving case. In the infinite measure preserving systems we observe logarithmic corrections to and polynomial scaling of the escape rate with hole length. Finally we conjecture a relationship between the wandering rate and the observed scaling of the escape rate.
Marcos Saraceno and Alfredo M Ozorio de Almeida 2016 J. Phys. A: Math. Theor. 49 145302
Operators in quantum mechanics—either observables, density or evolution operators, unitary or not—can be represented by c-numbers in operator bases. The position and momentum bases are in one-to-one correspondence with lagrangian planes in double phase space, but this is also true for the well known Wigner–Weyl correspondence based on translation and reflection operators. These phase space methods are here extended to the representation of superoperators. We show that the Choi–Jamiolkowsky isomorphism between the dynamical matrix and the linear action of the superoperator constitutes a 'double' Wigner or chord transform when represented in double phase space. As a byproduct several previously unknown integral relationships between products of Wigner and chord distributions for pure states are derived.
G Drótos and C Jung 2016 J. Phys. A: Math. Theor. 49 235101
The topic of this paper is hyperbolic chaotic scattering in a three degrees of freedom system. We generalize how shadows in the domain of the doubly differential cross-section are found: they are traced out by the appropriately filtered unstable manifolds of the periodic trajectories in the chaotic saddle. These shadows are related to the rainbow singularities in the doubly differential cross-section. As a result of this relation, we discover a method of how to recognize in the cross section a smoothly deformed image of the chaotic saddle, allowing the reconstruction of the symbolic dynamics of the chaotic saddle, its topology and its scaling factors.
Biological modelling
Show article list
A I Curatolo et al 2016 J. Phys. A: Math. Theor. 49 095601
We consider networks made of parallel lanes along which particles hop according to driven diffusive dynamics. The particles also hop transversely from lane to lane, hence indirectly coupling their longitudinal dynamics. We present a general method for constructing the phase diagram of these systems which reveals that in many cases their physics reduce to that of single-lane systems. The reduction to an effective single-lane description legitimizes, for instance, the use of a single TASEP to model the hopping of molecular motors along the many tracks of a single microtubule. Then, we show how, in quasi-2D settings, new phenomena emerge due to the presence of non-zero transverse currents, leading, for instance, to strong 'shear localization' along the network.
Maria Schwarzl et al 2016 J. Phys. A: Math. Theor. 49 225601
We study the degree of success of a single predator hunting a herd of prey on a two-dimensional square lattice landscape. We explicitly consider the self volume of the prey restraining their dynamics on the lattice. The movement of both predator and prey is chosen to include an intelligent, decision making step based on their respective sighting ranges, the radius in which they can detect the other species (prey cannot recognise each other besides the self volume interaction): after spotting each other the motion of prey and predator turns from a nearest neighbour random walk into directed escape or chase, respectively. We consider a large range of prey densities and sighting ranges and compute the mean first passage time for a predator to catch a prey as well as characterise the effective dynamics of the hunted prey. We find that the prey's sighting range dominates their life expectancy and the predator profits more from a bad eyesight of the prey than from his own good eye sight. We characterise the dynamics in terms of the mean distance between the predator and the nearest prey. It turns out that effectively the dynamics of this distance coordinate can be captured in terms of a simple Ornstein–Uhlenbeck picture. Reducing the many-body problem to a simple two-body problem by imagining predator and nearest prey to be connected by an effective Hookean bond, all features of the model such as prey density and sighting ranges merge into the effective binding constant.
Paul C Bressloff and Sean D Lawley 2016 J. Phys. A: Math. Theor. 49 245601
We consider diffusion on a tree with nodes that randomly switch between allowing and prohibiting particles to pass. We find exact expressions for various splitting probabilities and mean first passage times for a single diffusing particle and show how the many parameters in the problem, such as the node gating statistics and tree topology, contribute to these exit statistics. We also consider a concentration of particles that can always pass through interior branch nodes and determine how an intermittent source at one end of the tree affects the flux at the other end. The latter problem is motivated by applications to insect respiration.
Qingchu Wu and Haifeng Zhang 2016 J. Phys. A: Math. Theor. 49 345601
In this paper, we investigate the epidemic spreading on random and regular networks through a pairwise-type model with a general transmission rate to evaluate the influence of the node-weight distribution. By using block matrix theory, an epidemic threshold index is formulated to predict the epidemic outbreak. An upper bound of the epidemic threshold is obtained by analyzing the monotonicity of spectral radius for nonnegative matrices. Theoretical results suggest that the epidemic threshold is dependent on both matrices 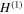 and
and  with the first matrix being related to the mean-field model while the second one reflecting the heterogeneous transmission rates. In particular, for a linear transmission rate, this study shows the negative correlation between the heterogeneity of weight distribution and the epidemic threshold, which is different from the results for existing results from the edge-weighted networks.
with the first matrix being related to the mean-field model while the second one reflecting the heterogeneous transmission rates. In particular, for a linear transmission rate, this study shows the negative correlation between the heterogeneity of weight distribution and the epidemic threshold, which is different from the results for existing results from the edge-weighted networks.
Mathematical physics
Show article list
R Campoamor-Stursberg et al 2016 J. Phys. A: Math. Theor. 49 035201
Ordinary differential equations (ODEs) and ordinary difference systems (OΔSs) invariant under the actions of the Lie groups  and
and 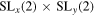 of projective transformations of the independent variables x and dependent variables y are constructed. The ODEs are continuous limits of the OΔSs, or conversely, the OΔSs are invariant discretizations of the ODEs. The invariant OΔSs are used to calculate numerical solutions of the invariant ODEs of order up to five. The solutions of the invariant numerical schemes are compared to numerical solutions obtained by standard Runge–Kutta methods and to exact solutions, when available. The invariant method performs at least as well as standard ones and much better in the vicinity of singularities of solutions.
of projective transformations of the independent variables x and dependent variables y are constructed. The ODEs are continuous limits of the OΔSs, or conversely, the OΔSs are invariant discretizations of the ODEs. The invariant OΔSs are used to calculate numerical solutions of the invariant ODEs of order up to five. The solutions of the invariant numerical schemes are compared to numerical solutions obtained by standard Runge–Kutta methods and to exact solutions, when available. The invariant method performs at least as well as standard ones and much better in the vicinity of singularities of solutions.
Fabio Deelan Cunden et al 2016 J. Phys. A: Math. Theor. 49 135202
In the last decade, spectral linear statistics on large dimensional random matrices have attracted significant attention. Within the physics community, a privileged role has been played by invariant matrix ensembles for which a two-dimensional Coulomb gas analogy is available. We present a critical revision of the Coulomb gas method in random matrix theory (RMT) borrowing language and tools from large deviations theory. This allows us to formalize an equivalent, but more effective and quicker route toward RMT free energy calculations. Moreover, we argue that this more modern viewpoint is likely to shed further light on the interesting issues of weak phase transitions and evaporation phenomena recently observed in RMT.
Robert Arthur et al 2016 J. Phys. A: Math. Theor. 49 165205
We explore boundary scattering in the sine-Gordon model with a non-integrable family of Robin boundary conditions. The soliton content of the field after collision is analysed using a numerical implementation of the direct scattering problem associated with the inverse scattering method. We find that an antikink may be reflected into various combinations of an antikink, a kink, and one or more breathers, depending on the values of the initial antikink velocity and a parameter associated with the boundary condition. In addition we observe regions with an intricate resonance structure arising from the creation of an intermediate breather whose recollision with the boundary is highly dependent on the breather phase.
Max R Atkin et al 2016 J. Phys. A: Math. Theor. 49 185201
We compute the partition function of the q-states Potts model on a random planar lattice with  allowed, equally weighted colours on a connected boundary. To this end, we employ its matrix model representation in the planar limit, generalising a result by Voiculescu for the addition of random matrices to a situation beyond free probability theory. We show that the partition functions with p and q − p colours on the boundary are related algebraically. Finally, we investigate the phase diagram of the model when
allowed, equally weighted colours on a connected boundary. To this end, we employ its matrix model representation in the planar limit, generalising a result by Voiculescu for the addition of random matrices to a situation beyond free probability theory. We show that the partition functions with p and q − p colours on the boundary are related algebraically. Finally, we investigate the phase diagram of the model when 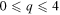 and comment on the conformal field theory description of the critical points.
and comment on the conformal field theory description of the critical points.
Alexandre Faribault et al 2016 J. Phys. A: Math. Theor. 49 185202
In this work we present a determinant expression for the domain-wall boundary condition partition function of rational (XXX) Richardson–Gaudin models which, in addition to  spins
spins 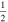 , contains one arbitrarily large spin S. The proposed determinant representation is written in terms of a set of variables which, from previous work, are known to define eigenstates of the quantum integrable models belonging to this class as solutions to quadratic Bethe equations. Such a determinant can be useful numerically since systems of quadratic equations are much simpler to solve than the usual highly nonlinear Bethe equations. It can therefore offer significant gains in stability and computation speed.
, contains one arbitrarily large spin S. The proposed determinant representation is written in terms of a set of variables which, from previous work, are known to define eigenstates of the quantum integrable models belonging to this class as solutions to quadratic Bethe equations. Such a determinant can be useful numerically since systems of quadratic equations are much simpler to solve than the usual highly nonlinear Bethe equations. It can therefore offer significant gains in stability and computation speed.
Jason Cantarella et al 2016 J. Phys. A: Math. Theor. 49 275202
Sampling equilateral closed polygons is of interest in the statistical study of ring polymers. Over the past 30 years, previous authors have proposed a variety of simple Markov chain algorithms (but have not been able to show that they converge to the correct probability distribution) and complicated direct samplers (which require extended-precision arithmetic to evaluate numerically unstable polynomials). We present a simple direct sampler which is fast and numerically stable, and analyze its runtime using a new formula for the volume of equilateral polygon space as a Dirichlet-type integral.
M V Berry 2016 J. Phys. A: Math. Theor. 49 305204
The Aharonov–Bohm (AB) function, describing a plane wave scattered by a flux line, is expanded asymptotically in a Fresnel-integral based series whose terms are smooth in the forward direction and uniformly valid in angle and flux. Successive approximations are valid for large distance r from the flux (or short wavelength) but are accurate even within one wavelength of it. Coefficients of all the terms are exhibited explicitly for the forward direction, enabling the high-order asymptotics to be understood in detail. The series is factorally divergent, with optimal truncation error exponentially small in r. Systematic resummation gives further exponential improvement. Terms of the series satisfy a resurgence relation: the high orders are related to the low orders. Discontinuities in the backward direction get smaller order by order, with systematic cancellation by successive terms. The relation to an earlier scheme based on the Cornu spiral is discussed.
N Crampe et al 2016 J. Phys. A: Math. Theor. 49 375201
The first result of the present paper is to provide classes of explicit solutions for integrable boundary matrices for the multi-species ASEP with an arbitrary number of species. All the solutions we have obtained can be seen as representations of a new algebra that contains the boundary Hecke algebra. The boundary Hecke algebra is not sufficient to build these solutions. This is the second result of our paper.
Timothy J Hollowood et al 2016 J. Phys. A: Math. Theor. 49 465201
Recently, two kinds of integrable deformations of the string world sheet theory in the gauge/gravity correspondence have been constructed (Delduc et al 2014 Phys. Rev. Lett. 112 051601; Hollowood et al 2014 J. Phys. A: Math. Theor. 47 495402). One class of these, the k deformations associated to the more general q deformations but with 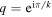 a root of unity, has been shown to be related to a particular discrete deformation of the principal chiral models and (semi-)symmetric space sigma models involving a gauged WZW model. We conjecture a form for the exact S-matrices of the bosonic integrable field theories of this type. The S-matrices imply that the theories have a hidden infinite dimensional affine quantum group symmetry. We provide some evidence, via quantum inverse scattering techniques, that the theories do indeed possess the finite-dimensional part of this quantum group symmetry.
a root of unity, has been shown to be related to a particular discrete deformation of the principal chiral models and (semi-)symmetric space sigma models involving a gauged WZW model. We conjecture a form for the exact S-matrices of the bosonic integrable field theories of this type. The S-matrices imply that the theories have a hidden infinite dimensional affine quantum group symmetry. We provide some evidence, via quantum inverse scattering techniques, that the theories do indeed possess the finite-dimensional part of this quantum group symmetry.
 case
case
Nalini Joshi et al 2016 J. Phys. A: Math. Theor. 49 495201
In this paper, we construct two lattices from the τ functions of  -surface q-Painlevé equations, on which quad-equations of ABS type appear. Moreover, using the reduced hypercube structure, we obtain the Lax pairs of the
-surface q-Painlevé equations, on which quad-equations of ABS type appear. Moreover, using the reduced hypercube structure, we obtain the Lax pairs of the  -surface q-Painlevé equations.
-surface q-Painlevé equations.
Quantum mechanics and quantum information theory
Show article list
Matthew A Graydon and D M Appleby 2016 J. Phys. A: Math. Theor. 49 085301
Complex projective t-designs, particularly sics and full sets of mutually unbiased bases, play an important role in quantum information. We introduce a generalization which we call conical t-designs. They include arbitrary rank symmetric informationally complete measurements (sims) and full sets of arbitrary rank mutually unbiased measurements (mums). They are deeply implicated in the description of entanglement (as we show in a subsequent paper). Viewed in one way a conical two-design is a symmetric decomposition of a separable Werner state (up to a normalization factor). Viewed in another way it is a certain kind of polytope in the Bloch body. In the Bloch body picture sims and full sets of mums form highly symmetric polytopes (a single regular simplex in the one case; the convex hull of a set of orthogonal regular simplices in the other). We give the necessary and sufficient conditions for an arbitrary polytope to be what we call a homogeneous conical two-design. This suggests a way to search for new kinds of projective two-design.
Alessandro Michelangeli and Paul Pfeiffer 2016 J. Phys. A: Math. Theor. 49 105301
We introduce a 3D model, and we study its stability, consisting of two distinct pairs of identical fermions coupled with a two-body interaction between fermions of different species, whose effective range is essentially zero (a so called (2+2)-fermionic system with zero-range interaction). The interaction is modelled by implementing the celebrated (and ubiquitous in the literature of this field) Bethe–Peierls contact condition with given two-body scattering length within the Krein–Višik–Birman theory of extensions of semi-bounded symmetric operators, in order to make the Hamiltonian a well-defined (self-adjoint) physical observable. After deriving the expression for the associated energy quadratic form, we show analytically and numerically that the energy of the model is bounded below, thus describing a stable system.
Patrick Hayden and Alex May 2016 J. Phys. A: Math. Theor. 49 175304
One of the most important properties of quantum information, and the one ultimately responsible for its cryptographic applications, is that it can not be copied. That statement, however, is not completely accurate. While the no-cloning theorem of quantum mechanics prevents quantum information from being copied in space, the reversibility of microscopic physics actually requires that the information be copied in time. In spacetime as a whole, therefore, quantum information is widely replicated but in a restricted fashion. We fully characterize which regions of spacetime can all hold the same quantum information. Because quantum information can be delocalized through quantum error correction and teleportation, it need not follow well-defined trajectories. Instead, replication of the information in any configuration of spacetime regions not leading to violations of causality or the no-cloning principle is allowed. To demonstrate this, we answer the operational question of exactly when the information can be summoned to a set of spacetime points, showing how to do so efficiently using a combination of teleportation and codeword-stabilized quantum codes. This provides a simple and complete description of where and when a qubit can be located in spacetime, revealing a remarkable variety of possibilities.
Takayuki Miyadera et al 2016 J. Phys. A: Math. Theor. 49 185301
The notion that any physical quantity is defined and measured relative to a reference frame is traditionally not explicitly reflected in the theoretical description of physical experiments where, instead, the relevant observables are typically represented as 'absolute' quantities. However, the emergence of the resource theory of quantum reference frames as a new branch of quantum information science in recent years has highlighted the need to identify the physical conditions under which a quantum system can serve as a good reference. Here we investigate the conditions under which, in quantum theory, an account in terms of absolute quantities can provide a good approximation of relative quantities. We find that this requires the reference system to be large in a suitable sense.
T G Philbin and J Anders 2016 J. Phys. A: Math. Theor. 49 215303
We consider the global thermal state of classical and quantum harmonic oscillators that interact with a reservoir. Ohmic damping of the oscillator can be exactly treated with a 1D scalar field reservoir, whereas general non-Ohmic damping is conveniently treated with a continuum reservoir of harmonic oscillators. Using the diagonalized Hamiltonian of the total system, we calculate a number of thermodynamic quantities for the damped oscillator: the mean force internal energy, mean force free energy, and another internal energy based on the free-oscillator Hamiltonian. The classical mean force energy is equal to that of a free oscillator, for both Ohmic and non-Ohmic damping no matter how strong the coupling to the reservoir. In contrast, the quantum mean force energy depends on the details of the damping and diverges for strictly Ohmic damping. These results give additional insight into the steady-state thermodynamics of open systems with arbitrarily strong coupling to a reservoir, complementing results for energies derived within dynamical approaches (e.g. master equations) in the weak-coupling regime.
W Roga et al 2016 J. Phys. A: Math. Theor. 49 235301
We investigate and compare three distinguished geometric measures of bipartite quantum correlations that have been recently introduced in the literature: the geometric discord, the measurement-induced geometric discord, and the discord of response, each one defined according to three contractive distances on the set of quantum states, namely the trace, Bures, and Hellinger distances. We establish a set of exact algebraic relations and inequalities between the different measures. In particular, we show that the geometric discord and the discord of response based on the Hellinger distance are easy to compute analytically for all quantum states whenever the reference subsystem is a qubit. These two measures thus provide the first instance of discords that are simultaneously fully computable, reliable (since they satisfy all the basic Axioms that must be obeyed by a proper measure of quantum correlations), and operationally viable (in terms of state distinguishability). We apply the general mathematical structure to determine the closest classical-quantum state of a given state and the maximally quantum-correlated states at fixed global state purity according to the different distances, as well as a necessary condition for a channel to be quantumness breaking.
Yu Cai et al 2016 J. Phys. A: Math. Theor. 49 305301
A dimension witness is a criterion that sets a lower bound on the dimension needed to reproduce the observed data. Three types of dimension witnesses can be found in the literature: device-dependent ones, in which the bound is obtained assuming some knowledge on the state and the measurements; device-independent prepare-and-measure ones, that can be applied to any system including classical ones; and device-independent Bell-based ones, that certify the minimal dimension of some entangled systems. Here we consider the Collins–Gisin–Linden–Massar–Popescu Bell-type inequality for four outcomes. We show that a sufficiently high violation of this inequality witnesses  and present a proof-of-principle experimental observation of such a violation. This presents a first experimental violation of the third type of dimension witness beyond qutrits.
and present a proof-of-principle experimental observation of such a violation. This presents a first experimental violation of the third type of dimension witness beyond qutrits.
F Benatti and R Floreanini 2016 J. Phys. A: Math. Theor. 49 305303
Many-body entanglement is studied within the algebraic approach to quantum physics in systems made of Majorana fermions. In this framework, the notion of separability stems from partitions of the algebra of observables and properties of the associated correlation functions, rather than on particle tensor products. This allows a complete characterization of non-separable Majorana fermion states to be obtained. These results may have direct application in quantum metrology: using Majorana systems, sub-shot-noise accuracy in parameter estimations can be achieved without preliminary resource-consuming, state entanglement operations.
Martin Idel et al 2016 J. Phys. A: Math. Theor. 49 445304
We propose and analyse a mathematical measure for the amount of squeezing contained in a continuous variable quantum state. We show that the proposed measure operationally quantifies the minimal amount of squeezing needed to prepare a given quantum state and that it can be regarded as a squeezing analogue of the 'entanglement of formation'. We prove that the measure is convex and subadditive and we provide analytic bounds as well as a numerical convex optimisation algorithm for its computation. By example, we then show that the amount of squeezing needed for the preparation of certain multi-mode quantum states can be significantly lower than naive state preparation suggests.
Krišjānis Prūsis et al 2016 J. Phys. A: Math. Theor. 49 455301
In typical discrete-time quantum walk algorithms, one measures the position of the walker while ignoring its internal spin/coin state. Rather than neglecting the information in this internal state, we show that additionally measuring it doubles the success probability of many quantum spatial search algorithms. For example, this allows Grover's unstructured search problem to be solved with certainty, rather than with probability 1/2 if only the walker's position is measured, so the additional measurement yields a search algorithm that is twice as fast as without it, on average. Thus the internal state of discrete-time quantum walks holds valuable information that can be utilized to improve algorithms. Furthermore, we determine conditions for which spatial search problems on regular graphs are amenable to this doubling of the success probability, and this involves diagrammatically analyzing search using degenerate perturbation theory and deriving a useful formula for how the quantum walk acts in its reduced subspace.
Field theory and string theory
Show article list
Matthew Buican and Takahiro Nishinaka 2016 J. Phys. A: Math. Theor. 49 045401
In a recent paper, we proposed closed-form expressions for the superconformal indices of the  and
and 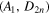 Argyres–Douglas (AD) superconformal field theories (SCFTs) in the Schur limit. Following up on our results, we turn our attention to the small S1 regime of these indices. As expected on general grounds, our study reproduces the S3 partition functions of the resulting dimensionally reduced theories. However, we show that in all cases—with the exception of the reduction of the
Argyres–Douglas (AD) superconformal field theories (SCFTs) in the Schur limit. Following up on our results, we turn our attention to the small S1 regime of these indices. As expected on general grounds, our study reproduces the S3 partition functions of the resulting dimensionally reduced theories. However, we show that in all cases—with the exception of the reduction of the  SCFT—certain imaginary partners of real mass terms are turned on in the corresponding mirror theories. We interpret these deformations as R symmetry mixing with the topological symmetries of the direct S1 reductions. Moreover, we argue that these shifts occur in any of our theories whose four-dimensional
SCFT—certain imaginary partners of real mass terms are turned on in the corresponding mirror theories. We interpret these deformations as R symmetry mixing with the topological symmetries of the direct S1 reductions. Moreover, we argue that these shifts occur in any of our theories whose four-dimensional 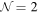 superconformal
superconformal  symmetry does not obey an SU(2) quantization condition. We then use our R symmetry map to find the four-dimensional ancestors of certain three-dimensional operators. Somewhat surprisingly, this picture turns out to imply that the scaling dimensions of many of the chiral operators of the four-dimensional theory are encoded in accidental symmetries of the three-dimensional theory. We also comment on the implications of our work on the space of general
symmetry does not obey an SU(2) quantization condition. We then use our R symmetry map to find the four-dimensional ancestors of certain three-dimensional operators. Somewhat surprisingly, this picture turns out to imply that the scaling dimensions of many of the chiral operators of the four-dimensional theory are encoded in accidental symmetries of the three-dimensional theory. We also comment on the implications of our work on the space of general  SCFTs.
SCFTs.
Nicolas Boulanger et al 2016 J. Phys. A: Math. Theor. 49 095402
We consider four-dimensional higher-spin (HS) theory at the first nontrivial order corresponding to the cubic action. All HS interaction vertices are explicitly obtained from Vasiliev's equations. In particular, we obtain the vertices that are not determined solely by the HS algebra structure constants. The dictionary between the Fronsdal fields and HS connections is found and the corrections to the Fronsdal equations are derived. These corrections turn out to involve derivatives of arbitrary order. We observe that the vertices not determined by the HS algebra produce naked infinities, when decomposed into the minimal derivative vertices and improvements. Therefore, standard methods can only be used to check a rather limited number of correlation functions within the HS AdS/CFT duality. A possible resolution of the puzzle is discussed.
Alba Grassi et al 2016 J. Phys. A: Math. Theor. 49 115401
The partition function of ABJ(M) theories on the three-sphere can be regarded as the canonical partition function of an ideal Fermi gas with a non-trivial Hamiltonian. We propose an exact expression for the spectral determinant of this Hamiltonian, which generalizes recent results obtained in the maximally supersymmetric case. As a consequence, we find an exact WKB quantization condition determining the spectrum which is in agreement with numerical results. In addition, we investigate the factorization properties and functional equations for our conjectured spectral determinants. These functional equations relate the spectral determinants of ABJ theories to consecutive ranks of gauge groups but the same Chern–Simons coupling.
Olivier Blondeau-Fournier et al 2016 J. Phys. A: Math. Theor. 49 125401
We consider the logarithmic negativity, a measure of bipartite entanglement, in a general unitary 1 + 1-dimensional massive quantum field theory, not necessarily integrable. We compute the negativity between a finite region of length r and an adjacent semi-infinite region, and that between two semi-infinite regions separated by a distance r. We show that the former saturates to a finite value, and that the latter tends to zero, as 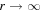 . We show that in both cases, the leading corrections are exponential decays in r (described by modified Bessel functions) that are solely controlled by the mass spectrum of the model, independently of its scattering matrix. This implies that, like the entanglement entropy (EE), the logarithmic negativity displays a very high level of universality, allowing one to extract information about the mass spectrum. Further, a study of sub-leading terms shows that, unlike the EE, a large-r analysis of the negativity allows for the detection of bound states.
. We show that in both cases, the leading corrections are exponential decays in r (described by modified Bessel functions) that are solely controlled by the mass spectrum of the model, independently of its scattering matrix. This implies that, like the entanglement entropy (EE), the logarithmic negativity displays a very high level of universality, allowing one to extract information about the mass spectrum. Further, a study of sub-leading terms shows that, unlike the EE, a large-r analysis of the negativity allows for the detection of bound states.
Marco Schäfer et al 2016 J. Phys. A: Math. Theor. 49 135402
We develop the worldline formalism for computations of composite operators such as the fluctuation induced energy-momentum tensor. As an example, we use a fluctuating real scalar field subject to Dirichlet boundary conditions. The resulting worldline representation can be evaluated by worldline Monte-Carlo methods in continuous spacetime. We benchmark this worldline numerical algorithm with the aid of analytically accessible single-plate and parallel-plate Casimir configurations, providing a detailed analysis of statistical and systematic errors. The method generalizes straightforwardly to arbitrary Casimir geometries and general background potentials.
 expansion
expansion
Simone Giombi et al 2016 J. Phys. A: Math. Theor. 49 135403
 expansion
PDF, Conformal QEDd, F-theorem and the
expansion
PDF, Conformal QEDd, F-theorem and the  expansion
expansion
We calculate the free energies F for U(1) gauge theories on the d dimensional sphere of radius R. For the theory with free Maxwell action we find the exact result as a function of d; it contains the term  consistent with the lack of conformal invariance in dimensions other than 4. When the U(1) gauge theory is coupled to a sufficient number Nf of massless four-component fermions, it acquires an interacting conformal phase, which in
consistent with the lack of conformal invariance in dimensions other than 4. When the U(1) gauge theory is coupled to a sufficient number Nf of massless four-component fermions, it acquires an interacting conformal phase, which in 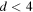 describes the long distance behavior of the model. The conformal phase can be studied using large Nf methods. Generalizing the d = 3 calculation in arXiv:1112.5342, we compute its sphere free energy as a function of d, ignoring the terms of order
describes the long distance behavior of the model. The conformal phase can be studied using large Nf methods. Generalizing the d = 3 calculation in arXiv:1112.5342, we compute its sphere free energy as a function of d, ignoring the terms of order  and higher. For finite Nf, following arXiv:1409.1937 and arXiv:1507.01960, we develop the
and higher. For finite Nf, following arXiv:1409.1937 and arXiv:1507.01960, we develop the  expansion for the sphere free energy of conformal QEDd. Its extrapolation to d = 3 shows very good agreement with the large Nf approximation for
expansion for the sphere free energy of conformal QEDd. Its extrapolation to d = 3 shows very good agreement with the large Nf approximation for  . For Nf at or below some critical value
. For Nf at or below some critical value 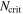 , the
, the  symmetric conformal phase of QED3 is expected to disappear or become unstable. By using the F-theorem and comparing the sphere free energies in the conformal and broken symmetry phases, we show that
symmetric conformal phase of QED3 is expected to disappear or become unstable. By using the F-theorem and comparing the sphere free energies in the conformal and broken symmetry phases, we show that  . As another application of our results, we calculate the one loop beta function in conformal QED6, where the gauge field has a four-derivative kinetic term. We show that this theory coupled to Nf massless fermions is asymptotically free.
. As another application of our results, we calculate the one loop beta function in conformal QED6, where the gauge field has a four-derivative kinetic term. We show that this theory coupled to Nf massless fermions is asymptotically free.
J S Dowker 2016 J. Phys. A: Math. Theor. 49 145401
I compute the conformal weights of the twist operators of free scalar fields for charged Rényi entropy in both odd and even dimensions. Explicit expressions can be found, in odd dimensions as a function of the chemical potential in the absence of a conical singularity and thence by images for all integer coverings. This method, developed some time ago, is equivalent, in results, to the replica technique. A review is given. The same method applies for even dimensions but a general form is more immediately available. For no chemical potential, the closed form in the covering order is written in an alternative way related to old trigonometric sums. Some derivatives are obtained. An analytical proof is given of a conjecture made by Bueno, Myers and Witczak-Krempa regarding the relation between the conformal weights and a corner coefficient (a universal quantity) in the Rényi entropy.
R R Metsaev 2016 J. Phys. A: Math. Theor. 49 175401
Using the BRST–BV approach, we consider totally symmetric arbitrary integer spin conformal fields propagating in flat space. For such fields, we obtain the ordinary-derivative BRST–BV Lagrangian that is invariant under gauge transformations. In our approach, the ordinary-derivative Lagrangian and gauge transformations are constructed in terms of the respective traceless gauge fields and traceless gauge transformation parameters. We also obtain a realization of conformal algebra symmetries on the space of fields and antifields entering the BRST–BV formulation of conformal fields.
Antal Jevicki and Junggi Yoon 2016 J. Phys. A: Math. Theor. 49 205401
We study interacting features of SN orbifold CFTs. Concentrating on characters (associated with SN Orbifold primaries) we first formulate a novel procedure for evaluating them through 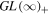 tracing. The result is a polynomial formula which we show gives results equivalent to those found by Bantay. From this we deduce a hierarchy of commuting Hamiltonians featuring locality in the induced space, and nonlinear string-type interactions.
tracing. The result is a polynomial formula which we show gives results equivalent to those found by Bantay. From this we deduce a hierarchy of commuting Hamiltonians featuring locality in the induced space, and nonlinear string-type interactions.
Matteo Beccaria and Arkady A Tseytlin 2016 J. Phys. A: Math. Theor. 49 295401
We find a simple relation between a free higher spin partition function on the thermal quotient of  and the partition function of the associated d-dimensional conformal higher spin field defined on the thermal quotient of
and the partition function of the associated d-dimensional conformal higher spin field defined on the thermal quotient of 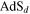 . Starting with a conformal higher spin field defined in
. Starting with a conformal higher spin field defined in  , one may also associate to with another conformal field in
, one may also associate to with another conformal field in  dimensions, thus iterating AdS/CFT. We observe that in the case of
dimensions, thus iterating AdS/CFT. We observe that in the case of 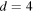 , this iteration leads to a trivial 3d higher spin conformal theory with parity-even non-local action: it describes a zero total number of dynamical degrees of freedom and the corresponding partition function is equal to 1.
, this iteration leads to a trivial 3d higher spin conformal theory with parity-even non-local action: it describes a zero total number of dynamical degrees of freedom and the corresponding partition function is equal to 1.
Domenico Orlando et al 2016 J. Phys. A: Math. Theor. 49 445403
We study Yang–Baxter deformations of the 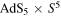 superstring with non-Abelian classical r-matrices which satisfy the homogeneous classical Yang–Baxter equation. By performing a supercoset construction, we can get deformed
superstring with non-Abelian classical r-matrices which satisfy the homogeneous classical Yang–Baxter equation. By performing a supercoset construction, we can get deformed  backgrounds. While this is a new area of research, the current understanding is that Abelian classical r-matrices give rise to solutions of type IIB supergravity, while non-Abelian classical r-matrices lead to solutions of the generalized supergravity equations. We examine here some examples of non-Abelian classical r-matrices and derive the associated backgrounds explicitly. All of the resulting backgrounds satisfy the generalized equations. For some of them, we derive 'T-dualized' backgrounds by adding a linear coordinate dependence to the dilaton and show that these satisfy the usual type IIB supergravity equations. Remarkably, some of the 'T-dualized' backgrounds are locally identical to undeformed
backgrounds. While this is a new area of research, the current understanding is that Abelian classical r-matrices give rise to solutions of type IIB supergravity, while non-Abelian classical r-matrices lead to solutions of the generalized supergravity equations. We examine here some examples of non-Abelian classical r-matrices and derive the associated backgrounds explicitly. All of the resulting backgrounds satisfy the generalized equations. For some of them, we derive 'T-dualized' backgrounds by adding a linear coordinate dependence to the dilaton and show that these satisfy the usual type IIB supergravity equations. Remarkably, some of the 'T-dualized' backgrounds are locally identical to undeformed  after an appropriate coordinate transformation, but this seems not to be generally the case.
after an appropriate coordinate transformation, but this seems not to be generally the case.
Fluid and plasma theory
Show article list
Koji Ohkitani 2016 J. Phys. A: Math. Theor. 49 015502
We study how late the first singularity can form in solutions of the Navier–Stokes equations and estimate the size of the potentially dangerous time interval, where it can possibly appear. According to Leray (1934), its size is estimated as 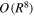 when normalized by the local existence time, for a general blowup of the enstrophy
when normalized by the local existence time, for a general blowup of the enstrophy 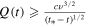 at
at  Here
Here  is the Reynolds number defined with initial energy E(0) and enstrophy Q(0). Applying dynamic scaling transformations, we give a general estimate parameterized by the behaviour of the scaled enstrophy. In particular, we show that the size is reduced to
is the Reynolds number defined with initial energy E(0) and enstrophy Q(0). Applying dynamic scaling transformations, we give a general estimate parameterized by the behaviour of the scaled enstrophy. In particular, we show that the size is reduced to  for a class of type II blow up of the form
for a class of type II blow up of the form 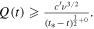 On the basis on the structure theorem of Leray (1934), we note that the self-similar and asymptotically self-similar blowup are ruled out for any singularities of weak solutions. We also apply the dynamic scaling to weak solutions with more than one singularities to show that the size is estimated as
On the basis on the structure theorem of Leray (1934), we note that the self-similar and asymptotically self-similar blowup are ruled out for any singularities of weak solutions. We also apply the dynamic scaling to weak solutions with more than one singularities to show that the size is estimated as  for the type II blowup above.
for the type II blowup above.
Wieslaw Larecki and Zbigniew Banach 2016 J. Phys. A: Math. Theor. 49 125501
The two-field radiation hydrodynamics in n spatial dimensions is derived from the kinetic theory of radiation. Both the full-moment (frequency-independent) and spectral (frequency-dependent) formulations of radiation hydrodynamics are considered. The derivation is based on the entropy principle of extended thermodynamics of gases. In the case of the full-moment hydrodynamics, the formulation of the entropy principle introduced by Boillat and Ruggeri (1997 Contin. Mech. Thermodyn. 9 205) is adapted and this suffices to determine the radiation pressure tensor. In the full-moment formulation, the equations of radiation hydrodynamics take the same form for all possible types of radiation statistics. In the spectral formulation, the different radiation pressure tensors are assigned to Bose–Einstein, Fermi–Dirac and Maxwell–Boltzmann statistics, and consequently the different hydrodynamic equations are obtained for each of those statistics types. In order to derive the equations of the spectral radiation hydrodynamics, the relations for the radiation pressure tensor implied by the entropy principle must be supplemented by the additional conditions. Considering the limit of small heat flux, we arrive at the linearized equations of radiation hydrodynamics which assume the same form in both the full-moment and spectral formulations.
Thiago F Viscondi et al 2016 J. Phys. A: Math. Theor. 49 165501
A method for extracting finite-dimensional Hamiltonian systems from a class of 2 + 1 Hamiltonian mean field theories is presented. These theories possess noncanonical Poisson brackets, which normally resist Hamiltonian truncation, but a process of beatification by coordinate transformation near a reference state is described in order to perturbatively overcome this difficulty. Two examples of four-wave truncation of Euler's equation for scalar vortex dynamics are given and compared: one a direct non-Hamiltonian truncation of the equations of motion, the other obtained by beatifying the Poisson bracket and then truncating.
V N Grebenev et al 2016 J. Phys. A: Math. Theor. 49 365501
We present a comprehensive study and full classification of the stationary solutions in Leith's model of turbulence with a generalised viscosity. Three typical types of boundary value problems are considered: Problems 1 and 2 with a finite positive value of the spectrum at the left (right) and zero at the right (left) boundaries of a wave number range, and Problem 3 with finite positive values of the spectrum at both boundaries. Settings of these problems and analysis of existence of their solutions are based on a phase–space analysis of orbits of the underlying dynamical system. One of the two fixed points of the underlying dynamical system is found to correspond to a 'sharp front' where the energy flux and the spectrum vanish at the same wave number. The other fixed point corresponds to the only exact power-law solution—the so-called dissipative scaling solution. The roles of the Kolmogorov, dissipative and thermodynamic scaling, as well as of sharp front solutions, are discussed.
Special issue articles
Show article list
N Kitanine et al 2016 J. Phys. A: Math. Theor. 49 104002
In the present article we study the form factors of quantum integrable lattice models solvable by the separation of variables (SoVs) method. It was recently shown that these models admit universal determinant representations for the scalar products of the so-called separate states (a class which includes in particular all the eigenstates of the transfer matrix). These results permit to obtain simple expressions for the matrix elements of local operators (form factors). However, these representations have been obtained up to now only for the completely inhomogeneous versions of the lattice models considered. In this article we give a simple algebraic procedure to rewrite the scalar products (and hence the form factors) for the SoV related models as Izergin or Slavnov type determinants. This new form leads to simple expressions for the form factors in the homogeneous and thermodynamic limits. To make the presentation of our method clear, we have chosen to explain it first for the simple case of the XXX Heisenberg chain with anti-periodic boundary conditions. We would nevertheless like to stress that the approach presented in this article applies as well to a wide range of models solved in the SoV framework.
Helen Au-Yang and Jacques H H Perk 2016 J. Phys. A: Math. Theor. 49 154003
Monodromy matrices of the  model are known to satisfy a Yang–Baxter equation with a six-vertex R-matrix as the intertwiner. The commutation relations of the elements of the monodromy matrices are completely determined by this R-matrix. We show the reason why in the superintegrable case the eigenspace is degenerate, but not in the general case. We then show that the eigenspaces of special CSOS models descending from the chiral Potts model are also degenerate. The existence of an
model are known to satisfy a Yang–Baxter equation with a six-vertex R-matrix as the intertwiner. The commutation relations of the elements of the monodromy matrices are completely determined by this R-matrix. We show the reason why in the superintegrable case the eigenspace is degenerate, but not in the general case. We then show that the eigenspaces of special CSOS models descending from the chiral Potts model are also degenerate. The existence of an 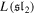 quantum loop algebra (or subalgebra) in these models is established by showing that the Serre relations hold for the generators. The highest weight polynomial (or the Drinfeld polynomial) of the representation is obtained by using the method of Baxter for the superintegrable case. As a byproduct, the eigenvalues of all such CSOS models are given explicitly.
quantum loop algebra (or subalgebra) in these models is established by showing that the Serre relations hold for the generators. The highest weight polynomial (or the Drinfeld polynomial) of the representation is obtained by using the method of Baxter for the superintegrable case. As a byproduct, the eigenvalues of all such CSOS models are given explicitly.
Manfred Opper et al 2016 J. Phys. A: Math. Theor. 49 114002
We consider the problem of solving TAP mean field equations by iteration for Ising models with coupling matrices that are drawn at random from general invariant ensembles. We develop an analysis of iterative algorithms using a dynamical functional approach that in the thermodynamic limit yields an effective dynamics of a single variable trajectory. Our main novel contribution is the expression for the implicit memory term of the dynamics for general invariant ensembles. By subtracting these terms, that depend on magnetizations at previous time steps, the implicit memory terms cancel making the iteration dependent on a Gaussian distributed field only. The TAP magnetizations are stable fixed points if a de Almeida–Thouless stability criterion is fulfilled. We illustrate our method explicitly for coupling matrices drawn from the random orthogonal ensemble.
Caterina De Bacco et al 2016 J. Phys. A: Math. Theor. 49 184003
Rare event statistics for random walks on complex networks are investigated using the large deviation formalism. Within this formalism, rare events are realised as typical events in a suitably deformed path-ensemble, and their statistics can be studied in terms of spectral properties of a deformed Markov transition matrix. We observe two different types of phase transition in such systems: (i) rare events which are singled out for sufficiently large values of the deformation parameter may correspond to localised modes of the deformed transition matrix; (ii) 'mode-switching transitions' may occur as the deformation parameter is varied. Details depend on the nature of the observable for which the rare event statistics is studied, as well as on the underlying graph ensemble. In the present paper we report results on rare events statistics for path averages of random walks in Erdős–Rényi and scale free networks. Large deviation rate functions and localisation properties are studied numerically. For observables of the type considered here, we also derive an analytical approximation for the Legendre transform of the large deviation rate function, which is valid in the large connectivity limit. It is found to agree well with simulations.
G Cigdem Yalcin et al 2016 J. Phys. A: Math. Theor. 49 154001
We analyse the probability densities of daily rainfall amounts at a variety of locations on Earth. The observed distributions of the amount of rainfall fit well to a q-exponential distribution with exponent q close to  . We discuss possible reasons for the emergence of this power law. In contrast, the waiting time distribution between rainy days is observed to follow a near-exponential distribution. A careful investigation shows that a q-exponential with
. We discuss possible reasons for the emergence of this power law. In contrast, the waiting time distribution between rainy days is observed to follow a near-exponential distribution. A careful investigation shows that a q-exponential with  yields the best fit of the data. A Poisson process where the rate fluctuates slightly in a superstatistical way is discussed as a possible model for this. We discuss the extreme value statistics for extreme daily rainfall, which can potentially lead to flooding. This is described by Fréchet distributions as the corresponding distributions of the amount of daily rainfall decay with a power law. Looking at extreme event statistics of waiting times between rainy days (leading to droughts for very long dry periods) we obtain from the observed near-exponential decay of waiting times extreme event statistics close to Gumbel distributions. We discuss superstatistical dynamical systems as simple models in this context.
yields the best fit of the data. A Poisson process where the rate fluctuates slightly in a superstatistical way is discussed as a possible model for this. We discuss the extreme value statistics for extreme daily rainfall, which can potentially lead to flooding. This is described by Fréchet distributions as the corresponding distributions of the amount of daily rainfall decay with a power law. Looking at extreme event statistics of waiting times between rainy days (leading to droughts for very long dry periods) we obtain from the observed near-exponential decay of waiting times extreme event statistics close to Gumbel distributions. We discuss superstatistical dynamical systems as simple models in this context.
Georg A Gottwald and Ian Melbourne 2016 J. Phys. A: Math. Theor. 49 174003
We present results on the broadband nature of the power spectrum  ,
,  , for a large class of nonuniformly expanding maps with summable and nonsummable decay of correlations. In particular, we consider a class of intermittent maps
, for a large class of nonuniformly expanding maps with summable and nonsummable decay of correlations. In particular, we consider a class of intermittent maps ![$f\;:[0,1]\to [0,1]$](https://content.cld.iop.org/journals/1751-8121/49/17/174003/revision1/jpaaa19efieqn3.gif) with
with  for
for 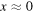 , where
, where 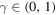 . Such maps have summable decay of correlations when
. Such maps have summable decay of correlations when  , and
, and  extends to a continuous function on
extends to a continuous function on ![$[0,2\pi ]$](https://content.cld.iop.org/journals/1751-8121/49/17/174003/revision1/jpaaa19efieqn9.gif) by the classical Wiener–Khintchine theorem. We show that
by the classical Wiener–Khintchine theorem. We show that  is typically bounded away from zero for Hölder observables. Moreover, in the nonsummable case
is typically bounded away from zero for Hölder observables. Moreover, in the nonsummable case 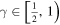 , we show that
, we show that  is defined almost everywhere with a continuous extension
is defined almost everywhere with a continuous extension 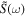 defined on
defined on 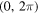 , and
, and 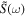 is typically nonvanishing.
is typically nonvanishing.
D Bombardelli et al 2016 J. Phys. A: Math. Theor. 49 320301
We introduce a series of articles reviewing various aspects of integrable models relevant to the anti-de Sitter (AdS)/conformal quantum field theory (CFT) correspondence. Topics covered in these reviews are: classical integrability, Yangian symmetry, factorized scattering, the Bethe ansatz, the thermodynamic Bethe ansatz, and integrable structures in (conformal) quantum field theory. In the present article we highlight how these concepts have found application in AdS/CFT, and provide a brief overview of the material contained in this series.
Otto G Berg et al 2016 J. Phys. A: Math. Theor. 49 364002
The helical structure of DNA imposes constraints on the rate of diffusion-limited protein binding. Here we solve the reaction–diffusion equations for DNA-like geometries and extend with simulations when necessary. We find that the helical structure can make binding to the DNA more than twice as fast compared to a case where DNA would be reactive only along one side. We also find that this rate advantage remains when the contributions from steric constraints and rotational diffusion of the DNA-binding protein are included. Furthermore, we find that the association rate is insensitive to changes in the steric constraints on the DNA in the helix geometry, while it is much more dependent on the steric constraints on the DNA-binding protein. We conclude that the helical structure of DNA facilitates the nonspecific binding of transcription factors and structural DNA-binding proteins in general.
Alexander Belavin and Vladimir Belavin 2016 J. Phys. A: Math. Theor. 49 41LT02
We compute the flat coordinates on the Frobenius manifolds arising on the deformation space of Gepner  chiral rings. The explicit form of the flat coordinates is important for exact solutions of models of topological CFT and 2D Liouville gravity. We describe the case k = 3, which is of particular interest because apart from the relevant chiral fields it contains a marginal one. Whereas marginal perturbations are relevant in different contexts, their analysis requires additional care compared to the relevant perturbations.
chiral rings. The explicit form of the flat coordinates is important for exact solutions of models of topological CFT and 2D Liouville gravity. We describe the case k = 3, which is of particular interest because apart from the relevant chiral fields it contains a marginal one. Whereas marginal perturbations are relevant in different contexts, their analysis requires additional care compared to the relevant perturbations.
Yunfeng Jiang et al 2016 J. Phys. A: Math. Theor. 49 454003
We develop analytical methods for computing the structure constant for three heavy operators, starting from the recently proposed hexagon approach. Such a structure constant is a semiclassical object, with the scale set by the inverse length of the operators playing the role of the Planck constant. We reformulate the hexagon expansion in terms of multiple contour integrals and recast it as a sum over clusters generated by the residues of the measure of integration. We test the method on two examples. First, we compute the semi-classical limit of the asymptotic three-point function of heavy operators at any coupling and show that it reproduces part of the results at strong coupling. Second, in the case of one non-BPS and two BPS operators at strong coupling we sum up all wrapping corrections associated with the opposite bridge to the non-trivial operator, or the 'bottom' mirror channel. We also give an alternative interpretation of the results in terms of a gas of fermions and show that they can be expressed compactly as an operator-valued super-determinant.
 as a quantum double
as a quantum double
Niklas Beisert et al 2016 J. Phys. A: Math. Theor. 49 434005
We derive the universal R-matrix of the quantum-deformed enveloping algebra of centrally extended  using Drinfeld's quantum double construction. We are led to enlarging the algebra by additional generators corresponding to an
using Drinfeld's quantum double construction. We are led to enlarging the algebra by additional generators corresponding to an  automorphism. For this maximally extended algebra we construct a consistent Hopf algebra structure where the extensions exhibit several uncommon features. We determine the corresponding universal R-matrix containing some non-standard functions. Curiously, this Hopf algebra has one extra deformation parameter for which the R-matrix does not factorize into products of exponentials.
automorphism. For this maximally extended algebra we construct a consistent Hopf algebra structure where the extensions exhibit several uncommon features. We determine the corresponding universal R-matrix containing some non-standard functions. Curiously, this Hopf algebra has one extra deformation parameter for which the R-matrix does not factorize into products of exponentials.
Ben Hoare and Stijn J van Tongeren 2016 J. Phys. A: Math. Theor. 49 434006
We consider various homogeneous Yang–Baxter deformations of the  superstring that can be obtained from the η-deformed superstring and related models by singular boosts. The jordanian deformations we obtain in this way behave similarly to the η-deformed model with regard to supergravity: T dualizing the classical sigma model it is possible to find corresponding solutions of supergravity, which, however, have dilatons that prevent T dualizing back. Hence the backgrounds of these jordanian deformations are not solutions of supergravity. Still, they do satisfy a set of recently found modified supergravity equations which implies that the corresponding sigma models are scale invariant. The abelian models that we obtain by singular boosts do directly correspond to solutions of supergravity. In addition to our main results we consider contraction limits of our main example, which do correspond to supergravity solutions.
superstring that can be obtained from the η-deformed superstring and related models by singular boosts. The jordanian deformations we obtain in this way behave similarly to the η-deformed model with regard to supergravity: T dualizing the classical sigma model it is possible to find corresponding solutions of supergravity, which, however, have dilatons that prevent T dualizing back. Hence the backgrounds of these jordanian deformations are not solutions of supergravity. Still, they do satisfy a set of recently found modified supergravity equations which implies that the corresponding sigma models are scale invariant. The abelian models that we obtain by singular boosts do directly correspond to solutions of supergravity. In addition to our main results we consider contraction limits of our main example, which do correspond to supergravity solutions.
S Hassani et al 2016 J. Phys. A: Math. Theor. 49 164003
We previously reported on a recursive method to generate the expansion of the lattice Green function (LGF) of the d-dimensional face-centered cubic lattice (fcc). The method was used to generate many coefficients for  and the corresponding linear differential equation has been obtained. In this paper, we show the strength and the limit of the method by producing the series and the corresponding linear differential equations for
and the corresponding linear differential equation has been obtained. In this paper, we show the strength and the limit of the method by producing the series and the corresponding linear differential equations for  . The differential Galois groups of these linear differential equations are shown to be symplectic for
. The differential Galois groups of these linear differential equations are shown to be symplectic for  and orthogonal for
and orthogonal for  . The recursion relation naturally provides a two-dimensional array
. The recursion relation naturally provides a two-dimensional array  where only the coefficients
where only the coefficients  correspond to the coefficients of the LGF of the
correspond to the coefficients of the LGF of the 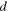 -dimensional fcc. The coefficients
-dimensional fcc. The coefficients 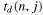 are associated to
are associated to  -finite bivariate series annihilated by linear partial differential equations that we analyze.
-finite bivariate series annihilated by linear partial differential equations that we analyze.
M L Glasser 2016 J. Phys. A: Math. Theor. 49 454004
The Fourier transforms of  and
and 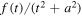 are shown to be related in terms of a Fredholm integral equation. Several examples are discussed.
are shown to be related in terms of a Fredholm integral equation. Several examples are discussed.
Topical reviews
Show article list
Denis S Grebenkov et al 2016 J. Phys. A: Math. Theor. 49 043001
We revise the Lévy construction of Brownian motion as a simple though rigorous approach to operate with various Gaussian processes. A Brownian path is explicitly constructed as a linear combination of wavelet-based 'geometrical features' at multiple length scales with random weights. Such a wavelet representation gives a closed formula mapping of the unit interval onto the functional space of Brownian paths. This formula elucidates many classical results about Brownian motion (e.g., non-differentiability of its path), providing an intuitive feeling for non-mathematicians. The illustrative character of the wavelet representation, along with the simple structure of the underlying probability space, is different from the usual presentation of most classical textbooks. Similar concepts are discussed for the Brownian bridge, fractional Brownian motion, the Ornstein-Uhlenbeck process, Gaussian free fields, and fractional Gaussian fields. Wavelet representations and dyadic decompositions form the basis of many highly efficient numerical methods to simulate Gaussian processes and fields, including Brownian motion and other diffusive processes in confining domains.
Alexander Nepomnyashchy and Sergey Shklyaev 2016 J. Phys. A: Math. Theor. 49 053001
The main subject of the present review is longwave oscillatory patterns in systems with conservation laws, that cannot be described by the complex Ginzburg–Landau equation. As basic examples, we consider nonlinear patterns created by Marangoni and buoyancy instabilities in pure and binary liquids, where the longwave nature of instabilities is related to conservation of the liquid volume, conservation of mass or approximate conservation of the mean temperature. Also, we discuss the excitation of longwave instabilities by a time-periodic parameter modulation.
Teiko Heinosaari et al 2016 J. Phys. A: Math. Theor. 49 123001
In the context of a physical theory, two devices, A and B, described by the theory are called incompatible if the theory does not allow the existence of a third device C that would have both A and B as its components. Incompatibility is a fascinating aspect of physical theories, especially in the case of quantum theory. The concept of incompatibility gives a common ground for several famous impossibility statements within quantum theory, such as 'no-cloning' and 'no information without disturbance'; these can be all seen as statements about incompatibility of certain devices. The purpose of this paper is to give a concise overview of some of the central aspects of incompatibility.
John Goold et al 2016 J. Phys. A: Math. Theor. 49 143001
This topical review article gives an overview of the interplay between quantum information theory and thermodynamics of quantum systems. We focus on several trending topics including the foundations of statistical mechanics, resource theories, entanglement in thermodynamic settings, fluctuation theorems and thermal machines. This is not a comprehensive review of the diverse field of quantum thermodynamics; rather, it is a convenient entry point for the thermo-curious information theorist. Furthermore this review should facilitate the unification and understanding of different interdisciplinary approaches emerging in research groups around the world.
Angnis Schmidt-May and Mikael von Strauss 2016 J. Phys. A: Math. Theor. 49 183001
This review is dedicated to recent progress in the field of classical, interacting, massive spin-2 theories, with a focus on ghost-free bimetric theory. We will outline its history and its development as a nontrivial extension and generalisation of nonlinear massive gravity. We present a detailed discussion of the consistency proofs of both theories, before we review Einstein solutions to the bimetric equations of motion in vacuum as well as the resulting mass spectrum. We introduce couplings to matter and then discuss the general relativity and massive gravity limits of bimetric theory, which correspond to decoupling the massive or the massless spin-2 field from the matter sector, respectively. More general classical solutions are reviewed and the present status of bimetric cosmology is summarised. An interesting corner in the bimetric parameter space which could potentially give rise to a nonlinear theory for partially massless spin-2 fields is also discussed. Relations to higher-curvature theories of gravity are explained and finally we give an overview of possible extensions of the theory and review its formulation in terms of vielbeins.
E Orlandini and S G Whittington 2016 J. Phys. A: Math. Theor. 49 343001
When a polymer molecule is subjected to a force (such as a tensile force) it responds and this response gives information about the thermodynamics and structural properties of the polymer. In recent years there have been a number of experimental developments, such as atomic force microscopy and optical tweezers, that allow individual polymer molecules to be pulled in various ways. This has resulted in a renewed theoretical interest in how polymers respond to applied forces. This review will focus on some particular aspects of this field. We shall be primarily interested in tensile forces and consider various scenarios, such as pulling an adsorbed polymer from a surface and pulling a polymer from one phase to another. In order to make theoretical progress one needs a model of the polymer and we shall focus on lattice models. Our emphasis will be on exactly solvable models such as Dyck and Motzkin paths, and on rigorous results for self-avoiding walk models and some relatives, though we shall also discuss scaling theories and some selected numerical results.
Gerardo Adesso et al 2016 J. Phys. A: Math. Theor. 49 473001
Quantum information theory is built upon the realisation that quantum resources like coherence and entanglement can be exploited for novel or enhanced ways of transmitting and manipulating information, such as quantum cryptography, teleportation, and quantum computing. We now know that there is potentially much more than entanglement behind the power of quantum information processing. There exist more general forms of non-classical correlations, stemming from fundamental principles such as the necessary disturbance induced by a local measurement, or the persistence of quantum coherence in all possible local bases. These signatures can be identified and are resilient in almost all quantum states, and have been linked to the enhanced performance of certain quantum protocols over classical ones in noisy conditions. Their presence represents, among other things, one of the most essential manifestations of quantumness in cooperative systems, from the subatomic to the macroscopic domain. In this work we give an overview of the current quest for a proper understanding and characterisation of the frontier between classical and quantum correlations (QCs) in composite states. We focus on various approaches to define and quantify general QCs, based on different yet interlinked physical perspectives, and comment on the operational significance of the ensuing measures for quantum technology tasks such as information encoding, distribution, discrimination and metrology. We then provide a broader outlook of a few applications in which quantumness beyond entanglement looks fit to play a key role.
Hamid Teimouri and Anatoly B Kolomeisky 2016 J. Phys. A: Math. Theor. 49 483001
The formation and growth of multi-cellular organisms and tissues from several genetically identical embryo cells is one of the most fundamental natural phenomena. These processes are stimulated and governed by multiple biological signaling molecules, which are also called morphogens. Embryo cells are able to read and pass genetic information by measuring the non-uniform concentration profiles of signaling molecules. It is widely believed that the establishment of concentration profiles of morphogens, commonly referred as morphogen gradients, is a result of complex biophysical and biochemical processes that might involve diffusion and degradation of locally produced signaling molecules. In this review, we discuss various theoretical aspects of the mechanisms for morphogen gradient formation, including stationary and transient dynamics, the effect of source delocalization, diffusion, different degradation mechanisms, and the role of spatial dimensions. Theoretical predictions are compared with experimental observations. In addition, we analyze the potential alternative mechanisms of the delivery of biological signals in embryo cells and tissues. Current challenges in understanding the mechanisms of morphogen gradients and future directions are also discussed.