Introduction
Published December 2017
•
Copyright © 2017 Morgan & Claypool Publishers
Pages 1-1 to 1-3
You need an eReader or compatible software to experience the benefits of the ePub3 file format.
Download complete PDF book, the ePub book or the Kindle book
Abstract
In Chapter 1 the statement of the problem is given and the results are described.
Introduction
Our method for creating materials with a desired refraction coefficient consists of
distributing many small impedance particles with prescribed boundary impedance. Let us
define first the notion of the refraction coefficient. Let  be a wave field satisfying the equation
be a wave field satisfying the equation
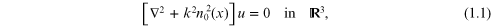
where  is the three-dimensional space,
is the three-dimensional space,  ,
,  is a wave number.
is a wave number.
The coefficient  is called the refraction coefficient of the
medium.
is called the refraction coefficient of the
medium.
We assume that
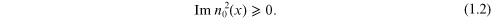
Physically, this means that the medium does not produce energy. We assume
that outside of an arbitrary large but fixed area, for example, a ball  ,
,  .
.
The basic question is:
Suppose  is the refraction coefficient of some material in
is the refraction coefficient of some material in  . How many particles of the characteristic dimension a
and the boundary impedance
. How many particles of the characteristic dimension a
and the boundary impedance  should be distributed in BR
in order to get a new material in BR
with the desired refraction coefficient
should be distributed in BR
in order to get a new material in BR
with the desired refraction coefficient  ?
?
The wavelength  in the medium with the refraction coefficient
in the medium with the refraction coefficient  can be calculated by the formula
can be calculated by the formula  . The smallness of a particle of the characteristic dimension
a is described by the relation
. The smallness of a particle of the characteristic dimension
a is described by the relation
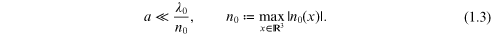
Wave scattering by the impedance particles in a medium is described by the equations
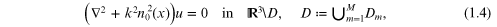

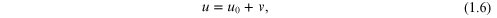

Here  is the incident field. It satisfies the equation:
is the incident field. It satisfies the equation:
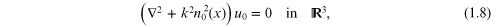
the dependence on k is dropped since  is constant, v is the scattered field,
Dm
is mth small particle, Sm
is its sufficiently smooth boundary (surface), N is a unit
normal to Sm
pointing out of Dm
,
is constant, v is the scattered field,
Dm
is mth small particle, Sm
is its sufficiently smooth boundary (surface), N is a unit
normal to Sm
pointing out of Dm
,  is the boundary impedance of Dm
, Im
is the boundary impedance of Dm
, Im  , M is the number of small particles. For simplicity
only we assume in what follows that
, M is the number of small particles. For simplicity
only we assume in what follows that  . In a separate section at the end of this book we explain why this
assumption is not important for our theory.
. In a separate section at the end of this book we explain why this
assumption is not important for our theory.
An important physical quantity d is defined as the minimal distance between neighboring particles

Let us assume that
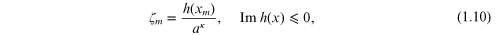
where  ,
,  is a continuous function in BR
,
is a continuous function in BR
,  is a number,
is a number,  .
.
The distribution of the small particles is described by the function
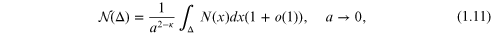
where  is an arbitrary open set,
is an arbitrary open set,  is a continuous function,
is a continuous function,  is the number of small particles in Δ. In particular,
is the number of small particles in Δ. In particular,
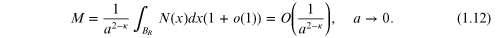
We prove that if the small particles are distributed by the law equation
(1.11), then
one can choose  that is boundary impedances, so that the solution to the many-body
scattering problem has a limit u, as
that is boundary impedances, so that the solution to the many-body
scattering problem has a limit u, as  , and this u solves the equation
, and this u solves the equation
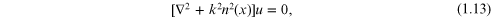
where the refraction coefficient  can be an arbitrary function satisfying the condition Im
can be an arbitrary function satisfying the condition Im  . Moreover, the limiting function
. Moreover, the limiting function  will be calculated explicitly:
will be calculated explicitly:

the constant c is defined by the formula
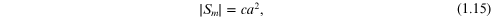
where  is the surface area of Sm
,
is the surface area of Sm
,  is the function from equation (1.10) and
is the function from equation (1.10) and  is the function from equation (1.11).
is the function from equation (1.11).
Our basic physical assumption is
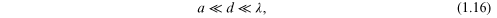
where d is defined in equation (1.9) and  . Assumption equation (1.16) means that multiple scattering is
essential: one cannot assume that the field acting on a particle Dm
is the incident field u0.
. Assumption equation (1.16) means that multiple scattering is
essential: one cannot assume that the field acting on a particle Dm
is the incident field u0.
From equation (1.14) it is already clear that if  can be chosen arbitrarily with Im
can be chosen arbitrarily with Im  then
then  can be obtained fairly arbitrarily.
can be obtained fairly arbitrarily.
In chapter 2 our theory of many-body wave scattering is presented for small impedance particles and formulas equations (1.13) and (1.14) are derived.
In chapter 3 a recipe for creating materials with a desired refraction coefficient is formulated and justified theoretically.
In chapter 4 we will discuss creating wave-focusing materials. These are materials such that a plane wave, scattered by such material, has a desired radiation pattern.
In chapter 5 some inverse scattering problems with non-over-determined scattering data are studied.
