Introduction
Published November 2015
•
Copyright © IOP Publishing Ltd 2015
Pages 1-1 to 1-27
You need an eReader or compatible software to experience the benefits of the ePub3 file format.
Download complete PDF book or the ePub book
Abstract
An introduction to many of the concepts that are central to the subject matter of this book. The topics include a preliminary survey of the different waves or excitations in solids, along with a brief discussion of their linear and nonlinear dynamical properties, some examples of the low-dimensional structures and arrays that will be of importance for later applications and also the experimental and theoretical techniques that are needed as tools in this study.
In this chapter we will introduce many of the concepts that are central to the subject matter of this book. The topics will include a preliminary survey of the different waves or excitations in solids, along with a brief discussion of their linear and nonlinear (NL) dynamical properties, some examples of the low-dimensional structures and arrays that will be of importance for later applications and also the experimental and theoretical techniques that will be needed as tools in this study.
We will be less concerned here with the static, or time-independent, behaviour of solids and instead focus on the temporal (and usual spatial) evolution of some characteristic property that can propagate through a solid or be localized in certain regions. Corresponding to the latter case the excitations mentioned above can be considered as just the wave-like Fourier components of a general propagating signal in the solid. Physically the signal might, for example, consist of optical waves, vibrations of the atoms in the solid, the fluctuating magnetization in a magnetic material, or the collective motion of charges in a plasma. In a finite-sized solid the excitations will be required to satisfy boundary conditions at the surfaces or interfaces and so their properties may become modified. The novel properties of the excitations in certain finite structures, sometimes taken in conjunction with their NL dynamics as explained later, are of fundamental interest scientifically and may lead to a wide variety of practical device applications.
1.1. Types of excitations or waves
1.1.1. Fundamentals of excitations
We start by briefly describing the 'bulk' (or 'volume') excitations that are characteristic of effectively unbounded solids, where there are no surface effects to be taken into account. Details may be found in standard textbooks on solid-state physics (see, e.g., Kittel [1], Ashcroft and Mermin [2], and Grosso and Parravicini [3]). The modifying effects of surfaces and interfaces will be introduced next by following, for example, an approach based on symmetry arguments adopted for geometries of thin films and multilayers as in the book by Cottam and Tilley [4]. From a consideration of the symmetry and crystal lattices we shall arrive, via reciprocal lattices and Brillouin zones, at a form of Bloch's theorem for the elementary excitations.
A bulk crystalline solid may be regarded as a three-dimensional (3D)
repetition in space of a basis or building block
consisting of one or more atoms. The basis can be associated with the
points on an infinitely extended lattice, which may be defined from
symmetry in terms of three fundamental non-coplanar translational
vectors, denoted by 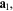
 and
and  It then follows that the vector R
connecting any two lattice points can be expressed as
It then follows that the vector R
connecting any two lattice points can be expressed as
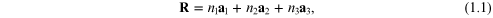
where n1, n2 and n3 take any integer values. Of course, the lattice may have
other symmetry operations, such as rotations and reflections, that also
leave the space lattice unchanged. We will see that the translations are
particularly important and they imply that any physical quantity  at a general position r in the system
satisfies
at a general position r in the system
satisfies

for any R given by equation (1.1). Depending on the context, the quantity f(r) might refer to a component of the magnetization vector or a charge density, for example.
The unit cell of a lattice is just the smallest volume
with the property that all space can be filled by periodic repetitions
of the unit cell for each lattice. Its specification is not unique, but
one simple choice is the parallelepiped formed by the basic vectors 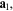
 and
and  Another construction is the
Wigner–Seitz unit cell formed by drawing the
perpendicular bisecting planes of the lattice vectors from any chosen
lattice point to its neighbouring sites. Details are given in, e.g.,
[1–3]. Some choices of unit cell are shown in figure 1.1 for the
special case of a two-dimensional (2D) oblique lattice with the basic
vectors
Another construction is the
Wigner–Seitz unit cell formed by drawing the
perpendicular bisecting planes of the lattice vectors from any chosen
lattice point to its neighbouring sites. Details are given in, e.g.,
[1–3]. Some choices of unit cell are shown in figure 1.1 for the
special case of a two-dimensional (2D) oblique lattice with the basic
vectors  and
and 
Figure 1.1. An oblique 2D space lattice with the basic vectors  and
and 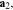 showing two choices for the unit cell. The one
on the left is a parallepiped and the Wigner–Seitz cell is
illustrated on the right.
showing two choices for the unit cell. The one
on the left is a parallepiped and the Wigner–Seitz cell is
illustrated on the right.
Download figure:
Standard image High-resolution imageThe next step is to introduce the reciprocal lattice.
The basic vectors 
 and
and  of this lattice in reciprocal space have the
properties in 3D that
of this lattice in reciprocal space have the
properties in 3D that
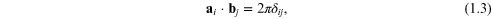
where i and j can take
values 1, 2 or 3, and  is the Kronecker delta (equal to unity if the
subscripts have the same value and zero otherwise). For example, we may
write
is the Kronecker delta (equal to unity if the
subscripts have the same value and zero otherwise). For example, we may
write  =
=  and so forth, with
and so forth, with 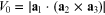 denoting the volume of the unit cell for the space
lattice (see, e.g., [1]). Since
denoting the volume of the unit cell for the space
lattice (see, e.g., [1]). Since  introduced in equation (1.2) is a periodic function
(generally in 3D) it can be expressed in terms of a Fourier series using
complex exponentials as
introduced in equation (1.2) is a periodic function
(generally in 3D) it can be expressed in terms of a Fourier series using
complex exponentials as
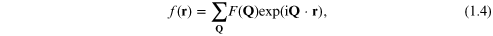
where the Q vectors are required to satisfy 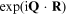 = 1. It is easily shown [1] that they are expressible
in terms of the basic vectors of the reciprocal lattice as
= 1. It is easily shown [1] that they are expressible
in terms of the basic vectors of the reciprocal lattice as
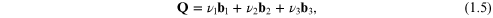
with 
 and
and  denoting integers. Finally we note that the unit cell
of the reciprocal lattice is known as the Brillouin
zone. The results are particularly straightforward in the
case of a simple-cubic (sc) space lattice with lattice parameter
a, because the reciprocal lattice is also sc. We
may choose for the space lattice
denoting integers. Finally we note that the unit cell
of the reciprocal lattice is known as the Brillouin
zone. The results are particularly straightforward in the
case of a simple-cubic (sc) space lattice with lattice parameter
a, because the reciprocal lattice is also sc. We
may choose for the space lattice
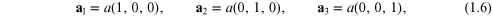
whereupon the basic vectors of the reciprocal lattice are simply
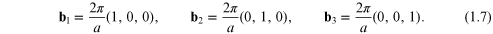
Now we discuss how the translational symmetries of the
space and reciprocal lattices influence the elementary excitations in an
unbounded solid. The most fundamental result is embodied in
Bloch's theorem [5], which
provides information about the spatial behaviour of the variable that
describes the amplitude of the excitations. This variable, which we will
denote generically as a function of position as  depends on the type of excitation. For example, it
could be the quantum-mechanical wave function in the case of electronic
states, an atomic displacement in the case of lattice vibrations (or
phonons), or the fluctuating magnetization in the case of spin waves
(SWs) (or magnons). These and other specific examples will be discussed
in more depth in later chapters after we consider some general
properties here. Bloch's theorem can be expressed generally
as
depends on the type of excitation. For example, it
could be the quantum-mechanical wave function in the case of electronic
states, an atomic displacement in the case of lattice vibrations (or
phonons), or the fluctuating magnetization in the case of spin waves
(SWs) (or magnons). These and other specific examples will be discussed
in more depth in later chapters after we consider some general
properties here. Bloch's theorem can be expressed generally
as
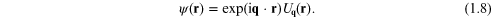
Here is a periodic amplitude function, just as in equation
(1.2), and the phase factor
is a periodic amplitude function, just as in equation
(1.2), and the phase factor 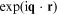 describes a plane-wave variation of the amplitude
describes a plane-wave variation of the amplitude  We shall not provide a proof of this result, since
this can be found in the solid-state physics textbooks cited earlier.
The wave vector
We shall not provide a proof of this result, since
this can be found in the solid-state physics textbooks cited earlier.
The wave vector  is evidently not unique, since it can be easily
checked that values differing by any reciprocal lattice
is evidently not unique, since it can be easily
checked that values differing by any reciprocal lattice  as defined in equation (1.5) will equally satisfy
the requirements of Bloch's theorem. Typically, as we will see later, an
energy eigenvalue E will be calculated for the dynamic
variable
as defined in equation (1.5) will equally satisfy
the requirements of Bloch's theorem. Typically, as we will see later, an
energy eigenvalue E will be calculated for the dynamic
variable  using its equation of motion, e.g., in the case of an
electronic excitation
using its equation of motion, e.g., in the case of an
electronic excitation  could be the spatial wave function which satisfies
Schrödinger's equation. On writing E =
could be the spatial wave function which satisfies
Schrödinger's equation. On writing E =  with
with  representing the angular frequency of the excitation,
it follows that we must have
representing the angular frequency of the excitation,
it follows that we must have
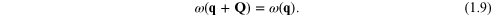
In the idealized case of an unbounded crystal lattice the
components of the vector q can take any real values, but
equation (1.9) tells us that it is sufficient to take only
q values that lie within the first Brillouin zone (the
Wigner–Seitz cell centred at q = 0). For the example of an
sc space lattice mentioned earlier this gives  =
=  with
with
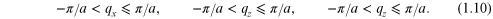
There are analogous results to equations (1.6), (1.7) and (1.10) for other 3D space lattices [1], such as body-centred cubic (bcc) and face-centred cubic (fcc) lattices.
While there are many 3D space lattices, there are relatively few in 2D.
In fact, there are only five instead of fourteen. As we will see later,
these 2D lattices will be important for thin films where there is
translational symmetry in the 2D planes of atoms parallel to the
surfaces, but not in the other dimension perpendicular to the surfaces.
Consequently Bloch's theorem will be modified, as we discuss later. A 2D
example, which is currently of considerable interest, is provided by
graphene, which can be produced in the form of
single sheets of atoms arranged in a 2D hexagonal or honeycomb space
lattice (see, e.g., [6, 7]). The lattice structure
is illustrated in figure 1.2 and it can be described
in terms of two vectors  and
and  that form the basis of a unit cell with two carbon
atoms per cell. There are two sublattices of carbon atoms, labelled
A and B, as shown. Relative to the
x- and y-coordinate axes we may
write
that form the basis of a unit cell with two carbon
atoms per cell. There are two sublattices of carbon atoms, labelled
A and B, as shown. Relative to the
x- and y-coordinate axes we may
write
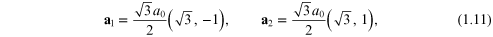
where  denotes the nearest-neighbour carbon–carbon distance.
Also the basic vectors of the reciprocal lattice are simply [7]
denotes the nearest-neighbour carbon–carbon distance.
Also the basic vectors of the reciprocal lattice are simply [7]

Figure 1.2. The spatial structure of a single sheet of graphene. Each carbon
atom lies on one of two interpenetrating sublattices labelled
A and B (shown here as red
and blue circles, respectively). A possible choice for the two
basic lattice vectors  and
and  is indicated, together with the corresponding
unit cell (shown shaded).
is indicated, together with the corresponding
unit cell (shown shaded).
Download figure:
Standard image High-resolution imageIn some other nanosystems to be considered later we might have just one direction in which there is a translational symmetry. For example, long nanowires and nanotubes that have a uniform, finite cross-sectional shape will exhibit translational symmetry with respect to their length coordinate only. Also one-dimensional (1D) linear-chain materials (such as the ferromagnetic chain pyroxene NaCrGe2O6 [8]) will have this property. By contrast, nanostructures that are finite in all three spatial dimensions will display no translational symmetry and are sometimes referred to as being zero-dimensional (0D).
1.1.2. Linear and nonlinear dynamics for excitations
Before looking further into the influence of the geometric structure on the excitations, it is useful to briefly consider how the excitations relate to the linear and NL aspects of the system dynamics. Although real physical systems might exhibit linear dynamics to a good approximation in many circumstances, it is nevertheless the case that NL behaviour will occur to some extent and may be enhanced under particular circumstances. It is to be expected that the excitations associated with the linear regime will consequently have their properties modified when nonlinearities are taken into account. It is important to enquire in what ways and to what degree this takes place and if there are practical effects to be utilized. Apart from this, we will find that there are some excitations associated with the NL regime of behaviour that have no counterpart in the linear approximation.
At this preliminary stage we will highlight some distinctions between the linear and NL dynamics of excitations, mainly by taking a few specific examples. These and other cases will then be explored in much more detail later, especially in chapter 7. Some general references covering NL dynamical phenomena, mostly for bulk properties, are the books by Yariv [9], Butcher and Cotter [10] and Mills [11] for NL optical materials and by Gurevich and Melkov [12] and Stancil and Prabakhar [13] for NL magnetic materials.
We start by considering an example of optical (electromagnetic) waves in
a dielectric material, ignoring for the moment any specifically magnetic
effects. The material is assumed to be homogeneous and sufficiently
large that we need not explicitly take account of boundary effects. The
response of the material to an external position- and time-dependent
electric field  is conventionally described in terms of a dielectric
function ε by writing
is conventionally described in terms of a dielectric
function ε by writing
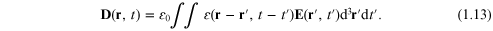
Here  is the permittivity of free space and
is the permittivity of free space and  is the electric displacement (see, e.g., [14, 15]). The
D and E vectors are also related to the
polarization P in the material by
is the electric displacement (see, e.g., [14, 15]). The
D and E vectors are also related to the
polarization P in the material by
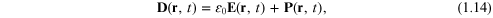
where  is the polarization induced in the material. Rather
than considering these quantities in terms of position and time, it is
more useful for the dynamics to make Fourier transforms to a wave vector
is the polarization induced in the material. Rather
than considering these quantities in terms of position and time, it is
more useful for the dynamics to make Fourier transforms to a wave vector  and angular frequency ω according to,
for example,
and angular frequency ω according to,
for example,
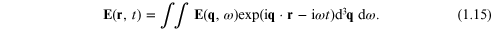
Then equation (1.13) can be re-expressed more compactly and conveniently as
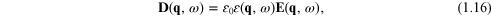
while the corresponding result for the polarization is
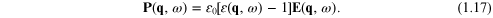
The q-dependence of the dielectric function
in the above two equations is known as spatial
dispersion and arises from the fact that the dielectric
term in equation (1.13) depends on the
spatial separation 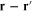 rather than on r and
rather than on r and  separately. However, in many cases this spatial
dispersion may vanish or be negligible and we have simply a
frequency-dependent dielectric function
separately. However, in many cases this spatial
dispersion may vanish or be negligible and we have simply a
frequency-dependent dielectric function  that is characteristic of the dynamical processes in
the material being considered. Examples will be given later.
that is characteristic of the dynamical processes in
the material being considered. Examples will be given later.
Before going any further we need to elaborate on two points regarding the
above discussion. The first is that, in general, the vectors
D and P may not necessarily be collinear
with E. The above relationships are still applicable
provided the scalar dielectric function,  or
or 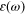 as appropriate, is replaced by a second-rank tensor or
equivalently a matrix in these cases. The second and more significant
point is that for small values of the electric field there is a
linear relationship, as expressed by equation
(1.16), between D and E. In other
words,
as appropriate, is replaced by a second-rank tensor or
equivalently a matrix in these cases. The second and more significant
point is that for small values of the electric field there is a
linear relationship, as expressed by equation
(1.16), between D and E. In other
words,  is a constant function that does not depend on
E and it is called the linear dielectric
function. At larger electric-field values there is usually
a NL regime in which the dielectric function becomes
dependent on E. A conventional approach in NL optics is to
expand the dielectric function as a power series in terms of components
of the electric-field components, as we describe in a later chapter.
Various different NL effects can then be identified depending on which
terms in the expansion are important. For example, the Kerr-type
nonlinearity involves an effective NL dielectric function
[10,
11]
of the form
is a constant function that does not depend on
E and it is called the linear dielectric
function. At larger electric-field values there is usually
a NL regime in which the dielectric function becomes
dependent on E. A conventional approach in NL optics is to
expand the dielectric function as a power series in terms of components
of the electric-field components, as we describe in a later chapter.
Various different NL effects can then be identified depending on which
terms in the expansion are important. For example, the Kerr-type
nonlinearity involves an effective NL dielectric function
[10,
11]
of the form
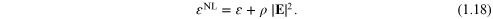
Here both the linear part  and the
coefficient ρ before the field-dependent term may, in
general, be functions of wave vector
and the
coefficient ρ before the field-dependent term may, in
general, be functions of wave vector  and frequency ω.
and frequency ω.
To probe further some distinctions between the linear and NL dynamics arising due to the form of the dielectric function, we now turn to the basic equation satisfied by the electric field. This is just the electromagnetic wave equation arising from Maxwell's equations [14, 15]:
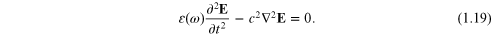
This result is the form appropriate for a transverse wave (i.e., when the
wave vector  specifying the propagation direction is perpendicular
to
specifying the propagation direction is perpendicular
to  ) and c is the velocity of light in a
vacuum. We note that the solution of this equation in the linear regime
is relatively straightforward, because the linear dielectric function
does not depend on
) and c is the velocity of light in a
vacuum. We note that the solution of this equation in the linear regime
is relatively straightforward, because the linear dielectric function
does not depend on  and so equation (1.19) is a linear
differential equation. We are ignoring spatial dispersion here. The
solution in this case where we assume an unbounded medium can be found
in a plane-wave
and so equation (1.19) is a linear
differential equation. We are ignoring spatial dispersion here. The
solution in this case where we assume an unbounded medium can be found
in a plane-wave ![$\mathrm{exp}[{\rm{i}}({\bf{q}}\cdot {\bf{r}}-\omega t)]$](https://content.cld.iop.org/books/10__1088_978-0-7503-1054-3/revision2/bk978-0-7503-1054-3ch1ieqn88.gif) form, yielding
form, yielding

This is just the implicit dispersion relation (ω versus
q relationship) arising when the electromagnetic
wave is coupled to the polarization field of the medium. The excitation
is generally referred to as a polariton. If the
dielectric function is just a constant and written as  where n is the refractive index of
the medium, we recover the usual dispersion relation ω
=
where n is the refractive index of
the medium, we recover the usual dispersion relation ω
= 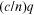 for a photon (light) with speed
c/n in the medium. By contrast, a
simple example of a frequency-dependent dielectric function occurs for
an electron plasma, as for the gas of electrons in a metal or
semiconductor in the presence of positive ions that ensure the overall
charge neutrality. The plasma oscillations [1, 2] of the electron gas are
known to define a characteristic angular frequency, the plasma frequency
for a photon (light) with speed
c/n in the medium. By contrast, a
simple example of a frequency-dependent dielectric function occurs for
an electron plasma, as for the gas of electrons in a metal or
semiconductor in the presence of positive ions that ensure the overall
charge neutrality. The plasma oscillations [1, 2] of the electron gas are
known to define a characteristic angular frequency, the plasma frequency  given by
given by 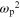 =
=  where n0 is the 3D concentration of electrons, each having mass
m and charge
where n0 is the 3D concentration of electrons, each having mass
m and charge  It can be shown (see also chapter 4)
that
It can be shown (see also chapter 4)
that
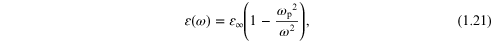
where  is the limiting dielectric constant at frequencies
well above
is the limiting dielectric constant at frequencies
well above  and damping has been neglected. Substituting this into
the expression in equation (1.20) and rearranging gives
the plasmon-polariton dispersion relation explicitly as
and damping has been neglected. Substituting this into
the expression in equation (1.20) and rearranging gives
the plasmon-polariton dispersion relation explicitly as
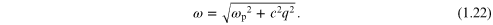
This simple dispersion relation is drawn as the solid
line in figure 1.3. We have also included for comparison the dashed line  which corresponds to the light line for propagation in
a vacuum. There are two limiting regions of interest for the polariton.
One is for
which corresponds to the light line for propagation in
a vacuum. There are two limiting regions of interest for the polariton.
One is for 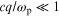 when
when  and the other is for
and the other is for  when
when  There is also a band gap of forbidden frequencies
where no plasmon-polaritons exist and this occurs here in the frequency
range from 0 to
There is also a band gap of forbidden frequencies
where no plasmon-polaritons exist and this occurs here in the frequency
range from 0 to 
Figure 1.3. Dispersion relation for a linear plasmon-polariton (solid line)
in a 3D material, as given by equation (1.22). The angular frequency, in terms of
dimensionless 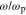 is plotted versus dimensionless wavenumber, in
terms of
is plotted versus dimensionless wavenumber, in
terms of 
Download figure:
Standard image High-resolution imageThe above discussion relates to an example of a bulk (or volume) excitation, since no account has been taken of any surface or boundary and the linear excitation propagates (or is wave-like) in all three spatial dimensions. Other linear types of polaritons may occur that are associated with surfaces and interfaces, and this behaviour will be one of the main topics in chapter 5.
We discussed earlier how NL effects could arise, for example, through a
Kerr-type form of the dielectric function, as in equation (1.18). Before concluding this section we will outline a case
of a NL polariton due to this term; more details will be given in
chapter 7
(but see also [4]). This example is related to the phenomenon known as
self-guiding and can occur for polaritons at an
interface (see [16, 17] for reviews). We start with a qualitative description by
recalling that within linear optics the guiding condition for a light
wave to remain localized (through multiple internal reflections) within
a film is that the refractive index of the film should exceed the
refractive index of the bounding medium on each side [14, 15]. It
might therefore be expected that, provided (i) ε and
ρ in equation (1.18) are both positive and
(ii) the electric-field term  can be localized with a large value near a surface,
the situation will be broadly analogous to a guiding film with a large
refractive index. The above conditions can, in fact, be realized as we
now demonstrate by considering an interface between a linear medium and
a Kerr NL medium.
can be localized with a large value near a surface,
the situation will be broadly analogous to a guiding film with a large
refractive index. The above conditions can, in fact, be realized as we
now demonstrate by considering an interface between a linear medium and
a Kerr NL medium.
Specifically we will assume that the NL medium fills the lower half-space  while a linear medium occupies the upper half-space
while a linear medium occupies the upper half-space  The interface between them corresponds to the plane
z = 0 and the system is assumed to be infinite in
the x- and y-coordinate directions. We
look for solutions for which the electric field is a s-polarized wave,
which means that it can be written as
The interface between them corresponds to the plane
z = 0 and the system is assumed to be infinite in
the x- and y-coordinate directions. We
look for solutions for which the electric field is a s-polarized wave,
which means that it can be written as  with its propagation being along the
x-direction. From Bloch's theorem and assuming an
angular frequency ω it follows that all
electromagnetic-field quantities are proportional to
with its propagation being along the
x-direction. From Bloch's theorem and assuming an
angular frequency ω it follows that all
electromagnetic-field quantities are proportional to 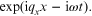 Substitution of equation (1.18) into the wave equation (1.19) yields
Substitution of equation (1.18) into the wave equation (1.19) yields
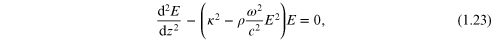
where we define κ, which is real for large enough qx , by
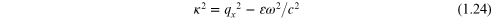
and we assume solutions exist where E is
real. The NL differential equation can then be solved by multiplying
each side of (1.23) by 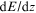 and integrating to obtain
and integrating to obtain
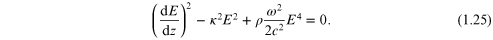
Here a constant of integration has been set to zero on
the assumption that both E and  tend to zero as
tend to zero as  inside the NL medium. Next, equation (1.25) can be rearranged as an expression for
inside the NL medium. Next, equation (1.25) can be rearranged as an expression for  as a function of z and directly
integrated, giving
as a function of z and directly
integrated, giving
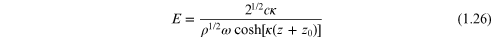
as the solution appropriate for 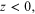 where z0 is another constant of integration. For completeness we
also need to consider the solution for E in the linear
medium (labelled 1) for
where z0 is another constant of integration. For completeness we
also need to consider the solution for E in the linear
medium (labelled 1) for 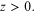 By contrast with equation (1.23) we now have a much simpler second-order linear
differential equation, for which the solution satisfying the requirement
By contrast with equation (1.23) we now have a much simpler second-order linear
differential equation, for which the solution satisfying the requirement 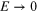 as
as  is
is

Here  by analogy with equation (1.24), with
by analogy with equation (1.24), with  denoting the dielectric constant of medium 1 and as
before we take
denoting the dielectric constant of medium 1 and as
before we take 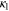 to be real. The constant E1 is easily found from the electromagnetic boundary condition
at the interface z = 0 that the tangential
electric-field components must be continuous. We are still left,
however, with the problem of finding the other constant
z0.
to be real. The constant E1 is easily found from the electromagnetic boundary condition
at the interface z = 0 that the tangential
electric-field components must be continuous. We are still left,
however, with the problem of finding the other constant
z0.
This kind of situation is typical of many problems involving NL excitations and in the present case it can be handled by finding another equation involving z0 from consideration of the power flow in the propagating wave. In electromagnetism this comes from the time-averaged Poynting vector [14, 15] and further discussion will be deferred to chapter 7. However, we have demonstrated here by the form of equation (1.26) that a spatially localized electromagnetic wave can occur due to the nonlinearity of the medium.
1.2. Survey of types of nanostructures
In the examples given so far, we have considered excitations in unbounded (bulk) media, in a 2D sheet (for graphene), or at the planar interface between two media. More generally there may be multiple boundaries (surfaces or interfaces) that affect the dimensionality and symmetries of the system, thus modifying the form of Bloch's theorem. Also, the boundaries introduce different length scales and here we will be mainly interested in effects in the range of nanometres (nm) up to micrometres (μm). We will now describe briefly some of the different nanostructures that will be considered in the following chapters. Examples are represented schematically in figure 1.4.
Figure 1.4. Schematic illustration of some types of nanostructures: (a) low-dimensional structures, (b) periodic multilayers or superlattices and (c) laterally patterned periodic structures.
Download figure:
Standard image High-resolution image1.2.1. Low-dimensional structures
In this category we have materials with reduced dimensionality as expressed in terms of the number of spatial dimensions in which there is translational symmetry. They include the 2D cases of thin films with finite thickness L and parallel planar surfaces, as well as sheets of atoms such as the graphene example mentioned earlier. They are characterized by a 2D space lattice associated with the planes of atoms parallel to the surfaces, as mentioned in subsection 1.1.1, and the form of Bloch's theorem will be modified slightly compared with equation (1.8) to become
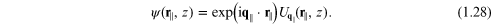
We have assumed that the z-axis is
chosen to be perpendicular to the surfaces, so the in-plane vectors are  and
and  The challenge in solving for the excitations in films
is finding the z-dependence of the amplitude term
The challenge in solving for the excitations in films
is finding the z-dependence of the amplitude term 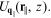
In the case of linear excitations in films we will often find later that
this z-dependence is expressible as a linear
combination of terms having the form  where
where  may be complex with a series of
allowed values labelled by j (see, e.g., [4]). There
are two possible situations that may arise. One is that
may be complex with a series of
allowed values labelled by j (see, e.g., [4]). There
are two possible situations that may arise. One is that  is real and thus it represents the third wave-vector
component of a bulk excitation in the film with total wave vector
is real and thus it represents the third wave-vector
component of a bulk excitation in the film with total wave vector  This bulk excitation is affected by the film surfaces
because it must satisfy boundary conditions there. The other possibility
is that
This bulk excitation is affected by the film surfaces
because it must satisfy boundary conditions there. The other possibility
is that  may have an imaginary part, which we denote as
may have an imaginary part, which we denote as  Then the
Then the  term will involve a real factor such as
term will involve a real factor such as  which is characteristic of a localized surface
excitation that decays with distance from one of the film surfaces. A
surface excitation can therefore be typically described in terms of a 2D
wave vector along with a decay length that is equal to
which is characteristic of a localized surface
excitation that decays with distance from one of the film surfaces. A
surface excitation can therefore be typically described in terms of a 2D
wave vector along with a decay length that is equal to 
The category of low-dimensional structures also includes nanowires (or nanorods), which have just one direction of translational symmetry (the axis along the length of the wire) and therefore the excitations are characterized by a 1D wave vector. The straightforward modification of Bloch's theorem in this case yields

where it is assumed here that the z-axis is along the translational symmetry axis.
Finally, we may have structures that are finite in all three dimensions, such as a small cuboid or a sphere. These have no translational symmetry (so Bloch's theorem does not apply) and they may be labelled as being 0D, such as the 'quantum dots' that have been of particular interest for semiconductors or flat 'platelets' or 'disks' for magnetic materials (see, e.g., [18, 19]). The low-dimensional structures mentioned here are illustrated schematically using examples in figure 1.4(a).
1.2.2. Multilayers and superlattices
If more than one material is utilized, then more elaborate cases of
nanostructures can arise than those in the previous subsection. One
simple possibility is to build up multilayers with alternating thin
films of two materials, denoted as A and
B, to form an  pattern of growth on a substrate material. Such an
example is provided in figure 1.4(b) for the materials
shown in different colours. The simplest case would be a bilayer
AB, but multilayers with a large number of layers
(e.g., hundreds or more) can be fabricated. In all cases these systems
would have the property of translational symmetry for lattice directions
parallel to the planar surfaces and interfaces. Thus the 2D Bloch's
theorem in equation (1.28) still applies, with
the only essential difference being that the term
pattern of growth on a substrate material. Such an
example is provided in figure 1.4(b) for the materials
shown in different colours. The simplest case would be a bilayer
AB, but multilayers with a large number of layers
(e.g., hundreds or more) can be fabricated. In all cases these systems
would have the property of translational symmetry for lattice directions
parallel to the planar surfaces and interfaces. Thus the 2D Bloch's
theorem in equation (1.28) still applies, with
the only essential difference being that the term 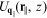 may have a more complicated dependence on
z. There may, for example, be excitations that are
localized only near the interfaces between A and
B layers.
may have a more complicated dependence on
z. There may, for example, be excitations that are
localized only near the interfaces between A and
B layers.
Another aspect of multilayers that makes them of special interest occurs
when all the A layers have identical properties
(composition, thickness, etc) to one another and likewise for all the
B layers. The structure then consists of repeats of
the same basic AB building block. If there is a large
number of these repeats, then a new symmetry operation emerges
corresponding to translations in the z-direction
through a periodicity length  where dA
and dB
denote the thicknesses of the individual A and
B layers. We then have an example of a
periodic superlattice, for which the inbuilt
artificial periodicity in the z-direction may be
associated with a new 1D Brillouin zone that extends in reciprocal space
from
where dA
and dB
denote the thicknesses of the individual A and
B layers. We then have an example of a
periodic superlattice, for which the inbuilt
artificial periodicity in the z-direction may be
associated with a new 1D Brillouin zone that extends in reciprocal space
from 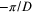 to
to 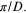 Since D is typically much larger than
the lattice parameter a of either constituent material,
this new Brillouin zone is smaller than the crystal Brillouin zone. This
can have striking consequences for the excitations that propagate as
waves in the perpendicular (z-)direction of the
superlattice. A smaller Brillouin zone can sometimes be advantageous as
regards the experimental techniques for studying the excitations and it
also leads to a 'folding' of the dispersion curves, as we will discuss
through examples in section 1.5 and later chapters.
Since D is typically much larger than
the lattice parameter a of either constituent material,
this new Brillouin zone is smaller than the crystal Brillouin zone. This
can have striking consequences for the excitations that propagate as
waves in the perpendicular (z-)direction of the
superlattice. A smaller Brillouin zone can sometimes be advantageous as
regards the experimental techniques for studying the excitations and it
also leads to a 'folding' of the dispersion curves, as we will discuss
through examples in section 1.5 and later chapters.
The concept of a superlattice was originally introduced by Esaki and Tsu
[20]
for ultrathin semiconductor multilayers where the layer thicknesses were
less than the electron mean free path, but currently the term is applied
more generally for multilayers that are either periodic or are generated
according to certain mathematical rules. In the former category we may
also have periodic arrangements with three (or more) components, 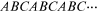 for example, as well as the two-component superlattice
described above. In the latter category we may include
quasi-periodic superlattices (see, e.g., [21], where
the sequencing of layers along the growth direction is quasi-periodic in
the sense that it involves two different fundamental periods whose ratio
is an irrational number. One way to achieve this is through the
Fibonacci sequence of numbers,
for example, as well as the two-component superlattice
described above. In the latter category we may include
quasi-periodic superlattices (see, e.g., [21], where
the sequencing of layers along the growth direction is quasi-periodic in
the sense that it involves two different fundamental periods whose ratio
is an irrational number. One way to achieve this is through the
Fibonacci sequence of numbers,  with integer
with integer  that is defined by the recursion relation
that is defined by the recursion relation
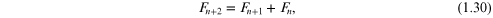
with the initial conditions  It is straightforward to prove that as
n becomes very large (
It is straightforward to prove that as
n becomes very large ( ) the ratio
) the ratio 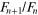 tends to the value
tends to the value 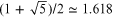 which is known as the golden mean. For the application
to Fibonacci superlattices some fundamental property of the layered
growth is developed by analogy with equation (1.30), as explained later. The excitations in quasi-periodic
superlattices have novel properties (e.g., regarding their localization,
multifractal behaviour, etc) that make them of special interest [22].
which is known as the golden mean. For the application
to Fibonacci superlattices some fundamental property of the layered
growth is developed by analogy with equation (1.30), as explained later. The excitations in quasi-periodic
superlattices have novel properties (e.g., regarding their localization,
multifractal behaviour, etc) that make them of special interest [22].
1.2.3. Laterally patterned structures
By contrast with the previous subsection we will now discuss some artificial nanostructures produced by a lateral arrangement (usually periodic) of elements such as that represented in figure 1.4(c). This shows an alternating sequence of stripes of two different materials deposited side-by-side on a planar surface, rather than stacked vertically. Interest in such structures was given impetus in 1987 through seminal work by Yablonovitch [23] and John [24], who studied artificial electromagnetic materials, typically in low dimensions, that have periodic modulation of the refractive index. This was originally undertaken with a view to control the propagation, localization and scattering of light, and led to periodic structures known as either photonic crystals or alternatively photonic band-gap materials for applications in optoelectronics. Some consequences for the photonic band structure in periodic cases are developed in section 1.5.
More recently, aided by advances in materials growth and fabrication on the sub-micron scale, other types of laterally patterned materials have been utilized to study phonons (hence phononic crystals), SWs or magnons (magnonic crystals; MCs) and plasmons (plasmonic crystals), among others. One of the characteristic features of these materials is the tailoring of the band structure of the excitations and the forbidden-frequency gaps (or band gaps) in the spectrum. We shall discuss these cases in more detail in later chapters. Just as with the superlattices in the previous subsection, effects will arise due to a modified Bloch's theorem and mini-Brillouin zones due to the artificial periodicity. The example depicted in figure 1.4(c) with a striped array is a 1D crystal in the lateral plane, but 2D patterning (as with a chess or checker board array) provides another case of interest.
1.3. Experimental techniques for dynamic properties
Although a wide range of different physical phenomena will contribute to the dynamic properties of materials, many of the same experimental techniques will be applicable. This will also be the case as regards the theoretical tools needed to study the excitations and so it is useful to give a broad introduction in this chapter and to provide some general references. The experimental aspects are covered first in this section and the theoretical topics will be described in section 1.4.
We will emphasize here the techniques that are most useful as regards the dynamical properties and characterization of the excitations. These include inelastic light scattering, inelastic particle scattering, electromagnetic techniques and magnetic (or spin) resonance methods, etc. A fuller account can be found in [4]. We do not describe here the sample growth and preparation techniques, or the analytical tools for surface and interface structural properties, since these are not the focus of this book and they have been extensively covered elsewhere (see, e.g., [19, 25, 26]).
Both Raman and Brillouin scattering of light by dense media involve an
inelastic process whereby the incident light of angular frequency 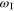 (or a photon of energy
(or a photon of energy 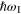 ) and wave vector
) and wave vector 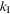 interact with the medium by creating or absorbing an
excitation and producing a scattered light beam. Although these effects were
discovered in the early part of the 20th century, it was not until much
later with the advent of the laser and other technical developments that
they were widely used for studying bulk and surface excitations. The
essential difference between the two techniques lies in the method used to
analyse the frequency of the scattered light; this involves a grating
spectrometer for Raman scattering (RS) (where the wavenumber shifts of the
light are typically in the range 5–4000 cm−1) and a Fabry–Pérot
interferometer for Brillouin scattering (where the wavenumber shifts are
below about 5 cm−1). Note that a wavenumber shift of 1
cm−1 corresponds to a 29.98 GHz frequency shift. We label the
excitation by ω and
interact with the medium by creating or absorbing an
excitation and producing a scattered light beam. Although these effects were
discovered in the early part of the 20th century, it was not until much
later with the advent of the laser and other technical developments that
they were widely used for studying bulk and surface excitations. The
essential difference between the two techniques lies in the method used to
analyse the frequency of the scattered light; this involves a grating
spectrometer for Raman scattering (RS) (where the wavenumber shifts of the
light are typically in the range 5–4000 cm−1) and a Fabry–Pérot
interferometer for Brillouin scattering (where the wavenumber shifts are
below about 5 cm−1). Note that a wavenumber shift of 1
cm−1 corresponds to a 29.98 GHz frequency shift. We label the
excitation by ω and 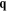 and the scattered light by
and the scattered light by  and
and  and the two possible processes (known as Stokes and
anti-Stokes scattering) are represented schematically in figure 1.5. When the
light scattering takes place in a bulk (effectively infinite) 3D transparent
material the energy and momentum are conserved and so
and the two possible processes (known as Stokes and
anti-Stokes scattering) are represented schematically in figure 1.5. When the
light scattering takes place in a bulk (effectively infinite) 3D transparent
material the energy and momentum are conserved and so

where the upper (lower) signs correspond to the Stokes
(anti-Stokes) case. The dispersion relations for the incident and scattered
light yield  and
and 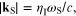 where
where  and
and  denote the corresponding values of the refractive index.
The above relations, together with the conservation properties in equation
(1.31), imply that only excitations with wave vectors near the
centre of the Brillouin zone in a bulk material are excited.
denote the corresponding values of the refractive index.
The above relations, together with the conservation properties in equation
(1.31), imply that only excitations with wave vectors near the
centre of the Brillouin zone in a bulk material are excited.
Figure 1.5. Representation of the (a) Stokes and (b) anti-Stokes processes of inelastic light scattering. The incident and scattered photons are depicted by solid lines and the created or absorbed excitation by a dashed line.
Download figure:
Standard image High-resolution imageThere are several modifications for the application of light scattering in low-dimensional and/or optically absorptive materials. First, with thin films and multilayers on the one hand, or nanowires and nanowire arrays on the other, the conservation of momentum will apply only in the 2D or 1D direction(s) where the system has translational symmetry. In the other dimension(s) there will be a spread of wave-vector components for the excitation, implying a spread of frequencies in the measured spectrum. The extent to which this occurs depends on the optical absorption (or imaginary part of the refractive index) in the material. If the absorption is large, which is typical for metals and some semiconductors, the light will penetrate only close to the surface of the material, so light scattering can be sensitive to surface properties and to the excitations localized there. In the case of 0D materials (or dots) none of the wave-vector components will be conserved. As well as providing information about the frequencies, light scattering also probes the intensities of the excitations. The scattering cross section is, in fact, related to the correlations between components of the electric field for the scattered light and this provides a connection between theory and experiment, as we describe later. Some general references for inelastic light scattering are [27] (mainly in bulk materials), [28, 29] (mainly in thin films and multilayers) and [30] (mainly in other low-dimensional materials).
Next we turn to the inelastic scattering of particles by the crystal excitations. In principle this process may involve larger momentum changes than encountered with light, so by contrast particle scattering may be useful for probing excitations throughout the entire Brillouin zone, depending on the type of particle involved. In electron energy loss spectroscopy (EELS), and in its high-resolution variant (HREELS), a beam of electrons is scattered from the surface of a material, as reviewed in [31, 32]. A typical geometry for the scattering of particles from a planar surface is shown in figure 1.6, where a surface excitation such as a phonon is emitted or absorbed in the process. The condition for conservation of energy yields
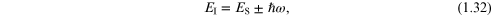
where we follow the notation in figure 1.6 and the upper (lower) sign refers to the creation (annihilation) case for the excitation. The other scattering condition corresponds to the conservation of the momentum component in the direction parallel to the surface plane, giving
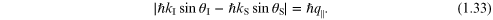
Also, we have the classical energy–momentum relations  and
and 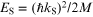 with M denoting the particle mass.
Generally for EELS or HREELS we can approximate by assuming
with M denoting the particle mass.
Generally for EELS or HREELS we can approximate by assuming  which is usually well satisfied (e.g., if
which is usually well satisfied (e.g., if 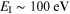 and
and 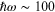 meV), implying
meV), implying 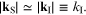 For the same reason we can also ignore Umklapp processes
in equation (1.33). It follows that, by varying the angles
For the same reason we can also ignore Umklapp processes
in equation (1.33). It follows that, by varying the angles 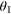 and
and  the in-plane wave vector can be varied across its 2D
Brillouin zone and the ω-versus-
the in-plane wave vector can be varied across its 2D
Brillouin zone and the ω-versus- dispersion relation for the surface excitation can be
investigated. An example of this type of analysis is provided by the work of
Lehwald et al [33] for phonons localized at a
Ni surface. Spin-polarized EELS has been used for magnetic excitations at
surfaces [34]. It involves employing a spin-polarized incident electron beam
together with a polarization analyser in the scattered beam.
dispersion relation for the surface excitation can be
investigated. An example of this type of analysis is provided by the work of
Lehwald et al [33] for phonons localized at a
Ni surface. Spin-polarized EELS has been used for magnetic excitations at
surfaces [34]. It involves employing a spin-polarized incident electron beam
together with a polarization analyser in the scattered beam.
Figure 1.6. Geometry for inelastic particle scattering from a planar surface of a material, where the incident and scattered beam are in the same vertical plane.
Download figure:
Standard image High-resolution imageThe inelastic scattering of particles that are much heavier than electrons
allows for larger momentum changes and hence offers the prospect of making
it easier (in principle) to study excitations with large wave vectors.
Inelastic neutron scattering is well established for studying bulk
excitations. However, neutrons interact only very weakly with materials and
have macroscopically large penetration depths, so this method is relatively
insensitive to surface effects. This drawback may be mitigated if the
surface or interface area is effectively increased (e.g., by using a
short-period superlattice) or if a neutron beam is used at grazing incidence
to a surface (see, e.g., [35]). However, in the context
of surface excitations, the inelastic scattering of small
neutral atoms, such as He atoms, has proved to be more useful. The He atoms
at suitable incident energies (e.g., of order 20 meV) will be scattered back
from a surface by essentially just the first monolayer (ML) of the material.
Also the atoms in the incident beam will have a de Broglie wavelength ( ) that is typically comparable with the lattice constant,
so the entire 2D Brillouin zone can be studied. The technique was pioneered
by Brusdeylins et al [36] using time-of-flight
spectroscopy to study surface phonons. The basic equations for the
scattering are essentially the same as for EELS, equations (1.32)
and (1.33), except that it is no longer true that
) that is typically comparable with the lattice constant,
so the entire 2D Brillouin zone can be studied. The technique was pioneered
by Brusdeylins et al [36] using time-of-flight
spectroscopy to study surface phonons. The basic equations for the
scattering are essentially the same as for EELS, equations (1.32)
and (1.33), except that it is no longer true that 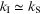 because of the larger particle mass here. In the case of a
90° scattering geometry (when
because of the larger particle mass here. In the case of a
90° scattering geometry (when  in figure 1.6) it is straightforward to
show that ω and q∥ are related by
in figure 1.6) it is straightforward to
show that ω and q∥ are related by
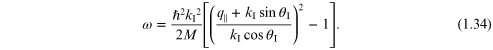
This allows the dispersion relation of a surface excitation to be deduced.
To conclude this section we briefly mention some experimental techniques that are specific to certain types of excitations. Others will be mentioned in later chapters. Magnetic resonance techniques are widely used for excitations in magnetic materials, both in the bulk and in low-dimensional geometries (see [29] for a review). At low power levels a microwave magnetic field (in a direction transverse to the magnetization) will couple linearly to the zero wave-vector SWs (magnons) in a ferromagnet, leading to the ferromagnetic resonance (FMR) condition when the frequencies of the field and excitation match. The analogous effect in antiferromagnets is called antiferromagnetic resonance (AFMR) and typically occurs at higher frequencies. In SW resonance (SWR) in ferromagnetic thin films the technique is used to excite selectively the standing SWs across the film thickness that have small but nonzero wave vectors. At higher power levels the oscillating (or 'pumping') magnetic field can be used to promote various NL SW processes in ferromagnets, as we will discuss in chapter 7.
Another area involving specialized techniques occurs with excitations that generate electromagnetic waves. These can be studied using optical methods that employ, for example, evanescent wave coupling in the region near closely positioned interfaces between media of different refractive index. This is the basis of the method of attenuated total reflection (ATR), which has been successfully applied to plasmons and polaritons (see chapters 4 and 5). Evanescent wave properties are also exploited in scanning near-field optical microscopy, which is a form of scanning probe microscopy.
1.4. Theoretical methods for dynamic properties
1.4.1. Equations of motion for excitations
Some of the theoretical considerations have already been mentioned in earlier parts of this chapter, particularly in subsection 1.1.2, where we presented some simple examples of linear and NL excitations. There we emphasized the role of an equation of motion for the excitation amplitude, e.g., Maxwell's wave equation for the electric field as in equation (1.19), along with boundary conditions and/or the use of Bloch's theorem to deal with spatial periodicity where needed.
From such an approach one would normally be able to deduce the excitation
frequency and hence a dispersion relation, as well as information about
the spatial variation in the case of a localized excitation. As
discussed earlier in section 1.2, a bulk excitation will
depend on a 3D wave vector  whereas a surface or interface excitation at a planar
interface will be characterized by a 2D wave vector
whereas a surface or interface excitation at a planar
interface will be characterized by a 2D wave vector  and one or more attenuation factors (or decay
lengths). Other considerations apply in 1D and 0D systems, as mentioned
before. Calculating the excitation frequencies in a low-dimensional
system normally involves having a set of homogeneous
equations of motion satisfied by the amplitude variable(s) in the
different parts of the system. These equations may either be
differential equations if a macroscopic (or continuum) approach is being
followed, as in the previous examples given for electromagnetic
excitations, or finite-difference equations if a microscopic approach is
used, as in a discrete-lattice model. Both approaches will be used
throughout the following chapters. Also, in some cases, numerical
simulation packages have been developed to carry out these calculations.
An example is the Object Oriented MicroMagnetic Framework (OOMMF)
project at the US National Institute of Standards and Technology, which
is applicable to studying a range of properties of micromagnetic
low-dimensional systems [37].
and one or more attenuation factors (or decay
lengths). Other considerations apply in 1D and 0D systems, as mentioned
before. Calculating the excitation frequencies in a low-dimensional
system normally involves having a set of homogeneous
equations of motion satisfied by the amplitude variable(s) in the
different parts of the system. These equations may either be
differential equations if a macroscopic (or continuum) approach is being
followed, as in the previous examples given for electromagnetic
excitations, or finite-difference equations if a microscopic approach is
used, as in a discrete-lattice model. Both approaches will be used
throughout the following chapters. Also, in some cases, numerical
simulation packages have been developed to carry out these calculations.
An example is the Object Oriented MicroMagnetic Framework (OOMMF)
project at the US National Institute of Standards and Technology, which
is applicable to studying a range of properties of micromagnetic
low-dimensional systems [37].
It is useful to briefly consider some other examples that involve a
homogeneous equation of motion, apart from the electromagnetic one given
previously. First we take the case of an infinite, isotropic elastic
medium with a longitudinal vibrational wave (an acoustic phonon)
propagating in one direction, which we label as the
z-direction. If we denote 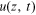 as the local displacement in the
z-direction of the medium, ρ as the
uniform density of the medium and
as the local displacement in the
z-direction of the medium, ρ as the
uniform density of the medium and 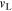 as the longitudinal sound wave velocity, the usual
linear wave equation with weak damping (constant
as the longitudinal sound wave velocity, the usual
linear wave equation with weak damping (constant 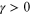 ) included is (see, e.g., [1, 3])
) included is (see, e.g., [1, 3])
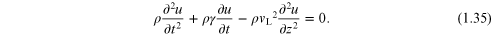
A solution is easily found by taking ![$u(z,t)\propto \mathrm{exp}[{\rm{i}}({qz}-\omega t)]$](https://content.cld.iop.org/books/10__1088_978-0-7503-1054-3/revision2/bk978-0-7503-1054-3ch1ieqn186.gif) which yields the condition
which yields the condition  In the limit of zero damping (
In the limit of zero damping ( ) this gives the usual acoustic-phonon dispersion
relation
) this gives the usual acoustic-phonon dispersion
relation 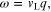 as expected.
as expected.
When a discrete-lattice approach is followed, leading to finite-difference equations for the spatial variables instead of differential equations, some special techniques are useful. One of these is the tridiagonal matrix (TDM) method, which is useful for surface and interface problems when the interactions are short range, often just between nearest neighbours. A general outline of the method is given in the appendix and some applications are discussed later, e.g., for the lattice dynamics of phonons in chapter 2 and for exchange-dominated SWs in ferromagnets in chapter 3.
A somewhat different situation will occur if the excitation is described in terms of a quantum-mechanical operator, rather than a classical amplitude as above. This will be so, for example, in the case of a magnetic system consisting of a lattice of atoms where each atom is associated with a spin angular-momentum operator (see chapter 3). If the quantum-mechanical system is represented by a Hamiltonian H, then the equation of motion for any operator A of the system is obtained from [38]
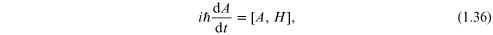
where ![$[A,H]\equiv ({AH}-{HA})$](https://content.cld.iop.org/books/10__1088_978-0-7503-1054-3/revision2/bk978-0-7503-1054-3ch1ieqn191.gif) denotes the commutator between the two operators. For
simplicity we shall henceforth usually take units such that
denotes the commutator between the two operators. For
simplicity we shall henceforth usually take units such that 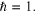 Equation (1.36) may be either a
linear or NL equation in A, depending on whether the
outcome of evaluating the commutator of the operator A
(for the excitation) with the Hamiltonian gives an expression that is
linear in A or has some other more complicated
dependence. Examples of both cases will arise later in this book, but it
is probably most clearly illustrated for magnons in ferromagnets (see
chapters 3 and 7).
Equation (1.36) may be either a
linear or NL equation in A, depending on whether the
outcome of evaluating the commutator of the operator A
(for the excitation) with the Hamiltonian gives an expression that is
linear in A or has some other more complicated
dependence. Examples of both cases will arise later in this book, but it
is probably most clearly illustrated for magnons in ferromagnets (see
chapters 3 and 7).
1.4.2. Linear-response theory for excitations
In many cases we are interested in other properties of the excitations apart from their dispersion relations. For example, we may need to know the relative statistical weighting (or spectral intensity) of the excitations or to find a scattering cross section to compare with experiment. This information can be provided by linear-response theory and we will now outline this method and then illustrate it with an example. The basis of the method is to calculate the response of the system to a small applied stimulus, taking care to choose the appropriate classical or quantum variables (relating to the excitation being studied). The response functions provide not only the dispersion relations for the relations but also the intensity-related information mentioned above. General accounts of linear-response theory are to be found, for example, in [4, 39] where the connection to Green functions is also explained. A comprehensive treatment in the context of low-dimensional systems can be found in [40]. Here (and also in the appendix) we will present, for later reference, only the important results.
We suppose that a time-dependent perturbation described by Hamiltonian  is applied to the system, where
f(t) is a scalar external field
that couples linearly to a system variable denoted by the operator
B. An example is when B is a
displacement from equilibrium in an elastic medium and
f(t) is a mechanical force. The
total Hamiltonian can be written as
is applied to the system, where
f(t) is a scalar external field
that couples linearly to a system variable denoted by the operator
B. An example is when B is a
displacement from equilibrium in an elastic medium and
f(t) is a mechanical force. The
total Hamiltonian can be written as
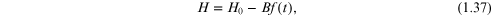
where H0 denotes the Hamiltonian for the unperturbed system, taken
to be in thermal equilibrium at time  At any later time the response of the system can be
expressed in terms of the change
At any later time the response of the system can be
expressed in terms of the change  produced in any other system variable corresponding to
an operator denoted as A. The procedure for doing this
is outlined in the appendix and the main conclusion is that
produced in any other system variable corresponding to
an operator denoted as A. The procedure for doing this
is outlined in the appendix and the main conclusion is that
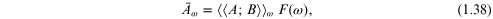
where 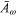 and
and  are defined to be the frequency Fourier components of
are defined to be the frequency Fourier components of 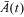 and
and  respectively. This result holds within a linear
approximation in terms of the perturbation term and the proportionality
factor written as
respectively. This result holds within a linear
approximation in terms of the perturbation term and the proportionality
factor written as 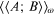 in equation (1.38) is identified as the
Fourier component of the Green function that describes correlations
between the operators A and B. The
above result establishes the role of Green functions as linear-response
functions, in the sense that they are just the same as the
proportionality factor between an applied stimulus to the system,
represented by
in equation (1.38) is identified as the
Fourier component of the Green function that describes correlations
between the operators A and B. The
above result establishes the role of Green functions as linear-response
functions, in the sense that they are just the same as the
proportionality factor between an applied stimulus to the system,
represented by  and the response that it produces, represented by
and the response that it produces, represented by  The formal definitions and some basic properties of
Green functions are given in the appendix.
The formal definitions and some basic properties of
Green functions are given in the appendix.
In order to illustrate the formalism for response functions and Green
functions, we return to the physical example of excitations in an
infinite elastic medium considered earlier in this section. The
homogeneous equation of motion for the displacement
u(z) for a longitudinal acoustic
(LA) wave in the z-direction was given by equation
(1.35), to which we now add a driving term (a perturbation)
which is chosen to represent a harmonic point force at position  in the system, i.e., we take
in the system, i.e., we take
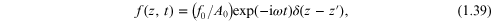
where f0 is an amplitude and A0 is the area presented by the system in the xy-plane. The total interaction energy with the system is
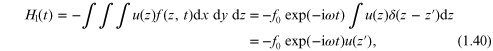
so it takes the general form assumed earlier. The equation of motion on generalizing (1.35) becomes

As anticipated, the outcome is that we now have an
inhomogeneous differential equation. We may first
take a common time dependence such as  leaving as the equation for the spatial
dependence
leaving as the equation for the spatial
dependence
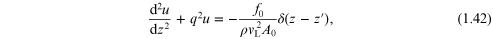
where the complex q2 is defined in the same way as following equation (1.35). We seek the solution that is bounded as  and has the correct behaviour as
and has the correct behaviour as  It may easily be verified that the result
is
It may easily be verified that the result
is
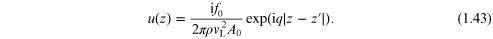
In the spirit of linear-response theory this is the
driven equation for u(z) due to a
harmonic force applied at point  From equation (1.38) we obtain the Green
function as
From equation (1.38) we obtain the Green
function as
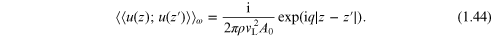
Since the above result is a function of  as expected for a system with translational symmetry,
we can re-express it by making a Fourier transform from the spatial
variables to a wave-vector component k in the
z-direction:
as expected for a system with translational symmetry,
we can re-express it by making a Fourier transform from the spatial
variables to a wave-vector component k in the
z-direction:
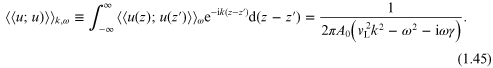
The last step for this result is accomplished by
splitting the range of integration into two parts with  and
and  We note that the condition for the energy denominator
to be zero yields the dispersion relation
We note that the condition for the energy denominator
to be zero yields the dispersion relation 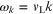 for the excitation (an acoustic phonon) if the damping
is ignored. This illustrates a general property for the denominator of
Green functions. Finally we may use equation (1.45) together with the fluctuation-dissipation theorem in
the appendix to obtain
for the excitation (an acoustic phonon) if the damping
is ignored. This illustrates a general property for the denominator of
Green functions. Finally we may use equation (1.45) together with the fluctuation-dissipation theorem in
the appendix to obtain  which is a measure of the spectral intensity (or
mean-square amplitude) of the excitation as a function of
k and ω. A numerical example of
the result appears in figure 1.7, where the peaks occur
for ω close to
which is a measure of the spectral intensity (or
mean-square amplitude) of the excitation as a function of
k and ω. A numerical example of
the result appears in figure 1.7, where the peaks occur
for ω close to 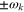 provided the damping is relatively small (
provided the damping is relatively small ( ). The peaks are unequal in height due to the
statistical-mechanical weighting, which depends on the temperature
T. This has consequences, for example, regarding
the difference in intensities observed between Stokes and anti-Stokes
peaks in inelastic light scattering, as we will discuss in chapters
2 and
3.
). The peaks are unequal in height due to the
statistical-mechanical weighting, which depends on the temperature
T. This has consequences, for example, regarding
the difference in intensities observed between Stokes and anti-Stokes
peaks in inelastic light scattering, as we will discuss in chapters
2 and
3.
Figure 1.7. The spectral intensity  versus reduced frequency
versus reduced frequency  for the acoustic phonons in an infinite
elastic medium (see the text). We denote
for the acoustic phonons in an infinite
elastic medium (see the text). We denote  for a fixed value of wave-vector component
k. The assumed numerical values of the
parameters correspond to dimensionless
for a fixed value of wave-vector component
k. The assumed numerical values of the
parameters correspond to dimensionless  and
and 
Download figure:
Standard image High-resolution image1.5. Photonic band gaps in periodic structures
We have already briefly mentioned periodic structures in subsections 1.2.2 and 1.2.3, which are typically formed from two or more materials, either as superlattices or as lateral arrays. The bands of excitations in such structures (i.e., their frequency versus wave-vector relationships) can be very complicated in general and particular features may sometimes arise, such as the appearance of band gaps at the mini-Brillouin-zone boundaries mentioned earlier. The properties for the occurrence and manipulation of such bands have led to the tremendous interest in band-gap materials, initially in the photonics case in optics (see [41] for a thorough review) but subsequently for other excitations as well. In this introductory chapter we present a simple formulation for a 1D photonic band-gap material (a photonic crystal) and discuss some extensions to 2D or 3D. This treatment will serve as a template for carrying out other calculations for periodic (and quasi-periodic) structures in the later chapters.
1.5.1. Bulk-slab model
Here we consider alternating layers of medium A and
medium B to form the superlattice structure depicted in
figure 1.8.
The layer thicknesses are dA
and dB
, both assumed to be large compared with the atomic lattice
parameters of the materials. The length associated with the artificial
periodicity is 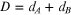 and so the 1D wave vector Q (the
so-called Bloch wave vector) in the z-direction
associated with this translational symmetry has a first Brillouin zone
corresponding to
and so the 1D wave vector Q (the
so-called Bloch wave vector) in the z-direction
associated with this translational symmetry has a first Brillouin zone
corresponding to  Further it will be assumed that the dielectric
functions are
Further it will be assumed that the dielectric
functions are  and
and  taken for simplicity to be the bulk dielectric
constants (independent of the excitation angular frequency
ω). This is sometimes referred to as the
bulk-slab model of a superlattice.
taken for simplicity to be the bulk dielectric
constants (independent of the excitation angular frequency
ω). This is sometimes referred to as the
bulk-slab model of a superlattice.
Figure 1.8. Geometry and notation for the calculation of the photonic (optical) band structure of a two-component alternating periodic superlattice. The wave propagation directions are taken to be in the xz plane.
Download figure:
Standard image High-resolution imageWe now employ standard results from electromagnetism for the optical wave
propagation in the layers, taken to be in the xz plane.
There are basically two cases, depending on whether the waves have
s-polarization (with electric-field vector  in the y-direction) or p-polarization
(with
in the y-direction) or p-polarization
(with  in the xz-plane). The wave-vector
component Q enters into the calculations through
Bloch's theorem in the form
in the xz-plane). The wave-vector
component Q enters into the calculations through
Bloch's theorem in the form
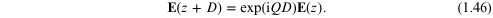
Also all field components will be taken to have
dependences on x and t as  where for completeness we have included a wave vector
qx
in the x-direction to allow for oblique
incidence of the optical waves at each interface.
where for completeness we have included a wave vector
qx
in the x-direction to allow for oblique
incidence of the optical waves at each interface.
The calculation for s-polarization will be shown first. The solution of the wave equation (1.19) for Ey in any layer will be a superposition of a forward- and a backward-travelling wave in the z-direction. Alternative forms can be written down, depending on whether the phases are taken relative to the lower (L) or upper (U) interface of each layer, giving

in an A layer (with  ) where qAz
must satisfy
) where qAz
must satisfy
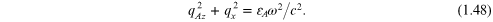
For the field in the adjacent layer B in
the same cell l (with  ) and with qBz
defined similarly to equation (1.48), we have
) and with qBz
defined similarly to equation (1.48), we have
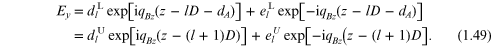
Using a matrix notation the amplitudes in equation (1.47) are related by
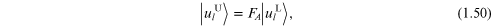
where we denote
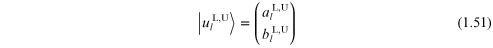
and FA is a 2 × 2 matrix given by
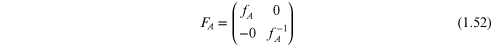
with phase term  Likewise for the other layer we write
Likewise for the other layer we write
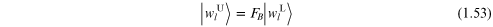
with analogous notations and definitions.
The electromagnetic boundary conditions at the 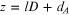 and
and  interfaces require that Ey
and Hx
are continuous (implying that Ey
and
interfaces require that Ey
and Hx
are continuous (implying that Ey
and  are continuous). These can be used to give additional
relationships between the column matrices of coefficients. The results
can eventually be expressed in matrix form as
are continuous). These can be used to give additional
relationships between the column matrices of coefficients. The results
can eventually be expressed in matrix form as
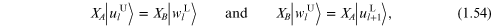
where
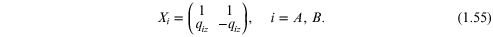
The equations (1.50), (1.53) and (1.54) may now be combined to give
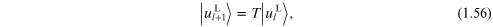
which relates amplitudes in cell l to
the equivalent part in cell  and introduces the transfer matrix T
given by
and introduces the transfer matrix T
given by
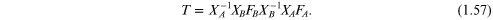
The transfer matrix has some useful properties, as we now
explain. First, it is unimodular in the sense that  which can be proved from the form of matrix products
in equation (1.57). Second, the
statement of Bloch's theorem in equation (1.46) is equivalent
to
which can be proved from the form of matrix products
in equation (1.57). Second, the
statement of Bloch's theorem in equation (1.46) is equivalent
to
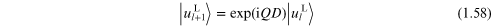
and therefore we have the property that
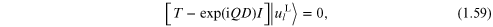
where I is the unit 2 × 2 matrix. There
is a similar equation obtained by relating  to
to  yielding
yielding
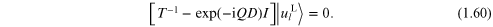
By adding equations (1.59) and (1.61) we find
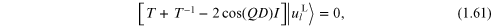
which holds for any cell l. Therefore,
from the property that  =
=  where 'tr' denotes the trace, we must
have
where 'tr' denotes the trace, we must
have
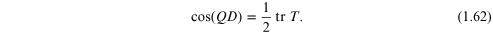
This is a general result, providing an implicit dispersion relation for the excitation frequencies in terms of the Bloch wave vector Q and the transfer matrix T.
Explicit evaluation shows that the diagonal elements of T in the present example are
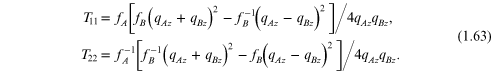
When these results are substituted into equation (1.62) we find after some algebraic manipulation that the dispersion relation in this case of s-polarization is
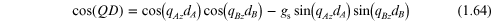
where
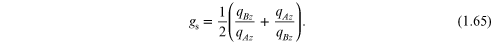
The calculation for the case of p-polarization is very
similar and it is found that equation (1.64) is still applicable
provided 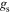 is replaced by
is replaced by  where
where
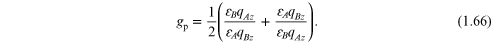
The dispersion equation in the general form represented by (1.64) occurs commonly for excitations in periodic structures, as we will see in later chapters. It is sometimes called the Rytov equation, since its first derivation is attributed to Rytov in the context of acoustic waves [42]. Full discussion of the results for the above optical superlattice, or photonic crystal, can be found in [41, 43]. We present a numerical example of a dispersion relation in figure 1.9 in the special case of normal incidence where qx = 0 and the distinction between s- and p-polarization vanishes. The plot is in dimensionless units for frequency ω versus Q. In the reduced-zone scheme used here the dispersion curves are 'folded back' and gaps open up at QD = 0 and π. In this example the band gaps (or stop bands) are relatively large because we have assumed a significant difference, or mismatch, between the dielectric constants of adjacent layers. If the dielectric constants are taken to be close in value, the gaps shrink to a small value.
Figure 1.9. Dispersion curves of frequency (in terms of  ) versus Bloch wave vector (in terms of
QD) for normal-incidence optical waves in a
1D photonic crystal consisting of a two-component alternating
periodic superlattice. The assumed parameters are
) versus Bloch wave vector (in terms of
QD) for normal-incidence optical waves in a
1D photonic crystal consisting of a two-component alternating
periodic superlattice. The assumed parameters are 
 and
and  The PBGs are shown as the shaded areas.
The PBGs are shown as the shaded areas.
Download figure:
Standard image High-resolution imageFinally we remark that the transfer-matrix method can straightforwardly be modified to apply other types of excitations, as well as to study the localized surface and/or interface modes (when they exist) in periodic and quasi-periodic structures that are either semi-infinite or finite in extent (in the z-direction). Results to illustrate this will be covered in some of the later chapters.
1.5.2. Photonic crystals in 2D and 3D
In the previous subsection it was demonstrated that stop bands would arise as a result of 1D periodicity in a superlattice. The interesting question arises as to whether it is possible to achieve 2D, or even 3D, arrays that would have stop bands or band gaps for optical signals at some frequencies and for both polarizations. The first investigations relating to this were made by Yablonovitch [23] in 1987, while related light localization studies were carried out around the same time by John [24]. A motivation for these early studies was the realization that a stop band with the properties mentioned would prohibit spontaneous emission of radiation in optical transitions and this could be utilized for semiconductor lasers and devices. However, subsequently a wide range of other quantum-optical device applications has emerged and an excellent reference is the book by Joannopoulos et al [41], which also covers the modelling techniques used to calculate the stop bands and the transmission characteristics.
The first realization of a full photonic band gap (PBG) material was due
to Yablonovitch et al [44] who formed a structure
that absorbed 15 GHz radiation for all spatial directions and
polarizations. It was made by drilling air holes at various angles into
a dielectric block. Such an arrangement, whilst effective, would be
impractical for scaling to the higher frequencies (shorter wavelengths)
required for most applications. Versatile alternative structures have
been based on the so-called 'woodpile' periodic arrangements of
semiconductor rods, in which each rod may have a rectangular cross
section with dimensions of order 1  and a length that is much larger. Such an arrangement
using rods of polycrystalline silicon (dielectric constant ∼13) on a Si
substrate is illustrated in figure 1.10. In this structure the
spatial alignments and separations between rods constitute an effective
face-centred tetragonal lattice symmetry and the stop band corresponds
to the 10–14.4
and a length that is much larger. Such an arrangement
using rods of polycrystalline silicon (dielectric constant ∼13) on a Si
substrate is illustrated in figure 1.10. In this structure the
spatial alignments and separations between rods constitute an effective
face-centred tetragonal lattice symmetry and the stop band corresponds
to the 10–14.4  range of wavelengths. Another PBG structure that has
been investigated (see [41]) is the 'inverse opal'
arrangement. These are formed by utilizing the property of microscopic
spheres (e.g., of silica, SiO2) to self-assemble into an fcc
lattice from a colloidal solution. The structure can then be inverted by
filling the voids between spheres with a high-dielectric material and
finally dissolving away the spheres.
range of wavelengths. Another PBG structure that has
been investigated (see [41]) is the 'inverse opal'
arrangement. These are formed by utilizing the property of microscopic
spheres (e.g., of silica, SiO2) to self-assemble into an fcc
lattice from a colloidal solution. The structure can then be inverted by
filling the voids between spheres with a high-dielectric material and
finally dissolving away the spheres.
Figure 1.10. SEM of a 3D photonic crystal with a 'woodpile' structure. The
rods are made of polycrystalline Si with widths 1.2  m. The stacking sequence shown here repeats
itself every four layers. Scale bar, 5
m. The stacking sequence shown here repeats
itself every four layers. Scale bar, 5 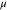 m. After Lin et al [45].
m. After Lin et al [45].
Download figure:
Standard image High-resolution imageAs well as the intense activity mentioned above with the focus on 3D PBG materials, there have also been advances in developing 2D structures [41]. In particular, there have been studies of structures with artificial 2D periodicity, including cases where the dielectric functions are dispersive, giving rise to plasmons, phonons and polaritons, for example. We will discuss some of these 2D cases in the later chapters.
References
- [1]Kittel C 2004 Introduction to Solid State Physics 8th edn (New York: Wiley)
- [2]Ashcroft N W and Mermin N D 1976 Solid State Physics (New York: Saunders College)
- [3]Grosso G and Parravicini G P 2013 Solid State Physics 2nd edn (Amsterdam: Academic)
- [4]Cottam M G and Tilley D R 2005 Introduction to Surface and Superlattice Excitations 2nd edn (Bristol: IOP)
- [5]Bloch F 1928 Z. Phys. 52 555
- [6]Novoselov K S, Geim A K, Morozov S V, Jiang D, Katsnelson M I, Grigorieva I V, Dubonos S V and Firsov A A 2005 Nature 438 197
- [7]Castro Neto A H, Guinea F, Peres N M R, Novosolov K S and Geim A K 2009 Rev. Mod. Phys. 81 109
- [8]Nénert G, Ritter C, Isobe M, Isnard O, Vasiliev A N and Ueda Y 2009 Phys. Rev. B 80 024402
- [9]Yariv A 1989 Quantum Electronics 3rd edn (New York: Wiley)
- [10]Butcher P N and Cotter D 1990 The Elements of Nonlinear Optics (Cambridge: Cambridge University Press)
- [11]Mills D L 1998 Nonlinear Optics 2nd edn (Berlin: Springer)
- [12]Gurevich A G and Melkov G A 1996 Magnetization Oscillations and Waves (Boca Raton, FL: CRC)
- [13]Stancil D D and Prabhakar A 2009 Spin Waves: Theory and Application (Heidelberg: Springer)
- [14]Jackson J D 1999 Classical Electrodynamics 3rd edn (New York: Wiley)
- [15]Griffiths D J 2012 Introduction to Electrodynamics 4th edn (Boston, MA: Addison-Wesley)
- [16]Stegeman G I, Seaton C T, Hetherington W M, Boardman A D and Egan P 1986 Electromagnetic Surface Excitations , ed R F Wallis and G I Stegeman (Berlin: Springer) p 261
- [17]Wendler L 1986 Phys. Stat. Solidi B 135 759
- [18]Weisbuch B and Vinter B 1991 Quantum Semiconductor Structures (Boston, MA: Academic)
- [19]Vollath D 2008 Nanomaterials (Weinheim: Wiley)
- [20]Esaki L and Tsu R 1970 IBM J. Dev. 14 61
- [21]MacDonald A H 1987 Interfaces, Quantum Wells, and Superlattices , ed C R Leavens and R Taylor (New York: Plenum) p 347
- [22]Albuquerque E L and Cottam M G 2003 Phys. Rep. 376 225
- [23]Yablonovich E 1987 Phys. Rev. Lett. 58 2059
- [24]John S 1987 Phys. Rev. Lett. 58 2486
- [25]Mitin V V, Kochelap V A and Stroscio M A 2008 Introduction to Nanoelectronics: Science, Nanotechnology, Engineering, and Applications (Cambridge: Cambridge University Press)
- [26]Aliofkhazraei M and Ali N 2012 Two-Dimensional Nanostructures (Boca Raton, FL: CRC)
- [27]Cottam M G and Lockwood D J 1986 Light Scattering in Magnetic Solids (New York: Wiley)
- [28]Cardona M and Güntherodt G (ed) 1989 Light Scattering in Solids vol 5 (Berlin: Springer)
- [29]Dutcher J 1995 Linear and Nonlinear Spin Waves in Magnetic Films and Superlattices , ed M G Cottam (Singapore: World Scientific) p 287
- [30]Hillebrands B and Ounadjela K (ed) 2003 Spin Dynamics in Confined Magnetic Structures vol 2 (Berlin: Springer)
- [31]Woodruff D P and Delchar T A 1986 Modern Techniques of Surface Science (Cambridge: Cambridge University Press)
- [32]Feldman L C and Mayer J W 1986 Fundamentals of Surface and Thin Film Analysis (Amsterdam: North-Holland)
- [33]Lehwald S, Szeftel J, Ibach H, Rahman T S and Mills D L 1983 Phys. Rev. Lett. 50 518
- [34]Hopster H 1994 Ultrathin Magnetic Structures vol 1 , ed J A C Bland and B Heinrich (Berlin: Springer)
- [35]Schreyer A, Schmitte T, Siebrecht R, Bödeker P, Zabel H, Lee S H, Erwin R W, Majkrzak C F, Kwo J and Hong M 2000 J. Appl. Phys. 87 5443
- [36]Brusdeylins G, Doak R B and Toennies J P 1981 Phys. Rev. Lett. 46 437
- [37]The Object Oriented MicroMagnetic Framework (OOMMF) project at ITL/NIST http://math.nist.gov/oommf
- [38]Bransden B H and Joachain C J 2000 Quantum Mechanics 2nd edn (Englewood Cliffs, NJ: Prentice-Hall)
- [39]Landau L D and Lifshitz E M 1980 Statistical Physics (Oxford: Pergamon)
- [40]Cottam M G and Maradudin A A 1984 Surface Excitations , ed V M Agranovich and R Loudon (Amsterdam: North-Holland) p 1
- [41]Joannopoulos J D, Johnson S G, Winn J N and Meade R D 2008 Photonic Crystals: Molding the Flow of Light 2nd edn (Princeton, NJ: Princeton University Press)
- [42]Rytov S M 1956 Sov. Phys. Acoust. 2 68
- [43]Yariv A and Yeh P 1984 Optical Waves in Crystals (New York: Wiley)
- [44]Yablonovitch E, Gmitter T J and Leung K M 1991 Phys. Rev. Lett. 67 2295
- [45]Lin S Y, Fleming J G, Hetherington D L, Smith B K, Biswas R, Ho K M, Sigalas M M, Zubrzycki W, Kurtz S R and Bur J 1998 Nature 394 251










