Probe method for measuring the diffusion coefficient in edge plasma

Several probe methods have been developed to measure the ion temperature in fusion plasmas.^1–5) In the edges of these plasmas, the ion temperature T_i has been found to exceed the electron temperature T_e in tokamaks such as DITE,⁶⁾ TEXTOR,⁷⁾ and JFT-2M.⁸⁾ In the plasmas with T_i > T_e, the effect of the presheath is small so the ions reach the probe with almost the thermal velocity. Furthermore, in the edge plasma, the movement of ions cannot always be treated as being completely collisionless. Since the magnetic field is strong, the diffusion becomes strongly anisotropic. In view of these facts, in this paper, the diffusion equation is applied under the condition of anisotropic flow due to a strong magnetic field.

Heretofore, the diffusion and thermal diffusion coefficients have been estimated from the e-folding length of the ion temperature and density.⁹⁾ The objective of this paper is to present a method to obtain the diffusion coefficient directly. The ion temperature can be estimated from the diffusion coefficient. The present probe method will be useful in high-density and high-temperature plasmas.

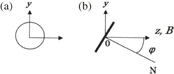
We assume that the double probe is composed of two electrodes: a disk and a sphere with radius a. We take the magnetic field B along the z-axis (cf. Fig. 1). The normal N of the disk at the center O pretends B by angle φ and the y-axis is perpendicular to the z-axis. Then, the x-axis can be automatically defined. The coordinates for the sphere are taken similarly.

Zoom In Zoom Out Reset image size

In the present paper, we consider the ion saturation current. The current–voltage characteristics are not considered except for the disk probe considered later in Eq. (19) concerning Bohm diffusion.

Considering that the dimension of the edge plasma is of the order of m while the size of the probe is of the order of mm, we treat the ion saturation current density j to the probe by using the diffusion equation, i.e., the macroscopic treatment by Bohm,¹⁰⁾ as

$$\begin{equation} j_{x} = -eD_{\bot}\frac{\partial n}{\partial x},\quad j_{y} = - eD_{\bot}\frac{\partial n}{\partial y},\quad j_{z} = -eD_{\|}\frac{\partial n}{\partial z}, \end{equation} \tag{ 1 }$$

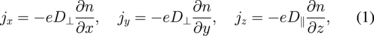
where n is the ion density, and D_∥ and D_⊥ are the diffusion coefficients parallel and perpendicular to B, respectively.

Applying the current continuity div j = 0 and transforming the coordinate system (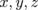$x,y,z$) to (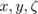$x,y,\zeta$), where ζ = (D_⊥/D_∥)^1/2z, we have, in the transformed coordinate,

$$\begin{equation} D_{\bot}\nabla^{2}n = 0. \end{equation} \tag{ 2 }$$

The current I to the probe is given by the surface integral as

$$\begin{equation} I = -e\sqrt{\alpha} D_{\|}\int \frac{\partial n}{\partial \mathbf{r}} \cdot d\mathbf{s} = -e\frac{D_{\bot}}{\sqrt{\alpha}}\int \frac{\partial n}{\partial \mathbf{r}}\cdot d\mathbf{s}, \end{equation} \tag{ 3 }$$

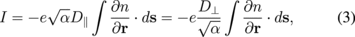
where α = D_⊥/D_∥ and note that the increment of density n by α^−1/2 arises owing to the contraction of the z-axis. Using the analogy to electromagnetism, the electric charge Q on the surface of an electrode is given by

$$\begin{equation} Q = -\varepsilon_{\text{o}}\int \frac{\partial V}{\partial \mathbf{r}} \cdot d\mathbf{s} = -C(V_{\text{s}} - V_{\text{o}}), \end{equation} \tag{ 4 }$$

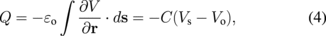
ε_o being the dielectric constant, C the capacitance of the electrode, and V_s and V_o the electrostatic potentials on the surface and at infinity, respectively.

Noting the analogy between Eqs. (3) and (4), i.e., the correspondence of I/(eα^1/2D_∥) to Q/ε_o and n to V, we obtain

$$\begin{equation} I = e\sqrt{\alpha} D_{\|}C(n_{\text{o}} - n_{\text{s}}), \end{equation} \tag{ 5 }$$

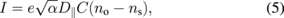
where n_s and n_o are the ion densities at the sheath edge and the plasma, respectively, and C is the equivalent capacitance of the electrode, where we assume, for simplicity, that the dielectric constant ε_o is contained in C.

The reduction in the ion density from n_o to n_s near the probe occurs as a result of the sink effect of the probe. Because of this effect, the density decreases towards the probe, while the potential decrease from the plasma toward the sheath edge is negligibly small.

When T_i > T_e, the effect of a presheath in front of the probe surface becomes negligibly small³⁾ (e.g., the Bohm criterion eV_B at T_i/T_e = 10 becomes eV_B/κT_e = 0.03 or eV_B/κT_i < 0.004 and decreases further with larger T_i/T_e). Hence, the current may be approximately given by the random current. It may be assumed further that the sheath thickness d_s is very small owing to the high plasma density in the edge plasma (in the present paper, the plasma parameter is assumed to be those of the edge plasma: n_o = 10¹¹–10¹² cm⁻³ and κT_e ∼ 10 eV. The Debye length λ_D becomes λ_D = 2.4–7.4 × 10⁻³ cm, which is much smaller than the assumed probe radius a of about 0.5 cm. Since d_s is about threefold λ_D, it becomes d_s ≪ a. In the edge plasma of about 10⁻³ Torr, the mean free path λ is much larger than the sheath thickness. That is, it is almost collision free inside the sheath). Therefore, the current at the probe surface, I, is given by the random current as

$$\begin{equation} I = \frac{eS}{4}n_{\text{s}}v_{\text{i}},\quad v_{\text{i}} = \sqrt{\frac{8\kappa T_{\text{i}}}{\pi M}}, \end{equation} \tag{ 6 }$$

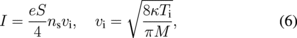
where S is the probe surface area, M is the ion mass and κ is the Boltzmann constant. Note that n_s must be different between the cases of sphere and disk electrodes. Eliminating n_s from Eqs. (5) and (6), we obtain

$$\begin{equation} i = \frac{I}{I_{\text{o}}} = \frac{D_{\|}C\sqrt{\alpha}}{Sv_{\text{i}}/4 + D_{\|}C\sqrt{\alpha}}, \end{equation} \tag{ 7 }$$

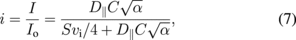
where I_o = eSn_ov_i/4; n_o the ion density in plasma.

Let us consider the current to disk electrode.

Because of the tilt of the surface vector relative to the magnetic field B by angle φ, the shape of the probe becomes an ellipse with axes a and b = a[α sin² φ + cos² φ]^1/2 in the coordinate ($x,y,\zeta$). Using the formula for the ellipsoid,¹¹⁾ the capacitance C_d is given by

$$\begin{equation} C_{\text{d}}/a = \frac{4\pi}{\mathrm{K}(k)}, \end{equation} \tag{ 8 }$$

where K is the complete elliptic integral of the first kind and the modulus k is given by

$$\begin{equation} k = \sqrt{1 - b^{2}/a^{2}} = \sqrt{1-\alpha} \sin \varphi. \end{equation} \tag{ 9 }$$

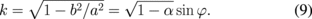
Substituting Eqs. (8) and (9) into Eq. (7), we can obtain the current for the disk, I_d. When φ = 0, we have α = 1, and k = 0 and hence K(k) = π/2. Then, C_d = 8a, which is the capacitance of a circular disk. As the magnetic becomes stronger and as φ becomes larger, k increases towards 1 and C_d decreases towards zero.

Next, consider the current to spherical electrode.

Because of the contraction of the z-axis, the sphere becomes an oblate spheroid with long and short axes a and α^1/2a, respectively. Using the formula for the spheroid,^11,13) the capacitance C_s is given by

$$\begin{equation} C_{\text{s}} = \frac{4\pi a\sqrt{1 - \alpha}}{\sin^{-1}\sqrt{1-\alpha}}. \end{equation} \tag{ 10 }$$

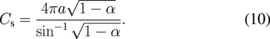
Substituting Eq. (10) into Eq. (7), we obtain the normalized current I_s for the sphere. In the case without magnetic field, we have α = 1. In this limit, using sin⁻¹ x ∼ x, we have C = 4πa, which is the capacitance of a sphere. As the magnetic field increases, α tends to zero. In the limit of α → 0, we obtain C = 8a, which is the capacitance of a circular disk.

The ratio R of currents for sphere I_s and disk electrodes I_d with radius a is obtained from Eq. (7) as follows:

$$\begin{equation} R \equiv \frac{I_{\text{s}}}{I_{\text{d}}} = 4\frac{C_{\text{s}}}{C_{\text{d}}} \cdot \frac{\pi a^{2}v_{\text{i}}/4 + D_{\|}C_{\text{d}}\sqrt{\alpha}}{\pi a^{2}v_{i} + D_{\|}C_{\text{s}}\sqrt{\alpha}}. \end{equation} \tag{ 11 }$$

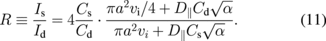
Using D = λv_i/3, where λ is the mean free path and v_i is the mean ion velocity, we finally have

$$\begin{equation} R = 4\frac{C_{\text{s}}}{C_{\text{d}}} \cdot \frac{1/4 + (\lambda/3\pi a)(C_{\text{d}}/a)\sqrt{\alpha}}{1 + (\lambda/3\pi a)(C_{\text{s}}/a)\sqrt{\alpha}}. \end{equation} \tag{ 12 }$$

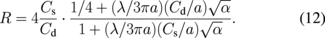
It is seen that R is a function of α with λ/a as a parameter.

The current ratio for φ = 0 (disk surface ⊥ B) becomes as follows.

For B = 0 (α = 1), we have C_d = 8a, and C_s = 4πa. Hence,

$$\begin{equation} R = 4 \cdot \frac{1 + (3\pi/32)a/\lambda}{1 + (3/4)a/\lambda}. \end{equation} \tag{ 13 }$$

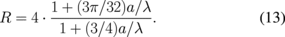
Because of a sink effect of the probe, R deviates from the surface ratio of 4. However, this effect is very small if a ≪ λ. In the limit of very strong B (α → 0), we have C_d = C_s = 8a. Hence, R tends to 1. Therefore, the dynamic range of R between B = 0 and ∞ becomes ∼4.

The current ratio for φ = 90° (disk surface ∥ B) becomes as follows.

For B = 0 (α = 1), R is given by Eq. (13).

For B ≠ 0 (α < 1), C_d decreases as B increases. From Eq. (12), R tends to C_s/C_d in the limit of α → 0 and increases to infinity. Although the dynamic range of R becomes large, this holds only in the region where φ deviates slightly from 90°.

In the above model, as the disk surface approaches φ = 90°, the current I_d becomes 0. However, actually, the effect of finite thickness will appear. In order to treat this problem, the disk probe can be constructed as a thin oblate spheroid with the major and minor axes a and d, (d ≪ a) respectively. When the thin spheroid rotates by φ, the lengths p₁, p₂, and p₃ of the three axes become p₁ = a, p₂ = a(cos² φ + α sin² φ)^1/2, and p₃ = d(sin² φ + α cos² φ)^1/2, respectively.

The capacitance of the ellipsoid is given by^12,13)

$$\begin{equation} \frac{1}{C} = \frac{1}{8\pi}\int_{0}^{\infty}\frac{d\xi}{\sqrt{(p_{1} + \xi)(p_{2} + \xi)(p_{3} + \xi)}}, \end{equation} \tag{ 14 }$$

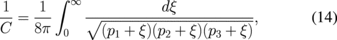
which can be reduced to analytic forms in limited cases.

For φ = 0,

$$\begin{equation} \frac{1}{C_{\text{d}}} = \frac{1}{4\pi \sqrt{a^{2} - d^{2}\alpha}} \cdot \cot^{-1}\left(\frac{\sqrt{d^{2}\alpha}}{\sqrt{a^{2} - d^{2}\alpha}}\right). \end{equation} \tag{ 15 }$$

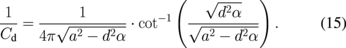
If α = 1, the probe becomes an elliptic body, i.e.,

$$\begin{equation} \frac{1}{C_{\text{d}}} = \frac{1}{4\pi \sqrt{a^{2} - d^{2}}} \cdot \cot^{-1}\left(\frac{d}{\sqrt{a^{2} - d^{2}}}\right). \end{equation} \tag{ 16 }$$

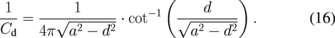
If α → 0, the probe becomes a circular disk, i.e., C_d = 8a.

For φ = 90°, if α = 1, the probe becomes an elliptic body, i.e., C_d is given by Eq. (16), and if α → 0, the probe becomes an elliptic plate, i.e.,

$$\begin{equation} \frac{1}{C_{\text{d}}} = \frac{\mathrm{K}(m)}{4\pi a};\quad m = \sqrt{1 - d^{2}/a^{2}}. \end{equation} \tag{ 17 }$$

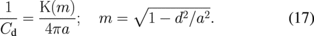
For the numerical calculation of the complete elliptic integral K, polynomial fittings¹⁴⁾ have been used.

Figure 2 shows examples of i_d and i_s as a function of α for λ/a = 30 with angle φ as a parameter. It is seen that both currents decrease with smaller α and that i_d shows a larger reduction with increasing φ.

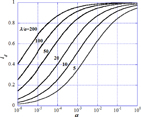
Zoom In Zoom Out Reset image size

Figure 3(a) shows the current ratio R = i_s/i_d of spherical to disk electrodes vs α for Λ/a = 50. Figure 3(b) shows details between φ = 80 and 90° in the range 10⁻⁶ < α < 10⁻³.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The angle dependence becomes more marked as φ approaches 90°, so the case of φ = 90° may be useful for the detection of the direction of magnetic field. On the other hand, the angle dependence is weak near 0°. This suggests that the design is easy for a disk surface perpendicular to B because the disk current is insensitive to small tilt.

Figure 4 shows the dependence on λ/a of the plane probe current i_d for the case of φ = 0° (surface ⊥ B) vs α. As λ/a increases (the pressure becomes lower or the probe is smaller), the dependence of i_d on λ/a becomes weaker at α > 10⁻³.

Zoom In Zoom Out Reset image size

A double probe consisting of a planar disk and a sphere with the same radius can be useful for the investigation of the diffusion coefficient in the edge plasma, that is, the ratio R of the saturation currents of the two electrodes can give α if the parameters λ/a and φ are known.

The ratio of diffusion coefficients α ≡ D_⊥/D_∥ for classical diffusion is

$$\begin{equation} \alpha = \frac{1}{1 + \omega^{2}\tau^{2}} = \frac{1}{1 + \omega^{2}\lambda^{2}(\pi M/8\kappa T_{\text{i}})}, \end{equation} \tag{ 18 }$$

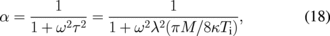
while α for Bohm diffusion is

$$\begin{equation} \alpha = \frac{3\pi T_{\text{e}}}{108T_{\text{i}}} \cdot \frac{1}{\omega \tau} = \frac{3\pi T_{\text{e}}}{108T_{\text{i}}}\cdot \frac{1}{\omega\lambda\sqrt{\pi M/8\kappa T_{\text{i}}}}, \end{equation} \tag{ 19 }$$

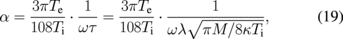
where D_⊥ = κT_e/16eB and D_∥ = λv_i/3 (λ: mean free path of ions) are used and ω and τ are the angular cyclotron frequency and the mean collision time of ions, respectively. Since α is a function of ωτ = ωλ/v_i, the value of T_i can be estimated from α using Eq. (18) in the case of classical diffusion. The retarding part of the current–voltage characteristics of the disk for φ = 0 can give T_e in the usual manner. Therefore, T_i can be estimated from α using Eq. (19) in the case of Bohm diffusion.

In summary, the applicable range of the present method is mainly in the edge plasma of helical and tokamak types whose parameters are n_o = 10¹⁷–10¹⁸ m⁻³, B of the order of Tesla and T_e ≫ T_i. Therefore, we have the condition λ_D < d_s ≪ a ≪ λ. It is almost collision free inside the sheath. The ion flow is anisotropic and governed by diffusion. The presheath is almost negligible but n_s < n_o owing to the sink effect of the probe.

For example, in the edge of Heliotron J, we have B = 1.4–1.6 T, T_e ∼ 20 eV, and n_o ∼ 7 × 10¹⁷ m⁻³. Using the collision cross section for hydrogen, σ ∼ 2 × 10¹⁶ cm²,¹⁵⁾ we have τ = 2.9 × 10⁻⁶ s and ω = 6.1 × 10⁷ s⁻¹. For the pressure of ∼10⁻³ Torr, we have λ = 20–50 cm. Then, λ/a = 40–100 in Figs. 2–4 are relevant values. The current ratio R = i_s/i_d shown in Figs. 3(a) and 3(b) serves to obtain D_⊥/D_∥. Using Eq. (18) or (19) depending on the diffusion modes, which must be determined by some other means, T_i is indirectly obtainable.

As an error source, the disk probe has no thickness. In order to reconcile this, a thin oblate spheroidal shape has been proposed, and the analytical form has been given. The accuracy of setting φ, especially near 90°, must be very high because R is very sensitive to φ. Other error sources such as probe supports and plasma noise, are common sources of error.

Acknowledgements