The Turbulence Magnetic Helicity Signature in the Interplanetary Medium: A Blackman–Tukey and Morlet Wavelet Analysis

Magnetic helicity is the dot product of the vector potential and magnetic field. The spectral magnetic helicity can determine the helicity associated with a spatial fluctuation as a function of wavenumber or of frequency when related to space by advection of fluctuations past a sensor (e.g., Matthaeus et al. 1982). With spectral magnetic helicity a handedness can be specified for fluctuations at a particular scale. Using a right-handed coordinate system, left-handed helicity corresponds to a clockwise rotation of the magnetic field in the xy plane when sampling in the positive z direction, and right-handed helicity counterclockwise. The spatial handedness is distinct from the temporal one used with respect to polarization in plasma physics.

Interplanetary fluctuations have a nonzero average magnetic helicity at small proton kinetic scales (e.g., Goldstein et al. 1994; Leamon et al. 1998a, 1998b, 1999; Hamilton et al. 2008; He et al. 2011; Podesta & Gary 2011; Smith et al. 2012; Markovskii et al. 2015, 2016). Toward small scales, the power spectrum breaks from a shallower inertial range to a steeper kinetic range (e.g., Smith et al. 2006; Alexandrova et al. 2009). An active energy cascade exists among the fluctuations, and energy dissipates at kinetic scales (e.g., Vasquez et al. 2007; MacBride et al. 2008; Stawarz et al. 2009). The dissipation range of turbulence can then overlap the kinetic range. The helicity generated at the kinetic scales could thereby indicate the nature of the fluctuations involved in the dissipation of the energy. Hereafter, the small-scale range is referred to as the kinetic range, but in circumstances where dissipation is of prime interest it is called the dissipation range.

The normalized magnetic helicity σ_m is given by kH_m/P_B, where H_m is the spectral magnetic helicity at wavenumber k and P_B is the trace of spectral magnetic power (e.g., see Markovskii & Vasquez 2016, their Equation (10)). The value of σ_m ranges from −1 to 1, where negative values correspond to right-handed helicity and positive values to left-handed helicity. The observed signature typically had positive values of σ_m when the interplanetary magnetic field was directed away from the Sun and negative when inward. Presuming a dominance of outward fluctuations from the Sun, these fluctuations are right-handed in the plasma frame.

Interpretations of the helicity signature have relied on the distinction between ions and electrons that occur near ion inertial and gyroradius scales and on solutions from both fluid and kinetic equations. At the plasma scales, wave modes in uniform media possess magnetic helicity (e.g., Gary 1986; Vasquez & Cargill 1993; Krauss-Varban et al. 1994; Hollweg 1999). The left-handed ion cyclotron mode, right-handed fast and kinetic Alfvén modes are the most important in solar wind applications (e.g., Leamon et al. 1999; Gary & Smith 2009; Chen et al. 2012; Smith et al. 2012).

The observed net helicity depends not only on the mode in the plasma frame but also on the propagation sense of the mode with respect to the background magnetic field B₀. There are two senses of propagation being either forward with B₀ or backward, and this sense is indicated by the sign of σ_m. For a single obliquely propagating mode, nonzero magnetic helicity develops for scales where ions and electrons must be given a separate treatment. The exception occurs for parallel propagation where the mode has the extremity of 1 for the absolute value of the normalized helicity $| {\sigma }_{{\rm{m}}}|$ at all scales. This corresponds to its circular polarization. An obliquely propagating wave mode has a smaller $| {\sigma }_{{\rm{m}}}|$ depending on the amount of departure from circular polarization. Typically with increasing wavenumber, the degree of circular polarization and $| {\sigma }_{{\rm{m}}}|$ increases for oblique propagation. When both senses of propagation occur for the same wave mode, the net $| {\sigma }_{{\rm{m}}}|$ approaches zero when the oppositely propagating waves have equal amplitudes. When different wave modes are combined, the effect on $| {\sigma }_{{\rm{m}}}|$ depends on their relative handedness and their relative sense of propagation.

The normalized cross-helicity σ_c can be used to deduce the relative fraction of wave energy associated with a sense of propagation and to identify handedness of the mode when combined with σ_m. The cross-helicity is the correlation between velocity and magnetic fluctuations and is normalized by the total fluctuation kinetic and magnetic energy. More wave energy is associated with forward propagation if σ_c < 0 and with backward if σ_c > 0. For small wavenumbers, a single Alfvén wave mode has $| {\sigma }_{{\rm{c}}}| =1$. In the inertial range of interplanetary turbulence, the small wavenumber approximation is valid. There the relative fraction of wave energy associated with a sense of propagation is directly proportional to σ_c. In the kinetic range, the wavenumbers are large enough that the magnitude of cross-helicity $| {\sigma }_{{\rm{c}}}|$ is not a direct measure of relative fraction and single wave modes need not have $| {\sigma }_{{\rm{c}}}| =1$.

The fluctuations are identified as right-handed according to the plasma physics convention if the magnetic helicity has the opposite sign compared to cross-helicity and left-handed if the sign is the same (Smith et al. 1983, 1984). The convention for right-handed sense can be expressed as σ_mσ_c < 0, and left-handed σ_mσ_c > 0.

Leamon et al. (1998a) examined the mean value of normalized magnetic helicity σ^int_m integrated over a frequency range within the dissipation range and its relationship with σ_c using Wind spacecraft data. Hamilton et al. (2008) followed with a much larger sample number using Advanced Composition Explorer spacecraft data integrating σ_m between 0.3 and 0.8 Hz. The value of σ_c was determined for inertial range scales and so was only considered to be a proxy at kinetic scales for the relative fraction of wave energy with propagation direction. The observed value of σ^int_m is around 0.3 when σ_c is near −1 and around −0.3 when σ_c is near +1. The trend is in accord with the dominance of the right-handed polarized wave modes.

Leamon et al. (1998a) were the first to offer an interpretation of this trend that Hamilton et al. (2008) supported. They considered that left-handed and right-handed fluctuations are equally generated by the turbulent cascade but left-handed polarized fluctuations are preferentially dissipated by ion cyclotron-resonant damping. A model in terms of the generation and destruction of left-handed and right-handed magnetic energy was constructed assuming fluctuation power is distributed isotropically with wave vector and that all fluctuations in the limit of a single type and a single sense of propagation have $| {\sigma }_{{\rm{m}}}| =1$ at the large wavenumbers corresponding to those of the dissipation range. Furthermore, the measured value of σ_c was taken to correspond with the energy fraction of fluctuations with different senses of propagation. In the limit where all left-handed polarized fluctuations were damped away, the trending slope between σ^int_m and σ_c was expected to be −1. The observed departure from this expected trend was used to calculate the relative rate of ion cyclotron-resonant damping. The observed slope led to the inference that two-thirds of the dissipation was ion cyclotron-resonant and the remainder could correspond to any other process, including damping at the Landau resonance.

An alternative interpretation had the right-handed magnetic helicity arising primarily from fluctuations with quasi-perpendicular wave vectors (He et al. 2011; Podesta & Gary 2011). Magnetohydrodynamic (MHD) turbulence can result in wave vectors that are quasi-parallel and quasi-perpendicular (e.g., Matthaeus et al. 1990; Bieber et al. 1996; Hamilton et al. 2008), but the energy cascade is strongest with the quasi-perpendicular wave vectors (e.g., Shebalin et al. 1983; Matthaeus et al. 1998; MacBride et al. 2008; Vasquez et al. 2014). Wavelet analyses of the magnetic helicity of interplanetary fluctuations have been done that reoganized the results according to a local mean evaluation of the magnetic field for each measurement at the particular scale examined (e.g., Horbury et al. 2008). This does have the effect of enhancing the wave vector anisotropy compared to a global mean B₀ (Matthaeus et al. 2012). The value of σ_m was then determined as a function of scale and the angle between the local mean field and sampling direction. A right-handed signature was found that corresponded with the quasi-perpendicular direction and a left-handed one with the quasi-parallel. The right-handed one has been interpreted as kinetic Aflvén wave modes involved in a turbulent energy cascade wherein the waves propagate and retain their linear properties (e.g., Howes & Quataert 2010). The quasi-parallel one has been interpreted as possibly the outcome of an electron heat flux instability (Podesta & Gary 2011).

Markovskii & Vasquez (2013a, 2013b, 2016) have conducted two-dimensional (2D) numerical hybrid simulations with particle protons and fluid electrons for strong turbulence bearing a magnetic helicity signature in the proton kinetic regime. This signature is generated among strongly turbulent fluctuations with no connection to wave modes. Markovskii & Vasquez (2013a, 2013b, 2016) followed the evolution of Alfvénic fluctuations with spatial wave vectors confined to a plane perpendicular to the magnetic field and finite σ_c. In the turbulence context, σ_c corresponds to the difference in Elsässer pseudo-energies and, for noncompressive fluctuations, nonlinear interactions vanish if $| {\sigma }_{{\rm{c}}}|$ is exactly unity. With this simulation wave vector configuration, a linear kinetic Alfvén wave-mode solution does not exist.

For a typical $| {\sigma }_{{\rm{c}}}| =0.8$, the simulated fluctuations developed a right-handed signature consistent with observations (Markovskii & Vasquez 2013a, 2013b, 2016; Markovskii et al. 2015, 2016). The signature also showed a peak of normalized magnetic helicity. This differs from a single kinetic Alfvén wave wherein the magnitude of the magnetic helicity asymptotes to a nearly constant value with increasing wavenumber (e.g., Hollweg 1999; Howes & Quataert 2010). The peak could be the result of dissipation and nonlinear effects. The position of the peak in wavenumber correlates with an inverse scale based on the square root of the sum of the proton and electron plasma pressure to magnetic pressure β ratio. The position was also in agreement with observations of signatures where a peak in the absolute value of the magnetic helicity was found (Markovskii et al. 2016). The simulations also showed that the signatures develop when $| {\sigma }_{{\rm{c}}}|$ had values near 1 rather than near 0. The peak magnitude of the normalized magnetic helicity increases weakly with increasing β. The magnitude of normalized magnetic helicity also increases with β for kinetic Alfvén wave modes, but single waves develop a plateau at higher wavenumbers rather than a peak and approach values near unity. Simulated protons were heated perpendicular to B₀ as is found in the solar wind. Linear kinetic Alfvén waves damp at the Landau resonance, and thereby heat protons parallel to B₀ (Stéfant 1970; Lysak & Lotko 1996; Quataert 1998).

In the present analysis parameters that potentially can affect the magnitude of the normalized magnetic helicity signature are examined for intervals where a peak has been found. Both Blackman–Tukey and Morlet wavelet spectra are utilized and compared. The wavelet method will be shown to permit an extension to shorter intervals. The global mean B₀ is used in the analysis because the Blackman–Tukey spectral method has always used this approach and because it directly addresses the disposition of the fluctuation energy in accordance with second-order moments (Matthaeus et al. 2012). The magnetic helicity is shown to be persistent through subdivision of the initial interval but is variable in magnitude. Fluctuations with quasi-perpendicular spatial wave vectors are shown to have a role in the observed right-handed signature. Model and simulation results are revisited. The magnitude of the peak normalized magnetic helicity is somewhat smaller than that predicted by the 2D simulations. The 2D simulations may characterize an upper bound for the peak magnitude. No trend between the peak magnitude and β is established though this is likely because it is obscured in the data. No current approach can be demonstrated to be consistent with all data concerning the magnetic helicity signature.

The outline of the paper is as follows: Section 2 explains the methods of the analysis and the data obtained by the Wind spacecraft. The results of the analysis are given in Section 3. Section 4 compares the observed magnetic helicity magnitude with theoretical and simulation predictions. Section 5 summarizes and discusses the results and conclusions.

Markovskii et al. (2015, 2016) developed a database of solar wind intervals with a magnetic helicity signature that has a peak and a power spectrum that could be interpreted in terms of a turbulent energy cascade. This database is used in the present analysis. The 92 ms magnetic data were obtained by Wind spacecraft (Lepping et al. 1995; Koval & Szabo 2013) between 2004 December 1 and 2005 December 31. During this period, the spacecraft was located near the L1 point. The solar wind intervals that sample the helicity spectra are chosen to be 100 minutes. More precisely, the interval length contains 65,536 regularly spaced samples, which is a power of 2. The Wind magnetic field measurements are in the GSE coordinates. The magnetic helicity calculation requires the RTN coordinate system. Therefore, the magnetic field was transformed to the RTN coordinates using ephemeris data.

Spectra are computed with the Blackman–Tukey algorithm (Blackman & Tukey 1958; Bieber et al. 1993), which gives the Fourier transform of the correlation tensor of the magnetic field $\langle {B}_{i}{B}_{j}\rangle$. The data are pre-whitened by a first-order difference filter and post-darkened on output (Chen 1989) to correct for power leakage in a sharply decreasing spectrum typical of the turbulence kinetic range. The power spectrum P_B is derived from the trace of the diagonal components of the tensor. The normalized reduced magnetic helicity spectrum is calculated from the off-diagonal $\langle {B}_{T}{B}_{N}\rangle$ component (Matthaeus et al. 1982)

$$\begin{eqnarray}&&{\sigma }_{{\rm{m}}}(\nu )=2\ \,\ \mathrm{Im}[\langle {B}_{T}{B}_{N}\rangle ]/{P}_{{\rm{B}}},\end{eqnarray} \tag{ 1 }$$

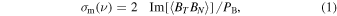
where ν is the frequency associated with the spacecraft time series of measured B in the RTN coordinate system at some integral lag of the sample time. The measured σ_m is said to be reduced because all fluctuation wave vectors are projected onto the direction of the spacecraft trajectory and combine to produce the measured magnetic helicity. With a single spacecraft trajectory, all components of the vector potential cannot be determined. Only a portion of the total normalized magnetic helicity σ^tot_m that can be present in association with all the components of the vector potential is, then, typically measured. Theory and simulations, generally, refer to σ^tot_m because they can fully specify the vector potential.

To determine the position and value of the magnetic helicity at the peak of a signature, the spectrum is fitted to an analytical function using the least-squares procedure:

$$\begin{eqnarray}&&{\sigma }_{m}={C}_{1}\exp \left[-\displaystyle \frac{1}{2}{\left(\displaystyle \frac{\nu -{C}_{2}}{{C}_{3}}\right)}^{2}\right]+{C}_{4}+{C}_{5}\nu +{C}_{6}{\nu }^{2},\end{eqnarray} \tag{ 2 }$$

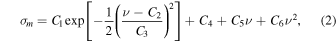
where C_i are the fitting constants. This combination of a Gaussian and a quadratic proves to be a simple and accurate expression for a spectrum with a peak. The position of the signature is taken to be the frequency where $| {\sigma }_{{\rm{m}}}|$ reached its maximum. The value of the signature σ^max_m is defined as the value σ_m (including the sign) at the maximum of $| {\sigma }_{{\rm{m}}}| .$

To interpret the properties of the helicity spectra, solar wind parameters of the corresponding intervals are obtained using the 96 s cadence proton plasma data from the Wind spacecraft (Ogilvie et al. 1995). The relevant parameters are the solar wind velocity, density, and isotropic proton thermal speed derived from nonlinear fitting to the ion current distribution function. Electron plasma data, specifically, the temperature derived from the total particle distribution are also necessary to this study (Ogilvie et al. 1995). The cadence of the electron data is 12 s.

In this paper, the helicity signature is also analyzed with a wavelet method. The Morlet wavelet function $\psi (\eta )\,={\pi }^{-1/4}{e}^{i{\omega }_{0}\eta }{e}^{-{\eta }^{2}/2}$ (Goupillaud et al. 1984) with ω₀ = 6 (Torrence & Compo 1998; Horbury et al. 2008) is used and η is the time normalized by the wavelet scale (see Torrence & Compo 1998). This function corresponds to a carrier wave modulated by a Gaussian envelope and localizes frequency at six times the scale of the wavelet. The magnetic helicity can be calculated with this function because it is complex.

A fast Fourier transform is used in the calculation of the wavelet spectrum for the entire interval, which is a power of 2 in terms of samples. Missing data are interpolated from data within the interval. The wavelet gives the spectrum as functions of time and scale. For the Morlet wavelet, the corresponding Fourier period is 1.03 times the scale. The global spectrum is calculated by integrating over the entire time domain separately for each period. The inverse of the period gives the corresponding frequency.

Section 3.1 presents the results from the 100 minute intervals obtained by the Wind spacecraft. Magnetic helicity spectra calculated with the Blackman–Tukey method are compared to those determined with the Morlet wavelet method. Signatures from each method are compared in terms of the position of the peaks of magnetic helicity, and in the sign and magnitude. The form and properties of the distribution of the magnitudes over all intervals are also examined and compared with each method. The obliquity angle, cross-helicity, and β from each interval are assessed to determine the conditions under which the magnetic helicity have been obtained. The relation between magnitude and cross-helicity and magnitude and β are then studied as these quantities have predicted effects on the magnetic helicity. The relations from both methods are compared and assessed.

Section 3.2 examines the persistence and variability of the magnetic helicity signature within subintervals. Variability is noted in the form of individual signatures and statistically by occurrence frequency of common forms and by the determination of the distribution of the relative change in the magnetic helicity magnitude. The contribution of the obliquity angle, cross-helicity, and β to the variation of magnetic helicity is treated by determining the change of obliquity angle, and the relative change of cross-helicity and β among the subintervals. Finally, the effect of shorter intervals on the relationship of magnitude to cross-helicity and to β is examined.

3.1. Analysis of 100 minute Intervals

Some examples of the spectra calculated with Blackman–Tukey and Morlet wavelet methods are shown in Figure 1. The position of the peak in the signature toward higher frequencies is consistent with both methods. The Morlet method yields a smoother time-averaged spectrum than does the Blackman–Tukey method. Figure 1(a) is a case where the two methods closely follow one another through the signature. About 30% of all cases have signature peaks within 20% of each other. More cases show a greater difference in magnitudes of the peak value such as those in Figures 1(b) and (c). The rare case is shown in Figure 1(d). Only about 4% of cases have a relative difference in peaks that are more than 80%. In no case did the sign of the signatures disagree.

Zoom In Zoom Out Reset image size

The positions of the peaks in the signatures ν_MW and ν_BT are close for each interval. The corresponding scatter plot in Figure 2 shows that the data points cluster tightly along the line of equal values. In 3 of 289 intervals, the signature was absent from the Morlet wavelet spectrum (e.g., Figure 1(d)), so the peak position could not be obtained. Markovskii et al. (2016) had established for the peak positions determined by the Blackman–Tukey method that the position in wavenumber based on the solar wind speed convecting the structure correlates with an inverse scale based on β^1/2. Since the Blackman–Tukey method agrees with the Morlet wavelet method with respect to signature position, the correlation with this inverse scale is obtained with either method.

Zoom In Zoom Out Reset image size

The values of the signatures were not equal to each other in each interval. Figure 3 displays the scatter plot of the signature magnitude $| {\sigma }_{{\rm{m}}}^{\max }|$. The average absolute difference between σ_BT and σ_MW is 0.07, which can be regarded as an uncertainty in the measured peak value. Nevertheless, statistically, the results of the two methods are not much different.

Zoom In Zoom Out Reset image size

Figure 4 plots the distribution functions of $| {\sigma }_{{\rm{m}}}^{\max }|$ for each method. The distributions show comparable maxima and spreads. A student's T-test (Trumpler & Weaver 1953) calculation found that the means of each distribution are very likely the same (probability equals 0.82). The Blackman–Tukey distribution extends to somewhat larger values than does the Morlet wavelet distribution and is less symmetrical about its maximum than is the Morlet. The differences here could result, in part, from a selection bias in that the peak signature was first chosen from intervals by applying the Blackman–Tukey method and choosing strong signatures from those intervals.

Zoom In Zoom Out Reset image size

The angle θ_B between the average magnetic field and radial direction is binned for the 100 minute intervals and plotted in Figure 5. The radial direction corresponds closely with the sampling direction. Most cases are quasi-perpendicular. A distribution maximum is found at 60° and a relative maximum near 120°. These are consistent with the sense of the Parker spiral angle at 1 au. Another relative maximum occurs at 85°, which shows that a number of intervals are sampled across the average magnetic field. Between 80° and 100°, there are 48 intervals. With these angles, nearly parallel propagating waves might not contribute to the sensible magnetic helicity.

Zoom In Zoom Out Reset image size

The parameter likely to have the strongest effect on the magnetic helicity is the cross-helicity. Strictly a correlation should not depend on the sign, and the absolute values are considered. Simulations (Markovskii & Vasquez 2016) found that the magnitude of the normalized magnetic helicity increases with β, and this also occurs for a kinetic Alfvén wave (e.g., Hollweg 1999). Thereby, the effect of plasma β is also examined.

The cross-helicity is taken from an average over the entire interval and is given by the formula:

$$\begin{eqnarray}&&{\sigma }_{{\rm{c}}}=2\displaystyle \frac{\sqrt{4\pi {m}_{{\rm{p}}}{n}^{\mathrm{avg}}}\,{(\delta {\boldsymbol{V}}\cdot \delta {\boldsymbol{B}})}^{\mathrm{avg}}}{{(4\pi {m}_{{\rm{p}}}{n}^{\mathrm{avg}}| \delta {\boldsymbol{V}}{| }^{2}+| \delta {\boldsymbol{B}}{| }^{2})}^{\mathrm{avg}}}.\end{eqnarray} \tag{ 3 }$$

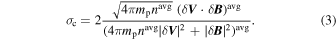
In Equation (3), m_p is the proton mass and the superscript "avg" denotes averaging over the interval. The vectors δV and δB have components $({V}_{x}-{V}_{x}^{\mathrm{avg}},{V}_{y}-{V}_{y}^{\mathrm{avg}},{V}_{z}-{V}_{z}^{\mathrm{avg}})$ and $({B}_{x}-{B}_{x}^{\mathrm{avg}},{B}_{y}-{B}_{y}^{\mathrm{avg}},{B}_{z}-{B}_{z}^{\mathrm{avg}})$ in GSE coordinates. The cross-helicity is taken from the volume average, by definition, in MHD and is a rugged invariant for incompressible and constant density media. The formulation in Equation (3) for spacecraft studies is based on this definition.

The plasma β is calculated as

$$\begin{eqnarray}&&\beta =\displaystyle \frac{8\pi \,{k}_{{\rm{B}}}\,{n}^{\mathrm{avg}}\,({T}_{{\rm{p}}}^{\mathrm{avg}}+{T}_{{\rm{e}}}^{\mathrm{avg}})}{{B}_{0}^{2}}.\end{eqnarray} \tag{ 4 }$$

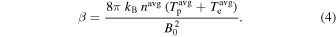
Here k_B is the Boltzmann constant, n is the number density, T_p and T_e are the proton and electron temperatures, and B²₀ is the squared average magnetic field intensity. The average magnetic field B₀ has the GSE components $({B}_{x}^{\mathrm{avg}},{B}_{y}^{\mathrm{avg}},{B}_{z}^{\mathrm{avg}})$. This definition of β is the one used in simulations and for linear waves in uniform media. Note that the combined thermal pressure does not include the alpha particles. They can contribute to the pressure during some solar wind intervals but on average are not expected to contribute significantly. If the relative abundance of the alpha particles is 5%, their temperature is four times the proton temperature, and the electron and proton temperatures are equal, then the effect of the alpha particles will be around 10%.

Figure 6(a) plots the dependence of σ_BT and Figure 6(b) σ_MW as a function of $| {\sigma }_{{\rm{c}}}|$. Correspondingly, Figures 6(c) and (d) show the dependence with β. Intervals with θ_B between 80° and 100° are marked with diamonds and the rest with crosses. There is an apparent correlation with $| {\sigma }_{{\rm{c}}}|$, but no trend is found with β. The relation between σ_MW and $| {\sigma }_{{\rm{c}}}|$ is particularly good with a fairly tight distribution about the trend near $| {\sigma }_{{\rm{c}}}| =1$ and only deviating nonuniformly near $| {\sigma }_{{\rm{c}}}| =0.3$. The intervals about 90° are distributed in much the same way as other angles.

Zoom In Zoom Out Reset image size

When the signed values of σ^max_m and σ_c are used, Markovskii et al. (2015) found a correlation. Every interval had the right-handed signature. Using the present data, a fit of the Blackman–Tukey results has ${\sigma }_{{\rm{m}}}^{\max }=-0.29{\sigma }_{{\rm{c}}}\,\mbox{--}\,0.01$ and of the Morlet results give the same. Even limiting to intervals with θ_B near 90° as shown by the diamonds in Figures 6(a) and (b) give nearly the same fits. The trend mainly joined values at the extremes of σ_c and in the diagonally opposed quadrants, where ${\sigma }_{{\rm{m}}}^{\max }{\sigma }_{{\rm{c}}}\lt 0$. The signed values overcome the incomplete sampling of cases with $| {\sigma }_{{\rm{m}}}^{\max }| \lt 0.1$ that could occur in the vicinity of σ_c = 0. The correlation is approximately consistent with the fit in Hamilton et al. (2008).

Hamilton et al. (2008) determined the correlation of signed σ_m with signed σ_c based on a value of σ^int_m integrated on a fixed domain of frequencies. A Blackman–Tukey analysis was used. Their database contained a number of cases with small values of $| {\sigma }_{{\rm{m}}}^{\mathrm{int}}|$ below 0.1. A re-examination of the results from Hamilton et al. (2008) finds that a correlation can be obtained when absolute values are used with a trend line ($| {\sigma }_{{\rm{m}}}^{\mathrm{int}}| =0.3| {\sigma }_{{\rm{c}}}|$) through the origin. The same trend line is followed by σ_MW as a function of $| {\sigma }_{{\rm{c}}}|$. The analysis of integrated and peak magnetic helicity appear to be consistent with one another.

There are far more intervals between β = 1 and 4 in Figures 6(c) and (d) than for β < 1. If a weak trend with β can be determined, it will need to occur between β = 1 and 4 where enough intervals have been obtained. A further binned analysis (not shown) of mean $| {\sigma }_{{\rm{m}}}|$ as functions of $| {\sigma }_{{\rm{c}}}|$ and β with β between 0.5 and 4.5 was made. Only for σ_MW and for $| {\sigma }_{{\rm{c}}}| \gt 0.8$ does an increasing trend of σ_MW with β occur. This trend could not be confirmed for the other bin values of $| {\sigma }_{{\rm{c}}}|$ or for any case with σ_BT. Moreover, the analysis followed below considered subdivisions of the intervals in terms of the Morlet wavelet results. These subintervals did not verify the trend for $| {\sigma }_{{\rm{c}}}| \gt 0.8$. Thereby, the results are inconclusive.

3.2. Analysis of 25 minute Subintervals

The 100 minute intervals were split into four 25 minute subintervals to study the persistence and variability of the magnetic helicity signatures. This subinterval size is about the smallest that could be expected for the correlation length of interplanetary turbulence and thus is likely below the actual correlation length. The subintervals may then not be independent. The task here is, however, to understand how the intervals are constituted with regards to the signature and to assess how background parameters, that could modify the helicity, vary.

The spectra in the subintervals are calculated only with the Morlet wavelet procedure. The Blackman–Tukey method produces more noise, and the signature is more difficult to identify. Figure 7 displays some examples of the spectra.

Zoom In Zoom Out Reset image size

Figure 7(a) shows a case where all four subintervals produce closely corresponding signatures. About 13% of cases all have peaks either within 0.05 or 20% of each other. An additional 40% of cases have three peaks within the same constraint as shown in Figure 7(b). Other cases have greater spread between signatures (Figure 7(c)) and a few (4%) show changes in sign. In no case does the peak magnitude exceed 0.5.

The occurrence frequency of cases like that in Figures 7(a)–(c) suggest that the signature is persistent in the subintervals but changes are also common. This behavior is examined with more detailed statistics. In several subintervals, the signature could not be identified. In this case, the whole interval was discarded. The intervals were also discarded when there was no plasma data coverage in one of the subintervals. This reduced the number of intervals in the database from 289 to 256. These 256 cases are used in the statistical studies below.

For each interval, the mean values over the four subintervals of the magnetic helicity

$$\begin{eqnarray}&&\langle {\sigma }_{{\rm{m}}}^{\max }\rangle =\,\displaystyle \frac{1}{4}\sum _{i=1}^{i=4}{({\sigma }_{{\rm{m}}}^{\max })}_{i}\end{eqnarray} \tag{ 5 }$$

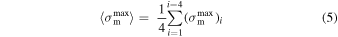
and other parameters were calculated along with the variability. The measure of the variability was taken to be equal to the standard deviation

$$\begin{eqnarray}&&{\rm{\Delta }}{\sigma }_{{\rm{m}}}^{\max }=\displaystyle \frac{1}{2}{\left(\sum _{i=1}^{i=4}{({({\sigma }_{{\rm{m}}}^{\max })}_{i}-\langle {\sigma }_{{\rm{m}}}^{\max }\rangle )}^{2}\right)}^{1/2}.\end{eqnarray} \tag{ 6 }$$

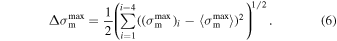
The distribution function of the relative variability of the magnetic helicity signature value ${\rm{\Delta }}{\sigma }_{{\rm{m}}}^{\max }/\,| \langle {\sigma }_{{\rm{m}}}^{\max }\rangle |$ is plotted in Figure 8. The distribution shows that the signature is persistent in the sense that it is present most of the time throughout the 100 minute intervals. At the same time, the variations of the signature are not small.

Zoom In Zoom Out Reset image size

The variability of the background parameters might affect the magnetic helicity. Since the spacecraft samples a reduced helicity, the variation of the obliquity angle of the average magnetic field with respect to the sampling direction θ_B is examined. The average magnetic field is now assessed in each subinterval. Figure 9 shows that the distribution of the standard deviation of the angle in degrees among the intervals following the same formulation used in Equation (6). There are significant variations here. Thereby, the variations of θ_B could be a factor in the variations of σ_m. Some of the variability with angle comes from the large-scale fluctuations within the 100 minute interval and thus does not indicate exactly how the underlying mean field varies with direction.

Zoom In Zoom Out Reset image size

For each interval, the average σ_c and β are computed from the subintervals. The distribution of ${\rm{\Delta }}{\sigma }_{{\rm{c}}}/| \langle {\sigma }_{{\rm{c}}}\rangle |$ is displayed in Figure 10 and ${\rm{\Delta }}\beta /\langle \beta \rangle$ in Figure 11. The core of the distribution for ${\rm{\Delta }}{\sigma }_{{\rm{c}}}/| \langle {\sigma }_{{\rm{c}}}\rangle |$ is narrower than for ${\rm{\Delta }}{\sigma }_{{\rm{m}}}^{\max }/\,| \langle {\sigma }_{{\rm{m}}}^{\max }\rangle |$. In part, this is consistent with the correlation between σ_MW and $| {\sigma }_{{\rm{c}}}|$. With the correlation, some portion of the scatter of ${\rm{\Delta }}{\sigma }_{{\rm{m}}}^{\max }/\,| \langle {\sigma }_{{\rm{m}}}^{\max }\rangle |$ can be assigned to cross-helicity. The remainder is then due to other causes.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The distribution for ${\rm{\Delta }}\beta /\langle \beta \rangle$ is somewhat wider in the core than is ${\rm{\Delta }}{\sigma }_{{\rm{m}}}^{\max }/\,| \langle {\sigma }_{{\rm{m}}}^{\max }\rangle |$. Possibly β variations contribute to σ_MW scatter but only weakly if its contribution is limited to the remainder after cross-helicity effects. Some of the variations with β represent measurement uncertainties, particularly for the temperatures, rather than true spatial variations. These variations can obscure weak trends that may exist between $| {\sigma }_{{\rm{m}}}^{\max }|$ and β.

Another source for scatter in ${\rm{\Delta }}{\sigma }_{{\rm{m}}}^{\max }/\,| \langle {\sigma }_{{\rm{m}}}^{\max }\rangle |$ could come from variability of cascade and dissipation rates. The cascade rate is dependent on σ_c, and the cascade rate is related to the dissipation rate. Since σ^max_m trends with σ_c, scatter could arise from rate variability. For noncompressive and steady conditions, the mean dissipation rate for MHD turbulent fluctuations obeys a third-moment equation (Politano & Pouquet 1998a, 1998b). Application of third moments to successive near-correlation length samples finds a variable rate of cascade or dissipation in the interplanetary medium (Coburn et al. 2014, 2015). Ensemble averages can reproduce mean dissipation rates that are consistent with inferred mean plasma heating rates (e.g., Stawarz et al. 2009). Yet, in a single sample, that rate varies widely about the ensemble mean, and this might contribute to σ^max_m variability between intervals. An intermittent cascade dynamic may also cause departures from a gyrotropic distribution of magnetic helicity and power about B₀ which could also generate scatter in σ^max_m.

Figure 12 plots the dependency of $| {\sigma }_{{\rm{m}}}^{\max }|$ separately as a function of $| {\sigma }_{{\rm{c}}}|$ and β for the subinterval results. The patterns found with 100 minute intervals remain. More intervals with small $| {\sigma }_{{\rm{c}}}|$ are present, and the trend appears stronger. Additional data at low β is found, but there continues to be no trend with β.

Zoom In Zoom Out Reset image size

Shorter sampling of these background parameters does not alter the relationships. A functional dependency on β is still elusive. A further binned analysis (not shown) of mean $| {\sigma }_{{\rm{m}}}|$ as functions of $| {\sigma }_{{\rm{c}}}|$ and β also did not reveal any trend with β.

Models and simulations of the fluctuation magnetic helicity determine the total magnetic helicity of the fluctuations since all wave vectors and associated components of the vector potential and magnetic field are known. Observations have only the magnetic helicity that can be reduced to the sampling and presumed radial direction that is based on measurements of the tangential and normal magnetic field components. To compare predictions and observed values, the distinction between the total and observed quantities needs to be specified. To reiterate, the total normalized magnetic helicity is denoted by σ^tot_m, and the observed value at one frequency by σ_m or its maximum value by $| {\sigma }_{{\rm{m}}}^{\max }|$, and the observed amount averaged over a range of frequencies by σ^int_m.

As a simple and illustrative case, the magnetic helicity associated with parallel propagating wave modes is first considered. These circularly polarized wave modes have $| {\sigma }_{{\rm{m}}}^{\mathrm{tot}}| =1$ at all wavenumbers unless there is a mixture of types or a mixture of forward and backward propagating waves. One fluctuating magnetic field component in such a wave can be characterized by ${ \mathcal A }\cos {kx}$ and the other by $\pm { \mathcal A }\sin {kx}$ where the spectral amplitude ${ \mathcal A }$ can vary with wavenumber k and the position x is along the direction of B₀. Both fluctuating components are perpendicular to B₀. Assuming a single mode type and one sense of propagation direction at all k, the measured $| {\sigma }_{{\rm{m}}}|$ is only equal to 1 when the sampling, radial direction is along B₀. At other sampling angles, the fluctuating tangential and normal magnetic field components would not show a circular polarization alone because the remaining fluctuating component of the waves would be found in the radial direction. The measured magnitude of helicity based on the tangential and normal components alone is $2{{ \mathcal A }}^{2}\cos {\theta }_{{\rm{B}}}$, where θ_B is restricted from 0° to 90°. On the other hand, the trace magnetic spectral power $2{{ \mathcal A }}^{2}$ is based on all directional components and so does not vary explicitly with θ_B. Implicitly, power in the helicity and trace spectrum are functions of k and both shift together to smaller wavenumbers along the radial direction consistent with cos θ_B. This alters only the position in wavenumber space for which to compare observed values of $| {\sigma }_{{\rm{m}}}|$. Allowing for this shift, the ratio of measured helicity to trace power $| {\sigma }_{{\rm{m}}}|$ varies only with cosθ_B since the spectral powers cancel. As such, the value of $| {\sigma }_{{\rm{m}}}|$ is consistent with the degree of apparent elliptical polarization in the tangential and normal components.

Since at 1 au the average θ_B is 56°, the average reduced magnetic helicity is cos 56° = 0.56. Toward θ_B = 90°, $| {\sigma }_{{\rm{m}}}|$ would tend to zero. In detail, Figure 5 shows that the value of θ_B varies considerably about 90°. At θ_B = 80°, no value of $| {\sigma }_{{\rm{m}}}^{\max }|$ should exceed $0.17| {\sigma }_{{\rm{c}}}|$, but this excludes all but two of the diamond points in Figures 6(a) and (b). This verifies that the fluctuations contributing to $| {\sigma }_{{\rm{m}}}^{\max }|$ are not exclusively from parallel propagating wave modes.

A second factor that diminishes the observed magnitude occurs when the observed magnetic helicity is integrated and averaged over a range of frequencies. Because a net helicity signature is not found in the inertial range, $| {\sigma }_{{\rm{m}}}|$ tends to ramp up from lower frequencies to higher ones in the dissipation range. If a peak is present, then $| {\sigma }_{{\rm{m}}}|$ will also decrease at frequencies past the frequency corresponding to the maximum value. When the average is taken over an interval, the obtained amount is dependent on the chosen end points of the integration. The consequences of this approach are more difficult to quantify generally. This uncertainty can be avoided by considering the maximum magnitude of $| {\sigma }_{{\rm{m}}}|$. Therefore, the focus here will be on the effects of the sampling direction.

Leamon et al. (1998a) developed a model of the generation and dissipation of magnetic helicity. They assumed an isotropic distribution of wave vectors and associated spectral power. At the large wavenumbers in the dissipation range, all fluctuations of a given sense of propagation were assumed to asymptote to $| {\sigma }_{{\rm{m}}}^{\mathrm{tot}}| =1$. This latter assumption is only an approximation for wave modes in that for the actual wavenumbers considered in the dissipation range the value of $| {\sigma }_{{\rm{m}}}^{\mathrm{tot}}|$ can be less than 1 and vary with θ_B and plasma conditions. They then assumed that a turbulent cascade generates energy equally in left-handed and right-handed spatial fluctuations that is balanced by dissipation of energy with a polarization dependence that favors the resonant cyclotron dissipation of propagating left-handed wave modes in the plasma frame. The sense of propagation direction was estimated based on the value of σ_c in the inertial range. From the model, the net σ^tot_m could be specified as a function of σ_c and the relative rate of nonresonant γ₀ to resonant γ_r dissipation. These damping rates are not restricted to linear ones. Their model can be expressed in terms of the ratio of resonant to total damping as

$$\begin{eqnarray}&&\displaystyle \frac{{\gamma }_{r}}{{\gamma }_{r}+{\gamma }_{0}}=\displaystyle \frac{2}{1-\tfrac{{\sigma }_{{\rm{c}}}}{{\sigma }_{{\rm{m}}}^{\mathrm{tot}}}}.\end{eqnarray} \tag{ 7 }$$

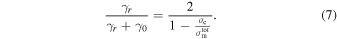
In effect, Leamon et al. (1998a) applied Equation (7) by replacing σ_c with the least-squares fit between σ_c and σ^int_m. Using a fit through the origin, they had ${\sigma }_{{\rm{c}}}=-1.90{\sigma }_{{\rm{m}}}^{\mathrm{int}}$. By equating σ^int_m with σ^tot_m, Equation (7) estimated that 69% of the energy cascade is dissipated by ion cyclotron-resonant processes.

There is a systematic correction not considered when the above model was applied to the solar wind. The observed magnetic helicity is generally some fraction f of the total and so ${\sigma }_{{\rm{m}}}^{\mathrm{int}}=f{\sigma }_{{\rm{m}}}^{\mathrm{tot}}$. To estimate the effect of the sampling direction, a Fourier mode configuration is considered in the present analysis, where each wave vector is associated with a circularly polarized fluctuation and so $| {\sigma }_{{\rm{m}}}^{\mathrm{tot}}| =1$. The wave vectors are then distributed uniformly over a half-sphere so as to represent fluctuations with the same sign of σ^tot_m and the same sense of propagation direction. Because every mode has circular polarization, it is sufficient to consider the projection of wave vectors to a single direction and at a particular wavenumber along that direction, say k_p. Also only the part of the power spectrum at wavenumbers k greater than k_p is necessary since the projection comes from wave vectors with larger magnitudes. With k_p representing a wavenumber in the dissipation range, the portion of the power spectrum used in calculations characterizes the dissipation range at higher k. The three-dimensional fluctuation spectral power in the dissipation range is taken to vary as k^−5.7. This corresponds to an omni-directional spectral index of −2.7, which is the observed mean value for interplanetary fluctuations in the dissipation range (Smith et al. 2006; Alexandrova et al. 2009).

The phase of each circularly polarized fluctuation is taken to be random. Perfect coherence would yield no difference between reduced and total in this case. Actual turbulent fluctuations are closer to the random phase, but there is some phase coherence associated with these fluctuations in the dissipation range; however, the amount is difficult to specify apart from simulation results of the turbulence. In the incoherent limit, an ensemble of 1000 cases, each with newly assigned random phases, is used to calculate that on average f = 0.81. In terms of the fit form and f, Equation (7) can be written as

$$\begin{eqnarray}&&\displaystyle \frac{{\gamma }_{r}}{{\gamma }_{r}+{\gamma }_{0}}=\displaystyle \frac{2}{1+1.90\,f}.\end{eqnarray} \tag{ 8 }$$

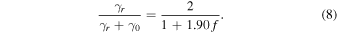
For f = 0.81, the amount of ion cyclotron damping increases to 79%. This value is still a lower bound in terms of systematic corrections because an integrated magnetic helicity was used.

A large relative amount of ion cyclotron damping is a reasonable conclusion based on the isotropic distribution of wave power that the model assumes. Away from the perpendicular directions to B₀, fluctuations would be expected to have a wave nature, and ion cyclotron resonance can be satisfied by propagating waves with left-handed polarization. However, the distribution of power is inferred to be anisotropic in the solar wind with more in quasi-perpendicular directions than quasi-parallel (Matthaeus et al. 1990; Bieber et al. 1996; Hamilton et al. 2008). This anisotropy could alter the partition of dissipation rate between ion cyclotron resonant and other processes and by the effect of sampling direction reduce the magnetic helicity to a value that can differ from that of an isotropic configuration of wave vectors.

Howes & Quataert (2010) considered a critical balanced model of highly oblique kinetic Alfvén wave modes in the limit of a single sense of propagation. For a sampling angle of 60^o, they calculated a value of $| {\sigma }_{{\rm{m}}}^{\max }|$ equal to 0.9. This reduced value then differs from the trend line for both σ_BT and σ_MW at $| {\sigma }_{{\rm{c}}}| =1$ by 310%. Since $| {\sigma }_{{\rm{m}}}^{\max }|$ can be no larger than 1, the maximum possible difference is only about 345%.

The above large discrepancy was noted by Howes & Quataert (2010) with regards to prior observational work and was deemed to have resulted by virtue of a significant change in the relative fraction of forward and backward propagating waves within the kinetic range. In that view, even though values of σ_c near ±1 are found in the inertial range that imply strongly outward propagation from the Sun that propagation dominance does not occur in the kinetic range. Nonlinear forces and effects must be brought to bear to reorder a directed nonlinear cascade with one sense of direction in the inertial range into a significantly modified one in the kinetic range. As such, the critical balanced model can only use the value of $| {\sigma }_{{\rm{m}}}^{\max }|$ as an indication of relative sense of propagation presuming that the kinetic Alfvén waves are present in the kinetic range and propagate very nearly in agreement with the linear wave-mode solutions. Analyses from Cluster spacecraft indicate that nonlinear corrections do apply to fluctuations in the kinetic range (e.g., Narita et al. 2011; Roberts et al. 2017).

Klein et al. (2014) considered an alternative explanation for the lower observed magnitudes of σ_m. They calculated that aliasing of kinetic Alfvén wave modes from higher wavenumbers and frequencies would cause the signature as seen by the spacecraft to decay toward zero at higher frequencies and limit the observed maximum magnitude. Markovskii et al. (2016) showed, however, that the positions of the signature in the database of peaks were at lower frequencies than were the predicted onset of significant aliasing.

Hybrid simulations of turbulent fluctuations with perpendicular wave vectors that have examined the resultant magnetic helicity signature have been made mostly for $| {\sigma }_{{\rm{c}}}| =0.8$ (e.g., Markovskii & Vasquez 2016). In addition, observations in the present analysis come mostly from intervals with β of the order of unity. The most relevant simulation for such cases has β = 1 wherein maximum $| {\sigma }_{{\rm{m}}}^{\mathrm{tot}}|$ is 0.6. This result, however, needs to be re-examined in the present analysis because it is the reduced $| {\sigma }_{{\rm{m}}}^{\max }|$ that is actually observed. A direct calculation of $| {\sigma }_{{\rm{m}}}^{\max }|$ was made with the spectrum obtained from simulation results. Taking the simulation grid to be the xy plane and B₀ along the z direction, a line can be taken that is oblique to B₀ at angle θ_B and so involves a z coordinate. Values of B from the simulation results can be assigned to this line using the fact that B depends only on x and y coordinates and so is independent of z. This yields a time series of B measurements corresponding to the manner in which a probe would acquire. For the purposes of determining the reduced magnetic helicity, the sampling line is taken to be along the R direction, and B is transformed to a coordinate system equivalent to RTN. For a fixed θ_B, this process is repeated for many different lines and at many times during the quasi-steady turbulent phase, and the final result is the average of all. Therefore, the resultant reduced $| {\sigma }_{{\rm{m}}}^{\max }|$ is an average value that should be compared to the average of observed values. The average value of $| {\sigma }_{{\rm{m}}}^{\max }|$ as a function of θ_B has also been obtained. The amount of reduction determined can be characterized by the factor 0.64 sin θ_B. For 1 au observations, the expected average θ_B is 56°, and for this θ_B, the predicted $| {\sigma }_{{\rm{m}}}^{\max }|$ is 0.32. Near $| {\sigma }_{{\rm{c}}}| =0.8$, the average of observed values is 0.23 according to the trend line and so the predicted value is 0.09 above which is a 40% relative difference. Compared to the tightly organized values of σ_MW near $| {\sigma }_{{\rm{c}}}| =0.8$ in Figure 6(b), the simulation predicted mean value even falls on the very high side of the observed range of individual values of σ_MW. Thus, the discrepancy is considered significant in that the essential physical circumstances responsible for the interplanetary magnetic helicity signature may not be completely represented within the 2D hybrid simulations.

It is possible that the discrepant 2D simulation results may be reconciled by the inclusion of electron kinetic effects or some other factor of importance to the solar wind that was missed. Another possibility is that the 2D simulation results define an upper bound for the magnitude of the normalized magnetic helicity. If the magnetic helicity maximizes in value with the perpendicular wave vectors relative to less oblique wave vectors, a full 3D configuration with a broad range of energized and quasi-perpendicular wave vectors might account for a smaller overall average for the normalized magnetic helicity. Moreover, the additional presence of a quasi-parallel component with the opposite sign of magnetic helicity as is observed by He et al. (2011) and Podesta & Gary (2011) and with less power than the quasi-perpendicular component would yield a right-handed but smaller net magnitude for the reduced magnetic helicity than is obtained with just the quasi-perpendicular component.

The examined magnetic helicity signatures peak at frequencies lower than the range where the power spectrum shows flattening, which is evidence of instrumental effects, and lower than the range where aliasing from higher frequencies would be anticipated (Markovskii et al. 2016). These signatures are then deemed to be resolved by the Wind magnetometer. The helicity associated with these signatures can then be compared to one another with confidence that significant contributions from higher frequencies have not been lost.

Blackman–Tukey and Morlet wavelet methods have been employed, and results compared with one another. Both methods yield positions for the signature that are correlated one-to-one. The signs of the magnetic helicity also agree in each interval. The magnitudes of the peak of normalized magnetic helicity do not correlate, and instead there is a range of uncertainty of ≈0.07. The results of each method do agree statistically. The Morlet wavelet method yields, however, a magnetic helicity spectrum that has less noise than does the Blackman–Tukey spectrum. When $| {\sigma }_{{\rm{m}}}^{\max }|$ is considered to be a function of $| {\sigma }_{{\rm{c}}}|$, the Morlet wavelet method shows a more organized and stronger trend. As such, the Morlet method was used to analyze the intervals separated into contiguous subintervals. Results from subintervals show that the magnetic helicity signature is persistent but variable. Signatures with smaller $| {\sigma }_{{\rm{m}}}^{\max }|$ were detected that better complete the existing trend between $| {\sigma }_{{\rm{m}}}^{\max }|$ and $| {\sigma }_{{\rm{c}}}|$. Relative variations of $| {\sigma }_{{\rm{m}}}^{\max }|$ were found to be larger than those of cross-helicity but less than those of β. Obliquity angle varies by about 20° within the subintervals.

In the analysis, the physical origin of the magnetic helicity signature was sought mainly by considering $| {\sigma }_{{\rm{m}}}^{\max }|$ as a function of $| {\sigma }_{{\rm{c}}}|$ and then separately as a function of β. There is a trend between $| {\sigma }_{{\rm{m}}}^{\max }|$ and $| {\sigma }_{{\rm{c}}}|$ that is consistent with Hamilton et al. (2008). The trend had been used to infer the relative rate of ion cyclotron damping of the turbulent energy cascade (Leamon et al. 1998a; Hamilton et al. 2008). The influence of the sampling direction was not previously considered, and this has been shown to systematically increase the rate of inferred cyclotron damping. There is no evident trend between $| {\sigma }_{{\rm{m}}}^{\max }|$ and β with values of β mostly sampled between 1 and 4.

Application of the Morlet wavelet method has most values for $| {\sigma }_{{\rm{m}}}^{\max }|$ smaller than 0.3 even when $| {\sigma }_{{\rm{c}}}|$ is near 1. These values are below the expected average of simulated turbulent fluctuations with perpendicular wave vectors (Markovskii & Vasquez 2013a, 2013b, 2016) and well below for kinetic Alfvén wave modes with the same sense of propagation direction. In addition, if any trend exists between $| {\sigma }_{{\rm{m}}}^{\max }|$ and β, it is likely obscured by the variability of $| {\sigma }_{{\rm{m}}}^{\max }|$ and β. Thereby, a comparison of model and simulation results as a function of β could not be convincingly done. More data or more precise measurements are needed. Fluctuations with oblique wave vectors would likely have some dependence on β, and with the establishment of that dependence, future approaches to explain the magnetic helicity signature could be more stringently verified.

At present the physical processes at work that provide for the interplanetary turbulence magnetic helicity signature are not satisfactorily understood. Predictions from models have drawn invariably from properties of linear wave modes. A direct one-to-one correspondence between the signature and the properties of the waves is not found. Instead the models had to interpret the observed signature in terms of the partition of dissipation rates (Leamon et al. 1998a) or of the sense of propagation within the kinetic range (Howes & Quataert 2010). At present, the accuracy of the predictions have not been verified.

Hybrid simulation results attempt to explain the signature and its properties directly (Markovskii & Vasquez 2013a, 2013b, 2016). This line of research has considered the proposition that the nonlinearity that brings about the energy cascade also alters the properties of the fluctuations from those defined by the exact linear wave-mode solutions from the governing equations. In pursuit of the validity of this proposition, the 2D perpendicular wave vector configuration was identified as a way to separate wave from turbulent fluctuations. In particular, no linear kinetic Alfvén wave-mode solution applies in this configuration. Yet the 2D approach, itself, does not confirm the proposition because the simulation reduced magnitude of magnetic helicity is larger than that obtained from the Morlet wavelet method for $| {\sigma }_{{\rm{c}}}|$ near 1. Nonetheless, the restriction of all wave vectors to the 2D plane perpendicular to B₀ gives results that come close in description of the interplanetary turbulence magnetic helicity signature. Likely the 3D wave vector configuration will need to be examined with simulations to reproduce the observations.

The Wind spacecraft data were obtained from CDAWeb (http://cdaweb.gsfc.nasa.gov). The authors are grateful to the Wind/IMF and Wind/SWE teams for making the data available. This work is supported by NSF SHINE grants AGS1357893 and AGS1622413.