Abstract
On account of its finite temperature, the unmagnetized intergalactic medium (IGM) is subject to thermal fluctuations. Due to the fundamental coupling between particles and fields in a plasma, the field fluctuations generate current densities by means of the Lorentz force and thereby affect both the density and the velocity fluctuations of the particles. Recently, a new damped, aperiodic mode was discovered that dominates field fluctuations in the IGM. Apart from its impact on the transport properties of the IGM that determine the propagation of cosmic rays, previous research has shown that this mode provides turbulent magnetic seed fields of 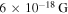 that are an essential ingredient in the generation of cosmic magnetic fields. The current investigation addresses the influence of the mode on the particle motion. In order to describe the corresponding state of the turbulence, both the spectrum and the integrated total value of the mode-driven proton velocity fluctuations are computed. It is found that the latter amounts to
that are an essential ingredient in the generation of cosmic magnetic fields. The current investigation addresses the influence of the mode on the particle motion. In order to describe the corresponding state of the turbulence, both the spectrum and the integrated total value of the mode-driven proton velocity fluctuations are computed. It is found that the latter amounts to 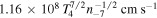 assuming a temperature of
assuming a temperature of 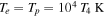 and a density of
and a density of 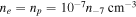 . This value is two orders of magnitude larger than the thermal velocity. If the IGM neutrals adopt the same velocities as the protons by mutual charge exchange and elastic collisions (ambipolar diffusion), atomic lines propagating through the IGM are expected to display spectral broadening, enhanced by a factor of 90 beyond the thermal level in the case of hydrogen. This opens the window to a first direct observation of the damped aperiodic mode. Other observational techniques such as dispersion measure, rotation measure, and scintillation data are not applicable in this case because the mode is a transverse one, and, as such, it does not induce the required density fluctuations, as is shown here.
. This value is two orders of magnitude larger than the thermal velocity. If the IGM neutrals adopt the same velocities as the protons by mutual charge exchange and elastic collisions (ambipolar diffusion), atomic lines propagating through the IGM are expected to display spectral broadening, enhanced by a factor of 90 beyond the thermal level in the case of hydrogen. This opens the window to a first direct observation of the damped aperiodic mode. Other observational techniques such as dispersion measure, rotation measure, and scintillation data are not applicable in this case because the mode is a transverse one, and, as such, it does not induce the required density fluctuations, as is shown here.
Export citation and abstract BibTeX RIS
1. Introduction
Due to the random motion of the discrete particles constituting a plasma, every state variable of the ensemble is subject to fluctuations. Although a microscopic phenomenon, fluctuations can have tremendous effects on macroscopic scales: they are involved in the formation of collisionless shock waves (Medvedev & Loeb 1999; Bret et al. 2013), affect the transport of relativistic cosmic rays (Dröge 2000; Schlickeiser 2011), and can provide the required seed fields for the genesis of cosmic magnetic fields (Schlickeiser 2012; Yoon et al. 2014).
Throughout the history of plasma physics, field fluctuations have been one of the major topics of research. Motivated by observations of a rich variety of wave modes ![$\propto \,\exp [{\imath }({\boldsymbol{k}}\cdot {\boldsymbol{r}}-\omega t)]$](https://content.cld.iop.org/journals/0004-637X/844/2/124/revision1/apjaa7d05ieqn5.gif) , these studies predominantly focused on weakly damped or weakly growing fluctuations that propagate a considerable distance (in multiples of the wavelength) before any significant modification of the amplitude occurs. In the spectral domain, this case corresponds to the limit
, these studies predominantly focused on weakly damped or weakly growing fluctuations that propagate a considerable distance (in multiples of the wavelength) before any significant modification of the amplitude occurs. In the spectral domain, this case corresponds to the limit 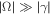 in terms of the complex frequency
in terms of the complex frequency 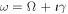 . It is a recent development that enhanced attention was paid to the opposite case of weakly propagating waves (such as the firehose and mirror modes) with
. It is a recent development that enhanced attention was paid to the opposite case of weakly propagating waves (such as the firehose and mirror modes) with  including the limit of aperiodic fluctuations with
including the limit of aperiodic fluctuations with 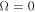 . The latter do not propagate at all; they solely grow or decay depending on the sign of γ. It should be noted that aperiodic modes are not a mathematical artifact but a well-established phenomenon that includes prominent examples like the Weibel and the filamentation fluctuations in unmagnetized plasmas (Fried 1959; Weibel 1959) and mirror and firehose fluctuations in magnetized plasmas.
. The latter do not propagate at all; they solely grow or decay depending on the sign of γ. It should be noted that aperiodic modes are not a mathematical artifact but a well-established phenomenon that includes prominent examples like the Weibel and the filamentation fluctuations in unmagnetized plasmas (Fried 1959; Weibel 1959) and mirror and firehose fluctuations in magnetized plasmas.
Theoretical investigations of these fluctuations require the proper analytical continuation of the wave equation to the entire complex plane. In the course of this, Felten et al. (2013) discovered a new transverse, damped, aperiodic mode that dominates the field fluctuations in an unmagnetized thermal plasma.
This is particularly notable considering that there are only three eigenmodes in an unmagnetized and stable plasma mentioned in the standard literature so far, namely the longitudinal Langmuir and ion acoustic waves as well as the transverse electromagnetic mode (i.e., light), all of which are propagating with a finite velocity. In contrast to these, the new mode merely describes nonpropagating, decaying fluctuations with the spatiotemporal behavior 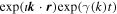 . The stability is guaranteed by the negative growth rate
. The stability is guaranteed by the negative growth rate 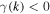 , and it ensures that the mode conserves the underlying equilibrium configuration. Thus, the damped aperiodic mode investigated here can be interpreted as the stable counterpart of the Weibel instability that, in contrast to the latter, occurs if no anisotropy remains in the distribution function. Since the associated fields are decaying with time, they must perpetually be re-excited in order to maintain a lasting fluctuation level. This is achieved by spontaneous field fluctuations that are entirely due to the discrete particle structure of the plasma. They are emitted in the whole ω–
, and it ensures that the mode conserves the underlying equilibrium configuration. Thus, the damped aperiodic mode investigated here can be interpreted as the stable counterpart of the Weibel instability that, in contrast to the latter, occurs if no anisotropy remains in the distribution function. Since the associated fields are decaying with time, they must perpetually be re-excited in order to maintain a lasting fluctuation level. This is achieved by spontaneous field fluctuations that are entirely due to the discrete particle structure of the plasma. They are emitted in the whole ω– spectrum, so they will always match the particular branch that corresponds to the dispersion relation of the damped aperiodic mode.
spectrum, so they will always match the particular branch that corresponds to the dispersion relation of the damped aperiodic mode.
Being a transverse mode, it sustains fluctuations not only of the electric field but also of the magnetic field. This is remarkable insofar as it is the only spontaneously excited mode in an unmagnetized equilibrium plasma with this property. Langmuir and ion acoustic waves are longitudinal, so they are not associated with magnetic field fluctuations. Electromagnetic waves, on the other hand, are not spontaneously excited because spontaneous emission is restricted to subluminal phase speeds. Consequently, the expected thermal level of magnetic field fluctuations is drastically enhanced by the mode.
This has deep implications for the early intergalactic medium (IGM), arguably the most important unmagnetized plasma. The radiation of the first stars at redshift 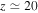 gave rise to the reionization of the universe after the dark ages. Photoionization models indicate a temperature of
gave rise to the reionization of the universe after the dark ages. Photoionization models indicate a temperature of 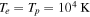 and a number density of
and a number density of 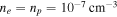 for the intergalactic electron–proton plasma shortly after the reionization onset at z = 4 (Hui & Gnedin 1997; Hui & Haiman 2003). Assuming these values, a strength of
for the intergalactic electron–proton plasma shortly after the reionization onset at z = 4 (Hui & Gnedin 1997; Hui & Haiman 2003). Assuming these values, a strength of 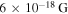 for the turbulent magnetic field is guaranteed on account of the new mode (Yoon et al. 2014). This value is larger than the field generated by the celebrated Biermann battery. In view of the high volume filling factor of almost 100% due to the omnipresence of the intergalactic plasma, spontaneous emission of field fluctuations is an ideal source of magnetic seed fields required for cosmic magnetogenesis. Considerably higher values are possible in the presence of an electron–positron pair beam traversing the IGM because it provides free energy and partially transforms the damped mode into an amplified one in certain spectral ranges (Kolberg et al. 2016).
for the turbulent magnetic field is guaranteed on account of the new mode (Yoon et al. 2014). This value is larger than the field generated by the celebrated Biermann battery. In view of the high volume filling factor of almost 100% due to the omnipresence of the intergalactic plasma, spontaneous emission of field fluctuations is an ideal source of magnetic seed fields required for cosmic magnetogenesis. Considerably higher values are possible in the presence of an electron–positron pair beam traversing the IGM because it provides free energy and partially transforms the damped mode into an amplified one in certain spectral ranges (Kolberg et al. 2016).
Due to the fundamental coupling between particles and fields that is characteristic for a plasma, the turbulent field fluctuations will inevitably affect the turbulent motion of electrons and protons. Thus, apart from the thermal velocity fluctuations, there is an additional contribution that is driven by the field fluctuations and in this sense by the mode itself. The knowledge of these modified fluctuation spectra gives an important insight into the state of the microturbulence.
The velocity fluctuations might also provide access to direct observations of the new mode that remain unavailable as yet. In contrast to the spacecraft instruments collecting solar wind data, in situ measurements of more distant astrophysical objects, unaffected by the influence of nearby stars, are not available.
Modern techniques to gather information about the turbulence of remote objects such as dispersion measure and scintillation data apply exclusively to compressional turbulence associated with density fluctuations. However, the mode under investigation is a transverse one, and transverse field fluctuations in an isotropic plasma are incompressible, as will be shown below. This property also constrains the applicability of Faraday rotation diagnostics. For incompressible turbulence in an unmagnetized and homogeneous plasma, one infers 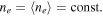 and
and 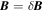 , so the rotation measure is given by
, so the rotation measure is given by
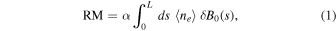
where 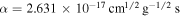 is a numerical constant and
is a numerical constant and 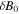 denotes the component of the magnetic field fluctuations along the line of sight. As the average of fluctuations is always zero, it is evident that incompressibility entails a vanishing average of the rotation measure:
denotes the component of the magnetic field fluctuations along the line of sight. As the average of fluctuations is always zero, it is evident that incompressibility entails a vanishing average of the rotation measure: 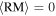 . This is plausible because the latter is sensitive to whether the fields along the line of sight point toward or away from the observer, and since the magnetic field fluctuations are randomly distributed, contributions to both orientations exist and cancel each other. Consequently, one is bound to resort to the variance instead:
. This is plausible because the latter is sensitive to whether the fields along the line of sight point toward or away from the observer, and since the magnetic field fluctuations are randomly distributed, contributions to both orientations exist and cancel each other. Consequently, one is bound to resort to the variance instead:

In the second line, the spatial homogeneity of the turbulence was taken into account, according to which the two-point correlations of the magnetic field fluctuations only depend on the difference of s and 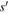 , i.e.,
, i.e., 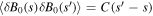 . As pointed out by Jokipii & Lerche (1969), the spectral correlation function C is an even function, so integrating by parts yields the result stated above. It is reasonable to assume that significant contributions to the correlation function only arise below a turbulence correlation length
. As pointed out by Jokipii & Lerche (1969), the spectral correlation function C is an even function, so integrating by parts yields the result stated above. It is reasonable to assume that significant contributions to the correlation function only arise below a turbulence correlation length 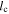 , but not beyond. Following Ruzmaikin et al. (1988), this scenario can be implemented by the model
, but not beyond. Following Ruzmaikin et al. (1988), this scenario can be implemented by the model 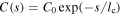 in order to obtain an order-of-magnitude estimate,
in order to obtain an order-of-magnitude estimate,
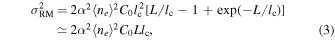
where it was assumed that the correlation length of the turbulence is much smaller than the distance traveled by the polarized rays through the fields. The former length can be estimated by the turbulence scale associated with the mode that was derived by Yoon et al. (2014), 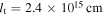 , yielding
, yielding

As mentioned earlier, the strength of the magnetic field fluctuations driven by the mode amounts to 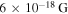 , so the component aligned to the line of sight is even below this value. Considering the smallness of
, so the component aligned to the line of sight is even below this value. Considering the smallness of  , it is evident that an observation of the mode by means of Faraday rotation is at least very demanding if not impossible.
, it is evident that an observation of the mode by means of Faraday rotation is at least very demanding if not impossible.
In view of these circumstances, the proton velocity fluctuations gain additional significance because the measurement of line broadening is a well-established tool for studying turbulence (Lazarian & Pogosyan 2006). Atomic or molecular lines of frequency  propagating through the IGM are subject to line broadening with an effective Doppler shift of
propagating through the IGM are subject to line broadening with an effective Doppler shift of
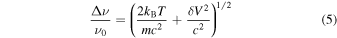
caused by the combined thermal and turbulent motion of the IGM neutrals (Rybicki & Lightman 1979). This might provide observational evidence for the damped, aperiodic mode if the velocity fluctuations driven by the latter are large enough in comparison with the thermal velocities. Since only the neutrals of the partially ionized IGM participate in this effect, this diagnostic technique crucially relies on the assumption that their motion is coupled to that of the protons by mutual charge exchange and elastic collisions (ambipolar diffusion). If such collisions are sufficiently frequent, the neutrals will adopt the velocity fluctuations of the protons that are under the permanent influence of the field fluctuations.
It is the purpose of the present paper to derive the spectrum and the integrated absolute value of the proton velocity fluctuations in the IGM that are driven by the damped, aperiodic mode. As outlined above, this provides some valuable insight into the turbulence state of the IGM. Moreover, a comparison of the resulting absolute value with the thermal speed will confirm that line broadening is a suitable tool for direct observations of the mode. These investigations continue the previous analyses by Yoon et al. (2014) and Kolberg et al. (2016), henceforth referred to as paper I and II, respectively. For the sake of readability, a corresponding shorthand notation for equation numbers will be used. For example, Equation (13) of paper II will be abbreviated as (II-13).
2. The Spectrum of the Velocity Fluctuations
In the kinetic model that is required for the description of noise arising from particle discreteness, the state of the plasma is completely determined by the phase space density
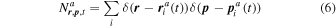
of every particle species a as well as the electric and magnetic fields, 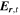 and
and 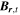 , respectively. The corresponding fluctuations are studied in the spectral domain, which is entered by performing a Fourier–Laplace transform of the Maxwell–Klimontovich equations. In the framework of linear plasma theory, the fluctuations of the Klimontovich function are composed of two contributions, the spontaneous and the induced fluctuations (Ichimaru 1977, 1992; Klimontovich 1982):
, respectively. The corresponding fluctuations are studied in the spectral domain, which is entered by performing a Fourier–Laplace transform of the Maxwell–Klimontovich equations. In the framework of linear plasma theory, the fluctuations of the Klimontovich function are composed of two contributions, the spontaneous and the induced fluctuations (Ichimaru 1977, 1992; Klimontovich 1982):
While the latter are proportional to the field fluctuations, the former are independent of the fields and in this sense spontaneous. These spontaneous fluctuations are entirely due to the particle discreteness of the plasma that gives rise to self-correlations of a point in spacetime with itself. If the distribution function is a thermal one, they are referred to as thermal noise, but in a more general context of arbitrary distributions they are also referred to as zero fluctuations or natural statistical fluctuations (Tsytovich 1989; Tolias et al. 2015). The linear coefficient  relating the induced fluctuations and the fields is determined by the particle distribution function
relating the induced fluctuations and the fields is determined by the particle distribution function  . Since the latter is isotropic in thermal equilibrium, it is reasonable to choose a coordinate system whose z axis is aligned with the wavevector
. Since the latter is isotropic in thermal equilibrium, it is reasonable to choose a coordinate system whose z axis is aligned with the wavevector  , and to introduce cylindrical coordinates p⊥, φ, and p∥ in momentum space. Then, an explicit expression for the coefficient can be extracted from (II-13):
, and to introduce cylindrical coordinates p⊥, φ, and p∥ in momentum space. Then, an explicit expression for the coefficient can be extracted from (II-13):
The associated fluctuations of number density and velocity can be defined as the respective integrals (Klimontovich 1982):
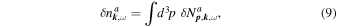

The contributions that are induced by the field fluctuations, therefore, are
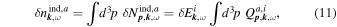
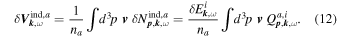
The computation of the first integral can be simplified by noticing that any gyrotropic function 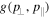 satisfies the symmetry relations (II-25) and (II-26):
satisfies the symmetry relations (II-25) and (II-26):

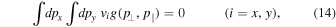
which remain valid even in the relativistic case 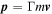 . As a direct consequence, one infers
. As a direct consequence, one infers
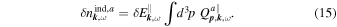
Thus, density fluctuations are solely induced by longitudinal field fluctuations, as claimed in the introduction. Therefore, the transverse mode investigated in this paper cannot be observed by techniques relying on dispersion measure, rotation measure, or scintillations.
Apart from a constant prefactor, the integral appearing in Equation (12) for the velocity fluctuations is determined by the linear susceptibility tensor associated with the corresponding particle species:
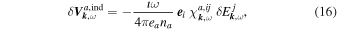

where 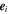 denotes the unit vector along the ith axis of the coordinate system. In the case of an isotropic distribution, this tensor is diagonal, as in (II-28)–(II-30):
denotes the unit vector along the ith axis of the coordinate system. In the case of an isotropic distribution, this tensor is diagonal, as in (II-28)–(II-30):
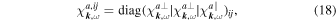
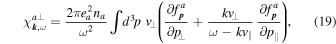
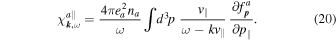
In general, therefore, the induced velocity fluctuations are driven by transverse and longitudinal field fluctuations:
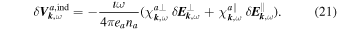
Since  is the induced current density of particle species a, this equation can be interpreted as Ohm's law. But in contrast to the formulation (II-16), the version above holds for each particle species separately without summing over a.
is the induced current density of particle species a, this equation can be interpreted as Ohm's law. But in contrast to the formulation (II-16), the version above holds for each particle species separately without summing over a.
Due to the random nature of the fluctuations, the physically meaningful quantities are the variances or the correlation functions rather than the fluctuations themselves:
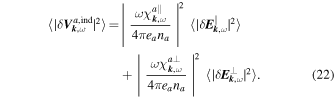
The field fluctuations in the plasma are governed by modes satisfying a dispersion relation 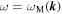 , and the fluctuations emitted into a particular mode are (Sitenko 1982)
, and the fluctuations emitted into a particular mode are (Sitenko 1982)
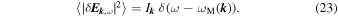
In the same fashion, the velocity fluctuations induced by the field fluctuations in the mode 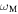 can be defined as
can be defined as
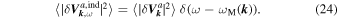
Since the damped, aperiodic mode investigated here is a transverse one, only the transverse field fluctuations contribute. In view of this, a comparison of the last three equations yields
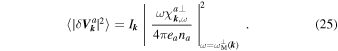
In order to proceed further, the dispersion relation of the mode as well as the underlying distribution function must be specified. The latter is a thermal Maxwell–Jüttner distribution:

where 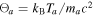 is the relativistic temperature and K2 denotes the modified Bessel function of the second kind and second order. As argued above, it will be assumed that the temperature
is the relativistic temperature and K2 denotes the modified Bessel function of the second kind and second order. As argued above, it will be assumed that the temperature 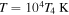 and the particle density
and the particle density 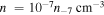 are the same for electrons and protons. The parameters T4 and
are the same for electrons and protons. The parameters T4 and 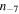 are unity in the case considered here, but they provide a convenient way to keep track of the temperature and density scaling. The dimensionless thermal velocity
are unity in the case considered here, but they provide a convenient way to keep track of the temperature and density scaling. The dimensionless thermal velocity 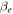 and the electron plasma frequency
and the electron plasma frequency 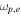 are
are
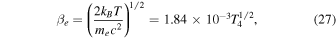
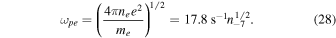
Since the thermal velocity of the electrons (and, therefore, also of the protons) is much smaller than unity, the IGM is a nonrelativistic plasma.
Under these circumstances, the transverse fluctuations are dominated by the damped, aperiodic mode 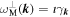 with
with 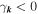 (Felten et al. 2013). In order to simplify the subsequent equations, it proves useful to introduce the dimensionless wavenumber κ and the dimensionless frequency y:
(Felten et al. 2013). In order to simplify the subsequent equations, it proves useful to introduce the dimensionless wavenumber κ and the dimensionless frequency y:
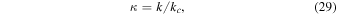
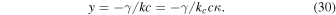
Since the mode is a damped one, the minus sign ensures that y is a positive number. The parameter kc is basically given by the inverse of the electron skin depth 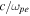 , accompanied by additional prefactors:
, accompanied by additional prefactors:
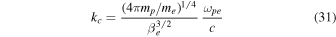
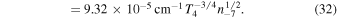
Due to this choice of normalization constants, the dispersion relation of the mode can be written in the simple form (Schlickeiser & Felten 2013)
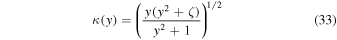
with
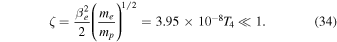
Schlickeiser & Felten (2013) also found an approximation for the inverse of the dispersion relation that is valid for both large and small wavenumbers:

Now that the dispersion relation of the mode is known, expression (25) for the velocity fluctuations can be evaluated. The susceptibility appearing there can be traced back to the integral 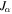 defined in (I-44):
defined in (I-44):
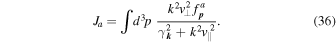
The reason is that Equation (19) implies
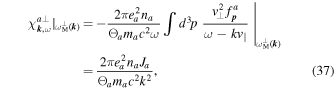
because the integral of an odd function vanishes if the integration limits are symmetric. Comparing this last equation with the result for 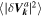 leads to
leads to
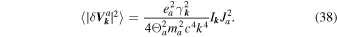
The only remaining unknowns,  and Ja, have already been computed in paper I in terms of the dimensionless variables κ and y defined above, specifically (I-50) and (I-51):
and Ja, have already been computed in paper I in terms of the dimensionless variables κ and y defined above, specifically (I-50) and (I-51):
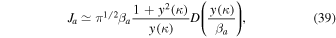
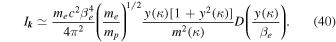
Here, 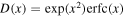 denotes an exponentially modulated complementary error function, and
denotes an exponentially modulated complementary error function, and 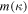 is given by Equation (I-42):
is given by Equation (I-42):
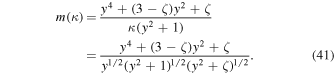
Therefore, the result for the spectrum of the proton velocity fluctuations reads
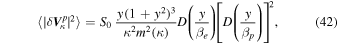
with
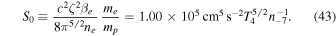
The spectrum in units of S0 is shown in Figure 1 for a plasma temperature of  .
.
Figure 1. Wavenumber spectrum of the proton velocity fluctuations driven by the transverse, damped, aperiodic mode in an isothermal electron–proton plasma at a temperature of 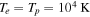 .
.
Download figure:
Standard image High-resolution image3. Integrated Spectrum of the Velocity Fluctuations
In order to compute the total value of the velocity fluctuations, the spectral contributions of the entire wavevector space must be collected. However, the corresponding integral diverges because the spectrum approaches a constant value for large wavenumbers. Such a problem is well known in plasma physics, most prominently from the logarithmic divergence displayed by the Landau collision integral. The customary treatment of this Coulomb logarithm will also be applied here, and that is to truncate the integral above a maximal wavenumber 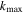 . The common choice for this critical value is the wavenumber associated with the classical distance of closest approach,
. The common choice for this critical value is the wavenumber associated with the classical distance of closest approach, 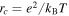 (Klimontovich 1982; Alexandrov et al. 1984):
(Klimontovich 1982; Alexandrov et al. 1984):
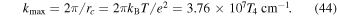
Since the spectrum (42) is isotropic with respect to  , the angular integration is trivial:
, the angular integration is trivial:
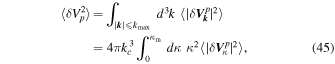
where
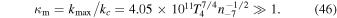
It is more convenient to perform the actual computation of this integral in terms of the variable y rather than κ. According to Equation (33), the corresponding transform of the differential is governed by
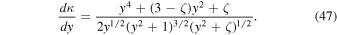
The new upper limit of the integral can be inferred from the inverse dispersion relation (35),
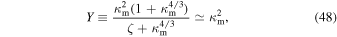
so one obtains

with

Assuming 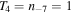 , a numerical computation of this integral yields
, a numerical computation of this integral yields  . In order to obtain its scaling with temperature and density, however, it must be calculated analytically. To this end, the function
. In order to obtain its scaling with temperature and density, however, it must be calculated analytically. To this end, the function 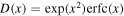 will be approximated by its asymptotic behavior (Abramowitz & Stegun 1972):
will be approximated by its asymptotic behavior (Abramowitz & Stegun 1972):
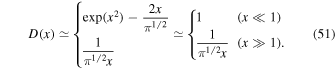
In order to apply this approximation, the range of integration must be dissected accordingly. Exploiting the inequalities 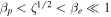 , one obtains
, one obtains
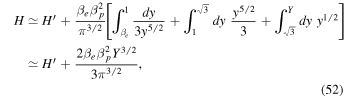
with
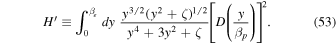
The remaining integral can be treated in the same fashion:
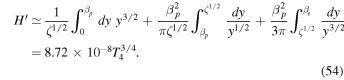
Considering scaling factors T4 and 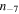 near unity once more,
near unity once more,  may safely be neglected in Equation (52) because it is many orders of magnitude smaller than the second term:
may safely be neglected in Equation (52) because it is many orders of magnitude smaller than the second term:
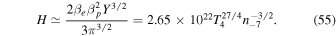
This analytical approximation agrees perfectly with the numerical result, so the temperature and density scaling may be considered reliable.
Plugging this result into Equation (49) and taking the square root afterwards leads to the desired proton velocity that is driven by the damped, aperiodic mode:
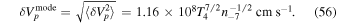
This value corresponds to 0.39% of the speed of light and, therefore, still remains within the nonrelativistic limit. It should be noted that this result is sensible to the artificial upper limit of the truncated integral because in view of Equation (55) it scales with 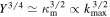 . The temperature dependency is even steeper (
. The temperature dependency is even steeper (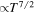 ), so the influence of the mode is expected to be more pronounced in hotter regions. For comparison, the thermal velocity is given by
), so the influence of the mode is expected to be more pronounced in hotter regions. For comparison, the thermal velocity is given by
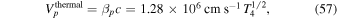
and hence two orders of magnitude smaller than the velocity fluctuations driven by the mode. This ratio increases rapidly with temperature as well (∝T 3). According to Equation (5), the relative line broadening is dominated by the damped aperiodic mode rather than the thermal velocities. For hydrogen it amounts to 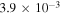 including the effects of the mode, as opposed to
including the effects of the mode, as opposed to 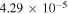 for purely thermal line broadening.
for purely thermal line broadening.
4. Summary and Conclusions
In this paper, the impact of the damped, aperiodic mode on the particle motion in the intergalactic plasma was investigated. The associated fluctuations are incompressible,  , because transverse field fluctuations in an isotropic plasma do not affect the density. This prevents access to observational evidence by means of dispersion measure, rotation measure, or scintillation data. The main results obtained here are the spectrum of the mode-driven proton velocity fluctuations, Equation (42), and their integrated total value. The latter amounts to
, because transverse field fluctuations in an isotropic plasma do not affect the density. This prevents access to observational evidence by means of dispersion measure, rotation measure, or scintillation data. The main results obtained here are the spectrum of the mode-driven proton velocity fluctuations, Equation (42), and their integrated total value. The latter amounts to 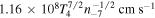 , which exceeds the thermal velocity by two orders of magnitude:
, which exceeds the thermal velocity by two orders of magnitude: 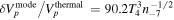 . Due to the pronounced temperature dependency, the influence of the mode prevails even more in hotter regions. As a consequence, the Doppler broadening of spectral lines traversing the IGM is dominated by the effects of the mode rather than the thermal velocity. In the case of hydrogen, the relative broadening becomes enhanced by a factor of 90.2 as compared to thermal broadening alone, which might provide the means to obtain observational evidence for the mode. However, this depends crucially on the assumption that the neutrals adopt the proton velocities by charge exchange or elastic collisions.
. Due to the pronounced temperature dependency, the influence of the mode prevails even more in hotter regions. As a consequence, the Doppler broadening of spectral lines traversing the IGM is dominated by the effects of the mode rather than the thermal velocity. In the case of hydrogen, the relative broadening becomes enhanced by a factor of 90.2 as compared to thermal broadening alone, which might provide the means to obtain observational evidence for the mode. However, this depends crucially on the assumption that the neutrals adopt the proton velocities by charge exchange or elastic collisions.
Despite the high fluctuation level of the proton velocities, it is not expected that instabilities are excited in turn because the underlying field fluctuations were derived from a spectral balance condition. In particular, the energy lost by the particles due to the excitation of fluctuations is balanced by the energy transferred from the fields to the particles. The situation may change, however, for sufficiently hot plasmas. With increasing temperature, the induced velocity fluctuations become comparable to the speed of light, thus entailing relativistic effects. At the same time, the thermal level of the field fluctuations is also enhanced and eventually leaves the linear regime considered here so that nonlinear effects become significant.
We thank the unknown referee for valuable comments on the manuscript. U.K. and R.S. acknowledge financial support by the Deutsche Forschungsgemeinschaft (grant Schl 201/32-1). P.H.Y. acknowledges NSF grant AGS1550566 to the University of Maryland, and the BK21 plus program from the National Research Foundation (NRF), Korea, to Kyung Hee University. He also acknowledges the Science Award Grant from the GFT, Inc., to the University of Maryland. Part of this work was carried out while P.H.Y. was visiting Ruhr University Bochum, Germany, which was made possible by the support from the Ruhr University Research School PLUS, funded by Germany's Excellence Initiative (DFG GSC 98/3), and by a Mercator fellowship awarded by the Deutsche Forschungsgemeinschaft through the grant Schl 201/31-1.




