Abstract
We carried out 2.5-dimensional resistive MHD simulations to study the formation mechanism of molecular loops observed by Fukui et al. in the Galactic central region. Since it is hard to form molecular loops by lifting up dense molecular gas, we study the formation mechanism of molecular gas in rising magnetic arcades. This model is based on the in situ formation model of solar prominences, in which prominences are formed by cooling instability in helical magnetic flux ropes formed by imposing converging and shearing motion at footpoints of the magnetic arch anchored to the solar surface. We extended this model to Galactic center scale (a few hundreds of parsecs). Numerical results indicate that magnetic reconnection taking place in the current sheet that formed inside the rising magnetic arcade creates dense blobs confined by the rising helical magnetic flux ropes. Thermal instability taking place in the flux ropes forms dense molecular filaments floating at high Galactic latitude. The mass of the filament increases with time and can exceed 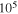
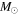 .
.
Export citation and abstract BibTeX RIS
1. Introduction
Molecular loops are found in the Galactic central region by NANTEN CO observations (Fukui et al. 2006; Fujishita et al. 2009; see Torii et al. 2010a, 2010b; Kudo et al. 2011, for detailed observations of these molecular loops). Fukui et al. (2006) proposed that Parker instability (Parker 1966) is a possible mechanism to create these molecular loops. This model is motivated by the systematic variation of the line-of-sight velocity along the loop; the velocity distribution can be explained by the motion of the dense gas sliding down along the rising magnetic loops formed by the Parker instability. Furthermore, large velocity dispersion observed around the footpoints of the loop can be explained by shock waves formed in the region where the supersonic downflow hits the galactic gas disk (Matsumoto et al. 1988, 1990; Shibata & Matsumoto 1991; Machida et al. 2009; Takahashi et al. 2009). Nevertheless, it is a puzzle how dense molecular gas (number density > 100 cm−3) can be levitated in warm interstellar medium (number density = a few cm−3). The levitated dense molecular filaments are similar to the solar prominences, whose density is 10–100 times larger than the surrounding solar corona. Note that solar prominences are warm gas with temperature 104 K, whereas molecular loops are cold molecular gas with temperature less than 100 K. Although the temperature and cooling mechanisms of solar prominences differ from those in molecular loops, the density ratio between the dense filament and ambient gas is similar. Torii et al. (2010b) discussed the possibility that the formation mechanism of molecular loops is similar to solar prominences. Understanding the physical process of the formation of solar prominences might be a key to revealing the formation mechanism of molecular loops.
Recently, Kaneko & Yokoyama (2015) proposed a model of in situ formation of solar prominence by condensation of hot coronal gas. They showed that magnetic flux ropes can be formed by converging/shearing motion for magnetic arches anchored to the solar photosphere. Dense plasma trapped in the flux rope is condensed by radiative cooling and can form cool, dense filaments observed as prominences.
In this paper, we present the results of 2.5-dimensional MHD simulations based on the model of solar prominences by Kaneko & Yokoyama (2015). The cooling/heating function is adopted from Inoue et al. (2006), in which radiative cooling by emission lines, the photoelectric effect on dust, cosmic rays, etc., are included. We demonstrate that dense loop-like structures near the Galactic center can be formed by condensation of the warm gas.
Our model and numerical settings are introduced in Section 2. Section 3 shows our numerical results. We compare the numerical results with observations. Section 4 is for summary and discussion.
2. Numerical Model
2.1. In Situ Formation Model of Galactic Prominence
We adopted the in situ formation model of prominences reported by Kaneko & Yokoyama (2015). Figure 1 schematically shows the formation mechanism of dense, cold filaments. We consider static magnetic arches at the initial state (Figure 1(a)). Subsequently, we impose converging and shearing motion at the footpoints of the arch to induce the rising motion of the arcade. Note that both the magnetic buoyancy around the loop top of the arch and the magnetic pressure gradient enhanced by the footpoint motion contribute to the rising motion of the arch. Current sheets can be formed inside the expanding magnetic arcade. Magnetic reconnection taking place in the current sheet forms rising dense plasmoids (Figure 1(b)). Since the plasmoid is confined by the helical magnetic fields, the warm gas accumulates around the bottom of the closed poloidal magnetic field lines (red arrows), where the cooling instability forms dense, cold filaments supported by magnetic tension force (Figure 1(c)). In this paper, since we neglect the variation of physical quantities perpendicular to the poloidal plane, the dense filaments are not arches but straight filaments. In three dimensions, the filaments can bend and form an arch, along which the molecular gas slides down.
Figure 1. Schematic picture of molecular loop formation. (a) Magnetic arches and footpoint motions. (b) Closed magnetic loops (helical magnetic fields in three dimensions) are formed by magnetic reconnection taking place in the arch, expanding by the imposed converging/shear motion. (c) Cooling instability taking place in the flux rope forms dense filaments (dark region).
Download figure:
Standard image High-resolution image2.2. Basic Equations and Numerical Scheme
The basic equations of resistive magnetohydrodynamics (MHD) are as follows:





where the anomalous resistivity η is assumed to depend on the current density J (see Kaneko & Yokoyama 2015) as

Here  = 3 × 1023 cm2 s−1 and Jc = 4.0 × 10−17 dyn
= 3 × 1023 cm2 s−1 and Jc = 4.0 × 10−17 dyn cm s−1. We adopt Cartesian coordinates
cm s−1. We adopt Cartesian coordinates  and assume translational symmetry with respect to y. The gravitational acceleration is assumed to be
and assume translational symmetry with respect to y. The gravitational acceleration is assumed to be  and gz = 3 × 10−9 cm s−2. The cooling function
and gz = 3 × 10−9 cm s−2. The cooling function  includes cooling and heating terms, and other symbols have their normal meaning. In the interstellar medium, cold neutral medium (CNM), with temperature 10–100 K, and warm medium (WM), with temperature 104 K, coexist by the balance of cooling and heating (Field et al. 1969; Wolfire et al. 1995, 2003). We adopted the cooling/heating function summarized by Inoue et al. (2006):
includes cooling and heating terms, and other symbols have their normal meaning. In the interstellar medium, cold neutral medium (CNM), with temperature 10–100 K, and warm medium (WM), with temperature 104 K, coexist by the balance of cooling and heating (Field et al. 1969; Wolfire et al. 1995, 2003). We adopted the cooling/heating function summarized by Inoue et al. (2006):



Here n is number density. Figure 2 shows a thermal equilibrium curve for the interstellar medium determined by the cooling/heating function (7)–(9). Two stable branches, WM (red branch) and CNM (blue branch), exist. In this paper we assume that cooling/heating takes place at the temperature range 400  K; otherwise, we set
K; otherwise, we set  in order for the dense, cold region to be resolved numerically with a moderate number of grid points. For simplicity, we neglect thermal conduction.
in order for the dense, cold region to be resolved numerically with a moderate number of grid points. For simplicity, we neglect thermal conduction.
Figure 2. Thermal equilibrium curve computed from the cooling/heating function adopted in this paper.
Download figure:
Standard image High-resolution imageThe basic equations are solved by applying the HLLD scheme (Miyoshi & Kusano 2005). Second-order accuracy in space is preserved by linearly interpolating the values at the cell interface and restricting them using the minmod limiter. The solenoidal condition  = 0 is satisfied by applying the generalized Lagrange multiplier (GLM) scheme proposed by Dedner et al. (2002). The cooling/heating term is included by the time-implicit method. This simulation code has been applied to MHD simulations of the interaction of jets with interstellar gas (Asahina et al. 2014).
= 0 is satisfied by applying the generalized Lagrange multiplier (GLM) scheme proposed by Dedner et al. (2002). The cooling/heating term is included by the time-implicit method. This simulation code has been applied to MHD simulations of the interaction of jets with interstellar gas (Asahina et al. 2014).
The size of the simulation box is −200 pc  200 pc, and 5 pc
200 pc, and 5 pc  2400 pc. The grid size is uniform with Δx = 1 pc and Δz = 0.5 pc.
2400 pc. The grid size is uniform with Δx = 1 pc and Δz = 0.5 pc.
2.3. Initial and Boundary Conditions
We assume a gravitationally stratified layer in hydrostatic equilibrium. The initial magnetic field is assumed to be force-free and given by



Initial distributions of density, temperature, and magnetic field are shown in Figure 3. We set ρ(z = 5 pc) = 2.8 × 10−24 g cm−3 and P(z = 5 pc) = 1.56 × 10−12 dyn cm−2 (T(z = 5 pc) = 6700 K). Here Hm = 200 pc and La = 200 pc denote magnetic scale height and half width of the magnetic arch, respectively. We assume a strong magnetic field to sustain the dense filaments. The plasma β (=Pgas/Pmag) is assumed to be β = 0.2 at the bottom of the simulation area (Ba = 1.54 × 10−5 G). The warm gas with temperature 6700–20,000 K is assumed to satisfy mechanical equilibrium and thermal equilibrium before converging and shearing motions are imposed. In the region where  900 pc, we assume a hot corona with Tcorona = 2 × 106 K.
900 pc, we assume a hot corona with Tcorona = 2 × 106 K.
Figure 3. Initial distribution of density (left), temperature (right), and magnetic field lines (solid curves).
Download figure:
Standard image High-resolution imageBoundary conditions in the x-direction are symmetric for ρ, P, Bz, vz and antisymmetric for Bx, By, vx, vy. Absorption boundary conditions are applied at the upper boundary. At the lower boundary, density and pressure are fixed to the initial value. Converging (vx) and shearing (vy) motions are imposed at footpoints of the magnetic arch as follows:


Here v0 is 4 km s−1.
3. Numerical Results and Comparison with Observation
3.1. Formation of a Dense Filament
Figure 4 shows the density and temperature distribution in the x–z plane at 30, 40, and 120 Myr. The arcade field squeezed by the converging motion and stretched by the shearing motion forms a current sheet around x = 0 inside the arcade. Magnetic reconnection taking place in the current sheet creates rising flux ropes inside which warm gas is confined. In this simulation, the flux rope is lifted up to ∼250 pc. Since the warm interstellar gas slides down along the closed magnetic field lines, the density around the bottom of the flux rope exceeds the threshold for the onset of the cooling instability. Thermal instability taking place in the dense region forms cold, dense filaments. The density of the filament becomes 10–100 times that of the initial state. The dense filament is lifted up to 100–200 pc and sustained for 100 Myr. The length and thickness of the filament at 120 Myr are ∼60 pc in the vertical direction and 6–8 pc in the x-direction, respectively.
Figure 4. Density (left panels) and temperature (right panels) distribution and magnetic field lines (solid lines) at 30 Myr (top), 40 Myr (middle), and 120 Myr (bottom).
Download figure:
Standard image High-resolution imageFigure 5 enlarges the region where dense filaments are formed. Arrows show velocity vectors. The warm gas infalls along the magnetic field lines. The speed of the warm gas accumulating toward the filament is about 2 km s−1. Figure 6 shows the distribution of By at t = 120 Myr. Since By is amplified by shearing motion, By becomes strong inside the magnetic flux rope. The flux rope corresponds to the blue-purple region in Figure 6, where  5.5 μG. Magnetic field lines inside the flux rope have a helical shape, as schematically shown in Figure 1(b).
5.5 μG. Magnetic field lines inside the flux rope have a helical shape, as schematically shown in Figure 1(b).
Figure 5. Density distribution (color), magnetic field lines (solid line), and velocities (arrows).
Download figure:
Standard image High-resolution imageFigure 6. Distribution of By and magnetic field lines (solid line).
Download figure:
Standard image High-resolution imageRed dots in Figure 7 show the pressure and number density at each grid point. At the initial state (Figure 7(a)), warm gas is located on the thermal equilibrium curve (solid line). The dashed line shows the isothermal line at T = 400 K, and the dot-dashed line shows that at T = 20,000 K. Figure 7(b) plots pressure P and number density n at t = 120 Myr. Since the warm gas infalling along the closed magnetic field lines compresses the gas around the bottom of the flux rope (x = 0 pc), the number density exceeds the threshold for the cooling instability and deviates from the warm gas branch. The dense, cool gas is transformed to the CNM, where temperature is less than 400 K. Since we cut off cooling when  K to numerically resolve the filament, the CNM is located at the isothermal line at T = 400 K.
K to numerically resolve the filament, the CNM is located at the isothermal line at T = 400 K.
Figure 7. Pressure and number density at 0 Myr (left panel) and 120 Myr (right panel). The solid curve shows the thermal equilibrium curve. The dashed line shows the isothermal line at T = 400 K, and the dot-dashed line shows that at T = 20,000 K.
Download figure:
Standard image High-resolution imageFigure 8 shows the time evolution of density, pressure, and temperature at x = 0 pc and z = 105 pc. The initially warm gas ( 4 K) is compressed during 30–50 Myr. Consequently, density and pressure increase and temperature slightly decreases. At t = 50 Myr, the gas is located in the thermally unstable region in the P–n diagram. Figure 8 shows that pressure and temperature decrease owing to the cooling instability and the density continues to increase. Finally, a cool (T = 400 K), dense filament is formed.
4 K) is compressed during 30–50 Myr. Consequently, density and pressure increase and temperature slightly decreases. At t = 50 Myr, the gas is located in the thermally unstable region in the P–n diagram. Figure 8 shows that pressure and temperature decrease owing to the cooling instability and the density continues to increase. Finally, a cool (T = 400 K), dense filament is formed.
Figure 8. Time evolution of density (top), pressure (middle), and temperature (bottom) at x = 0 pc and z = 105 pc.
Download figure:
Standard image High-resolution imageFigure 9 shows the vertical distribution of temperature at x = 0 pc at 120 Myr. The dense filament locates at z = 100–160 pc. Meanwhile, a high-temperature (T = 35,000–70,000 K) region appears at z = 330–450 pc. The hot region is formed by shock waves formed by the upward flow. When the temperature of the shocked gas exceeds 20,000 K, the region stays in a high-temperature state.
Figure 9. Vertical distribution of temperature at x = 0 pc at 120 Myr (solid line) and initial temperature profile (dashed line).
Download figure:
Standard image High-resolution imageFigure 10 shows the column density of the dense gas ( K), the unstable neutral medium (UNM) in the temperature range 500 K
K), the unstable neutral medium (UNM) in the temperature range 500 K  5000 K, and the warm gas in the temperature range 5000 K
5000 K, and the warm gas in the temperature range 5000 K  7000 K, at 120 Myr for the line-of-sight direction parallel to the x-axis. The column density of the dense filament is ∼1.0 × 10−3 g cm−2 (column number density = 6 × 1020 cm−2) around the bottom of the dense filament. The column density of the UNM is largest at 1.0 × 10−4 g cm−2 (column number density = 6 × 1019 cm−2). The column density of the warm gas is 3 × 10−4 g cm−2 above the top of the dense filament. The dense gas can be observed by CO emission, and the UNM and the warm gas can be observed by 21 cm line emission by neutral hydrogen. Torii et al. (2010b) compared the distribution of CO emission and H i emission and found that they coincide in loop 1. In our simulation, the distribution of the UNM coincides with the dense filament, but the warm gas above the dense filament has comparable column density to the dense filament.
7000 K, at 120 Myr for the line-of-sight direction parallel to the x-axis. The column density of the dense filament is ∼1.0 × 10−3 g cm−2 (column number density = 6 × 1020 cm−2) around the bottom of the dense filament. The column density of the UNM is largest at 1.0 × 10−4 g cm−2 (column number density = 6 × 1019 cm−2). The column density of the warm gas is 3 × 10−4 g cm−2 above the top of the dense filament. The dense gas can be observed by CO emission, and the UNM and the warm gas can be observed by 21 cm line emission by neutral hydrogen. Torii et al. (2010b) compared the distribution of CO emission and H i emission and found that they coincide in loop 1. In our simulation, the distribution of the UNM coincides with the dense filament, but the warm gas above the dense filament has comparable column density to the dense filament.
Figure 10. Black line: vertical distribution of column density of the dense gas ( 500 K); blue and red lines: unstable neutral gas (500 K
500 K); blue and red lines: unstable neutral gas (500 K  5000 K) and warm gas (5000 K
5000 K) and warm gas (5000 K  7000 K), respectively. The line-of-sight direction is parallel to the x-axis.
7000 K), respectively. The line-of-sight direction is parallel to the x-axis.
Download figure:
Standard image High-resolution imageThe column density estimated from the CO emission is 3 × 1021 cm−2 around the top of loop 1, and the H i column number density of loop 1 obtained from the 21 cm line emission is 6 × 1020 cm−2 (Torii et al. 2010b). These column densities are five times larger than that of our simulation and will be discussed in the next subsection.
3.2. Mass of the Filament
In this section, we would like to estimate the mass levitated in the cold, dense filament and compare the numerical results with observations. NANTEN observations indicate that the projected lengths of two loops (loop 1 and loop 2) are ∼500 and ∼300 pc, respectively. They are lifted up to ∼220 and ∼300 pc, and the total mass of each loop was estimated to be 8 × 
 (Fukui et al. 2006). If we take the average value of projected lengths of two loops and assume that the shape of the loops is a half circle, the average length of the loop is 400 pc × π/2 ∼ 600 pc. In our simulation results at 120 Myr, the dense filament (
(Fukui et al. 2006). If we take the average value of projected lengths of two loops and assume that the shape of the loops is a half circle, the average length of the loop is 400 pc × π/2 ∼ 600 pc. In our simulation results at 120 Myr, the dense filament ( K) is lifted up to 100–200 pc. The mass of the filament can be estimated to be 112
K) is lifted up to 100–200 pc. The mass of the filament can be estimated to be 112  times the length of the loop in the y-direction in units of pc. In other words, the total mass of the dense filament is 7 × 104
times the length of the loop in the y-direction in units of pc. In other words, the total mass of the dense filament is 7 × 104  if we assume that the length of the filament in the y-direction is 600 pc.
if we assume that the length of the filament in the y-direction is 600 pc.
The total mass of the dense filament in the simulation is consistent with the lower limit of the mass estimated from observations. However, Torii et al. (2010b) estimated by detailed analysis of the NANTEN 12CO and 13CO(J = 1–0) observations that the total mass of these two loops is 1.4 × 106  and 1.9 × 106
and 1.9 × 106  , respectively. These values are an order of magnitude larger than those of our simulation. The smaller total mass of the molecular loop in our simulation can be due to the lower density of the WM,
, respectively. These values are an order of magnitude larger than those of our simulation. The smaller total mass of the molecular loop in our simulation can be due to the lower density of the WM,  = 2.8 × 10−24 g cm−3, that we assumed at the bottom of our simulation box at z = 5 pc. One possibility is that the heating rate Γ is larger in the Galactic central region. When
= 2.8 × 10−24 g cm−3, that we assumed at the bottom of our simulation box at z = 5 pc. One possibility is that the heating rate Γ is larger in the Galactic central region. When  = 10−25 erg s−1, since the thermal equilibrium condition gives
= 10−25 erg s−1, since the thermal equilibrium condition gives  (z = 5 pc, GC) ∼ 1.4 × 10−23 g cm−3, the total mass of the filament can be 5 times that for
(z = 5 pc, GC) ∼ 1.4 × 10−23 g cm−3, the total mass of the filament can be 5 times that for  (z = 5 pc) = 2.8 × 10−24 g cm−3. Another possibility is the coexistence of the molecular gas with warm gas at the initial state. According to Sofue & Nakanishi (2016), the fraction of molecular gas fmol =
(z = 5 pc) = 2.8 × 10−24 g cm−3. Another possibility is the coexistence of the molecular gas with warm gas at the initial state. According to Sofue & Nakanishi (2016), the fraction of molecular gas fmol =  /(
/( +
+  ) ∼ 0.8 at z ∼ 20 pc in the Galactic central region, where
) ∼ 0.8 at z ∼ 20 pc in the Galactic central region, where  is the density of molecular hydrogen and VWM and VH2 are the volume fractions of the warm gas and molecular hydrogen, respectively. This means that when
is the density of molecular hydrogen and VWM and VH2 are the volume fractions of the warm gas and molecular hydrogen, respectively. This means that when  = 2.8 × 10−24 g cm−3 and
= 2.8 × 10−24 g cm−3 and  = 2.8 × 10−22 g cm−3, the volume fraction of the molecular hydrogen VH2 ∼ 0.04. Since the mean density of the two-phase medium is ρ =
= 2.8 × 10−22 g cm−3, the volume fraction of the molecular hydrogen VH2 ∼ 0.04. Since the mean density of the two-phase medium is ρ =  +
+  = 1.4 × 10−23 g cm−3, the total mass of the filament can be 5 times that for the WM with
= 1.4 × 10−23 g cm−3, the total mass of the filament can be 5 times that for the WM with  = 2.8 × 10−24 g cm−3. The third possibility is the larger size of the magnetic arch. We assumed that the half width of the magnetic arch is 200 pc. When the magnetic arch is larger, it forms a larger flux rope and more mass accumulates inside the rope, so that the total mass of the dense filament can be larger.
= 2.8 × 10−24 g cm−3. The third possibility is the larger size of the magnetic arch. We assumed that the half width of the magnetic arch is 200 pc. When the magnetic arch is larger, it forms a larger flux rope and more mass accumulates inside the rope, so that the total mass of the dense filament can be larger.
Here we would like to point out that the mass of the dense filament increases with time. Figure 11 shows the time evolution of the total mass of the dense filament. As we have shown in Figure 5, warm gas in the magnetic flux rope continuously falls down toward the filament along magnetic field lines. The maximum mass of the filament can be estimated by assuming that all the gas inside a flux rope falls into the filament. The mass inside the flux rope corresponding to the blue-purple region in Figure 6 is 3.5 × 105  , assuming that the depth in the y-direction is 600 pc.
, assuming that the depth in the y-direction is 600 pc.
Figure 11. Time evolution of total mass of a dense filament.
Download figure:
Standard image High-resolution image4. Summary and Discussion
The idea of "Galactic prominence" was addressed in Morris (2006) and Torii et al. (2010b) to explain the formation mechanism of the molecular loops found in the Galactic central region. The essential component that sustains the prominence is a strong magnetic field, which enables the dense filament to be levitated against gravity. In Fukui et al. (2006), the observed velocity gradient along the loop and the large velocity dispersion around the footpoint of the loop were explained by the sliding motion of the molecular gas along the magnetic loop formed by the Parker instability. However, since the dense molecular gas in the equatorial region is hard to lift by magnetic buoyancy, the molecular gas should be formed in situ in the rising magnetic loops. A possible mechanism of the in situ formation of molecular gas is compression of the warm neutral medium by magnetic loops buoyantly rising by the Parker instability. Magnetohydrodynamic simulations by Takahashi et al. (2009), however, showed that the maximum density of the dense shell that formed around the top of the rising magnetic loops is too small to trigger the cooling instability. We may need a preexisting dense gas layer to trigger the cooling instability. In this paper, we applied the in situ formation model of solar prominences by Kaneko & Yokoyama (2015) to the Galactic gas disk and demonstrated that dense, cold filaments can be formed by the cooling instability. Since we assumed translational symmetry to simulate the prominence formation by 2.5D MHD simulation, we cannot reproduce the velocity gradient along the loop, which needs 3D simulation.
Recently, ESA's Herschel space observatory carried out detailed observations of dense filaments in our Galaxy (Palmeirim et al. 2013; Schisano et al. 2014; Wang et al. 2015). Filaments whose length ranges from a few parsecs to 100 pc are found along the Galactic plane. Three-dimensional magnetohydrodynamic simulations by Wareing et al. (2016) demonstrated that the dense filaments can be formed by thermal instability in a magnetized interstellar medium without assuming colliding flows or other external effects. Filaments with a higher aspect ratio can be formed by a stronger magnetic field.
In our simulation, the total mass of the dense filament is 7 × 104  at t = 120 Myr. It is smaller than the 1.6 × 106
at t = 120 Myr. It is smaller than the 1.6 × 106  observed for loop 1 by NANTEN. The total mass of the filament can be larger if we take into account the enhanced heating in the Galactic center and the coexistence of the molecular gas with the WM. The mass of the filament can be larger when the size of the magnetic arcade is larger.
observed for loop 1 by NANTEN. The total mass of the filament can be larger if we take into account the enhanced heating in the Galactic center and the coexistence of the molecular gas with the WM. The mass of the filament can be larger when the size of the magnetic arcade is larger.
In this paper, we neglected cooling when  400 K. If we include cooling in this temperature range, the dense filaments can be thinner. We will need more grid points to resolve such filaments. Since the thickness of the filament becomes less than the Field's length, we may need to include thermal conduction. According to Inoue et al. (2006), the thermal conductivity drives turbulence in the two-phase interstellar medium if we resolve the Field's length of the warm gas (∼0.1 pc). Such turbulence may thicken the dense filament and enable us to compare the numerical results more quantitatively with observations. We would like to report the results of such simulations in subsequent papers.
400 K. If we include cooling in this temperature range, the dense filaments can be thinner. We will need more grid points to resolve such filaments. Since the thickness of the filament becomes less than the Field's length, we may need to include thermal conduction. According to Inoue et al. (2006), the thermal conductivity drives turbulence in the two-phase interstellar medium if we resolve the Field's length of the warm gas (∼0.1 pc). Such turbulence may thicken the dense filament and enable us to compare the numerical results more quantitatively with observations. We would like to report the results of such simulations in subsequent papers.
We appreciate discussion and helpful comments by M. Machida, T. Hanawa, T. Kaneko, Y. Kudoh, and Y. Matsumoto. The simulation codes we adopted in our simulation were developed by Y. Asahina. C.H. Peng appreciates the scholarship from the Interchange Association, Japan. Numerical computations were carried out on Cray XC30 at the Center for Computational Astrophysics, National Astronomical Observatory of Japan. This work was supported by JSPS KAKENHI Grant Number 16H03954.














