On the Existence of Regular and Irregular Outer Moons Orbiting the Pluto–Charon System

Since its discovery in 1930 (Tombaugh 1946) the dwarf planet Pluto has provided us with valuable information on the origin of the solar system: its structure, its dynamical evolution, and its basic building blocks. It was the first object to be discovered in the Kuiper Belt and suggest its existence; its orbital resonance with Neptune and high inclination provided strong evidence for Neptune migration (Malhotra 1993), and thereby provided important clues into the early history of the solar system and its assemblage. The discovery of its close companion (Charon Christy & Harrington 1978) revealed the existence of a new type of planetary systems, binary planetesimals/dwarf-planets, and its close and tidally locked configuration provided further clues for its collisional origin (Canup 2005; for properties of Kuiper Belt objects (KBOs) see Brown 2012 and references therein).

A series of discoveries in recent years showed the existence of no less than four additional satellites, including Styx, Nix, Kerberos, and Hydra orbiting Pluto on circular orbits with semimajor axes ranging between ∼42 and 65 K km, i.e., residing between ∼0.007–0.011 of the system Hill radius, ${R}_{\mathrm{Hill}}={a}_{P}{(1-{e}_{P})({m}_{P}/3{m}_{\odot })}^{1/3};$ where a_P, e_P, and m_P are the semimajor axis (SMA) of the orbit of Pluto around the Sun, the orbital eccentricity, and the mass of Pluto, respectively; m_⊙ is the mass of the Sun (Brozović et al. 2015 and references therein). These recent findings gave rise to a series of studies on the formation, stability, and evolution of this extended system (Brown 2002; Lee & Peale 2006; Stern et al. 2006; Ward & Canup 2006; Lithwick & Wu 2008a, 2008b; Canup 2011; Youdin et al. 2012; Giuliatti Winter et al. 2013; Cheng et al. 2014b; Giuliatti Winter et al. 2014, 2015; Kenyon & Bromley 2014; Bromley & Kenyon 2015; Porter & Stern 2015) that could not only shed light on the origin of the Pluto system but also provide new clues to the understanding of the growth of the planetary system in general, as well as on migration and resonant capture processes in planetesimal disks. Better understanding of the properties of the Pluto system and its constituents is therefore invaluable for advancing our knowledge of the solar system, its building blocks, and its origins. The New-Horizons mission, launched in 2006, was designed to explore the Pluto–Charon system and help accomplish these goals (Young et al. 2008). New Horizons recently made its close flyby near the Pluto–Charon system and provided new constraints on the system are therefore invaluable for interpreting New Horizons data and their implications for the origins of Pluto and the solar system history.

Here we show that secular evolutionary processes due to gravitational perturbations by the Sun, previously neglected, may have played a major role in the initial formation of the Pluto system as well as in the later evolution of its satellite system and its configuration to this day. The Pluto–Charon system is thought to be a result of a collision of two approximately like-sized bodies (Kenyon & Bromley 2014). Though most of the collisional debris is strongly bound at short period orbits, some material can even be ejected from the system. The post-collision energetics of the debris therefore spans a wide range, giving rise to the possibility of loosely bound debris at a wide orbit. Moreover, the post-impact debris disk expands with time, driving some of the debris to wider orbits (Kenyon & Bromley 2014). These aspects, together with the known existence of many wide-orbit KBO binaries (Naoz et al. 2010), suggests that the Pluto–Charon system may host wide-orbit outer moons beyond the currently observed one, which either formed in situ post-impact or were otherwise captured (e.g., Goldreich et al. 2002). As we discuss below, our finding provides direct predictions for the possible orbits of outer moons in the Pluto–Charon system, if such exist. In particular, we show that co-planar planetesimal rings cannot exist beyond a specific critical separation from Pluto–Charon (significantly smaller than the Hill radius of the system), and that any moon residing beyond this critical separation must be an irregular, inclined, and/or eccentric moon. Moreover, we constrain the orbital phase space regimes (SMA, eccentricity, inclination) in which dust, planetesimal rings, and/or outer moons can exist on dynamically and secularly stable orbits.

Charon is Pluto's closest and largest moon, with SMA of a_C ∼ 19.4 K km (period of 6.387 days) and mass ∼1.52 × 10²⁴ g (mass ratio of μ = m_c/m_P = 0.116). It revolves around Pluto on a tidally locked (i.e., in double synchronous state) circular orbit with an inclination of I ∼ 119° in respect to the orbit of Pluto around the Sun (which in itself is inclined in an angle of ∼17° in respect to the ecliptic plane). Together with the Sun, the Pluto–Charon system comprises a hierarchical triple system, with Pluto and Charon orbiting each other in an inner binary orbit and their center of mass orbiting the Sun in an outer binary orbit. The evolution of such hierarchical gravitating triple systems may give rise to secular dynamical processes, in which the outer third body perturbs the orbit of the inner binary, leading to secular precession of the inner binary, typically exciting its eccentricity. In particular, triples with high mutual inclinations between the inner and outer orbits (typically >∼40°, and somewhat lower for eccentric systems) are subject to quasi-periodic secular evolution resulting in a coherence liberation/oscillation of the inner binary. This quasi-periodic behavior called Lidov–Kozai (LK) cycles (Kozai 1962; Lidov 1962), which could affect Pluto's satellites as well as other solar system binary planetesimals (Perets & Naoz 2009) and satellites of the gas-giants (Carruba et al. 2002; Tremaine et al. 2009; Tamayo et al. 2013a, 2013b). Such LK evolution leads to the inner orbit precession and in turn gives rise to high amplitude eccentricity and inclination oscillations that occur on the LK precession timescales, which are much longer than the orbital period.

In principle, the high mutual inclination of the Charon-Pluto system makes it highly susceptible to such LK secular evolution, and in the absence of other forces it would have lead to a collision between Pluto and Charon. However, such processes are highly sensitive to any additional perturbations of the system precession. In particular, the effects of the tidal forces between Pluto and Charon at their current separation lead to a significant precession of their orbital periapsis, which will be denoted ${\dot{g}}_{C}$. This, in turn, quenches any LK secular evolution, and keeps Pluto and Charon on a stable circular orbit, with no variations of the orbital eccentricity and the mutual inclination in respect to the orbit around the Sun.

The strong dependence of the tidal forces on the satellite separation renders the tidal effects on Pluto's four other known satellites negligible. However, periapsis precession can still be induced by the non-point-mass gravitational potential of the inner Pluto–Charon binary (Lee & Peale 2006; Hamers et al. 2015a), similar to the case of circumbinary planets (Hamers et al. 2015b; Martin et al. 2015; Muñoz & Lai 2015) or orbiting an oblate object Tremaine et al. (2009). In this case, if the inner-binary-induced precession timescale, τ_PC, is shorter than the LK precession timescale, τ_LK, the orbit will not liberate/oscillate on the LK timescale, and the LK secular evolution will be quenched. If, on the other hand, the LK period is shorter than the precession timescale, the binary-induced precession is slow and the orbit has sufficient time to liberate/oscillate and build-up significant LK oscillations. The critical SMA at which these timescales become comparable is given by (Figure 2; see Appendix A for full derivation)

$$\begin{eqnarray}&&{a}_{\mathrm{crit}}={\left[\displaystyle \frac{3}{8}\displaystyle \frac{{a}_{C}^{2}{a}_{P}^{3}{m}_{P}{m}_{C}{(1-{e}_{p}^{2})}^{3/2}(5{\theta }^{2}-1)}{({m}_{P}+{m}_{C}){(1-{e}_{m}^{2})}^{2}{m}_{\odot }}\right]}^{1/5},\end{eqnarray} \tag{ 1 }$$

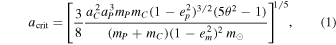
where parameters with sub-indexes PC correspond to the orbital parameters of the Pluto–Charon orbit, and the m index refers to the orbital parameters of the orbiting moon. The inner orbit SMA for Pluto–Charon mutual orbit is a_C; the SMA of the moon orbit around Pluto–Charon is given by a_m; the eccentricity of the outer orbit is e_m; the arguments of the pericenter of the inner and outer orbits are g_C, g_m, respectively, and $\theta \equiv \cos i$ is the cosine of the inclination between the two orbit planes denoted by i. Charon mass is given by m_C and the mass of the Sun is denoted by m_⊙. See Figure 1 for a diagram of the discussed system.

Zoom In Zoom Out Reset image size

It is important to note that we do not account for the precession caused by Pluto's other moons because of their negligible mass. From Equations (3) and (15), we see that the ${\dot{g}}_{m}\propto {m}_{C}{a}_{C}^{2}$. In comparison, for the most massive and distant moon, Hydra with a_Hydra ≈ 64,738 km and m_Hydra = 5 · 10¹⁶ km, we get ${m}_{\mathrm{Hydra}}{a}_{\mathrm{Hydra}}^{2}/{m}_{C}{a}_{C}^{2}\approx 3\cdot {10}^{-6}$, which is negligible.

In Figure 2, we compare the satellite precession timescales due to the inner-binary-induced precession with the precession timescales due to LK secular evolution. The opposite dependence of these two precession timescales on the orbital separation give rise to a critical separation at which they equalize, as derived in Equation (1). Beyond the critical separation, a_crit, at which the timescales become comparable, satellites/rings become highly susceptible to LK secular evolution. The effect of the inner binary can be combined with the full secular equations of motion of the quadruple system (Pluto–Charon+outer satellite+the Sun) to derive the full orbital evolution of the outer satellite in time. We use such derivations to find the maximal inclination and eccentricities attained by an initially co-planar satellite orbiting Pluto–Charon on a circular orbit, as a function of the satellite initial separation from Pluto (Figure 2). As can be seen, the LK secular timescale is longer than the binary-induced precession timescale for satellites at small separations, including the current locations of Pluto satellites. LK evolution induced eccentricity and inclination oscillations are completely quenched in these regions below a_crit, allowing for the stable orbits of the currently known satellites. However, beyond this point, LK oscillations are not (or are only partially) quenched. Satellites in these regions experience large amplitude eccentricity and inclination oscillations. In principle, satellites excited to high eccentricities might even cross the orbits of the inner satellites at pericenter approach or extend beyond the Hill stable region at apocenter. The former case leads to strong interactions with the inner satellites; such a satellite will eventually destabilize the satellite system or collide with one of the inner moons. In the latter case, the perturbations by the Sun will destabilize the orbit of the moon, likely ejecting it from the system or sending into crossing orbits with the inner moons (see examples in Figure 3). Regions in which such instabilities occur are therefore excluded regions where outer satellites cannot survive (Figure 4).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

We can therefore exclude the existence of moons with some given orbital parameters a, i, e if they do not follow the stability criteria (Grishin et al. 2016)

$$\begin{eqnarray}{a}_{\mathrm{Hydra}} & \lt & a[1-{e}_{\max }(a,i,e)]\,\mathrm{and}\ a[1+1/4{e}_{\max }^{2}(a,i,e)]\\ & \lt & 0.5{R}_{\mathrm{Hill}}\end{eqnarray} \tag{ 2 }$$

where e_max(a, i, e) is the maximal eccentricity of the moon during an LK cycle (which can be analytically or numerically derived from the coupled secular evolution equations of the orbital parameters; including both binary precession and LK precession terms; see Figure 5 and Appendix B). Note that the average Keplerian separation is given by $a(1+1/2{e}_{\max }^{2})$ but numerical exploration for triple stability suggests a somewhat better fit with a pre-factor of one-fourth for the upper stability criteria $a(1+1/4{e}_{\max }^{2})\lt 0.5{R}_{\mathrm{Hill}}$. Frouard et al. (2010) showed that eccentricity plays a rule in the stability of triple systems. Note that not far beyond the critical separation, the LK timescale becomes much shorter than the binary-precession timescale, at which point the secular evolution is completely dominated by LK evolution, and the binary precession terms can be neglected, i.e., for such large separations one can use the analytic solution for e_max during LK oscillations, ${e}_{\max }={[1-(5/3){\cos }^{2}I]}^{1/2}$ Lidov (1962), which is independent of the separation. This criterion therefore provides a robust map of the excluded and allowed orbital phase regions in which outer moons may exist in the Pluto–Charon system. Moreover, the current stable configuration of the known inner satellite system can therefore be used to constrain the region where farther satellites can exist.

Zoom In Zoom Out Reset image size

In this section, we present our grid based numerical calculation for the stability of additional moons/rings to the Pluto–Charon system. Each integration is determined by three parameters: the initial eccentricity e_initial, the initial SMA a, and the initial inclination i. Given these parameters, we integrate the secular equations of motion and check if the stability condition from Equation (2) is met. We present the stability grid for five different initial eccentricities: ${e}_{\mathrm{initial}}=\{0,0.1,0.2,0.3,0.5\}$, for each eccentricity, we integrated 100 different SMA in log spacing, 10⁻³ au < a < 1.8 × 10⁻² au and 20 different initial inclination, in linear spacing −80° < i < 15. For each pair of a and i (see example in Figure 3), we checked the stability criteria and deduced whether this set up is stable (white) or unstable (black) see Figure 6. We note that stable orbits are not regular because the $a\gt {a}_{\mathrm{crit}}\approx 0.004\,\mathrm{au}\ ({\rm{600,000}}\,\mathrm{km})$. In Appendix C, we present the rest of the grid integration, for different initial eccentricities the excluded parameter space is similar (see Figure 7).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

For initially circular co-planar moons with a > a_crit, ${e}_{\max }\backsimeq 0.78$ and we get ${a}_{\mathrm{crit}}(1-{e}_{\max })\gt {a}_{\mathrm{Hydra}}$, i.e., such moons never evolve to hydra crossing orbits. This can be seen in Figure 4 showing that initially regular moons on co-planar circular orbits beyond ${a}_{{\rm{m}}\_\mathrm{crit}}$ evolve through LK cycles and can obtain high inclinations and eccentricities, but their trajectories never cross the orbits of the inner moons. Such moons, even if they were initially formed on co-planar circular orbits ("regular" moons) cannot sustain such orbits; they secularly evolve, and if observed they are expected to be irregular moons, with non-negligible eccentricity and/or inclination in respect to the Pluto–Charon orbit. Moreover, initially regular outer moons can exist only in a limited outer region beyond the critical separation, as satellites at even larger separations cross the Hill stability radius. Large regions of the orbital phase space are therefore excluded by these criteria for the existence of moons.

Our results therefore constrain the maximal extension where regular moons and non-self-gravitating planetesimal disks can exist around the Pluto–Charon system. We can therefore predict that any moons residing beyond the critical separation, if such exist, will be eccentric/inclined irregular moons, and we map the specific orbits allowed for such moons. These findings also show that secular LK evolution could play a major role in the formation and evolution of the Pluto–Charon outer system and satellites, if such exist.

In the canonical two-body problem, the bodies are treated as point particles. Any deviation from the point mass approximation changes the solution, and the orbital evolution. For example, if we change the primary from a point mass to an oblate sphere, the resulting orbit of the secondary will be a precessing ellipse (Cheng et al. 2014a) as would be the case if we were to change the primary point mass to a stable binary system. In the latter case, the secondary orbits the center of mass of the inner binary in a precessing Keplerian ellipse, similar to the case of the Pluto–Charon system and its co-planar zero eccentricity moons (Lee & Peale 2006). In the following, we describe the precession rate for the more general case. Following similar derivations (Ford et al. 2000; Blaes et al. 2002; Naoz et al. 2013a; Michaely & Perets 2014; Hamers et al. 2015a), we find that the precession rate of the outer orbit due to the inner orbit, is given by (the inner Pluto–Charon orbit is constant)

$$\begin{eqnarray}\displaystyle \frac{{{dg}}_{m}}{{dt}} & = & 3{C}_{2}\left\{\displaystyle \frac{2\theta }{{G}_{C}}[2+{e}_{C}^{2}(3-5\cos 2{g}_{C})]\right\}\\ & & +3{C}_{2}\left\{\displaystyle \frac{1}{{G}_{m}}[4+6{e}_{C}^{2}+(5{\theta }^{2}-3)\right.\\ & & \times (2+3{e}_{C}^{2}-5{e}_{C}^{2}\cos 2{g}_{C})]\phantom{\rule{}{3ex}}\},\end{eqnarray} \tag{ 3 }$$

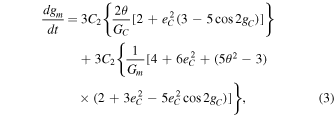
where

$$\begin{eqnarray}&&{C}_{2}=\displaystyle \frac{{{Gm}}_{P}{m}_{C}{m}_{m}}{16({m}_{P}+{m}_{C}){a}_{m}{(1-{e}_{m}^{2})}^{3/2}}{\left(\displaystyle \frac{{a}_{C}}{{a}_{m}}\right)}^{2},\end{eqnarray} \tag{ 4 }$$

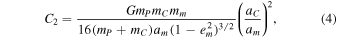
the inner and outer angular momenta are

$$\begin{eqnarray}&&{G}_{C}=\displaystyle \frac{{m}_{P}{m}_{C}}{{m}_{P}+{m}_{C}}\sqrt{G({m}_{P}+{m}_{C}){a}_{C}(1-{e}_{\mathrm{PC}}^{2})}\end{eqnarray} \tag{ 5 }$$

$$\begin{eqnarray}&&{G}_{m}=\displaystyle \frac{{m}_{m}({m}_{P}+{m}_{C})}{{m}_{P}+{m}_{C}+{m}_{m}}\sqrt{G({m}_{P}+{m}_{C}+{m}_{m}){a}_{m}(1-{e}_{m}^{2})}.\end{eqnarray} \tag{ 6 }$$

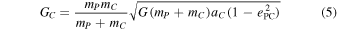
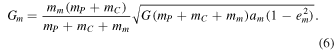
For the Pluto–Charon case e_C = 0, due to tidal interaction, and equation therefore reduces to

$$\begin{eqnarray}&&\displaystyle \frac{{{dg}}_{m}}{{dt}}=6{C}_{2}\left(\displaystyle \frac{2\theta }{{G}_{C}}+\displaystyle \frac{5{\theta }^{2}-1}{{G}_{m}}\right).\end{eqnarray} \tag{ 7 }$$

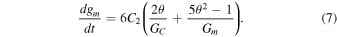
Equation (7) sets a timescale for the orbit precession. Note that if the precession timescale is comparable to the LK timescale, the precession quenches the LK cycling effects on the system. In order to compare the timescales, we can use the approximation in which Pluto and Charon are considered as a single object with the joint total mass. The outer orbit is the orbit on which Pluto orbits the Sun and the inner orbit is the satellite orbit around the Pluto–Charon system. In order to find the SMA on which the precession and LK timescales are equal, we need to equate the LK timescale and the precession timescale and solve for a_m, the inner orbit SMA:

$$\begin{eqnarray}&&6{C}_{2}\left(\displaystyle \frac{2\theta }{{G}_{C}}+\displaystyle \frac{5{\theta }^{2}-1}{{G}_{m}}\right)={\left(\displaystyle \frac{{{dg}}_{m}}{{dt}}\right)}_{\mathrm{Kozai}}\end{eqnarray} \tag{ 8 }$$

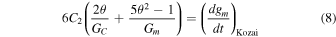
where (dg_m/dt)_Kozai is given by

$$\begin{eqnarray}&&{\left(\displaystyle \frac{{{dg}}_{m}}{{dt}}\right)}_{\mathrm{Kozai}}\approx \displaystyle \frac{{G}^{1/2}{m}_{\odot }{a}_{m}^{3/2}}{{({m}_{P}+{m}_{C}+{m}_{m})}^{1/2}{a}_{p}^{3}{(1-{e}_{P}^{2})}^{3/2}}\end{eqnarray} \tag{ 9 }$$

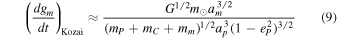
where e_p is Pluto's orbital eccentricity and G is Newton's constant. In the general case, we can solve this equation numerically. However, in the test particle limit we can neglect the first term in the parenthesis of the left hand side and solve for a_m analytically. We can see this fact if we compare the importance of the two terms:

$$\begin{eqnarray}&&\displaystyle \frac{2\theta /{G}_{C}}{(5{\theta }^{2}-1)/{G}_{m}}=\kappa {m}_{m}\left(\displaystyle \frac{2\theta }{5{\theta }^{2}-1}\right)\end{eqnarray} \tag{ 10 }$$

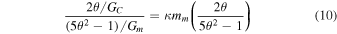
where κ is constant with units. We can see the in the test particle limit ${m}_{m}\,\longmapsto \,0$, the first term is negligible except in an extreme case. In the case of a specific moon inclination that satisfies the following condition

$$\begin{eqnarray}&&5{\theta }^{2}-1=0,\end{eqnarray} \tag{ 11 }$$

which corresponds to

$$\begin{eqnarray}&&{\cos }^{2}i=\displaystyle \frac{1}{5}.\end{eqnarray} \tag{ 12 }$$

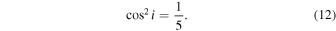
If the approximation is fulfilled, then we can solve for a_m and get the critical a_m

$$\begin{eqnarray}&&{a}_{\mathrm{crit}}^{5}=\displaystyle \frac{3}{8}\displaystyle \frac{{a}_{C}^{2}{a}_{P}^{3}{m}_{P}{m}_{C}{(1-{e}_{p}^{2})}^{3/2}(5{\theta }^{2}-1)}{({m}_{P}+{m}_{C}){(1-{e}_{m}^{2})}^{2}\,{m}_{\odot }}.\end{eqnarray} \tag{ 13 }$$

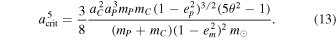
Upon close inspection of (13), one can notice an interesting feature of the dynamics. Due to the term $(1-{e}_{m}^{2})$ in the denominator, eccentric orbits are more stable, with respect to Kozai oscillations than circular ones, which is counterintuitive.

The maximal eccentricity obtained by a moon during its long-term evolution can be derived by solving the full coupled secular evolution equations. However, one can derive approximate analytic solutions in some specific cases. In the following, we derive the maximal eccentricity for a moon on an initially co-planar circular orbit around the inner binary.

The precession rate of the moon's orbit is given by adding the LK precession rate in the quadrupole expansion and to the binary precession by the inner Pluto–Charon system:

$$\begin{eqnarray}&&\displaystyle \frac{{{dg}}_{m}}{{dt}}={\left(\displaystyle \frac{{{dg}}_{m}}{{dt}}\right)}_{\mathrm{percession}}+{\left(\displaystyle \frac{{{dg}}_{m}}{{dt}}\right)}_{\mathrm{Kozai}}\end{eqnarray} \tag{ 14 }$$

$$\begin{eqnarray}\displaystyle \frac{{{dg}}_{m}}{{dt}} & = & \displaystyle \frac{3}{8}\displaystyle \frac{{G}^{1/2}{m}_{P}{m}_{C}{a}_{C}^{2}(5{\theta }^{2}-1)}{{({m}_{P}+{m}_{C})}^{3/2}{a}_{m}^{7/2}{(1-{e}_{m}^{2})}^{2}}\\ & & +\displaystyle \frac{3}{4}\displaystyle \frac{{G}^{1/2}{m}_{S}{a}_{m}^{3/2}}{{({m}_{P}+{m}_{C})}^{1/2}{a}_{p}^{3}{(1-{e}_{P}^{2})}^{3/2}}(2-5{\sin }^{2}{g}_{m}{\sin }^{2}i)\end{eqnarray} \tag{ 15 }$$

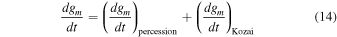
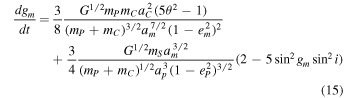
and from the definition of a_crit, see Equation (13), we can substitute to get

$$\begin{eqnarray}&&\displaystyle \frac{{{dg}}_{m}}{{dt}}=\displaystyle \frac{(3/2)\pi }{{T}_{\mathrm{Kozai}}}\left[(2-5{\sin }^{2}{g}_{m}{\sin }^{2}i)+\displaystyle \frac{4}{3}{\left(\displaystyle \frac{{a}_{\mathrm{crit}}}{{a}_{m}}\right)}^{5}\right]\end{eqnarray} \tag{ 16 }$$

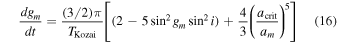
if we redefine t into a more convenient coordinate

$$\begin{eqnarray}&&\tau \equiv t\times \displaystyle \frac{(3/2)\pi }{{T}_{\mathrm{Kozai}}}\end{eqnarray} \tag{ 17 }$$

$$\begin{eqnarray}\displaystyle \frac{{{dg}}_{m}}{d\tau } & = & 2-5{\sin }^{2}{g}_{m}{\sin }^{2}i+\displaystyle \frac{4}{3}{\left(\displaystyle \frac{{a}_{\mathrm{crit}}}{{a}_{m}}\right)}^{5}\\ & = & \left(2+\displaystyle \frac{4}{3}{\left(\displaystyle \frac{{a}_{\mathrm{crit}}}{{a}_{m}}\right)}^{5}-5{\sin }^{2}{g}_{m}{\sin }^{2}i\right)\end{eqnarray} \tag{ 18 }$$

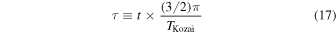
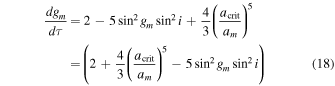
as an immediate result, we get that when the ratio a_crit/a_m tends to zero, the precession rate tends to the standard LK rate and therefore the standard e_max. The standard LK treatment for the test particle problem leads to an additional constant of motion

$$\begin{eqnarray}&&2=5{\sin }^{2}{g}_{m}{\sin }^{2}i\end{eqnarray} \tag{ 19 }$$

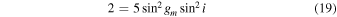
(for derivation see, e.g., Valtonen & Karttunen 2006a). In our system, the correction to the maximal eccentricity is due to the term that is proportional to a_crit/a_m. Therefore, the constant of motion is

$$\begin{eqnarray}&&2+\displaystyle \frac{4}{3}{q}^{5}=5{\sin }^{2}{g}_{m}{\sin }^{2}i\end{eqnarray} \tag{ 20 }$$

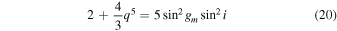
where we define q ≡ a_crit/a_m. From Equation (20), we can get the relation between g_m and sin i. Together with the secular evolution of the orbit eccentricity (for the full equation, see Ford et al. 2000; Blaes et al. 2002) we get the following condition

$$\begin{eqnarray}&&{\sin }^{2}i\gt \displaystyle \frac{2+\tfrac{4}{3}{q}^{5}}{5}.\end{eqnarray} \tag{ 21 }$$

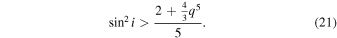
Using the conservation of inner orbit angular momentum equation

$$\begin{eqnarray}&&\sqrt{1-{e}_{0}^{2}}\cos {i}_{0}=\sqrt{1-{e}_{\max }^{2}}\sqrt{1-\displaystyle \frac{2+\tfrac{4}{3}{q}^{5}}{5}}\end{eqnarray} \tag{ 22 }$$

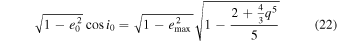
for initially circular orbit the eccentricity vanishes e₀ = 0

$$\begin{eqnarray}&&{\cos }^{2}{i}_{0}=(1-{e}_{\max }^{2})\left(\displaystyle \frac{3-\tfrac{4}{3}{q}^{5}}{5}\right)\end{eqnarray} \tag{ 23 }$$

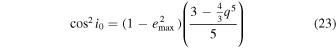
and therefore the maximal eccentricity is given by

$$\begin{eqnarray}&&{e}_{\max }=\sqrt{1-{\cos }^{2}{i}_{0}\displaystyle \frac{5}{3-\tfrac{4}{3}{q}^{5}}}\end{eqnarray} \tag{ 24 }$$

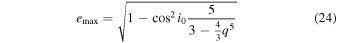
note that for

$$\begin{eqnarray}&&3\lt \displaystyle \frac{4}{3}{q}^{5}\end{eqnarray} \tag{ 25 }$$

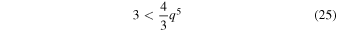
the maximal eccentricity is ill defined; in these cases, a_m is well below a_crit and the secular LK evolution is completely quenched.

We integrated the stability grid for additional initial eccentricities ${e}_{\mathrm{initial}}=\{0,0.1,0.2,0.3,0.5\}$, and we present the results in Figure 7. We note that the structure of the excluded parameter space is very similar.