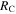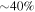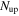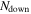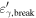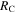Abstract
Gamma-ray bursts (GRBs) are promising as sources of neutrinos and cosmic rays. In the internal shock scenario, blobs of plasma emitted from a central engine collide within a relativistic jet and form shocks, leading to particle acceleration and emission. Motivated by present experimental constraints and sensitivities, we improve the predictions of particle emission by investigating time-dependent effects from multiple shocks. We produce synthetic light curves with different variability timescales that stem from properties of the central engine. For individual GRBs, qualitative conclusions about model parameters, neutrino production efficiency, and delays in high-energy gamma-rays can be deduced from inspection of the gamma-ray light curves. GRBs with fast time variability without additional prominent pulse structure tend to be efficient neutrino emitters, whereas GRBs with fast variability modulated by a broad pulse structure can be inefficient neutrino emitters and produce delayed high-energy gamma-ray signals. Our results can be applied to quantitative tests of the GRB origin of ultra-high-energy cosmic rays, and have the potential to impact current and future multi-messenger searches.
Export citation and abstract BibTeX RIS
1. Introduction
The most energetic particles discovered—ultra-high-energy cosmic rays (UHECRs), above 109 GeV, and high-energy astrophysical neutrinos, above 100 TeV—are detected with regularity, but their sources remain unknown. The extreme physical conditions required to reach these energies restrict the potential source classes. Gamma-ray bursts (GRBs) are one such class. They are the most luminous transient electromagnetic astrophysical phenomena: they emit gamma-rays up to ∼100 GeV, concentrated in only a few tens of seconds. Their observed high luminosities and inferred high particle densities make them prime candidate sources of UHECRs and neutrinos.
One of the leading explanations of GRB emission is the fireball model (Rees & Mészáros 1992). In it, a central engine—likely, a black hole—injects plasma blobs with different relativistic speeds into the jet flow. When they collide with one another, they create mildly relativistic shocks in which their kinetic energy is transformed into internal energy that is radiated away as high-energy particles (Paczynski & Xu 1994; Rees & Mészáros 1994). If the jets contain enough baryons, then protons (Milgrom & Usov 1995; Vietri 1995; Waxman 1995) and nuclei (Murase et al. 2008; Wang et al. 2008) can be accelerated by the shocks into UHECRs which, upon interacting with source photons, create pions and other mesons. Their decays produce PeV gamma-rays and neutrinos (Waxman & Bahcall 1997).
In recent years, IceCube has started testing the hypothesis of GRBs as sources of high-energy neutrinos (Abbasi et al. 2012; Aartsen et al. 2015a, 2016). The simplest versions of the fireball model are now in tension with the data. In these, the neutrino flux prediction for a burst is based on the emission from a single representative plasma blob collision in the jet—this is known as the one-zone approach.
While high-luminosity GRBs cannot account for the diffuse high-energy astrophysical neutrino signal detected by IceCube (Tamborra & Ando 2015; Aartsen et al. 2016), they persist as interesting objects because of the following two reasons. First, they can still be the sources of UHECRs. This can happen if UHECR emission and neutrino emission are not tightly correlated (Baerwald et al. 2013), a possibility that we consider in the present work. Second, they are attractive targets for neutrino telescopes because timing and directional gamma-ray information can be used to reduce neutrino backgrounds. They are ideal sites to look for joint gamma-ray and neutrino signals.
In this paper, we focus on the connection between gamma-rays, UHECRs, and neutrinos in individual GRBs. Unlike most of the existing literature, we consider the multi-messenger emission from a multitude of different plasma collisions along the jet, each one occurring under different physical conditions—this is known as the multi-zone approach.
We construct synthetic GRB light curves—curves of photon rate versus time—that successfully reproduce generic features of real ones. We identify the properties of the central engine that lead to such light curves, and study the consequences for different messengers. For example, light curves dominated by broad pulses overlaid with fast variability imply a "disciplined" engine that ejects shells with little spread in speed at any given time. In such cases, the neutrino production efficiency can be low, and high-energy gamma-ray signals can reach Earth delayed with respect to low-energy signals. Conversely, light curves with no broad pulse structure hint at likely efficient neutrino emitters. We also test the robustness of the assumptions going into the minimal neutrino flux estimate found in Bustamante et al. (2015).
This paper is organized as follows. In Section 2, we comment on GRB emission models. In Section 3, we introduce our multi-zone simulation and a sample of GRBs computed with it. In Section 4, we compute the gamma-ray and neutrino light curves for each of them. In Section 5, we calculate their associated quasi-diffuse neutrino fluxes and show that different types of particles are emitted from different regions in the jet. In Section 6, we show that, for some GRBs, delays between the light curves in different energy bands are possible, and why. We summarize and conclude in Section 7. Appendix
2. One-zone versus Multi-zone Emission
GRBs are conceivably fueled by matter accretion, either in the collapse of a massive star—long-duration bursts, lasting  s—or in the merging of two neutron stars or a neutron star and a black hole—short-duration bursts, lasting
s—or in the merging of two neutron stars or a neutron star and a black hole—short-duration bursts, lasting  . The central engine, likely a newly formed black hole, emits two relativistic matter jets in opposite directions. When one of them points toward Earth, we might detect it as a GRB. We focus on long-duration bursts because they have higher gamma-ray luminosity (
. The central engine, likely a newly formed black hole, emits two relativistic matter jets in opposite directions. When one of them points toward Earth, we might detect it as a GRB. We focus on long-duration bursts because they have higher gamma-ray luminosity (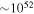 erg s−1), represent
erg s−1), represent 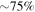 of observed bursts, and their emission mechanism has been more deeply studied.
of observed bursts, and their emission mechanism has been more deeply studied.
In the internal shock scenario of the fireball model, internal plasma collisions within the jet account for particle emission during the initial, or prompt, phase of the burst, which typically lasts 10–100 s. Ultimately, the jet reaches the circumburst medium, triggering a late emission phase—the afterglow. We will focus exclusively on the prompt phase, where PeV neutrino emission is well-motivated. This is the energy range where existing water-Cherenkov neutrino telescopes, like IceCube and ANTARES, are most sensitive. However, the internal shock scenario, while successful, is not without issues, which we introduce below.
The GRB prompt emission mechanism has been under debate for years (see reviews by Piran 1999; Mészáros 2006; Kumar & Zhang 2014; Mészáros et al. 2015; Pe'er 2015). In the classical model, prompt gamma-ray emission in the MeV range is attributed to optically thin synchrotron emission from non-thermal electrons accelerated at internal shocks (Rees & Mészáros 1994), possibly supplemented by a thermal component from the fireball. Indeed, there are observational indications of such a thermal component (see, e.g., Pe'er 2012; Guiriec et al. 2011). However, this classical internal shock model has difficulty explaining the data, including the low-energy spectral index (Preece et al. 1998), radiation efficiency (Kumar 1999; Zhang et al. 2007), and spectral energy relations (Amati et al. 2002; Yonetoku et al. 2004).
Among alternative theories, photospheric emission models became popular after the Fermi satellite was launched (Thompson 1994; Rees & Mészáros 2005; Pe'er et al. 2006; Ioka et al. 2007; Giannios 2008; Beloborodov 2010; Lazzati et al. 2013). In them, the bulk of the prompt emission is attributed to quasi-thermal emission from below the photosphere, i.e., from the region where gamma-rays are unable to escape due to high optical depth to electron-photon scattering. Amid different versions of photospheric emission models, dissipative photosphere models have been discussed both theoretically and observationally, due to their appealing implications (Beloborodov 2013; Hascoet et al. 2013; Vurm et al. 2013). Some authors consider the superposition of pure thermal emission to explain the prompt emission spectrum (Lundman et al. 2013).
Magnetic reconnection models have also been largely of interest (Mészáros & Rees 1997; Lyutikov & Blandford 2003; Zhang & Yan 2011; Bošnjak & Kumar 2012; McKinney & Uzdensky 2012), due to certain advantages (Kumar & Zhang 2014), though detailed microphysics is much more uncertain. For example, they can explain the high polarization observed in some GRBs (Gotz et al. 2009; Yonetoku et al. 2012) and the absence of bright thermal emission (Zhang & Pe'er 2009; Gao & Zhang 2015).
Even though the classical internal shock model has several theoretical issues, internal shocks may still play an important role in the dissipation of the outflowing kinetic energy. For instance, some photospheric emission models require sub-photospheric dissipation that is often attributed to internal shocks (Rees & Mészáros 2005). Magnetic reconnection may also be driven by shocks beyond the photosphere (Zhang & Yan 2011). Even in the optically thin internal shock model, the observed spectra can be explained by synchrotron emission with some modifications such as stochastic acceleration of electrons in the shock downstream (Bykov & Mészáros 1996; Murase et al. 2012; Asano & Terasawa 2015).
In the internal shock model, shell collisions inside the jet are responsible for the shape of the GRB light curves. They typically have a fast time variability 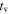 , of ∼10–100 ms (Bhat 2013; Golkhou et al. 2015), frequently superposed on top of slower pulse structure (Ramirez-Ruiz & Fenimore 1999; Nakar & Piran 2002b). Since the light curve reflects the particularities of the central emitter and jet propagation (Nakar & Piran 2002a; Lopez-Camara et al. 2016; Zhang et al. 2016), no two are equal, though they can be classified on the basis of their morphology.
, of ∼10–100 ms (Bhat 2013; Golkhou et al. 2015), frequently superposed on top of slower pulse structure (Ramirez-Ruiz & Fenimore 1999; Nakar & Piran 2002b). Since the light curve reflects the particularities of the central emitter and jet propagation (Nakar & Piran 2002a; Lopez-Camara et al. 2016; Zhang et al. 2016), no two are equal, though they can be classified on the basis of their morphology.
One-zone collision models assume average shell properties—such as an average speed or Lorentz factor 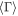 —derived from gamma-ray observations. Neutrino emission is computed for a single representative collision (Dermer & Atoyan 2003; Guetta et al. 2004) and is scaled by the total number of collisions—roughly,
—derived from gamma-ray observations. Neutrino emission is computed for a single representative collision (Dermer & Atoyan 2003; Guetta et al. 2004) and is scaled by the total number of collisions—roughly, 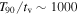 , with
, with 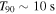 the burst duration—to yield the flux for the whole burst, implying that all collisions are identical (see, e.g., Asano 2005).
the burst duration—to yield the flux for the whole burst, implying that all collisions are identical (see, e.g., Asano 2005).
However, it is unrealistic that all collisions occur at the same radius. The main reason is that all shells would have to be emitted with precisely tuned speeds. A different reason comes from the fact that energy deposited in the afterglow cannot be too large; therefore, a sizable part of the energy must be dissipated during the preceding prompt phase. Because dissipation of kinetic energy into radiation scales with the difference of the Lorentz factors of the colliding shells, this implies that the differences must be large. In fact, there is considerable spread in the inferred values of bulk Lorentz factors of GRBs observed by the Fermi satellite (Ackermann et al. 2012). Assuming for the Lorentz factors a broad or bi-modal distribution leads to efficient dissipation of kinetic energy in the prompt phase (Kumar 1999; Zhang et al. 2007). As a consequence, collisions occur at many positions throughout the jet, from below the photosphere—where gamma-rays cannot escape—to the circumburst medium, and that particle emission will be different for each collision.
The impact of a distribution7
of Lorentz factors or emission radii have been addressed qualitatively (Murase & Nagataki 2006) and quantitatively (Guetta et al. 2001a, 2001b; Bustamante et al. 2015; Globus et al. 2015). For example, Bustamante et al. (2015) predicted a minimal quasi-diffuse prompt neutrino flux from super-photospheric collisions, at the level of  per flavor, which is presently below the sensitivity of IceCube. In later sections, we discuss the relationship among different types of messengers in multiple-collision models, focusing on how the properties of the central engine impact the GRB light curves and neutrino emission efficiency.
per flavor, which is presently below the sensitivity of IceCube. In later sections, we discuss the relationship among different types of messengers in multiple-collision models, focusing on how the properties of the central engine impact the GRB light curves and neutrino emission efficiency.
IceCube recently discovered a diffuse astrophysical flux of neutrinos between about 30 TeV and 2 PeV (Aartsen et al. 2013a, 2013b, 2014a, 2014b, 2015b, 2015c). However, no individual neutrinos are associated to known GRBs (Abbasi et al. 2012; Aartsen et al. 2015a, 2016). The resulting upper limit, extrapolated from a catalog of bursts, is about an order of magnitude below the diffuse flux. Thus, it is unlikely that classical high-luminosity GRBs are the main origin of the observed IceCube neutrinos (Laha et al. 2013; Murase & Ioka 2013; Bustamante et al. 2015). (However, low-luminosity classes of GRBs can describe the diffuse neutrino flux without violating the stacking limits (Murase et al. 2006; Gupta & Zhang 2007), subject to their assumed source density.)
Nevertheless, this does not preclude GRBs from being the dominant sources of UHECRs. So far, results of these observational searches have been interpreted mostly in the context of one-zone models (Waxman & Bahcall 1997; Guetta et al. 2004; He et al. 2012; Hümmer et al. 2012; Li 2012). While the plain one-zone ansatz with commonly assumed parameters with values that are favorable for the UHECR explanation, is starting to be challenged by IceCube data (He et al. 2012; Hümmer et al. 2012), it is not fully ruled out yet.
Another important aspect is that the relationship between neutrino and cosmic-ray emission depends on the UHECR escape mechanism (Baerwald et al. 2013). It has been shown that, depending on the parameter values, a fraction of cosmic rays must directly escape from the sources without neutrino production (Baerwald et al. 2013). Earlier approaches focused on the emission of neutrons only (Ahlers et al. 2011), which leads to a stringent relation between the neutrino and cosmic-ray fluxes. Consequently, bounds on GRB neutrinos translate into bounds on the GRB parameter space; see Baerwald et al. (2015) for the bounds in the one-zone model. Further quantitative tests are necessary to test the possibility that UHECRs mainly come from GRBs, especially taking into account the effects from multiple collisions.
3. Simulating Collisions in a GRB Jet
We study the prompt emission phase of the GRB in the internal shock scenario by simulating collisions of many propagating plasma blobs. Our simulations are based on Kobayashi et al. (1997) and Daigne & Mochkovitch (1998). See Appendix
Figure 1 illustrates the evolution of the blobs along the jet. To simplify the computations, we take them to be spherical shells. The simulation starts with the central engine emitting 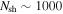 shells. Each one propagates at a different relativistic speed; typically, they have Lorentz factors of
shells. Each one propagates at a different relativistic speed; typically, they have Lorentz factors of 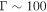 . After some time, they catch up to one another, collide inelastically, and merge into new shells. At collisionless shocks generated during the collisions, a fraction of the kinetic energy of the colliding shells is used for particle acceleration and creation, and becomes the internal energy of the newly created shells. The new shells cool instantly by emitting high-energy particles, continue propagating in the jet, and may collide again. Each simulation in this work comprises about 1000 collisions, as almost all initial shells collide.
. After some time, they catch up to one another, collide inelastically, and merge into new shells. At collisionless shocks generated during the collisions, a fraction of the kinetic energy of the colliding shells is used for particle acceleration and creation, and becomes the internal energy of the newly created shells. The new shells cool instantly by emitting high-energy particles, continue propagating in the jet, and may collide again. Each simulation in this work comprises about 1000 collisions, as almost all initial shells collide.
Figure 1. Illustration of the initialization, evolution, and collision of plasma shells in our simulations. See the main text and Appendix
Download figure:
Standard image High-resolution imageNon-thermal electrons receive a fraction 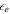 of the internal energy of the new shell, protons receive a fraction
of the internal energy of the new shell, protons receive a fraction 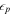 , and magnetic fields receive a fraction
, and magnetic fields receive a fraction 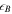 . Because electrons cool quickly via synchrotron emission,
. Because electrons cool quickly via synchrotron emission, 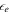 can also be regarded as the energy fraction of radiated gamma-rays. We assume that there is energy equipartition between electrons and magnetic fields, and 10 times more energy in protons (Abbasi et al. 2010; Hümmer et al. 2012), i.e.,
can also be regarded as the energy fraction of radiated gamma-rays. We assume that there is energy equipartition between electrons and magnetic fields, and 10 times more energy in protons (Abbasi et al. 2010; Hümmer et al. 2012), i.e., 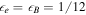 and
and  see Appendix
see Appendix  can be regarded as the non-thermal baryon loading factor, defined as the ratio of cosmic-ray energy to radiation energy (Murase & Nagataki 2006).
can be regarded as the non-thermal baryon loading factor, defined as the ratio of cosmic-ray energy to radiation energy (Murase & Nagataki 2006).
The volume of the shell (see Appendix
In a shell collision, if both protons and electrons are accelerated up to sufficiently high energies, 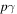 interactions create pions via the
interactions create pions via the 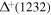 resonance and other processes. High-energy gamma-rays are produced in
resonance and other processes. High-energy gamma-rays are produced in  (and by synchrotron and inverse-Compton radiation by electrons), while high-energy neutrinos are produced in
(and by synchrotron and inverse-Compton radiation by electrons), while high-energy neutrinos are produced in 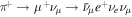 (and, via additional production channels, by its charge-conjugated version). The pion production efficiency is, on average,
(and, via additional production channels, by its charge-conjugated version). The pion production efficiency is, on average,  this is the fraction of proton energy received by pions. It is distributed roughly evenly among the pion decay products, so each neutrino carries
this is the fraction of proton energy received by pions. It is distributed roughly evenly among the pion decay products, so each neutrino carries 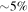 of the proton energy. Therefore, production of PeV neutrinos requires 20 PeV protons.
of the proton energy. Therefore, production of PeV neutrinos requires 20 PeV protons.
At the source, for the protons, we assume a power-law spectrum 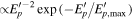 , with
, with  the proton energy, as expected from Fermi acceleration (primed quantities are in the shock rest frame). The maximum proton energy
the proton energy, as expected from Fermi acceleration (primed quantities are in the shock rest frame). The maximum proton energy 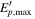 is computed by balancing the acceleration rate, and the synchrotron, adiabatic, and photohadronic energy loss rates (Baerwald et al. 2013).
is computed by balancing the acceleration rate, and the synchrotron, adiabatic, and photohadronic energy loss rates (Baerwald et al. 2013).
For the target photons, we assume a broken power-law spectrum, Equation (14), which resembles the gamma-ray spectrum observed at Earth. This assumption is certainly justified beyond the photosphere, from where the photons can escape. Note that we neither generate the photon spectrum from first principles, nor explain its origin, which typically includes radiation processes such as inverse-Compton scattering, synchrotron emission, and bremsstrahlung. The Band function can be reproduced by invoking various effects, such as the slow heating of electrons (Bykov & Mészáros 1996; Murase et al. 2012; Asano & Terasawa 2015). In this sense, our approach is model-independent; this comes at the expense of insight on the radiation processes at work and their detailed individual implications on secondary production. To calculate the secondary particle production, we use the state-of-the-art NeuCosmA (Hümmer et al. 2012) software (see Appendix
UHECRs are emitted via two mechanisms: either  interactions transform protons into neutrons, which escape the merged shell, and later beta-decay back into protons (Mannheim et al. 2001), or protons directly leak out of the shell without interacting. The latter situation occurs if the proton Larmor radius—determined by the physical conditions in the shell—exceeds the shell width at the highest energies; see Baerwald et al. (2013) for a detailed discussion. This direct escape produces a hard proton spectrum (it is dubbed a "high-pass filter" in Globus et al. 2015). Direct proton escape dominates over neutron escape only when the photon densities are low. Therefore, neutrino production associated with neutron escape is higher than that associated with direct proton escape (Mannheim et al. 2001).
interactions transform protons into neutrons, which escape the merged shell, and later beta-decay back into protons (Mannheim et al. 2001), or protons directly leak out of the shell without interacting. The latter situation occurs if the proton Larmor radius—determined by the physical conditions in the shell—exceeds the shell width at the highest energies; see Baerwald et al. (2013) for a detailed discussion. This direct escape produces a hard proton spectrum (it is dubbed a "high-pass filter" in Globus et al. 2015). Direct proton escape dominates over neutron escape only when the photon densities are low. Therefore, neutrino production associated with neutron escape is higher than that associated with direct proton escape (Mannheim et al. 2001).
Gamma-rays are produced throughout the jet. However, they only escape if they are produced above the "photosphere," i.e., the radius below which Thomson scattering occurs frequently enough to effectively trap them (see Appendix
For super-photospheric collisions, the gamma-rays are still attenuated in energy and produce particle cascades, via electron–positron pair-production processes inside shells (see below). After gamma-rays leave the source, they scatter off cosmological photon fields—microwave, optical, infrared—and their energies are degraded down to a few hundred GeV or lower. UHECRs also lose energy through photohadronic interactions and inelastic scattering off cosmological photons. Neutrinos are affected only by the adiabatic cosmological expansion, which changes their energies by, at most, a factor of a few.
We normalize the gamma-ray emission of our simulated bursts to typical time-integrated GRB gamma-ray energies,  erg (in the source reference frame). This is equated to the sum energy emitted by all collisions, sub- and super-photospheric (Equation (13)). In our simulated bursts, about
erg (in the source reference frame). This is equated to the sum energy emitted by all collisions, sub- and super-photospheric (Equation (13)). In our simulated bursts, about 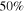 of the energy is liberated in super-photospheric collisions.
of the energy is liberated in super-photospheric collisions.
4. Synthetic Light Curves
GRB light curves are highly irregular. They are extremely variable, and a fraction of GRBs have minimum variability timescales of ms (Golkhou et al. 2015). The time resolution of the detector imposes a lower bound on the variability timescale that can be inferred. Pulses typically have a duration of ∼1 s with an asymmetric structure (Ramirez-Ruiz & Fenimore 1999; Nakar & Piran 2002b), and some GRBs show distinct quiescent time between the pulses.
In the internal shock scenario, the shape of the GRB light curve is the result of shell collisions (Kobayashi et al. 1997; Daigne & Mochkovitch 1998; Beloborodov 2000; Spada et al. 2000; Kobayashi & Sari 2001; Daigne & Mochkovitch 2003; Aoi et al. 2010). When shells collide, a gamma-ray pulse and a neutrino pulse are emitted. The superposition of all pulses emitted during the evolution of the burst makes up the light curve. Different features in the light curves are due to differences in the distribution of collision radii, as determined by the initial speeds of the shells, imprinted on them by the central emitter. See Appendix
The simulation parameters from our benchmark model from Bustamante et al. (2015) are re-branded here as "GRB 1." Note that we slightly adjusted the collision model;8
therefore, the results are not exactly the same as in Bustamante et al. (2015). Most notably, collisions occur on average at slightly lower radii now. The initial values of shell Lorentz factors, 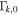 , are randomly sampled from a log-normal distribution defined by the characteristic value
, are randomly sampled from a log-normal distribution defined by the characteristic value 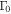 and the amplitude of fluctuations AΓ:
and the amplitude of fluctuations AΓ:

where the random variable x follows a Gaussian distribution, 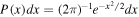 . When
. When 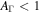 , the mean value
, the mean value 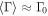 and the variance
and the variance  . When
. When 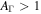 , the mean value and variance are significantly affected by fluctuations. Large
, the mean value and variance are significantly affected by fluctuations. Large 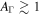 are typically required for the efficient conversion of kinetic energy to radiated energy (Kobayashi & Sari 2001), since the latter is proportional to the difference in speeds between two colliding shells. In addition,
are typically required for the efficient conversion of kinetic energy to radiated energy (Kobayashi & Sari 2001), since the latter is proportional to the difference in speeds between two colliding shells. In addition, 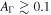 is necessary for the number of collisions to be large, i.e.,
is necessary for the number of collisions to be large, i.e., 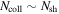 . The light curve for GRB 1 is in Figure 4. It is dominated by fast variability, which is determined by the ratio of T90 to
. The light curve for GRB 1 is in Figure 4. It is dominated by fast variability, which is determined by the ratio of T90 to  , on the order of tens of ms, which is typical for GRBs.
, on the order of tens of ms, which is typical for GRBs.
Figure 2 shows selected real gamma-ray light curves that have slower structure overlaid with fast variability. In the internal shock scenario, the slower structure can be produced by modifying the behavior of the engine. We can change the widths of the initial shells, the separations between them or the spread AΓ, emit shells intermittently, ramp up or down the Lorentz factors during shell emission, or make them oscillate (see also Daigne & Mochkovitch 1998).
Figure 2. Selected GRB light curves, detected by BATSE (Paciesas et al. 1999) in the  range (channels 1–4); from left to right: GRB920513, GRB931008, GRB940210, and GRB920627. The implied time resolution is 64 ms.
range (channels 1–4); from left to right: GRB920513, GRB931008, GRB940210, and GRB920627. The implied time resolution is 64 ms.
Download figure:
Standard image High-resolution imageTable 1 lists our sample simulations, GRBs 1–6, where we have implemented these options. We have chosen parameter values such that the associated synthetic light curves reproduce features similar to Figure 2.
Table 1. Description of Simulated GRBs 1–6
| Model |
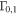
|
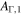
|
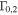
|
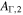
|
Tp |
|
|
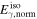 (erg) (erg) |
Description |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 500 | 1.0 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | 1053 | Fixed Γ and AΓ; benchmark from Bustamante et al. (2015) |
| 2 | 500 | 1.0 | 50 | 0.1 | ⋯ | ⋯ | ⋯ | 1053 | Linear speedup of Γ |
| 3 | 50 | 0.1 | 500 | 0.1 | 0.34 | ⋯ | ⋯ | 1053 | Sawtooth Γ (linear slowdown three times) with narrow distribution |
| 4 | 50 | 0.1 | 500 | 1.0 | 0.2 | ⋯ | ⋯ | 1053 | Oscillating Γ (five periods) with increasing distribution width |
| 5 | 50 | 0.1 | 500 | 0.1 | 0.2 | ⋯ | ⋯ | 1053 | Oscillating Γ (four periods) with lower amplitude increasing and narrow distribution |
| 6 | 50 | 0.1 | 500 | 1.0 | 1/8 | 250 | 250 | 1053 | Oscillating Γ (four periods) with distribution widening up; in addition, engine intermittent: 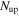 pulses followed by pulses followed by 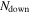 pulses; corresponds to increasing Lorentz factor during uptime pulses; corresponds to increasing Lorentz factor during uptime |
Note. Common values for all models: 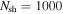 ,
, 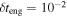 s,
s, 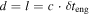 ,
, 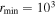 km,
km, 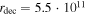 km, z = 2,
km, z = 2, 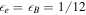 ,
, 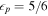 , and
, and 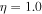 (acceleration efficiency; Baerwald et al. 2013). See Table 3 for an explanation of each parameter. The period Tp for the oscillating cases refers to Γ changing between
(acceleration efficiency; Baerwald et al. 2013). See Table 3 for an explanation of each parameter. The period Tp for the oscillating cases refers to Γ changing between 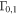 and
and 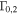 , and AΓ changing between
, and AΓ changing between 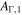 and
and 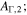 Tp is a fraction of the total number of emitted shells. This means that Γ and
Tp is a fraction of the total number of emitted shells. This means that Γ and 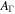 change between first and second value with a factor
change between first and second value with a factor 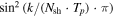 , where k is the index of the shell (
, where k is the index of the shell ( ). For GRB 5, the lower amplitude increases from
). For GRB 5, the lower amplitude increases from 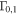 to
to 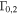 linearly with k.
linearly with k.
Download table as: ASCIITypeset image
Figure 3 shows the randomly sampled initial values of the Lorentz factors 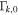 of the shells in GRBs 1–6, as a function of initial radius
of the shells in GRBs 1–6, as a function of initial radius 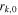 . See Table 1 for descriptions of the underlying distributions.
. See Table 1 for descriptions of the underlying distributions.
Figure 3. Initial values of the Lorentz factors of the shells in GRBs 1–6, at the start of the simulations. See Table 1 for descriptions of the underlying distributions of initial Lorentz factors in each simulation.
Download figure:
Standard image High-resolution imageFigure 4 shows that the synthetic gamma-ray and neutrino light curves for GRBs 1–6. GRB 1 has fast time variability without prominent features. GRB 2 has a speedup in Γ during shell emission; a single pulse is overlaid with fast variability. For a slowdown, the pulse occurs earlier and the light curve is time-inverted. However, the efficiency is much lower in this case because the fast shells are emitted first. GRB 3 has three pulses with linear slowdown. The second and third pulses collide with slow shells from the preceding pulse and therefore contribute more strongly to the light curve than the first pulse. GRBs 4 and 6 have more oscillating periods. GRB 5 is oscillating as well, but its lower amplitude increases linearly during emission. Comparison with Figure 2 reveals that GRB 3 was inspired by GRB931008; GRBs 4 and 6, by case GRB920627; and GRB 5, by cases GRB920513 and GRB940210. Appendix
Figure 4. Synthetic gamma-ray and neutrino light curves for the simulated GRBs 1–6, from collisions beyond the photosphere. Photon and neutrino counts are in arbitrary units, obtained by multiplying the flux times a factor of 106 GeV−1 cm2 s.
Download figure:
Standard image High-resolution imageMost GRB light curves detected by Fermi (Ajello et al. 2013; von Kienlin et al. 2014) do not have prominent features like the ones in Figure 2. The reason why the latter are featured in the literature more often than simpler single-pulse or fast-variability light curves is possibly a selection effect (i.e., they are more interesting to show and study). From that perspective, it is conceivable that GRBs 3–6 are not "typical" GRBs.
The light curves of GRBs 3 and 5 are qualitatively different from the others in one key aspect: they have a dominant, broad pulse structure overlaid with fast time variability, whereas in the other bursts the fast component is more relevant. This feature can be traced back to the input parameters in Table 1: GRBs 3 and 5 have a "disciplined" central engine that emits shells within a narrow Γ distribution ( ), while the average Γ changes slowly. Therefore, most collisions occur at larger radii compared to the cases where the spread in Γ is larger. We will see that this also affects the neutrino production efficiency in the case of GRB 5.
), while the average Γ changes slowly. Therefore, most collisions occur at larger radii compared to the cases where the spread in Γ is larger. We will see that this also affects the neutrino production efficiency in the case of GRB 5.
The internal shock model has been invoked as a successful model to explain irregular features of the GRB light curve (Kobayashi et al. 1997; Daigne & Mochkovitch 1998; Beloborodov 2000; Spada et al. 2000; Kobayashi & Sari 2001; Daigne & Mochkovitch 2003; Aoi et al. 2010). However, because the classical internal shock model is being challenged, light-curve predictions of alternative models have also been extensively investigated. In particular, it has been shown that turbulence or magnetic reconnection models can better explain the observed structure of the GRB light curve (Lazar et al. 2009; Narayan & Kumar 2009; Zhang & Zhang 2014; Beniamini & Granot 2016). Some recent studies suggested that GRB light curves may consist of the superposition of slow and fast components, as inferred by a gradual depletion of the fast component at low energies (Vetere et al. 2006). Sub-structures of the observed GRB pulses can be easily accounted for by assuming relativistic motions in the bulk of a relativistic jet. Although their origins are unclear at present, such relativistic motions could be realized in the ICMART model (Zhang & Zhang 2014). Compared to these explanations, our pulse structure comes from the properties of the engine rather than the jet.
Figure 4 shows that there is no linear correlation between the heights of gamma-ray and neutrino pulses. This is because the height of a neutrino pulse is, via the pion production efficiency, more sensitive to the collision radius than the height of a gamma-ray pulse, i.e., it depends on the proton and photon densities, which drop  , where
, where 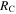 is the collision radius.
is the collision radius.
There are no long time delays between gamma-ray and neutrino pulses: they are within T90 (see Equation (23)) of each other. There may be, however, short delays. For example, in GRB 3, the neutrino peak corresponding to the first large gamma-ray peak is suppressed. So the first gamma-ray detection will have occurred ∼20 s, before the neutrino instrument triggers. In GRB 4, the quiescent periods of gamma-ray and neutrino emission coincide, which may be exploited by neutrino telescopes to set further time window cuts.
In GRB 5, the fast time variability gives rise to neutrino spikes, whereas the longer pulses seen in gamma-rays are hardly present in neutrinos. Indeed, the rise time of the spike of particle emission associated with one collision depends strongly on Γ (see Equation (18)) and, consequently, it is  . Therefore, faster rises—sharper structures—are created by collisions at smaller radii, where the neutrino production efficiency is higher.
. Therefore, faster rises—sharper structures—are created by collisions at smaller radii, where the neutrino production efficiency is higher.
Table 2 lists the parameters output by GRBs 1–6. GRBs 1, 2, 4, and 5 have time variabilities of 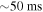 and durations of
and durations of  . In GRB 3, the duration (
. In GRB 3, the duration (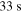 ) and time variability (
) and time variability (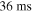 ) are smaller because mainly two of the three peaks contribute. In GRB 6, pulses are separated by a downtime and, therefore, duration and variability are larger (
) are smaller because mainly two of the three peaks contribute. In GRB 6, pulses are separated by a downtime and, therefore, duration and variability are larger (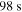 and
and 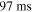 , respectively).
, respectively).
Table 2. Parameters Output by Simulated GRBs 1–6
| Model |
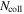
|
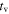 (ms) (ms) |
T90 (s) |
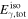 (erg) (erg) |
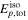 (erg) (erg) |
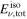 (erg) (erg) |
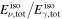 
|
ε 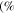 ) ) |
|---|---|---|---|---|---|---|---|---|
| 1 | 987 | 53 | 54.0 |
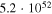
|
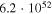
|
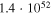
|
26.9 | 26.8 |
| 2 | 999 | 47 | 47.0 |
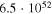
|
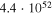
|

|
14.3 | 19.6 |
| 3 | 951 | 33 | 35.5 |
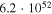
|

|
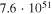
|
12.3 | 10.5 |
| 4 | 987 | 52 | 52.6 |
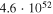
|
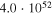
|

|
20.4 | 21.7 |
| 5 | 990 | 57 | 57.9 |
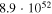
|
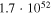
|
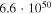
|
0.7 | 10.6 |
| 6 | 985 | 97 | 98.0 |
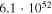
|
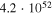
|
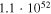
|
18.0 | 23.6 |
Note. The parameters are variability timescale (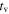 ), total energy emitted as gamma-rays (
), total energy emitted as gamma-rays (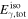 ), as protons (
), as protons (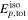 ), and as neutrinos (
), and as neutrinos (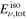 ), ratio between neutrino and gamma-ray energies (
), ratio between neutrino and gamma-ray energies ( ), and overall emission efficiency ε. Energies are computed using super-photospheric collisions only. Only protons in the UHECR energy range, above
), and overall emission efficiency ε. Energies are computed using super-photospheric collisions only. Only protons in the UHECR energy range, above 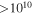 GeV, are counted. The efficiency ε is defined as the ratio of total energy dissipated by all types of particles (gamma-rays, protons, neutrinos) to the total kinetic energy initially available.
GeV, are counted. The efficiency ε is defined as the ratio of total energy dissipated by all types of particles (gamma-rays, protons, neutrinos) to the total kinetic energy initially available.
Download table as: ASCIITypeset image
The dissipation efficiency ε of a burst in Table 2 is the ratio between total energy dissipated by all types of particles in super-photospheric collisions and total kinetic energy available at the start of the simulation. Most simulations9
have high 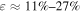 , which reasonably agrees with previous work (Beloborodov 2000). The efficiency is lower in cases with narrow Γ distribution, as expected.
, which reasonably agrees with previous work (Beloborodov 2000). The efficiency is lower in cases with narrow Γ distribution, as expected.
The gamma-ray emission efficiency 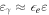 is about 10 times smaller since most of the dissipation energy is assumed to be carried by protons rather than electrons. Here,
is about 10 times smaller since most of the dissipation energy is assumed to be carried by protons rather than electrons. Here, 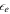 is the fraction of energy in electrons and photons; see Appendix
is the fraction of energy in electrons and photons; see Appendix
5. Multi-messenger Emission
Here we discuss the emission of multiple messengers and their relation.
5.1. Weak versus Strong Neutrino Emitters
The time-integrated neutrino fluence of a simulated burst, for a baryon-rich jet, roughly scales as (Bustamante et al. 2015)

assuming a fixed photon break energy (see Appendix 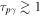 to
to 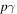 interactions, ε is the energy dissipation efficiency, and
interactions, ε is the energy dissipation efficiency, and  is the total energy emitted as gamma-rays in super-photospheric collisions. Unlike one-zone predictions (Waxman & Bahcall 1997; Guetta et al. 2004; He et al. 2012; Hümmer et al. 2012; Li 2012), the fluence does not depend on the average Lorentz factor of the shells.
is the total energy emitted as gamma-rays in super-photospheric collisions. Unlike one-zone predictions (Waxman & Bahcall 1997; Guetta et al. 2004; He et al. 2012; Hümmer et al. 2012; Li 2012), the fluence does not depend on the average Lorentz factor of the shells.
Figure 5 shows 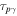 as a function of
as a function of 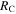 for collisions in GRBs 1 and 5. In GRB 1, a strong neutrino emitter, about 60 in 1000 collisions occurred above the photosphere—so that they were optically thin to Thomson scattering—and were still optically thick to photomeson production. The other simulations with broad Γ distributions have similar results. Therefore, the first factor in Equation (2) is ∼0.05 for strong neutrino emitters. The energy dissipation efficiency in Table 2 lies around
for collisions in GRBs 1 and 5. In GRB 1, a strong neutrino emitter, about 60 in 1000 collisions occurred above the photosphere—so that they were optically thin to Thomson scattering—and were still optically thick to photomeson production. The other simulations with broad Γ distributions have similar results. Therefore, the first factor in Equation (2) is ∼0.05 for strong neutrino emitters. The energy dissipation efficiency in Table 2 lies around 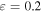 for these GRBs. As a result, for fixed
for these GRBs. As a result, for fixed  , the quasi-diffuse neutrino flux that we infer below (Bustamante et al. 2015) is relatively robust.
, the quasi-diffuse neutrino flux that we infer below (Bustamante et al. 2015) is relatively robust.
Figure 5. Optical depth 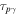 for all collisions in GRBs 1 (top) and 5 (bottom) as a function of collision radius. The horizontal line corresponds to
for all collisions in GRBs 1 (top) and 5 (bottom) as a function of collision radius. The horizontal line corresponds to 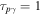 . Black filled rectangles are sub-photospheric collisions, red filled dots are super-photospheric collisions, where the dominant UHECR component is neutron escape, and blue unfilled dots are super-photospheric collisions where the dominant component is direct proton escape.
. Black filled rectangles are sub-photospheric collisions, red filled dots are super-photospheric collisions, where the dominant UHECR component is neutron escape, and blue unfilled dots are super-photospheric collisions where the dominant component is direct proton escape.
Download figure:
Standard image High-resolution imageThe situation is different for GRBs 3 and 5. They have lower efficiencies 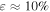 . More importantly, they have no optically thick collisions close to the photosphere; see the bottom panel of Figure 5 for GRB 5. The reason is that they emit shells with a variable but narrow Lorentz factor distribution (see Figure 3) that tends to induce collisions at larger radii, where photon densities are low and, therefore, so is neutrino production efficiency. In particular, this makes GRB 5 our weakest neutrino emitter, i.e., it has the lowest ratio of emitted neutrino energy to gamma-ray energy beyond the photosphere. While the same effect should also make GRB 3 a weak neutrino emitter, its neutrino flux is still on a level with our other examples. The reason for this comes from its very specific initial shell setup. It consists of three narrow pulses, each with decreasing Γ. The collisions are therefore dominated by the first, fast shells of a pulse running into the preceding pulse—these shells have largely different Lorentz factors; in particular, the differences are larger than in GRB 5. Most of the neutrino emission comes from these first collisions, which happen below and slightly above the photosphere.
. More importantly, they have no optically thick collisions close to the photosphere; see the bottom panel of Figure 5 for GRB 5. The reason is that they emit shells with a variable but narrow Lorentz factor distribution (see Figure 3) that tends to induce collisions at larger radii, where photon densities are low and, therefore, so is neutrino production efficiency. In particular, this makes GRB 5 our weakest neutrino emitter, i.e., it has the lowest ratio of emitted neutrino energy to gamma-ray energy beyond the photosphere. While the same effect should also make GRB 3 a weak neutrino emitter, its neutrino flux is still on a level with our other examples. The reason for this comes from its very specific initial shell setup. It consists of three narrow pulses, each with decreasing Γ. The collisions are therefore dominated by the first, fast shells of a pulse running into the preceding pulse—these shells have largely different Lorentz factors; in particular, the differences are larger than in GRB 5. Most of the neutrino emission comes from these first collisions, which happen below and slightly above the photosphere.
We saw that GRBs with light curves dominated by fast variability are likely to be strong neutrino emitters. However, the reverse conclusion does not hold. While both GRBs 3 and 5 have gamma-ray light curves with broad pulses overlaid with fast variability, only GRB 5 is a weak neutrino emitter. Therefore, in the multi-zone internal shock model, we can tell, by inspection of the gamma-ray light curve alone, whether or not a GRB is likely to be a strong neutrino emitter. Conclusions about weak neutrino emitters require a closer inspection of the specific light-curve morphology.
Figure 6 shows, in the top panel, the neutrino fluence for GRB 2. The neutrino fluence follows the behavior of 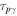 from Figure 5 (which is shown there for different examples). The average fluence per collision drops stronger than approximately
from Figure 5 (which is shown there for different examples). The average fluence per collision drops stronger than approximately 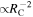 . In principle, the fluence from sub-photospheric collisions is high, due to the high extrapolated photon density; however, we do not use those collisions in our flux calculations.
. In principle, the fluence from sub-photospheric collisions is high, due to the high extrapolated photon density; however, we do not use those collisions in our flux calculations.
Figure 6. Muon-neutrino (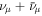 ) fluence (top) and maximum cosmic-ray energy (in source frame, bottom) for collisions in GRB 2. The legend is the same as for Figure 5. In the bottom panel, the UHECR range
) fluence (top) and maximum cosmic-ray energy (in source frame, bottom) for collisions in GRB 2. The legend is the same as for Figure 5. In the bottom panel, the UHECR range 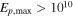 GeV is shaded.
GeV is shaded.
Download figure:
Standard image High-resolution image5.2. Quasi-diffuse Neutrino Flux
We derive the all-sky quasi-diffuse 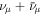 flux
flux 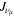 associated with a particular simulated GRB by scaling its fluence by the rate of long-duration GRBs,
associated with a particular simulated GRB by scaling its fluence by the rate of long-duration GRBs,  per year, i.e.,
per year, i.e., 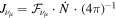 . Since this flux does not contain contributions from sub-photospheric collisions, it is effectively a lower limit on the prompt GRB neutrino flux. For our original benchmark, GRB 1, Bustamante et al. (2015) found that the flux is robust against variations in burst parameters like
. Since this flux does not contain contributions from sub-photospheric collisions, it is effectively a lower limit on the prompt GRB neutrino flux. For our original benchmark, GRB 1, Bustamante et al. (2015) found that the flux is robust against variations in burst parameters like 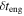 (see Table 3) and
(see Table 3) and 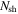 . We will discuss below how it depends on underlying assumptions, and what the corresponding fluxes are for GRBs 2–6.
. We will discuss below how it depends on underlying assumptions, and what the corresponding fluxes are for GRBs 2–6.
Table 3. Main Parameters of the Burst Simulation
| Parameter | Description | Type | Units | Notes |
|---|---|---|---|---|
| Burst initialization | ||||

|
Initial number of shells | Input | ⋯ | ⋯ |
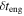
|
Uptime of the engine | Input | s | ⋯ |
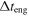
|
Downtime of the engine | Input | s | ⋯ |
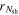
|
Distance from innermost shell to central emitter | Input | km | Default: 103 km |
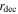
|
Deceleration radius (circumburst medium starts) | Input | km | Default: 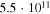 km km |
| AΓ | Fluctuation amplitude of 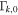 distribution distribution |
Input | ⋯ | ⋯ |

|
Initial bulk kinetic energy of shells | Input | erg | Common to all initial shells |
| z | Redshift of the emitter | Input | ⋯ | Used to calculate 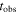 , Equation (5): z = 2 by default , Equation (5): z = 2 by default |
| l | Initial shell width | Internal | km | Common to all initial shells: 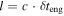
|
| d | Initial separation between consecutive shells | Internal | km | Common to all initial shell pairs: d = l by default |
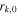
|
Initial radius of the kth shell, | Internal | km |
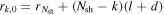
|
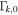
|
Initial bulk Lorentz factor of the kth shell | Internal | ⋯ | Sampled from the pre-defined Γ distribution |

|
Initial mass of the kth shell | Internal | GeV |
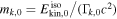
|
| Burst evolution | ||||
| t | Time in the source frame | Internal | s | ⋯ |
| rk | Radius of the kth shell | Internal | km | Grows as 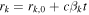
|
| lk | Width of the kth shell | Internal | km | Changes only in collisions |
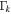
|
Bulk Lorentz factor of the kth shell | Internal | ⋯ | Changes only in collisions |
| mk | Mass of the kth shell | Internal | GeV | Changes only in collisions |
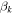
|
Bulk speed of the kth shell | Internal | ⋯ |
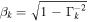
|
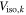
|
Isotropically equivalent volume of the kth shell | Internal | km3 |

|
|
Bulk kinetic energy of the kth shell | Internal | erg | Changes only in collisions |
|
Mass density of the kth shell | Internal | GeV km−3 |

|
| Shell collisions | ||||

|
Mass of the fast (slow) colliding shell | Internal | GeV | ⋯ |

|
Bulk Lorentz factor of the fast (slow) shell | Internal | ⋯ | ⋯ |
|
Lorentz factor of the forward (reverse) shock | Internal | ⋯ | See Equation (9) |
|
Speed of the forward (reverse) shock | Internal | ⋯ |
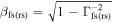
|
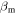
|
Bulk speed of the merged shell | Internal | ⋯ |
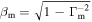
|
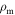
|
Mass density of the merged shell | Internal | GeV km−3 | See Equation (10) |
|
Collision time (source frame) | Internal | s | ⋯ |
|
Total number of collisions | Output | ⋯ | ⋯ |
|
Collision time (observer's frame) | Output | s | See Equation (5) |
|
Bulk Lorentz factor of the merged shell | Output | ⋯ | See Equation (7) |

|
Internal energy liberated in the collision | Output | erg | See Equation (6) |

|
Width of the merged shell | Output | km | See Equation (8) |
| RC | Collision radius | Output | km | ⋯ |
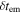
|
Time for reverse shock to cross fast shell | Output | s | See Equation (17) |
Note. All quantities are expressed in the source (engine) frame, except for 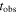 , which is in the observer's frame.
, which is in the observer's frame.
Download table as: ASCIITypeset image
Figure 7 shows the fluxes for GRBs 1–6. For all but GRB 5, the flux is  around 1 PeV—this is close to the value found for GRB 1 in Bustamante et al. (2015). For GRB 5, the flux is somewhat lower because it has fewer optically thick collisions, which is in agreement with Equation (2). (For GRB 3, the same could be expected, but instead it has a higher neutrino flux, as explained in Section 5.1.) Most real light curves lack the non-trivial features seen in GRB 5 (and GRB 3), and are therefore likely strong neutrino emitters. So it is conceivable that most bursts are instead like GRBs 1, 2, 4, and 6, and that the quasi-diffuse flux lies indeed at the level predicted using those bursts.
around 1 PeV—this is close to the value found for GRB 1 in Bustamante et al. (2015). For GRB 5, the flux is somewhat lower because it has fewer optically thick collisions, which is in agreement with Equation (2). (For GRB 3, the same could be expected, but instead it has a higher neutrino flux, as explained in Section 5.1.) Most real light curves lack the non-trivial features seen in GRB 5 (and GRB 3), and are therefore likely strong neutrino emitters. So it is conceivable that most bursts are instead like GRBs 1, 2, 4, and 6, and that the quasi-diffuse flux lies indeed at the level predicted using those bursts.
Figure 7. All-sky quasi-diffuse 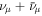 fluxes in our simulated multi-zone GRBs 1–6. Numerical one-zone predictions (Hümmer et al. 2012) are included for comparison; they are calculated using the average burst parameters computed as in Appendix
fluxes in our simulated multi-zone GRBs 1–6. Numerical one-zone predictions (Hümmer et al. 2012) are included for comparison; they are calculated using the average burst parameters computed as in Appendix 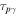 is larger (red/light) or smaller (blue/dark) than unity. The IceCube 2016 upper limit was calculated using their latest reported detector effective area and exposure in a stacked GRB search using tracks coming from the Northern Hemisphere (Aartsen et al. 2016).
is larger (red/light) or smaller (blue/dark) than unity. The IceCube 2016 upper limit was calculated using their latest reported detector effective area and exposure in a stacked GRB search using tracks coming from the Northern Hemisphere (Aartsen et al. 2016).
Download figure:
Standard image High-resolution imageIceCube has searched for correlations between neutrino arrival directions and positions of known GRBs (Abbasi et al. 2012; Aartsen et al. 2015a, 2016). No significant signal from GRBs has been found, in consistency with our prediction. Figure 7 includes the differential upper bound from Abbasi et al. (2012).
One-zone and multi-zone models have similar (average) burst parameters and compute the flux of secondaries similarly. However, Figure 7 shows that fluxes calculated with the multi-zone model are typically lower than with the one-zone model (Hümmer et al. 2012; see dashed curves in Figure 7). The reason is that all shells are assumed to have the same collision radius in the one-zone model, which tends to be underestimated: since the neutrino production efficiency decreases nonlinearly with the collision radius, the average value of the collision radius is, in general, not representative of the neutrino production. Nevertheless, we could define a single effective collision radius for neutrino production in the one-zone model that is different from the radius for gamma-rays; this would be done by folding in the production efficiency calculated with the fraction of collisions occurring at that radius. The average or representative jet parameters—such as the typical collision radius—are derived from gamma-ray observations (see Appendix
5.3. Cosmic Rays
From Table 2, we can see that all of the GRBs 1–6 are relatively efficient cosmic-ray emitters, though the required energy output per GRB, of at least 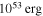 in the discussed energy range, should likely be a factor of a few larger to explain UHECR observations.10
Within the presented model, it is conceivable that GRBs are the sources of UHECRs.
in the discussed energy range, should likely be a factor of a few larger to explain UHECR observations.10
Within the presented model, it is conceivable that GRBs are the sources of UHECRs.
The connection between cosmic rays and neutrinos depends on how UHECRs escape the shells. Photohadronic interactions will transform protons into neutrons; neutrinos will also be produced. If all cosmic rays escape as neutrons ("neutron escape") the connection is strong (Mannheim et al. 2001; Ahlers et al. 2011): one neutrino of each flavor is expected per observed UHECR proton. This possibility can be clearly ruled out (Abbasi et al. 2012; Baerwald et al. 2015). However, at the highest energies, when the proton Larmor radius exceeds the shell width, protons can directly escape the shells without interacting in them, which leads to a hard spectrum ("direct escape"). In addition, diffusion may lead to escape depending on properties of magnetic fields.
In each merged shell, one or another escape component dominates,11 depending on the properties of the shell (Baerwald et al. 2013). If we consider escape processes other than neutron escape, which is implicitly assumed in most of the previous literature (Waxman & Bahcall 1997; Dermer & Atoyan 2003; Guetta et al. 2004; Murase & Nagataki 2006), the latest IceCube data cannot exclude GRBs as the sources of UHECRs even in a one-zone model, but constraints on the average shell parameters can be obtained from the efficient neutrino production (Baerwald et al. 2015).
Figure 6 shows, in the bottom panel, the maximum proton energy 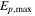 to which protons are accelerated in collisions in GRB 2, as a function of collision radius. Below the photosphere (black boxes), proton synchrotron losses dominate and
to which protons are accelerated in collisions in GRB 2, as a function of collision radius. Below the photosphere (black boxes), proton synchrotron losses dominate and 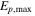 increases with
increases with  . Around
. Around 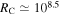 –
–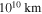 , protons reach 1010 GeV and higher. This is where UHECRs are emitted. At large
, protons reach 1010 GeV and higher. This is where UHECRs are emitted. At large 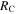 , falling magnetic fields yield lower acceleration rates and energies. Neutron emission is correlated with efficient neutrino production, since neutrons and charged pions are produced together in
, falling magnetic fields yield lower acceleration rates and energies. Neutron emission is correlated with efficient neutrino production, since neutrons and charged pions are produced together in 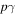 interactions. However, this occurs only in a few collisions, in a narrow range of low collision radii, where proton and photon densities are high; see red dots. In effect, cosmic-ray emission via neutron escape is limited by Equation (2). Most collisions occur at larger radii, so that the average collision radius for CR emission tends to be higher than for neutrinos (blue circles). There, particle densities are low enough for direct proton escape to dominate, without associated neutrino production. Given that only few collisions are neutron-dominated, the pure neutron escape assumptions for GRBs (Ahlers et al. 2011) cannot be justified. However, a quantitative statement requires further study beyond the scope of this work because it depends on the relative contribution between neutron-dominated and direct escape-dominated shells. For a discussion of UHECR nuclei, see Bustamante et al. (2015) and Globus et al. (2015).
interactions. However, this occurs only in a few collisions, in a narrow range of low collision radii, where proton and photon densities are high; see red dots. In effect, cosmic-ray emission via neutron escape is limited by Equation (2). Most collisions occur at larger radii, so that the average collision radius for CR emission tends to be higher than for neutrinos (blue circles). There, particle densities are low enough for direct proton escape to dominate, without associated neutrino production. Given that only few collisions are neutron-dominated, the pure neutron escape assumptions for GRBs (Ahlers et al. 2011) cannot be justified. However, a quantitative statement requires further study beyond the scope of this work because it depends on the relative contribution between neutron-dominated and direct escape-dominated shells. For a discussion of UHECR nuclei, see Bustamante et al. (2015) and Globus et al. (2015).
5.4. Multi-messenger Emission from Different Radii
Figure 8 shows a key feature of the multi-zone GRB model that is not captured by the one-zone model: that neutrinos, gamma-rays, and UHECR protons are emitted from different regions of the jet (Bustamante et al. 2015). This holds regardless of the difference in burst parameters among GRBs 1–6. Neutrinos are produced close to the photosphere, as discussed above. UHECRs tend to be produced at somewhat larger radii. At low radii, UHECRs escape as neutrons; at larger radii, most UHECRs escape directly as protons. Gamma-rays tend to come from even larger radii. While their production is more evenly distributed in collision radius, at low radii, pair production ( ) drives their energy down, so high-energy gamma-rays mainly come from large radii.
) drives their energy down, so high-energy gamma-rays mainly come from large radii.
Figure 8. Energy output as a function of collision radius in neutrinos, UHECR protons (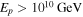 ), and gamma-rays. The approximate photospheric and (assumed) circumburst radius are marked, as well as the UHECR escape regions where either neutron escape or direct escape dominates.
), and gamma-rays. The approximate photospheric and (assumed) circumburst radius are marked, as well as the UHECR escape regions where either neutron escape or direct escape dominates.
Download figure:
Standard image High-resolution image6. Delayed High-energy Gamma-Rays
The detection of time delays between gamma-ray signals in different energy bands can provide insight into the dynamics of the GRB central engine and jet.
The maximum energy with which a photon can escape the shell where it is created is limited by the optical depth 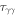 to pair production via
to pair production via 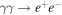 . A photon of a certain energy escapes only if
. A photon of a certain energy escapes only if 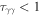 . Close to the central engine, photon density and, therefore, optical depth, are high. Bustamante et al. (2015) showed that only low-energy gamma-rays escape from that region. Higher-energy gamma-rays escape at larger radii. In this section, we explore whether the different shell opacities lead to time delays between gamma-ray energy bands.
. Close to the central engine, photon density and, therefore, optical depth, are high. Bustamante et al. (2015) showed that only low-energy gamma-rays escape from that region. Higher-energy gamma-rays escape at larger radii. In this section, we explore whether the different shell opacities lead to time delays between gamma-ray energy bands.
Figure 9—top row, left panel—shows that, in GRB 1, 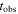 is quite uniformly distributed in
is quite uniformly distributed in 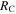 , especially between 108 and
, especially between 108 and 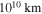 , i.e., above the photosphere. The central panel shows that for many collisions in this range the maximum gamma-ray energy is limited by pair production, while, from 109 km up, an increasing number of collisions is unaffected by it. However, the right panel shows that no separation exists between the arrival times of gamma-rays limited and not limited by pair production. In other words, at any time during the burst, low- and high-energy gamma-rays arrive indistinctly at Earth from everywhere inside the jet.
, i.e., above the photosphere. The central panel shows that for many collisions in this range the maximum gamma-ray energy is limited by pair production, while, from 109 km up, an increasing number of collisions is unaffected by it. However, the right panel shows that no separation exists between the arrival times of gamma-rays limited and not limited by pair production. In other words, at any time during the burst, low- and high-energy gamma-rays arrive indistinctly at Earth from everywhere inside the jet.
Figure 9. Collision time in the observer's frame as a function of collision radius (left column), and maximum gamma-ray energy in the source frame as a function of collision radius (central column) and time (right column), for collisions in GRBs 1 (top row) and 5 (bottom row). In the left column, collisions between older shells—that have undergone multiple mergers—are darker, while collisions between younger collisions are lighter; the solid black lines are the average trends. In the central and right columns, collisions are labeled as in Figure 6. Energy ranges accessible by Fermi-GBM, Fermi-LAT, and CTA are shaded. Arrows ( ) represent collisions where the maximum gamma-ray energy is not limited by pair production.
) represent collisions where the maximum gamma-ray energy is not limited by pair production.
Download figure:
Standard image High-resolution imageFor GRB 5 (Figure 9, bottom row), the situation is different. The average  increases with
increases with 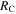 between 109 and
between 109 and  , i.e., some early (
, i.e., some early (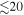 s) gamma-ray detections come from mid-range radii, while all late detections tend to come from large radii. As a result, some early gamma-rays have lower energies, in the upper Fermi-LAT and lower CTA bands, limited by pair production. Later detections, coming from larger radii, will have consistently higher energies, not limited by pair production. There is also an impact on the neutrino light curve: Figure 4 shows that the neutrino flux is much lower for later collisions, which come from larger radii, where neutrino production is inefficient. This behavior is characteristic of bursts with narrow Γ distribution, where collisions tend to occur at large radii and late in the jet evolution.
s) gamma-ray detections come from mid-range radii, while all late detections tend to come from large radii. As a result, some early gamma-rays have lower energies, in the upper Fermi-LAT and lower CTA bands, limited by pair production. Later detections, coming from larger radii, will have consistently higher energies, not limited by pair production. There is also an impact on the neutrino light curve: Figure 4 shows that the neutrino flux is much lower for later collisions, which come from larger radii, where neutrino production is inefficient. This behavior is characteristic of bursts with narrow Γ distribution, where collisions tend to occur at large radii and late in the jet evolution.
Figure 10 shows the gamma-ray light curves in different energy bands for GRBs 3 and 5, our two simulations with narrow Γ distributions . To produce them, we have assumed that the power-law photon density in the source extends to high enough energies.12 GRB 3 has a delayed start of a few seconds in the LAT band compared to the first detected peak in GBM, and of ∼10 s in the higher-energy CTA band. These delays depend strongly on the energy threshold of the instrument. In GRB 5, the LAT peak follows the GBM peak after ∼2 s, and the signal in CTA grows to comparable levels ∼10 s later. For this GRB, the suppression affects mainly the first peak in the light curve (the overall normalization of the light curves is arbitrary, but the relative normalization among the different energy bands is fixed). The early suppression of high-energy emission is consistent with observations; see, e.g., Castignani et al. (2014).
Figure 10. Gamma-ray light curves—using super-photospheric collisions only—for GRBs 3 and 5, in different energy bands: Fermi-GBM: 10−6–10−2 GeV; Fermi-LAT: 10−1–102 GeV; and CTA: 102–106 GeV.
Download figure:
Standard image High-resolution imageFigure 11. Schematic illustration of the collision process between two plasma shells, and the ensuing emission of high-energy particles.
Download figure:
Standard image High-resolution imageSince bursts with time delays between energy bands have narrow Γ distributions, they are associated with light curves with broad pulses overlaid with fast variability and possibly weak neutrino emitters (see Section 4). It is possible, in principle, to use the observation of delays in population studies to find how common these GRBs actually are, which affects the neutrino flux from the full GRB population.
To summarize, our predictions are as follows.
- 1.In GRBs with light curves that have broader pulses overlaid with fast variability, time delays in different wavelength bands are possible.
- 2.Compared to detection in the GBM energy band (10−6–10−2 GeV), typical delays are a few seconds long in the LAT band (10−1–102 GeV) and ∼10 s in the CTA band (102–106 GeV).
- 3.If such delays are observed, the GRB can be a weak neutrino emitter.
- 4.The fundamental reason for these apparent delays is an early suppression—rather than an actual delay—of high-energy gamma-rays coming from smaller
 , where the radiation densities are higher and the gamma-rays cannot escape. This effect is only observable if observation time and
, where the radiation densities are higher and the gamma-rays cannot escape. This effect is only observable if observation time and  in the collisions are correlated.
in the collisions are correlated.
An example of a GRB that could match these predictions is GRB 080916C (Abdo et al. 2009).
These predictions are a qualitative summary based on examples GRB 1–6, which we believe to be representative of a larger set of examples that we have produced. Quantitative results depend on the chosen parameter values, which reflects the observation that no two light curves are identical. Figure 9 captures the central feature we observe in all examples that exhibit a lag: for these, there is a correlation between  and
and 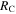 (within the range of
(within the range of  values in which the maximal photon energy depends on
values in which the maximal photon energy depends on 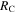 ). This correlation can be traced back to the engine emitting shells in a relatively narrow range of values of Γ. The lags in Figure 10 are clearly visible, though one can see some differences concerning their interpretation. For example, for GRB 3, the first tall peak in the CTA band is clearly delayed by several seconds with respect to the Fermi-GBM band, whereas, for GRB 5, the precise size of the lag depends on the instrument threshold of CTA.
). This correlation can be traced back to the engine emitting shells in a relatively narrow range of values of Γ. The lags in Figure 10 are clearly visible, though one can see some differences concerning their interpretation. For example, for GRB 3, the first tall peak in the CTA band is clearly delayed by several seconds with respect to the Fermi-GBM band, whereas, for GRB 5, the precise size of the lag depends on the instrument threshold of CTA.
7. Summary and Conclusions
We have simulated the evolution of a baryon-rich GRB jet in the internal shock scenario of the fireball model, by keeping track of all relativistic plasma shells that propagate in it, of the collisions between shells, and of the gamma-rays, protons, and neutrinos emitted at the shocks produced during the collisions. Unlike traditional one-zone models that extrapolate the behavior of the whole burst from a single representative collision, our multi-zone simulations consider many such collisions, each happening under different physical conditions.
We have demonstrated that it is possible to generate the various features observed in GRB light curves by varying the behavior of the central emitter, in particular, the initial speeds with which it puts out shells (see Section 4). The initial speeds determine where collisions between shells will occur during the jet evolution. In this approach, one can relate the properties of the central emitter to observables.
If the initial distribution of shell speeds is "disciplined" or narrow—even if the average speed changes with time—the associated gamma-ray light curve will have one or more broad pulses overlaid with fast time variability. The associated neutrino flux can be low, because collisions tend to occur at large collision radii. In addition, there is a correlation between observation time and collision radius, which implies that early-time collisions occur at low radii, where radiation densities are high, and high-energy gamma-ray signals are suppressed. As a consequence, we expect delays in the light curves in the Fermi-LAT energy band with respect to the ones in the Fermi-GBM band of a few seconds, and in the CTA band with respect to the Fermi-GBM band of the order of 10 seconds.
If the distribution of speeds is broader, collisions occur over a wide range of collision radii and the light curve is dominated by fast time variability. In this case, neutrino production is always efficient, because, typically, several collisions occur where the radiation densities are high. In this case, we do not expect delays between gamma-ray wavelength bands, because there is not a strong correlation between observation time and collision radius. Inspection of many GRB light curves reveals that most are actually simple, while the ones typically presented in the literature tend to be the more interesting cases with non-trivial features. This means the class of bursts with broad speed distributions may be more representative of the "typical" GRB.
We have also qualitatively confirmed the findings from Bustamante et al. (2015) for very different parameter sets. Notably, we have shown that, regardless of the initial speed distribution of the shells, different messengers come from different regions of the same GRB: neutrinos predominantly come from regions close to the center, UHECR protons come from intermediate regions, and high-energy gamma-rays tend to come from regions further out from the center, where photon densities are low enough that their energies are not limited by pair production on source photons. We have also confirmed the minimal predicted neutrino flux around 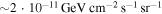 per flavor around 1 PeV, as long as a significant fraction of the GRBs has broad initial shell speed distributions, which explain observations better; see, e.g., our examples GRB 1, 2, 4, and 6.
per flavor around 1 PeV, as long as a significant fraction of the GRBs has broad initial shell speed distributions, which explain observations better; see, e.g., our examples GRB 1, 2, 4, and 6.
Our main results and conclusions are based exclusively on collisions that occur above the photosphere, where photons are not trapped by Thomson scattering. This allows us to assume that the photon spectra in the shells have the same form as the observed spectra at Earth.
Our results could be exploited in targeted GRB neutrino searches, such as the ones performed by IceCube, to cull a smaller catalog of GRBs that are specially likely to be strong neutrino sources. The non-observation of neutrinos from bursts in such a catalog—where associated backgrounds are smaller—could result in stronger upper bounds on prompt high-energy GRB neutrino emission. Our results could also be tested in different gamma-ray wavelength bands: we do not expect significant delays in GRBs with fast time variability without underlying pulse structure.
Due to their high luminosity, short duration, and the high angular precision with which they are detected, GRBs are arguably our best chance at finding a high-energy neutrino counterpart to electromagnetic emission. The study presented here is a step toward a necessary, realistic multi-messenger understanding of GRBs. The observation of these neutrinos would be a smoking-gun signature of high baryonic loading, and thus of the paradigm that GRBs could be the sources of the UHECRs.
The authors thank John Beacom, Denise Boncioli, Valerie Connaughton, Željka Bošnjak, and Eli Waxman for useful discussion and comments on the manuscript. M.B. acknowledges the hospitality of DESY Zeuthen during the completion of this work. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant No. 646623). M.B. acknowledges support from NSF Grant PHY-1404311. The work of K.M. is supported by NSF Grant PHY-1620777.
Appendix A: Model Description
Here we describe our GRB jet simulation, based on Kobayashi et al. (1997) and Daigne & Mochkovitch (1998).
A.1. Overview
The central object in a GRB (e.g., the black hole created by a collapsing massive star) emits collimated, relativistic jets that are rich in baryons, which we assume to be protons. When one of the jets points toward Earth, the gamma-ray emission from it may be detected as a GRB. We simulate the particle emission from this jet.
Since we are located inside the opening angle of the jet, we cannot distinguish between the emission geometry of a collimated jet and that of spherical, isotropic emission. For simplicity, we develop our formalism under such an isotropically equivalent scenario. In it, the central engine emits spherical plasma shells that propagate outward along the jet at relativistic speeds. We simulate their propagation and collisions between them, which produce high-energy gamma-rays, protons, and neutrinos.
The simulation covers only the coasting phase of the GRB, during which shells propagate at constant speed, except when they collide. In the preceding, acceleration phase, they reached their maximum individual speeds, limited by the available kinetic energy and their masses. The coasting phase ends when the shells reach the circumburst medium; there, they decelerate, and might produce an afterglow. The acceleration and deceleration phases are not part of the simulation.
In our simulation, shells propagate in one dimension. At any time during the simulation, the kth shell is characterized by four basic parameters: rk, the shell radius, as measured from the emitter (i.e., the position of the shell inside the jet); lk, the shell width; 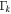 , the shell bulk Lorentz factor; and mk, the shell mass.
, the shell bulk Lorentz factor; and mk, the shell mass.
When two shells collide, they merge into a new shell, with width, speed, and mass calculated from the properties of the shells that collided. The new shell continues propagating in the jet flow and may collide again. Collisions are inelastic. The new shell cools instantly by radiating away its internal energy via particle emission. We compute collisions numerically, following Kobayashi et al. (1997) and Daigne & Mochkovitch (1998), as detailed below.
Table 3 describes all the relevant simulation parameters. Unless otherwise noted, quantities therein and in the text are expressed in the source reference frame.
A.2. Burst Initialization
In the simulation, before shell propagation starts, the central engine has already emitted  shells. Each one is described by the initial tuple
shells. Each one is described by the initial tuple  . Shells closer to the engine are labeled with higher indices.
. Shells closer to the engine are labeled with higher indices.
The behavior of the engine is described by two timescales13
: an "uptime,"  , during which it emits one shell, followed by a "downtime,"
, during which it emits one shell, followed by a "downtime,"  , during which it is inactive. The former determines the initial shell width,
, during which it is inactive. The former determines the initial shell width,  , which we assume to be common for all shells, and the latter determines the initial separation between consecutive shells,
, which we assume to be common for all shells, and the latter determines the initial separation between consecutive shells, 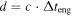 . Thus, each of the initial shells is located at position
. Thus, each of the initial shells is located at position  , where
, where  is the distance from the innermost shell to the emitter, which is an input parameter of the simulation. Results do not depend on
is the distance from the innermost shell to the emitter, which is an input parameter of the simulation. Results do not depend on 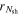 strongly, unless its value is too large; see Table 3.
strongly, unless its value is too large; see Table 3.
We choose the values of l and d to reproduce the timescale of pulses in observed light curves (Nakar & Piran 2002a). If 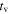 is the GRB variability timescale, i.e., the characteristic duration of peaks in the light curve, and
is the GRB variability timescale, i.e., the characteristic duration of peaks in the light curve, and 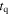 is the characteristic quiescent time between consecutive peaks, we expect that, roughly,
is the characteristic quiescent time between consecutive peaks, we expect that, roughly, 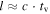 and
and  (Kobayashi et al. 1997; Aoi et al. 2010). In the internal shock model, d and l should be comparable. The simulations in Kobayashi et al. (1997) set d = l, while Aoi et al. (2010) set
(Kobayashi et al. 1997; Aoi et al. 2010). In the internal shock model, d and l should be comparable. The simulations in Kobayashi et al. (1997) set d = l, while Aoi et al. (2010) set 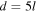 . In our simulations, we chose
. In our simulations, we chose 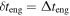 , such that
, such that  .
.
The variability timescale of a simulated burst is not an input parameter of the simulation, but a result of it. For our choices of simulation parameter values, we find that the variability timescale, obtained from the post-simulation synthetic light curve (see Appendix A.4), is close to the input value of 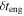 .
.
The initial values of the shell Lorentz factors follow a pre-defined distribution. In the benchmark scenario GRB 1, it is a log-normal distribution; see Section 4. Table 1 describes the distributions used in GRBs 2–6.
There are two typical schemes to assign initial masses 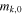 to the shells: the equal-mass assumption, i.e.,
to the shells: the equal-mass assumption, i.e., 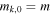 for all k; and the equal-energy assumption, i.e.,
for all k; and the equal-energy assumption, i.e.,  , with
, with 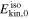 the initial bulk kinetic energy, assumed common to all shells. Our simulation uses the latter, since it appears to match observations more closely (Nakar & Piran 2002a).
the initial bulk kinetic energy, assumed common to all shells. Our simulation uses the latter, since it appears to match observations more closely (Nakar & Piran 2002a).
A.3. Burst Evolution
We simulate the coasting phase of the jet, during which shell speeds do not change while they propagate and expand. In our simplified treatment, the shell width and mass also stay constant.14
Therefore, the shell volume 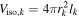 grows
grows 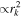 and mass density
and mass density 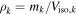 decreases
decreases 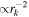 . Since the shell mass and Lorentz factor are constant during propagation, its bulk kinetic energy
. Since the shell mass and Lorentz factor are constant during propagation, its bulk kinetic energy 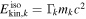 is constant as well. Speed, width, and mass change only in collisions.
is constant as well. Speed, width, and mass change only in collisions.
At the start of the simulation, we calculate the collision time for all pairs of neighboring shells, i.e.,
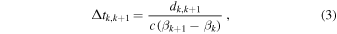
where  is the separation between shells k and
is the separation between shells k and  . The time interval until the next collision occurs is the minimum of these times, i.e.,
. The time interval until the next collision occurs is the minimum of these times, i.e.,
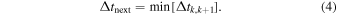
We increase the simulation time to  . The collision radius
. The collision radius  is set to the radius of the innermost colliding shell. Light emitted from this collision will be detected by a distant observer at time
is set to the radius of the innermost colliding shell. Light emitted from this collision will be detected by a distant observer at time
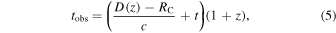
where 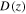 is the light-travel distance to the emitter with redshift z. These equations satisfy well-known relations in the internal shock scenario,
is the light-travel distance to the emitter with redshift z. These equations satisfy well-known relations in the internal shock scenario, 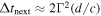 and
and  . All shells propagate to their new positions
. All shells propagate to their new positions 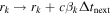 , the time interval for the next collision is calculated, and the process is repeated. (The term
, the time interval for the next collision is calculated, and the process is repeated. (The term 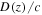 is just an offset: it will disappear when, in the simulation output, the first emission is set to start at
is just an offset: it will disappear when, in the simulation output, the first emission is set to start at 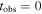 .)
.)
We distinguish between the shell bulk kinetic energy, 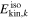 , and its internal energy,
, and its internal energy,  . The former is related to the motion of the compact shell, measured in the source rest frame, while the latter is the aggregated kinetic energy of particles moving randomly inside the shell, measured in the shock rest frame.
. The former is related to the motion of the compact shell, measured in the source rest frame, while the latter is the aggregated kinetic energy of particles moving randomly inside the shell, measured in the shock rest frame.
In a collision, the kinetic energy of the two colliding shells is used partly as bulk kinetic energy for the new shell and partly as its internal energy. For simplicity, we assume that the new shell immediately cools by prompt particle emission; see Kobayashi & Sari (2001) for alternative treatments. While collision details depend on modeling of hydrodynamical properties (Daigne & Mochkovitch 2003), here we adopt the simple collision prescription for the relativistic limit introduced in Kobayashi et al. (1997), which we outline below. Figure 11 is a schematic illustration of the collision process.
In the collision of a slow (s) and a fast (f) shell, the internal energy of the merged (m) shell is the difference of kinetic energy before and after the collision, i.e.,
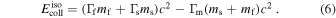
We assume that this amount of internal energy of the merged shell is radiated away as secondary particles. From momentum and energy conservation, and assuming  , the Lorentz factor of the merged shell is
, the Lorentz factor of the merged shell is
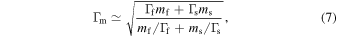
which reduces to  if
if  . Its width is given by (Kobayashi et al. 1997; Aoi et al. 2010)
. Its width is given by (Kobayashi et al. 1997; Aoi et al. 2010)
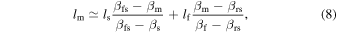
where 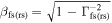 is the speed of the forward (reverse) shock, whose Lorentz factor is
is the speed of the forward (reverse) shock, whose Lorentz factor is
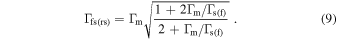
The volume of the new shell is 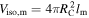 . The density is different between the shocked faster shell and shocked slower shell. The new shell has an average density obtained from the assumption of an inelastic collision
. The density is different between the shocked faster shell and shocked slower shell. The new shell has an average density obtained from the assumption of an inelastic collision 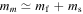 already implied in Equation (6), i.e.,
already implied in Equation (6), i.e.,
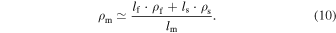
Therefore, its mass is 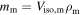 , and its kinetic energy is
, and its kinetic energy is 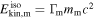 . After the collision, the original fast shell is removed from the simulation and the new shell replaces the former slow shell. It is then propagated with the remaining shells in the jet.
. After the collision, the original fast shell is removed from the simulation and the new shell replaces the former slow shell. It is then propagated with the remaining shells in the jet.
If a shell reaches the circumburst medium, where it decelerates, it is removed from the simulation. Following Rees & Mészáros (1992), we assume  km for the radius at which this happens (see, e.g., Equation (15) in Mészáros 2006).
km for the radius at which this happens (see, e.g., Equation (15) in Mészáros 2006).
The simulation finishes when all shells have reached the circumburst medium, all shells have merged into a single remaining shell, or all remaining shells are ordered outward with increasing Lorentz factor, so that no more collisions are possible. The output lists  collisions,
collisions,
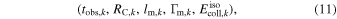
where  . The minimum
. The minimum  is taken to be the start of the observation time of the burst and is set to zero. Collisions are arranged so that
is taken to be the start of the observation time of the burst and is set to zero. Collisions are arranged so that  .
.
Figure 12 shows the time evolution (in the source frame) of macroscopic burst parameters in one of our simulations: average shell mass  (subscripts of zero indicates values at simulation start), standard deviation of the Lorentz factor15
(subscripts of zero indicates values at simulation start), standard deviation of the Lorentz factor15
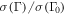 , and total available internal energy of the burst
, and total available internal energy of the burst 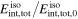 . The latter is calculated directly as
. The latter is calculated directly as 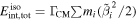 , where
, where 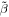 is the speed in the CM-frame.16
The numerical results of our simulation match the analytical power-law estimates from Beloborodov (2000), which assume that fluctuations in the initial Lorentz factors are small, i.e.,
is the speed in the CM-frame.16
The numerical results of our simulation match the analytical power-law estimates from Beloborodov (2000), which assume that fluctuations in the initial Lorentz factors are small, i.e., 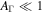 . Deviations occur at late times, when the number of remaining shells is low and the analytical predictions are no longer applicable. This late deviation depends strongly on the random initial setup, so we show ranges obtained after running 1000 different simulations.
. Deviations occur at late times, when the number of remaining shells is low and the analytical predictions are no longer applicable. This late deviation depends strongly on the random initial setup, so we show ranges obtained after running 1000 different simulations.
Figure 12. Time evolution, in the source frame, of average shell mass 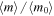 , standard deviation of the Lorentz factor
, standard deviation of the Lorentz factor 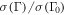 , and total internal energy of a burst,
, and total internal energy of a burst, 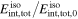 . The ranges are from our numerical results from a 1000 simulations run with random setups for the parameter values
. The ranges are from our numerical results from a 1000 simulations run with random setups for the parameter values 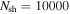 ,
, 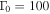 ,
, 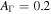 ,
, 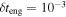 s, d = l, z = 2, and
s, d = l, z = 2, and 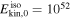 erg. Solid and dashed lines come from Figure 1 in Beloborodov (2000) for the same parameter set and refer to numerical calculations and analytical estimates respectively.
erg. Solid and dashed lines come from Figure 1 in Beloborodov (2000) for the same parameter set and refer to numerical calculations and analytical estimates respectively.
Download figure:
Standard image High-resolution imageChanging the collision dynamics can affect the burst efficiency—i.e., the fraction of kinetic energy dissipated as secondaries—and the radii where most of the gamma-ray energy is dissipated. Changes could include re-converting a fraction of collision energy into kinetic energy, partially inelastic collisions, or even fully penetrating shells. We explore simple modifications of our collision model in Appendix B.
A.4. Gamma-Ray Observables
The internal energy of a merged shell is split among electrons, magnetic field, and protons. They receive a fraction 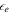 ,
, 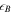 , and
, and 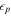 , respectively. We assume energy equipartition between electrons and photons and fix
, respectively. We assume energy equipartition between electrons and photons and fix 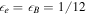 and
and 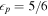 , since this yields the frequently used value of baryonic loading
, since this yields the frequently used value of baryonic loading 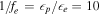 (Waxman & Bahcall 1999; Abbasi et al. 2012). Thus, the kth collision dissipates an energy
(Waxman & Bahcall 1999; Abbasi et al. 2012). Thus, the kth collision dissipates an energy  as gamma-rays, and energy
as gamma-rays, and energy 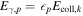 as protons, and supports a magnetic energy density of
as protons, and supports a magnetic energy density of 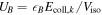 . The latter translates into a magnetic field intensity, in the shock rest frame, of
. The latter translates into a magnetic field intensity, in the shock rest frame, of
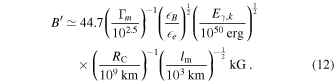
We normalize these individual energies by requiring that the total dissipated energy as gamma-rays, an experimentally accessible quantity,
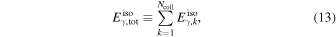
matches a given value  erg. This also fixes the energy in protons and magnetic field.
erg. This also fixes the energy in protons and magnetic field.
Our simulation does not generate the photon spectrum in the shell. Instead, as in Aoi et al. (2010), Abbasi et al. (2012), we assume that its shape is that of observed GRB spectra. We parametrize the spectrum as a broken power law, i.e.,

Primed quantities are in the shock rest frame. We fix17
 ,
, 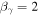 , and
, and  .
.
The photon spectrum in each shell is normalized via
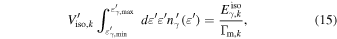
where the minimum and maximum energies are 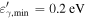 and
and 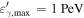 , respectively (Aoi et al. 2010). Pair production via
, respectively (Aoi et al. 2010). Pair production via 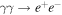 may limit the maximum energy of escaping photons; see Figure 9, right column.
may limit the maximum energy of escaping photons; see Figure 9, right column.
Each collision emits a gamma-ray pulse. The superposition of all pulses, propagated to Earth, is the light curve of the burst; see Section 4. Following Kobayashi et al. (1997), we parametrize the luminosity of the pulse from the kth collision (in the observer's frame) as a peaked profile, with a fast rise and exponential decay ("FRED"), i.e.,

where the emission timescale, i.e., the time at which the reverse shock crosses the fast shell, is
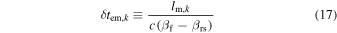
and the "rise time,"

is the time elapsed since the start of the emission until the peak luminosity is reached. For an illustration, see Figure 1 in Kobayashi et al. (1997). The peak luminosity is
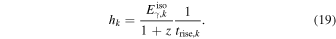
The time t in the source frame is related to  through
through
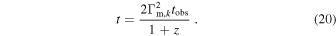
Hence, the synthetic light curve Lγ is
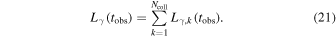
Unless noted otherwise, we only show the light curves for collisions beyond the photosphere (see Section 4), while we use all collisions for the normalization in Equation (13). In our simulations, the fraction of energy dissipated below the photosphere is around 50%, so that the total super-photospheric energy output in gamma-rays is around half of 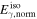 .
.
In Section 6, we showed light curves in different energy bands. Each band spans the range ![$[{E}_{\gamma ,\mathrm{low}}^{\mathrm{band}},{E}_{\gamma ,\mathrm{high}}^{\mathrm{band}}]$](https://content.cld.iop.org/journals/0004-637X/837/1/33/revision1/apjaa4417ieqn301.gif) , with
, with 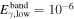 , 10−1, 102 GeV, and
, 10−1, 102 GeV, and 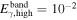 , 102, 106 GeV, for Fermi-GBM, Fermi-LAT, and CTA, respectively. To compute the gamma-ray contribution of the kth collision to each band, we calculate the fraction
, 102, 106 GeV, for Fermi-GBM, Fermi-LAT, and CTA, respectively. To compute the gamma-ray contribution of the kth collision to each band, we calculate the fraction
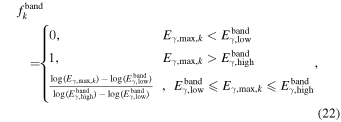
where  is the maximum gamma-ray energy emitted by the collision. The light curve for each band is then simply calculated using Equation (21), replacing
is the maximum gamma-ray energy emitted by the collision. The light curve for each band is then simply calculated using Equation (21), replacing  . Note that this simplified treatment assumes that the product of instrument response times flux is approximately constant within the anticipated energy band—which is typically a good estimate within the energy bands the instruments are designed for. A more detailed model for the instrument response or a different shape of the target photon spectrum at TeV energies—which we assumed to be a power law beyond the break—will not affect the qualitative shape of the light curves, but may slightly change the relative power in different energy bands or light-curve peaks.
. Note that this simplified treatment assumes that the product of instrument response times flux is approximately constant within the anticipated energy band—which is typically a good estimate within the energy bands the instruments are designed for. A more detailed model for the instrument response or a different shape of the target photon spectrum at TeV energies—which we assumed to be a power law beyond the break—will not affect the qualitative shape of the light curves, but may slightly change the relative power in different energy bands or light-curve peaks.
The burst duration and variability timescale 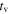 are derived from the light curve. For the duration, we use T90, the time elapsed between the detection of 5% and 95% of the total gamma-ray energy, i.e.,
are derived from the light curve. For the duration, we use T90, the time elapsed between the detection of 5% and 95% of the total gamma-ray energy, i.e.,
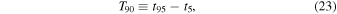
where
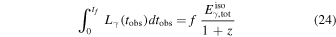
and f = 0.05 or 0.95. The variability timescale is estimated as

This procedure yields values of  close to
close to  .
.
In some cases (e.g., Figure 7), we have compared simulation results to "standard" estimators from the one-zone model:
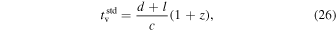
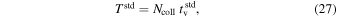
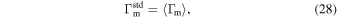
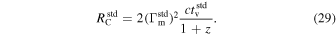
A.5. Neutrinos and Cosmic-rays
In analogy to gamma-rays, the proton and neutrino spectra of the complete burst are obtained by summing over the spectra emitted by all the individual collisions.
We compute secondary particle production using the NeuCosmA software (Baerwald et al. 2012; Hümmer et al. 2012; Baerwald et al. 2013). This assumes a proton density  , with the maximum proton energy
, with the maximum proton energy 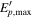 obtained from balancing the acceleration rate (with perfect efficiency) with synchrotron, adiabatic, and photohadronic energy loss rates (Baerwald et al. 2013). The proton density is normalized like the photon density, Equation (15), but replacing
obtained from balancing the acceleration rate (with perfect efficiency) with synchrotron, adiabatic, and photohadronic energy loss rates (Baerwald et al. 2013). The proton density is normalized like the photon density, Equation (15), but replacing 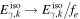 . Secondary pion, muon, and kaon spectra, and, consequently, neutrino spectra are computed as in Hümmer et al. (2012), which includes magnetic field effects on the secondaries, state-of-the-art normalization of the spectra, helicity-dependent muon decays, and flavor mixing.
. Secondary pion, muon, and kaon spectra, and, consequently, neutrino spectra are computed as in Hümmer et al. (2012), which includes magnetic field effects on the secondaries, state-of-the-art normalization of the spectra, helicity-dependent muon decays, and flavor mixing.
Following Baerwald et al. (2013), UHECRs escape from each shell as neutrons, produced in photohadronic interactions ("neutron escape"), and as protons that leak out of the shell when their Larmor radius exceeds the shell thickness ("direct escape"). At the highest energies, protons can always leak out—provided their maximum energy is limited by adiabatic cooling. However, which escape component dominates in each shell depends on the optical depth to photohadronic interactions of the shell in question. Figure 13 is a schematic illustration of the components contributing to UHECR emission depending on the optical depth of the merged shell. (If magnetic fields decay fast enough in the bulk of the shell, the direct escape component may be larger. However, this possibility is not contemplated in our framework.)
Figure 13. Schematic illustration of the UHECR emission from a merged shell produced in a collision, when the shell is optically thin (left) and thick (right) to 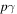 and
and  interactions.
interactions.
Download figure:
Standard image High-resolution imageOur main results, e.g., our light curves and neutrino spectra, are based only on shell collisions that occurred above the photosphere. Below it, Thomson scattering off electrons keeps the photons trapped in the shell. Since our adopted photon spectra are chosen to reproduce observed gamma-ray spectra, we cannot accurately calculate secondary production below the photosphere, where the photon spectra might be different. We mark "sub-photospheric" collisions clearly as such (see, e.g., Figures 5 and 6) and exclude them from our flux calculations. Excluding sub-photospheric collisions does not qualitatively change the shape of the light curves. However, in cases with broader pulse structures, the onset of each pulse is usually dominated by sub-photospheric collisions. Excluding these collisions slightly delays the onset of each peak.
The optical depth to Thomson scattering is calculate from shell properties. Since shells are, on average, electrically neutral, the electron density is equal to the proton density, i.e.,

where mp is the proton mass. This assumes that electron–positron pair production does not increase the electron and positron densities significantly. The optical depth to Thomson scattering is then
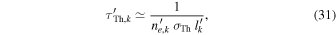
with 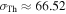 fm2 the Thomson cross-section. A collision is sub-photospheric if
fm2 the Thomson cross-section. A collision is sub-photospheric if 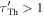 .
.
For a burst with 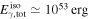 ,
, 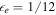 , and a dissipation efficiency of
, and a dissipation efficiency of 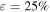 (such as GRB 1), the initial kinetic energy per shell is about
(such as GRB 1), the initial kinetic energy per shell is about  if 1000 collisions occur. This yields
if 1000 collisions occur. This yields 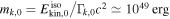 for
for 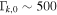 . From Equations (30) and (31), the photospheric radius of the kth shell is
. From Equations (30) and (31), the photospheric radius of the kth shell is
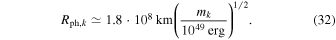
Bustamante et al. (2015) showed that, since the photohadronic optical depth scales similarly to Equation (31) (replacing 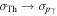 ), the pion production efficiency at the photosphere is independent of the isotropic volume and only weakly dependent on
), the pion production efficiency at the photosphere is independent of the isotropic volume and only weakly dependent on 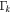 . The total neutrino flux of the burst is dominated by a few collisions that occur just above the photosphere, where the pion production efficiency is highest.
. The total neutrino flux of the burst is dominated by a few collisions that occur just above the photosphere, where the pion production efficiency is highest.
Appendix B: Additional Simulations
Here we include four additional examples of GRB simulations, GRBs 7–10, that complement the ones showed in the main text. Table 4 describes the simulations. Figure 14 shows the corresponding light curves.
Figure 14. Synthetic gamma-ray and neutrino light curves for the simulated GRBs 7–10, from collisions beyond the photosphere. Photon counts are in arbitrary units, obtained by multiplying the flux times a factor of 106 GeV−1 cm2 s.
Download figure:
Standard image High-resolution imageTable 4. Description of Simulated GRBs 7–10
| Model |
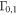
|
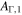
|
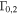
|
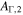
|
Tp |
|
|
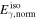 (erg) (erg) |
Description |
|---|---|---|---|---|---|---|---|---|---|
| 7 | 5 | ⋯ | 1500 | ⋯ | ⋯ | ⋯ | ⋯ | 1053 | Box-like Γ distribution |
| 8 | 50 | 0.1 | 500 | 1.0 | ⋯ | ⋯ | ⋯ | 1053 | Linear speedup of Γ |
| 9 | 500 | 1.0 | ⋯ | ⋯ | ⋯ | 100 | 100 | 1052 | 100 pulses separated by 100 pulse-times |
| 10 | 500 | 1.0 | ⋯ | ⋯ | ⋯ | 300 | 350 | 1052 | 300 pulses separated by 350 pulse-times |
Note. Common values for all models: 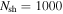 ,
, 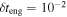 s,
s, 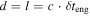 ,
, 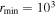 km,
km, 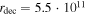 km, z = 2,
km, z = 2, 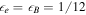 ,
, 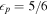 ,
, 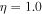 (acceleration efficiency, see Baerwald et al. 2013). See Table 3 for an explanation of each parameter.
(acceleration efficiency, see Baerwald et al. 2013). See Table 3 for an explanation of each parameter.
Download table as: ASCIITypeset image
The light curves of GRB 7 and GRB 8 are similar to that of GRB 1; see Figure 4. The light curves of GRB 9 and GRB 10 are similar to that of GRB 4 and GRB 6.
The similarities in the light curves exist in spite of fundamental differences between the behavior of the engine. This illustrates our point that the qualitative behavior of the examples shown in this work are representative of a larger class of models.
Appendix C: Alternative Collision Dynamics
Here we discuss the impact of modifications to our canonical collision model, which is used in the main text and described in Appendix A. We focus on alternative scenarios that can be easily implemented in our framework; that is, we assume that, in each collision, the colliding shells merge and do not consider the case in which they reflect off each other, as in Kobayashi & Sari (2001).
One extreme modification is to remove colliding shells from the system after they collide and radiate, which means that multiple collisions are not allowed. This makes simulation results insensitive to details of how shells are treated after colliding. However, removing the shells will modify the whole system, since, in the canonical collision model, collisions among old shells, and between young and old shells, occurred relatively early on.
Figure 15 shows the effect on the quasi-diffuse neutrino flux of applying this modification to a simulation that has the same parameters as our reference case, GRB 1. The modified case is labeled "no multiple collisions." The collision energies were normalized using 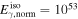 erg. The number of collisions is reduced to 499, about half that of the reference GRB 1 model. The modification results in a higher neutrino flux, because, by forbidding multiple-time collisions, most collisions—all of them first-time—occur at low radii, around
erg. The number of collisions is reduced to 499, about half that of the reference GRB 1 model. The modification results in a higher neutrino flux, because, by forbidding multiple-time collisions, most collisions—all of them first-time—occur at low radii, around  km. As we normalize to the same total energy, the per-collision normalization is slightly higher, which further increases the neutrino flux.
km. As we normalize to the same total energy, the per-collision normalization is slightly higher, which further increases the neutrino flux.
Figure 15. Three modifications to the canonical collision model described in Appendix A and applied to GRB 1. The modified case with no multiplication collisions (green dotted) uses the same per-collision normalization as the reference case (orange, solid). The other two modifications—50% of internal energy reconverted to kinetic energy (blue, dotted–dashed) and 50% radiated with 50% reconverted (red, dashed)—are normalized so in each case the burst yields 1053 erg in gamma-rays when adding sub-photospheric and super-photospheric collisions.
Download figure:
Standard image High-resolution imageAnother modification is to assume that only a fraction η of the internal energy in each collision, Equation (6), is attributed to the non-thermal spectra of the secondaries, while 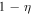 is instantly reconverted into kinetic energy of the merged shell. This fraction
is instantly reconverted into kinetic energy of the merged shell. This fraction 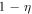 can, for instance, describe a fraction of thermal protons not directly participating in the prompt emission. For simplicity, we assume that the extra kinetic energy translates into an instantaneous increase of the Lorentz factor the merged shell after cooling:
can, for instance, describe a fraction of thermal protons not directly participating in the prompt emission. For simplicity, we assume that the extra kinetic energy translates into an instantaneous increase of the Lorentz factor the merged shell after cooling: ![${{\rm{\Gamma }}}_{{\rm{m}}}=[(1-\eta ){E}_{\mathrm{coll}}^{\mathrm{iso}}+{E}_{\mathrm{kin},{\rm{m}}}^{\mathrm{iso}}]/{m}_{{\rm{m}}}$](https://content.cld.iop.org/journals/0004-637X/837/1/33/revision1/apjaa4417ieqn343.gif) .
.
However, another modification is linked to our assumption that protons can only directly escape the merged shells—and not leave them by diffusion (Baerwald et al. 2013) or other processes—which implies that a substantial fraction of the non-thermal baryonic energy will remain trapped by the magnetic fields and eventually be reconverted into kinetic energy. The typical fraction ξ of electromagnetic energy and non-thermal baryonic energy, which is actually radiated for this escape process, is 40%–50%, estimated from energy partition and from the proportion of baryonic energy in the UHECR energy range compared to the full energy range. To account for this, we consider that the amount of internal energy used for computing the secondary production is still given by Equation (6), but we modify the dynamics so that a fraction of internal energy is reconverted into kinetic energy. This case does not include a fraction of energy going into thermal protons, unlike the previous case.
Figure 15 shows the result of both of these modifications to the kinetic and radiated energy, for the case 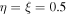 . In both cases, the burst was normalized to yield 1053 erg in gamma-rays when adding sub-photospheric and super-photospheric collisions. The number of collisions is similar to that of the reference GRB 1 model. Because the Lorentz factors of the merged shells are higher due to the increased kinetic energy, collisions occur further out in the jet, where particle densities are lower and neutrino production is less efficient. As a result, the neutrino flux associated with these two modifications is slightly lower than the one associated with the reference case, especially if only a fraction η of the energy is radiated. Therefore, the minimal super-photospheric flux prediction of
. In both cases, the burst was normalized to yield 1053 erg in gamma-rays when adding sub-photospheric and super-photospheric collisions. The number of collisions is similar to that of the reference GRB 1 model. Because the Lorentz factors of the merged shells are higher due to the increased kinetic energy, collisions occur further out in the jet, where particle densities are lower and neutrino production is less efficient. As a result, the neutrino flux associated with these two modifications is slightly lower than the one associated with the reference case, especially if only a fraction η of the energy is radiated. Therefore, the minimal super-photospheric flux prediction of 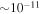 GeV cm−2 s−1 s−1 holds.
GeV cm−2 s−1 s−1 holds.
The neutrino flux scales with the fraction η going into the non-thermal spectra (and magnetic field), which means that, for 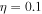 , it would be about one order of magnitude lower than our nominal case. On the other hand, the result is rather insensitive to the fraction of reconverted non-thermal energy
, it would be about one order of magnitude lower than our nominal case. On the other hand, the result is rather insensitive to the fraction of reconverted non-thermal energy  . This means that for the combined case—a fraction η into non-thermal spectra and a fraction
. This means that for the combined case—a fraction η into non-thermal spectra and a fraction  of non-thermal energy reconverted—we expect that the result is dominated by the effect of η.
of non-thermal energy reconverted—we expect that the result is dominated by the effect of η.
Finally, the three modifications to the collision dynamics that we have explored do not affect our conclusion about the distribution of particle emission with collision radii: neutrinos still come from low radii, UHECR protons come from intermediate radii, and gamma-rays come from large radii.
Footnotes
- 7
Guetta et al. (2004), Becker et al. (2006), Stamatikos (2006), and Baerwald et al. (2012) studied the complementary problem of calculating, in the one-zone approach, the expected neutrino flux from individual GRBs using their observed electromagnetic properties, and the impact of distributions of model parameter values on the quasi-diffuse flux.
- 8
The main difference compared to the earlier computation in Bustamante et al. (2015) is that, before, we determined which two shells should collide next by computing the absolute value of the times needed for all contiguous shells to collide, and selecting the two shells with the minimum value, whereas now we include causality (so that slower shells cannot catch up with faster ones). We also fixed a problem with the maintenance of the collision data lists (the shell speed was not always updated correctly). As explained in the main text, these modifications do not qualitatively change the results for GRB 1 nor our conclusions.
- 9
Bursts reach higher efficiencies (
 ) if they have a square-pulse ("box-like") distribution of Γ. Since this distribution is unrealistic, we do not discuss it further.
) if they have a square-pulse ("box-like") distribution of Γ. Since this distribution is unrealistic, we do not discuss it further. - 10
For details, see Section 2 in Baerwald et al. (2015), where the dependence on the source evolution is also discussed. Such an increase can be achieved either by a somewhat larger gamma-ray luminosity or by a somewhat larger baryonic loading.
- 11
- 12
This might overestimate the relative height of the light curve in the Fermi-LAT band.
- 13
This is strictly true for the simulated GRBs 1–5. GRB 6 has an overlaid time structure: the engine has an overall active period, where it emits
 shells, followed by a quiescent period that lasts for
shells, followed by a quiescent period that lasts for  pulses. See Table 1.
pulses. See Table 1. - 14
Depending on the internal energy, shell spreading is important especially after collisions. Recent dedicated simulations take into account this effect, but it is neglected in the simplest versions, like the one we have adopted (Aoi et al. 2010).
- 15
The reference Beloborodov (2000) refers to this as
 . However, we repeated the derivations of their analytical estimates, which are consistent only when interpreting this as the standard deviation.
. However, we repeated the derivations of their analytical estimates, which are consistent only when interpreting this as the standard deviation. - 16
The general relation between the total internal, or free, energy of a gas,
 , and its volume is given by
, and its volume is given by  , where γ is the adiabatic index. For the relativistic gas in a shell,
, where γ is the adiabatic index. For the relativistic gas in a shell,  and
and  .
. - 17
It is uncertain how
 changes with
changes with  , since the scaling expected in the internal shock model has a problem (Daigne & Mochkovitch 2003), which is why we prefer to set the photon spectra to observations. However, depending on the origin of the prompt gamma-ray emission—e.g., synchrotron radiation, inverse-Compton scattering—one can implement model-specific assumptions, as in Guetta et al. (2001a, 2001b; though the models therein are already in tension with GRB neutrino searches by IceCube (Abbasi et al. 2012; Aartsen et al. 2015a)). To correctly calculate the photon break energy for each collision, one needs a time-dependent radiative code, as implemented in Bošnjak et al. (2008). Detailed information on mildly relativistic collisionless physics, such as the injection Lorentz factor (which depends on the number fraction of accelerated particles (Eichler & Waxman 2005)), is also necessary. However, such an improvement will not change our conclusions in Section 7.
, since the scaling expected in the internal shock model has a problem (Daigne & Mochkovitch 2003), which is why we prefer to set the photon spectra to observations. However, depending on the origin of the prompt gamma-ray emission—e.g., synchrotron radiation, inverse-Compton scattering—one can implement model-specific assumptions, as in Guetta et al. (2001a, 2001b; though the models therein are already in tension with GRB neutrino searches by IceCube (Abbasi et al. 2012; Aartsen et al. 2015a)). To correctly calculate the photon break energy for each collision, one needs a time-dependent radiative code, as implemented in Bošnjak et al. (2008). Detailed information on mildly relativistic collisionless physics, such as the injection Lorentz factor (which depends on the number fraction of accelerated particles (Eichler & Waxman 2005)), is also necessary. However, such an improvement will not change our conclusions in Section 7.