Abstract
We study the link between baryons and dark matter (DM) in 240 galaxies with spatially resolved kinematic data. Our sample spans 9 dex in stellar mass and includes all morphological types. We consider (1) 153 late-type galaxies (LTGs; spirals and irregulars) with gas rotation curves from the SPARC database, (2) 25 early-type galaxies (ETGs; ellipticals and lenticulars) with stellar and H i data from ATLAS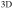 or X-ray data from Chandra, and (3) 62 dwarf spheroidals (dSphs) with individual-star spectroscopy. We find that LTGs, ETGs, and "classical" dSphs follow the same radial acceleration relation: the observed acceleration (
or X-ray data from Chandra, and (3) 62 dwarf spheroidals (dSphs) with individual-star spectroscopy. We find that LTGs, ETGs, and "classical" dSphs follow the same radial acceleration relation: the observed acceleration ( ) correlates with that expected from the distribution of baryons (
) correlates with that expected from the distribution of baryons (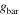 ) over 4 dex. The relation coincides with the 1:1 line (no DM) at high accelerations but systematically deviates from unity below a critical scale of ∼10−10 m s−2. The observed scatter is remarkably small (
) over 4 dex. The relation coincides with the 1:1 line (no DM) at high accelerations but systematically deviates from unity below a critical scale of ∼10−10 m s−2. The observed scatter is remarkably small (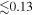 dex) and largely driven by observational uncertainties. The residuals do not correlate with any global or local galaxy property (e.g., baryonic mass, gas fraction, and radius). The radial acceleration relation is tantamount to a natural law: when the baryonic contribution is measured, the rotation curve follows, and vice versa. Including ultrafaint dSphs, the relation may extend by another 2 dex and possibly flatten at
dex) and largely driven by observational uncertainties. The residuals do not correlate with any global or local galaxy property (e.g., baryonic mass, gas fraction, and radius). The radial acceleration relation is tantamount to a natural law: when the baryonic contribution is measured, the rotation curve follows, and vice versa. Including ultrafaint dSphs, the relation may extend by another 2 dex and possibly flatten at 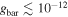 m s−2, but these data are significantly more uncertain. The radial acceleration relation subsumes and generalizes several well-known dynamical properties of galaxies, like the Tully–Fisher and Faber–Jackson relations, the "baryon-halo" conspiracies, and Renzo's rule.
m s−2, but these data are significantly more uncertain. The radial acceleration relation subsumes and generalizes several well-known dynamical properties of galaxies, like the Tully–Fisher and Faber–Jackson relations, the "baryon-halo" conspiracies, and Renzo's rule.
Export citation and abstract BibTeX RIS
1. Introduction
The flat rotation curves of spiral galaxies (Bosma 1978; Rubin et al. 1978) provided clear empirical evidence for mass discrepancies in galactic systems, which are commonly attributed to nonbaryonic dark matter (DM). Over the past 40 years, the relations between the baryonic and dynamical properties of galaxies have been intensively debated considering all different galaxy types: early-type galaxies (ETGs) like ellipticals and lenticulars (e.g., Faber & Jackson 1976; Djorgovski & Davis 1987; Dressler et al. 1987; Cappellari 2016), late-type galaxies (LTGs) like spirals and irregulars (e.g., Rubin et al. 1985; van Albada & Sancisi 1986; Persic & Salucci 1991; van der Kruit & Freeman 2011), and dwarf spheroidals (dSphs) in the Local Group (e.g., Mateo 1998; Battaglia et al. 2008; Strigari et al. 2008; Walker et al. 2009b).
LTGs follow a tight baryonic Tully–Fisher (Tully & Fisher 1977) relation (BTFR), linking the baryonic mass (stars plus gas) to the flat rotation velocity  (e.g., McGaugh et al. 2000; Verheijen 2001; Lelli et al. 2016b). Similarly, ETGs follow the Faber–Jackson relation (Faber & Jackson 1976), linking stellar mass and stellar velocity dispersion
(e.g., McGaugh et al. 2000; Verheijen 2001; Lelli et al. 2016b). Similarly, ETGs follow the Faber–Jackson relation (Faber & Jackson 1976), linking stellar mass and stellar velocity dispersion  . den Heijer et al. (2015) show that ETGs with extended H i disks (tracing
. den Heijer et al. (2015) show that ETGs with extended H i disks (tracing  ) follow the same BTFR as LTGs. If
) follow the same BTFR as LTGs. If  is used to estimate
is used to estimate  , the most luminous dSphs adhere to the BTFR, but the ultrafaint dSphs seem to deviate (McGaugh & Wolf 2010), possibly hinting at out-of-equilibrium dynamics due to tides from the host galaxy.
, the most luminous dSphs adhere to the BTFR, but the ultrafaint dSphs seem to deviate (McGaugh & Wolf 2010), possibly hinting at out-of-equilibrium dynamics due to tides from the host galaxy.
The BTFR is a "global" scaling relation between the baryonic and dynamical masses of galaxies. Sancisi (2004) further advocates for a "local" Tully–Fisher kind of relation, linking baryons and dynamics on a radial basis. For LTGs, indeed, it has become clear that the rotation curve shape and the baryonic mass distribution are closely related (Kent 1987; Corradi & Capaccioli 1990; Casertano & van Gorkom 1991; McGaugh 2004, 2005; Sancisi 2004; Noordermeer et al. 2007; Swaters et al. 2009, 2012, 2014; Lelli et al. 2010, 2013, 2016b). A similar coupling is also observed in ETGs (Serra et al. 2016).
Several works try to parameterize this baryon–DM coupling using different approaches (Sanders 1990; Persic & Salucci 1991; McGaugh 1999, 2004, 2014; Swaters et al. 2009, 2014; Lelli et al. 2013, 2016a; Walker & Loeb 2014). In particular, McGaugh (2004) defines the "mass discrepancy" as  at every radius, where
at every radius, where  is the observed rotation curve and
is the observed rotation curve and  is the baryonic contribution from the distribution of stars and gas. McGaugh (2004) finds that the mass discrepancy anticorrelates with the baryonic acceleration7
is the baryonic contribution from the distribution of stars and gas. McGaugh (2004) finds that the mass discrepancy anticorrelates with the baryonic acceleration7
 (see also Sanders 1990), leading to a mass discrepancy–acceleration relation (MDAR). The sample of McGaugh (2004), however, has heterogeneous surface photometry in different bands, so one needs to pick a different stellar mass-to-light ratio (
(see also Sanders 1990), leading to a mass discrepancy–acceleration relation (MDAR). The sample of McGaugh (2004), however, has heterogeneous surface photometry in different bands, so one needs to pick a different stellar mass-to-light ratio ( ) for each galaxy to compute
) for each galaxy to compute  . McGaugh (2004) shows that the scatter in the MDAR and BTFR can be simultaneously minimized by choosing an optimal
. McGaugh (2004) shows that the scatter in the MDAR and BTFR can be simultaneously minimized by choosing an optimal  for each galaxy, corresponding to the prescriptions of modified Newtonian dynamics (MOND; Milgrom 1983). This approach evinces the existence of a tight MDAR but does not enable measurement of its shape and scatter. Besides, the location of ETGs and dSphs on the MDAR was not addressed.
for each galaxy, corresponding to the prescriptions of modified Newtonian dynamics (MOND; Milgrom 1983). This approach evinces the existence of a tight MDAR but does not enable measurement of its shape and scatter. Besides, the location of ETGs and dSphs on the MDAR was not addressed.
To improve the situation, we built the Spitzer Photometry and Accurate Rotation Curves (SPARC) database: a sample of 175 disk galaxies (S0 to dIrr) with homogeneous [3.6] surface photometry and high-quality H i/Hα rotation curves (Lelli et al. 2016a, hereafter Paper I). Several lines of evidence suggest that  does not vary strongly at [3.6] (McGaugh & Schombert 2014, 2015; Meidt et al. 2014; Schombert & McGaugh 2014), so one can effectively use a single value of
does not vary strongly at [3.6] (McGaugh & Schombert 2014, 2015; Meidt et al. 2014; Schombert & McGaugh 2014), so one can effectively use a single value of  for disk galaxies of different masses and morphologies. This is a major improvement over previous studies.
for disk galaxies of different masses and morphologies. This is a major improvement over previous studies.
In McGaugh et al. (2016), we provide a concise summary of our results from 153 SPARC galaxies. Here we present a more extensive analysis, including 25 ETGs and 62 dSphs. Specifically, we study the local link between baryons and DM using a parameterization that minimizes observational uncertainties and degeneracies. We plot the baryonic acceleration ( ) against the total acceleration (
) against the total acceleration ( ) instead of the mass discrepancy (
) instead of the mass discrepancy ( ). This has two key advantages: (1) the two axes are fully independent (photometry versus kinematics as in the BTFR), and (2) the uncertainties on
). This has two key advantages: (1) the two axes are fully independent (photometry versus kinematics as in the BTFR), and (2) the uncertainties on  only enter in
only enter in  . This parameterization is also used by Scarpa (2006) for pressure-supported systems and by Wu & Kroupa (2015) for rotation-supported galaxies using the best-fit data of McGaugh (2004). We find that
. This parameterization is also used by Scarpa (2006) for pressure-supported systems and by Wu & Kroupa (2015) for rotation-supported galaxies using the best-fit data of McGaugh (2004). We find that  correlates with
correlates with  over ∼4 dex (∼6 dex including ultrafaint dSphs). This radial acceleration relation is remarkably tight: the observed scatter is only 0.13 dex and is largely driven by observational uncertainties.
over ∼4 dex (∼6 dex including ultrafaint dSphs). This radial acceleration relation is remarkably tight: the observed scatter is only 0.13 dex and is largely driven by observational uncertainties.
We start by describing our galaxy samples and associated data (Section 2). Next, we study the radial acceleration relation of LTGs (Section 3), test different normalizations of  (Section 4.1), and explore different choices of the dependent x variable (Section 4.2). We then investigate the same relation for ETGs (Section 5) and dSphs (Section 6). Finally, we discuss the link with other dynamical laws of galaxies (Section 7) and the implications for galaxy formation models and alternative theories (Section 8).
(Section 4.1), and explore different choices of the dependent x variable (Section 4.2). We then investigate the same relation for ETGs (Section 5) and dSphs (Section 6). Finally, we discuss the link with other dynamical laws of galaxies (Section 7) and the implications for galaxy formation models and alternative theories (Section 8).
2. Galaxy Sample and Data Analysis
Our sample comprises 240 galaxies of all main morphological types. Figure 1 shows their structural properties, using Spitzer photometry for LTGs (Paper I) and ETGs (Section 2.2) and V-band photometry for dSphs (Section 2.3). Our sample covers the widest possible range of galaxy properties, spanning 9 dex in stellar mass, 5 dex in effective surface density, and 3 dex in effective radius.8 The cold gas fractions range from ∼90% in dIrrs to virtually zero in dSphs. Here we describe photometric and kinematic data for our subsamples of 153 LTGs, 25 ETGs, and 62 dSphs.
Figure 1. Structural properties of the 240 galaxies in our sample. The stellar mass is plotted against the effective radius (top panel) and effective surface density (bottom panel). Different symbols indicate different galaxy types as given by the legend. For dSphs, large symbols show the classical satellites of the Milky Way and M31, while small symbols indicate ultrafaint dSphs and more isolated dSphs (like Tucana and Cetus). Stellar masses and effective surface densities are computed using the mass-to-light ratios in Table 1.
Download figure:
Standard image High-resolution image2.1. Late-type Galaxies
We consider 153 galaxies from the SPARC database, providing [3.6] surface brightness profiles, H i/Hα rotation curves, and mass models (Paper I). SPARC spans a wide range of disk properties and contains representatives of all late-type morphologies, from bulge-dominated spirals to gas-dominated dwarf irregulars. Three SPARC galaxies are classified as lenticulars by de Vaucouleurs et al. (1991): we consider them among the LTGs to have a clear separation from the S0s of Atlas (Cappellari et al. 2011), having different types of data (Section 2.2).
(Cappellari et al. 2011), having different types of data (Section 2.2).
Paper I describes the analysis of [3.6] images, the collection of rotation curves, and the derivation of mass models. SPARC contains a total of 175 galaxies, but we exclude 12 objects where the rotation curve may not trace the equilibrium gravitational potential (quality flag Q = 3) and 10 face-on galaxies ( ) with uncertain velocities due to large
) with uncertain velocities due to large  corrections (see Paper I). This does not introduce any selection bias because galaxy disks are randomly oriented on the sky.
corrections (see Paper I). This does not introduce any selection bias because galaxy disks are randomly oriented on the sky.
2.1.1. The Total Gravitational Field of LTGs
LTGs possess a dynamically cold H i disk, so the observed rotation curve  directly traces the gravitational potential at every radius. Corrections for pressure support are relevant only in the smallest dwarf galaxies with
directly traces the gravitational potential at every radius. Corrections for pressure support are relevant only in the smallest dwarf galaxies with  km s−1 (e.g., Lelli et al. 2012). The total gravitational field is given by
km s−1 (e.g., Lelli et al. 2012). The total gravitational field is given by

where  is the total potential (baryons and DM).
is the total potential (baryons and DM).
The uncertainty on  is estimated as
is estimated as

The errors on the rotation velocity ( ), disk inclination (
), disk inclination ( ), and galaxy distance (
), and galaxy distance ( ) are described in Paper I. Here we consider only velocity points with
) are described in Paper I. Here we consider only velocity points with  . A minimum accuracy of 10% ensures that
. A minimum accuracy of 10% ensures that  is not affected by strong noncircular motions or kinematic asymmetries. This criterion removes only ∼15% of our data (from 3149 to 2693 points), which are primarily in the innermost or outermost galaxy regions. Dropping this criterion does not change our results: it merely increases the observed scatter as expected from less accurate data. The mean error on
is not affected by strong noncircular motions or kinematic asymmetries. This criterion removes only ∼15% of our data (from 3149 to 2693 points), which are primarily in the innermost or outermost galaxy regions. Dropping this criterion does not change our results: it merely increases the observed scatter as expected from less accurate data. The mean error on  is 0.1 dex.
is 0.1 dex.
2.1.2. The Baryonic Gravitational Field of LTGs
We compute the gravitational field in the galaxy midplane by numerically solving Poisson's equation, using the observed radial density profiles of gas and stars and assuming a nominal disk thickness (see Paper I):

Specifically, the expected velocity  is given by
is given by

where  and
and  are the stellar mass-to-light ratios of disk and bulge, respectively (see Section 2.4).
are the stellar mass-to-light ratios of disk and bulge, respectively (see Section 2.4).
The uncertainty on  is estimated considering a typical 10% error on the H i flux calibration and a 25% scatter on
is estimated considering a typical 10% error on the H i flux calibration and a 25% scatter on  . The latter is motivated by stellar population synthesis models (McGaugh 2014; Meidt et al. 2014; Schombert & McGaugh 2014) and the BTFR (McGaugh & Schombert 2015; Lelli et al. 2016b). Uncertainties in the Spitzer photometric calibration are negligible. Note that
. The latter is motivated by stellar population synthesis models (McGaugh 2014; Meidt et al. 2014; Schombert & McGaugh 2014) and the BTFR (McGaugh & Schombert 2015; Lelli et al. 2016b). Uncertainties in the Spitzer photometric calibration are negligible. Note that  is distance independent because both
is distance independent because both  and R linearly vary with D. The mean error on
and R linearly vary with D. The mean error on  is 0.08 dex, but this is a lower limit because it neglects uncertainties due to the adopted 3D geometry (vertical disk structure and bulge flattening) and the possible (minor) contribution of molecular gas (see Paper I for details). This may add another ∼20% uncertainty to points at small radii.
is 0.08 dex, but this is a lower limit because it neglects uncertainties due to the adopted 3D geometry (vertical disk structure and bulge flattening) and the possible (minor) contribution of molecular gas (see Paper I for details). This may add another ∼20% uncertainty to points at small radii.
2.2. Early-type Galaxies
ETGs generally lack high-density H i disks, so one cannot derive gas rotation curves that directly trace  at every radius. Different tracers, however, have been extensively explored. Integral field units (IFUs) have made it possible to study the 2D stellar kinematics of ETGs, revealing that ∼85% of them are rotating (see Cappellari 2016, for a review). X-ray telescopes like Chandra and XMM have been used to probe the hot gas and trace total mass profiles assuming hydrostatic equilibrium (see Buote & Humphrey 2012, for a review). Progress has also been made using discrete kinematical tracers (planetary nebulae and globular clusters) and strong gravitational lensing (see Gerhard 2013 for a review).
at every radius. Different tracers, however, have been extensively explored. Integral field units (IFUs) have made it possible to study the 2D stellar kinematics of ETGs, revealing that ∼85% of them are rotating (see Cappellari 2016, for a review). X-ray telescopes like Chandra and XMM have been used to probe the hot gas and trace total mass profiles assuming hydrostatic equilibrium (see Buote & Humphrey 2012, for a review). Progress has also been made using discrete kinematical tracers (planetary nebulae and globular clusters) and strong gravitational lensing (see Gerhard 2013 for a review).
Here we consider two different data sets of ETGs: (1) 16 ETGs from Atlas (Cappellari et al. 2011) that have inner rotating stellar components (Emsellem et al. 2011) and outer low-density H i disks or rings (den Heijer et al. 2015), and (2) nine ETGs with relaxed X-ray halos. These two data sets roughly correspond to two different "families" of ETGs (e.g., Kormendy & Bender 1996; Kormendy 2009; Cappellari 2016): rotating ETGs from Atlas
(Cappellari et al. 2011) that have inner rotating stellar components (Emsellem et al. 2011) and outer low-density H i disks or rings (den Heijer et al. 2015), and (2) nine ETGs with relaxed X-ray halos. These two data sets roughly correspond to two different "families" of ETGs (e.g., Kormendy & Bender 1996; Kormendy 2009; Cappellari 2016): rotating ETGs from Atlas are either lenticulars or disky ellipticals, while X-ray ETGs are generally giant boxy ellipticals. Three X-ray ETGs are part of Atlas
are either lenticulars or disky ellipticals, while X-ray ETGs are generally giant boxy ellipticals. Three X-ray ETGs are part of Atlas : NGC 4261 and NGC 4472 are classified as "slow rotators" (essentially nonrotating galaxies), while NGC 4649 is classified as a "fast rotator" but actually lies at the boundary of the classification (
: NGC 4261 and NGC 4472 are classified as "slow rotators" (essentially nonrotating galaxies), while NGC 4649 is classified as a "fast rotator" but actually lies at the boundary of the classification ( ). These X-ray ETGs are representative of "classic" pressure-supported ellipticals, possibly metal-rich, anisotropic, and mildly triaxial. Appendix
). These X-ray ETGs are representative of "classic" pressure-supported ellipticals, possibly metal-rich, anisotropic, and mildly triaxial. Appendix
2.2.1. The Total Gravitational Field of Rotating ETGs
Our sample of rotating ETGs is drawn from Serra et al. (2016). Despite the significant amount of rotation, the stellar components of these ETGs are dynamically hot ( ), so pressure support needs to be taken into account. Cappellari et al. (2013) build Jeans anisotropic models (JAM), fitting the stellar velocity field, the velocity dispersion map, and the r-band image of the galaxy. These models assume that (1) the galaxy is axisymmetric and the velocity ellipsoid is nearly oblate (
), so pressure support needs to be taken into account. Cappellari et al. (2013) build Jeans anisotropic models (JAM), fitting the stellar velocity field, the velocity dispersion map, and the r-band image of the galaxy. These models assume that (1) the galaxy is axisymmetric and the velocity ellipsoid is nearly oblate ( ), (2) the total mass distribution follows the light distribution, and (3) the r-band mass-to-light ratio is constant with radius. The JAM models return the maximum circular velocity
), (2) the total mass distribution follows the light distribution, and (3) the r-band mass-to-light ratio is constant with radius. The JAM models return the maximum circular velocity  within the IFU field of view (typically one effective radius). We use this quantity to estimate
within the IFU field of view (typically one effective radius). We use this quantity to estimate  We assume a formal error of 10% on
We assume a formal error of 10% on  (similar to typical H i data), but we stress that
(similar to typical H i data), but we stress that  is not directly observed and remains somewhat model dependent.
is not directly observed and remains somewhat model dependent.
The situation is much simpler at large radii because H i disks or rings directly trace the gravitational potential. den Heijer et al. (2015) analyze H i velocity fields and position–velocity diagrams for these 16 ETGs, providing a velocity measurement in the outer parts (VH i). Hence, we have  . In principle, high-resolution H i observations may trace the full rotation curve in the outer parts of these ETGs, but we are currently limited to a single, average value. Therefore, we have "rotation curves" with two points: an inner point from IFU data (via JAM models) and an outer point from H i data.
. In principle, high-resolution H i observations may trace the full rotation curve in the outer parts of these ETGs, but we are currently limited to a single, average value. Therefore, we have "rotation curves" with two points: an inner point from IFU data (via JAM models) and an outer point from H i data.
For NGC 2974, we note a small discrepancy between the values of  and VH i reported by Serra et al. (2016) and Weijmans et al. (2008). The latter is an in-depth study providing the full stellar, Hα, and H i rotation curves. We adopt the values from Weijmans et al. (2008).
and VH i reported by Serra et al. (2016) and Weijmans et al. (2008). The latter is an in-depth study providing the full stellar, Hα, and H i rotation curves. We adopt the values from Weijmans et al. (2008).
2.2.2. The Total Gravitational Field of X-Ray ETGs
We consider nine ETGs from Humphrey et al. (2006, 2008, 2009, 2011, 2012). This series of papers provides a homogeneous analysis of deep X-ray observations from Chandra and XMM. The X-ray data give accurate density and temperature profiles, so one can directly compute the enclosed total mass  using the equation of hydrostatic equilibrium (see Buote & Humphrey 2012, for a review). The main assumptions are (1) the hot gas is in hydrostatic equilibrium, (2) the system is spherically symmetric, and (3) the thermal pressure dominates over nonthermal components like magnetic pressure or turbulence. For our nine ETGs, these assumptions are realistic (Buote & Humphrey 2012).
using the equation of hydrostatic equilibrium (see Buote & Humphrey 2012, for a review). The main assumptions are (1) the hot gas is in hydrostatic equilibrium, (2) the system is spherically symmetric, and (3) the thermal pressure dominates over nonthermal components like magnetic pressure or turbulence. For our nine ETGs, these assumptions are realistic (Buote & Humphrey 2012).
We consider total mass profiles from the "classic" smoothed inversion approach (see Buote & Humphrey 2012). This technique is nonparametric (no specific potential is assumed a priori) and provides the enclosed mass at specific radii. The sampling is determined by the quality of the data, that is, by "smoothing" the temperature and density profiles to ensure that the resulting mass profile monotonically increases with radius. This technique is closest to the derivation of rotation curves in LTGs. The "observed acceleration" is then given by

where G is Newton constant and r is the 3D radius.
Four of these ETGs (NGC 1407, NGC 4261, NGC 4472, and NGC 4649) belong to groups with 10 to 60 known members, so the outer mass profile may be tracing the group potential instead of the galaxy potential (Humphrey et al. 2006). For these galaxies, we restrict our analysis to  . This radius is determined by computing rotation curves from the mass profiles. For example, NGC 4261 has a relatively flat rotation curve within
. This radius is determined by computing rotation curves from the mass profiles. For example, NGC 4261 has a relatively flat rotation curve within  but starts to rise at larger radii, reaching velocities of ∼700 km s−1 at 100 kpc. Clearly, such a rotation curve cannot be due to the galaxy potential. The other five ETGs are relatively isolated, so we use the full mass profile out to ∼15
but starts to rise at larger radii, reaching velocities of ∼700 km s−1 at 100 kpc. Clearly, such a rotation curve cannot be due to the galaxy potential. The other five ETGs are relatively isolated, so we use the full mass profile out to ∼15  .
.
We also exclude data at  for three basic reasons: (1) intermittent feedback from active galactic nuclei may introduce significant turbulence, breaking the assumption of hydrostatic equilibrium at small radii (Buote & Humphrey 2012); (2) the gravitational effect of central black holes may be important (Humphrey et al. 2008, 2009), but these dark components are not included in our baryonic mass models (Section 2.2.3); and (3) X-ray ETGs generally have steep luminosity profiles (Sérsic index ≳4, e.g., Kormendy 2009) that may be smeared by the limited spatial resolution of Spitzer, leading to inaccurate mass models in the innermost parts. This quality criterion retains 80 out of 97 points.
for three basic reasons: (1) intermittent feedback from active galactic nuclei may introduce significant turbulence, breaking the assumption of hydrostatic equilibrium at small radii (Buote & Humphrey 2012); (2) the gravitational effect of central black holes may be important (Humphrey et al. 2008, 2009), but these dark components are not included in our baryonic mass models (Section 2.2.3); and (3) X-ray ETGs generally have steep luminosity profiles (Sérsic index ≳4, e.g., Kormendy 2009) that may be smeared by the limited spatial resolution of Spitzer, leading to inaccurate mass models in the innermost parts. This quality criterion retains 80 out of 97 points.
2.2.3. The Baryonic Gravitational Field of ETGs
For consistency with SPARC, we collect [3.6] images from the Spitzer archive and derive surface photometry using the same procedures as in Paper I. For two objects (NGC 1521 and NGC 6798), Spitzer images are not available: we use WISE images at 3.2 μm (W1 band) and convert W1 profiles to [3.6] adopting W1 – [3.6] = 0.11. For these two ETGs, we do not consider the innermost regions ( pixels) due to the limited spatial resolution of WISE. The surface brightness profiles are used to calculate
pixels) due to the limited spatial resolution of WISE. The surface brightness profiles are used to calculate  (Equation (3)). Stellar mass-to-light ratios are discussed in Section 2.4. We neglect the contribution of cold gas (H i or H2) as this is a minor dynamical component for ETGs and can be safely ignored (Weijmans et al. 2008). For X-ray ETGs, the contribution of hot gas is calculated assuming spherical symmetry and using published density profiles (see Appendix
(Equation (3)). Stellar mass-to-light ratios are discussed in Section 2.4. We neglect the contribution of cold gas (H i or H2) as this is a minor dynamical component for ETGs and can be safely ignored (Weijmans et al. 2008). For X-ray ETGs, the contribution of hot gas is calculated assuming spherical symmetry and using published density profiles (see Appendix
Among our rotating ETGs, 12 of 16 galaxies are morphologically classified as lenticulars, while the remaining four ellipticals may have face-on disks, as revealed by their stellar kinematics (see, e.g., Cappellari 2016). We perform nonparametric bulge–disk decompositions using the same strategy as in Paper I. In particular, structures in the luminosity profiles due to bars or lenses are assigned to the disk. We assume that bulges are spherical, while disks have an exponential vertical distribution with scale height  (see Paper I).
(see Paper I).
All X-ray ETGs are classified as ellipticals, with the exception of NGC 1332 (S0). For this galaxy, we perform a bulge–disk decomposition, while the other X-ray ETGs are treated as spherically symmetric systems.
2.3. Dwarf Spheroidals
For every currently known dSph in the Local Group, we collected distances, V-band magnitudes, half-light radii, ellipticities, and velocity dispersions from the literature. We only exclude Sagittarius and Bootes III, which are heavily disrupted satellites of the Milky Way (MW; Ibata et al. 1994; Carlin et al. 2009). In Appendix  ) are derived from high-resolution individual-star spectroscopy and their errors are indicative. The reliability of these measurements depends on the available number of stars, the possible contaminations from foreground objects and binary stars, and the dynamical state of the galaxy (e.g., Walker et al. 2009c; McConnachie & Côté 2010; McGaugh & Wolf 2010; Minor et al. 2010).
) are derived from high-resolution individual-star spectroscopy and their errors are indicative. The reliability of these measurements depends on the available number of stars, the possible contaminations from foreground objects and binary stars, and the dynamical state of the galaxy (e.g., Walker et al. 2009c; McConnachie & Côté 2010; McGaugh & Wolf 2010; Minor et al. 2010).
In general, the data quality for "classical" dSphs and "ultrafaint" dSphs is markedly different. Classical dSphs were discovered during the 20th century, and their properties have been steadily refined over the years. Ultrafaint dSphs have been discovered during the past ∼10 years with the advent of the Sloan Digital Sky Survey (e.g., Willman et al. 2005) and Dark Energy Survey (e.g., Koposov et al. 2015a). Their properties remain uncertain due to their extreme nature: some ultrafaint dSphs are less luminous than a single giant star! In our opinion, it is still unclear whether all these objects deserve the status of "galaxies," or whether they are merely overdensities in the stellar halo of the host galaxy. Hence, caution is needed to interpret the data of ultrafaint dSphs.
2.3.1. The Total Gravitational Field of dSphs
Dwarf spheroidals typically lack a rotating gas disk and have a fully pressure-supported stellar component. The gravitational field cannot be directly estimated at every radius due to degeneracies between the projected velocity dispersion ( ) and the velocity dispersion anisotropy. Several studies, however, show that the total mass within the half-light radius (hence,
) and the velocity dispersion anisotropy. Several studies, however, show that the total mass within the half-light radius (hence,  ) does not strongly depend on anisotropy and can be estimated from the average
) does not strongly depend on anisotropy and can be estimated from the average  (Walker et al. 2009b; Wolf et al. 2010; Amorisco & Evans 2011). Following Wolf et al. (2010), we have
(Walker et al. 2009b; Wolf et al. 2010; Amorisco & Evans 2011). Following Wolf et al. (2010), we have

where  is the deprojected 3D half-light radius. Equation (6) assumes that (1) the system is spherically symmetric, (2) the projected velocity dispersion profile is fairly flat near
is the deprojected 3D half-light radius. Equation (6) assumes that (1) the system is spherically symmetric, (2) the projected velocity dispersion profile is fairly flat near  , and (3)
, and (3)  traces the equilibrium potential. These assumptions are sensible for classical dSphs, but remain dubious for many ultrafaint dSphs (McGaugh & Wolf 2010). The error on
traces the equilibrium potential. These assumptions are sensible for classical dSphs, but remain dubious for many ultrafaint dSphs (McGaugh & Wolf 2010). The error on  is estimated considering formal errors on
is estimated considering formal errors on  and
and  (including distance uncertainties).
(including distance uncertainties).
We note that the brightest satellites of M31 (NGC 147, NGC 185, and NGC 205) are sometimes classified as dwarf ellipticals (dEs). Their stellar components show significant rotation at large radii (Geha et al. 2010), similar to dEs in galaxy clusters (e.g., van Zee et al. 2004). At  , however, the stellar velocity dispersion of these galaxies is much larger than the stellar rotation, so Equation (6) still provides a sensible estimate of
, however, the stellar velocity dispersion of these galaxies is much larger than the stellar rotation, so Equation (6) still provides a sensible estimate of  .
.
2.3.2. The Baryonic Gravitational Field of dSphs
The baryonic gravitational field at  is given by
is given by

where  is the V-band stellar mass-to-light ratio. We assume
is the V-band stellar mass-to-light ratio. We assume  /L⊙ as suggested by studies of resolved stellar populations. For example, de Boer et al. (2012a, 2012b) derive accurate star formation histories for Fornax and Sculptor using deep color–magnitude diagrams and assuming a Kroupa (2001) initial mass function (IMF), which is very similar to the Chabrier (2003) IMF. The inferred stellar masses imply
/L⊙ as suggested by studies of resolved stellar populations. For example, de Boer et al. (2012a, 2012b) derive accurate star formation histories for Fornax and Sculptor using deep color–magnitude diagrams and assuming a Kroupa (2001) initial mass function (IMF), which is very similar to the Chabrier (2003) IMF. The inferred stellar masses imply  /L⊙ for Fornax and
/L⊙ for Fornax and  /L⊙ for Sculptor, adopting a gas-recycling efficiency of 30%. The error on
/L⊙ for Sculptor, adopting a gas-recycling efficiency of 30%. The error on  is estimated considering a 25% scatter on
is estimated considering a 25% scatter on  (2.0 ± 0.5 M⊙/L⊙) and formal errors on
(2.0 ± 0.5 M⊙/L⊙) and formal errors on  and
and  .
.
2.4. Stellar Mass-to-light Ratios at 3.6 
The stellar mass-to-light ratio at 3.6 μm is known to show a smaller scatter and weaker dependence on color than in optical bands (e.g., McGaugh & Schombert 2014; Meidt et al. 2014). When comparing ETGs and LTGs, however, it is sensible to distinguish between different structural components and galaxy types, given their different metallicities and star formation histories (SFHs). Here we consider four different cases: (1) the star-forming disks of LTGs, (2) the bulges of LTGs, (3) the bulges and disks of rotating ETGs (S0 and disky E), and (4) X-ray ETGs (massive and metal-rich). We use the stellar population synthesis (SPS) models of Schombert & McGaugh (2014), which assume a Chabrier (2003) IMF and include metallicity evolution. We consider constant SFHs for the disks of LTGs and exponentially declining SFHs for the other cases, exploring different timescales and metallicities. Our fiducial values are summarized in Table 1. These values are in good agreement with different SPS models (McGaugh & Schombert 2014; Meidt et al. 2014; Norris et al. 2016).
Table 1. Fiducial Stellar Mass-to-light Ratios
| Galaxy Component |

|
|---|---|
| Disks of LTGs (Sa to Irr) | 0.5 M⊙/L⊙ |
| Bulges of LTGs (Sa to Sb) | 0.7 M⊙/L⊙ |
| Rotating ETGs (S0 and disky E) | 0.8 M⊙/L⊙ |
| X-ray ETGs (Giant metal-rich E) | 0.9 M⊙/L⊙ |
| Dwarf Spheroidals (V-band) | 2.0 M⊙/L⊙ |
Note. The values of  refer to 3.6 μm apart for dwarf spheroidals (V-band). We adopt a Chabrier (2003) IMF and the SPS models of Schombert & McGaugh (2014).
refer to 3.6 μm apart for dwarf spheroidals (V-band). We adopt a Chabrier (2003) IMF and the SPS models of Schombert & McGaugh (2014).
Download table as: ASCIITypeset image
For LTGs, our value for  agrees with resolved stellar populations in the LMC (Eskew et al. 2012), provides sensible gas fractions (Paper I), and minimizes the scatter in the BTFR (Lelli et al. 2016b). The BTFR scatter is very small for a fixed value of
agrees with resolved stellar populations in the LMC (Eskew et al. 2012), provides sensible gas fractions (Paper I), and minimizes the scatter in the BTFR (Lelli et al. 2016b). The BTFR scatter is very small for a fixed value of  at [3.6], so the actual
at [3.6], so the actual  cannot vary wildly among different galaxies. The role of
cannot vary wildly among different galaxies. The role of  is further investigated in Section 4.1.
is further investigated in Section 4.1.
3. Radial Acceleration Relation for Late-type Galaxies
3.1. General Results for LTGs
Figure 2 displays mass models for each SPARC galaxy (left) and their location on the  plane (right). Figure 3 (top left) shows the resulting radial acceleration relation for our 153 LTGs. Since we have ∼2700 independent points, we use a 2D heat map (blue color scale) and bin the data in
plane (right). Figure 3 (top left) shows the resulting radial acceleration relation for our 153 LTGs. Since we have ∼2700 independent points, we use a 2D heat map (blue color scale) and bin the data in  (red squares). The radial acceleration relation is remarkably tight. Note that
(red squares). The radial acceleration relation is remarkably tight. Note that  and
and  are fully independent.
are fully independent.
Figure 2. A movie shows how each individual SPARC galaxy adds to the radial acceleration relation. The galaxy name and its total baryonic mass are indicated at the top. The left panel shows the observed rotation curve (dots) and the expected baryonic contributions: gas (dotted line), stellar disk (dashed line), bulge (dash-dotted line), and total baryons (solid line). The right panel shows the galaxy location on the  plane; the cumulative amount of data points is indicated at the top left corner. The radial acceleration relation (right panel) evinces a remarkable regularity between baryons and dynamics, in spite of the large diversity in individual mass models (left panel). This movie is also available on the SPARC web page (astroweb.cwru.edu/SPARC) in different formats.
plane; the cumulative amount of data points is indicated at the top left corner. The radial acceleration relation (right panel) evinces a remarkable regularity between baryons and dynamics, in spite of the large diversity in individual mass models (left panel). This movie is also available on the SPARC web page (astroweb.cwru.edu/SPARC) in different formats.
(An animation of this figure is available.)
Download figure:
Video Standard image High-resolution imageFigure 3. Radial acceleration relation for LTGs. The total gravitational field ( ) is derived at every radius from the rotation curve, while the baryonic gravitational field (
) is derived at every radius from the rotation curve, while the baryonic gravitational field ( ) is calculated from the distribution of stars and gas. Top left: the blue color scale represents 2693 independent data points. Red squares and dashed lines show the mean and standard deviation of binned data, respectively. The dotted line indicates the 1:1 relation. Dash-dotted and solid lines show error-weighted fits using Equations (9) and (11), respectively. Top right: each galaxy is plotted by a solid line, color-coded by the effective baryonic surface density. Bottom: same as the top right panel but we separate high-mass (left) and low-mass (right) galaxies. In all panels, the small dot in the bottom right corner shows the typical error bars on individual data points.
) is calculated from the distribution of stars and gas. Top left: the blue color scale represents 2693 independent data points. Red squares and dashed lines show the mean and standard deviation of binned data, respectively. The dotted line indicates the 1:1 relation. Dash-dotted and solid lines show error-weighted fits using Equations (9) and (11), respectively. Top right: each galaxy is plotted by a solid line, color-coded by the effective baryonic surface density. Bottom: same as the top right panel but we separate high-mass (left) and low-mass (right) galaxies. In all panels, the small dot in the bottom right corner shows the typical error bars on individual data points.
Download figure:
Standard image High-resolution imageFigure 3 (top right) show the radial acceleration relation using a solid line for each LTG. In this plot, one cannot appreciate the actual tightness of the relation because many lines fall on top of each other and a few outliers become prominent to the eye. This visualization, however, illustrates how different galaxies cover different regions of the relation. We color-code each galaxy by the equivalent baryonic surface density (McGaugh 2005):

where  is the total baryonic mass, and
is the total baryonic mass, and  is the radius where
is the radius where  is maximum. In the bottom panels of Figure 3, we also separate high-mass and low-mass galaxies at
is maximum. In the bottom panels of Figure 3, we also separate high-mass and low-mass galaxies at  . This value is similar to the characteristic mass in the
. This value is similar to the characteristic mass in the  relation from abundance matching (Moster et al. 2013) and may correspond to the transition between cold and hot modes of gas accretion (Dekel & Birnboim 2006).
relation from abundance matching (Moster et al. 2013) and may correspond to the transition between cold and hot modes of gas accretion (Dekel & Birnboim 2006).
High-mass, high-surface-brightness (HSB) galaxies cover the high-acceleration portion of the relation: they are baryon dominated in the inner parts and become DM dominated in the outer regions. Low-mass, low-surface-brightness (LSB) galaxies cover the low-acceleration portion: the DM content is already significant at small radii and systematically increases with radius. Strikingly, in the central portion of the relation ( m s−2), the inner radii of low-mass galaxies overlap with the outer radii of high-mass ones. The rotating gas in the inner regions of low-mass galaxies seems to relate to that in the outer regions of high-mass galaxies.
m s−2), the inner radii of low-mass galaxies overlap with the outer radii of high-mass ones. The rotating gas in the inner regions of low-mass galaxies seems to relate to that in the outer regions of high-mass galaxies.
3.2. Fits, Scatter, and Residuals
We fit a generic double power law:

where α and β are the asymptotic slopes for  and
and  , respectively. We rename
, respectively. We rename

The data are fitted using the Python orthogonal distance regression algorithm (scipy.odr), considering errors in both variables. We do not fit the binned data, but the individual 2693 points. The fit results are listed in Table 2 together with alternative choices of  (Section 4.1) and of the dependent variable x (Section 4.2). For our fiducial relation, we find
(Section 4.1) and of the dependent variable x (Section 4.2). For our fiducial relation, we find  and
and  , implying that the relation is consistent with unity at high accelerations. The outer slope β is ∼0.60.
, implying that the relation is consistent with unity at high accelerations. The outer slope β is ∼0.60.
Table 2. Fits to the Radial Acceleration Relation of LTGs Using a Double Power Law (Equation (9))
| x variable | x and  units units |

|

|
α | β |

|

|
Scatter (dex) |
|---|---|---|---|---|---|---|---|---|

|
10−10 m s−2 | 0.5 | 0.7 | 0.94 ± 0.06 | 0.60 ± 0.01 | 2.3 ± 1.1 | 2.6 ± 0.8 | 0.13 |

|
10−10 m s−2 | 0.5 | 0.5 | 1.03 ± 0.07 | 0.60 ± 0.01 | 2.3 ± 0.6 | 1.8 ± 0.7 | 0.14 |

|
10−10 m s−2 | 0.2 | 0.2 | 1.59 ± 1.32 | 0.77 ± 0.01 | 10 ± 22 | 22 ± 37 | 0.15 |
| g⋆ | 10−10 m s−2 | 0.5 | 0.7 | 0.79 ± 0.01 | 0.24 ± 0.01 | 0.16 ± 0.02 | 0.40 ± 0.03 | 0.13 |

|
M⊙ pc−2 | 0.5 | 0.7 | 0.64 ± 0.03 | 0.09 ± 0.01 | 9.3 ± 2.1 | 0.48 ± 0.03 | 0.25 |

|
M⊙ pc−2 | 0.5 | 0.0 | 0.56 ± 0.02 | 0.08 ± 0.01 | 6.8 ± 1.4 | 0.45 ± 0.03 | 0.23 |
Note. In all cases, the y variable is the observed radial acceleration  , and the units of
, and the units of  are 10−10 m s−2.
are 10−10 m s−2.
Download table as: ASCIITypeset image
The residuals around Equation (9), however, are slightly asymmetric and offset from zero. The results improve by fitting the following function (McGaugh 2008, 2014):

where the only free parameter is  . For
. For  , Equation (11) gives
, Equation (11) gives  , in line with the values of α,
, in line with the values of α,  , and
, and  found above. For
found above. For  , Equation (11) imposes a low-acceleration slope of 0.5. A slope of 0.5 actually provides a better fit to the low-acceleration data than 0.6 does (see Figure 3). We find
, Equation (11) imposes a low-acceleration slope of 0.5. A slope of 0.5 actually provides a better fit to the low-acceleration data than 0.6 does (see Figure 3). We find  m s−2. Considering a 20% uncertainty in the normalization of
m s−2. Considering a 20% uncertainty in the normalization of ![${{\rm{\Upsilon }}}_{[3.6]}$](https://content.cld.iop.org/journals/0004-637X/836/2/152/revision1/apjaa5b2cieqn145.gif) , the systematic error is
, the systematic error is  m s−2.
m s−2.
Equation (11) is inspired by MOND (Milgrom 1983). It is important, however, to keep data and theory well separated: Equation (11) is empirical and provides a convenient description of the data with a single free parameter  . In the specific case of MOND, the empirical constant
. In the specific case of MOND, the empirical constant  is equivalent to the theoretical constant a0, and
is equivalent to the theoretical constant a0, and  coincides with the interpolation function ν, connecting Newtonian and Milgromian regimes. Notably, Equation (11) is reminiscent of the Planck law connecting the Rayleigh–Jeans and Wien regimes of electromagnetic radiation, where the Planck constant h plays a role similar to that of
coincides with the interpolation function ν, connecting Newtonian and Milgromian regimes. Notably, Equation (11) is reminiscent of the Planck law connecting the Rayleigh–Jeans and Wien regimes of electromagnetic radiation, where the Planck constant h plays a role similar to that of  .
.
The residuals around Equation (11) are represented by a histogram in Figure 4 (top left). They are symmetric around zero and well fitted by a Gaussian, indicating that there are no major systematics. The Gaussian fit returns a standard deviation of 0.11 dex. This is slightly smaller than the measured rms scatter (0.13 dex) due to a few outliers. Outlying points generally come from galaxies with uncertain distances (e.g., from flow models within 15 Mpc) or poorly sampled rotation curves. Outliers are also expected if galaxies (or regions within galaxies) have a  different from our fiducial values due to, for example, enhanced star formation activity or unusual extinction.
different from our fiducial values due to, for example, enhanced star formation activity or unusual extinction.
Figure 4. Residuals after subtracting Equation (11) from the radial acceleration relation. The top left panel shows a histogram with Poissonian ( ) error bars and a Gaussian fit. The other panels show the residuals against radius (top right), stellar surface density at R (bottom left), and local gas fraction
) error bars and a Gaussian fit. The other panels show the residuals against radius (top right), stellar surface density at R (bottom left), and local gas fraction  at R (bottom right). Squares and dashed lines show the mean and standard deviation of binned residuals, respectively. The bar in the bottom right corner shows the anticipated scatter from observational uncertainties.
at R (bottom right). Squares and dashed lines show the mean and standard deviation of binned residuals, respectively. The bar in the bottom right corner shows the anticipated scatter from observational uncertainties.
Download figure:
Standard image High-resolution imageWe constrain the observed scatter between 0.11 dex (Gaussian fit) and 0.13 dex (measured rms). These values are surprisingly small by astronomical standards. The intrinsic scatter must be even smaller since observational errors and intrinsic variations in  are not negligible. The mean expected scatter equals
are not negligible. The mean expected scatter equals

where the partial derivative considers the variable slope of the relation. This explains the vast majority of the observed scatter, leaving little room for any intrinsic scatter. Clearly, the intrinsic scatter is either zero or extremely small. This is truly remarkable.
The other panels of Figure 4 show the residuals versus several local quantities: radius R, stellar surface density at R, and gas fraction  at R. The tiny residuals display no correlation with any of these quantities: the Pearson's, Spearman's, and Kendall's coefficients range between −0.2 and 0.1.
at R. The tiny residuals display no correlation with any of these quantities: the Pearson's, Spearman's, and Kendall's coefficients range between −0.2 and 0.1.
Figure 5 shows the residuals versus several global quantities: baryonic mass, effective radius, effective surface brightness, and global gas fraction  . We do not find any statistically significant correlation with any of these quantities. Similarly, we find no correlation with flat rotation velocity, disk scale length, disk central surface brightness, and disk inclination. Strikingly, the deviations from the radial acceleration relation do not depend on any intrinsic galaxy property, either locally or globally defined.
. We do not find any statistically significant correlation with any of these quantities. Similarly, we find no correlation with flat rotation velocity, disk scale length, disk central surface brightness, and disk inclination. Strikingly, the deviations from the radial acceleration relation do not depend on any intrinsic galaxy property, either locally or globally defined.
Figure 5. Residuals vs. baryonic mass (top left), effective radius (top right), effective surface brightness (bottom left), and global gas fraction (bottom right). Squares and dashed lines show the mean and standard deviation of binned residuals, respectively. The vertical clumps of data are due to individual objects: each galaxy contributes with several points to the radial acceleration relation.
Download figure:
Standard image High-resolution image4. Alternative Relations for Late-type Galaxies
4.1. The Stellar Mass-to-light Ratio
In the previous sections, we used  and
and  at [3.6]. These values are motivated by SPS models (Schombert & McGaugh 2014) using a Chabrier (2003) IMF. They are in agreement with independent estimates from different SPS models (Meidt et al. 2014; Norris et al. 2016) and resolved stellar populations in the LMC (Eskew et al. 2012). They also provide sensible gas fractions (Paper I) and minimize the BTFR scatter (Lelli et al. 2016b). The DiskMass survey, however, reports smaller values of
at [3.6]. These values are motivated by SPS models (Schombert & McGaugh 2014) using a Chabrier (2003) IMF. They are in agreement with independent estimates from different SPS models (Meidt et al. 2014; Norris et al. 2016) and resolved stellar populations in the LMC (Eskew et al. 2012). They also provide sensible gas fractions (Paper I) and minimize the BTFR scatter (Lelli et al. 2016b). The DiskMass survey, however, reports smaller values of  in the K band (Martinsson et al. 2013; Swaters et al. 2014), corresponding to ∼0.2
in the K band (Martinsson et al. 2013; Swaters et al. 2014), corresponding to ∼0.2  at [3.6] (see Paper I). Here we investigate the effects that different normalizations of
at [3.6] (see Paper I). Here we investigate the effects that different normalizations of  have on the radial acceleration relation.
have on the radial acceleration relation.
Figure 6 (left) shows our fiducial relation, while Figure 6 (middle) shows the case of  to isolate the role of bulges. Clearly, bulges affect only the high-acceleration portion of the relation. We fit a double power law (Equation (9)) and provide fit results in Table 2. The fit parameters are consistent with those from our fiducial relation, indicating that bulges play a minor role. The observed scatter increases by 0.01 dex. For
to isolate the role of bulges. Clearly, bulges affect only the high-acceleration portion of the relation. We fit a double power law (Equation (9)) and provide fit results in Table 2. The fit parameters are consistent with those from our fiducial relation, indicating that bulges play a minor role. The observed scatter increases by 0.01 dex. For  , the relation slightly deviates from the 1:1 line. Our fiducial value of
, the relation slightly deviates from the 1:1 line. Our fiducial value of  implies that bulges are truly maximal.
implies that bulges are truly maximal.
Figure 6. The radial acceleration relation using different normalizations of the stellar mass-to-light ratio. Symbols are the same as in Figure 3. A relation between  and
and  persists even for low stellar mass-to-light ratio, corresponding to submaximal baryonic disks.
persists even for low stellar mass-to-light ratio, corresponding to submaximal baryonic disks.
Download figure:
Standard image High-resolution imageFigure 6 (right) shows the radial acceleration relation using  . For these low values of
. For these low values of  , baryonic disks are submaximal and DM dominates everywhere (as found by the DiskMass survey). The radial acceleration relation, however, still exists: it is simply shifted in location. This happens because the shape of
, baryonic disks are submaximal and DM dominates everywhere (as found by the DiskMass survey). The radial acceleration relation, however, still exists: it is simply shifted in location. This happens because the shape of  closely relates to the shape of
closely relates to the shape of  , as noticed early by van Albada & Sancisi (1986) and Kent (1987). For
, as noticed early by van Albada & Sancisi (1986) and Kent (1987). For  , the relation shows only a weak curvature since the inner and outer parts of galaxies are almost equally DM dominated. Fitting a double power law, we find that both
, the relation shows only a weak curvature since the inner and outer parts of galaxies are almost equally DM dominated. Fitting a double power law, we find that both  and
and  are not well constrained and depend on the initial parameter estimates, whereas α and β are slightly more stable. The values in Table 2 are indicative. In any case, the observed scatter significantly increases to 0.15 dex. The same happens with the BTFR (Lelli et al. 2016b). The quality of both relations is negatively impacted by low
are not well constrained and depend on the initial parameter estimates, whereas α and β are slightly more stable. The values in Table 2 are indicative. In any case, the observed scatter significantly increases to 0.15 dex. The same happens with the BTFR (Lelli et al. 2016b). The quality of both relations is negatively impacted by low  .
.
Interestingly, the high-acceleration slope of the relation is consistent with 1 for any choice of  (Table 2). This supports the concept of baryonic dominance in the inner parts of HSB galaxies. If HSB galaxies were strongly submaximal, they could have a slope different from unity, as seen in DM-dominated LSB galaxies. Our fiducial normalization of
(Table 2). This supports the concept of baryonic dominance in the inner parts of HSB galaxies. If HSB galaxies were strongly submaximal, they could have a slope different from unity, as seen in DM-dominated LSB galaxies. Our fiducial normalization of  seems natural as it places the high end of the radial acceleration relation on the 1:1 line.
seems natural as it places the high end of the radial acceleration relation on the 1:1 line.
4.2. Purely Stellar Relations
We now investigate alternative versions of the radial acceleration relation using only stellar quantities and neglecting the H i gas. This is interesting for two reasons.
- 1.IFU surveys like CALIFA (García-Lorenzo et al. 2015) and MANGA (Bundy et al. 2015) are providing large galaxy samples with spatially resolved kinematics, but they usually lack H i data. The availability of both gas and stellar maps is one of the key advantages of SPARC. Local scaling relations between stars and dynamics, therefore, can provide a benchmark for such IFU surveys.
- 2.One might suspect that the radial acceleration relation is the end product of a self-regulated star formation process, where the total gravitational field (
 ) sets the local stellar surface density. If true, one may expect that the stellar surface density correlates with
) sets the local stellar surface density. If true, one may expect that the stellar surface density correlates with  better than with
better than with  .
.
In Figure 7, we plot  versus the stellar gravitational field (
versus the stellar gravitational field ( ), the total stellar surface density (
), the total stellar surface density ( ), and the stellar surface density of the disk (
), and the stellar surface density of the disk ( ). The tightest correlation is given by the stellar gravitational field. We recall that this quantity is obtained considering the entire run of
). The tightest correlation is given by the stellar gravitational field. We recall that this quantity is obtained considering the entire run of  with radius (Casertano 1983): Newton's shell theorem does not hold for a flattened mass distribution, so the distribution of mass outside a given radius R also affects the gravitational potential at R. The most fundamental relation involves the gravitational potential, not merely the local stellar density. This cannot be trivially explained in terms of self-regulated star formation via disk stability: it is the full run of
with radius (Casertano 1983): Newton's shell theorem does not hold for a flattened mass distribution, so the distribution of mass outside a given radius R also affects the gravitational potential at R. The most fundamental relation involves the gravitational potential, not merely the local stellar density. This cannot be trivially explained in terms of self-regulated star formation via disk stability: it is the full run of  with R (and its derivatives) to determine the quantity that best correlates with the observed acceleration at every R, not just the local
with R (and its derivatives) to determine the quantity that best correlates with the observed acceleration at every R, not just the local  .
.
Figure 7. Alternative versions of the radial acceleration relation using only photometric data. The observed acceleration at R is plotted against the corresponding stellar gravitational field  (left), the total stellar surface density
(left), the total stellar surface density  (middle), and the disk stellar surface density
(middle), and the disk stellar surface density  (right). Symbols are the same as in Figure 3.
(right). Symbols are the same as in Figure 3.
Download figure:
Standard image High-resolution imageThe use of g⋆ instead of  changes the shape of the relation: the curvature is now more acute because the data deviate more strongly from the 1:1 line below ∼10−10 m s−2. This is the unavoidable consequence of neglecting the gas contribution. Nevertheless, the observed scatter in the
changes the shape of the relation: the curvature is now more acute because the data deviate more strongly from the 1:1 line below ∼10−10 m s−2. This is the unavoidable consequence of neglecting the gas contribution. Nevertheless, the observed scatter in the  relation is the same as in the
relation is the same as in the  relation. Hence, one can use [3.6] surface photometry to predict rotation curves with a ∼15% error (modulo uncertainties on distance and inclination). We perform this exercise for ETGs in the next section.
relation. Hence, one can use [3.6] surface photometry to predict rotation curves with a ∼15% error (modulo uncertainties on distance and inclination). We perform this exercise for ETGs in the next section.
5. Radial Acceleration Relation for Early-type Galaxies
5.1. General Results for ETGs
We now study the location of ETGs on the radial acceleration relation. Figure 8 (left) shows rotating ETGs from Atlas with two different measurements of
with two different measurements of  (Section 2.2.1): one at small radii from JAM modeling of IFU data (Cappellari et al. 2013) and one at large radii from H i data (den Heijer et al. 2015). Figure 8 (right) shows X-ray ETGs with detailed mass profiles from Chandra and XMM observations (Section 2.2.2): each galaxy contributes with multiple points, similar to LTGs. For all ETGs, we derived Spitzer [3.6] photometry and built mass models (Section 2.2.3): this gives estimates of
(Section 2.2.1): one at small radii from JAM modeling of IFU data (Cappellari et al. 2013) and one at large radii from H i data (den Heijer et al. 2015). Figure 8 (right) shows X-ray ETGs with detailed mass profiles from Chandra and XMM observations (Section 2.2.2): each galaxy contributes with multiple points, similar to LTGs. For all ETGs, we derived Spitzer [3.6] photometry and built mass models (Section 2.2.3): this gives estimates of  that are fully independent from
that are fully independent from  and comparable with those of LTGs. Our fiducial
and comparable with those of LTGs. Our fiducial  values are listed in Table 1: different values would systematically shift the data in the horizontal direction without changing our overall results.
values are listed in Table 1: different values would systematically shift the data in the horizontal direction without changing our overall results.
Figure 8. Radial acceleration relation adding rotating ETGs from Atlas (left) and X-ray ETGs with accurate mass profiles (right). Each ETG is represented with a different color, as given by the legend. In the left panel, squares show measurements within 1
(left) and X-ray ETGs with accurate mass profiles (right). Each ETG is represented with a different color, as given by the legend. In the left panel, squares show measurements within 1  from JAM models of IFU data (Cappellari et al. 2013), while diamonds show measurements at large radii from H i data (den Heijer et al. 2015). The other symbols are the same as in Figure 3. In some cases, the JAM models may overestimate the true circular velocity (see Section 5).
from JAM models of IFU data (Cappellari et al. 2013), while diamonds show measurements at large radii from H i data (den Heijer et al. 2015). The other symbols are the same as in Figure 3. In some cases, the JAM models may overestimate the true circular velocity (see Section 5).
Download figure:
Standard image High-resolution imageFigure 8 shows that ETGs follow the same relation as LTGs. X-ray and H i data probe a broad range of accelerations in different ETGs and nicely overlap with LTGs. The IFU data probe a narrow dynamic range at high accelerations, where we have only a few measurements from bulge-dominated spirals. In general, the IFU data lie on the 1:1 relation with some scatter, reinforcing the notion that ETGs have negligible DM content in the inner parts (Cappellari 2016). The same results are given by X-ray data at small radii, probing high-acceleration regions. Some IFU data show significant deviations above the 1:1 line, but these are expected. The values of  from JAM models are not fully empirical and may overestimate the true circular velocity, as we discuss below.
from JAM models are not fully empirical and may overestimate the true circular velocity, as we discuss below.
Davis et al. (2013) compare the predictions of JAM models with interferometric CO data using 35 ETGs with inner molecular disks. In ∼50% of the cases, they find good agreement. For another ∼20%, the CO is disturbed or rotates around the polar plane of the galaxy, so it cannot be compared with JAM models. For the remaining ∼30%, there is poor agreement: the JAM models tend to predict systematically higher circular velocities than those observed in CO. An incidence of 30% is consistent with the deviant points in Figure 8. We have three ETGs in common with Davis et al. (2013). NGC 3626 (dark orange) shows good agreement between CO and JAM velocities and lies close to the 1:1 line, as expected. On the contrary, NGC 2824 (pink) and UGC 6176 (dark blue) show higher JAM velocities than observed in CO: these are among the strongest outliers in Figure 8.
Janz et al. (2016) discuss the location of ETGs on the MDAR, which is equivalent to the radial acceleration relation after subtracting the 1:1 line. Janz et al. (2016) use JAM models of IFU data and find that ETGs follow an MDAR similar to LTGs, but with a small offset. For LTGs, they use data from McGaugh (2004), which rely on optical photometry. The apparent offset disappears using the more accurate SPARC data with [3.6] photometry. Moreover, Janz et al. (2016) use globular clusters to trace the outer gravitational potential of ETGs and find potential deviations from the MDAR at low  . These deviations may simply point to possible deviations from the assumed isotropy of globular cluster orbits. Both H i and X-ray data show that there are no significant deviations at low accelerations: ETGs and LTGs do follow the same relation within the uncertainties.
. These deviations may simply point to possible deviations from the assumed isotropy of globular cluster orbits. Both H i and X-ray data show that there are no significant deviations at low accelerations: ETGs and LTGs do follow the same relation within the uncertainties.
5.2. Predicted Rotation Curves for ETGs
Given the uncertainties, we do not fit the radial acceleration relation including ETGs. This exercise has little value because the 2693 points of LTGs would dominate over the 28 points of rotating ETGs and the 80 points of X-ray ETGs. Instead, we use the radial acceleration relation of LTGs (Equation (11)) to predict the full rotation curves of rotating ETGs. These may be tested in future studies combining CO, Hα, and H i observations. We show three examples in Figure 9. NGC 2859 (left) exemplifies ∼50% of our mass models: the predicted rotation curve agrees with both IFU and H i measurements (as expected from Figure 8). NGC 3522 exemplifies ∼20% of our cases: the H i velocity point is reproduced, but the IFU measurement is not (although the peak radius is reproduced). This suggests that JAM models may have overestimated the true circular velocity (as discussed in Section 5.1). NGC 3998 exemplifies the remaining ∼30%: both IFU and H i measurements are not reproduced within 1σ, but there are systematic shifts. This may be accounted for by changing the distance, inclination, or  .
.
Figure 9.
Mass models for three rotating ETGs with extended H i disks. Top panels: the [3.6] surface brightness profiles (red dots) and exponential fits to the outer regions (dashed line). Open circles show extrapolated values for bulge (purple) and disk (red) components from nonparametric decompositions. Bottom panels: velocity contributions due to the bulge (purple dash-dotted line), stellar disk (red dashed line), and total baryons (blue solid line), adopting  /L⊙. The black line and gray band show the predicted rotation curve using the radial acceleration relation of LTGs (Equation (11)) and considering a scatter of 0.13 dex. The inner square shows the maximum velocity from JAM modeling of IFU data. The outer circle shows the rotation velocity from H i data (den Heijer et al. 2015). The arrows indicate the galaxy effective radius (red) and 2.2 disk scale lengths (gray). Similar figures for all ETGs are available as a figure set. (The complete figure set (16 images) is available.)
/L⊙. The black line and gray band show the predicted rotation curve using the radial acceleration relation of LTGs (Equation (11)) and considering a scatter of 0.13 dex. The inner square shows the maximum velocity from JAM modeling of IFU data. The outer circle shows the rotation velocity from H i data (den Heijer et al. 2015). The arrows indicate the galaxy effective radius (red) and 2.2 disk scale lengths (gray). Similar figures for all ETGs are available as a figure set. (The complete figure set (16 images) is available.)
Download figure:
Standard image High-resolution imageIn general, we predict that the rotation curves of ETGs should rise quickly in the central regions, decline at intermediate radii, and flatten in the outer parts. The difference between peak and flat rotation velocities can be ∼20%, for example, 50 km s−1 for galaxies with  km s−1. This is analogous to bulge-dominated spirals (Casertano & van Gorkom 1991; Noordermeer et al. 2007). Similar conclusions are drawn by Serra et al. (2016).
km s−1. This is analogous to bulge-dominated spirals (Casertano & van Gorkom 1991; Noordermeer et al. 2007). Similar conclusions are drawn by Serra et al. (2016).
6. Radial Acceleration Relation for Dwarf Spheroidal Galaxies
6.1. General Results for dSphs
We now investigate the location of dSphs on the radial acceleration relation. For these objects, we have only one measurement per galaxy near the half-light radii, assuming spherical symmetry and dynamical equilibrium (see Section 2.3). These data are compiled in Appendix
In Figure 10 (left), we plot all available data. Large symbols indicate the "classical" satellites of the MW (Carina, Draco, Fornax, Leo I, Leo II, Sculptor, Sextans, and Ursa Minor) and Andromeda (NGC 147, NGC 185, NGC 205, And I, And II, And III, And V, And VI, and And VII). Classical dSphs follow the same relation as LTGs within the errors. The brightest satellites of Andromeda adhere to the relation at  , which are typically found in the outer parts of high-mass HSB disks or in the inner parts of low-mass LSB disks (see Figure 4, bottom). Similarly, the brightest satellites of the MW overlap with LSB disks at
, which are typically found in the outer parts of high-mass HSB disks or in the inner parts of low-mass LSB disks (see Figure 4, bottom). Similarly, the brightest satellites of the MW overlap with LSB disks at  .
.
Figure 10. Location of dSphs on the radial acceleration relation, using all available data (left) and data that satisfy quality criteria (right; see Section 6.2). Circles and diamonds distinguish between MW and M31 satellites. Large symbols indicate classical satellites, while small symbols show ultrafaint satellites and more isolated dSphs (like Cetus and Tucana; see, e.g., Pawlowski & McGaugh 2014). The other symbols and lines are the same as in Figure 3. The dashed-dotted line is a fit to Equation (14) using high-quality dSphs.
Download figure:
Standard image High-resolution imageIn Figure 10 (left), small symbols show the "ultrafaint" dSphs. They seem to extend the relation by a further ∼2 dex in  but display large scatter. These objects, however, have much less accurate data than other galaxies. Photometric properties are estimated using star counts, after candidate stars are selected using color–magnitude diagrams and template isochrones. Velocity dispersions are often based on few stars and may be systematically affected by contaminants (Walker et al. 2009c), unidentified binary stars (McConnachie & Côté 2010), and out-of-equilibrium kinematics (McGaugh & Wolf 2010). Differences of a few km s−1 in
but display large scatter. These objects, however, have much less accurate data than other galaxies. Photometric properties are estimated using star counts, after candidate stars are selected using color–magnitude diagrams and template isochrones. Velocity dispersions are often based on few stars and may be systematically affected by contaminants (Walker et al. 2009c), unidentified binary stars (McConnachie & Côté 2010), and out-of-equilibrium kinematics (McGaugh & Wolf 2010). Differences of a few km s−1 in  would significantly impact the location of ultrafaint dSphs on the plot. Hence, the shape of the radial acceleration relation at
would significantly impact the location of ultrafaint dSphs on the plot. Hence, the shape of the radial acceleration relation at  remains very uncertain.
remains very uncertain.
6.2. Ultrafaint dSphs: A Low-acceleration Flattening?
As an attempt to constrain the low-acceleration shape of the relation, we apply three quality criteria.
- 1.The velocity dispersion is measured using more than eight stars to avoid systematics due to binary stars and velocity outliers (see Appendix A.3 of Collins et al. 2013). This removes eight satellites (four of the MW and four of M31).
- 2.
- 3.The tidal field of the host galaxy does not strongly affect the internal kinematics of the dSphs.
To apply the last criterion, we estimate the tidal acceleration from the host galaxy at the half-light radii:

where  is the distance from the host (MW or M31), and
is the distance from the host (MW or M31), and  is its total mass. We assume a total mass of
is its total mass. We assume a total mass of  for the MW and
for the MW and  for M31. These assumptions do not strongly affect our quality cut. We exclude dSphs with
for M31. These assumptions do not strongly affect our quality cut. We exclude dSphs with  since tides are comparable to the internal gravity. This removes four M31 satellites, reducing our dSph sample to 35 objects.
since tides are comparable to the internal gravity. This removes four M31 satellites, reducing our dSph sample to 35 objects.
We note that the observed velocity dispersion may be inflated by nonequilibrium kinematics, so  may be overestimated, and the criterion
may be overestimated, and the criterion  may miss some tidally affected dSphs. For example, Bootes I (Roderick et al. 2016) and And XXVII (Collins et al. 2013) show tidal features but are not excluded by our criterion. Nevertheless, these two objects are not strong outliers from the relation. Conversely, the ellipticity criterion correctly excludes some dSphs that show signs of disruption, like Ursa Minor (Palma et al. 2003), Hercules (Roderick et al. 2015), and Leo V (Collins et al. 2016).
may miss some tidally affected dSphs. For example, Bootes I (Roderick et al. 2016) and And XXVII (Collins et al. 2013) show tidal features but are not excluded by our criterion. Nevertheless, these two objects are not strong outliers from the relation. Conversely, the ellipticity criterion correctly excludes some dSphs that show signs of disruption, like Ursa Minor (Palma et al. 2003), Hercules (Roderick et al. 2015), and Leo V (Collins et al. 2016).
In Figure 10 (right), we enforce these quality criteria. Several outliers are removed, and the scatter substantially decreases. Ultrafaint dSphs seem to trace a flattening in the relation at  . This possible flattening is in line with the results of Strigari et al. (2008), who found that dSphs have a constant total mass of ∼107
. This possible flattening is in line with the results of Strigari et al. (2008), who found that dSphs have a constant total mass of ∼107  within 300 pc. Clearly, if
within 300 pc. Clearly, if  const, the inferred mass will necessarily be constant within any chosen radii in parsecs (see Walker et al. 2010 for a similar result).
const, the inferred mass will necessarily be constant within any chosen radii in parsecs (see Walker et al. 2010 for a similar result).
Despite the large uncertainties, it is tempting to fit the radial acceleration relation including ultrafaint dSphs. We tried both Equations (9) and (11) but found unsatisfactory results because the putative low-acceleration flattening is not represented by these functional forms. Moreover, the fit is dominated by LTGs because dSphs have large errors. If we neglect the errors, we find a reasonable fit with the following function:

where the free parameters are  and
and  . This is similar to Equation (11), but the additional term imposes a flattening at
. This is similar to Equation (11), but the additional term imposes a flattening at  for
for  . We find
. We find

The observed rms scatter is still small (0.14 dex). We stress that the "acceleration floor" expressed by  may be real or an intrinsic limitation of the current data. In a ΛCDM context, this putative low-acceleration flattening may be linked to the steep mass function of DM halos: dwarf galaxies spanning a broad range in stellar mass may form in DM halos spanning a narrow range in virial mass (as also implied by abundance-matching studies). Future studies may shed new light on this issue.
may be real or an intrinsic limitation of the current data. In a ΛCDM context, this putative low-acceleration flattening may be linked to the steep mass function of DM halos: dwarf galaxies spanning a broad range in stellar mass may form in DM halos spanning a narrow range in virial mass (as also implied by abundance-matching studies). Future studies may shed new light on this issue.
6.3. dSphs with Chemodynamically Distinct Components
The radial acceleration relation is a local scaling law that combines data at different radii in different galaxies. In general, dSphs cannot probe this local nature because robust estimates of  can only be obtained near the half-light radius, where the effects of anisotropy are small (e.g., Wolf et al. 2010). Some dSphs, however, show chemodynamically distinct stellar components (Tolstoy et al. 2004; Battaglia et al. 2006): one can distinguish between a metal-rich (MR) and a metal-poor (MP) component, with the former more centrally concentrated and kinematically colder than the latter. These two components can be used to trace the gravitational field at different radii in the same dSph (Battaglia et al. 2008; Walker & Peñarrubia 2011), so they provide two independent points on the radial acceleration relation.
can only be obtained near the half-light radius, where the effects of anisotropy are small (e.g., Wolf et al. 2010). Some dSphs, however, show chemodynamically distinct stellar components (Tolstoy et al. 2004; Battaglia et al. 2006): one can distinguish between a metal-rich (MR) and a metal-poor (MP) component, with the former more centrally concentrated and kinematically colder than the latter. These two components can be used to trace the gravitational field at different radii in the same dSph (Battaglia et al. 2008; Walker & Peñarrubia 2011), so they provide two independent points on the radial acceleration relation.
In Figure 11, we investigate the distinct stellar components of Fornax and Sculptor using data from Walker & Peñarrubia (2011). Both components lie on the radial acceleration relation within the observed scatter, confirming its local nature. For both galaxies, the two components have approximately the same stellar mass, but the MP component has significantly larger  , leading to lower values of
, leading to lower values of  . Even though the two components have different velocity dispersions, the value of
. Even though the two components have different velocity dispersions, the value of  is nearly the same. Velocity dispersions and half-light radii seem to conspire to give a constant
is nearly the same. Velocity dispersions and half-light radii seem to conspire to give a constant  , in line with the apparent flattening of the relation at low
, in line with the apparent flattening of the relation at low  . We repeated the same exercise using different data from G. Battaglia (2017, private communication) and find only minor differences.
. We repeated the same exercise using different data from G. Battaglia (2017, private communication) and find only minor differences.
Figure 11. Same as Figure 10 (right) but considering the chemodynamically distinct components of Sculptor (red) and Fornax (green). Stars and pentagons correspond to the metal-rich and metal-poor components, respectively. These two components have different spatial distributions and kinematics, providing two measurements of  at different radii.
at different radii.
Download figure:
Standard image High-resolution image7. Relation to Other Dynamical Laws
In the previous sections, we showed that LTGs, ETGs, and dSphs follow a tight radial acceleration relation: the observed acceleration correlates with that due to the baryonic distribution. This is summarized in Figure 12 (left).
Figure 12. Left: the radial acceleration relation considering all galaxy types. The color scale represents ∼2700 points from 153 LTGs: blue squares and dashed lines show the mean and standard deviation of the binned data, respectively. Red circles and orange diamonds indicate rotating ETGs and X-ray ETGs, respectively. Small gray hexagons show dSphs: the large green hexagons show the mean and standard deviation of binned data. Right: the mass discrepancy–acceleration relation, where the vertical axis shows  . This is equivalent to subtracting the 1:1 line from the radial acceleration relation. Symbols are the same as in the left panel.
. This is equivalent to subtracting the 1:1 line from the radial acceleration relation. Symbols are the same as in the left panel.
Download figure:
Standard image High-resolution imageTo facilitate the comparison with previous works, the right panel of Figure 12 shows the "mass discrepancy"  versus
versus  . This plot is referred to as MDAR (McGaugh 2004, 2014). Clearly, the mass discrepancy is not some random value but is closely related to the baryonic gravitational field. In particular, ultrafaint dSphs are heavily DM dominated (
. This plot is referred to as MDAR (McGaugh 2004, 2014). Clearly, the mass discrepancy is not some random value but is closely related to the baryonic gravitational field. In particular, ultrafaint dSphs are heavily DM dominated ( ), but their insignificant baryonic content can be used to predict
), but their insignificant baryonic content can be used to predict  despite the domination of DM. The observed scatter increases at high and low accelerations, but this is likely due to less precise data: the derivation of the total gravitational field for dSphs and ETGs is more complex than for LTGs due to the lack of a high-density gas disk. We also stress that the MDAR axes are no longer independent, so it is preferable to use the radial acceleration relation.
despite the domination of DM. The observed scatter increases at high and low accelerations, but this is likely due to less precise data: the derivation of the total gravitational field for dSphs and ETGs is more complex than for LTGs due to the lack of a high-density gas disk. We also stress that the MDAR axes are no longer independent, so it is preferable to use the radial acceleration relation.
The radial acceleration relation subsumes and generalizes several well-known dynamical properties of galaxies: (1) the BTFR (McGaugh et al. 2000), (2) the "dichotomy" between HSB and LSB galaxies (de Blok & McGaugh 1997; Tully & Verheijen 1997), (3) the central density relation (Lelli et al. 2013, 2016c), (4) the "baryon-halo conspiracy" (van Albada & Sancisi 1986), (5) Renzo's rule (Sancisi 2004), (6) the Faber–Jackson relation (Faber & Jackson 1976), and (7) the  relation (Serra et al. 2016). In the following, we discuss the interplay between these different dynamical laws.
relation (Serra et al. 2016). In the following, we discuss the interplay between these different dynamical laws.
7.1. Baryonic Tully–Fisher Relation
The BTFR is a consequence of the bottom-end portion of the radial acceleration relation. At large radii, we have

The former equation is straightforward since  is defined as the mean value along the flat part of the rotation curve (e.g., Lelli et al. 2016b). The latter equation is reasonably accurate since the monopole term typically dominates the baryonic potential beyond the bright stellar disk. The BTFR considers a single value of
is defined as the mean value along the flat part of the rotation curve (e.g., Lelli et al. 2016b). The latter equation is reasonably accurate since the monopole term typically dominates the baryonic potential beyond the bright stellar disk. The BTFR considers a single value of  and
and  for each galaxy. The radial acceleration relation, instead, considers each individual point along the flat part of the rotation curve and the corresponding enclosed baryonic mass. For LTGs and ETGs, the low-acceleration slope of the relation is fully consistent with 0.5, and hence
for each galaxy. The radial acceleration relation, instead, considers each individual point along the flat part of the rotation curve and the corresponding enclosed baryonic mass. For LTGs and ETGs, the low-acceleration slope of the relation is fully consistent with 0.5, and hence

This eliminates the radial dependence and gives a BTFR with a slope of 4. A different bottom-end slope of the radial acceleration relation would preserve the radial dependence and imply a correlation between the BTFR residuals and some characteristic radius, contrary to the observations (e.g., Lelli et al. 2016b). We stress that these results are completely empirical. Remarkably, this phenomenology was anticipated by Milgrom (1983).
7.2. HSB–LSB Dichotomy and Central Density Relation
HSB galaxies have steeply rising rotation curves and can be described as "maximum disks" in their inner parts (e.g., van Albada & Sancisi 1986), whereas LSB galaxies have slowly rising rotation curves and are DM dominated at small radii (e.g., de Blok & McGaugh 1997). Lelli et al. (2013) find that the inner slope of the rotation curve correlates with the central surface brightness, indicating that dynamical and baryonic densities are closely related. In Lelli et al. (2016c), we estimate the central dynamical density  of SPARC galaxies using a formula from Toomre (1963). We find that
of SPARC galaxies using a formula from Toomre (1963). We find that  correlates with the central stellar density
correlates with the central stellar density  over 4 dex, leading to a central density relation (see also Swaters et al. 2014).
over 4 dex, leading to a central density relation (see also Swaters et al. 2014).
The shape of the central density relation is similar to that of the radial acceleration relation. These two relations involve similar quantities in natural units (G = 1), but there are major conceptual differences between them.
- 1.The radial acceleration relation unifies points from different radii in different galaxies, whereas the central density relation relates quantities measured at
 in every galaxy. The latter relation can be viewed as a special case of the former for
in every galaxy. The latter relation can be viewed as a special case of the former for  .
. - 2.Poisson's equation is applied along the "baryonic axis" of the radial acceleration relation (
 ), while it is used along the "dynamical axis" of the central density relation (
), while it is used along the "dynamical axis" of the central density relation ( ) via Equation (16) of Toomre (1963). Basically, these two relations address the same problem in reverse directions: (i) in the radial acceleration relation, we start from the observed density distribution to obtain the expected dynamics
) via Equation (16) of Toomre (1963). Basically, these two relations address the same problem in reverse directions: (i) in the radial acceleration relation, we start from the observed density distribution to obtain the expected dynamics  and compare it with the observed dynamics
and compare it with the observed dynamics  (ii) in the central density relation, we start from the observed dynamics to obtain the expected surface density
(ii) in the central density relation, we start from the observed dynamics to obtain the expected surface density  and compare it with the observed surface density
and compare it with the observed surface density  .
.
7.3. Baryon-halo Conspiracy and Renzo's Rule
In a seminal paper, van Albada & Sancisi (1986) pointed out that the rotation curves of spiral galaxies show no indication of the transition from the baryon-dominated inner regions to the DM-dominated outer parts. Hence, the relative distributions of baryons and DM must "conspire" to keep the rotation curve flat. Similarly, the total surface density profiles of ETGs are nearly isothermal, leading to flat rotation curves and a "bulge-halo conspiracy" (e.g., Treu et al. 2006; Humphrey et al. 2012; Cappellari et al. 2015). The concept of "baryon-halo conspiracy" is embedded in the smooth shape of the radial acceleration relation, progressively deviating from the 1:1 line to the DM-dominated regime at low accelerations.
Despite being remarkably flat, rotation curves can show features (bumps and wiggles), especially in their inner parts. Renzo's rule states that "for any feature in the luminosity profile there is a corresponding feature in the rotation curve, and vice versa" (Sancisi 2004). This concept is embedded by the radial acceleration relation, linking photometry and dynamics on a radial basis. It is also generalized: the fundamental relation does not involve merely the local surface density of stars, but also the local gravitational field (via Poisson's equation) due to the entire density distribution of baryons (Section 4.2).
7.4. Faber–Jackson and  Relations
Relations
The Faber–Jackson and  relations also seem to be a consequence of the radial acceleration relation. Serra et al. (2016) considers a sample of 16 rotating ETGs and find that
relations also seem to be a consequence of the radial acceleration relation. Serra et al. (2016) considers a sample of 16 rotating ETGs and find that  linearly correlates with VH i, where
linearly correlates with VH i, where  (den Heijer et al. 2015). They report
(den Heijer et al. 2015). They report

with an observed scatter of only 0.05 dex. The extremely small scatter suggests that the  relation is most fundamental for ETGs (see also Pizzella et al. 2005; Courteau et al. 2007). Serra et al. (2016) discuss that the
relation is most fundamental for ETGs (see also Pizzella et al. 2005; Courteau et al. 2007). Serra et al. (2016) discuss that the  relation implies a close link between the inner baryon-dominated regions (probed by
relation implies a close link between the inner baryon-dominated regions (probed by  or
or  ) and the outer DM-dominated parts (probed by VH i). This link is made explicit in Figure 8: ETGs follow the same radial acceleration relation as LTGs, combining inner and outer parts of galaxies into a single smooth relation.
) and the outer DM-dominated parts (probed by VH i). This link is made explicit in Figure 8: ETGs follow the same radial acceleration relation as LTGs, combining inner and outer parts of galaxies into a single smooth relation.
den Heijer et al. (2015) show that rotating ETGs follow the same BTFR as LTGs:

Hence, a baryonic Faber–Jackson relation follows:

The radial acceleration relation appears to be the most fundamental scaling law of galaxies, encompassing previously known dynamical properties. It links the central density relation at R = 0 and the BTFR at large radii. The smooth connection between the baryon-dominated and DM-dominated regimes generalizes concepts like the disk-halo conspiracy and Renzo's rule for LTGs, as well as the Faber–Jackson and  relations for ETGs. The radial acceleration relation is tantamount to a natural law, a sort of Kepler's law for galaxies.
relations for ETGs. The radial acceleration relation is tantamount to a natural law, a sort of Kepler's law for galaxies.
8. Implications
8.1. Implications for the DM Distribution
In this work we have not considered any specific model for the DM halo. Empirically, there is no reason to do so. For LTGs and ETGs, the detailed DM distribution directly follows from the radial acceleration relation. The gravitational field due to DM can be written entirely in terms of the baryonic field (see also McGaugh 2004):

where  is given by either Equation (9) or Equation (11). Note that Equation (14) is unrealistic in this context because it would imply that rotation curves start to rise as
is given by either Equation (9) or Equation (11). Note that Equation (14) is unrealistic in this context because it would imply that rotation curves start to rise as  beyond
beyond  m s−2. Equation (14) is just a convenient function to include ultrafaint dSphs in the radial acceleration relation. For a spherical DM halo, the enclosed mass is
m s−2. Equation (14) is just a convenient function to include ultrafaint dSphs in the radial acceleration relation. For a spherical DM halo, the enclosed mass is

The observed baryonic distribution specifies the DM distribution. There is no need to fit arbitrary halo models.
8.2. Implications for Galaxy Formation Models
8.2.1. General Implications and Conceptual Issues
In a ΛCDM cosmology, the process of galaxy formation is highly stochastic. DM halos grow by hierarchical merging and accrete gas via hot or cold modes, depending on their mass and redshift (Dekel & Birnboim 2006). Gas is converted into stars via starbursts or self-regulated processes, leading to diverse star formation histories. Supernova explosions, stellar winds, and active galactic nuclei can inject energy into the ISM and potentially drive gas outflows, redistributing both mass and angular momentum (Governato et al. 2010; Di Cintio et al. 2014; Madau et al. 2014). Despite the complex and diverse nature of these processes, galaxies follow tight scaling laws. Regularity must somehow emerge from stochasticity. This issue is already puzzling in the context of global scaling laws, like the Tully–Fisher and Faber–Jackson relations, but is exacerbated in the context of the radial acceleration relation, due to its local nature.
The ΛCDM model is known to face severe problems with both the rotation curves of disk galaxies (e.g., Moore et al. 1999; de Blok et al. 2001; McGaugh et al. 2007; Kuzio de Naray et al. 2009) and the dynamics of dSphs (e.g., Boylan-Kolchin et al. 2011; Walker & Peñarrubia 2011; Pawlowski et al. 2014). Recently, Oman et al. (2015) pointed out the "unexpected diversity of dwarf galaxy rotation curves." This statement is correct from a pure ΛCDM perspective since little variation is expected in the DM distribution at a given mass. However, it misses a key observational fact: the diversity of rotation curve shapes is fully accounted for by the diversity in baryonic mass distributions (Sancisi 2004; Swaters et al. 2012; Lelli et al. 2013; Karukes & Salucci 2017). For example, IC 2574 and F583-1 are identified by Oman et al. (2015) as problematic cases for ΛCDM (see their Figure 5). Still, these galaxies fall on the observed radial acceleration relation (Figure 13). From an empirical perspective, their slowly rising rotation curves are fully expected due to their low surface brightnesses (Lelli et al. 2013). The real problem is not "diversity," but the remarkable regularity in the baryon–DM coupling. Similarly, the "cusp-core" and "too-big-to-fail" problems are merely symptoms of a broader issue for ΛCDM: rotation curves can be predicted from the baryonic distribution, even for galaxies that appear to be entirely DM dominated!
Figure 13. Same as Figure 3 (top left) but we highlight F583-1 and IC 2574. These two LSB galaxies are identified by Oman et al. (2015) as challenging cases for ΛCDM, yet they fall on the radial acceleration relation within the observed scatter. The shifts with respect to the main relation may be due to variations in  .
.
Download figure:
Standard image High-resolution imageA satisfactory model of galaxy formation should explain four conceptual issues: (1) the physical origin of the acceleration scale g†, (2) the physical origin of the low-acceleration slope (consistent with 0.5), (3) the intrinsic tightness of the relation, and (4) the lack of correlations between residuals and other galaxy properties.
8.2.2. Comparison with Hydrodynamical Simulations
Wu & Kroupa (2015) compared the data of McGaugh (2004) with cosmological simulations of galaxy formation (Agertz et al. 2011; Guedes et al. 2011; Aumer et al. 2013; Marinacci et al. 2014), finding poor agreement. On the other hand, Santos-Santos et al. (2016) find reasonable agreement between the data of McGaugh (2014) and 22 model galaxies from zoom-in simulations of small volumes. This is encouraging, but more simulated galaxies are needed to quantify the theoretical scatter around these relations and have a proper comparison with observations. For example, Keller & Wadsley (2017) find good agreement between the SPARC relation and 18 simulated galaxies, but their model galaxies span only a factor of 15 in mass covering less than  of the SPARC mass range. To conclude that "ΛCDM is fully consistent with the SPARC acceleration law," the simulated galaxies should at least span the same ranges in luminosity, surface brightness, size, and gas fraction as the data.
of the SPARC mass range. To conclude that "ΛCDM is fully consistent with the SPARC acceleration law," the simulated galaxies should at least span the same ranges in luminosity, surface brightness, size, and gas fraction as the data.
Recently, Ludlow et al. (2016) analyzed simulated galaxies from the EAGLE and APOSTOLE projects. This work significantly increases the statistics and mass range with respect to Santos-Santos et al. (2016) and Keller & Wadsley (2017) but present several problems.
- 1.Ludlow et al. (2016) fit the simulated data using our Equation (11) but find
 instead of
instead of  . The discrepancy is 90σ (rnd) and 7.5σ (sys). This indicates that simulations predict too much DM in galaxies, which is a persistent problem for ΛCDM (e.g., McGaugh et al. 2007; Kuzio de Naray et al. 2009). Indeed, the same simulations were used by the same group to reach the opposite conclusion: many real galaxies show a putative "inner mass deficit" with respect to ΛCDM expectations (Oman et al. 2015).
. The discrepancy is 90σ (rnd) and 7.5σ (sys). This indicates that simulations predict too much DM in galaxies, which is a persistent problem for ΛCDM (e.g., McGaugh et al. 2007; Kuzio de Naray et al. 2009). Indeed, the same simulations were used by the same group to reach the opposite conclusion: many real galaxies show a putative "inner mass deficit" with respect to ΛCDM expectations (Oman et al. 2015). - 2.Ludlow et al. (2016) compare the theoretical scatter from the numerical simulations with the observed scatter. This is not appropriate because the observed scatter is largely driven by observational errors (see Section 3.2 and McGaugh et al. 2016). One should compare to the intrinsic scatter, which is either zero or extremely small (
 dex). The theoretical scatter from Ludlow et al. (2016), though small (0.09 dex), is still too large compared to the observations.
dex). The theoretical scatter from Ludlow et al. (2016), though small (0.09 dex), is still too large compared to the observations. - 3.Ludlow et al. (2016) compute
 and
and  assuming spherical symmetry instead of estimating the gravitational potential in the disk midplane. The difference between spherical and disk geometry is not terribly large, but it is significant. This introduces systematics that are hard to address.
assuming spherical symmetry instead of estimating the gravitational potential in the disk midplane. The difference between spherical and disk geometry is not terribly large, but it is significant. This introduces systematics that are hard to address. - 4.
In summary, several key properties of the radial acceleration relation are not reproduced by the current generation of cosmological simulations. The claim that this relation is "a natural outcome of galaxy formation in CDM halos" has yet to be demonstrated.
8.2.3. Comparison with Semiempirical Models
Di Cintio & Lelli (2016) investigated the BTFR and MDAR using a simple, analytic, semiempirical model. They assign disk galaxies to DM halos using abundance-matching prescriptions and specify the distribution of gas and stars using observed scaling relations. This is the most optimistic ΛCDM model imaginable: baryonic physics is assumed to work just right to form realistic galaxies, while the properties of DM halos are taken from simulations (with or without the effects of baryons). This model can reproduce the overall shape of the MDAR, hence the radial acceleration relation. This is not trivial: the DM fractions from abundance matching depend on the relation between the theoretical halo mass function and the observed stellar mass function. There is no guarantee that they should reproduce the mass discrepancies observed in real galaxies.
While promising, the model of Di Cintio & Lelli (2016) predicts significant intrinsic scatter around the MDAR and correlations between residuals and radius (see their Figure 2). In ΛCDM the intrinsic scatter is driven by scatter in the baryonic-to-halo mass ratio, the mass–concentration relation of DM halos, the mass–size relation of stellar disks, and so on. These sources of scatter are unavoidable in any hierarchical DM model of galaxy formation. Similar results are found by Desmond (2017) using a similar semiempirical approach and a sophisticated statistical framework: even models with zero scatter on abundance-matching prescriptions predict too-large scatter!
The radial acceleration relation cannot be an accident of faulty data. If there were systematic errors (due to, e.g., beam smearing), even a tight intrinsic relation would be washed out. In contrast, the only way to increase the intrinsic scatter is if we have overestimated the uncertainties. We are confident that our errors are not overestimated. We assume relatively small variations in  (0.11 dex) and neglect some sources of error, like that in the vertical density distribution of disks and bulges. There is simply little room for intrinsic scatter.
(0.11 dex) and neglect some sources of error, like that in the vertical density distribution of disks and bulges. There is simply little room for intrinsic scatter.
8.3. Implications for Alternative Theories
The tightness of the radial acceleration relation and the lack of residual correlations may suggest the need for a revision of the standard DM paradigm. We envisage two general scenarios: (1) we need new fundamental laws of physics rather than DM, or (2) we need new physics in the dark sector leading to a baryon–DM coupling.
8.3.1. New Laws of Physics Rather than Dark Matter?
Scenario I includes MOND (Milgrom 1983), modified gravity (Moffat 2016), entropic gravity (Verlinde 2016), conformal gravity (O'Brien & Mannheim 2012), and fifth forces (Burrage et al. 2016). Strikingly, Milgrom (1983) predicted the existence of the radial acceleration relation 33 years ago when only a few rotation curves were available (Bosma 1978; Rubin et al. 1978) and no detailed mass models were built. MOND can be viewed either as modified gravity (MG) by changing Poisson's equation (Bekenstein & Milgrom 1984; Milgrom 2010) or modified inertia (MI) by changing the second law of Newton (Milgrom 1994, 2006). Several relativistic extensions of MOND have been proposed (see Famaey & McGaugh 2012), but it is unclear whether they can reproduce the cosmic microwave background and the formation of cosmic structures (McGaugh 2015).
The basic tenet of MOND is that dynamics become scale-invariant below a critical acceleration scale a0 (Milgrom 2009): the equations of motion remain unchanged under the transformation  . Scale-invariance specifies the bottom-end behavior of the radial acceleration relation:
. Scale-invariance specifies the bottom-end behavior of the radial acceleration relation:  , where
, where  for test particles on circular orbits far from a given mass distribution (Milgrom 2014). In MG theories,
for test particles on circular orbits far from a given mass distribution (Milgrom 2014). In MG theories,  for all orbits in all spherical systems, but it could vary from galaxy to galaxy (or even within the same galaxy) in nonspherical systems like disk galaxies. In MI theories,
for all orbits in all spherical systems, but it could vary from galaxy to galaxy (or even within the same galaxy) in nonspherical systems like disk galaxies. In MI theories,  for circular orbits in dynamically cold systems like H i disks, but it may differ from unity if there are chaotic orbits or significant pressure support, like in the stellar components of ETGs and dSphs.
for circular orbits in dynamically cold systems like H i disks, but it may differ from unity if there are chaotic orbits or significant pressure support, like in the stellar components of ETGs and dSphs.
For LTGs, ETGs, and classic dSphs, we find that the relation is consistent with a low-acceleration slope of 0.5 and  for every galaxy, in agreement with general MOND predictions. For ultrafaint dSphs, the outer slope seems to be shallower than 0.5 (Figure 10). This result must be taken with caution because (1) the data of ultrafaint dSphs are much more uncertain than those of other galaxies, (2) we cannot robustly estimate
for every galaxy, in agreement with general MOND predictions. For ultrafaint dSphs, the outer slope seems to be shallower than 0.5 (Figure 10). This result must be taken with caution because (1) the data of ultrafaint dSphs are much more uncertain than those of other galaxies, (2) we cannot robustly estimate  at different radii (as in LTGs and ETGs) and test possible variations of α from galaxy to galaxy, and (3) in MOND we expect many dSphs to be affected by the external field effect (EFE), as we discuss below. In any case, Figure 10 suggests some sort of organizing principle.
at different radii (as in LTGs and ETGs) and test possible variations of α from galaxy to galaxy, and (3) in MOND we expect many dSphs to be affected by the external field effect (EFE), as we discuss below. In any case, Figure 10 suggests some sort of organizing principle.
We note that the intrinsic scatter around the radial acceleration relation could distinguish between MI and MG theories. In MI theories, the relation  holds exactly for circular orbits (Milgrom 1994), so the radial acceleration relation should have zero intrinsic scatter. In MG theories, the above relation is valid only for spherically symmetric systems (Bekenstein & Milgrom 1984). For flattened systems like LTGs, the predicted
holds exactly for circular orbits (Milgrom 1994), so the radial acceleration relation should have zero intrinsic scatter. In MG theories, the above relation is valid only for spherically symmetric systems (Bekenstein & Milgrom 1984). For flattened systems like LTGs, the predicted  can show significant differences with respect to the algebraic relation (Brada & Milgrom 1995), potentially causing some small intrinsic scatter in the radial acceleration relation. The current data cannot distinguish between tiny or null intrinsic scatter.
can show significant differences with respect to the algebraic relation (Brada & Milgrom 1995), potentially causing some small intrinsic scatter in the radial acceleration relation. The current data cannot distinguish between tiny or null intrinsic scatter.
8.3.2. New Physics in the Dark Sector?
Scenario II includes theories like dark fluids (Zhao & Li 2010; Khoury 2015) and dipolar DM particles subjected to gravitational polarization (Blanchet & Le Tiec 2008, 2009). By construction, these theories reconcile the successes of ΛCDM on cosmological scales with those of MOND on galaxy scales, so they can explain the radial acceleration relation for LTGs and ETGs. The situation is more complex for dSphs because they are not isolated, and the internal gravitational field can be comparable to the gravitational field from the host galaxy ( ). In pure MOND theories (scenario I), this leads to the EFE: the strong equivalence principle is violated, and the internal dynamics of a system can be affected by an external field (Bekenstein & Milgrom 1984). This is not necessarily the case in hybrid theories (scenario II), so dSphs may help distinguish between fundamental dynamics (I) or new dark-sector physics (II).
). In pure MOND theories (scenario I), this leads to the EFE: the strong equivalence principle is violated, and the internal dynamics of a system can be affected by an external field (Bekenstein & Milgrom 1984). This is not necessarily the case in hybrid theories (scenario II), so dSphs may help distinguish between fundamental dynamics (I) or new dark-sector physics (II).
Inspired by the EFE, we plot the radial acceleration relation replacing  with
with  (Figure 14). For LTGs, we assume
(Figure 14). For LTGs, we assume  as these are relatively isolated systems. For dSphs, we estimate
as these are relatively isolated systems. For dSphs, we estimate  as
as

where  has the same meaning as in Section 6 but
has the same meaning as in Section 6 but  is now the baryonic mass of the host. Strikingly, ultrafaint dSphs now lie on the same relation as more luminous galaxies. Note that
is now the baryonic mass of the host. Strikingly, ultrafaint dSphs now lie on the same relation as more luminous galaxies. Note that  depends on the distance from the host and can vary by ∼2 dex from galaxy to galaxy. It is surprising that this variable factor shifts dSphs roughly on top of the relation for LTGs.
depends on the distance from the host and can vary by ∼2 dex from galaxy to galaxy. It is surprising that this variable factor shifts dSphs roughly on top of the relation for LTGs.
Figure 14. The radial acceleration relation replacing  with
with  , where
, where  is the baryonic gravitational field from the host galaxy (either M31 or MW). dSphs are color-coded by the ratio
is the baryonic gravitational field from the host galaxy (either M31 or MW). dSphs are color-coded by the ratio  , which quantifies the entity of the horizontal shift. The other symbols are the same as in Figure 10.
, which quantifies the entity of the horizontal shift. The other symbols are the same as in Figure 10.
Download figure:
Standard image High-resolution imageWe stress, however, that this is not a standard MOND implementation of the EFE. In the quasi-linear formulation of MOND (Milgrom 2010), the EFE can be approximated by Equation (60) of Famaey & McGaugh (2012):

where ν is the interpolation function (equivalent to the shape of the radial acceleration relation). Basically, Figure 14 neglects the negative term in Equation (24), driving nonlinearity in  . This term is important because it ensures the required Newtonian limit:
. This term is important because it ensures the required Newtonian limit:  for
for  . Neglecting this term, we would have
. Neglecting this term, we would have  when either
when either  or
or  , leading to some strange results. For example, the internal dynamics of globular clusters would depend on their location within the MW. The location of ultrafaint dSphs in Figure 14 may be a coincidence or perhaps hint at some deeper physical meaning.
, leading to some strange results. For example, the internal dynamics of globular clusters would depend on their location within the MW. The location of ultrafaint dSphs in Figure 14 may be a coincidence or perhaps hint at some deeper physical meaning.
9. Summary and Conclusions
We study local scaling relations between baryons and dynamics in galaxies. Our sample includes 240 galaxies with spatially resolved kinematic data, spanning ∼9 dex in baryonic mass and covering all morphological types. We consider (1) 153 LTGs (spirals and irregulars) from the SPARC database, (2) 25 ETGs (ellipticals and lenticulars) with stellar and H i kinematics from Atlas or X-ray observations from Chandra and XMM, and (3) 62 dSphs in the Local Group with individual-star spectroscopy. Our results can be summarized as follows.
or X-ray observations from Chandra and XMM, and (3) 62 dSphs in the Local Group with individual-star spectroscopy. Our results can be summarized as follows.
- 1.For LTGs, the observed acceleration (from the rotation curve) correlates with the baryonic gravitational field (from the distributions of gas and stars) over ∼4 dex. This relation combines ∼2700 data points at different radii in different galaxies. The outer parts of high-mass HSB galaxies smoothly overlap with the inner parts of low-mass LSB ones.
- 2.The observed scatter is very small (
 dex) and is largely driven by observational uncertainties: the radial acceleration relation has little (if any) intrinsic scatter. The tiny residuals show no correlation with either local or global galaxy properties. There is no hint of a second parameter.
dex) and is largely driven by observational uncertainties: the radial acceleration relation has little (if any) intrinsic scatter. The tiny residuals show no correlation with either local or global galaxy properties. There is no hint of a second parameter. - 3.The radial acceleration relation holds for any reasonable choice of
 . The high-end slope is always consistent with 1, suggesting that HSB galaxies are baryon dominated in their inner parts.
. The high-end slope is always consistent with 1, suggesting that HSB galaxies are baryon dominated in their inner parts. - 4.The stellar surface density correlates with
 less tightly than with
less tightly than with  or g⋆. The fundamental relation involves the baryonic gravitational field via Poisson's equation, considering the entire surface density distribution, not merely the local surface density at R.
or g⋆. The fundamental relation involves the baryonic gravitational field via Poisson's equation, considering the entire surface density distribution, not merely the local surface density at R. - 5.ETGs follow the same radial acceleration relation as LTGs. We predict the full rotation curves of rotating ETGs using the radial acceleration relation of LTGs and the observed [3.6] luminosity profiles.
- 6.The most luminous dSphs overlap with LTGs and ETGs on the radial acceleration relation, whereas ultrafaint dSphs seem to extend the relation ∼2 dex lower in
 . If the data are trimmed with basic quality criteria, ultrafaint dSphs may possibly trace a low-acceleration flattening in the relation. If confirmed, this would explain the constant value of the total mass found by Strigari et al. (2008).
. If the data are trimmed with basic quality criteria, ultrafaint dSphs may possibly trace a low-acceleration flattening in the relation. If confirmed, this would explain the constant value of the total mass found by Strigari et al. (2008).
The radial acceleration relation describes the local link between baryons and dynamics in galaxies, encompassing and generalizing several well-known galaxy scaling laws. This is tantamount to a natural law, a sort of Kepler law for galactic systems. A tight coupling between baryons and DM is difficult to understand within the standard ΛCDM cosmology. Our results may point to the need for a revision of the current DM paradigm.
F.L. thanks G. Battaglia, F. Fraternali, G. Pezzulli, R. Sancisi, and M. Verheijen for many inspiring discussions over the years. Support for this work was provided by NASA through Hubble Fellowship grant #HST-HF2-51379.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. This publication was made possible through the support of a grant from the John Templeton Foundation. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the John Templeton Foundation.
Appendix A: Sample of Early-type Galaxies
Table 3 gives the properties of 25 ETGs. The horizontal line distinguishes between rotating ETGs from Atlas and X-ray ETGs with Chandra data.
and X-ray ETGs with Chandra data.
- Column (1) gives the galaxy name.
- Column (2) gives the Hubble type using the RC3 morphological classification (de Vaucouleurs et al. 1991).
- Column (3) gives the adopted distance.
- Column (5) gives the total luminosity at 3.6 μm.
- Column (6) gives the effective radius encompassing one-half of the total [3.6] luminosity.
- Column (7) gives the effective surface brightness.
- Column (8) gives the exponential disk scale length.
- Column (9) gives the central disk surface brightness.
Column (11) gives the references for the kinematic or X-ray data: (1) Serra et al. (2016), (2) Weijmans et al. (2008), (3) Humphrey et al. (2011), (4) Humphrey et al. (2009), (5) Humphrey et al. (2006), (6) Humphrey et al. (2012), (8) Humphrey et al. (2008).
Table 3. Sample of Early-type Galaxies
| Galaxy | T | D | Met. |
![${L}_{[3.6]}$](https://content.cld.iop.org/journals/0004-637X/836/2/152/revision1/apjaa5b2cieqn132.gif)
|

|

|

|

|
References |
|---|---|---|---|---|---|---|---|---|---|
| (Mpc) | ( ) ) |
(kpc) | (L⊙ pc−2) | (kpc) | (L⊙ pc−2) | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
| Rotating ETGs | |||||||||
| NGC 2685 | S0 | 16.1 ± 4.8 | 1 | 30.0 ± 0.3 | 1.92 | 1284.8 | 3.19 | 413.8 | (1) |
| NGC 2824 | S0 | 39.6 ± 9.9 | 1 | 39.6 ± 0.7 | 1.09 | 5209.9 | 5.00 | 84.1 | (1) |
| NGC 2859 | S0 | 26.2 ± 6.5 | 1 | 89.1 ± 0.8 | 1.59 | 5608.3 | 2.51 | 603.7 | (1) |
| NGC 2974 | E4 | 22.1 ± 2.8 | 2 | 116.9 ± 1.1 | 3.02 | 1516.5 | 3.44 | 1530.5 | (2) |
| NGC 3522 | E | 25.2 ± 3.2 | 2 | 13.2 ± 0.2 | 1.42 | 1039.5 | 2.47 | 254.0 | (1) |
| NGC 3626 | S0 | 22.9 ± 2.5 | 2 | 74.6 ± 0.7 | 2.43 | 2017.6 | 2.52 | 1891.6 | (1) |
| NGC 3838 | S0 | 23.1 ± 5.8 | 1 | 22.5 ± 0.2 | 1.03 | 3410.6 | 1.99 | 417.7 | (1) |
| NGC 3941 | S0 | 12.4 ± 1.6 | 2 | 43.7 ± 0.4 | 1.42 | 3474.0 | 1.30 | 4373.5 | (1) |
| NGC 3945 | S0 | 22.8 ± 5.7 | 1 | 126.3 ± 1.2 | 2.50 | 3197.6 | 7.22 | 209.3 | (1) |
| NGC 3998 | S0 | 14.2 ± 1.8 | 2 | 56.2 ± 0.5 | 1.01 | 8807.0 | 1.46 | 2998.0 | (1) |
| NGC 4203 | S0 | 15.3 ± 2.0 | 2 | 61.7 ± 0.6 | 1.85 | 2093.3 | 1.85 | 2132.2 | (1) |
| NGC 4262 | S0 | 16.6 ± 1.8 | 2 | 29.0 ± 0.3 | 0.69 | 9480.5 | 2.90 | 43.74 | (1) |
| NGC 4278 | E1-2 | 15.4 ± 2.0 | 2 | 82.6 ± 0.1 | 1.63 | 4884.6 | 2.57 | 992.7 | (1) |
| NGC 5582 | E | 28.1 ± 3.6 | 2 | 55.2 ± 0.5 | 3.07 | 930.7 | 3.86 | 686.8 | (1) |
| NGC 6798 | S0 | 37.3 ± 9.3 | 1 | 69.1 ± 0.6 | 3.30 | 992.7 | 3.29 | 974.6 | (1) |
| UGC 6176 | S0 | 39.3 ± 9.8 | 1 | 29.0 ± 0.5 | 1.18 | 3317.6 | 1.80 | 1049.1 | (1) |
| X-ray ETGs | |||||||||
| NGC 720 | E5 | 26.1 ± 0.0 | 2 | 234.5 ± 0.1 | 4.5 | 1857.1 | ... | ... | (3) |
| NGC 1332 | S0 | 24.5 ± 0.0 | 2 | 211.0 ± 0.1 | 2.7 | 4579.6 | 3.17 | 6498.7 | (4) |
| NGC 1407 | E0 | 28.2 ± 0.0 | 2 | 540.1 ± 0.1 | 7.8 | 1408.7 | ... | ... | (5) |
| NGC 1521 | E3 | 69.5 ± 0.0 | 2 | 532.6 ± 0.1 | 10.1 | 825.7 | ... | ... | (6) |
| NGC 4125 | E6 | 24.0 ± 0.0 | 2 | 303.1 ± 0.1 | 5.7 | 1448.2 | ... | ... | (5) |
| NGC 4261 | E2 | 32.4 ± 0.0 | 2 | 345.4 ± 0.1 | 4.5 | 2635.3 | ... | ... | (4) |
| NGC 4472 | E2 | 16.1 ± 0.0 | 2 | 447.6 ± 0.1 | 5.2 | 2587.2 | ... | ... | (4) |
| NGC 4649 | E2 | 17.4 ± 0.0 | 2 | 345.7 ± 0.1 | 3.6 | 4293.7 | ... | ... | (7) |
| NGC 6482 | E: | 57.9 ± 0.0 | 1 | 427.9 ± 3.9 | 4.4 | 3410.6 | ... | ... | (5) |
Note. Column 4 gives the distance method: (1) Virgocentric infall model (as in Paper I), (2) surface brightness fluctuations (from Tully et al. 2013). Column 10 gives references for the kinematic or X-ray data: (1) Serra et al. (2016), (2) Weijmans et al. (2008), (3) Humphrey et al. (2011), (4) Humphrey et al. (2009), (5) Humphrey et al. (2006), (6) Humphrey et al. (2012), (7) Humphrey et al. (2008).
Download table as: ASCIITypeset image
Appendix B: Catalog of Dwarf Spheroidals
Table 4 gives the properties of 62 dSphs in the Local Group. The horizontal line distinguishes between MW and M31 satellites (whichever is closer). Objects like Tucana and Cetus are relatively isolated, but they are considered as "satellites" for simplicity. Galaxies are listed in alphabetic order, but we start with the "classic" satellites and follow with the ultrafaint ones. Bolded galaxies represent our high-quality sample (see Section 6).
- Column (1) gives the galaxy name.
- Column (2) gives the heliocentric distance derived from the tip of the red giant branch method or variable stars.
- Column (3) gives the distance to the host galaxy.
- Column (4) gives the total luminosity in the V band, adopting a solar absolute magnitude of 4.83.
- Column (5) gives the deprojected 3D half-light radii (
 ; see Wolf et al. 2010).
; see Wolf et al. 2010). - Column (6) gives the observed ellipticity.
- Column (7) gives the observed mean velocity dispersion.
- Column (8) gives the number of stars used to estimate the mean velocity dispersion
 .
. - Column (9) gives the baryonic acceleration (Equation (6)).
- Column (10) gives the observed acceleration (Equation (7)).
Column (11) gives references for distances, structural parameters, and velocity dispersions, respectively. They are coded as follows: 1. Pietrzyński et al. (2009), 2. Irwin & Hatzidimitriou (1995), 3. Walker et al. (2009c), 4. Bonanos et al. (2004), 5. Martin et al. (2008), 6. Walker et al. (2007), 7. Bellazzini et al. (2004), 8. Mateo et al. (2008), 9. Bellazzini et al. (2005), 10. Koch et al. (2007), 11. Pietrzyński et al. (2008), 12. Lee et al. (2009), 13. Carrera et al. (2002), 14. Walker et al. (2009b), 15. Dall'Ora et al. (2006), 16. Okamoto et al. (2012), 17. Koposov et al. (2011), 18. Walsh et al. (2008), 19. Koch et al. (2009), 20. Simon & Geha (2007), 21. Greco et al. (2008), 22. Belokurov et al. (2007), 23. Muñoz et al. (2010), 24. Sand et al. (2009), 25. Adén et al. (2009), 26. Koposov et al. (2015a), 27. Koposov et al. (2015b), 28. Martin et al. (2015), 29. Kirby et al. (2015), 30. Moretti et al. (2009), 31. de Jong et al. (2010), 32. Walker et al. (2009a), 33. Irwin et al. (2007), 34. de Jong et al. (2008), 35. Sand et al. (2012), 36. Simon et al. (2011), 37. Belokurov et al. (2009), 38. Kirby et al. (2013), 39. Bernard et al. (2009), 40. McConnachie (2012), 41. Fraternali et al. (2009), 42. Okamoto et al. (2008), 43. Zucker et al. (2006), 44. Willman et al. (2006), 45. Willman et al. (2011), 46. Conn et al. (2012), 47. Geha et al. (2010), 48. McConnachie et al. (2005), 49. Geha et al. (2006), 50. McConnachie & Irwin (2006), 51. Tollerud et al. (2012), 52. Ho et al. (2012), 53. Chapman et al. (2007), 54. Collins et al. (2013), 55. Brasseur et al. (2011), 56. Kalirai et al. (2009), 57. Collins et al. (2015), 58. McConnachie et al. (2008), 59. Martin et al. (2009), 60. Richardson et al. (2011), 61. Slater et al. (2015), 62. Tollerud et al. (2013), 63. Salomon et al. (2015), 64. Martin et al. (2013b), 65. Martin et al. (2014), 66. Kirby et al. (2014), 67. Martin et al. (2013a), 68. Cook et al. (1999).
Table 4. Catalog of Dwarf Spheroidals in the Local Group
| Galaxy | D⊙ |

|

|

|
 |

|
N⋆ |

|

|
References |
|---|---|---|---|---|---|---|---|---|---|---|
| (kpc) | (kpc) | (L⊙) | (pc) | (km s−1) | (m s−2) | (m s−2) | ||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) |
| Carina | 105+6−6 | 107 | 5.57 ± 0.20 | 273 ± 45 | 0.33 | 6.60+1.20−1.20 | 774 | −12.15+0.27−0.27 | −10.81+0.18−0.18 | 1, 2, 3 |
| Draco | 76+5−5 | 76 | 5.45 ± 0.08 | 244 ± 9 | 0.31 | 9.10+1.20−1.20 | 413 | −12.18+0.14−0.14 | −10.48+0.12−0.12 | 4, 5, 6 |
| Fornax | 147+12−12 | 149 | 7.31 ± 0.12 | 792 ± 58 | 0.30 | 11.70+0.90−0.90 | 2483 | −11.35+0.17−0.17 | −10.77+0.08−0.08 | 1, 2, 3 |
| Leo I | 254+19−16 | 258 | 6.74 ± 0.12 | 298 ± 29 | 0.21 | 9.20+0.40−0.40 | 328 | −11.06+0.18−0.18 | −10.56+0.06−0.06 | 7, 2, 8 |
| Leo II | 233+15−15 | 236 | 5.87 ± 0.12 | 219 ± 52 | 0.13 | 6.60+0.70−0.70 | 171 | −11.67+0.26−0.26 | −10.71+0.14−0.14 | 9, 2, 10 |
| Sculptor | 86+6−6 | 86 | 6.36 ± 0.20 | 311 ± 46 | 0.32 | 9.20+1.10−1.10 | 1365 | −11.48+0.26−0.26 | −10.58+0.13−0.13 | 11, 2, 3 |
| Sextans | 86+4−4 | 89 | 5.64 ± 0.20 | 748 ± 66 | 0.35 | 7.90+1.30−1.30 | 441 | −12.96+0.24−0.24 | −11.09+0.15−0.15 | 12, 2, 3 |
| Ursa Minor | 76+4−4 | 78 | 5.45 ± 0.20 | 398 ± 44 | 0.54 | 9.50+1.20−1.20 | 212 | −12.60+0.25−0.25 | −10.66+0.12−0.12 | 13, 2, 14 |
| Bootes I | 66+3−3 | 64 | 4.29 ± 0.08 | 283 ± 7 | 0.22 | 4.60+0.80−0.60 | 65 | −13.47+0.14−0.14 | −11.14+0.15−0.12 | 15, 16, 17 |
| Bootes II | 42+2−2 | 40 | 3.02 ± 0.36 | 61 ± 24 | 0.21 | 10.50+7.40−7.40 | 5 | −13.40+0.50−0.53 | −9.75+0.63−0.64 | 18, 5, 19 |
| Canes Venatici I | 216+8−8 | 216 | 5.08 ± 0.08 | 647 ± 27 | 0.30 | 7.60+0.40−0.40 | 214 | −13.40+0.14−0.14 | −11.06+0.05−0.05 | 16, 16, 20 |
| Canes Venatici II | 160+5−4 | 161 | 4.10 ± 0.08 | 101 ± 5 | 0.23 | 4.60+1.00−1.00 | 25 | −12.76+0.14−0.14 | −10.69+0.19−0.19 | 21, 16, 20 |
| Coma Berenices | 44+4−4 | 45 | 3.46 ± 0.24 | 79 ± 6 | 0.36 | 4.60+0.80−0.80 | 59 | −13.19+0.27−0.27 | −10.59+0.16−0.16 | 22, 23, 20 |
| Hercules | 133+6−6 | 128 | 4.42 ± 0.16 | 175 ± 22 | 0.67 | 3.72+0.91−0.91 | 18 | −12.92+0.22−0.22 | −11.11+0.22−0.22 | 24, 24, 25 |
| Horologium I | 79+0−0 | 79 | 3.29 ± 0.04 | 40 ± 5 | 0.28 | 4.90+2.80−0.90 | 5 | −12.78+0.17−0.15 | −10.24+0.50−0.17 | 26, 26, 27 |
| Hydra II | 134+10−10 | 131 | 3.87 ± 0.12 | 88 ± 17 | 0.01 | 4.50+0.00−4.50 | 13 | −12.88+0.28−0.19 | −10.65+0.12−0.87 | 28, 28, 29 |
| Leo IV | 154+5−5 | 155 | 3.91 ± 0.08 | 149 ± 47 | 0.04 | 3.30+1.70−1.70 | 18 | −13.30+0.30−0.30 | −11.15+0.47−0.47 | 30, 16, 20 |
| Leo V | 175+9−9 | 176 | 4.02 ± 0.16 | 125 ± 47 | 0.50 | 2.40+2.40−1.40 | 5 | −13.03+0.38−0.38 | −11.35+0.88−0.53 | 31, 31, 32 |
| Leo T | 417+19−19 | 422 | 5.57 ± 0.07 | 160 ± 10 | 0.10 | 7.50+1.60−1.60 | 19 | −11.70+0.14−0.14 | −10.47+0.19−0.19 | 33, 34, 20 |
| Pisces II | 196+15−15 | 195 | 3.64 ± 0.16 | 70 ± 18 | 0.33 | 5.40+3.60−2.40 | 7 | −12.91+0.29−0.29 | −10.39+0.59−0.40 | 35, 35, 29 |
| Reticulum II | 30+15−15 | 31 | 3.01 ± 0.04 | 42 ± 2 | 0.59 | 3.22+1.64−0.49 | 18 | −13.10+0.13−0.12 | −10.62+0.49−0.25 | 26, 26, 27 |
| Segue I | 23+2−2 | 28 | 2.54 ± 0.32 | 28 ± 9 | 0.48 | 3.70+1.40−1.10 | 71 | −13.22+0.45−0.42 | −10.33+0.36−0.29 | 22, 5, 36 |
| Segue II | 35+2−2 | 41 | 2.94 ± 0.12 | 43 ± 6 | 0.15 | 2.60+0.00−2.60 | 25 | −13.17+0.20−0.20 | −10.81+0.06−0.87 | 37, 37, 38 |
| Tucana | 887+49−49 | 883 | 5.75 ± 0.08 | 273 ± 52 | 0.48 | 15.80+4.10−3.10 | 17 | −11.98+0.21−0.21 | −10.05+0.24−0.19 | 39, 40, 41 |
| Ursa Major I | 97+4−4 | 101 | 4.14 ± 0.12 | 190 ± 46 | 0.80 | 7.60+1.00−1.00 | 39 | −13.27+0.27−0.26 | −10.53+0.16−0.15 | 42, 5, 20 |
| Ursa Major II | 32+4−4 | 38 | 3.54 ± 0.20 | 123 ± 6 | 0.50 | 6.70+1.40−1.40 | 20 | −13.49+0.23−0.23 | −10.45+0.19−0.19 | 43, 23, 20 |
| Willman I | 38+7−7 | 43 | 3.01 ± 0.28 | 25 ± 5 | 0.47 | 4.00+0.80−0.80 | 40 | −12.63+0.33−0.36 | −10.20+0.20−0.22 | 44, 5, 45 |
| NGC 147 | 712+19−21 | 118 | 7.84 ± 0.04 | 672 ± 23 | 0.41 | 16.00+1.00−1.00 | 520 | −10.67+0.12−0.12 | −10.43+0.06−0.06 | 46, 40, 47 |
| NGC 185 | 620+18−19 | 181 | 7.84 ± 0.04 | 565 ± 7 | 0.15 | 24.00+1.00−1.00 | 442 | −10.52+0.12−0.12 | −10.00+0.04−0.04 | 46, 40, 47 |
| NGC 205 | 824+27−27 | 46 | 8.52 ± 0.04 | 594 ± 107 | 0.43 | 35.00+5.00−5.00 | 725 | −9.88+0.19−0.19 | −9.70+0.15−0.15 | 48, 40, 49 |
| And I | 727+17−18 | 68 | 6.58 ± 0.04 | 772 ± 85 | 0.22 | 10.20+1.90−1.90 | 51 | −12.06+0.15−0.15 | −10.88+0.17−0.17 | 46, 50, 51 |
| And II | 630+15−15 | 195 | 6.85 ± 0.08 | 1355 ± 142 | 0.20 | 9.25+1.10−1.10 | 531 | −12.27+0.16−0.16 | −11.21+0.11−0.11 | 46, 50, 52 |
| And III | 723+24−18 | 86 | 5.89 ± 0.12 | 427 ± 43 | 0.52 | 4.70+1.80−1.80 | 43 | −12.23+0.18−0.18 | −11.30+0.34−0.34 | 46, 50, 53 |
| And V | 742+22−21 | 113 | 5.55 ± 0.08 | 365 ± 57 | 0.18 | 10.50+1.10−1.10 | 85 | −12.43+0.19−0.19 | −10.53+0.11−0.11 | 46, 50, 51 |
| And VI | 783+25−25 | 268 | 6.44 ± 0.08 | 537 ± 54 | 0.41 | 12.40+1.50−1.30 | 43 | −11.88+0.16−0.16 | −10.55+0.11−0.10 | 48, 50, 54 |
| And VII | 762+35−35 | 217 | 6.98 ± 0.12 | 965 ± 52 | 0.13 | 13.00+1.00−1.00 | 136 | −11.85+0.17−0.17 | −10.77+0.07−0.07 | 48, 50, 51 |
| And IX | 600+23−91 | 182 | 4.97 ± 0.44 | 582 ± 23 | 0.12 | 10.90+2.00−2.00 | 32 | −13.42+0.45−0.45 | −10.70+0.17−0.16 | 46, 40, 51 |
| And X | 827+25−23 | 92 | 5.13 ± 0.40 | 312 ± 41 | 0.44 | 3.90+1.20−1.20 | 22 | −12.72+0.43−0.43 | −11.32+0.27−0.27 | 46, 55, 56 |
| And XI | 763+106−29 | 102 | 4.70 ± 0.48 | 210 ± 9 | 0.24 | 7.60+4.00−2.80 | 5 | −12.80+0.49−0.49 | −10.57+0.46−0.33 | 46, 40, 54 |
| And XII | 928+136−40 | 181 | 4.55 ± 0.48 | 432 ± 72 | 0.39 | 4.00+0.00−4.00 | 8 | −13.58+0.51−0.51 | −11.44+0.07−0.87 | 46, 40, 54 |
| And XIII | 760+156−126 | 115 | 4.45 ± 0.48 | 230 ± 24 | 0.54 | 5.80+2.00−2.00 | 12 | −13.12+0.50−0.50 | −10.85+0.31−0.32 | 46, 40, 51 |
| And XIV | 793+179−23 | 161 | 5.37 ± 0.20 | 434 ± 212 | 0.31 | 5.30+1.00−1.00 | 48 | −12.76+0.48−0.48 | −11.20+0.27−0.29 | 46, 40, 51 |
| And XV | 626+35−79 | 174 | 5.69 ± 0.12 | 294 ± 12 | 0.24 | 4.00+1.40−1.40 | 29 | −12.11+0.17−0.17 | −11.28+0.31−0.31 | 46, 40, 51 |
| And XVI | 476+29−44 | 319 | 5.53 ± 0.12 | 164 ± 9 | 0.29 | 5.80+1.10−0.90 | 20 | −11.76+0.17−0.17 | −10.70+0.17−0.14 | 46, 40, 57 |
| And XVII | 727+25−39 | 67 | 5.34 ± 0.16 | 299 ± 31 | 0.27 | 6.50+3.30−2.70 | 16 | −12.47+0.21−0.21 | −10.86+0.44−0.36 | 46, 55, 57 |
| And XIX | 821+148−32 | 116 | 5.52 ± 0.24 | 1799 ± 52 | 0.17 | 4.70+1.60−1.40 | 26 | −13.84+0.26−0.26 | −11.92+0.30−0.27 | 46, 58, 54 |
| And XX | 741+52−42 | 128 | 4.39 ± 0.32 | 127 ± 36 | 0.30 | 7.10+3.90−2.50 | 4 | −12.67+0.45−0.39 | −10.42+0.50−0.32 | 46, 58, 54 |
| And XXI | 827+25−23 | 135 | 5.85 ± 0.24 | 1004 ± 123 | 0.20 | 4.50+1.20−1.00 | 32 | −13.01+0.28−0.28 | −11.71+0.24−0.20 | 46, 59, 54 |
| And XXII | 920+139−32 | 275 | 4.66 ± 0.32 | 223 ± 60 | 0.56 | 2.80+1.90−1.40 | 10 | −12.89+0.41−0.41 | −11.47+0.60−0.45 | 46, 59, 54 |
| And XXIII | 748+21−31 | 127 | 6.00 ± 0.20 | 1034 ± 97 | 0.40 | 7.10+1.00−1.00 | 42 | −12.88+0.24−0.24 | −11.32+0.13−0.13 | 46, 60, 54 |
| And XXIV | 898+42−28 | 169 | 5.32 ± 0.20 | 633 ± 52 | 0.25 | 7.30+0.00−7.30 | 12 | −13.14+0.24−0.24 | −11.09+0.04−0.87 | 46, 60, 54 |
| And XXV | 736+69−23 | 90 | 5.75 ± 0.20 | 742 ± 70 | 0.25 | 3.00+1.20−1.10 | 26 | −12.85+0.24−0.24 | −11.93+0.35−0.32 | 46, 60, 54 |
| And XXVI | 754+164−218 | 103 | 4.77 ± 0.20 | 253 ± 30 | 0.25 | 8.60+2.80−2.20 | 6 | −12.90+0.25−0.25 | −10.55+0.31−0.25 | 46, 60, 54 |
| And XXVII | 1214+474−42 | 482 | 5.45 ± 0.20 | 679 ± 253 | 0.40 | 14.80+4.30−3.10 | 8 | −13.07+0.40−0.40 | −10.50+0.30−0.30 | 46, 60, 54 |
| And XXVIII | 811+48−48 | 384 | 5.39 ± 0.16 | 285 ± 12 | 0.43 | 4.90+1.60−1.60 | 18 | −12.37+0.20−0.20 | −11.09+0.29−0.29 | 61, 61, 62 |
| And XXIX | 829+42−42 | 198 | 5.33 ± 0.12 | 377 ± 30 | 0.29 | 5.70+1.20−1.20 | 24 | −12.68+0.18−0.18 | −11.08+0.19−0.19 | 61, 61, 62 |
| And XXX | 681+78−32 | 145 | 5.20 ± 0.00 | 306 ± 45 | 0.38 | 11.80+7.70−4.70 | 8 | −12.63+0.17−0.17 | −10.35+0.57−0.36 | 46, 63, 54 |
| And XXXI | 756+28−44 | 262 | 6.61 ± 0.28 | 1231 ± 132 | 0.43 | 10.30+0.90−0.90 | 126 | −12.43+0.31−0.32 | −11.08+0.09−0.09 | 64, 64, 65 |
| And XXXII | 772+56−61 | 140 | 6.83 ± 0.28 | 1376 ± 340 | 0.50 | 8.40+0.60−0.60 | 212 | −12.31+0.37−0.36 | −11.30+0.13−0.12 | 64, 64, 65 |
| Cetus | 779+43−43 | 688 | 6.44 ± 0.08 | 791 ± 75 | 0.33 | 8.30+1.00−1.00 | 11 | −12.22+0.16−0.16 | −11.07+0.11−0.11 | 39, 50, 66 |
| Perseus I | 785+65−65 | 351 | 6.04 ± 0.28 | 391 ± 143 | 0.43 | 4.20+3.60−4.20 | 12 | −12.00+0.43−0.45 | −11.36+0.76−0.88 | 67, 67, 65 |
| Pisces I | 769+24−24 | 268 | 5.98 ± 0.04 | 560 ± 53 | 0.20 | 7.90+5.30−2.90 | 4 | −12.37+0.14−0.14 | −10.97+0.58−0.32 | 48, 40, 68 |
Notes. The total luminosity of Leo T includes one-half of the gas mass, giving the actual total baryonic mass for 
 . Galaxies in bold are included in our high-quality sample (see Section 6).
. Galaxies in bold are included in our high-quality sample (see Section 6).
Footnotes
- 7
In this paper, the general term "acceleration" will always refer to the centripetal radial acceleration.
- 8
The effective radius
 is defined as the geometrical radius
is defined as the geometrical radius  that encompasses half of the total luminosity. The effective surface density
that encompasses half of the total luminosity. The effective surface density  is then simply
is then simply  .
.














































