Abstract
Electron acceleration in solar flares is well known to be efficient at generating energetic particles that produce the observed bremsstrahlung X-ray spectra. One mechanism proposed to explain the observations is electron acceleration within contracting magnetic islands formed by magnetic reconnection in the flare current sheet. In a previous study, a numerical magnetohydrodynamic simulation of an eruptive solar flare was analyzed to estimate the associated electron acceleration due to island contraction. That analysis used a simple analytical model for the island structure and assumed conservation of the adiabatic invariants of particle motion. In this paper, we perform the first-ever rigorous integration of the guiding-center orbits of electrons in a modeled flare. An initially isotropic distribution of particles is seeded in a contracting island from the simulated eruption, and the subsequent evolution of these particles is followed using guiding-center theory. We find that the distribution function becomes increasingly anisotropic over time as the electrons' energy increases by up to a factor of five, in general agreement with the previous study. In addition, we show that the energized particles are concentrated on the Sunward side of the island, adjacent to the reconnection X-point in the flare current sheet. Furthermore, our analysis demonstrates that the electron energy gain is dominated by betatron acceleration in the compressed, strengthened magnetic field of the contracting island. Fermi acceleration by the shortened field lines of the island also contributes to the energy gain, but it is less effective than the betatron process.
Export citation and abstract BibTeX RIS
1. Introduction
Electron acceleration during solar flare events has received great attention for several decades, because a significant portion of energy released during a flare is transformed into hard X- or γ-radiation as accelerated electrons interact with a dense background (Hudson & Ryan 1995; Kontar et al. 2011; Vilmer et al. 2011; White et al. 2011). As this type of radiation is a signature of bremsstrahlung, these observations are a clear indication of a highly energetic electron population present in the system. Radiation spectra registered by various spacecraft allow us to infer the electrons' distribution function. A well-known power law, 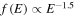 , is commonly found throughout many data sets (Holman et al. 2003), implying that an efficient process drives electron acceleration during solar flare events.
, is commonly found throughout many data sets (Holman et al. 2003), implying that an efficient process drives electron acceleration during solar flare events.
Although the existence of such a process is undoubted, its nature is poorly understood. The primary difficulty is the lack of in situ observations of the acceleration regions. The electron population may evolve and change properties before it emits bremsstrahlung, therefore, affecting the observed radiation spectrum (Agueda et al. 2009; Holman et al. 2011). Researchers are faced with the problem of distinguishing which observed features are caused by the acceleration process rather than acquired later. One frequently observed feature that needs to be explained by any acceleration mechanism is the high time variability of observed radiation (Holman et al. 2011). This is likely an indication of the mechanism being intermittent in nature.
Several candidates for the underlying acceleration mechanism have been proposed. Drake et al. (2006a) proposed a mechanism that is based on the dynamics of plasmoids formed in flare current sheets and the response of the electrons moving within them. Plasmoids, often referred to as magnetic islands, are flux ropes, formed between pairs of reconnection regions (X-points, X-lines, or nulls), that subsequently move, contract, and possibly coalesce within the sheet. On the kinetic scale, plasmoid electrons experience Fermi acceleration due to the contraction of the field lines on which they reside, increasing their energy of motion parallel to the magnetic field. In regions where the local magnetic-field strength rises with time, the energy of electron motion perpendicular to the field increases due to betatron acceleration.
The island-contraction mechanism for electron acceleration has been extensively studied in recent years. The present paper is an extension of the study by Guidoni et al. (2016), which utilized the physical properties of an MHD simulation of a coronal mass ejection/eruptive flare to estimate electron energy gains in individual islands in the flare current sheet. In this paper, we track the particles by performing the first-ever rigorous integration of the guiding-center orbits of electrons in a modeled flare.
2. Physics
2.1. Dynamics of Electrons
As described by Drake et al. (2006a, 2010), the mechanism underlying the electron acceleration can be understood in terms of conservation of the adiabatic invariants of particle motion (Northrop 1963) within an evolving plasmoid.
The first invariant is associated with the particle's gyration about magnetic-field lines. It is referred to as the magnetic moment of the particle, μ:
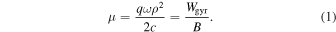
Here ω is the gyrofrequency, ρ is the particle's gyroradius, q is its electric charge, Wgyr is its kinetic energy of gyration, B is the magnitude of the magnetic field, and c is the speed of light. As the particle moves within the plasmoid, the value of the local magnetic field may increase or decrease. Conservation of the magnetic moment implies that the gyration energy Wgyr simultaneously increases or decreases, respectively. In a static magnetic field, the total particle energy W is preserved, so the energy of parallel motion 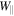 decreases or increases to compensate for the change in Wgyr. If
decreases or increases to compensate for the change in Wgyr. If 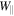 decreases, this leads to the phenomenon of magnetic mirroring. In a time-dependent magnetic field, on the other hand, an increase in the field strength leads to an increase in the gyration energy; however, the parallel energy does not decrease. The increase in total energy in this case is due to the associated induced electric field. This phenomenon is referred to as betatron acceleration.
decreases, this leads to the phenomenon of magnetic mirroring. In a time-dependent magnetic field, on the other hand, an increase in the field strength leads to an increase in the gyration energy; however, the parallel energy does not decrease. The increase in total energy in this case is due to the associated induced electric field. This phenomenon is referred to as betatron acceleration.
The second invariant is associated with the particle's motion along field lines in geometries that support closed orbits, either mirroring or transiting. It is referred to as the parallel action, J:
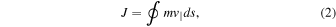
where the integral of the parallel momentum 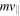 is taken along the field line coordinate s over one mirroring period or one loop of a transiting spiral, respectively. In the case of the magnetic configuration considered in the present paper, the plasmoid contracts after formation, thus reducing the length of the particle's path. Under this condition, conservation of the action invariant implies an increase in the velocity magnitude and kinetic energy of parallel motion,
is taken along the field line coordinate s over one mirroring period or one loop of a transiting spiral, respectively. In the case of the magnetic configuration considered in the present paper, the plasmoid contracts after formation, thus reducing the length of the particle's path. Under this condition, conservation of the action invariant implies an increase in the velocity magnitude and kinetic energy of parallel motion,  and
and 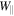 , respectively. As for the first invariant, this momentum and energy transfer to the particle occurs through the intermediary of the electric field and generalizes Fermi's mechanism (Fermi 1954) for accelerating particles via reflection off moving magnetic mirrors.
, respectively. As for the first invariant, this momentum and energy transfer to the particle occurs through the intermediary of the electric field and generalizes Fermi's mechanism (Fermi 1954) for accelerating particles via reflection off moving magnetic mirrors.
These simple considerations of conservation of adiabatic invariants within a plasmoid show that the magnetic-field evolution can strongly affect the motion of individual particles. If the local plasma conditions within a plasmoid experience a significant change during its evolution, the energies of the particles trapped within the plasmoid will also change significantly. The primary particle species affected by this mechanism is the electron species (Guidoni et al. 2016). For that reason they are the focus of this work.
In order to conserve the second invariant, the electrons need to close their orbits (mirroring or transiting) much more rapidly than the ambient magnetic field changes. This condition is usually met for energetic electrons, since their thermal speed is much larger than the bulk speed of the electron-ion plasma.
The effect of the acceleration per individual electron within a single contracting island is expected to be modest (Drake et al. 2006a). For example, Guidoni et al. (2016) found an increase in energy below a factor of five. This result is extended, and generally confirmed, by the analysis presented in this paper.
2.2. Dynamics of Plasmoids
During a solar flare, magnetic free energy is released via reconnection and energy is transferred from magnetic field to plasma. As mentioned in Section 2.1, the evolution of a single plasmoid does not produce a big impact on the electron population, and therefore cannot ultimately explain the observed energetic radiation.
The key idea is that reconnection occurs at many locations during a solar flare (Sheeley et al. 2004; Drake et al. 2006b; Fermo et al. 2010; Karpen et al. 2012), yielding a large number of plasmoids. Apart from simple contraction, these plasmoids can coalesce together as considered by Drake et al. (2013) and Zank et al. (2014). Interaction and merger of many plasmoids might eventually lead to a large energy gain by the electron population. In this work, however, we only consider the effect of acceleration in a single magnetic island.
3. Numerical Approach
3.1. MHD Simulation
The background plasma conditions have been simulated with the Adaptively Refined Magnetohydrodynamics (MHD) Solver (ARMS) code (DeVore 1991). A detailed description of this simulation can be found in Guidoni et al. (2016). For the sake of simplicity, a 2.5D setting is adopted, i.e., the system is assumed to have axial symmetry. Ideal MHD is assumed. The flare is triggered according to the principles discussed in Karpen et al. (2012) and earlier papers on the breakout mechanism for solar eruptions (e.g., Antiochos et al. 1999). The modeled current sheet, as expected, is populated by several X-points separated by plasmoids, which are usually referred to as magnetic islands under 2.5D conditions. Because the current sheet forms in the initially low-lying, sheared magnetic field that powers the eruptive flare, the magnetic field in the sheet has a strong component in the translationally invariant direction (out of the plane in Figure 1).
Figure 1. Extracted field line projections. Diamond shapes are the fluid elements obtained via the extraction procedure described in Section 3.3. The effectiveness and accuracy of the procedure are demonstrated with well-resolved features of the field lines at the parts stretched toward the X-point (toward the left axis).
Download figure:
Standard image High-resolution imageA number of islands were well resolved on the adaptive mesh. Their shape, evolution, and life cycle were carefully tracked. The simulation revealed the presence of one persistent X-point with smaller ones generated near it, some moving Sunward until reaching and merging with the flare arcade, others moving outward and merging with the erupting coronal mass ejection.
Those islands that were present in the system for a significantly long time and had clear features were chosen for investigation to test the acceleration mechanism of Drake et al. (2006a). Since ARMS does not include a particle-tracking capability, only theoretical estimates could be made. We found that individual electrons should gain up to a factor of five in energy (Guidoni et al. 2016). The simulated MHD data for Island 2 of Guidoni et al. (2016) was exported and used as input for the particle simulation described below.
3.2. Particle Simulation
The electron population's evolution has been simulated with the Adaptive Mesh Particle Simulator (AMPS) code developed at the University of Michigan and successfully used by Tenishev et al. (2008, 2010, 2013).
Rather than directly integrating Newton's equations of motions for the electrons in the electromagnetic field, 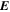 and
and 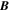 , which would be prohibitively expensive (see below), we elected to integrate the equations for guiding-center motion (Northrop 1963). In this model, the dominant motions are (1) the displacement of the guiding center parallel to the magnetic field with velocity
, which would be prohibitively expensive (see below), we elected to integrate the equations for guiding-center motion (Northrop 1963). In this model, the dominant motions are (1) the displacement of the guiding center parallel to the magnetic field with velocity 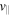 , (2) the
, (2) the 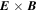 drift perpendicular to the magnetic field, with velocity
drift perpendicular to the magnetic field, with velocity 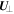 , and (3) the fast gyration also perpendicular to the magnetic field, with velocity
, and (3) the fast gyration also perpendicular to the magnetic field, with velocity 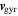 . The electron kinetic energy W is then given by
. The electron kinetic energy W is then given by
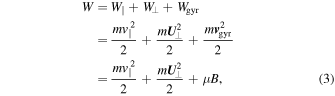
where m is the electron's mass and μ is its magnetic moment introduced in Equation (1). Additional terms, such as the gradient-B and curvature drifts, contribute small corrections to the perpendicular velocity and kinetic energy of the guiding center (see Northrop 1963, and the estimates below). This implies that the guiding centers perfectly follow the magnetic-field lines to first order, since the 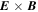 velocity is the cross-field advection rate of the field lines in the ideal-MHD simulation.
velocity is the cross-field advection rate of the field lines in the ideal-MHD simulation.
The total rate of change of 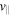 , following the electron's orbit, is
, following the electron's orbit, is
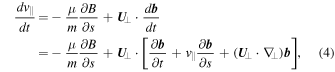
where 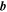 is the local direction of the magnetic field, s is the distance along the magnetic field. The first term in Equation (4) describes the effect of magnetic mirroring on the parallel motion. As was mentioned previously, and will become evident below, this term represents a redistribution between the parallel and perpendicular energies of the electron along its orbit. The second term contains both time- and space-dependent variations of the magnetic-field direction along the orbit. As demonstrated in detail by Northrop (1963), among other effects these terms give rise to the increase of parallel energy due to Fermi's mechanism.
is the local direction of the magnetic field, s is the distance along the magnetic field. The first term in Equation (4) describes the effect of magnetic mirroring on the parallel motion. As was mentioned previously, and will become evident below, this term represents a redistribution between the parallel and perpendicular energies of the electron along its orbit. The second term contains both time- and space-dependent variations of the magnetic-field direction along the orbit. As demonstrated in detail by Northrop (1963), among other effects these terms give rise to the increase of parallel energy due to Fermi's mechanism.
The total rate of change of the 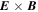 velocity is
velocity is
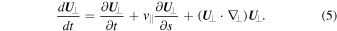
As will be shown below, direct contribution of 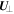 to the electron's kinetic energy is small, being quadratic in the
to the electron's kinetic energy is small, being quadratic in the 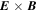 velocity. Indirectly, however, the
velocity. Indirectly, however, the 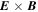 drift is extremely important, as it is responsible for advecting and compressing the magnetic-field lines (whose electric fields accelerate the electrons) within the evolving plasmoids.
drift is extremely important, as it is responsible for advecting and compressing the magnetic-field lines (whose electric fields accelerate the electrons) within the evolving plasmoids.
From the results above, we now can compute the rate of change of the electron's energy,
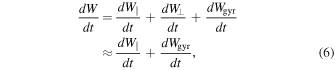
upon neglecting the contribution due to the 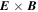 drift. Using Equation (4), we find for the parallel energy
drift. Using Equation (4), we find for the parallel energy 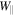 that
that
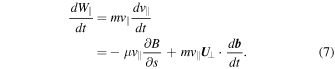
For the gyration energy Wgyr we have, recalling the invariance of μ,
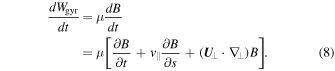
Combining Equations (7) and (8), and noting the cancellation of the common magnetic mirroring terms (the first and second, respectively), for the total energy change we finally obtain
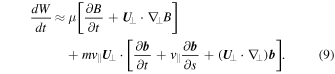
In this equation, the two terms on the first line come from the change in the gyration energy, and are commonly identified as betatron acceleration terms. Clearly, they arise from changes in the magnetic-field strength due either to a local compression or rarefaction of the flux density (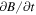 ) or to an advection of the field line into a region of spatially varying flux density (
) or to an advection of the field line into a region of spatially varying flux density (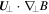 ). The three terms on the second line come from the change in the parallel energy, and are commonly identified as Fermi acceleration terms. They arise from changes in the field direction due to a local reorientation of the field (
). The three terms on the second line come from the change in the parallel energy, and are commonly identified as Fermi acceleration terms. They arise from changes in the field direction due to a local reorientation of the field (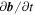 ), to parallel motion of the electron into a region of differing direction (
), to parallel motion of the electron into a region of differing direction (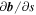 ), or to perpendicular advection of the field line into a region of differing direction (
), or to perpendicular advection of the field line into a region of differing direction (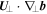 ).
).
The great benefit of utilizing the guiding-center approximation in our simulation is the elimination of the enormous restriction on the time step. The scale of this restriction is demonstrated by the following estimation. The value of the magnetic field in the region of interest is 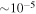 T, which results in a gyration period of
T, which results in a gyration period of 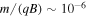 s, where q is the electron's charge. In order to simulate a process that lasts 10 minutes, one would need to perform at least half a trillion time steps per electron. Since the number of test electrons per field line needed to produce reliable statistics is of the order of a million, the problem would be virtually impossible to simulate on modern hardware. Thus, the adoption of guiding-center motion equations greatly facilitates simulation of the problem.
s, where q is the electron's charge. In order to simulate a process that lasts 10 minutes, one would need to perform at least half a trillion time steps per electron. Since the number of test electrons per field line needed to produce reliable statistics is of the order of a million, the problem would be virtually impossible to simulate on modern hardware. Thus, the adoption of guiding-center motion equations greatly facilitates simulation of the problem.
In order for their motion to be adiabatic, electrons need to move fast enough. The Alfvén speed in the domain is 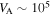 m s−1. For this reason, the speed range of electron injection was chosen to be between
m s−1. For this reason, the speed range of electron injection was chosen to be between 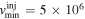 m s−1 and
m s−1 and 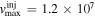 m s−1. The electrons in this energy range were randomly sampled from the Maxwellian distribution
m s−1. The electrons in this energy range were randomly sampled from the Maxwellian distribution
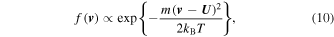
where kB is the Boltzmann constant and T and  are local plasma temperature and bulk velocity.
are local plasma temperature and bulk velocity.
With the energy range set as above, one can estimate the contribution of the cross-field drift to the motion of electrons' guiding centers (Northrop 1963). Under ideal MHD, the  drift accounts for the advection of the magnetic-field lines and, therefore, for the cross-field motion of electrons attached to them. Its magnitude,
drift accounts for the advection of the magnetic-field lines and, therefore, for the cross-field motion of electrons attached to them. Its magnitude, 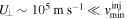 , has a negligible contribution to the total electron energy (see Equations (4) and (9)). However, the advection is responsible for both the betatron and Fermi acceleration of electrons as they sample regions with varying magnetic-field strength and direction. The gradient and curvature drifts both are on the order of
, has a negligible contribution to the total electron energy (see Equations (4) and (9)). However, the advection is responsible for both the betatron and Fermi acceleration of electrons as they sample regions with varying magnetic-field strength and direction. The gradient and curvature drifts both are on the order of 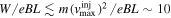 m s−1, where
m s−1, where 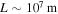 (see Figure 2) is the characteristic spatial scale of the magnetic field's geometry. The drift associated with acceleration of the field lines' advection,
(see Figure 2) is the characteristic spatial scale of the magnetic field's geometry. The drift associated with acceleration of the field lines' advection, 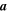 , is
, is 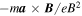 . With the characteristic time of change
. With the characteristic time of change 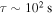 (see Figure 2), the estimate for this drift is
(see Figure 2), the estimate for this drift is  m s−1. Therefore, the cross-field drift that may displace electrons from their original field lines is much less significant than
m s−1. Therefore, the cross-field drift that may displace electrons from their original field lines is much less significant than 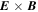 drift and can be neglected in the guiding-center equations. Overall, one may safely assume that each electron stays on the same field line throughout the simulation.
drift and can be neglected in the guiding-center equations. Overall, one may safely assume that each electron stays on the same field line throughout the simulation.
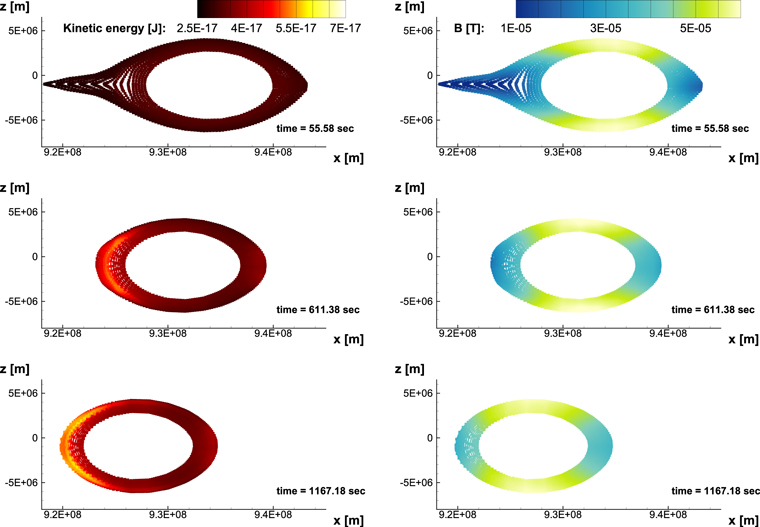
Figure 2. Evolution of a magnetic island over time. Left column: colors indicate average kinetic energy of electrons; right column: colors indicate magnitude of background magnetic field. Electrons gain most energy when magnetic field changes most rapidly, as seen in the stretched sections of field lines.
Download figure:
Standard image High-resolution image3.3. Data Structure
It is also worth noting that the guiding-center approximation is naturally tied to the notion of the magnetic-field lines. Thus, the underlying physics of the process motivates improvements in the numerical approach. Since the motion of high energy electrons is essentially one-dimensional, as viewed on a larger scale, and follows the magnetic-field lines, it is most practical to adopt a data structure that takes advantage of it.
Rather than utilizing a Cartesian grid, a linear structure that follows a magnetic-field line has been developed. Under the assumption of axial symmetry used to simulate the background field and plasma (see Section 3.1), which reduces the dimensionality of the problem, we introduce a scalar potential for poloidal (out of the plane of Figure 2) components of the magnetic field as well as the magnetic flux function, Ψ. The latter quantity greatly simplifies the problem of field line extraction, while keeping high accuracy. The procedure is as follows.
The poloidal projection of a magnetic-field line is defined as a line of constant value of Ψ. If one chooses a starting point for a magnetic loop, it is possible to extract the whole loop point-by-point.
The initial point, X0, is taken at an arbitrary location within the magnetic island. The value of the magnetic flux function, 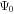 , must be the same for all points associated with this magnetic loop. The candidate point is taken in the direction of the magnetic field, then it is corrected via gradient descent iterations until the value of the magnetic flux function is sufficiently close to
, must be the same for all points associated with this magnetic loop. The candidate point is taken in the direction of the magnetic field, then it is corrected via gradient descent iterations until the value of the magnetic flux function is sufficiently close to 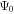 .
.
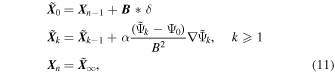
where  is the last extracted point on the field line,
is the last extracted point on the field line,  is the magnetic field at this location,
is the magnetic field at this location, 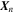 is the point being extracted, k enumerates iterations,
is the point being extracted, k enumerates iterations, 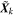 and
and 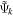 are values at iteration k,
are values at iteration k,  is the limit of iterations, δ controls distance between consecutive extracted points, and α controls stability of gradient descent.
is the limit of iterations, δ controls distance between consecutive extracted points, and α controls stability of gradient descent.
The effectiveness and accuracy of this procedure are demonstrated in Figure 1. As one can see, even complex features such as the stretched parts of field lines near an X-point additionally complicated with low values of the magnetic field are carefully resolved.
Each point thus extracted moves with the local plasma velocity. Under ideal MHD, frozen-in conditions apply, hence allowing us to trace the evolution of an individual field line via following motion of fluid elements extracted along it.
Although only the poloidal projections of field lines were extracted, the full 3D plasma velocity is used to update their state. The new locations of thus-obtained fluid elements are then projected to the original poloidal plane. The same procedure was applied to the electron motion.
The background plasma data from our ARMS simulation are imported into AMPS, with a data file cadence of 1 s. To maintain higher accuracy, linear time interpolation between files is used. Extracted field lines are regularly updated with each plasma fluid element being moved with the velocity of the background plasma and corrected via gradient descent to match the original value of Ψ0, which should be preserved under ideal MHD.
Another reason why our approach is better suited for particle tracking in the current case is the issue with electrons staying within the island. While the physical reason for electrons to escape the island is the cross-field drift, artificial electron leakage from the island is observed when a full 3D simulation on a regular grid is performed. Since the field evolves rapidly, an electron on the edge of the island commonly finds itself outside the island when the plasma state is updated. Such electrons escape the domain and information is lost. Our solution is to correct the position of an electron in order to put it back into the island (Equation (11)). With the adopted field-aligned data structure, this problem was effectively non-existent. Since all electrons are essentially attached to field lines, they cannot escape the island due to non-physical reasons.
4. Results
The particle-tracking simulation started after an island was fully formed. Evolution of the electron population was prominent throughout all contraction process. Results are presented in this section.
First, a significant change in energy is observed. The evolution of the average electron kinetic energy, together with the magnitude of the background magnetic field, is shown in Figure 2. It is clearly seen that the most rapid change in energy occurs near the stretched parts of field lines. These are the locations where electrons experience betatron and Fermi acceleration, as the newly reconnected magnetic field retracts and thus carries electrons away from the reconnection regions. The energy increase is much higher on the left (Sunward) side of the island than on the right, because the initial shape of the outward side is smoother and, therefore, undergoes less intense change in the background field. Also, the magnetic field increases more in magnitude on the sunward side as seen in Figure 2. The initial field strength is lower there because it is closer to the corresponding X-point. As described in Section 2.1, an increase in magnetic-field strength leads to an increase in the gyration energy of electrons due to the betatron effect. In addition, the island contracts overall and the electrons experience slow but steady energy gain throughout the whole island, producing an increase in the parallel energy due to Fermi acceleration.
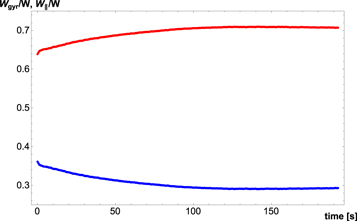
In order to determine the relative importance of betatron and Fermi acceleration in our analysis, we tracked the population's energy partition as shown in Figure 3. The fractions of gyration and parallel energy, 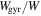 and
and 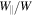 , respectively, are displayed as red and blue curves. Both Wgyr and
, respectively, are displayed as red and blue curves. Both Wgyr and 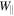 increase with time, so both acceleration mechanisms are active, but Wgyr clearly increases faster than
increase with time, so both acceleration mechanisms are active, but Wgyr clearly increases faster than 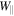 . Thus, the betatron mechanism dominates the acceleration of particles in our simulation. This result differs from that reported by Drake et al. (2006a), who found only a small contribution by the betatron effect in the nearly incompressible evolution of their kinetic simulation. Indeed, a more recent and comprehensive analysis of acceleration mechanisms in kinetic reconnection by Dahlin et al. (2014) shows that the betatron effect actually slightly cools (decelerates) electrons in their system, due to a field strength reduction in the islands after they form. In contrast, our flare simulation (Guidoni et al. 2016) is highly compressible. The strong compression of the island leads to a substantial, indeed dominant, contribution of betatron acceleration to the total energy gain of the electrons.
. Thus, the betatron mechanism dominates the acceleration of particles in our simulation. This result differs from that reported by Drake et al. (2006a), who found only a small contribution by the betatron effect in the nearly incompressible evolution of their kinetic simulation. Indeed, a more recent and comprehensive analysis of acceleration mechanisms in kinetic reconnection by Dahlin et al. (2014) shows that the betatron effect actually slightly cools (decelerates) electrons in their system, due to a field strength reduction in the islands after they form. In contrast, our flare simulation (Guidoni et al. 2016) is highly compressible. The strong compression of the island leads to a substantial, indeed dominant, contribution of betatron acceleration to the total energy gain of the electrons.
Figure 3. Evolution of partition of particle energy between 0 and 200 s from the start of the simulation: red curve is the fraction of gyration energy 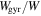 , blue curve is the fraction of energy of parallel motion
, blue curve is the fraction of energy of parallel motion  .
.
Download figure:
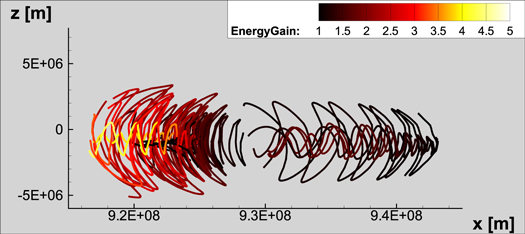
Standard image High-resolution imageWhile the average energy increase is approximately two, some electrons experience an energy gain of up to five, as shown in Figure 4: the electrons that bounce between mirror points close to the reconnection region. These electrons reside in the acceleration region throughout the lifetime of the trapping island, as is reflected in the higher average energy gain in this region in Figure 2. This is consistent with the analysis in Guidoni et al. (2016): the energy gain depends on the initial pitch angle of the electrons. In kinetic simulations by Oka et al. (2010), the simulated electrons experienced an energy gain of ∼1.25 after being trapped in a magnetic island. However, that study considered relativistic electrons, while in the present work the classical approximation is still valid.
Figure 4. Trajectories of selected individual particles. Energy gain is the highest for particles that bounce between mirror points close to the reconnection region and are subject to betatron and Fermi acceleration continuously throughout the process.
Download figure:
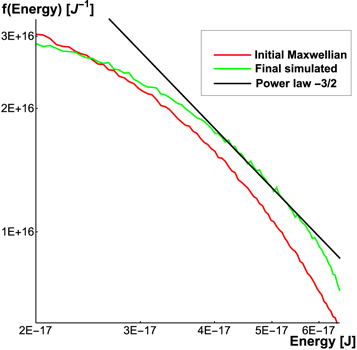
Standard image High-resolution imageFinally, the change in the overall energy distribution, sampled over all electrons injected into the island (2 × 106), is demonstrated in Figure 5. The initial energy distribution is Maxwellian (see Section 2.1). In response to island contraction, its high energy tail moved closer to the ubiquitous 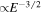 power law that is commonly found in the distribution of suprathermal electrons (Drake et al. 2006b). Moreover, the basic assumption of Drake et al. (2006a) is that electrons experience acceleration multiple times in several magnetic islands. Therefore, when electrons visit many islands, we expect that the final distribution may approach a power law with a spectral index even closer to that observed. Such multiple visits to successive islands also seem necessary to obtain the energy amplifications required to understand hard X-ray emissions in flares. Whether the dominant mechanism is betatron or Fermi acceleration, or both are comparably important, the amplification by passage through a single island seems to be limited to a factor of five or less. Thus, as concluded by both Drake et al. (2006a) and Guidoni et al. (2016), accelerated electrons would have to visit several islands in order to attain the high energies observed.
power law that is commonly found in the distribution of suprathermal electrons (Drake et al. 2006b). Moreover, the basic assumption of Drake et al. (2006a) is that electrons experience acceleration multiple times in several magnetic islands. Therefore, when electrons visit many islands, we expect that the final distribution may approach a power law with a spectral index even closer to that observed. Such multiple visits to successive islands also seem necessary to obtain the energy amplifications required to understand hard X-ray emissions in flares. Whether the dominant mechanism is betatron or Fermi acceleration, or both are comparably important, the amplification by passage through a single island seems to be limited to a factor of five or less. Thus, as concluded by both Drake et al. (2006a) and Guidoni et al. (2016), accelerated electrons would have to visit several islands in order to attain the high energies observed.
Figure 5. Initial and final electron energy distribution. Curves are shown on a log–log scale. The low energy part of the final distribution (green solid) drops due to the lack of particles below the cutoff energy and bears no physical significance. At the end of the simulation, the high energy tail of the distribution moved slightly closer to a power law with index −1.5.
Download figure:
Standard image High-resolution image5. Discussion
Our particle-tracking simulation shows a clear average energy gain on the order of two for electrons trapped in a single magnetic island, with some electrons reaching a gain of approximately five. This is consistent with the results of Guidoni et al. (2016). We also found that, although the final electron energy distribution did not reach a power law after contraction of one magnetic island, it is significantly different from the initial Maxwellian. Our study also revealed that betatron acceleration, rather than Fermi acceleration, is responsible for most of the energy gain.
In a more realistic scenario, i.e., for a flare occurring at active-region scales rather than the global scale of the Guidoni et al. (2016) MHD simulation, the plasmoids occupy a smaller volume. Because the drift velocity scales inversely with island size, electrons would escape more easily and reach other acceleration regions, thus undergoing additional acceleration. We expect the resulting electron distribution to more closely resemble a power law when the whole process is repeated many times via electrons traveling in multiple contracting islands. Islands merging as studied in Drake et al. (2013) is yet another opportunity to boost the acceleration process. However, Guidoni et al. (2016) found that very few islands merged in the model flare current sheet.
The approach utilized in this work assumes that the energetic electron population does not significantly affect the magnetic-field evolution, and the MHD and particle simulations were performed independently. On the other hand, self-consistent plasma simulations have shown that about half of the magnetic energy of a magnetic island is transferred to the energetic electrons (Drake et al. 2006a).
The final conclusion of this study is that the island-contraction acceleration mechanism of Drake et al. (2006a) is a promising candidate to explain the energetic electron population observed in solar flares. The present study also finds that, when compressibility is included, the dominant source of electron acceleration in contracting islands is the betatron mechanism, rather than the Fermi process.
The work performed at the University of Michigan was partially supported by National Science Foundation grants AGS-1322543 and PHY-1513379, NASA grant NNX13AG25G, the European Union's Horizon 2020 research and innovation program under grant agreement No 637302 PROGRESS. We would also like to acknowledge high-performance computing support from Pleiades operated by NASA's Advanced Supercomputing Division.