ABSTRACT
Estimates of the source sky location for gravitational wave signals are likely to span areas of up to hundreds of square degrees or more, making it very challenging for most telescopes to search for counterpart signals in the electromagnetic spectrum. To boost the chance of successfully observing such counterparts, we have developed an algorithm that optimizes the number of observing fields and their corresponding time allocations by maximizing the detection probability. As a proof-of-concept demonstration, we optimize follow-up observations targeting kilonovae using telescopes including the CTIO-Dark Energy Camera, Subaru-HyperSuprimeCam, Pan-STARRS, and the Palomar Transient Factory. We consider three simulated gravitational wave events with 90% credible error regions spanning areas from 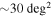 to
to 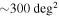 . Assuming a source at
. Assuming a source at 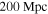 , we demonstrate that to obtain a maximum detection probability, there is an optimized number of fields for any particular event that a telescope should observe. To inform future telescope design studies, we present the maximum detection probability and corresponding number of observing fields for a combination of limiting magnitudes and fields of view over a range of parameters. We show that for large gravitational wave error regions, telescope sensitivity rather than field of view is the dominating factor in maximizing the detection probability.
, we demonstrate that to obtain a maximum detection probability, there is an optimized number of fields for any particular event that a telescope should observe. To inform future telescope design studies, we present the maximum detection probability and corresponding number of observing fields for a combination of limiting magnitudes and fields of view over a range of parameters. We show that for large gravitational wave error regions, telescope sensitivity rather than field of view is the dominating factor in maximizing the detection probability.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
The detection of gravitational waves (GWs) from the inspiral and merger of binary black-hole systems (Abbott et al. 2016a, 2016b) has marked the beginning of the GW astronomy era. With the advanced interferometric detectors, GWs are expected to be observed from a number of additional source types, including the mergers of binary neutron stars (BNS), and neutron star-black hole (NSBH) systems. For these other sources the presence of matter from the neutron star (NS) components, in such a violent interaction with its companion, makes it likely that electromagnetic (EM) emission will be generated. The joint detection of a GW signal and its EM counterpart is therefore of particular interest (Kasliwal & Nissanke 2014). A coincident EM observation together with the detection of GWs from these sources would lead to a deeper and more comprehensive understanding of these objects. A successful EM follow-up observation triggered by a GW event can greatly improve the identification and localization of the host galaxy, bring us a more accurate estimate of the distance and energy involved, and provide better understanding of the merger hydrodynamics and the local environment of the progenitor (Bloom et al. 2009; Kulkarni & Kasliwal 2009; Phinney 2009). Additionally, knowledge obtained by EM follow-up observations may break the modeling degeneracies of binary properties and confirm the association between the GW source and its EM counterpart. Moreover, successfully locating the EM counterpart of a GW event could increase the confidence in the GW detection (Blackburn et al. 2015).
Among many other potential EM counterparts of GW events, it has been argued that kilonovae are strong candidates for GW signals from BNS and NSBH mergers (Li & Paczynski 1998; Metzger & Berger 2011; Tanvir et al. 2013) and can improve the rate estimate for NSBH (LIGO-P1600304 2016). We therefore focus our discussion solely on kilonovae. Kilonovae are predicted to produce an optical/infrared and isotropic quasithermal transient, and are thought to originate from the hot neutron-rich matter ejected from BNS mergers and NSBH mergers (Metzger et al. 2010). This ejection triggers r-process nucleosynthesis, the radioactive decay of which sustains the high temperature of the ejecta and powers the kilonovae. Kilonovae can be  times brighter than a nova (peak luminosity
times brighter than a nova (peak luminosity  ) (Metzger et al. 2015), but given the expected rate of BNS events, their corresponding distances make kilonovae relatively dim EM transients. In addition, according to Metzger & Berger (2011), a kilonova only maintains its peak luminosity for hours to days after merger. However, more recent calculations including the opacity of the r-process elements (Barnes & Kasen 2013; Grossman et al. 2014; Tanaka et al. 2014) indicate that this timescale is likely to be days to weeks. Three detections are currently associated with the short-duration gamma-ray bursts GRB 130603B (Berger et al. 2013; Tanvir et al. 2013), GRB 060614 (Jin et al. 2015; Yang et al. 2015), and GRB 050709 (Jin et al. 2016).
) (Metzger et al. 2015), but given the expected rate of BNS events, their corresponding distances make kilonovae relatively dim EM transients. In addition, according to Metzger & Berger (2011), a kilonova only maintains its peak luminosity for hours to days after merger. However, more recent calculations including the opacity of the r-process elements (Barnes & Kasen 2013; Grossman et al. 2014; Tanaka et al. 2014) indicate that this timescale is likely to be days to weeks. Three detections are currently associated with the short-duration gamma-ray bursts GRB 130603B (Berger et al. 2013; Tanvir et al. 2013), GRB 060614 (Jin et al. 2015; Yang et al. 2015), and GRB 050709 (Jin et al. 2016).
In this work, we consider scenarios consistent with only two or three operating GW detectors. For such a network the sky location estimate for a GW event can cover a large part of the sky ( (Singer et al. 2014)), posing a significant challenge to telescopes with field of views (FOVs) of order
(Singer et al. 2014)), posing a significant challenge to telescopes with field of views (FOVs) of order  trying to find counterpart signals in the EM spectrum. (For larger detector networks it has been shown that the size of GW sky localization error regions can be considerably reduced (Fairhurst 2011; Nissanke et al. 2011, 2013; Veitch et al. 2012; Rodriguez et al. 2014).) Observing and confidently detecting kilonovae demands long exposure times even for powerful telescopes. It has been proposed that the infrared sensitivity of the planned James Webb Space Telescope (JWST) may enable detections with short exposure times, thus compensating for its small FOV (Bartos et al. 2016). The use of galaxy catalogs may also provide prior information on the direction of an event (Kulkarni & Kasliwal 2009; Nuttall & Sutton 2010; White et al. 2011; Nissanke et al. 2013; Fan et al. 2014; Bartos et al. 2015; Gehrels et al. 2016; Singer et al. 2016b). Nonetheless, even with JWST and galaxy catalogs, the observation time can still span an entire night, which may make target-of-opportunity BNS merger observations less attractive.
trying to find counterpart signals in the EM spectrum. (For larger detector networks it has been shown that the size of GW sky localization error regions can be considerably reduced (Fairhurst 2011; Nissanke et al. 2011, 2013; Veitch et al. 2012; Rodriguez et al. 2014).) Observing and confidently detecting kilonovae demands long exposure times even for powerful telescopes. It has been proposed that the infrared sensitivity of the planned James Webb Space Telescope (JWST) may enable detections with short exposure times, thus compensating for its small FOV (Bartos et al. 2016). The use of galaxy catalogs may also provide prior information on the direction of an event (Kulkarni & Kasliwal 2009; Nuttall & Sutton 2010; White et al. 2011; Nissanke et al. 2013; Fan et al. 2014; Bartos et al. 2015; Gehrels et al. 2016; Singer et al. 2016b). Nonetheless, even with JWST and galaxy catalogs, the observation time can still span an entire night, which may make target-of-opportunity BNS merger observations less attractive.
Given that current and future EM telescopes will be subject to limited observational resources, we might ask how we can maximize the detection probability of a GW-triggered kilonova signature. We have developed an algorithm to answer this question, and here we present the results of a proof-of-concept demonstration applied to four different telescopes including the Subaru-HyperSuprimeCam (HSC)5
(Miyazaki et al. 2012), CTIO-Dark Energy Camera (DEC) (Bernstein et al. 2012), Pan-Starrs6
(Kaiser et al. 2002), and the Palomar Transient Factory (PTF) (Law et al. 2009) for three different simulated GW events. This algorithm takes as inputs GW sky localization information, and returns a guidance strategy for time allocation and telescope pointing for a given EM telescope. In this paper we restrict the discussion to kilonovae from BNS mergers and leave the discussion of kilonova from NSBH for future study. This is in part because our chosen GW data set from Singer et al. (2014) only contains BNS mergers. However, we recall that there is no theoretical restriction preventing us from applying our algorithm using other EM counterpart models, and neither is it restricted to using only GW sky maps from compact binary coalescence (CBC) events. Other methods for improving the detection probability by finding observing fields exist, such as that presented in Ghosh et al. (2015) and Rana et al. (2016). However, the former mostly considers fixed field locations and is concerned with telescopes with large fields of view. The latter primarily focuses on the setting and rising of the Sun to be the only constraining factors of the coverage of the GW sky localization error region. It has been shown in Rana et al. (2016) that observing fields with predefined locations may cover a slightly higher GW probability than methods allowing the fields to move freely on the sky if the telescopes are to observe  fields. These methods could be potentially used to improve our method. However, given the peak luminosity of kilonovae, their likely distances, and the amount of available observation time, most telescopes will in reality only be able to observe a few fields if required to reach the depth necessary to capture kilonovae as EM-counterparts. In addition, unlike the aforementioned studies, our method distinguishes itself by considering optimization of the time allocation given to the observing fields.
fields. These methods could be potentially used to improve our method. However, given the peak luminosity of kilonovae, their likely distances, and the amount of available observation time, most telescopes will in reality only be able to observe a few fields if required to reach the depth necessary to capture kilonovae as EM-counterparts. In addition, unlike the aforementioned studies, our method distinguishes itself by considering optimization of the time allocation given to the observing fields.
This paper is organized as follows: the method is introduced in Section 2, and we describe the implementation in Section 3. The results obtained with the algorithm and a discussion of these results are given in Section 4. The possible future directions of this work are provided in Section 6, and our conclusions are presented in Section 7.
2. METHOD
As a proof-of-concept of our general EM follow-up method, here we have chosen to focus on kilonovae counterpart signatures. We have also adopted some simplifications that will be relaxed in future studies. We assume that the available observation time is short compared to the luminosity variation timescale of a kilonova. This is validated by the fact that the luminosity variation timescale of a kilonova is estimated to be several days to a week, which is longer than a reasonable continuous EM observation. This approximation allows us to assume that a kilonova has constant luminosity during the observation period. We also only consider the use of R-band luminosity information, but the method we present can be extended to other regions of the EM spectrum. We note that kilonovae are predicted to have higher peak luminosities in the i band, but we do not consider the i band in this study for two reasons: (1) although kilonovae luminosity indeed peaks higher at i band, the difference is not dramatic, and (2) the SDSS survey for science indicates that the sky brightness is one magnitude brighter in i band than in R band, counteracting the increase in the peak luminosity of kilonovae in i band. In reality, identifying a target EM counterpart requires tracking the light curves of the object, leading to several observations of the same point in the sky over several days. However, in this work we deal with the problem of detection, rather than identification. We consider only single observations and calculate optimized pointing directions and durations for a constrained total observation length and constant luminosity. Subsequent observations for the purpose of identifying variation within a field can be achieved by repeating our proposed observing strategy at some later time.
In general, GW events could be localized to ≳100 deg2, which is much larger than a typical EM telescope FOV ( ). We therefore do not consider the telescope rotation around its own axis, and throughout this work, reference to single telescope pointing therefore implies a rectangular charge-coupled device (CCD) image with edges parallel to lines of longitude and circles of latitude.
). We therefore do not consider the telescope rotation around its own axis, and throughout this work, reference to single telescope pointing therefore implies a rectangular charge-coupled device (CCD) image with edges parallel to lines of longitude and circles of latitude.
We also assume that the prior information from a GW trigger can be approximated as having independent sky location and distance probability distributions. Generally, this may not be the case, but our mathematical treatment can be greatly simplified under this assumption. We note that the sky maps available for our chosen data set (discussed in Section 3) naturally lend themselves to this approximation since no distance information was computed as part of the rapid sky localization study reported in Singer et al. (2012).7 The final assumption is that the EM telescope can see every direction regardless of the location of the Sun, Moon, and the horizon. The issue of optimization of EM follow-up observations under the time-critical constraints such as those imposed by a source dipping below the horizon is explored in Rana et al. (2016).
2.1. Bayesian Framework
We use  to denote the successful detection of an EM counterpart. The probability of this occurring depends on the size of the FOV ω of the selected telescope, the observed sky locations
to denote the successful detection of an EM counterpart. The probability of this occurring depends on the size of the FOV ω of the selected telescope, the observed sky locations  , and the exposure time τ. The posterior probability of successful detection is then given by
, and the exposure time τ. The posterior probability of successful detection is then given by

Here, I is prior information that includes the parameters of the selected telescope, such as its photon collecting area  , filter, and CCD efficiency. For a particular observation, the number of photons N collected by the telescope is
, filter, and CCD efficiency. For a particular observation, the number of photons N collected by the telescope is

where m is the apparent magnitude of the observed source. The threshold count N* is the criterion for detection determined by the signal-to-noise ratio (S/N) threshold, background noise, and the sensitivity of the selected telescope. The value of N* is given by Equation (2) with input values of m and τ corresponding to the detection threshold of the selected telescope (see Table 1). The constant 1010 in Equation (2) is the number of photons per second at m = 0. In practice, the value of N* should also account for the change in background light accumulated for different choices of observation time τ, but for simplicity, we ignore this effect here. Since the number of photons expected from a target EM counterpart depends on its absolute magnitude M, distance R from the telescope, and how likely it is that the GW event is located within the field being observed, Equation (1) can be expanded such that

The quantity  is the probability of receiving N photons from a source, given its absolute magnitude M, distance R, and observation time τ, and is described by a Poisson distribution. Since we assume that the prior distribution on the distance to the target EM counterpart is statistically independent of the prior distribution on its sky location, Equation (3) can be written as
is the probability of receiving N photons from a source, given its absolute magnitude M, distance R, and observation time τ, and is described by a Poisson distribution. Since we assume that the prior distribution on the distance to the target EM counterpart is statistically independent of the prior distribution on its sky location, Equation (3) can be written as

where


Table 1. Telescope Parameters
| Telescope | Aperture | FOV | Exposure | Sensitivity |

|
|---|---|---|---|---|---|
| (m) | (deg2) | (s) | (5σ mag | ||
| in R band) | (m−2) | ||||
| DEC | 4.0 | 3.0 | 50 | 23.7 | 162.0 |
| HSC | 8.2 | 1.13a | 30 | 24.5 | 46.5 |
| Pan-Starrs | 1.8 | 7.0 | 60 | 22.0 | 930.5 |
| PTF | 1.2 | 7.0 | 60 | 20.6 | 3378.3 |
| LSST | 6.7 | 9.6 | 15 | 24.5 | 23.26 |
Note.
aThe full HSC FOV is 1.77 deg2, but ∼20% is used for calibration purposes.Download table as: ASCIITypeset image
It should be noted that the GW sky localization information used for this work has been marginalized over distance, meaning that the GW information represents a two-dimensional (2D) error region projected onto the sky. However, as a reasonable approximation, the marginalized (and therefore missing) low-latency distance uncertainty can be approximated by a Gaussian distribution (Veitch et al. 2015; Singer et al. 2016a). Hence we assume a Gaussian prior with mean  and standard deviation
and standard deviation  for the distance. We note that in more general cases, specifically for GW events with low S/N, this Gaussian approximation becomes invalid. In principle, any form of positional information can be incorporated into our analysis, and therefore our method can be adapted to include more realistic GW distance information. Further constraints from galaxy catalogs can also be incorporated into our method (Fan et al. 2014).
for the distance. We note that in more general cases, specifically for GW events with low S/N, this Gaussian approximation becomes invalid. In principle, any form of positional information can be incorporated into our analysis, and therefore our method can be adapted to include more realistic GW distance information. Further constraints from galaxy catalogs can also be incorporated into our method (Fan et al. 2014).
We assume the least informative prior on the peak luminosity such that  . It then follows that the prior on the peak magnitude is given by
. It then follows that the prior on the peak magnitude is given by

where we assume M has a prior range of  as defined by the peak magnitudes of the models in Barnes & Kasen (2013).
as defined by the peak magnitudes of the models in Barnes & Kasen (2013).
The probability of EM detection as defined in Equation (1) only considers one observing field. Given the size of a GW sky localization error region, and the typical size of an EM telescope FOV, the number of fields needed to be considered is  . If an error region enclosing 90% of the GW probability covers
. If an error region enclosing 90% of the GW probability covers  and the EM telescope FOV is
and the EM telescope FOV is  , the maximum number n of fields8
required to cover the error region at 90% can be estimated as
, the maximum number n of fields8
required to cover the error region at 90% can be estimated as  .
.
One might assume that observing as many fields as possible is optimal, but we show below that telescope time is better spent by observing k fields, where k lies in the range ![$[1,n]$](https://content.cld.iop.org/journals/0004-637X/834/1/84/revision1/apjaa4cd1ieqn23.gif) . This occurs when it becomes more beneficial to observe a particular field for longer than observing a new field.
. This occurs when it becomes more beneficial to observe a particular field for longer than observing a new field.
For a given total observation time T, we are free to choose which fields we observe, and we can also determine the observation time allocated to each field. We represent these quantities by the vectors  and
and  , respectively, where k is the total number of chosen fields. Maximizing the detection probability of a kilonova amounts to finding the values of these vectors and the value of k, which maximizes
, respectively, where k is the total number of chosen fields. Maximizing the detection probability of a kilonova amounts to finding the values of these vectors and the value of k, which maximizes

The choices of  are subject to the constraint that
are subject to the constraint that

where T0 represents the time required to slew between telescope pointings and/or perform CCD readout, and is equal to  . We treat T0 as independent of the angular distance between pointings.
. We treat T0 as independent of the angular distance between pointings.
The expression we have for the kilonova detection probability (Equation (7)) as a function of the number of observed fields depends on our choice of field location and observation time within each field. Given a number of fields k, we begin choosing fields with a greedy algorithm, which is described in Section 3. Once the k fields have been chosen, they are represented by  and Equation (7) is maximized over the parameter vector
and Equation (7) is maximized over the parameter vector  to obtain the optimal kilonova detection probability. This is then repeated for each k in the range
to obtain the optimal kilonova detection probability. This is then repeated for each k in the range ![$[1,n]$](https://content.cld.iop.org/journals/0004-637X/834/1/84/revision1/apjaa4cd1ieqn30.gif) to find the optimal number of observed fields k.
to find the optimal number of observed fields k.
3. IMPLEMENTATION
In this section we describe the processes for applying the GW sky localization information and generating the optimal observing strategy. The flow chart in Figure 1 is a visual representation of this process.
Figure 1. The process for generating an optimized observing strategy. Our algorithm takes two inputs: the GW sky localization information, and a set of telescope parameters. After integrating over the number of received photons N, the source distance R, and the source absolute magnitude M, the algorithm returns the probability of detection of an EM kilonova signal  as a function of the field observation time τ. In parallel, for each choice of the total number of observed fields k, the algorithm selects the fields using a greedy algorithm. Based on the enclosed GW probability within each field, the corresponding optimized observation times are computed using a Lagrange multiplier approach. The total EM detection probability is then output for each choice of k.
as a function of the field observation time τ. In parallel, for each choice of the total number of observed fields k, the algorithm selects the fields using a greedy algorithm. Based on the enclosed GW probability within each field, the corresponding optimized observation times are computed using a Lagrange multiplier approach. The total EM detection probability is then output for each choice of k.
Download figure:
Standard image High-resolution imageAs shown in Figure 1, we require information regarding the sky position of the GW source, which we obtain from the BAYESTAR algorithm (Singer & Price 2016) (other algorithms for low-latency GW sky localization exist, such as that proposed by Chen & Holz 2015). This algorithm outputs GW sky localization information using a HEALPix9 coverage of the sky. Each HEALPix point corresponds to a value of the GW probability and represents an equal area of the sky. BAYESTAR can rapidly (in ∼10 s) generate event location information and has been shown in Singer et al. (2014) to closely match results from more computationally intensive off-line Bayesian inference methods (Veitch et al. 2015). The simulated GW events used in this work are from BNS systems and taken directly from the data set used in Singer et al. (2014).
In this work, we consider follow-up observations using four telescopes (HSC, DEC, Pan-Starrs, and PTF) for three simulated representative GW events (see Table 2) that are studied assuming three total observation times  . For any telescope, GW event, and total observation time, the first stage of our procedure is to calculate the maximum number of fields n required to cover the sky area enclosed by the 90% probability contour of the GW sky region.
. For any telescope, GW event, and total observation time, the first stage of our procedure is to calculate the maximum number of fields n required to cover the sky area enclosed by the 90% probability contour of the GW sky region.
Table 2. Simulated GW Event Parameters
| Event IDa | S/N | 90% Region | Chirp Mass |
|---|---|---|---|

|

|
||
| 28700 | 16.8 | 302 | 1.33 |
| 19296 | 24.3 | 103 | 1.28 |
| 18694 | 24.0 | 28.2 | 1.31 |
Note.
aThe Event ID is that given to the events used in Singer et al. (2014).Download table as: ASCIITypeset image
In order to identify the possible observing fields for a given GW event, the greedy algorithm identifies the least number of HEALPix locations on the sky whose sum of GW probability is equal to the desired confidence level (in our case 90%). Then, assuming that each of those points represents the center of an observing field we compute the sum of GW probability from each HEALPix point whose center lies within each of those fields. The field returning the maximum sum of the GW probability among those fields will be the first field. Subsequent fields are found by the same procedure, with the HEALPix points in the previous fields ignored. The summed probability within each field is an accurate approximation to the quantity  as defined in Equation 5(a). The n selected fields are labeled in the order with which they are chosen, and hence their label indicates their rank in terms of enclosed GW probability. Therefore the first
as defined in Equation 5(a). The n selected fields are labeled in the order with which they are chosen, and hence their label indicates their rank in terms of enclosed GW probability. Therefore the first  fields represent our optimized choice of the values of
fields represent our optimized choice of the values of  in Equation (7).
in Equation (7).
As shown in Equations (4), 5(b), and (7), the detection probability achieved by observing k selected fields can be expressed as the sum of the product of the EM and GW probabilities in each field. For each value of k in the range ![$[1,n]$](https://content.cld.iop.org/journals/0004-637X/834/1/84/revision1/apjaa4cd1ieqn38.gif) we apply a Lagrange multiplier to find the solution for the values
we apply a Lagrange multiplier to find the solution for the values  that maximize the detection probability given by Equation (7). This is subject to the constraints defined in Equation (8), and the value of k that returns the highest detection probability is identified as the optimal solution. The analysis therefore guides us as to which subset of fields should be observed with the selected telescope and how much time should be allocated to each of those selected fields given the total observation time constraint.
that maximize the detection probability given by Equation (7). This is subject to the constraints defined in Equation (8), and the value of k that returns the highest detection probability is identified as the optimal solution. The analysis therefore guides us as to which subset of fields should be observed with the selected telescope and how much time should be allocated to each of those selected fields given the total observation time constraint.
4. RESULTS
In this section we present the results of our algorithm using our four example telescopes applied to the follow-up of three simulated GW events. These events are taken from the data set used in Singer et al. (2014) and are designated with the IDs 28700, 19296, and 18694. The error regions for these events each cover  ,
,  , and
, and  , respectively, and details of these events are presented in Table 2. These events were chosen to represent the potential variation in sky localization ability of a global advanced detector network. We highlight that the actual injected distances for our chosen events are
, respectively, and details of these events are presented in Table 2. These events were chosen to represent the potential variation in sky localization ability of a global advanced detector network. We highlight that the actual injected distances for our chosen events are  ,
,  , and
, and  , respectively, while for our analysis we have assumed a distance of
, respectively, while for our analysis we have assumed a distance of  for each event. However, the validity of this work is not undermined. The injected events were originally simulated assuming a two-detector aLIGO first observational run configuration. Our analysis assumes a two- (three-) detector design sensitivity aLIGO configuration. The S/N and sky localization for an event at
for each event. However, the validity of this work is not undermined. The injected events were originally simulated assuming a two-detector aLIGO first observational run configuration. Our analysis assumes a two- (three-) detector design sensitivity aLIGO configuration. The S/N and sky localization for an event at  in the latter configuration is comparable (to within factors of ∼few) to events at a few tens
in the latter configuration is comparable (to within factors of ∼few) to events at a few tens  for the former configuration.
for the former configuration.
Figure 2 shows the optimized tiling of observing fields obtained using the greedy algorithm approach. For each telescope we show sky maps of the GW probability overlaid with the 90% coverage tiling choices for the three representative GW events. The FOVs of the telescopes range from  to
to  , and as such, the required number and location of tilings differ accordingly. The largest and smallest number of observation tilings are 230 and 7 for the largest GW error region (ID 28700) using HSC and for the smallest error region (ID 18694) using either Pan-Starrs or PTF,––– respectively.
, and as such, the required number and location of tilings differ accordingly. The largest and smallest number of observation tilings are 230 and 7 for the largest GW error region (ID 28700) using HSC and for the smallest error region (ID 18694) using either Pan-Starrs or PTF,––– respectively.
Figure 2. The optimized locations of the observing fields covering 90% of the GW probability for each telescope and for each of the three simulated GW events. Each row of plots corresponds to the four different telescopes (a) HSC, (b) DEC, (c) Pan-Starrs, and (d) PTF. Within each row we show the optimized observing field locations for the  event (ID 28700) on the left, the
event (ID 28700) on the left, the  event (ID 19296) in the center, and the
event (ID 19296) in the center, and the  event (ID 18694) on the right. In each plot the GW sky error is shown as a shaded region with the color bar indicating the value of the posterior probability density.
event (ID 18694) on the right. In each plot the GW sky error is shown as a shaded region with the color bar indicating the value of the posterior probability density.
Download figure:
Standard image High-resolution imageEach of the event maps is the result of an analysis assuming only two GW detectors. Without a third detector, the sky location of an event is restricted to a thin band of locations consistent with the single time-delay measurement between detectors. This degeneracy is partially broken with the inclusion of antenna response information resulting in extended arc structures. The third event that we consider (ID 18694) has sufficient S/N and suitable orientation with respect to the detector network for the sky region to be well localized and only partially extended with two detectors. We consider this event to be approximately representative of sky maps obtained from a three-detector network. We also note that given the imperfect duty factors of both the initial and advanced detectors, it is highly likely that future detections will be made while one or more detectors are offline. We therefore use the first two example events (ID 28700 and 19296) as simultaneously representative of such a two-detector scenario and of the potential situation in which a third detector is significantly less sensitive than the other two.
Figures 3–5 display the results of the simulated EM follow-up observations for the events labeled 28700, 19296, and 18694, respectively. From the top panels to the bottom panels, the assumed total observation times are 6 hr, 4 hr, and 2 hr. The plots on the left of the figure show the optimized detection probability  as a function of the total observed number of fields k. The plots on the right of the figure display the optimal time allocations corresponding to the value of k returning the highest detection probability (indicated by a circular marker in the detection probability plots on the left of the figure). The indices refer to the labels assigned to the fields when they are chosen by the greedy algorithm.
as a function of the total observed number of fields k. The plots on the right of the figure display the optimal time allocations corresponding to the value of k returning the highest detection probability (indicated by a circular marker in the detection probability plots on the left of the figure). The indices refer to the labels assigned to the fields when they are chosen by the greedy algorithm.
Figure 3. The results of simulated EM follow-up observations for the  GW event (ID 28700). We show the optimized EM detection probability as a function of the number of observing fields (left) and the allocated observing times for the optimal number of fields (right). The subfigures (a), (b) and (c) show results from three different total observation times for 6 hr, 4 hr, and 2 hr, respectively. For each total observation time, the four solid curves in each plot correspond to the optimal time allocation strategy applied to each of the four telescopes. The dashed lines show results for the equal time strategy. The solid markers and the circles indicate the number of observing fields at which the maximum detection probability is achieved using the optimal time allocation strategy and the equal time strategy, respectively.
GW event (ID 28700). We show the optimized EM detection probability as a function of the number of observing fields (left) and the allocated observing times for the optimal number of fields (right). The subfigures (a), (b) and (c) show results from three different total observation times for 6 hr, 4 hr, and 2 hr, respectively. For each total observation time, the four solid curves in each plot correspond to the optimal time allocation strategy applied to each of the four telescopes. The dashed lines show results for the equal time strategy. The solid markers and the circles indicate the number of observing fields at which the maximum detection probability is achieved using the optimal time allocation strategy and the equal time strategy, respectively.
Download figure:
Standard image High-resolution imageWe highlight the asymptotic behavior of the detection probability curves in Figures 3–5. This is due to a particular feature of our algorithm and is explained as follows. As the number of fields are increased, we approach an optimal value k* where to observe an addition field with any finite observation time would reduce the detection probability. This occurs where the gains from an additional field are outweighed by the losses incurred by reducing the lengths of the observations of the other fields. In this case, for a given value of k above the optimal value, the optimal choice is to allocate  to all fields with index greater than k*. If we know that we will allocate no time to these fields, then we also have no need to slew to them or to readout from the CCD. Hence the optimal time allocations and the detection probability for values of
to all fields with index greater than k*. If we know that we will allocate no time to these fields, then we also have no need to slew to them or to readout from the CCD. Hence the optimal time allocations and the detection probability for values of  remain constant at the maximum value.
remain constant at the maximum value.
Figure 4. The results of simulated EM follow-up observations for the  GW event (ID 19296). We show the optimized EM detection probability as a function of the number of observing fields (left) and the allocated observing times for the optimal number of fields (right). The subfigures (a), (b), and (c) show results from three different total observation times for 6 hr, 4 hr, and 2 hr, respectively. For each total observation time, the four solid curves in each plot correspond to the optimal time allocation strategy applied to each of the four telescopes. The dashed lines show results for the equal time strategy. The solid markers and the circles indicate the number of observing fields at which the maximum detection probability is achieved using the optimal time allocation strategy and the equal time strategy, respectively.
GW event (ID 19296). We show the optimized EM detection probability as a function of the number of observing fields (left) and the allocated observing times for the optimal number of fields (right). The subfigures (a), (b), and (c) show results from three different total observation times for 6 hr, 4 hr, and 2 hr, respectively. For each total observation time, the four solid curves in each plot correspond to the optimal time allocation strategy applied to each of the four telescopes. The dashed lines show results for the equal time strategy. The solid markers and the circles indicate the number of observing fields at which the maximum detection probability is achieved using the optimal time allocation strategy and the equal time strategy, respectively.
Download figure:
Standard image High-resolution imageAs a comparison, we introduce a second observing strategy for time allocation in which all the fields are observed with equal time. We call this method the equal time strategy. For each value of k, subject to the total observation time constraints and slew/readout time, the time allocated to each field is given by  . The values of
. The values of  obtained using this strategy are plotted as dashed lines in the plots on the left of Figures 3–5. The time allocations corresponding to the peaks of the dashed lines are plotted as flat lines (constant equal values) in the plots on the right of the figures. The resulting maximal probabilities and corresponding optimal number of fields for both time allocation strategies are given in Table 3 for all simulated events and total observation times. We also indicate the relative gains in detection probability obtained using our fully optimized (Lagrange multiplier) approach relative to the equal time strategy.
obtained using this strategy are plotted as dashed lines in the plots on the left of Figures 3–5. The time allocations corresponding to the peaks of the dashed lines are plotted as flat lines (constant equal values) in the plots on the right of the figures. The resulting maximal probabilities and corresponding optimal number of fields for both time allocation strategies are given in Table 3 for all simulated events and total observation times. We also indicate the relative gains in detection probability obtained using our fully optimized (Lagrange multiplier) approach relative to the equal time strategy.
Figure 5. The results of simulated EM follow-up observations for the  GW event (ID 18694). We show the optimized EM detection probability as a function of the number of observing fields (left) and the allocated observing times for the optimal number of fields (right). The subfigures (a), (b), and (c) show results from three different total observation times for 6 hr, 4 hr, and 2 hr, respectively. For each total observation time, the four solid curves in each plot correspond to the optimal time allocation strategy applied to each of the four telescopes. The dashed lines show results for the equal time strategy. The solid markers and the circles indicate the number of observing fields at which the maximum detection probability is achieved using the optimal time allocation strategy and the equal time strategy respectively.
GW event (ID 18694). We show the optimized EM detection probability as a function of the number of observing fields (left) and the allocated observing times for the optimal number of fields (right). The subfigures (a), (b), and (c) show results from three different total observation times for 6 hr, 4 hr, and 2 hr, respectively. For each total observation time, the four solid curves in each plot correspond to the optimal time allocation strategy applied to each of the four telescopes. The dashed lines show results for the equal time strategy. The solid markers and the circles indicate the number of observing fields at which the maximum detection probability is achieved using the optimal time allocation strategy and the equal time strategy respectively.
Download figure:
Standard image High-resolution imageTable 3. The EM Detection Probability Using Both the Optimal and Equal Time Strategies
| Telescope | Event ID | Strategy | EM Detection Probability (Optimal Number of Fields) | Relative Gain | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 hr | 4 hr | 2 hr | 6 hr | 4 hr | 2 hr | ||||||
| HSC | 28700 | LMa | 66.4% | (226) | 58.0% | (167) | 41.6% | (94) | 1.4% | 1.0% | 0.3% |
| ETb | 65.0% | (198) | 57.0% | (155) | 41.3% | (90) | |||||
| 19296 | LM | 78.1% | (106) | 75.1% | (100) | 65.3% | (76) | 1.1% | 1.4% | 1.6% | |
| ET | 77.0% | (103) | 73.7% | (93) | 63.7% | (71) | |||||
| 18694 | LM | 93.7% | (47) | 92.7% | (45) | 89.1% | (37) | 0.8% | 1.2% | 1.7% | |
| ET | 92.9% | (47) | 91.5% | (44) | 87.4% | (36) | |||||
| DEC | 28700 | LM | 49.4% | (69) | 41.7% | (56) | 28.1% | (35) | 1.4% | 1.0% | 0.5% |
| ET | 48.0% | (60) | 40.7% | (51) | 27.6% | (34) | |||||
| 19296 | LM | 71.5% | (50) | 64.7% | (41) | 52.6% | (19) | 4.3% | 3.8% | 1.1% | |
| ET | 67.2% | (39) | 60.9% | (32) | 51.5% | (17) | |||||
| 18694 | LM | 85.3% | (16) | 81.7% | (16) | 73.0% | (16) | 2.3% | 3.0% | 3.9% | |
| ET | 83.0% | (16) | 78.7% | (16) | 69.1% | (13) | |||||
| Pan-Starrs | 28700 | LM | 34.6% | (20) | 28.5% | (14) | 19.0% | (9) | 1.2% | 0.5% | 0.2% |
| ET | 33.4% | (17) | 28.0% | (13) | 18.8% | (9) | |||||
| 19296 | LM | 57.4% | (12) | 50.1% | (10) | 36.2% | (8) | 1.5% | 1.0% | 0.4% | |
| ET | 55.9% | (11) | 49.1% | (10) | 35.8% | (7) | |||||
| 18694 | LM | 77.2% | (7) | 71.5% | (7) | 59.7% | (5) | 4.0% | 3.7% | 1.4% | |
| ET | 73.2% | (6) | 67.8% | (5) | 58.3% | (3) | |||||
| PTF | 28700 | LM | 17.7% | (9) | 13.0% | (6) | 7.1% | (3) | 0.2% | 0.1% | 0.0% |
| ET | 17.5% | (8) | 12.9% | (6) | 7.1% | (3) | |||||
| 19296 | LM | 34.1% | (7) | 25.8% | (6) | 14.6% | (3) | 0.3% | 0.2% | 0.0% | |
| ET | 33.8% | (7) | 25.6% | (5) | 14.6% | (3) | |||||
| 18694 | LM | 56.9% | (4) | 50.1% | (3) | 34.9% | (3) | 0.8% | 0.9% | 1.4% | |
| ET | 56.1% | (3) | 49.2% | (3) | 33.5% | (3) | |||||
Notes.
aLM: Lagrange multiplier. bET: Equal time strategy.Download table as: ASCIITypeset image
In Figure 6 we provide an insight into the detection potential of future telescopes and those not included in our analysis. We have computed the detection probability  and corresponding optimal number of fields k as a function of arbitrary FOV and telescope sensitivity. We define this sensitivity via the quantity
and corresponding optimal number of fields k as a function of arbitrary FOV and telescope sensitivity. We define this sensitivity via the quantity  , the number of photons per m2 required for detection (see Equation (2)). For this general case we consider only a 6 hr total observation of each of the three simulated events. For reference we include the four telescopes we considered before plus the proposed Large Synoptic Survey Telescope (LSST) (Abell et al. 2009), which are plotted with points indicating their locations in the FOV and the telescope sensitivity plane. The relevant parameters for all included telescopes are given in Table 1.
, the number of photons per m2 required for detection (see Equation (2)). For this general case we consider only a 6 hr total observation of each of the three simulated events. For reference we include the four telescopes we considered before plus the proposed Large Synoptic Survey Telescope (LSST) (Abell et al. 2009), which are plotted with points indicating their locations in the FOV and the telescope sensitivity plane. The relevant parameters for all included telescopes are given in Table 1.
Figure 6. Contours of EM follow-up performance of kilonovae as a function of the size of telescope FOV and sensitivity assuming a 6 hr total observation. We show results for the three simulated GW events (a) event ID 28700,  , (b) event ID 19296
, (b) event ID 19296  , and event 18694
, and event 18694  . For each event we plot contours of equal detection probability (left) and the corresponding optimal number of observing fields (right). Overlayed for reference on all plots are the locations of the telescopes considered in this work (including the proposed LSST).
. For each event we plot contours of equal detection probability (left) and the corresponding optimal number of observing fields (right). Overlayed for reference on all plots are the locations of the telescopes considered in this work (including the proposed LSST).
Download figure:
Standard image High-resolution image5. DISCUSSION
The behavior of the detection probability as a function of the number of observed fields (as shown in Figures 3–5) shows that the two time-allocation strategies produce similar detection probabilities. In all cases the optimized approach gives marginally greater probability. As listed in Table 3, we see that for the particular cases examined in this work, the fully optimal approach leads to a typical gain of a few percent in detection probability over the equal time strategy. The greatest gains of  are obtained for the DEC telescope. These relatively modest gains suggests that spreading observation time equally is close to optimal at the optimal number of observing fields k*. We also note that the number of fields at which the peak detection probability is achieved is similar for both strategies, but always marginally lower for the equal time approach.
are obtained for the DEC telescope. These relatively modest gains suggests that spreading observation time equally is close to optimal at the optimal number of observing fields k*. We also note that the number of fields at which the peak detection probability is achieved is similar for both strategies, but always marginally lower for the equal time approach.
Both strategies clearly indicate that with a given telescope, a number of fields exist at which the probability of a successful EM follow-up is maximized for a given GW event and a fixed amount of total observation time. In other words, exploring more or fewer fields than necessary will result in a decrease in detection probability. Although one would expect that the probability of a successful EM follow-up first increases with the number of observed fields, a drop occurs when so many fields are observed that only short-exposure observations in some or all of the observed fields are allowed, given that the observation time is fixed. This trade-off between exploring new fields and achieving increased depth within fields is broadly consistent with Nissanke et al. (2013). For the same event, the peak detection probabilities increase overall as the total observation time increases. For the same telescope, the detection probability increases as the size of error region decreases. This is expected since smaller error regions mean that a telescope requires fewer fields to cover that region at a given confidence. By examining the curves in Figures 3–5, it can be seen that an increase in the total observation time shifts the position of the peak to more fields, but does not change the general shape of the function.
The time allocations shown in the plots on the right of Figures 3–5 are those computed for the optimal number of fields. In all cases, our optimal strategy ensures that proportionally more time will be assigned to those fields containing the greater fraction of GW probability (the lower index fields). In general, the range in observation times per field spans ∼1 order of magnitude for a given optimized observation. A surprising feature of these distributions is that the optimal time allocations can therefore differ by factors of a few per field with respect to the equal time distribution. However, both distributions result in very similar detection probabilities. Recently, Coughlin & Stubbs (2016) have produced an analytic result for the distribution of observing times under a number of simplifying assumptions, including a uniform prior on peak luminosity. They recommend that the time spent per field should be proportional to the prior GW probability in each field to the 2/3 power. We find that our numerical results are broadly consistent with this result, but again highlight that the relative gains in detection probability are quite insensitive to the time allocation distribution.
Figure 6 shows our results from another perspective, namely the optimal performance of any existing or future telescope of arbitrary sensitivity and FOV. As mentioned in Section 2, our treatment of the detection threshold criterion N* is simplified, and hence these results should be treated as illustrative rather than definitive. However, as might be expected, a telescope with poor sensitivity and small FOV will be unlikely to detect an EM counterpart unless the GW event is particularly well localized.
That LSST should explore more fields than PTF for these GW events may seem slightly confusing at first glance as the LSST FOV is larger than that of the PTF. This is because LSST is far more sensitive than PTF and can therefore explore as many fields as needed to cover the entire error region. In comparison, PTF has to spend a considerable fraction of its total observation time on each of its observed fields, which results in PTF being only able to observe a limited number of fields.
In general, the achieved EM detection probabilities are more sensitive to the telescope parameters for events with smaller error regions. For example, imagine that a telescope with a  FOV and a R-band limiting magnitude of 20.3 in 30 s (
FOV and a R-band limiting magnitude of 20.3 in 30 s ( ) needed to raise the detection probability
) needed to raise the detection probability  by 10%. For event 18694, where the size of the 90% credible region is
by 10%. For event 18694, where the size of the 90% credible region is  , it could either increase its FOV by a factor of
, it could either increase its FOV by a factor of  , or reduce its limiting magnitude to
, or reduce its limiting magnitude to  in 30 s. However, if the 90% credible region is
in 30 s. However, if the 90% credible region is  , as for event 28700, it would have to either further increase its FOV by a factor of
, as for event 28700, it would have to either further increase its FOV by a factor of  , or enhance its limiting magnitude to
, or enhance its limiting magnitude to  in 30 s to have the same improvement factor.
in 30 s to have the same improvement factor.
In addition, at high sensitivity the contours in Figure 6 appear to be almost flat, which means that as the size of the GW error region becomes larger, the FOV of a telescope has negligible impact on the detection probability  . For the design of future EM telescopes performing follow-up observations of GW events, there will likely be a trade-off between sensitivity and FOV. This result implies that for GW triggers with relatively large error regions, sensitivity, rather than FOV, is the dominant factor determining EM follow-up success. However, we recall that this result is based on particular choices of source and corresponding prior on the source luminosity (see Equation (6)). Different choices may have different impacts on the outcome of our method.
. For the design of future EM telescopes performing follow-up observations of GW events, there will likely be a trade-off between sensitivity and FOV. This result implies that for GW triggers with relatively large error regions, sensitivity, rather than FOV, is the dominant factor determining EM follow-up success. However, we recall that this result is based on particular choices of source and corresponding prior on the source luminosity (see Equation (6)). Different choices may have different impacts on the outcome of our method.
6. FUTURE WORK
This work considers source sky error regions based solely on the information obtained from low-latency GW sky localization (Singer & Price 2016). One may also include galaxy catalogs to further constrain source locations within our existing Bayesian approach. In this work, the GW source distance was assumed to be statistically independent of its sky location. In the future we plan to use more realistic distance information (Singer et al. 2016b), which will enhance the effectiveness of our follow-up optimization strategy.
Moreover, since telescopes are distributed at various latitudes and longitudes on the Earth, different telescopes are able to see different parts of the sky at different times. As has been studied by Rana et al. (2016), we would include the effect of observation prioritization when considering the diurnal cycle and for instances where GW sky error regions may pass below the horizon during a follow-up observation. Depending on the type of telescope, we would also incorporate factors such as the obscuration of the source by the Sun and/or Moon.
In this work, we ask the question of detecting kilonovae rather than identifying and characterizing them. The task of source identification is more demanding and will require the ability to differentiate our desired sources from contaminating backgrounds such as SNe and M-dwarf flares. One way to accomplish this is to perform multiple observations of the same fields. In this case, a tentative detection is followed by an observation of the candidate for a period of time until the source allows it to be classify as a kilonova or contaminating noise (Nissanke et al. 2013; Cowperthwaite & Berger 2015). As mentioned in Section 2, simply repeating our proposed observations would enable the identification of variable objects for deeper follow-ups. However, a more involved procedure could incorporate light-curve information into our strategy, thereby jointly optimizing the pointings used in both the detection and identification stages. This more complex strategy is left for future implementation.
7. CONCLUSION
In summary, we have demonstrated a proof-of-concept method for quantifying and maximizing the probability of a successful EM follow-up of a candidate GW event. We applied this method to kilonovae counterparts, but we emphasize that this method is versatile and applicable to any EM counterpart model. We showed that an optimal number of fields exists on which time should be spent, and that observing more or fewer fields will result in a decrease in the detection probability. This analysis was based on the assumptions of a static telescope with unconstrained pointings, a kilonova source at constant peak luminosity, and the independence of statistical uncertainty between the distance and the GW trigger sky location.
Our approach takes as inputs the GW sky localization information, and the characteristics of the selected telescope. The method selects the observed field locations with a greedy algorithm and then uses Lagrange multipliers to compute the time allocation for those fields based on maximizing the detection probability. We have tested the algorithm by optimizing the EM follow-up observations of the HSC, DEC, Pan-Starrs, and PTF telescopes for three simulated GW events. By comparing the results of our methods with the results of equally dividing the observation time among the observed fields, we have shown that both strategies return similar results, with our method producing marginally higher detection probabilities.
In addition, we have provided estimates for the EM follow-up performance of a general telescope of arbitrary sensitivity and FOV. These results indicate that in terms of telescope design, the likelihood of its success in the follow-up of kilonova signals is approximately independent of the FOV for reasonably sensitive telescopes.
To extend this work, it may be helpful to consider including constraints from galaxy catalogs on source location. In addition, the assumptions that the kilonova luminosity is constant during the observation period, a more realistic treatment of the source distance, and consideration of the dynamics of the telescope with respect to the source should be investigated. Finally, the inclusion of multiple observations of the same fields should be implemented to help distinguish kilonovae from contaminating sources.
We thank our colleague Xilong Fan, who provided insight and expertise that greatly assisted the research. We also thank Keiichi Maeda, Tomoki Morokuma, Hsin-Yu Chen, and Daniel Holz for assistance and comments that hugely improved the manuscript. This research is supported by The Scottish Universities Physics Alliance and Science and Technology Facilities Council. C. M. is supported by a Glasgow University Lord Kelvin Adam Smith Fellowship and the Science and Technology Research Council (STFC) grant No. ST/ L000946/1.
Footnotes
- 5
- 6
- 7
The rapid sky localization algorithm BAYESTAR has since been updated to also provide rapid distance posteriors (Singer et al. 2016a).
- 8
In practice, n can be slightly larger because of overlapping fields.
- 9









