ABSTRACT
Mass and radius are two of the most fundamental properties of an astronomical object. Increasingly, new planet discoveries are being announced with a measurement of one of these quantities, but not both. This has led to a growing need to forecast the missing quantity using the other, especially when predicting the detectability of certain follow-up observations. We present an unbiased forecasting model built upon a probabilistic mass–radius relation conditioned on a sample of 316 well-constrained objects. Our publicly available code, Forecaster, accounts for observational errors, hyper-parameter uncertainties, and the intrinsic dispersions observed in the calibration sample. By conditioning our model on a sample spanning dwarf planets to late-type stars, Forecaster can predict the mass (or radius) from the radius (or mass) for objects covering nine orders of magnitude in mass. Classification is naturally performed by our model, which uses four classes we label as Terran worlds, Neptunian worlds, Jovian worlds, and stars. Our classification identifies dwarf planets as merely low-mass Terrans (like the Earth) and brown dwarfs as merely high-mass Jovians (like Jupiter). We detect a transition in the mass–radius relation at 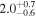 M⊕, which we associate with the divide between solid, Terran worlds and Neptunian worlds. This independent analysis adds further weight to the emerging consensus that rocky super-Earths represent a narrower region of parameter space than originally thought. Effectively, then, the Earth is the super-Earth we have been looking for.
M⊕, which we associate with the divide between solid, Terran worlds and Neptunian worlds. This independent analysis adds further weight to the emerging consensus that rocky super-Earths represent a narrower region of parameter space than originally thought. Effectively, then, the Earth is the super-Earth we have been looking for.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Over the last two decades, astronomers have discovered thousands of extrasolar worlds (see exoplanets.org; Han et al. 2014), filling in the parameter space from moon-sized planets (e.g., Barclay et al. 2013) to brown dwarfs many times more massive than Jupiter (e.g., Deleuil et al. 2008). Over 98% of these detections have come from radial velocity, microlensing, or transit surveys, yet each of these methods only directly measures the mass (M) or radius (R) of the planet, not both.1
This leads to the common situation where it is necessary to forecast what the missing quantity is based on the other. A typical case would be when one needs to predict the detectability of a potentially observable effect for a resource-intensive, time-competitive observing facility, which in some way depends upon the missing quantity. For example, the TESS mission (Ricker et al. 2014) will soon start detecting hundreds, possibly thousands, of nearby transiting planets for which the radius, but not the mass, will be measured. Planets with radii consistent with super-Earths will be of great interest for follow up and so radial velocity facilities will need to forecast the detectability, which is proportional to the planet mass, for each case. Conversely, the CHEOPS mission (Broeg et al. 2013) will try to detect the transits of planets discovered with radial velocities, necessitating a forecast of the radius based upon the mass.
In those two examples, the objective was to forecast the missing quantity in order to predict the feasibility of actually measuring it. However, the value of forecasting the mass/radius for the purposes of predicting detectability extends beyond this. As another example, exoplanet transit spectroscopy is expected to be a major function of the upcoming JWST mission (Seager et al. 2009). At the first-order level, the detectability of an exoplanet atmosphere is proportional to the scale height, H, which in turn is proportional to  . Given the limited supply of cryogen on board JWST, discoveries of future Earth-analog candidates may be found with insufficient time to reasonably schedule a radial velocity campaign first (if even detectable at all). Therefore, there will likely be a critical need to accurately forecast the scale height of new planet discoveries from just either the mass or (more likely) the radius.
. Given the limited supply of cryogen on board JWST, discoveries of future Earth-analog candidates may be found with insufficient time to reasonably schedule a radial velocity campaign first (if even detectable at all). Therefore, there will likely be a critical need to accurately forecast the scale height of new planet discoveries from just either the mass or (more likely) the radius.
Forecasting the mass/radius of an object based on the other quantity is most obviously performed using a mass–radius (MR) relation. Such relations are known to display sharp changes at specific locations, such as the transition from brown dwarfs to hydrogen-burning stars (e.g., see Hatzes & Rauer 2015). These transition points can be thought of as bounding a set of classes of astronomical objects, where the classes are categorized using the features of the inferred MR relation. In this case then, it is apparent that inference of the MR relation enables both classification and forecasting.
Classification is more than a taxonomical enterprise; it can have dramatic implications in astronomy. Perhaps the most famous example of classification in astronomy is the Hertzsprung–Russell (HR) diagram (Hertzsprung 1909; Russell 1914) for luminosity versus effective temperature, which revealed the distinct regimes of stellar evolution. A common concern in classification is that the very large number of possible features against which to frame the problem can be overwhelming. Mass and radius, though, are not random and arbitrary choices for framing such a problem. Rather, they are two of the most fundamental quantities describing any object in the cosmos and indeed represent two of the seven base quantities in the International System of Units (SI).
The value of classification extends beyond guiding physical understanding—it even affects the design of future instrumentation. As an example, the boundary between terrestrial planets and Neptune-like planets represents a truncation of the largest allowed habitable Earth-like body. The location of this boundary strongly affects estimates of the occurrence rate of Earth-like planets ( ) and thus in turn the design requirements of future missions needed to characterize such planets (Dalcanton et al. 2015). To illustrate this, using the occurrence rate posteriors of Foreman-Mackey et al. (2014),
) and thus in turn the design requirements of future missions needed to characterize such planets (Dalcanton et al. 2015). To illustrate this, using the occurrence rate posteriors of Foreman-Mackey et al. (2014),  decreases by 42% when altering the definition of Earth analogs from
decreases by 42% when altering the definition of Earth analogs from  R⊕ to
R⊕ to  R⊕. In order to maintain the same exo-Earth yield for the proposed HDST mission, this change corresponds to a 27% increase in the required mirror diameter (using the yield equation in Section 3.5.4 of Dalcanton et al. 2015).
R⊕. In order to maintain the same exo-Earth yield for the proposed HDST mission, this change corresponds to a 27% increase in the required mirror diameter (using the yield equation in Section 3.5.4 of Dalcanton et al. 2015).
We therefore argue that both forecasting and classification using the masses and radii of astronomical bodies will, at the very least, be of great utility for present/future missions and may also provide meaningful insights to guide our interpretation of these objects. Accordingly, the primary objective of this work is to build a statistically rigorous and empirically calibrated model
- 1.to forecast the mass/radius of an astronomical object based on a measurement of the other, and
- 2.for the classification of astronomical bodies based on their observed masses and/or radii.
The layout of this paper is as follows. In Section 2, we outline our model for the MR relation, which is used to enable forecasting and classification. In Section 3, we describe the regression algorithm used to conduct a Bayesian parameter estimation of our model parameters. The results, in terms of both classification and forecasting, are discussed separately in Sections 4 and 5. We summarize the main findings of our work in Section 6.
2. MODEL
2.1. Choosing a Model
We begin by describing the rationale behind the model used in this work. As discussed in Section 1 (and demonstrated later in Section 3), the two primary goals of this paper are both achievable through the use of an MR relation and this defines the approach in this work. Broadly speaking, such a relation can be cast as either a parametric (e.g., a polynomial) or non-parametric model (e.g., a nearest neighbor algorithm).
Parametric models, in particular power laws, have long been popular for modeling the MR relation with many examples even in the recent literature (e.g., Valencia et al. 2006; Weiss et al. 2013; Hatzes & Rauer 2015; Wolfgang et al. 2015; Zeng et al. 2016). In our case, we note that such models are more straightforward for hierarchical Bayesian modeling (which we argue to be necessary later), since they allow for a simple prescription of the Bayesian network. Moreover, based on those earlier cited works, power laws ostensbily do an excellent job of describing the data and the greater flexibility afforded by non-parametric methods is not necessary. Accordingly, we adopt the power-law prescription in this work.
As noted earlier, the use of power laws to describe the MR relation is common in the literature. However, many of the assumptions and model details in these previous implementations would make forecasts based on these relations problematic. We identify three key aspects of the model proposed in this work with differentiate our work from previous studies.
[1] Largest data range: Inferences of the MR relation often censor the available data to a specific subset of parameter space (for example, Wolfgang et al. 2015 consider the  R⊕ exoplanets). While it is inevitable that certain subjective choices will be made by those analyzing the MR relation, a more physically motivated choice for the parameter limits can be established. Ideally, this range should be as large as possible such that forecasting is unlikely to encounter the extrema, leading to truncation errors. A natural lower bound is an object with sufficient mass to achieve hydrostatic equilibrium leading to a nearly spherical shape and thus a well-defined radius (a planemo), which would encompass dwarf planets. As an upper bound, late-type stars take longer than a Hubble time to leave the main sequence a so should exhibit a relatively tight trend between mass and radius.
R⊕ exoplanets). While it is inevitable that certain subjective choices will be made by those analyzing the MR relation, a more physically motivated choice for the parameter limits can be established. Ideally, this range should be as large as possible such that forecasting is unlikely to encounter the extrema, leading to truncation errors. A natural lower bound is an object with sufficient mass to achieve hydrostatic equilibrium leading to a nearly spherical shape and thus a well-defined radius (a planemo), which would encompass dwarf planets. As an upper bound, late-type stars take longer than a Hubble time to leave the main sequence a so should exhibit a relatively tight trend between mass and radius.
[2] Fitted transitions: As a by-product of using such a wide mass range, several transitional regions are traversed where the MR relation exhibits sharp changes. For example, the onset of hydrogen burning leads to a dramatic change in the MR relation versus brown dwarfs (Hatzes & Rauer 2015). In previous works, such transitional points are often held as fixed, assumed locations (e.g., Weiss & Marcy 2014 assume a physically motivated, but not freely inferred, break at 1.5 R⊕). In contrast, we here seek to make a more agnostic, data-driven inference without imposing any assumed transition points from theory or previous data-driven inferences. In this way, the uncertainty in these transitions is propagated into the inference of all other parameters defining our model, leading to more robust uncertainty estimates for both forecasting and classification. Accordingly, in this work, the MR relation is described by a broken power law with freely fitted transition points (in addition to the other parameters).
[3] Probabilistic modeling: While mass can be considered to be the primary influence on the size of an object, many second-order terms will also play a role. As an example, rocky planets of the same mass but different core-mass fractions will exhibit distinct radii (Zeng et al. 2016). When viewed in the MR plane then, a particular choice of mass will not correspond to a singular radius value. Rather, a distribution of radii is expected, as a consequence of the numerous hidden second-order effects influencing the size. Statistically speaking then, the MR relation is expected to be probabilistic, rather than deterministic. A probabilistic model fundamentally relaxes the assumption that the underlying model (in our case a broken power law) is the "correct" or "true" description of the data, allowing an approximate model to absorb some (although it can never be all) of the error caused by model misspecification (in our case via an intrinsic dispersion). Naturally, the closer one's underlying model is to the truth, the smaller this probabilistic dispersion needs to be, and in the ultimate limit of a perfect model the probabilistic model tends toward a deterministic one. Since we do not make the claim that a broken power law is the true description of the MR relation, the probabilistic model is essential for reliable forecasting, as it enables predictions in spite of the fact our model is understood to not represent the truth.
While each of these three key features have been applied to MR relations in some form independently, a novel quality of our methodology is to adopt all three. For example, Wolfgang et al. (2015) inferred a probabilistic power law conditioned on the masses and radii of 90 exoplanets with radii below 8 R⊕. This range crosses the expected divide between solid planets and those with significant gaseous envelopes at 1.5–2.0 R⊕ (Lopez & Fortney 2014) and so the authors tried truncating the data at 1.6 R⊕ as an alternative model. In this work, we argue that the transitional points can actually be treated as free parameters in the model, enabling us to infer (rather than assume) their location and test theoretical predictions. Additionally, the data need not be censored at  R⊕, and the wider range makes a forecasting model less susceptible to truncation issues at the extrema (we point out that Wolfgang et al. 2015 did not set out to develop a forecasting model explicitly, and thus this is not a criticism of their work, but rather just an example of how our work differs from previous studies).
R⊕, and the wider range makes a forecasting model less susceptible to truncation issues at the extrema (we point out that Wolfgang et al. 2015 did not set out to develop a forecasting model explicitly, and thus this is not a criticism of their work, but rather just an example of how our work differs from previous studies).
2.2. Data Selection
Having broadly established the motivation (see Section 1) and requirements (see Section 2.1) for our model, we will use the rest of Section 2 to provide a more detailed account of our methodology. To begin, we first define our basic criteria for a data point (a mass and radius measurement) to be included in what follows. Since our work focuses on the MR relation, all included objects must fundamentally have a well-defined mass and radius. While the former is universally true, the latter requires that the object have a nearly spherical shape. Low-mass objects, for example the comet 67P/Churyumov-Gerasimenko, may not have sufficient self-gravity to overcome rigid body forces and assume a hydrostatic equilibrium shape (i.e., nearly spherical). The corresponding threshold mass limit should lie somewhere between the most massive body that is known to not be in hydrostatic equilibrium (Iapetus;  kg; Sheppard 2016) and the least massive body confirmed to be in hydrostatic equilibrium (Rhea;
kg; Sheppard 2016) and the least massive body confirmed to be in hydrostatic equilibrium (Rhea;  kg; Sheppard 2016). This leads us to adopt a boundary condition of
kg; Sheppard 2016). This leads us to adopt a boundary condition of  kg for all objects considered in this work.
kg for all objects considered in this work.
As for the upper limit, we choose the maximum mass to be that of a star that must still lie on the main sequence within a Hubble time. The lifetime of a star is dependent upon its mass and luminosity, to first order. Given that the Sun will spend 10 Gyr on the main sequence and  , then the lifetime
, then the lifetime  . This results in an upper limit of
. This results in an upper limit of  M⊙ (
M⊙ ( kg) for
kg) for  Gyr (where we set
Gyr (where we set  km s−1; Planck Collaboration et al. 2014). Therefore, between our lower and upper limits, there is a difference of nine orders of magnitude in mass and three orders of magnitude in radius.
km s−1; Planck Collaboration et al. 2014). Therefore, between our lower and upper limits, there is a difference of nine orders of magnitude in mass and three orders of magnitude in radius.
We performed a literature search for all objects within this range with a mass and radius measurement available. For solar system moons, we used The Giant Planet Satellite and Moon Page2 (Sheppard 2016) which is curated by Scott Sheppard (Sheppard & Jewitt 2003; Sheppard et al. 2005, 2006) and for the planets we used the NASA Planetary Fact Sheet3 (Williams 2016). For extrasolar planets, we used the TEPCat catalog4 of "well-studied transiting planets," curated by John Southworth (Southworth 2008, 2009, 2010, 2011, 2012). Brown dwarfs and low-mass stars were drawn from a variety of sources, which we list (along with all other objects used in this work) in Table 1.
Table 1. Masses and Radii Used for This Study
| Name | Mass | Radius | Reference |
|---|---|---|---|
| NGC 6791 KR V20 |
 M⊙ M⊙ |
 R⊙ R⊙ |
Torres et al. (2010) |
| HD 124784 |
 M⊙ M⊙ |
 R⊙ R⊙ |
Torres et al. (2010) |
| Parenago 1478 |
 M⊙ M⊙ |
 R⊙ R⊙ |
Torres et al. (2010) |
| HD 7700 |
 M⊙ M⊙ |
 R⊙ R⊙ |
Torres et al. (2010) |
| BD+34 4217 |
 M⊙ M⊙ |
 R⊙ R⊙ |
Torres et al. (2010) |
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
In order to later fit these data sources to an MR model, it is necessary to define a likelihood function for each datum. We later (see Section 2.9) make the assumption that for a quoted mass (or radius) measurement of  , one can reasonably approximate
, one can reasonably approximate  . This assumption is a poor one for low signal-to-noise data, especially for upper limit constraints only, where M (or R) is more likely to follow an asymmetric profile centered near zero. Without knowledge of the correct likelihood function, we argue that such data are best excluded in what follows.
. This assumption is a poor one for low signal-to-noise data, especially for upper limit constraints only, where M (or R) is more likely to follow an asymmetric profile centered near zero. Without knowledge of the correct likelihood function, we argue that such data are best excluded in what follows.
For this reason, we apply a 3σ cut to both mass ( ) and radius (
) and radius ( ). In what follows, we assume that both the mass and radius measurements follow a normal distribution, which is symmetric. For those data that have substantially asymmetric errors (
). In what follows, we assume that both the mass and radius measurements follow a normal distribution, which is symmetric. For those data that have substantially asymmetric errors ( ) then, we only use cases where the errors differ by less than 10% (i.e.,
) then, we only use cases where the errors differ by less than 10% (i.e.,  ). Together, these cuts remove 16% of the initial data, which, as discussed later in Section 3.3, do not bias (or even noticeably influence) our final results. Next, we take the average of both errors
). Together, these cuts remove 16% of the initial data, which, as discussed later in Section 3.3, do not bias (or even noticeably influence) our final results. Next, we take the average of both errors  as the standard deviation of the normal distribution. In the end, we have 316 objects in total which are listed in Table 1.
as the standard deviation of the normal distribution. In the end, we have 316 objects in total which are listed in Table 1.
The data span a diverse range of environments, with a variety orbital periods, insolations, metallicities, etc. Since these terms are not used in our analysis, the results presented here should be thought of as an MR relation marginalized over all of these other terms. Once again, we stress that the effects of these terms is naturally absorbed by the probabilistic framework of our model, meaning that forecasts may be made about any new data, provided it can be considered representative of the data used for our analysis.
2.3. Probabilistic Broken Power Law
We elect to model the MR relation with a probabilistic broken power law, for the reasons described in Section 2.1. By probabilistic, we mean that this model includes intrinsic dispersion in the MR relation to account for additional variance beyond that of the formal measurement uncertainties. This dispersion represents the variance observed in nature itself around our broken power-law model. To put this in context, a deterministic MR power law would be described by

where  and
and  are the mass and radius of the object, respectively, and
are the mass and radius of the object, respectively, and  and
and  are the parameters describing the power law. However, it is easy to conceive of two objects with the exact same mass but different compositions, thereby leading to different radii. For this reason, we argue that a deterministic model provides an unrealistic description of the MR relation. In the probabilistic model, for any given mass there is a corresponding distribution of radii. In this work, we assume a normal distribution in the logarithm of the radius. The mean of the distribution takes the result of the deterministic model, and the standard deviation is the intrinsic dispersion, a new free parameter.
are the parameters describing the power law. However, it is easy to conceive of two objects with the exact same mass but different compositions, thereby leading to different radii. For this reason, we argue that a deterministic model provides an unrealistic description of the MR relation. In the probabilistic model, for any given mass there is a corresponding distribution of radii. In this work, we assume a normal distribution in the logarithm of the radius. The mean of the distribution takes the result of the deterministic model, and the standard deviation is the intrinsic dispersion, a new free parameter.
A power-law relation can be converted to a linear relation by taking the logarithm on both axes. In practice, we take the logarithm base 10 of both mass and radius in Earth units, and use a linear relation to fit them. In what follows, we will use  and
and  to represent mass and radius, and
to represent mass and radius, and  and
and  to represent
to represent  and
and  . The power-law relation turns into
. The power-law relation turns into

where  ,
,  , and
, and  . In what follows, we will use
. In what follows, we will use  as the normal distribution, where μ is the mean and σ is the standard deviation. The corresponding probabilistic relation in log scale becomes
as the normal distribution, where μ is the mean and σ is the standard deviation. The corresponding probabilistic relation in log scale becomes

On a logarithmic scale, the data still approximately follow normal distributions, because the logarithm of a normal distribution is approximately a normal distribution when the standard deviation is small relative to the mean, which is true here since we made a 3σ cut in both mass and radius. The original data,  , will turn into
, will turn into  , where
, where  and
and  .
.
We consider it more reasonable to assume that the intrinsic dispersion in radius will be a fractional dispersion rather than an absolute dispersion. For example, the dispersion of Earth-radius planets might be ![${ \mathcal O }[0.1\,{R}_{\oplus }]$](https://content.cld.iop.org/journals/0004-637X/834/1/17/revision1/apjaa4b8cieqn53.gif) but for stars it should surely be much larger in an absolute sense. Since a fractional dispersion on a linear scale corresponds to an absolute dispersion on logarithmic scale, this assumption is naturally accounted for by our model. To implement the probabilistic model, we employ a hierarchical Bayesian model, or HBM for short.
but for stars it should surely be much larger in an absolute sense. Since a fractional dispersion on a linear scale corresponds to an absolute dispersion on logarithmic scale, this assumption is naturally accounted for by our model. To implement the probabilistic model, we employ a hierarchical Bayesian model, or HBM for short.
2.4. Hierarchical Bayesian Modeling
The difference between an HBM and the more familiar Bayesian method is that HBMs have two sets of parameters: a layer of hyper parameters,  , on top of the local parameters,
, on top of the local parameters,  (see Hogg et al. 2010 for a pedagogical explanation). The local parameters usually describe the properties of each individual datum, while the hypers describe the overall ensemble properties. For example, in this work, the local parameters are the true
(see Hogg et al. 2010 for a pedagogical explanation). The local parameters usually describe the properties of each individual datum, while the hypers describe the overall ensemble properties. For example, in this work, the local parameters are the true  ,
,  (or
(or  ,
,  ) of all the objects, and the hyper parameters,
) of all the objects, and the hyper parameters,  , are those that represent the broken power law. This hierarchical structure is illustrated in Figure 1, which may be compared to the analogous graphical model shown in Figure 1 of Wolfgang et al. (2015). Some of the first applications of this method are Loredo & Wasserman (1995), Graziani & Lamb (1996), and Hogg et al. (2010) (in exoplanet research).
, are those that represent the broken power law. This hierarchical structure is illustrated in Figure 1, which may be compared to the analogous graphical model shown in Figure 1 of Wolfgang et al. (2015). Some of the first applications of this method are Loredo & Wasserman (1995), Graziani & Lamb (1996), and Hogg et al. (2010) (in exoplanet research).
Figure 1. Graphical model of the HBM used to infer the probabilistic MR relation in this work. Yellow ovals represent hyper parameters, white ovals represent the true local parameters, and gray ovals represent data inputs. All objects on the plate have N members.
Download figure:
Standard image High-resolution imageFor the local parameters, we define a mass,  , and radius,
, and radius,  , term for each object, giving 632 local variables. In practice, the
, term for each object, giving 632 local variables. In practice, the  local parameters are related to the
local parameters are related to the  term through the broken power law and each realization of the hyper parameters. In total then, our model includes 632 local parameters and a compact set of hyper parameters, as described later in the Markov Chain Monte Carlo (MCMC) subsection.
term through the broken power law and each realization of the hyper parameters. In total then, our model includes 632 local parameters and a compact set of hyper parameters, as described later in the Markov Chain Monte Carlo (MCMC) subsection.
2.5. Continuous Broken Power-law Model
Plotting the masses and radii on a log–log scale (as shown later in Figure 3), it is clear that a single, continuous power law is unable to provide a reasonable description of the data. For example, one might reasonably expect that the Neptune-like planets follow a different MR relation from the terrestrial planets, since the voluminous gaseous envelope of the former dominates their radius (Lopez & Fortney 2014). This therefore argues in favor of using a segmented (or broken) power law.
At least three fundamentally distinct regimes are expected using some simple physical insights: a segment each for terrestrial planets, gas giants, and stars. Indeed, the MR data clearly show distinct changes in the power-index, corresponding to the transition points between each segment. However, a visual inspection also reveals a turnover in the MR relation at around a Saturn mass. Therefore, from one roughly Saturn mass to the onset of stars, there is a strong case for a fourth segment, which we consequently include in our model. Later, in Section 3.2, we perform a model comparison of a three-segment versus four-segment model to validate the fact that the four-segment broken power law is strongly favored.
Our favored model consists of 12 free hyper parameters: 1 offset ( ), 4 slopes (
), 4 slopes ( ), 4 intrinsic dispersions (
), 4 intrinsic dispersions ( ), and 3 transition points (
), and 3 transition points ( ). Critically then, we actually fit for the location of transition points and include an independent intrinsic dispersion for each segment (making our model probabilistic). Also note that the "slopes" in log–log space are the power-law indices in linear space. The hyper-parameter vector is therefore
). Critically then, we actually fit for the location of transition points and include an independent intrinsic dispersion for each segment (making our model probabilistic). Also note that the "slopes" in log–log space are the power-law indices in linear space. The hyper-parameter vector is therefore

There is only one free parameter for the offset since we impose the condition that each segment of the power law is connected, i.e., a continuous broken power law. By requiring that two segments meet at the transition point between them, we can derive the offsets for the rest of the segments. At each transition point  ,
,

We can now iteratively derive the other offsets as

2.6. Hyper Priors
The hyper priors, that is, the priors on the hyper parameters, are selected to be sufficiently broad to allow an extensive exploration of parameter space and to be identical for each segment. Uniform priors are used for the location parameters, namely the offset,  , and transition points,
, and transition points,  . For scale parameters, namely the intrinsic dispersion
. For scale parameters, namely the intrinsic dispersion  , we adopt log-uniform priors.
, we adopt log-uniform priors.
For the slope parameters, we do not want to constrain them to a specific range, so we use the normal distribution with a large variance. This leads to a prior that is approximately uniform in any small region yet loosely constrains the MCMC walkers to the relevant scale of the data. A detailed list of the priors is provided in Table 2.
Table 2. Description and Posterior of Hyper Parameters
 term term |
Description | Credible Interval |
|---|---|---|
 R⊕ R⊕ |
Power-law constant for the Terran (T-class) worlds MR relation |
 R⊕ R⊕ |

|
Power-law index of Terran worlds; 
|

|

|
Power-law index of Neptunian worlds; 
|

|

|
Power-law index of Jovian worlds; 
|

|

|
Power-law index of Stellar worlds; 
|

|

|
Fractional dispersion of radius for the Terran MR relation |
 % % |

|
Fractional dispersion of radius for the Neptunian MR relation |
 % % |

|
Fractional dispersion of radius for the Jovian MR relation |
 % % |

|
Fractional dispersion of radius for the Stellar MR relation |
 % % |
 M⊕ M⊕ |
Terran-to-Neptunian transition point |
 M⊕ M⊕ |
 M⊕ M⊕ |
Neptunian-to-Jovian class transition point |
 MJ MJ |
 M⊕ M⊕ |
Jovian-to-Stellar class transition point |
 M⊙ M⊙ |
Note. The prior distributions of the hyper parameters are 

![${\mathrm{log}}_{10}[{\sigma }_{{ \mathcal R }}^{(1-4)}]\sim { \mathcal U }(-3,2);$](https://content.cld.iop.org/journals/0004-637X/834/1/17/revision1/apjaa4b8cieqn104.gif)
 .
.
Download table as: ASCIITypeset image
2.7. Two Different Categories of Local Parameters
The local parameters in our model are formally  and
and  , although in practice
, although in practice  does not need to be fitted explicitly since it is derived from the realization of the broken power law (as described in more detail later).
does not need to be fitted explicitly since it is derived from the realization of the broken power law (as described in more detail later).
Even for  though, there are two categories that we must distinguish between. Objects within the solar system tend to have very precise measurements of their fundamental properties such that their formal uncertainties are negligible relative to the uncertainties encountered for extrasolar objects, for which we must account for the measurement uncertainty in our model.
though, there are two categories that we must distinguish between. Objects within the solar system tend to have very precise measurements of their fundamental properties such that their formal uncertainties are negligible relative to the uncertainties encountered for extrasolar objects, for which we must account for the measurement uncertainty in our model.
For objects with negligible error, we simply fix  and
and  , since
, since  . For objects in the second category,
. For objects in the second category,  are set to be independently uniformly distributed in [−4, 6]. Throughout the paper, we will use
are set to be independently uniformly distributed in [−4, 6]. Throughout the paper, we will use  to denote a uniform distribution, where a and b are the lower and upper bounds of the distribution, so for example
to denote a uniform distribution, where a and b are the lower and upper bounds of the distribution, so for example

2.8. Inverse Sampling
We use the inverse sampling method to sample the parameters  and
and  . By inverse sampling, we mean that the walkers directly sample in the probability space rather than the parameter space itself. By directly walking in the prior probability space with a Gaussian function as our proposal distribution, inverse sampling is more efficient than walking in real space plus likelihood penalization (see Devroye 1986 for further details on the inverse sampling method).
. By inverse sampling, we mean that the walkers directly sample in the probability space rather than the parameter space itself. By directly walking in the prior probability space with a Gaussian function as our proposal distribution, inverse sampling is more efficient than walking in real space plus likelihood penalization (see Devroye 1986 for further details on the inverse sampling method).
For each jump in the MCMC chain, we sample a probability,  , for each parameter with
, for each parameter with  . We then determine this parameter's cumulative distribution from its prior probability distribution. With
. We then determine this parameter's cumulative distribution from its prior probability distribution. With  and the cumulative distribution, we can then calculate the corresponding sample of the parameter.
and the cumulative distribution, we can then calculate the corresponding sample of the parameter.
The equations of the prior distributions of  and
and  are already shown in Table 2 and Equation (7). With inverse sampling, the effects of the priors have already been accounted for, meaning that we do not need to add the prior probabilities of a parameter into the total log-likelihood function.
are already shown in Table 2 and Equation (7). With inverse sampling, the effects of the priors have already been accounted for, meaning that we do not need to add the prior probabilities of a parameter into the total log-likelihood function.
2.9. Total Log-likelihood
As discussed above, since  and
and  are drawn with inverse sampling, then there is no need to add corresponding penalty terms to the log-likelihood function. The total log-likelihood is now based on how we sample
are drawn with inverse sampling, then there is no need to add corresponding penalty terms to the log-likelihood function. The total log-likelihood is now based on how we sample  from
from  and
and  , and the relations among
, and the relations among  ,
,  , and the data. The relations are given by
, and the data. The relations are given by

When  , the above equation can be interpreted as
, the above equation can be interpreted as  , which corresponds to the case where measurement errors are zero. This is also true for
, which corresponds to the case where measurement errors are zero. This is also true for  , such that
, such that

and

where we define

Combining Equations (9) and (10), we have

Equation (12) shows that if we have already sampled  and
and  , we no longer need to sample
, we no longer need to sample  since
since  can be directly related to
can be directly related to  and
and  . From Equations (8) and (12), we can see that the total log-likelihood of the model is
. From Equations (8) and (12), we can see that the total log-likelihood of the model is


Note that in the above, we assume the mass and radius have no covariance, which is almost always true given the independent methods of their measurement.
3. ANALYSIS
3.1. Parameter Inference with Markov Chain Monte Carlo
We used the MCMC method with the Metropolis algorithm (Metropolis et al. 1953) to explore the parameter space and infer the posterior distributions for both the hyper and local parameters. The Metropolis algorithm uses jumping walkers, proceeding by accepting or rejecting each jump by comparing its likelihood with that of the previous step. Since we have 12 hyper parameters and 316 data points (corresponding to 316  ), the walker jumps in a probability hyper-cube of (12+316) dimensions.
), the walker jumps in a probability hyper-cube of (12+316) dimensions.
We begin by running five independent initial chains for 500,000 accepted steps each, seeding the parameters  from 0.5, 2, and 4 with Gaussian distributions of sigma one (but keeping all others terms drawn seeded from a random sample from the hyper priors).
from 0.5, 2, and 4 with Gaussian distributions of sigma one (but keeping all others terms drawn seeded from a random sample from the hyper priors).
We identify the burn-in point by eye, searching for the instant where the local variance in the log-likelihood (with respect to chain step) stabilizes to a relatively small scatter in comparison to the initial steps. This burn-in point tended to occur after ≃200,000 accepted steps, largely driven by the fact that both the hyper and local parameters were not seeded from a local minimum (with the exception of  ) and therefore required a substantial number of steps to converge.
) and therefore required a substantial number of steps to converge.
Combining these initial chains, we chose 10 different realizations that have the highest log-likelihood but also not too close to each other. We then start 10 new independent chains, where each chain is seeded from one of the top 200 log-like solutions found from the stacked initial chains. We run each of these 10 chains for 107 trials with acceptance rate  (i.e., 500,000 accepted steps each) and find, as expected, that each chain is burnt-in right from the beginning.
(i.e., 500,000 accepted steps each) and find, as expected, that each chain is burnt-in right from the beginning.
To check for adequate mixing, we calculated the effective length, defined as the length of the chain divided by the correlation length, where the correlation length is defined as  (Tegmark et al. 2004). We find that the sum of the effective lengths exceeds 2000 (i.e., is
(Tegmark et al. 2004). We find that the sum of the effective lengths exceeds 2000 (i.e., is  ), indicating good mixing. We also verified that the Gelman–Rubin statistic (Gelman & Rubin 1992) dropped below 1.1 (it was 1.02), indicating that the chains had converged. Finally, we thinned the 10 chains by a factor of 100 and stacked them together, which gives a combined chain of length of 106. The hyper-parameter posteriors, available at github.com/chenjj2/forecaster, are shown as a triangle plot in Figure 2. We list the median and corresponding 68.3% confidence interval of each hyper-parameter posterior in Table 2. Our model, evaluated at the spatial median of the hyper parameters, is shown in Figure 3 compared to the data on which it was conditioned. The spatial median simply finds the sample from the joint posterior that minimizes the Euclidean distance to all other samples.
), indicating good mixing. We also verified that the Gelman–Rubin statistic (Gelman & Rubin 1992) dropped below 1.1 (it was 1.02), indicating that the chains had converged. Finally, we thinned the 10 chains by a factor of 100 and stacked them together, which gives a combined chain of length of 106. The hyper-parameter posteriors, available at github.com/chenjj2/forecaster, are shown as a triangle plot in Figure 2. We list the median and corresponding 68.3% confidence interval of each hyper-parameter posterior in Table 2. Our model, evaluated at the spatial median of the hyper parameters, is shown in Figure 3 compared to the data on which it was conditioned. The spatial median simply finds the sample from the joint posterior that minimizes the Euclidean distance to all other samples.
Figure 2. Triangle plot of the hyper-parameter joint posterior distribution (generated using corner.py [github.com/dfm/corner.py.git]; Foreman-Mackey 2016). Contours denote the 0.5σ, 1.0σ, 1.5σ, and 2.0σ confidence intervals.
Download figure:
Standard image High-resolution imageFigure 3. Mass–radius relation from dwarf planets to late-type stars. Points represent the 316 data points against which our model is conditioned, with the data key in the top left. Although we do not plot the error bars, both radius and mass uncertainties are accounted for. The red line shows the mean of our probabilistic model and the surrounding light and dark gray regions represent the associated 68% and 95% confidence intervals, respectively. The plotted model corresponds to the spatial median of our hyper-parameter posterior samples.
Download figure:
Standard image High-resolution image3.2. Model Comparison
The model with four segments was at first selected by visual inspection of the data. Two of the three transition points, T(1) and T(3), occur at locations that can be associated with physically well-motivated boundaries (planets accreting volatile envelopes Rogers 2015, and hydrogen burning Dieterich et al. 2014), whereas the T(2) transition is not as physically intuitive.
In order to demonstrate that this model is statistically favored over the three-segment model, we repeated all of the fits for a simpler three-segment model. We seed the remaining two transition points from the approximate locations of T(1) and T(3) found from the four-segment model fit. We label this model as  and the four-segment model used earlier as
and the four-segment model used earlier as  .
.
For this simpler model,  uses only two transition points, which break the data into three different segments. To implement this model, the only difference is that the hyper-parameter vector
uses only two transition points, which break the data into three different segments. To implement this model, the only difference is that the hyper-parameter vector  becomes
becomes

We find that the maximum log-likelihood of  is considerably less than that of
is considerably less than that of  , less by 34.16 (corresponding to
, less by 34.16 (corresponding to  for 316 data points) at the gain of just three fewer free parameters. The marginal likelihood cannot be easily computed in the very high dimensional parameter space of our problem, and the Bayesian and Akaike information criteria (BIC, Schwarz 1978 and AIC, Akaike 1974) are also both invalid for such high dimensionality. Instead, we used the Deviance information criterion (DIC, Spiegelhalter et al. 2002), a hierarchical modeling generalization of the AIC, to compare the two models. When comparing two models with the DIC, the smaller value is understood to the preferred model. We find that
for 316 data points) at the gain of just three fewer free parameters. The marginal likelihood cannot be easily computed in the very high dimensional parameter space of our problem, and the Bayesian and Akaike information criteria (BIC, Schwarz 1978 and AIC, Akaike 1974) are also both invalid for such high dimensionality. Instead, we used the Deviance information criterion (DIC, Spiegelhalter et al. 2002), a hierarchical modeling generalization of the AIC, to compare the two models. When comparing two models with the DIC, the smaller value is understood to the preferred model. We find that  and
and  , indicating a strong preference for model
, indicating a strong preference for model  .
.
3.3. The Effect of our Data Cuts
As discussed earlier in Section 2.2, our data cuts removed 16% of the initial data considered. Since these points are low S/N data, they, by definition, have a weak effect on the likelihood function. As evident in Figure 3, there is an abundance of precise data constraining the slope parameters in each segment and none of the segments can be described as residing in a poorly constrained region. Given that the transition points are defined as the intercept of the slopes, they too are well constrained by virtue of the construction of our model. Critically, then, a paucity of data at the actual transition point locations (as is true for T(1)) has little influence on our inference of their locations. In order for the results of this work to be significantly affected by the exclusion of these low S/N data then, these points would have to have modified the inference of the slope parameters.
To demonstrate this effect is negligible, we consider the Neptunian segment in isolation, since it strongly affects the critical transition T(1) and features the largest fraction of excluded points (24%). Since the excluded data were due to lossy mass measurements, we ignore the radius errors and perform a simple weighted linear least-squares regression with and without the excluded data, where we approximate the observations to be normally distributed. We find that the slope parameter, S(2), changes from 0.782 ± 0.058 to 0.784 ± 0.050 by re-introducing the excluded data, illustrating the negligible impact of these data.
3.4. Injection/Recovery Tests
In order to verify the robustness of our algorithm, we created 10 fake data sets and blindly ran our algorithm again on each. The data sets are generated by making a random, fair draw from our joint posteriors (both the local and hyper parameters), ensuring that each draw is from a different effective chain. We then re-ran our original algorithm as before, except the number of steps in the final chain is reduced by a factor of 10 for computational expedience.
We computed the 1σ and 2σ credible intervals on each hyper-parameter and compare them to the injected truth in Figure 4. As evident from this figure, we are able to easily recover all of the inputs to within the expected range, validating the robustness of the main results presented in this work.
Figure 4. Each sub-panel shows the residuals of a hyper-parameter in our model, as computed between 10 injected truths and the corresponding recovered values. The black square denotes the recovered posterior median and the dark and light gray bars denote the 1σ and 2σ confidence intervals. The green horizontal bar marks the zero-point expected for a perfect recovery.
Download figure:
Standard image High-resolution image4. CLASSIFICATION
4.1. Classification with an MR Relation
A unique aspect of this work was to use freely fitted transitional points in our MR relation. As discussed earlier, these transitional points essentially classify the data between distinct categories, where the class boundaries occur in mass and are defined using the feature of  . Such classes are evident even from visual inspection of the MR data (see Figure 3), but our Bayesian inference of a self-consistent probabilistic broken power law provides statistically rigorous estimates of these class boundaries. In what follows, we discuss the implications of the inferred locations of the class boudnaries (
. Such classes are evident even from visual inspection of the MR data (see Figure 3), but our Bayesian inference of a self-consistent probabilistic broken power law provides statistically rigorous estimates of these class boundaries. In what follows, we discuss the implications of the inferred locations of the class boudnaries ( ,
,  , and
, and  ).
).
4.2. Naming the Classes
Rather than refer to each class as segments 1, 2, 3, and 4, we here define a name for each class to facilitate a more physically intuitive discussion of the observed properties. A naming scheme based on the physical processes operating is appealing but ultimately disingenuous since our model is deliberately chosen to be a data-driven inference, free of physical assumptions about the mechanics and evolution sculpting these worlds. We consider it more appropriate, then, to name each class based on a typical and well-known member.
For segment 2, Neptune and Uranus are typical members and are of course very similar to one another in basic properties. We therefore consider this class to define a sub-sample of Neptune-like worlds, or "Neptunian" worlds more succinctly. Similarly, we identify Jupiter as a typical member of segment 3, unlike Saturn which lies close to a transitional point. Accordingly, we define this sub-sample to be representative of Jupiter-like worlds, or "Jovian" worlds.
For the hydrogen-burning late-type stars of segment 4, these objects can be already classified by their spectral types spanning M, K, and late-type G dwarfs. Rather than refer to them as M/K/late-G class stars, we simply label them as stars for the sake of this work and for consistency with the "worlds" taxonomy dub them "Stellar" worlds.
Finally, we turn to segment 1, which is comprised largely of solar system members and thus all of which are relatively well-known. The objects span dwarf planets to terrestrial planets, silicate worlds to icy worlds, making naming this broad class quite challenging. Additionally, calling this class Earth-like worlds would be confusing given the usual association of this phrase with habitable, Earth analogs. For consistency with the naming scheme used thus far, we decided that dubbing these objects as "Terran" worlds to be the most appropriate.
4.3.
 : The Terran–Neptunian Worlds Divide
: The Terran–Neptunian Worlds Divide
From masses of ∼10−4 M⊕ to a couple of Earth masses, we find that a continuous power law of  provides an excellent description of these Terran worlds. No break is observed between "dwarf planets" and "planets." If the Terrans displayed a constant mean density, then we would expect
provides an excellent description of these Terran worlds. No break is observed between "dwarf planets" and "planets." If the Terrans displayed a constant mean density, then we would expect  , and so the slightly depressed measured index indicates modest compression with increasing mass (
, and so the slightly depressed measured index indicates modest compression with increasing mass ( ). Our result is in close agreement with theoretical models, which typically predict
). Our result is in close agreement with theoretical models, which typically predict  for Earth-like compositions (e.g., see Valencia et al. 2006).
for Earth-like compositions (e.g., see Valencia et al. 2006).
We find the first transition to be located at  M⊕, defining the transition from Terrans to Neptunians. After this point, the density trend reverses with
M⊕, defining the transition from Terrans to Neptunians. After this point, the density trend reverses with  , indicating the accretion of substantial volatile gas envelopes. This transition is not only evident in the power-law index, but also in the intrinsic dispersion, which increases by a factor of
, indicating the accretion of substantial volatile gas envelopes. This transition is not only evident in the power-law index, but also in the intrinsic dispersion, which increases by a factor of  from Terrans to Neptunians. This transition point is of major interest to the community, since it caps the possibilities of rocky, habitable super-Earth planets, with implications for future missions designs (e.g., see Dalcanton et al. 2015).
from Terrans to Neptunians. This transition point is of major interest to the community, since it caps the possibilities of rocky, habitable super-Earth planets, with implications for future missions designs (e.g., see Dalcanton et al. 2015).
Our result is compatible with independent empirical and theoretical estimates of this transition. Starting with the former, we compare our result to Rogers (2015), who sought the transition in radius rather than mass. This was achieved by identifying radii thayt exceed that of a solid planet, utilizing a principle first proposed by Kipping et al. (2013). Assuming an Earth-like compositional model, the radius threshold was inferred to be  R⊕ (Rogers 2015). Our result may be converted to a radius by using our derived relation. However, since our model imposes intrinsic radius dispersion (i.e., the probabilistic nature of our model), then the uncertainty in radius is somewhat inflated by this process. Nevertheless, we may convert our mass posterior samples to fair radii realizations using our Forecaster public code (described later in Section 5).5
Accordingly, we find that the transition occurs at
R⊕ (Rogers 2015). Our result may be converted to a radius by using our derived relation. However, since our model imposes intrinsic radius dispersion (i.e., the probabilistic nature of our model), then the uncertainty in radius is somewhat inflated by this process. Nevertheless, we may convert our mass posterior samples to fair radii realizations using our Forecaster public code (described later in Section 5).5
Accordingly, we find that the transition occurs at  R⊕, which is fully compatible with Rogers (2015).
R⊕, which is fully compatible with Rogers (2015).
A comparison to theory comes from Lopez & Fortney (2014), who scale down compositional models of gaseous planets to investigate the minimum size of a H-/He-rich sub-Neptune. From this theoretical exercise, the authors estimate that 1.5 R⊕ is the minimum radius of a H-/He-rich sub-Neptune, which is also compatible with our measurement. Therefore, despite the fact that we do not impose any physical model (unlike Lopez & Fortney 2014 & Rogers 2015), our broken power-law model recovers the transition from Terrans and Neptunians.
4.4.
 : The Jovian–Stellar Worlds Divide
: The Jovian–Stellar Worlds Divide
Another well-understood transition is recovered by our model at  M⊙, which we interpret as the onset of hydrogen burning. As with the Terran–Neptunian worlds transition, we may compare this to other estimates of the critical boundary. In the recent work of Dieterich et al. (2014), the authors performed a detailed observational campaign around this boundary. Inspecting the
M⊙, which we interpret as the onset of hydrogen burning. As with the Terran–Neptunian worlds transition, we may compare this to other estimates of the critical boundary. In the recent work of Dieterich et al. (2014), the authors performed a detailed observational campaign around this boundary. Inspecting the  –R plane, the authors identify a minimum at
–R plane, the authors identify a minimum at  R⊙, which corresponds to ≃0.072 M⊙ with the 5 Gyr isochrones6
of Baraffe et al. (1998). Based on this, we conclude that the result is fully compatible with our own prediction.
R⊙, which corresponds to ≃0.072 M⊙ with the 5 Gyr isochrones6
of Baraffe et al. (1998). Based on this, we conclude that the result is fully compatible with our own prediction.
From stellar modeling, estimates of the minimum mass for hydrogen burning range from 0.07 M⊙ to 0.09 M⊙ (Burrows et al. 1993, 1997; Baraffe et al. 1998, 2003; Chabrier et al. 2000; Saumon & Marley 2008). Therefore, both independent observational studies and theoretical estimates are consistent with our broken power-law estimate.
4.5.
 : The Neptunian–Jovian Worlds Divide
: The Neptunian–Jovian Worlds Divide
We find strong evidence for a transition in our broken power law at  MJ, corresponding to the transition between Neptunians and Jovians. While this transition has been treated as an assumed, fixed point in previous works (e.g., Weiss et al. 2013 adopt a fixed transition at 150 M⊕ or 0.47 MJ), our work appears to be the first instance of a data-driven inference of this transition.
MJ, corresponding to the transition between Neptunians and Jovians. While this transition has been treated as an assumed, fixed point in previous works (e.g., Weiss et al. 2013 adopt a fixed transition at 150 M⊕ or 0.47 MJ), our work appears to be the first instance of a data-driven inference of this transition.
A plausible physical interpretation of this boundary is that Neptunians rapidly grow in radius as more mass is added, depositing more gaseous envelope to their outer layers. Eventually, the object's mass is sufficient for gravitational self-compression to start reversing the growth, leading into the Jovians. The existence of such a transition is not unexpected, but our model allows for an actual measurement of its location.
We infer the significance of this transition to be high at nearly 10σ (see Section 3.2), motivating us to propose that this transition is physically real and that a class of Jovians is taxonomically rigorous in the mass–radius plane. A defining feature of the Jovian worlds is that the MR power-index is close to zero (−0.04 ± 0.02), with radius being nearly degenerate with respect to mass.
We find that brown dwarfs are absorbed into this class, displaying no obvious transition (also see Figure 1) at ∼13 MJ, the canonical threshold for brown dwarfs (Spiegel et al. 2011), as was also argued by Hatzes & Rauer (2015). When viewed in terms of mass and radius then, brown dwarfs are merely high-mass members of a continuum of Jovians and more closely resemble "planets" than "stars."
The fact that the Neptunian-to-Jovian transition occurs at around one Saturn mass is generally incompatible with theoretical predictions of a H-/He-rich planet, such as Saturn. Calculations by Zapolsky & Salpeter (1969) predict that a cold sphere of H/He is expected to reach a maximum size somewhere between 1.2 MJ to 3.3 MJ. The suite of models produced by Fortney et al. (2007) for H-/He-rich giant planets, for various insolations and metallicities, peaks at masses between ∼2.5 MJ to ∼5.2 MJ. Nevertheless, Jupiter and Saturn have similar radii (within 20%) to one another despite a factor of three difference in mass, crudely indicating that Jovians commence at a mass less than or equal to that of Saturn.
5. FORECASTING
5.1. Forecaster: An Open-source Package
Using our probabilistic model for MR relation inferred in this work, it is possible to now achieve our primary objective: to forecast the mass (or radius) of an object given the radius (or mass). Crucially, our forecasting model can propagate not only the measurement uncertainty on the inputs (easily achieved using Monte Carlo draws), but also the uncertainty in the model itself thanks to the probabilistic nature of our model. Thus, even for an input with perfect measurement error (i.e., none), our forecasting model will still return a probability distribution for the forecasted quantity, due to (i) our measurement uncertainty in the hyper parameters describing the model and (ii) the intrinsic variability seen in nature herself around the imposed model.
To enable the community to make use of this, we have written a Python package, Forecaster
7
(MIT license), which allows a user to input a mass (or radius) posterior and return a radius (or mass) forecasted distribution. Alternatively, one can simply input a mean and standard deviation of mass (or radius), and the package will return an forecasted mean and standard deviation of the radius (or mass), This code works for any object with mass in the range of  M⊕, 3 × 105 M⊕(0.87 M⊙)], or [0.1 R⊕, 100 R⊕ (9 RJ)].
M⊕, 3 × 105 M⊕(0.87 M⊙)], or [0.1 R⊕, 100 R⊕ (9 RJ)].
We present the details of how we use the MR relation we obtained to forecast one quantity from the other below.
5.2. Forecasting Radius
Predicting radius given mass is straightforward from our model. If the input is the mean and standard deviation of mass, Forecaster will first generate a vector of masses,  , following a normal distribution truncated within the mass range. Otherwise, the code will accept the input mass posterior as
, following a normal distribution truncated within the mass range. Otherwise, the code will accept the input mass posterior as  . Forecaster will then randomly choose n realizations of the hyper parameters from the hyper posteriors derived in this work. A radius will be drawn for each
. Forecaster will then randomly choose n realizations of the hyper parameters from the hyper posteriors derived in this work. A radius will be drawn for each  with each set of hyper parameters
with each set of hyper parameters  , as
, as

The output in this case is a vector of radius  . It is worth pointing out that since our model uses a Gaussian distribution, it is possible that the predicted radius for a given mass turns out to be so small that no current physical composition model can explain it. However, we choose not to truncate the prediction with any theoretical model and let our code users to choose what is suitable for them.
. It is worth pointing out that since our model uses a Gaussian distribution, it is possible that the predicted radius for a given mass turns out to be so small that no current physical composition model can explain it. However, we choose not to truncate the prediction with any theoretical model and let our code users to choose what is suitable for them.
5.3. Forecasting Mass
Mass cannot be directly sampled given  with our model. To sample mass, Forecaster first creates a grid of mass as
with our model. To sample mass, Forecaster first creates a grid of mass as  in the whole mass range of our model. Similarly, we then randomly choose n sets of hyper parameters from the hyper posteriors of our model. For each radius
in the whole mass range of our model. Similarly, we then randomly choose n sets of hyper parameters from the hyper posteriors of our model. For each radius  , Forecaster calculates the probability
, Forecaster calculates the probability  of
of  given
given  with
with  . Finally, Forecaster samples
. Finally, Forecaster samples  from
from  with
with  . The output in this case is a vector of mass
. The output in this case is a vector of mass  .
.
5.4. Examples: Kepler-186f and Kepler-452b
An illustrative example of Forecaster in action, we here forecast the masses of arguably the two most Earth-like planets discovered by Kepler, Kepler-186f and Kepler-452b.
Kepler-186f was discovered by Quintana et al. (2014), reported to have  R⊕ and receiving
R⊕ and receiving  % the insolation received by the Earth. A re-analysis by Torres et al. (2015) refined the radius to
% the insolation received by the Earth. A re-analysis by Torres et al. (2015) refined the radius to  R⊕ and we use the radius posterior samples from that work as our input to Forecaster. As shown in Figure 5, we predict a mass of
R⊕ and we use the radius posterior samples from that work as our input to Forecaster. As shown in Figure 5, we predict a mass of  M⊕, with 59% of the samples lying within the Terrans classification. Therefore, in agreement with the discovery paper of Quintana et al. (2014), we also predict that Kepler-186f is most likely a rocky planet.
M⊕, with 59% of the samples lying within the Terrans classification. Therefore, in agreement with the discovery paper of Quintana et al. (2014), we also predict that Kepler-186f is most likely a rocky planet.
Figure 5. Posterior distributions of the radius (measured) and mass (forecasted) of two habitable-zone small planets, with predictions produced by Forecaster (triangle plots generated using corner.py (http://github.com/dfm/corner.py.git); Foreman-Mackey 2016).
Download figure:
Standard image High-resolution imageKepler-452b was discovered by Jenkins et al. (2015) and was found to have a very similar insolation to that of the Earth, differing by a factor of just  . The reported radius of
. The reported radius of  R⊕ means that Kepler-452b would be unlikely to be rocky using the definition resulting from the analysis of Rogers (2015). Using the reported radius with Forecaster predicts that
R⊕ means that Kepler-452b would be unlikely to be rocky using the definition resulting from the analysis of Rogers (2015). Using the reported radius with Forecaster predicts that  M⊕, with only 13% of samples lying within the Terran worlds classification (see Figure 5). Therefore, in contrast to the discovery paper of Jenkins et al. (2015), we predict that Kepler-452b is unlikely to be a rocky planet.
M⊕, with only 13% of samples lying within the Terran worlds classification (see Figure 5). Therefore, in contrast to the discovery paper of Jenkins et al. (2015), we predict that Kepler-452b is unlikely to be a rocky planet.
6. DISCUSSION
In this work, we have developed a new package, called Forecaster, to predict the mass (or radius) of an object based on the radius (or mass). Our code uses a new probabilistic mass–radius relation that has been conditioned on the masses or radii of 316 objects spanning dwarf planets to late-type stars. Aside from enabling forecasting, this exercise naturally performs classification of the observed population, since we fit for the transitional points. Since the observed population has been classified in this way, future objects can also be probabilistically classified, which is another feature of Forecaster.
As discussed in Section 1, expected applications may include a newly discovered transiting planet candidate that could have its mass forecasted in order to estimate the detectability with radial velocities. Conversely, a newly discovered planet found via radial velocities may be considered for transit follow up, and our code can predict the detectability given the present constraints. Another example might be to forecast the scale height of a small planet found by TESS for atmospheric follow up with JWST, where Forecaster would also calculate the probability of the object being a Terran world.
The classification aspect of our work, which is essentially a free by-product of our approach, provides some interesting insights:
- 1.There is no discernible change in the MR relation from Jupiter to brown dwarfs. Brown dwarfs are merely high-mass planets, when classified using their size and mass.
- 2.There is no discernible change in the MR relation from dwarf planets to the Earth. Dwarf planets are merely low-mass planets, when classified using their size and mass.
- 3.The transition from Neptunians to Jovians occurs at
 MJ, meaning that Saturn is close to being the largest occuring Neptunian world. This is the first empirical inference of this divide.
MJ, meaning that Saturn is close to being the largest occuring Neptunian world. This is the first empirical inference of this divide. - 4.The transition from Terrans to Jovians occurs at
 M⊕, meaning that the Earth is close to being the largest occuring solid world. Rocky "super-Earths," then, can be argued to be a fictional category.
M⊕, meaning that the Earth is close to being the largest occuring solid world. Rocky "super-Earths," then, can be argued to be a fictional category.
This latter point may seem remarkable given that "super-Earths" have become part of the astronomical lexicon. The large number of 2–10 M⊕ planets discovered is often cited as evidence that super-Earths are very common and thus the solar system's makeup is unusual (Haghighipour 2013). However, if the boundary between Terran and Neptunian worlds is shifted down to 2 M⊕, the solar system is no longer unusual. Indeed, by our definition three of the eight solar system planets are Neptunian worlds, which are the most common type of planet around other Sun-like stars (Foreman-Mackey et al. 2014).
As shown earlier, while our value is lower than previous estimates, it is fully compatible with previous estimates from both theory (e.g., see Lopez & Fortney 2014) and independent population studies (e.g., see Rogers 2015). The uncertainty on our inference of this key transition is large (∼33%) due to the paucity of objects with >3σ precision masses and radii in the Earth-mass regime. Future work could hopefully improve the precision to ∼10% by using a larger sample, which will inevitably be found in the coming years, or by extending our method to include lossier measurements and upper limits by directly re-fitting the original observations (which was beyond the scope of this work). In any case, these divides are unlikely sharp, with counter-examples such as the M⊕ mass Neptunian world KOI-314c (Kipping et al. 2015).
A wholly independent line of thinking can also be shown to support the provocative hypothesis that the divide between Terran and Neptunian worlds is much lower than the canonical 10 M⊕ limit. Recently, Simpson (2016) made a Bayesian argument using population bias to infer that inhabited, Terran worlds should have radii of  R⊕ to 95% confidence. Assuming an Earth-like core-mass fraction, this limit corresponds to 2.0 M⊕ (Zeng et al. 2016). This is also compatible with our determination and again argues for effectively a paucity of Super-Earths. It may be, then, that the Earth is the super-Earth we have been looking for all along.
R⊕ to 95% confidence. Assuming an Earth-like core-mass fraction, this limit corresponds to 2.0 M⊕ (Zeng et al. 2016). This is also compatible with our determination and again argues for effectively a paucity of Super-Earths. It may be, then, that the Earth is the super-Earth we have been looking for all along.
Footnotes
- 1
Except for the rare cases of systems displaying invertible transit timing variations.
- 2
- 3
- 4
- 5
- 6
Although the point slightly precedes the first point in the Baraffe et al. (1998) grid, requiring a small linear extrapolation to compute.
- 7
https://github.com/chenjj2/forecaster; an archival version 1.0 of this code can be found at https://doi.org/10.5281/zenodo.164450 (Chen & Kipping 2016).













