The JPL Planetary and Lunar Ephemerides DE440 and DE441

The inertial coordinate frame of the planetary and lunar ephemerides is connected to the International Celestial Reference System (ICRS). The current ICRS realization is achieved by VLBI measurements of the positions of extragalactic radio sources (i.e., quasars) defined in the Third Realization of the International Celestial References Frame (ICRF3; Charlot et al. 2020), which is adopted by the International Astronomical Union (IAU). The orbits of the inner planets are tied to ICRF3 via VLBI measurements of Mars-orbiting spacecraft (Konopliv et al. 2016) with respect to quasars with positions known in the ICRF. Overall, the orientations of inner planet orbits are aligned with ICRF3 with an average accuracy of about 0.2 mas (Folkner & Border 2015; Folkner et al. 2014; Park et al. 2015). The orbits of Jupiter and Saturn are tied to ICRF3 via VLBA measurements of Juno and Cassini spacecraft (Jones et al. 2020), respectively.

The solar system barycenter (SSBC) is defined as (Estabrook 1971)

$$\begin{eqnarray}&&{{\boldsymbol{r}}}_{\mathrm{ssbc}}=\left(\displaystyle \sum _{i}{\mu }_{i}^{* }{{\boldsymbol{r}}}_{i}\right)/\left(\displaystyle \sum _{i}{\mu }_{i}^{* }\right).\end{eqnarray} \tag{ 1 }$$

Here, the summation is over all bodies with finite mass, r _i , is the position of body i, and ${\mu }_{i}^{* }$ is defined as

$$\begin{eqnarray}&&{\mu }_{i}^{* }={{GM}}_{i}\left(1+\displaystyle \frac{1}{2{c}^{2}}{v}_{i}^{2}-\displaystyle \frac{1}{2{c}^{2}}\displaystyle \sum _{j\ne i}\displaystyle \frac{{{GM}}_{j}}{{r}_{{ij}}}\right),\end{eqnarray} \tag{ 2 }$$

where GM_i is the mass parameter of body i, c is the speed of light, v_i is the barycentric speed of body i, and ${r}_{{ij}}=\left|{{\boldsymbol{r}}}_{i}-{{\boldsymbol{r}}}_{j}\right|$ is the distance between bodies i and j.

For DE440, the bodies used for computing the SSBC were the Sun, barycenters of eight planetary systems, the Pluto system barycenter, 343 asteroids, 30 KBOs, and a KBO ring representing the main Kuiper belt. The 343 asteroids were the same set of asteroids used in DE430, which consist of ∼90% of the total asteroid-belt mass. The mass of the 30 largest known KBOs were from Pitjeva & Pitjev (2018). The circular KBO ring was modeled as 36 point masses with equal mass located in the ecliptic plane with a semimajor axis of 44 au, with the ring mass estimated.

Figure 2 shows the motion of the SSBC relative to the Sun for 100 years (2000–2100), which is sometimes called the solar inertial motion (SIM). Compared to DE430, SSBC has shifted by ∼100 km, which is mainly due to the addition of KBOs. It is important to note that, to the first order, Earth orbits around the Sun, not around the SSBC. This point is reflected in Figure 3, which shows the time history of the closest (e.g., perihelion) and farthest (e.g., aphelion) points of the Earth–Moon barycenter (EMB) relative to the Sun and the SSBC. The near-constant distance of the perihelion and aphelion of the EMB relative to the Sun indicates that SIM does not affect the orbit of Earth relative to the Sun.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

JPL's DE series are integrated using the barycentric dynamical time (TDB), which is defined relative to the barycentric coordinate time (TCB; Petit & Luzum 2009). All of the data used to compute DE440 and DE441 had the intrinsic time tag in the coordinated universal time (UTC), which differs from the international atomic time (TAI) by leap seconds (i.e., TAI = UTC + leap seconds). In order to process these UTC-tagged measurements, the conversion from UTC to TDB would be needed (Soffel et al. 2003; Petit & Luzum 2009). Once the TAI time is computed, 32.184 s are added to compute the terrestrial time (TT; i.e., TT = TAI + 32.184 s). The conversion from TT to TDB (in Julian days) is given by

$$\begin{eqnarray}\begin{array}{c}\begin{array}{c}\begin{array}{ccc}{\rm{T}}{\rm{D}}{\rm{B}}-{\rm{T}}{\rm{T}} & = & \displaystyle \frac{{L}_{G}-{L}_{B}}{1-{L}_{B}}\left({\rm{T}}{\rm{D}}{\rm{B}}-{T}_{0}\right)+\displaystyle \frac{1-{L}_{G}}{1-{L}_{B}}{{\rm{T}}{\rm{D}}{\rm{B}}}_{0}\\ & & +\,\displaystyle \frac{1-{L}_{G}}{1-{L}_{B}}\mathop{\mathop{\displaystyle \int }\limits^{{\rm{T}}{\rm{D}}{\rm{B}}}}\limits_{{T}_{0}+{{\rm{T}}{\rm{D}}{\rm{B}}}_{0}}\displaystyle \frac{1}{{c}^{2}}\left(\displaystyle \frac{{v}_{{\rm{E}}}^{2}}{2}+{w}_{0E}+{w}_{{LE}}\right)dt\\ & & +\,\displaystyle \frac{1}{{c}^{2}}{{\boldsymbol{v}}}_{{\rm{E}}}\cdot \left({{\boldsymbol{r}}}_{S}-{{\boldsymbol{r}}}_{{\rm{E}}}\right)\\ & & -\,\displaystyle \frac{1-{L}_{G}}{1-{L}_{B}}\mathop{\mathop{\displaystyle \int }\limits^{{\rm{T}}{\rm{D}}{\rm{B}}}}\limits_{{T}_{0}+{{\rm{T}}{\rm{D}}{\rm{B}}}_{0}}\displaystyle \frac{1}{{c}^{4}}\left(-\displaystyle \frac{{v}_{{\rm{E}}}^{4}}{8}-\displaystyle \frac{3}{2}{v}_{{\rm{E}}}^{2}{w}_{0E}\right.\\ & & +\,\left.4{{\boldsymbol{v}}}_{{\rm{E}}}\cdot {{\boldsymbol{w}}}_{{iE}}+\displaystyle \frac{1}{2}{w}_{0E}^{2}+{{\rm{\Delta }}}_{{\rm{E}}}\right)dt\\ & & +\,\displaystyle \frac{1}{{c}^{4}}\left(3{w}_{0E}+\displaystyle \frac{{v}_{{\rm{E}}}^{2}}{2}\right){{\boldsymbol{v}}}_{{\rm{E}}}\cdot \left({{\boldsymbol{r}}}_{S}-{{\boldsymbol{r}}}_{{\rm{E}}}\right),\end{array}\end{array}\end{array}\,\end{eqnarray} \tag{ 3 }$$

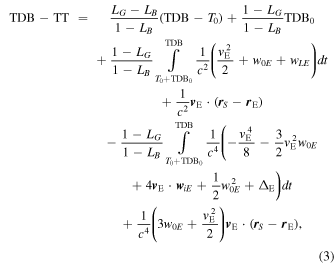
where L_G = 6.969290134 × 10⁻¹⁰ defines the rate of TT with respect to geocentric coordinate time (TCG), L_B = 1.550519768 × 10⁻⁸ defines the rate of TDB with respect to TCB, T₀ is 2443144.5003725 Julian days, ${\mathrm{TDB}}_{0}=-65.5\times \tfrac{{10}^{-6}}{86400}$ days, v_E is the velocity of the Earth, v _E is the velocity vector of the Earth, r _E is the position vector of the Earth, and r _S is the position vector of a measurement station. The potential term w_0E is defined as

$$\begin{eqnarray}&&{w}_{0E}=\displaystyle \sum _{i\ne E}\displaystyle \frac{{{GM}}_{i}}{{r}_{{iE}}},\end{eqnarray} \tag{ 4 }$$

with the summation over all bodies other than Earth. The potential due to external oblate figures w_LE is defined as

$$\begin{eqnarray}&&{w}_{{LE}}=-\displaystyle \frac{{{GM}}_{\odot }{J}_{2\odot }}{{\left|{{\boldsymbol{r}}}_{\odot }-{{\boldsymbol{r}}}_{{\rm{E}}}\right|}^{3}}\displaystyle \frac{{R}_{\odot }^{2}}{2}\left(3\sin {\varphi }_{{\rm{E}},\odot }^{2}-1\right),\end{eqnarray} \tag{ 5 }$$

where J_2⊙ is the unnormalized second-degree gravitational zonal harmonic of the Sun, R_⊙ is the solar radius, and φ_E,⊙ is the heliocentric ecliptic latitude of Earth. The term w_iE is defined as

$$\begin{eqnarray}&&{{\boldsymbol{w}}}_{{iE}}=\displaystyle \sum _{i\ne E}\displaystyle \frac{{{GM}}_{i}{{\boldsymbol{v}}}_{i}}{{r}_{{iE}}},\end{eqnarray} \tag{ 6 }$$

where the summation is over all bodies other than Earth. Lastly, Δ_E is defined as

$$\begin{eqnarray}\begin{array}{rcl}{{\rm{\Delta }}}_{{\rm{E}}} & = & \displaystyle \sum _{i\ne E}\displaystyle \frac{{{GM}}_{i}}{{r}_{{iE}}}-2{v}_{i}^{2}+\displaystyle \sum _{j\ne i}\displaystyle \frac{{{GM}}_{j}}{{r}_{{ij}}}+\displaystyle \frac{1}{2}{\left(\displaystyle \frac{{{\boldsymbol{v}}}_{i}\cdot \left({{\boldsymbol{r}}}_{{\rm{E}}}-{{\boldsymbol{r}}}_{i}\right)}{{r}_{{iE}}}\right)}^{2}\\ & & \left.+\displaystyle \frac{1}{2}{{\boldsymbol{a}}}_{i}\cdot \left({{\boldsymbol{r}}}_{{\rm{E}}}-{{\boldsymbol{r}}}_{i}\right)\right],\end{array}\end{eqnarray} \tag{ 7 }$$

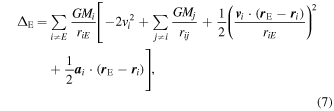
where a _i is the acceleration of body i and the summation is over all bodies.

LLR measures the round-trip light time of a laser pulse between an Earth LLR station and a retroreflector on the Moon. Thus, LLR data are not only sensitive to where the Moon is, but they are also sensitive to its orientation.

The orientation of lunar exterior (mantle and crust, hereafter referred to as the mantle) is defined by the principal axes (PAs) of the undistorted lunar mantle, and thus its moment of inertia matrix is diagonal. The directions of the PAs are taken from analyses of the Gravity Recovery and Interior Laboratory (GRAIL) data (Konopliv et al. 2013; Lemoine et al. 2013). The Euler angles that define the rotation from the PA frame to the inertial ICRF3 frame are: ϕ_m , the angle from the X-axis of the inertial frame along the XY plane to the intersection of the mantle equator; θ_m , the inclination of the mantle equator from the inertial XY plane; and ψ_m , the longitude from the intersection of the inertial XY plane with the mantle equator along the mantle equator to the prime meridian. The rotation from the lunar PA frame (i.e., lunar mantle frame) to ICRF3 is given as

$$\begin{eqnarray}&&{{\boldsymbol{r}}}_{I}={{ \mathcal R }}_{z}\left(-{\phi }_{m}\right){{ \mathcal R }}_{x}\left(-{\theta }_{m}\right){{ \mathcal R }}_{z}\left(-{\psi }_{m}\right){{\boldsymbol{r}}}_{\mathrm{PA}}.\end{eqnarray} \tag{ 8 }$$

The Euler angles ϕ_m , θ_m , and ψ_m are also known as lunar libration angles, stored in the DE440 and DE441 files. The rotation matrices use the right-hand rule and are defined as

$$\begin{eqnarray}{{ \mathcal R }}_{x}\left(\alpha \right)=\left[\begin{array}{ccc}1 & 0 & 0\\ 0 & +\cos \alpha & +\sin \alpha \\ 0 & -\sin \alpha & +\cos \alpha \end{array}\right],\end{eqnarray} \tag{ 9 }$$

$$\begin{eqnarray}{{ \mathcal R }}_{y}\left(\alpha \right)=\left[\begin{array}{ccc}+\cos \alpha & 0 & -\sin \alpha \\ 0 & 1 & 0\\ +\sin \alpha & 0 & +\cos \alpha \end{array}\right],\end{eqnarray} \tag{ 10 }$$

$$\begin{eqnarray}{{ \mathcal R }}_{z}\left(\alpha \right)=\left[\begin{array}{ccc}+\cos \alpha & +\sin \alpha & 0\\ -\sin \alpha & +\cos \alpha & 0\\ 0 & 0 & 1\end{array}\right].\end{eqnarray} \tag{ 11 }$$

These lunar libration angles are integrated simultaneously with the orbital motion. The equations of motion for the lunar libration angles are

$$\begin{eqnarray}&&{\dot{\phi }}_{m}=\left({\omega }_{m,x}\sin {\psi }_{m}+{\omega }_{m,y}\cos {\psi }_{m}\right)/\sin {\theta }_{m},\end{eqnarray} \tag{ 12 }$$

$$\begin{eqnarray}&&{\dot{\theta }}_{m}={\omega }_{m,x}\cos {\psi }_{m}-{\omega }_{m,y}\sin {\psi }_{m},\end{eqnarray} \tag{ 13 }$$

$$\begin{eqnarray}&&{\dot{\psi }}_{m}={\omega }_{m,z}-{\dot{\phi }}_{m}\cos {\theta }_{m},\end{eqnarray} \tag{ 14 }$$

where ω_m,x , ω_m,y , and ω_m,z represent the components of the lunar mantle angular velocity ω _m expressed in the mantle frame. The time derivatives of ω _m are given in Section 4.

The lunar orientation model includes a fluid core. The orientation of the core with respect to the ICRF is represented by the Euler angles ϕ_c , θ_c , and ψ_c , which are also numerically integrated. Since the shape of the core/mantle boundary is modeled as fixed to the frame of the mantle, it is more convenient to express the core angular velocities with respect to the mantle frame. The time derivatives of the core Euler angles are then given by

$$\begin{eqnarray}&&{\dot{\phi }}_{c}={\omega }_{c,z}^{\dagger }-{\dot{\psi }}_{c}\cos {\theta }_{c},\end{eqnarray} \tag{ 15 }$$

$$\begin{eqnarray}&&{\dot{\theta }}_{c}={\omega }_{c,x}^{\dagger },\end{eqnarray} \tag{ 16 }$$

$$\begin{eqnarray}&&{\dot{\psi }}_{c}=-{\omega }_{c,y}^{\dagger }/\sin {\theta }_{c},\end{eqnarray} \tag{ 17 }$$

where the core angular velocity ω _c is related to the angular velocity ${{\boldsymbol{\omega }}}_{c}^{\dagger }$ in a frame defined by the intersection of the core equator with the inertial XY plane by

$$\begin{eqnarray}&&{{\boldsymbol{\omega }}}_{c}^{\dagger }={{ \mathcal R }}_{z}\left({\phi }_{c}-{\phi }_{m}\right){{ \mathcal R }}_{x}\left(-{\theta }_{m}\right){{ \mathcal R }}_{z}\left(-{\psi }_{m}\right){{\boldsymbol{\omega }}}_{{\boldsymbol{c}}}.\end{eqnarray} \tag{ 18 }$$

The time derivatives of ω _c are given in Section 4.

Most of lunar cartographic products are defined relative to the DE421 mean-Earth/mean-rotation (MER) frame. The MER frame is defined by the X-axis pointing toward the mean-Earth direction and the Z-axis pointing toward the mean-rotation axis direction. The rotation from the DE440 PA frame to the DE421 MER frame is estimated by comparing the coordinates of the lunar retroreflectors estimated in the DE440 PA frame and the retroreflector coordinates in the DE421 MER frame, which yield

$$\begin{eqnarray}\begin{array}{rcl}{{\boldsymbol{r}}}_{\mathrm{MER},\mathrm{DE}421} & = & {{ \mathcal R }}_{x}\left(-0\buildrel{\prime\prime}\over{.} 2785\right){{ \mathcal R }}_{y}\left(-78\buildrel{\prime\prime}\over{.} 6944\right)\\ & & \times {{ \mathcal R }}_{z}\left(-67\buildrel{\prime\prime}\over{.} 8526\right){{\boldsymbol{r}}}_{\mathrm{PA},\mathrm{DE}440}.\end{array}\end{eqnarray} \tag{ 19 }$$

Table 1 shows the five lunar retroreflector positions in the DE440 PA frame and the corresponding lunar retroreflector positions in the DE421 MER frame.

Only the long-term change of the Earth orientation is modeled in the ephemeris integration. The Earth orientation model used for DE440 and DE441 is based on a long-term precession model (Vondrak et al. 2011) and a modified nutation model based on the IAU 1980 precession model including only terms with a period of 18.6 years.

The Earth pole unit vector in the inertial frame, p _E, can be computed by the following steps.

First, the mean longitude of the ascending node of the lunar orbit measured on the ecliptic plane from the mean equinox of date is computed by

$$\begin{eqnarray}\begin{array}{rcl}{\rm{\Omega }} & = & 125^\circ {02}^{{\prime} }40\buildrel{\prime\prime}\over{.} 280-1934^\circ {08}^{{\prime} }10\buildrel{\prime\prime}\over{.} 539T\\ & & +7\buildrel{\prime\prime}\over{.} 455{T}^{2}+0\buildrel{\prime\prime}\over{.} 008{T}^{3},\end{array}\end{eqnarray} \tag{ 20 }$$

where T is the TDB time in Julian centuries (36,525 days) from J2000.0. The nutation angles in longitude, Δψ, and obliquity, Δε, are given by

$$\begin{eqnarray}&&{\rm{\Delta }}\psi =-17\buildrel{\prime\prime}\over{.} 1996\sin {\rm{\Omega }},\end{eqnarray} \tag{ 21 }$$

$$\begin{eqnarray}&&{\rm{\Delta }}\varepsilon =9\buildrel{\prime\prime}\over{.} 2025\cos {\rm{\Omega }}.\end{eqnarray} \tag{ 22 }$$

The true pole of date unit vector, p _d , is computed by rotating the Earth-fixed pole vector by the effect of the 18.6 year nutation term to give

$$\begin{eqnarray}&&{{\boldsymbol{p}}}_{d}\,=\,\left[\begin{array}{c}\sin \left({\rm{\Delta }}\psi \right)\sin \left(\overline{\varepsilon }+{\rm{\Delta }}\varepsilon \right)\\ \cos \left({\rm{\Delta }}\psi \right)\sin \left(\overline{\varepsilon }+{\rm{\Delta }}\varepsilon \right)\cos \left(\overline{\varepsilon }\right)-\cos \left(\overline{\varepsilon }+{\rm{\Delta }}\varepsilon \right)\sin \left(\overline{\varepsilon }\right)\\ \cos \left({\rm{\Delta }}\psi \right)\sin \left(\overline{\varepsilon }+{\rm{\Delta }}\varepsilon \right)\sin \left(\overline{\varepsilon }\right)+\cos \left(\overline{\varepsilon }+{\rm{\Delta }}\varepsilon \right)\cos \left(\overline{\varepsilon }\right)\end{array}\right],\,\end{eqnarray} \tag{ 23 }$$

where the mean obliquity $\bar{\varepsilon }$ is given by

$$\begin{eqnarray}\begin{array}{rcl}\bar{\varepsilon } & = & 84381\buildrel{\prime\prime}\over{.} 448-46\buildrel{\prime\prime}\over{.} 815T\\ & & -\,0\buildrel{\prime\prime}\over{.} 00059{T}^{2}+0\buildrel{\prime\prime}\over{.} 001813{T}^{3}.\end{array}\end{eqnarray} \tag{ 24 }$$

The pole unit vector in the inertial frame p _E is computed by precessing the pole of date to inertial coordinates using the long-term precession model (Vondrak et al. 2011) plus an estimated frame offset in x and y rotations,

$$\begin{eqnarray}&&{{\boldsymbol{p}}}_{{\rm{E}}}={{ \mathcal R }}_{V}{{ \mathcal R }}_{x}\left(-{{\rm{\Phi }}}_{x}\right){{ \mathcal R }}_{y}\left(-{{\rm{\Phi }}}_{y}\right){{\boldsymbol{p}}}_{d},\end{eqnarray} \tag{ 25 }$$

where Φ_x and Φ_y are the estimated offsets of the EME2000 pole from the ICRF pole and the precession matrix ${{ \mathcal R }}_{V}$ is given by

$$\begin{eqnarray}&&{{ \mathcal R }}_{V}=\left[\begin{array}{c}\left({\boldsymbol{n}}\times {\boldsymbol{k}}\right)/\left|{\boldsymbol{n}}\times {\boldsymbol{k}}\right|\\ {\boldsymbol{n}}\times \left({\boldsymbol{n}}\times {\boldsymbol{k}}\right)/\left|{\boldsymbol{n}}\times \left({\boldsymbol{n}}\times {\boldsymbol{k}}\right)\right|\\ {\boldsymbol{n}}/\left|{\boldsymbol{n}}\right|\end{array}\right],\end{eqnarray} \tag{ 26 }$$

where k is the ecliptic pole vector and n is the mean equatorial pole vector, derived from polynomial fits to a numerically integrated long-term orientation of Earth (Vondrak et al. 2011). The $\left|\cdot \right|$ operator represents the norm of a vector.

The point-mass interaction between planetary bodies is governed by the parameterized post-Newtonian (PPN) formulation (Will & Nordtvedt 1972; Moyer 2003)

$$\begin{eqnarray}\begin{array}{rcl}{{\boldsymbol{a}}}_{i,\mathrm{pm}-\mathrm{pm}} & = & \displaystyle \sum _{j\ne i}\displaystyle \frac{{{GM}}_{j}\left({{\boldsymbol{r}}}_{j}-{{\boldsymbol{r}}}_{i}\right)}{{r}_{{ij}}^{3}}1-\displaystyle \frac{2\left(\beta +\gamma \right)}{{c}^{2}}\\ & & \times \displaystyle \sum _{k\ne i}\displaystyle \frac{{{GM}}_{k}}{{r}_{{ik}}}-\displaystyle \frac{2\beta -1}{{c}^{2}}\displaystyle \sum _{k\ne j}\displaystyle \frac{{{GM}}_{k}}{{r}_{{jk}}}\\ & & +\,\gamma {\left(\displaystyle \frac{{v}_{i}}{c}\right)}^{2}+\left(1+\gamma \right){\left(\displaystyle \frac{{v}_{j}}{c}\right)}^{2}-\displaystyle \frac{2\left(1+\gamma \right)}{{c}^{2}}{{\boldsymbol{v}}}_{i}\cdot {{\boldsymbol{v}}}_{j}\\ & & \left.-\ \displaystyle \frac{3}{2{c}^{2}}{\left[\displaystyle \frac{\left({{\boldsymbol{r}}}_{i}-{{\boldsymbol{r}}}_{j}\right)\cdot {{\boldsymbol{v}}}_{j}}{{r}_{{ij}}}\right]}^{2}+\displaystyle \frac{1}{2{c}^{2}}\left({{\boldsymbol{r}}}_{j}-{{\boldsymbol{r}}}_{i}\right)\cdot {{\boldsymbol{a}}}_{j}\right\}\\ & & +\displaystyle \frac{1}{{c}^{2}}\displaystyle \sum _{j\ne i}\displaystyle \frac{{{GM}}_{j}}{{r}_{{ij}}^{3}}\left\{\left[{{\boldsymbol{r}}}_{i}-{{\boldsymbol{r}}}_{j}\right]\cdot \left[\left(2+2\gamma \right){{\boldsymbol{v}}}_{i}\right.\right.\\ & & -\left.\left.\left(1+2\gamma \right){{\boldsymbol{v}}}_{j}\right]\right\}\left({{\boldsymbol{v}}}_{i}-{{\boldsymbol{v}}}_{j}\right)\\ & & +\displaystyle \frac{\left(3+4\gamma \right)}{2{c}^{2}}\displaystyle \sum _{j\ne i}\displaystyle \frac{{{GM}}_{j}{{\boldsymbol{a}}}_{j}}{{r}_{{ij}}},\end{array}\end{eqnarray} \tag{ 27 }$$

where the summations are over all bodies, and β and γ are the Eddington–Robertson–Schiff parameters representing the measure of nonlinearity in the superposition law for gravity and the amount of space curvature produced by a unit rest mass, respectively, and are constrained to unity as predicted by the general theory of relativity (GTR).

DE440 integrated the same set of bodies (i.e., Sun, barycenter of eight planets, the Moon, Pluto barycenter, and 343 asteroids) used in DE430, but also included perturbations from 30 KBOs and a KBO ring discussed in Section 2.2. The key mass parameters used in DE440 are shown in Table 2, and all other relevant parameters are given in the comment blocks of the DE440 and DE441 files.

Table 2. Planetary Masses Used in DE440 and DE441

Parameter	Value
GMSun	132712440041.279419 km3 s−2 (estimated from DE440)
GMMercury	22031.868551 km3 s−2 (Konopliv et al. 2020)
GMVenus	324858.592000 km3 s−2 (Konopliv et al. 1999)
GMEarth	398600.435507 km3 s−2 (estimated from DE440)
GMMars System	42828.375816 km3 s−2 (Konopliv et al. 2016)
GMJupiter System	126712764.100000 km3 s−2 (SSD JPL 2020)
GMSaturn System	37940584.841800 km3 s−2 (SSD JPL 2020)
GMUranus System	5794556.400000 km3 s−2 (Jacobson 2014)
GMNeptune System	6836527.100580 km3 s−2 (Jacobson 2009)
GMPluto System	975.500000 km3 s−2 (Brozovic et al. 2015)
GMMoon	4902.800118 km3 s−2 (estimated from DE440)
${{GM}}_{\mathrm{Ceres}}$	62.62890 km3 s−2 (Park et al. 2016; Konopliv et al. 2018; Park et al. 2019, 2020a)
GMVesta	17.288245 km3 s−2 (Konopliv et al. 2014; Park et al. 2014)

Download table as:  ASCIITypeset image

Nonspherical gravitational interaction has been modeled using a spherical harmonic expansion. For Earth, the interaction of the zonal harmonics up to the fifth degree and the point masses of the Moon, Sun, Mercury, Venus, Mars, Jupiter, and Saturn have been modeled. For the Moon, the interaction of a degree and order 6 gravity field and the point masses of Earth, Sun, Mercury, Venus, Mars, Jupiter, and Saturn have been modeled. For the Sun, the interaction of the second-degree zonal harmonic with all other bodies has been modeled.

The acceleration due to an extended body can be represented as

$$\begin{eqnarray}&&\begin{array}{l}\left[\begin{array}{c}\ddot{\xi }\\ \ddot{\eta }\\ \ddot{\zeta }\end{array}\right]=\,-\displaystyle \frac{{GM}}{{r}^{2}}\left\{\displaystyle \sum _{n=2}^{{n}_{1}}{J}_{n}{\left(\displaystyle \frac{R}{r}\right)}^{n}\left[\begin{array}{c}\left(n+1\right){P}_{n}\left(\sin \varphi \right)\\ 0\\ -\cos \varphi {P}_{n}^{{\prime} }\left(\sin \varphi \right)\end{array}\right]\right.+\displaystyle \sum _{n=2}^{{n}_{2}}{\left(\displaystyle \frac{R}{r}\right)}^{n}\\ \left.\times \displaystyle \sum _{m=1}^{n}\left[\begin{array}{c}-\left(n+1\right){P}_{{nm}}\left(\sin \varphi \right)\left(+{C}_{{nm}}\cos m\lambda +{S}_{{nm}}\sin m\lambda \right)\\ m\sec \varphi {P}_{{nm}}\left(\sin \varphi \right)\left(-{C}_{{nm}}\sin m\lambda +{S}_{{nm}}\cos m\lambda \right)\\ \cos \varphi {P}_{{nm}}^{{\prime} }\left(\sin \varphi \right)\left(+{C}_{{nm}}\cos m\lambda +{S}_{{nm}}\sin m\lambda \right)\end{array}\right]\right\},\end{array}\end{eqnarray} \tag{ 28 }$$

where the ξ η ζ coordinate system is defined such that the ξ-axis is defined outward from the extended body to the point mass, the ξ ζ-plane contains the figure spin-pole of the extended body, and the η-axis completes the triad. Here, r is the distance between the two bodies; n₁ and n₂ represent the maximum degrees of the zonal and nonzonal spherical harmonic coefficients, respectively; P_n and P_nm represent the unnormalized degree-n Legendre polynomial and associated Legendre function with degree-n and order-m, respectively; ${P}_{n}^{{\prime} }$ and ${P}_{{nm}}^{{\prime} }$ represent the derivative of P_n and P_nm with respect to $\sin \varphi$, respectively; J_n represents the degree-n zonal harmonic coefficient; C_nm and S_nm represent the nonzonal spherical harmonic coefficients for the extended body; R represents the reference radius of the extended body; and λ and φ represent the longitude and latitude of the point mass in the extended-body fixed coordinate system. Once the accelerations are computed in the body fixed frame, they are transformed into the inertial frame for integration.

There is also an interaction between the figure of an extended body and a point mass, often called the indirect acceleration. Given a _i,figi−pmj , which denotes the acceleration of the extended body i interacting with the point-mass external body j expressed in an inertial frame, the corresponding indirect acceleration of the point mass, a _j,figi−pmj , is

$$\begin{eqnarray}&&{{\boldsymbol{a}}}_{j,\mathrm{fig}i-\mathrm{pm}j}=-\displaystyle \frac{{m}_{i}}{{m}_{j}}{{\boldsymbol{a}}}_{i,\mathrm{fig}i-\mathrm{pm}j}.\end{eqnarray} \tag{ 29 }$$

For the Moon, the second-degree spherical harmonic coefficients vary with time due to distortion by tides and rotation. These coefficients are computed from the moment of inertia tensors as a function of time and the detailed description is given in Section 4. The second-degree spherical harmonic coefficients are given by

$$\begin{eqnarray}&&{J}_{2,M}\left(t\right)=\displaystyle \frac{2{I}_{33,T}\left(t\right)-\left[{I}_{11,T}\left(t\right)+{I}_{22,T}\left(t\right)\right]}{2{m}_{{\rm{M}}}{R}_{{\rm{M}}}^{2}},\end{eqnarray} \tag{ 30 }$$

$$\begin{eqnarray}&&{C}_{22,M}\left(t\right)=\displaystyle \frac{{I}_{22,T}\left(t\right)-{I}_{11,T}\left(t\right)}{4{m}_{{\rm{M}}}{R}_{{\rm{M}}}^{2}},\end{eqnarray} \tag{ 31 }$$

$$\begin{eqnarray}&&{C}_{21,M}\left(t\right)=\displaystyle \frac{-{I}_{13,T}\left(t\right)}{{m}_{{\rm{M}}}{R}_{{\rm{M}}}^{2}},\end{eqnarray} \tag{ 32 }$$

$$\begin{eqnarray}&&{S}_{21,M}\left(t\right)=\displaystyle \frac{-{I}_{23,T}\left(t\right)}{{m}_{{\rm{M}}}{R}_{{\rm{M}}}^{2}},\end{eqnarray} \tag{ 33 }$$

$$\begin{eqnarray}&&{S}_{22,M}\left(t\right)=\displaystyle \frac{-{I}_{12,T}\left(t\right)}{2{m}_{{\rm{M}}}{R}_{{\rm{M}}}^{2}},\end{eqnarray} \tag{ 34 }$$

where I_ij,T represent the elements of the total lunar moment of inertia matrix (see Section 4), m_M is the lunar mass, and R_M is the lunar radius.

The lunar orbit is affected by the tides raised on Earth by the Sun and Moon. The tidal distortion of Earth can be modeled using the second-degree gravitational Love numbers, k_2j,E , where the order j is 0, 1, and 2 for long-period, diurnal, and semidiurnal responses, respectively. See Section 2.2 in Williams & Boggs (2016) for more information.

A time-delay tidal model has been applied to account for the tidal dissipation. The distorted response of Earth is delayed with respect to the tide-raising forces from the Moon or Sun. The appropriate time delay depends on the period of each tidal component. Consequently, different time delays have been employed for each order j. To allow for time delays shifting across the diurnal and semidiurnal frequency bands, separate time delays are associated with Earth's rotation and the lunar orbit.

The acceleration of the Moon due to the Earth tides is evaluated separately for the tides raised by the Sun and the tides raised by the Moon. The Earth tides depend on the position of the tide-raising body with respect to Earth, r _T , where T can denote either the Sun or the Moon. The position of the tide-raising body is evaluated at an earlier time $t-{\tau }_{j}^{{\prime} }$, where ${\tau }_{j}^{{\prime} }$ denotes the orbital time lag, for long-period (j = 0), diurnal (j = 1), and semi-diurnal (j = 2) responses. The rotational distortion of Earth is delayed by a rotational time lag τ_j , so that the distortion leads the direction to the tide-raising body by an angle $\dot{\theta }{\tau }_{j}$, where $\dot{\theta }$ is the rotation rate of Earth. The long-period zonal tides (j = 0) do not depend on the rotation of Earth, so τ_j = 0. The acceleration of the Moon due to the distorted Earth depends on the position of the Moon with respect to Earth ( r ) and on the modified position vector for the tide-raising body (${{\boldsymbol{r}}}_{j}^{* }$) that is given for each order j by

$$\begin{eqnarray}&&{{\boldsymbol{r}}}_{j}^{* }={{ \mathcal R }}_{{\rm{E}}}^{T}{{ \mathcal R }}_{z}\left(-\dot{\theta }{\tau }_{j}\right){{ \mathcal R }}_{{\rm{E}}}{{\boldsymbol{r}}}_{T}\left(t-{\tau }_{j}^{{\prime} }\right),\end{eqnarray} \tag{ 35 }$$

where ${{ \mathcal R }}_{{\rm{E}}}$ rotates the time-delayed position of the tide-raising body with respect to Earth from the inertial frame to the Earth fixed frame and ${{ \mathcal R }}_{z}$ here means a right-handed rotation of the vector ${{\boldsymbol{r}}}_{T}\left(t-{\tau }_{j}^{{\prime} }\right)$ by the angle $-\dot{\theta }{\tau }_{j}$ about Earth's rotation axis.

For evaluation of the acceleration of the Moon, the vectors r (Moon with respect to Earth) and ${{\boldsymbol{r}}}_{j}^{* }$ (time-delayed position of a tide-raising body with respect to Earth) are expressed in cylindrical coordinates with the Z-axis perpendicular to Earth's equator so that r = ρ + z and ${{\boldsymbol{r}}}_{j}^{* }={{\boldsymbol{\rho }}}_{j}^{* }+{{\boldsymbol{z}}}_{j}^{* }$.

The acceleration of the Moon due to the tide raised on Earth by each tide-raising body (Sun or Moon), a _M,tide is given by

$$\begin{eqnarray}\begin{array}{rcl}{{\boldsymbol{a}}}_{{\rm{M}},\mathrm{tide}} & = & \displaystyle \frac{3}{2}\left(\displaystyle \frac{{m}_{{\rm{E}}}+{m}_{{\rm{M}}}}{{m}_{{\rm{E}}}}\right)\displaystyle \frac{{{Gm}}_{T}{R}_{{\rm{E}}}^{5}}{{r}^{5}}\displaystyle \frac{{k}_{20,E}}{{r}_{1}^{* 5}}\left(\left[2{z}_{0}^{* 2}{\boldsymbol{z}}+{\rho }_{0}^{* 2}{\boldsymbol{\rho }}\right]\right.\\ & & -\left.\displaystyle \frac{5\left[{\left({{zz}}_{0}^{* }\right)}^{2}+\tfrac{1}{2}{\left(\rho {\rho }_{0}^{* }\right)}^{2}\right]{\boldsymbol{r}}}{{r}^{2}}+{r}_{0}^{* 2}{\boldsymbol{r}}\right)\\ & & +\displaystyle \frac{{k}_{21,E}}{{r}_{1}^{* 5}}\left(\left[2\left({\boldsymbol{\rho }}\cdot {{\boldsymbol{\rho }}}_{1}^{* }\right){{\boldsymbol{z}}}_{1}^{* }+{{zz}}_{1}^{* }{{\boldsymbol{\rho }}}_{1}^{* }\right]-\displaystyle \frac{10{{zz}}_{1}^{* }\left({\boldsymbol{\rho }}\cdot {{\boldsymbol{\rho }}}_{1}^{* }\right){\boldsymbol{r}}}{{r}^{2}}\right)\\ & & \,+\displaystyle \frac{{k}_{22,E}}{{r}_{2}^{* 5}}\left(\left[2\left({\boldsymbol{\rho }}\cdot {{\boldsymbol{\rho }}}_{2}^{* }\right){{\boldsymbol{\rho }}}_{2}^{* }-{\rho }_{2}^{* 2}{\boldsymbol{\rho }}\right]\right.\\ & & \left.-\left.\displaystyle \frac{5\left[{\left({\boldsymbol{\rho }}\cdot {{\boldsymbol{\rho }}}_{2}^{* }\right)}^{2}-\tfrac{1}{2}{\left(\rho {\rho }_{2}^{* }\right)}^{2}\right]{\boldsymbol{r}}}{{r}^{2}}\right)\right\},\end{array}\end{eqnarray} \tag{ 36 }$$

where m_T is the mass of the tide-raising body.

The tidal acceleration due to tidal dissipation is implicit in the above acceleration. Tides raised on Earth by the Moon do not influence the motion of the EMB. The effect of Sun-raised tides on the barycentric motion is not considered.

The tidal bulge leads the Moon and its gravitational attraction accelerates the Moon forward and retards Earth's spin. Energy and angular momentum are transferred from Earth's rotation to the lunar orbit. Consequently, the Moon moves away from Earth, the lunar orbit period lengthens, and Earth's day becomes longer. Some energy is dissipated in Earth rather than being transferred to the orbit.

In DE440, the acceleration of each body other than the Sun due to the gravito-magnetic effect of GTR, also known as the LT effect, has been implemented (Moyer 2003; Park et al. 2017):

$$\begin{eqnarray}&&{{\boldsymbol{a}}}_{i,\mathrm{LT}}=2{{\boldsymbol{\Omega }}}_{{\rm{i}}}\times {{\boldsymbol{v}}}_{i},\end{eqnarray} \tag{ 37 }$$

where the LT angular velocity vector Ω_I is given by

$$\begin{eqnarray}&&{{\boldsymbol{\Omega }}}_{{\rm{i}}}=\displaystyle \frac{\left(1+\gamma \right)G}{2{c}^{2}{r}_{i}^{3}}\left[-{\boldsymbol{J}}+\displaystyle \frac{3\left({\boldsymbol{J}}\cdot {{\boldsymbol{r}}}_{i}\right){{\boldsymbol{r}}}_{i}}{{r}_{i}^{2}}\right],\end{eqnarray} \tag{ 38 }$$

$$\begin{eqnarray}&&{\boldsymbol{J}}={C}_{\odot }{M}_{\odot }{R}_{\odot }^{2}{\omega }_{\odot }\widehat{{\boldsymbol{p}}},\end{eqnarray} \tag{ 39 }$$

where G is the universal gravitational constant, γ is the Eddington–Robertson–Schiff parameter from Section 3.1, c is the speed of light, r _i is position of the body with respect to the Sun, M_⊙ is the Sun's mass, C_⊙ is the Sun's polar moment of inertia divided by $\left({M}_{\odot }{R}_{\odot }^{2}\right)$, where ${C}_{\odot }/({M}_{\odot }{R}_{\odot }^{2})=0.06884$, R_⊙ is the Sun's equatorial radius (696,000 km), ω_⊙ the is Sun's rotation rate (14.1844 deg/day), and $\widehat{{\boldsymbol{p}}}$ is the unit spin-pole direction of the Sun (R.A. of 28613 and decl. of 6387; Archinal et al. 2018).

The LT effect is small, but it is important for fitting the MESSENGER range data (Park et al. 2017). Overall, the LT effect causes Mercury's perihelion to precess at the rate of about −00020/Julian century, which is about 7% of the precession caused by the solar oblateness.

Photons carry energy and momentum so there is a very small force directed away from the Sun. Like Newtonian gravity, solar radiation pressure depends on the inverse-square distance of the Sun. A simple solar radiation pressure model has been implemented for Earth and the Moon, with accelerations given by

$$\begin{eqnarray}&&{{\boldsymbol{a}}}_{{\rm{E}},\mathrm{srp}}=-{\varepsilon }_{{\rm{E}},\mathrm{srp}}\displaystyle \frac{{{GM}}_{\mathrm{Sun}}{{\boldsymbol{r}}}_{\mathrm{SE}}}{{r}_{\mathrm{SE}}^{3}},\end{eqnarray} \tag{ 40 }$$

$$\begin{eqnarray}&&{{\boldsymbol{a}}}_{{\rm{M}},\mathrm{srp}}=-{\varepsilon }_{{\rm{M}},\mathrm{srp}}\displaystyle \frac{{{GM}}_{\mathrm{Sun}}{{\boldsymbol{r}}}_{\mathrm{SM}}}{{r}_{\mathrm{SM}}^{3}},\end{eqnarray} \tag{ 41 }$$

where the acceleration due to solar radiation pressure is a very small fraction of gravitational acceleration (Vokrouhlický 1997), i.e., ε_E,srp = 2 × 10⁻¹⁴ for Earth and ε_M,srp =1.44 × 10⁻¹³ for the Moon. Here, r _SE is the inertial Sun-to-Earth position vector and r _SM is the inertial Sun-to-Moon position vector.

In a rotating system, the change in angular velocity ω is related to torques N by

$$\begin{eqnarray}&&{\boldsymbol{N}}=\displaystyle \frac{d}{{dt}}\left({\boldsymbol{I}}{\boldsymbol{\omega }}\right)+{\boldsymbol{\omega }}\times {\boldsymbol{I}}{\boldsymbol{\omega }},\end{eqnarray} \tag{ 42 }$$

where I is the moment of inertia tensor. The second term on the right-hand side puts the time derivative into the rotating system. The total lunar moment of inertia I _T , which is the sum of the moment of inertia of the mantle I _m and the moment of inertia of the core I _c , is proportional to the mass m_M times the square of the radius R_M. Because the fractional uncertainty in the constant of gravitation G is much larger than that for the lunar mass parameter Gm_M, Equation (42) is evaluated in the integration with both sides multiplied by G.

The components of vectors can be given in the inertial frame, mantle frame, or other frames. Since the moment of inertia matrices are nearly diagonal in the mantle frame, there is great convenience to inverting matrices and performing the matrix multiplications in the mantle frame. The resulting vector components can then be rotated to other frames if desired.

The moment of inertia of the mantle varies with time due to tidal distortions. The distortions are functions of the lunar position and rotational velocities computed at time t − τ_m , where τ_m is a time lag determined from the fits to the LLR data. The time delay allows for dissipation when flexing the Moon. The time derivative of the angular velocity of the mantle is given by

$$\begin{eqnarray}\begin{array}{rcl}{\dot{{\boldsymbol{\omega }}}}_{{\rm{m}}} & = & {{\boldsymbol{I}}}_{{\rm{m}}}^{-1}\displaystyle \sum _{j\ne M}{{\boldsymbol{N}}}_{{\rm{M}},\mathrm{fig}M-\mathrm{pm}j}+{{\boldsymbol{N}}}_{{\rm{M}},\mathrm{fig}M-\mathrm{fig}E}-{\dot{{\boldsymbol{I}}}}_{{\rm{m}}}{{\boldsymbol{\omega }}}_{{\rm{m}}}\\ & & -\left.\left({{\boldsymbol{\omega }}}_{{\rm{m}}}-{{\boldsymbol{\nu }}}_{\mathrm{gp}}\right)\times {{\boldsymbol{I}}}_{{\rm{m}}}{{\boldsymbol{\omega }}}_{{\rm{m}},}+{{\boldsymbol{N}}}_{\mathrm{cmb}},\right],\end{array}\end{eqnarray} \tag{ 43 }$$

where I _m is the lunar mantle moment of inertia matrix, N _M,figM−pmj is the torque on the lunar mantle due to the point-mass body j, N _{M,figM−figE} is the torque on the lunar mantle due to the interaction between the extended figure of the Moon and the extended figure of Earth, ν _gp is the angular rate due to geodetic precession, and N _cmb is the torque due to the interaction between lunar mantle and core. The geodetic precession rate is defined as

$$\begin{eqnarray}&&{{\boldsymbol{\nu }}}_{\mathrm{gp}}={\boldsymbol{L}}\left[\displaystyle \frac{\left(1+2\gamma \right)}{2{c}^{2}}{{\boldsymbol{v}}}_{\mathrm{EM}}\times \left(\displaystyle \frac{{{GM}}_{\mathrm{Earth}}{{\boldsymbol{r}}}_{\mathrm{EM}}}{{r}_{\mathrm{EM}}^{3}}+\displaystyle \frac{{{GM}}_{\mathrm{Sun}}{{\boldsymbol{r}}}_{\mathrm{SM}}}{{r}_{\mathrm{SM}}^{3}}\right)\right],\end{eqnarray} \tag{ 44 }$$

where L is the rotation matrix from the mean J2000 frame to the lunar body fixed (i.e., selenographic) frame, v _EM is the inertial Earth-to-Moon velocity vector, r _EM is the inertial Earth-to-Moon position vector, and r _SM is the inertial Sun-to-Moon position vector.

The fluid core is assumed to be rotating like a solid and constrained by the shape of the core–mantle boundary at the interior of the mantle, with the moment of inertia constant in the frame of the mantle. The time derivative of the angular velocity of the core expressed in the mantle frame is given by

$$\begin{eqnarray}&&{\dot{{\boldsymbol{\omega }}}}_{c}={{\boldsymbol{I}}}_{c}^{-1}\left[-\left({{\boldsymbol{\omega }}}_{{\rm{m}}}-{{\boldsymbol{\nu }}}_{\mathrm{gp}}\right)\times {{\boldsymbol{I}}}_{{\rm{c}}}{{\boldsymbol{\omega }}}_{{\rm{c}}}-{{\boldsymbol{N}}}_{\mathrm{cmb}}\right],\end{eqnarray} \tag{ 45 }$$

where I _c is the lunar core moment of inertia matrix.

In the mantle frame, the undistorted moment of inertia of the mantle and the moment of inertia of the core are diagonal. The undistorted total moment of inertia ${\widetilde{{\boldsymbol{I}}}}_{T}$ is given by

$$\begin{eqnarray}{\widetilde{{\boldsymbol{I}}}}_{T}=\left[\begin{array}{ccc}{A}_{T} & 0 & 0\\ 0 & {B}_{T} & 0\\ 0 & 0 & {C}_{T}\end{array}\right],\end{eqnarray} \tag{ 46 }$$

with A_T , B_T , and C_T given by

$$\begin{eqnarray}&&{A}_{T}=\displaystyle \frac{2\left(1-{\beta }_{L}{\gamma }_{L}\right)}{\left(2{\beta }_{L}-{\gamma }_{L}+{\beta }_{L}{\gamma }_{L}\right)}{m}_{{\rm{M}}}{R}_{{\rm{M}}}^{2}{\tilde{J}}_{2,M},\end{eqnarray} \tag{ 47 }$$

$$\begin{eqnarray}&&{B}_{T}=\displaystyle \frac{2\left(1+{\gamma }_{L}\right)}{\left(2{\beta }_{L}-{\gamma }_{L}+{\beta }_{L}{\gamma }_{L}\right)}{m}_{{\rm{M}}}{R}_{{\rm{M}}}^{2}{\tilde{J}}_{2,M},\end{eqnarray} \tag{ 48 }$$

$$\begin{eqnarray}&&{C}_{T}=\displaystyle \frac{2\left(1+{\beta }_{L}\right)}{\left(2{\beta }_{L}-{\gamma }_{L}+{\beta }_{L}{\gamma }_{L}\right)}{m}_{{\rm{M}}}{R}_{{\rm{M}}}^{2}{\tilde{J}}_{2,M},\end{eqnarray} \tag{ 49 }$$

where m_M is the mass of the Moon, R_M is the reference radius of the Moon, ${\tilde{J}}_{2,M}$ is the second-degree zonal harmonic of the undistorted Moon, and β_L and γ_L are ratios of the undistorted moments of inertia given by

$$\begin{eqnarray}&&{\beta }_{L}=\displaystyle \frac{\left({C}_{T}-{A}_{T}\right)}{{B}_{T}},\end{eqnarray} \tag{ 50 }$$

$$\begin{eqnarray}&&{\gamma }_{L}=\displaystyle \frac{\left({B}_{T}-{A}_{T}\right)}{{C}_{T}}.\end{eqnarray} \tag{ 51 }$$

The undistorted total moment of inertia and the second-degree zonal harmonic of the undistorted Moon are not the same as the mean values since the tidal distortions have non-zero averages.

We assume that the lunar rotation aligns an oblate core–mantle boundary with the equator. Then the moment of inertia of the core I _c is given by

$$\begin{eqnarray}{{\boldsymbol{I}}}_{c}={\alpha }_{c}{C}_{T}\left[\begin{array}{ccc}1-{f}_{c} & 0 & 0\\ 0 & 1-{f}_{c} & 0\\ 0 & 0 & 1\end{array}\right]=\left[\begin{array}{ccc}{A}_{c} & 0 & 0\\ 0 & {B}_{c} & 0\\ 0 & 0 & {C}_{c}\end{array}\right],\end{eqnarray} \tag{ 52 }$$

where α_c = C_c /C_T is the ratio of the core polar moment of inertia to the undistorted total polar moment of inertia and f_c is the core oblateness. Distortion of the core moment of inertia is not considered.

The undistorted moment of inertia of the mantle is the difference between the undistorted total moment of inertia and the core moment of inertia:

$$\begin{eqnarray}&&{\widetilde{{\boldsymbol{I}}}}_{m}={\widetilde{{\boldsymbol{I}}}}_{T}-{{\boldsymbol{I}}}_{c}.\end{eqnarray} \tag{ 53 }$$

The moment of inertia of the mantle varies with time due to tidal distortion by Earth and spin distortion,

$$\begin{eqnarray}\begin{array}{l}{I}_{m}\left(t\right)={\widetilde{{\boldsymbol{I}}}}_{m}-\displaystyle \frac{{k}_{2,M}{m}_{{\rm{E}}}{R}_{{\rm{M}}}^{5}}{{r}^{5}}\left[\begin{array}{ccc}{x}^{2}-\displaystyle \frac{1}{3}{r}^{2} & {xy} & {xz}\\ {xy} & {y}^{2}-\displaystyle \frac{1}{3}{r}^{2} & {yz}\\ {xz} & {yz} & {z}^{2}-\displaystyle \frac{1}{3}{r}^{2}\end{array}\right]\\ +\displaystyle \frac{{k}_{2,M}{R}_{{\rm{M}}}^{5}}{3G}\left[\begin{array}{ccc}{\omega }_{m,x}^{2}-\displaystyle \frac{1}{3}\left({\omega }_{m}^{2}-{n}^{2}\right) & {\omega }_{m,x}{\omega }_{m,y} & {\omega }_{m,x}{\omega }_{m,z}\\ {\omega }_{m,x}{\omega }_{m,y} & {\omega }_{m,y}^{2}-\displaystyle \frac{1}{3}\left({\omega }_{m}^{2}-{n}^{2}\right) & {\omega }_{m,y}{\omega }_{m,z}\\ {\omega }_{m,x}{\omega }_{m,z} & {\omega }_{m,y}{\omega }_{m,z} & {\omega }_{m,z}^{2}-\displaystyle \frac{1}{3}\left({\omega }_{m}^{2}+2{n}^{2}\right)\end{array}\right],\end{array}\end{eqnarray} \tag{ 54 }$$

where the position vector of Earth relative to Moon, r , and the angular velocity of the mantle, ω _m , are evaluated at time t − τ_m ; k_2,M is the lunar potential Love number; m_E is the mass of Earth; R_M is the reference radius of the Moon; r is the Earth–Moon distance; x, y, and z are the components of the position of Earth relative to the Moon referred to the mantle frame; ω_m,x , ω_m,y , ω_m,z are the components of ω _m in the mantle frame; and n is the lunar mean motion.

The rate of change of the mantle's moment of inertia is given by

$$\begin{eqnarray}\begin{array}{l}{\dot{{\boldsymbol{I}}}}_{m}=\displaystyle \frac{5{k}_{2,M}{m}_{{\rm{E}}}{R}_{{\rm{M}}}^{5}{\boldsymbol{r}}\cdot \dot{{\boldsymbol{r}}}}{{r}^{7}}\left[\begin{array}{ccc}{x}^{2}-\displaystyle \frac{1}{3}{r}^{2} & {xy} & {xz}\\ {xy} & {y}^{2}-\displaystyle \frac{1}{3}{r}^{2} & {yz}\\ {xz} & {yz} & {z}^{2}-\displaystyle \frac{1}{3}{r}^{2}\end{array}\right]\\ -\,\displaystyle \frac{{k}_{2,M}{m}_{{\rm{E}}}{R}_{{\rm{M}}}^{5}}{{r}^{5}}\left[\begin{array}{ccc}2\left(x\dot{x}-\displaystyle \frac{1}{3}{\boldsymbol{r}}\cdot \dot{{\boldsymbol{r}}}\right) & x\dot{y}+\dot{x}y & x\dot{z}+\dot{x}z\\ x\dot{y}+\dot{x}y & \left(y\dot{y}-\displaystyle \frac{1}{3}{\boldsymbol{r}}\cdot \dot{{\boldsymbol{r}}}\right) & y\dot{z}+\dot{y}z\\ x\dot{z}+\dot{x}z & y\dot{z}+\dot{y}z & 2\left(z\dot{z}-\displaystyle \frac{1}{3}{\boldsymbol{r}}\cdot \dot{{\boldsymbol{r}}}\right)\end{array}\right]\\ +\,\displaystyle \frac{{k}_{2,M}{R}_{{\rm{M}}}^{5}}{3G}\left[\begin{array}{ccc}2\left({\omega }_{m,x}{\dot{\omega }}_{m,x}-\displaystyle \frac{1}{3}{{\boldsymbol{\omega }}}_{m}\cdot {\dot{{\boldsymbol{\omega }}}}_{m}\right) & {\omega }_{m,x}{\dot{\omega }}_{m,y}+{\dot{\omega }}_{m,x}{\omega }_{m,y} & {\omega }_{m,x}{\dot{\omega }}_{m,z}+{\dot{\omega }}_{m,x}{\omega }_{m,z}\\ {\omega }_{m,x}{\dot{\omega }}_{m,y}+{\dot{\omega }}_{m,x}{\omega }_{m,y} & 2\left({\omega }_{m,y}{\dot{\omega }}_{m,y}-\displaystyle \frac{1}{3}{{\boldsymbol{\omega }}}_{m}\cdot {\dot{{\boldsymbol{\omega }}}}_{m}\right) & {\omega }_{m,y}{\dot{\omega }}_{m,z}+{\dot{\omega }}_{m,y}{\omega }_{m,z}\\ {\omega }_{m,x}{\dot{\omega }}_{m,z}+{\dot{\omega }}_{m,x}{\omega }_{m,z} & {\omega }_{m,y}{\dot{\omega }}_{m,z}+{\dot{\omega }}_{m,y}{\omega }_{m,z} & 2\left({\omega }_{m,z}{\dot{\omega }}_{m,z}-\displaystyle \frac{1}{3}{{\boldsymbol{\omega }}}_{m}\cdot {\dot{{\boldsymbol{\omega }}}}_{m}\right)\end{array}\right].\end{array}\end{eqnarray} \tag{ 55 }$$

The torque on the Moon due to an external point-mass A is given by

$$\begin{eqnarray}&&{{\boldsymbol{N}}}_{{\rm{M}},\mathrm{fig}M-\mathrm{pm}A}={M}_{{\rm{M}}}{{\boldsymbol{r}}}_{{AM}}\times {{\boldsymbol{a}}}_{{\rm{M}},\mathrm{fig}M-\mathrm{pm}A},\end{eqnarray} \tag{ 56 }$$

where r _AM is the position of the point mass relative to the Moon and a _M,figM−pmA is the acceleration of the Moon due to the interaction of the extended figure of the Moon with the point-mass A, as described in Section 3.2. Torques are computed for the figure of the Moon interacting with Earth, the Sun, Mercury, Venus, Mars, Jupiter, and Saturn.

It can be shown that torques due to the interaction of the figure of the Moon with the figure of Earth are important for the orientation of the Moon (Eckhardt 1981). The three most significant terms of the torque are

$$\begin{eqnarray}\begin{array}{rcl}{{\boldsymbol{N}}}_{{\rm{M}},\mathrm{figM}-\mathrm{figE}} & = & \displaystyle \frac{15{{GM}}_{{\rm{E}}}{R}_{{\rm{E}}}^{2}{J}_{2,E}}{2{r}_{\mathrm{EM}}^{5}}\left\{\left(1-7{\sin }^{2}{\varphi }_{{\rm{M}},{\rm{E}}}\right)\right.\\ & & \times \left[{\widehat{{\boldsymbol{r}}}}_{\mathrm{EM}}\times {{\boldsymbol{I}}}_{{\rm{M}}}{\widehat{{\boldsymbol{r}}}}_{\mathrm{EM}}\right]\\ & & +2\sin {\varphi }_{{\rm{M}},{\rm{E}}}\left[{\widehat{{\boldsymbol{r}}}}_{\mathrm{EM}}\times {{\boldsymbol{I}}}_{{\rm{M}}}{\widehat{{\boldsymbol{p}}}}_{{\rm{E}}}+{\widehat{{\boldsymbol{p}}}}_{{\rm{E}}}\times {{\boldsymbol{I}}}_{{\rm{M}}}{\widehat{{\boldsymbol{r}}}}_{\mathrm{EM}}\right]\\ & & -\displaystyle \frac{2}{5}\left[{\widehat{{\boldsymbol{p}}}}_{{\boldsymbol{E}}}\times {{\boldsymbol{I}}}_{{\rm{M}}}{\widehat{{\boldsymbol{p}}}}_{{\rm{E}}}\right],\end{array}\end{eqnarray} \tag{ 57 }$$

where ${\widehat{{\boldsymbol{p}}}}_{{\rm{E}}}$ is the direction vector of Earth's pole and ${\widehat{{\boldsymbol{r}}}}_{\mathrm{EM}}$ is the direction vector of Earth from the Moon, I _M is the lunar moment of inertia tensor, R_E is the reference radius of Earth, and φ_M,E is defined by $\sin {\varphi }_{{\rm{M}},{\rm{E}}}={\widehat{{\boldsymbol{r}}}}_{\mathrm{EM}}\cdot {\widehat{{\boldsymbol{p}}}}_{{\rm{E}}}$.

The torque on the mantle due to the interaction between the core and mantle is evaluated in the mantle frame and is given by

$$\begin{eqnarray}&&{{\boldsymbol{N}}}_{\mathrm{cmb}}={k}_{v}\left({{\boldsymbol{\omega }}}_{c}-{{\boldsymbol{\omega }}}_{m}\right)+\left({C}_{c}-{A}_{c}\right)\left({\widehat{{\boldsymbol{z}}}}_{m}\cdot {{\boldsymbol{\omega }}}_{m}\right)\left({\widehat{{\boldsymbol{z}}}}_{m}\times {{\boldsymbol{\omega }}}_{c}\right),\end{eqnarray} \tag{ 58 }$$

where ${\widehat{{\boldsymbol{z}}}}_{m}$ is a unit vector in the mantle frame aligned with the polar axis. Parameter k_v is for the viscous interaction at the core–mantle boundary. The torque on the core is the negative of the torque on the mantle.

The orbit of the Moon is determined from the LLR data, and Figure 4 shows the one-way residuals of the LLR data over about 50 years. In the last few years, data were available from the Observatoire de la Côte d'Azur, Apache Point, Matera, and Wettzell sites. The rms residual of the early LLR data (∼1970–1980) is about 20 cm while the rms residual of the recent LLR data is about 1.3 cm.

Zoom In Zoom Out Reset image size

The orbit of Mercury is mainly determined from the MESSENGER radio range data, and Figure 5 shows the one-way range residuals over about 4 years. The rms residual of the MESSENGER ranges is about 0.7 m.

Zoom In Zoom Out Reset image size

The orbit of Venus is mainly determined from the Venus Express radio range data, and Figure 6 shows the one-way range residuals over about 6.5 years. The rms residual of the Venus Express ranges is about 8 m.

Zoom In Zoom Out Reset image size

The shape of Mars' orbit is mainly constrained by the radio range data of Mars orbiters, and Figure 7 shows the one-way range residuals of Mars Express (MEX), Mars Global Surveyor (MGS), Mars Odyssey (ODY), and Mars Reconnaissance Orbiter (MRO). The rms residual of the MEX ranges is about 2 m and the rms residuals of the MGS, ODY, and MRO ranges are about 0.7 m. The orientation of Mars' orbit is mainly constrained by VLBI measurements of the Mars orbiters, and Figure 8 shows the VLBI residuals of the Goldstone–Madrid and Goldstone–Canberra baselines. The rms residual of the Goldstone–Madrid baseline is about 0.25 mas and the rms residual of the Goldstone–Canberra baseline is about 0.18 mas.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The shape of Jupiter's orbit is mainly constrained by the Juno radio range data, and Figure 9 shows the one-way range residuals over about 4 years. The rms residual of the Juno ranges is about 13 m. The orientation of Jupiter's orbit is mainly constrained by the VLBA data of the Juno spacecraft, and Figure 10 shows the Juno VLBA residuals over about 2 years. The rms residual of the Juno VLBA data in R.A. is about 0.4 mas and the rms residual of the Juno VLBA data in decl. is about 0.6 mas.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The shape of Saturn's orbit is mainly constrained by the Cassini radio range data, and Figure 11 shows the one-way range residuals over about 13 years. The rms residual of the Cassini ranges is about 3 m. The orientation of Saturn's orbit is mainly constrained by the VLBA data of the Cassini spacecraft, and Figure 12 shows the Cassini VLBA residuals over about 13 years. The rms residual of the Cassini VLBA data in R.A. is about 0.6 mas and the rms residual of the Cassini VLBA data in decl. is about 0.8 mas if the two obvious outliers are included, and 0.35 and 0.36 mas if they are excluded.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The orbits of Uranus and Neptune are mainly constrained by astrometry and radio range measurements to the Voyager flybys and they are statistically consistent with DE430 (see Folkner et al. 2014).

The orbit of Pluto is mainly determined by astrometry, and Figure 13 shows the residuals of the stellar occultation measurements from Desmars et al. (2019). The rms residuals of the stellar occultations are about 8 mas in R.A. and about 11 mas in decl.

Zoom In Zoom Out Reset image size