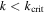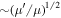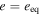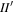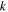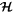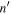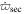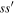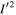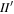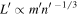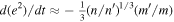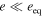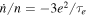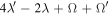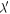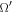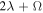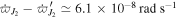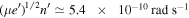ABSTRACT
Several pairs of solar system satellites occupy mean motion resonances (MMRs). We divide these into two groups according to their proximity to exact resonance. Proximity is measured by the existence of a separatrix in phase space. MMRs between Io–Europa, Europa–Ganymede, and Enceladus–Dione are too distant from exact resonance for a separatrix to appear. A separatrix is present only in the phase spaces of the Mimas–Tethys and Titan–Hyperion MMRs, and their resonant arguments are the only ones to exhibit substantial librations. Could there be a causal connection between the libration amplitude and the presence of a separatrix? Our suspicions were aroused by Goldreich & Schlichting, who demonstrate that sufficiently deep in a MMR, eccentricity damping could destabilize librations. However, our investigation reveals that libration amplitudes in both the Mimas–Tethys and Titan–Hyperion MMRs are fossils. Although the Mimas–Tethys MMR is overstable, its libration amplitude grows on the tidal damping timescale of Mimas's inclination, which is considerably longer than a Hubble time. On the other hand, the Titan–Hyperion MMR is stable, but tidal damping of Hyperion's eccentricity is too weak to have affected the amplitude of its libration.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
An influential paper by Roy & Ovenden (1954) established that the number of mean motion resonances (MMRs) between pairs of solar system satellites exceeds that expected from a random distribution of mean motions. Subsequently, Goldreich (1965) proposed that MMRs form as the result of convergent outward migration of satellite orbits driven by tidal torques from their parent planets. He argued that this could account for the origin of the MMRs between the Saturnian satellites, Mimas–Tethys and Enceladus–Dione but not that between Titan–Hyperion.3 He also suggested that MMRs between the Jovian satellites Io–Europa and Europa–Ganymede were tidal in origin.
MMR formation by convergent migration associated with tidal torques is widely accepted. For a long time, tidal torques were assumed to arise from an unspecified mechanism of damping associated with the equilibrium tide. Recent astrometric analyses of both historical and Cassini data by Lainey et al. (2015) challenge this assumption. Outward migration rates are much faster than expected, especially for satellites that orbit far from Saturn. Fuller et al. (2016) propose an explanation involving resonance lock between frequencies of tides and those of normal modes or waves. They favor g-modes but also mention inertial waves (Ogilvie 2014). Either possibility suggests that Saturn possesses a stably stratified core or layer which evolves on a timescale comparable to its lifetime.
Conventionally, the tidal torque acting on a satellite was assumed to depend only on the satellite's mass and orbit and internal properties of the planet. Conventional tidal torques include both equilibrium tides and various cases of dynamic tides. Tidal torques with resonance lock are particular cases of dynamic tides. They differ from conventional tidal torques in one crucial aspect. Their strength of the torque depends upon whether the satellite is involved in an MMR with another satellite. For example, suppose resonant lock enforces a fixed outward migration of a satellite's semimajor axis and that satellite enters into an MMR with an outer satellite. Subsequently, the tidal torque acting on the inner satellite would increase as angular momentum is transferred from the inner to the outer satellite. Moreover, if prior to the formation of the MMR, the tidal torque on the outer satellite also involved resonance lock, it would decrease after the MMR were established. We view resonance lock as an extremely promising hypothesis. However, at this point the properties of the internal planetary modes it relies on are not well-identified. In addition, we find it confusing to switch back and forth between conventional tides and those involving resonance lock. Thus we delay discussions related to resonance lock until the end (Section 5). Unless specified otherwise, everything before that section is discussed under the implicit assumption of conventional tidal torques.
Convergent migration does not guarantee the formation of an MMR so the probability of capture into resonance is an important quantity. Initial steps toward calculating it were taken by Allan (1969) and Sinclair (1972) who estimated a small, 0.04, capture probability for the MMR between Mimas–Tethys. Yoder (1979) developed an accurate diagrammatic method and Henrard (1982) showed how capture probabilities were related to adiabatic invariants. Following Henrard (1982), Borderies & Goldreich (1984) derived simple expressions for capture probabilities.
It is natural to wonder how long an MMR, once formed, will last. Lin & Papaloizou (1979) noted that there exists an equilibrium state for some MMRs in which convergence toward exact resonance is halted by tidal damping of one or both of the resonant satellites' orbital eccentricities. In a more recent development, it was found that eccentricity damping may promote librational overstability leading to passage through resonance provided a separatrix is present at the equilibrium state (Meyer & Wisdom 2008; Goldreich & Schlichting 2014).
Before classifying MMRs, we digress to summarize our current understanding of librational stability. Rapid secular apsidal precession due to Saturn's large quadrupole moment separates first-order e- and e'-type MMRs with resonant arguments 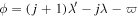 and
and 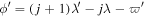 by more than their librational widths.4
Thus each type may be treated independently of the other. Goldreich & Schlichting (2014) derived an analytic criterion for librational overstability of a first-order e-MMR. They proved that above a limiting eccentricity, satellite tides render ϕ overstable. Moreover, if the eccentricity is so large that a separatrix is present, passage through resonance would ensue. Delisle et al. (2015) and Deck & Batygin (2015) examined a related problem and found that first-order e'-MMRs are stable. Moreover, Meyer & Wisdom (2008) found the Mimas–Enceladus 3:2 e'-MMR and the Enceladus–Dione 2:1 e'-MMR to be permanent once formed. To avoid definite MMR capture, they proposed that
by more than their librational widths.4
Thus each type may be treated independently of the other. Goldreich & Schlichting (2014) derived an analytic criterion for librational overstability of a first-order e-MMR. They proved that above a limiting eccentricity, satellite tides render ϕ overstable. Moreover, if the eccentricity is so large that a separatrix is present, passage through resonance would ensue. Delisle et al. (2015) and Deck & Batygin (2015) examined a related problem and found that first-order e'-MMRs are stable. Moreover, Meyer & Wisdom (2008) found the Mimas–Enceladus 3:2 e'-MMR and the Enceladus–Dione 2:1 e'-MMR to be permanent once formed. To avoid definite MMR capture, they proposed that 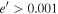 initially. This reduces the capture probability but does not annihilate it. In this paper, we analyze e'-MMRs and find them to be stable except for extreme choices of a parameter, p, that is not realized in tidal damping of eccentricity (see Appendix
initially. This reduces the capture probability but does not annihilate it. In this paper, we analyze e'-MMRs and find them to be stable except for extreme choices of a parameter, p, that is not realized in tidal damping of eccentricity (see Appendix
The crucial difference between e- and e'-MMRs involves the effect of eccentricity damping due to tides the planet raises in the satellite. By decreasing orbital energy at constant orbital angular momentum5 , these tides act to decrease a satellite's semimajor axis. Thus eccentricity damping opposes convergent migration in e-MMRs and promotes it in e'-MMRs.
A puzzle then arises. Saturn's oblateness causes elliptical orbits to precess in a prograde fashion at a rate that declines with increasing semimajor axis. Thus during convergent outward migration, e'-MMRs are encountered before e-MMRs. Yet despite their permanence once formed, only the 4:3 MMR between Titan and Hyperion is of e' type in the Saturn system. This puzzle does not have great statistical significance, but it is worth bearing in mind.
Our paper is structured as follows. Section 2 presents a physical picture of librational overstability. We divide satellite MMRs into two groups. Group I contains the pairs Io–Europa, Europa–Ganymede, and Enceladus–Dione. Their resonant arguments exhibit small librations. We treat this group in Section 3. Group II contains the remaining MMRs, Mimas–Tethys and Titan–Hyperion. Their resonant arguments show large librations. We analyse this group in Section 4. Section 6 consists of two parts. The first compares resonant and tidal torques and speculates about how Lainey et al. (2012) might have erred in concluding that Mimas is migrating toward Saturn. The second part describes some vestiges of past MMRs. Particular attention is given to the orbital eccentricity of Mimas and the possibility that Mimas possesses an internal ocean. Our final section focuses on resonance lock and its effect on the dynamics of MMRs. We relegate technical details to the Appendix. These include a table listing relevant parameters for satellites involved in MMRs, stability analysis of the e'-MMR, and details regarding the resonant dynamics of MMRs that are not covered in the main text.
2. CLASSIFICATION OF MMRS
We begin by reviewing selected features of e-MMR following the description given in Goldreich & Schlichting (2014), where e-MMR refers to first-order, eccentricity type, MMR perturbing the inner body. In Appendix 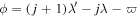 , where λ and ϖ denote mean longitude and longitude of pericenter, and a prime labels the outer body. We assume that the orbits of both satellites lie in the planet's equatorial plane. We can also neglect the orbital eccentricity of the outer satellite. For the moment it suffices to treat the inner satellite as a test particle. Although this is a special example, the physical concepts we emphasize apply more generally to both eccentricity-type and inclination-type MMRs.
, where λ and ϖ denote mean longitude and longitude of pericenter, and a prime labels the outer body. We assume that the orbits of both satellites lie in the planet's equatorial plane. We can also neglect the orbital eccentricity of the outer satellite. For the moment it suffices to treat the inner satellite as a test particle. Although this is a special example, the physical concepts we emphasize apply more generally to both eccentricity-type and inclination-type MMRs.
As described above, the dynamical system has two degrees of freedom. Because the outer satellite moves on a circular orbit, the Jacobi constant of the inner satellite, 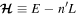 , is a constant of motion.6
Denoting the Jacobi constant by
, is a constant of motion.6
Denoting the Jacobi constant by  is deliberate. It is the Hamiltonian corresponding to the conjugate coordinate and momentum, ϕ and e2. Moreover, because λ and ϖ only appear in the combination
is deliberate. It is the Hamiltonian corresponding to the conjugate coordinate and momentum, ϕ and e2. Moreover, because λ and ϖ only appear in the combination  , the other combination
, the other combination  is an ignorable coordinate. This implies the existence of a second constant of motion labeled k by Goldreich & Schlichting (2014). Expressions for k and
is an ignorable coordinate. This implies the existence of a second constant of motion labeled k by Goldreich & Schlichting (2014). Expressions for k and  read:
read:
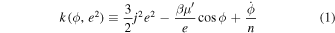
and
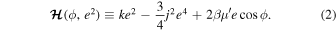
In the above, β is a j-dependent constant of order unity and 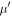 is the ratio of the mass of the outer satellite to that of the planet. The expression for
is the ratio of the mass of the outer satellite to that of the planet. The expression for 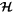 is derived from the linearized equations of motion as described in Eckart (1960). The canonical coordinate, ϕ, and momentum, e2, satisfy Hamilton's equations
is derived from the linearized equations of motion as described in Eckart (1960). The canonical coordinate, ϕ, and momentum, e2, satisfy Hamilton's equations 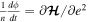 and
and 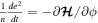 .
.
At fixed k, the system is constrained to move along level curves of 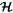 . At the maximum value of
. At the maximum value of 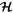 , denoted
, denoted 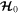 ,
,  . Corresponding to
. Corresponding to 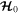 , there exists a nested set of periodic orbits for which conjunctions occur at pericenter passage;
, there exists a nested set of periodic orbits for which conjunctions occur at pericenter passage;  when
when 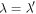 . Orbital eccentricities, e0, increase with proximity of n to the exact resonance value,
. Orbital eccentricities, e0, increase with proximity of n to the exact resonance value, ![${n}_{r}=[(j+1)n-{\dot{\varpi }}_{\sec }]/j$](https://content.cld.iop.org/journals/1538-3881/153/1/17/revision1/ajaa4b0bieqn22.gif) , according to7
, according to7
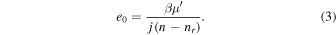
Note that this fixed point exists only if 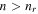 .
.
Setting  in Equation (1), we obtain a relation between e0 and k. Comparing this relation with that given by Equation (3), we observe that k increases with proximity to exact resonance although not at all linearly. The topology of the level curves of
in Equation (1), we obtain a relation between e0 and k. Comparing this relation with that given by Equation (3), we observe that k increases with proximity to exact resonance although not at all linearly. The topology of the level curves of  undergoes a qualitative change across
undergoes a qualitative change across
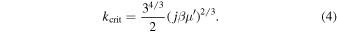
For 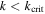 there is one stable fixed point at
there is one stable fixed point at 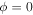 and
and 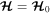 whereas two additional fixed points, one stable and the other unstable, are present for
whereas two additional fixed points, one stable and the other unstable, are present for  . Both additional fixed points are located at
. Both additional fixed points are located at  , but
, but 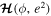 has a local minimum at the former, which we denote by
has a local minimum at the former, which we denote by 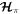 , and a saddle point at the latter.8
A second set of nested periodic orbits corresponds to
, and a saddle point at the latter.8
A second set of nested periodic orbits corresponds to 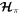 . These are pertinent to our investigation. They lie beyond exact resonance,
. These are pertinent to our investigation. They lie beyond exact resonance, 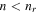 , and since
, and since 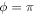 , conjunction coincides with apoapse passage. Thus for
, conjunction coincides with apoapse passage. Thus for 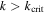 , there is a door to escape from resonance. Librational overstability leading to passage through the inner separatrix is the way to open it. Again, eccentricity increases with proximity to exact resonance;
, there is a door to escape from resonance. Librational overstability leading to passage through the inner separatrix is the way to open it. Again, eccentricity increases with proximity to exact resonance;

2.1. Tidal Evolution
We consider systems in which the planet's spin frequency  . Then the tides the satellites raise in the planet produce positive torques that cause their orbits to expand.9
We denote the tidal timescale for orbit expansion by
. Then the tides the satellites raise in the planet produce positive torques that cause their orbits to expand.9
We denote the tidal timescale for orbit expansion by 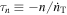 .10
To ensure convergent migration, we further assume that
.10
To ensure convergent migration, we further assume that  . We take the inner satellite's spin to be synchronous with its mean motion. Thus tides raised by the planet in the satellite dissipate energy at constant angular momentum. We denote the timescale for eccentricity damping by
. We take the inner satellite's spin to be synchronous with its mean motion. Thus tides raised by the planet in the satellite dissipate energy at constant angular momentum. We denote the timescale for eccentricity damping by 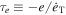 . From Peale (1999) we have,
. From Peale (1999) we have,
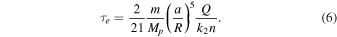
It is important to bear in mind that  and
and 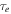 set the timescales for tidal evolution of n and e for an isolated satellite. Within a MMR, the resonant transfer of angular momentum and energy between satellites modifies these timescales. Eccentricity damping is assumed to be dominated by dissipation associated with the equilibrium tide in the satellite. This is probably appropriate for rocky/icy satellites since frequencies of internal elastic modes are much higher than epicyclic frequencies. However, the effect on eccentricity of dynamics tides the satellite excites in the planet could be important.
set the timescales for tidal evolution of n and e for an isolated satellite. Within a MMR, the resonant transfer of angular momentum and energy between satellites modifies these timescales. Eccentricity damping is assumed to be dominated by dissipation associated with the equilibrium tide in the satellite. This is probably appropriate for rocky/icy satellites since frequencies of internal elastic modes are much higher than epicyclic frequencies. However, the effect on eccentricity of dynamics tides the satellite excites in the planet could be important.
Tides cause both k and 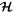 to evolve. Tidal evolution is slow in comparison to the periods characteristic of motions around the level curves of
to evolve. Tidal evolution is slow in comparison to the periods characteristic of motions around the level curves of 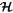 . The evolution of k and
. The evolution of k and 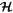 are governed by11
are governed by11
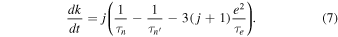
and

Convergent migration, i.e., 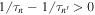 , tends to increase k whereas eccentricity damping acts to reduce it. In practice, the slow tidal evolution of k and
, tends to increase k whereas eccentricity damping acts to reduce it. In practice, the slow tidal evolution of k and 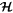 is evaluated by averaging the right-hand sides of Equations (7) and (8) over a period of the motion around the level curves of
is evaluated by averaging the right-hand sides of Equations (7) and (8) over a period of the motion around the level curves of 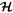 with k and
with k and 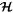 held fixed.
held fixed.
From Equation (7), we see that 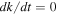 at
at 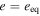 , where
, where

Thus k increases almost linearly with time until it approaches 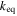 where
where 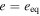 . If
. If  the system cannot escape from MMR. On the other hand, if
the system cannot escape from MMR. On the other hand, if 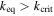 , librational instability will ensue leading to passage through the inner branch of the separatrix and approach to the stable fixed point that lies within it (see Figure 1). This transition signifies escape from the e-MMR and occurs on timescale
, librational instability will ensue leading to passage through the inner branch of the separatrix and approach to the stable fixed point that lies within it (see Figure 1). This transition signifies escape from the e-MMR and occurs on timescale 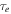 (Goldreich & Schlichting 2014). However, librations are always stable for e'-MMRs, independent of whether
(Goldreich & Schlichting 2014). However, librations are always stable for e'-MMRs, independent of whether 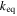 is larger or smaller than
is larger or smaller than 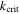 , as shown in the subsection "stability of equilibrium" of Appendix
, as shown in the subsection "stability of equilibrium" of Appendix
Figure 1. Contour plots of the Hamiltonian (top) and the corresponding cross section along the 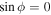 axis (bottom) for
axis (bottom) for 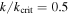 (left) and
(left) and 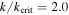 (right). Negative values on the bottom x-axes correspond to
(right). Negative values on the bottom x-axes correspond to 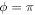 . Stable fixed points are marked by a square at
. Stable fixed points are marked by a square at 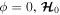 and a circle at
and a circle at 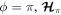 . A diamond is attached to the unstable fixed point at the intersection of the inner (thick-dashed) and outer (thick-solid) branches of the separatrix.
. A diamond is attached to the unstable fixed point at the intersection of the inner (thick-dashed) and outer (thick-solid) branches of the separatrix.
Download figure:
Standard image High-resolution imageEnergy dissipated by damping orbital eccentricity is deposited as heat inside the inner satellite at a rate
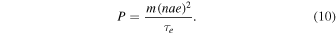
Substituting  given by Equation (9) into Equation (10) sets a
given by Equation (9) into Equation (10) sets a 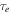 independent upper bound on the tidal heating rate;
independent upper bound on the tidal heating rate;
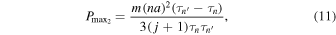
where the subscript "2" means that this power corresponds to two satellites locked in resonance.
Evolution of 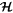 also deserves examination. From Equation (8), it is obvious that convergent migration acts to increase
also deserves examination. From Equation (8), it is obvious that convergent migration acts to increase 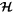 whereas eccentricity damping tends to decrease it. A stronger result is that convergent migration drives
whereas eccentricity damping tends to decrease it. A stronger result is that convergent migration drives 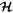 toward
toward 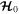 even as it causes
even as it causes 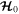 to grow. This result may be derived by noting that, in the absence of eccentricity damping, the area within a level curve describing librations about
to grow. This result may be derived by noting that, in the absence of eccentricity damping, the area within a level curve describing librations about 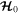 is an adiabatic invariant under convergent migration (Goldreich & Schlichting 2014). Librations around
is an adiabatic invariant under convergent migration (Goldreich & Schlichting 2014). Librations around  and
and 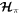 are analogous to anticyclones and cyclones in which Coriolis and pressure forces are in stable balance around pressure maxima and minima. Librational overstability promoted by eccentricity damping is analogous to the spreading and weakening of an anticyclone by friction.
are analogous to anticyclones and cyclones in which Coriolis and pressure forces are in stable balance around pressure maxima and minima. Librational overstability promoted by eccentricity damping is analogous to the spreading and weakening of an anticyclone by friction.
We classify the MMRs of satellite pairs in the solar system into two groups, one with 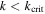 and the other with
and the other with  (Table 1). We emphasize the distinguishing features of the members in each group and investigate their origin.
(Table 1). We emphasize the distinguishing features of the members in each group and investigate their origin.
Table 1. Satellite Pairs in MMR
| Argument | Satellites | Class | k |

|
|
|---|---|---|---|---|---|
| 1 |
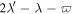
|
Io–Europa |

|
−4.60 × 10−3 | 1.54 × 10−3 |
| 2 |
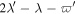
|
Io–Europa |

|
−8.77 × 10−4 | 1.27 × 10−3 |
| 3 |
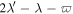
|
Europa–Ganymede |
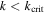
|
−6.38 × 10−3 | 3.26 × 10−3 |
| 4 |

|
Mimas–Tethys |
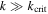
|
2.25 × 10−3 | 5.32 × 10−6 |
| 5 |
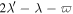
|
Enceladus–Dione |
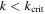
|
−2.76 × 10−4 | 2.76 × 10−4 |
| 6 |
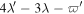
|
Titan–Hyperion |
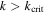
|
6.39 × 10−2 | 1.15 × 10−2 |
Note. The names of the satellites are ordered as "inner satellite–outer satellite". The concepts of k and 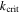 are the same for all MMRs although their specific definitions vary. For the 1st, 3rd and 5th MMR, k and
are the same for all MMRs although their specific definitions vary. For the 1st, 3rd and 5th MMR, k and 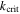 follow the formulas in Goldreich & Schlichting (2014). Expressions for k and
follow the formulas in Goldreich & Schlichting (2014). Expressions for k and 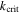 appropriate to the 2nd, 4th and 6th MMR are provided in the appendix. The
appropriate to the 2nd, 4th and 6th MMR are provided in the appendix. The 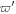 in the arguments for the 2nd and 6th MMRs imply that it is the outer body's eccentricity which is excited.
in the arguments for the 2nd and 6th MMRs imply that it is the outer body's eccentricity which is excited.
Download table as: ASCIITypeset image
3. GROUP I: 
All MMRs with  are first order eccentricity-type and exhibit only small librations about
are first order eccentricity-type and exhibit only small librations about 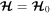 . The 1st, 2nd and 3rd entries in Table 1 involve pairs of Jupiter's Galilean satellites. Each of these satellites is also a member of the Laplace three-body resonance. The 2nd entry is special in that it is the outer body's eccentricity that is perturbed. The 4th entry is the only MMR in Saturn's satellite system for which
. The 1st, 2nd and 3rd entries in Table 1 involve pairs of Jupiter's Galilean satellites. Each of these satellites is also a member of the Laplace three-body resonance. The 2nd entry is special in that it is the outer body's eccentricity that is perturbed. The 4th entry is the only MMR in Saturn's satellite system for which 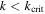 .
.
Table 2. Eccentricity Comparison
| Satellites |
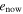
|
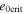
|
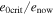
|
|---|---|---|---|
| Io–Europa (e) | 0.0041 | 0.037 | 9.024 |
| Io–Europa (e') | 0.009 | 0.0238 | 2.532 |
| Europa–Ganymede | 0.009 | 0.0538 | 48.91 |
| Enceladus–Dione | 0.0047 | 0.0157 | 3.340 |
Note. Comparison of the current and critical values of e. Io–Europa (e') signifies that this row shows the corresponding values for e'.
Download table as: ASCIITypeset image
Table 3. Parameters
| Satellite |
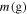
|
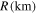
|

|
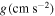
|

|

|
Type |
|---|---|---|---|---|---|---|---|
| Mimas | 3.7 × 1022 | 198 | 7.7 × 10−5 | 6.4 | 1.14 | 2700 | Icy |
| Enceladus | 1.1 × 1023 | 252 | 5.3 × 10−5 | 11.4 | 1.6 | 2000 | Icy |
| Tethys | 6.2 × 1023 | 531 | 3.85 × 10−5 | 14.7 | 0.984 | 500 | Icy |
| Dione | 1.1 × 1024 | 561 | 2.65 × 10−5 | 23.3 | 1.48 | 200 | Icy |
| Titan | 1.3 × 1026 | 2576 | 4.56 × 10−6 | 135.2 | 1.88 | 9 | rocky/icy |
| Hyperion | 5.6 × 1021 | 135 | 3.42 × 10−6 | 2 | 0.544 | 2.6 × 104 | icy |
| Io | 8.9 × 1025 | 1822 | 4.1 × 10−5 | 179.6 | 3.53 | 40 | rocky |
| Europa | 4.8 × 1025 | 1561 | 2.0 × 10−5 | 131.4 | 3.01 | 80 | rocky |
| Ganymede | 1.5 × 1026 | 2634 | 1.0 × 10−5 | 142.8 | 1.94 | 8 | rocky/icy |
Note. To calculate  , we apply
, we apply 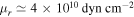 for icy satellite,
for icy satellite, 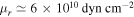 for rocky/icy satellite, and
for rocky/icy satellite, and 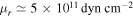 for rocky satellite. For Saturn, we adopt
for rocky satellite. For Saturn, we adopt 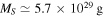 and
and 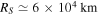 . For Jupiter, we adopt
. For Jupiter, we adopt 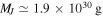 , and
, and 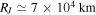 . All parameters except
. All parameters except 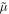 are taken from Seidelmann (1992).
are taken from Seidelmann (1992).
Download table as: ASCIITypeset image
Ideally, Table 1 would have a 4th column displaying calculated values for  . Unfortunately, there are too many uncertain parameters to make calculating
. Unfortunately, there are too many uncertain parameters to make calculating 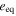 a useful exercise. Values of the tidal Love number, k2, and the tidal quality factor, Q for both the planet and the perturbed satellite enter into Equation (9) for
a useful exercise. Values of the tidal Love number, k2, and the tidal quality factor, Q for both the planet and the perturbed satellite enter into Equation (9) for 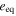 . Jupiter and Saturn are fluid bodies and reasonable estimates of their tidal Love numbers exist (Gavrilov & Zharkov 1977). Reliable estimates for tidal Love numbers of solid satellites are also possible, but there is compelling evidence that, as a result of tidal heating, Io, Europa, and Enceladus have undergone limited internal melting.12
Melting enhances k2, but without knowing its extent, we cannot determine by how much. Our ability to estimate tidal Q's is poor. The mechanism responsible for tidal dissipation in Jupiter and Saturn remains a topic of active investigation (Ogilvie 2014). In the past, estimates for the Q of Jupiter and Saturn were made by assuming that the satellites formed contemporaneously with their planet and that the MMRs resulted from tidal evolution (Goldreich 1965; Goldreich & Soter 1966). Recent astrometric analyses of the secular accelerations of Jupiter's Galilean satellites are consistent with these assumptions but those for Saturn's inner satellites (Lainey et al. 2009, 2012, 2015) imply that either the satellites are younger than the planet or, more likely, dynamic tides rather than equilibrium tides are responsible for their rapid outward migrations. Estimates of tidal Q for solid material are also fraught with uncertainty as relevant parameters such as composition, porosity, grain size and temperature are poorly constrained.
. Jupiter and Saturn are fluid bodies and reasonable estimates of their tidal Love numbers exist (Gavrilov & Zharkov 1977). Reliable estimates for tidal Love numbers of solid satellites are also possible, but there is compelling evidence that, as a result of tidal heating, Io, Europa, and Enceladus have undergone limited internal melting.12
Melting enhances k2, but without knowing its extent, we cannot determine by how much. Our ability to estimate tidal Q's is poor. The mechanism responsible for tidal dissipation in Jupiter and Saturn remains a topic of active investigation (Ogilvie 2014). In the past, estimates for the Q of Jupiter and Saturn were made by assuming that the satellites formed contemporaneously with their planet and that the MMRs resulted from tidal evolution (Goldreich 1965; Goldreich & Soter 1966). Recent astrometric analyses of the secular accelerations of Jupiter's Galilean satellites are consistent with these assumptions but those for Saturn's inner satellites (Lainey et al. 2009, 2012, 2015) imply that either the satellites are younger than the planet or, more likely, dynamic tides rather than equilibrium tides are responsible for their rapid outward migrations. Estimates of tidal Q for solid material are also fraught with uncertainty as relevant parameters such as composition, porosity, grain size and temperature are poorly constrained.
An upper bound to the current time-average rate of dissipation within Io, Europa, and Ganymede is set by assuming the two-body MMRs between Io–Europa and Europa–Ganymede have existed for tss, the entire age of the solar system (Goldreich & Mitchell 2010)13
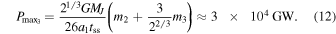
But infrared measurements made by the Galileo orbiter find Io's net luminosity to be closer to 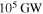 (Veeder et al. 2012). Although the observed power is only three times larger than
(Veeder et al. 2012). Although the observed power is only three times larger than 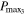 , it is hard to adjust the coefficients and parameters in Equation (12) to account for this discrepancy. This suggests that the tidal power dissipated in Io varies and so does its orbital eccentricity (Ojakangas & Stevenson 1986).14
How large might Io's eccentricity have been and could it ever have exceeded
, it is hard to adjust the coefficients and parameters in Equation (12) to account for this discrepancy. This suggests that the tidal power dissipated in Io varies and so does its orbital eccentricity (Ojakangas & Stevenson 1986).14
How large might Io's eccentricity have been and could it ever have exceeded 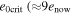 , see Table 2)? Models by Ojakangas & Stevenson (1986) suggest not, since the most extreme eccentricity they reach is
, see Table 2)? Models by Ojakangas & Stevenson (1986) suggest not, since the most extreme eccentricity they reach is 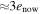 . According to Lainey et al. (2009), currently Io's semimajor axis is decreasing as might be expected if the satellite's orbital eccentricity were damping following an episode of higher than average tidal heating. Tides convert orbital energy into heat at fixed angular momentum and hence cause a to decrease.
. According to Lainey et al. (2009), currently Io's semimajor axis is decreasing as might be expected if the satellite's orbital eccentricity were damping following an episode of higher than average tidal heating. Tides convert orbital energy into heat at fixed angular momentum and hence cause a to decrease.
Next we examine the MMR between Enceladus and Dione. All the tidal heating occurs in Enceladus so we appeal to Equations (10) and (11) for guidance. Infrared observations from the Cassini orbiter indicate that between 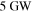 and
and 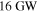 of power is being radiated from hot spots associated with long cracks in the south polar region of Enceladus (Spencer et al. 2013; Howett et al. 2014). Even
of power is being radiated from hot spots associated with long cracks in the south polar region of Enceladus (Spencer et al. 2013; Howett et al. 2014). Even 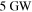 would be difficult to account for if the expansion of Enceladus's orbit were due to dissipation of its equilibrium tide with Saturn's
would be difficult to account for if the expansion of Enceladus's orbit were due to dissipation of its equilibrium tide with Saturn's 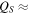 18,000 (Meyer & Wisdom 2007). However, it is compatible with rates of outward migration of Saturn's satellites reported by Lainey et al. (2015) which, under the assumption of equilibrium tides, requires QS to be 10 times smaller than that adopted by Meyer & Wisdom (2007). All this suggests another type of tidal interaction must prevail. In this context, we find particularly appealing the hypothesis by Fuller et al. (2016) of resonance lock with dynamical tides particularly appealing.
18,000 (Meyer & Wisdom 2007). However, it is compatible with rates of outward migration of Saturn's satellites reported by Lainey et al. (2015) which, under the assumption of equilibrium tides, requires QS to be 10 times smaller than that adopted by Meyer & Wisdom (2007). All this suggests another type of tidal interaction must prevail. In this context, we find particularly appealing the hypothesis by Fuller et al. (2016) of resonance lock with dynamical tides particularly appealing.
3.1. Similarities and Differences between Io and Enceladus
Although their current eccentricities are small, Io and Enceladus exhibit unmistakable signatures of thermal activity. Noting that tidal power dissipation is 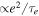 , we apply Equation (10) to calculate the
, we apply Equation (10) to calculate the 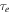 required to match each satellite's current power output. Then we compare this value of
required to match each satellite's current power output. Then we compare this value of 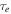 to that calculated from interior models. In each case, the theoretical value for
to that calculated from interior models. In each case, the theoretical value for 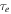 exceeds the required one, suggesting that Io and Enceladus may be in cooling phases of limit cycles.
exceeds the required one, suggesting that Io and Enceladus may be in cooling phases of limit cycles.
For Io to dissipate 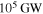 with e = 0.0041 requires
with e = 0.0041 requires 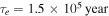 . A uniform density model with
. A uniform density model with 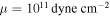 , as appropriate for a solid body composed of silicates, yields
, as appropriate for a solid body composed of silicates, yields 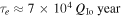 . Thus it is not a stretch to imagine that with e enhanced by a factor of 3, tidal dissipation in Io could match the satellite's current net luminosity.
. Thus it is not a stretch to imagine that with e enhanced by a factor of 3, tidal dissipation in Io could match the satellite's current net luminosity.
For Enceladus to dissipate  with e = 0.0047 requires
with e = 0.0047 requires 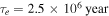 . Our models for Enceladus are all spherically symmetric and contain a rigid core with
. Our models for Enceladus are all spherically symmetric and contain a rigid core with 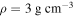 . The core is encased in a layer of water with
. The core is encased in a layer of water with 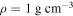 overlain by a shell of ice with
overlain by a shell of ice with 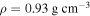 and
and 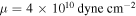 . In the absence of an ocean, we calculate
. In the absence of an ocean, we calculate 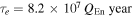 . So tidal dissipation in a solid model falls far short of matching Enceladus's current net luminosity. Models with thin ice shells overlying thick oceans do better. For example, a model with an ice shell
. So tidal dissipation in a solid model falls far short of matching Enceladus's current net luminosity. Models with thin ice shells overlying thick oceans do better. For example, a model with an ice shell 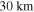 thick, as estimated by Iess et al. (2014), Thomas et al. (2016), yields
thick, as estimated by Iess et al. (2014), Thomas et al. (2016), yields 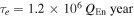 . An enhancement of e by a factor of 3 and a
. An enhancement of e by a factor of 3 and a 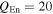 would be a possible fit. Note however that the enhanced e would make
would be a possible fit. Note however that the enhanced e would make 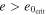 (see Table 2).
(see Table 2).
From the above discussion, it appears that an enhancement of eccentricity is needed to match the current luminosities of both Io and Enceladus. This indicates their orbits were more eccentric in the past, yielding higher heating rates during which the satellites stored thermal energy. Then they entered cooling phases and their eccentricities damped. Thus these satellites may undergo limit cycles, alternating between heating and cooling phases, and that currently they are in the latter phase.
4. GROUP II: 
The Mimas–Tethys 4:2  -MMR and the Titan–Hyperion 4:3 e'-MMR are the only examples of MMRs between solar system satellites for which
-MMR and the Titan–Hyperion 4:3 e'-MMR are the only examples of MMRs between solar system satellites for which  . Unlike the MMRs with
. Unlike the MMRs with 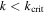 , their resonant arguments exhibit large librations. Could this be a sign that they are experiencing librational overstability as described in Section 2.1? Below we argue that these librations did not arise from overstability but are fossils that survived following capture into MMR. We bolster this claim by demonstrating that neither the inclination of Mimas nor the eccentricity of Hyperion has suffered significant damping.
, their resonant arguments exhibit large librations. Could this be a sign that they are experiencing librational overstability as described in Section 2.1? Below we argue that these librations did not arise from overstability but are fossils that survived following capture into MMR. We bolster this claim by demonstrating that neither the inclination of Mimas nor the eccentricity of Hyperion has suffered significant damping.
4.1. Mimas–Tethys
At present, Mimas and Tethys occupy a 4:2 mixed-inclination 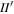 MMR. The leading resonant term in the disturbing function has coefficient
MMR. The leading resonant term in the disturbing function has coefficient  where inclination is measured relative to Saturn's equatorial plane. The resonant argument
where inclination is measured relative to Saturn's equatorial plane. The resonant argument 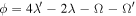 with Ω the longitude of the ascending node. Currently, ϕ is librating around zero with amplitude
with Ω the longitude of the ascending node. Currently, ϕ is librating around zero with amplitude 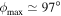 (Seidelmann 1992). Lowest-order inclination MMRs are of second order because the distance between the satellites involves the cosine of the mutual inclination of their orbital planes,
(Seidelmann 1992). Lowest-order inclination MMRs are of second order because the distance between the satellites involves the cosine of the mutual inclination of their orbital planes,  . Here I,
. Here I,  , Ω,
, Ω, 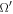 are inclinations and longitudes of ascending nodes measured with respect to the equatorial plane of Saturn.15
are inclinations and longitudes of ascending nodes measured with respect to the equatorial plane of Saturn.15
Mimas almost certainly passed the I2 MMR prior to being captured in the 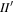 MMR (Murray & Dermott 1999). This would have excited I to a value that persisted and thus affected its capture probability into the
MMR (Murray & Dermott 1999). This would have excited I to a value that persisted and thus affected its capture probability into the 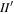 MMR (analytic work by e.g., Sinclair 1972; Luan 2014, numerical work by e.g., Champenois & Vienne 1999). The large separation between neighboring second-order inclination type MMRs, i.e., I2,
MMR (analytic work by e.g., Sinclair 1972; Luan 2014, numerical work by e.g., Champenois & Vienne 1999). The large separation between neighboring second-order inclination type MMRs, i.e., I2, 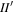 and
and 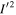 ensures that adjacent MMRs barely affect the dynamics of the
ensures that adjacent MMRs barely affect the dynamics of the 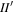 MMR.16
MMR.16
Tethys is significantly more massive than Mimas, 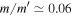 , and the two satellites have similar orbital inclinations,
, and the two satellites have similar orbital inclinations, 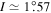 and
and 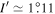 (Seidelmann 1992). In Appendix
(Seidelmann 1992). In Appendix
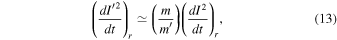
where "r" denotes resonance. Thus it seems likely that Tethys's inclination originates from passage through some other MMR, e.g., Tethys–Dione 4:6 inclination-type MMR. A similar hypothesis has been investigated for the origin of the anomalously large inclination of the Uranian satellite Miranda (Tittemore & Wisdom 1989; Malhotra & Dermott 1990).
The dynamics of the Mimas–Tethys mixed inclination 4:2 MMR is analogous to that of the eccentricity type resonance discussed in Section 2. With the replacement of  by
by  where
where 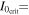 is defined in Equation (40), Figure 1 applies equally well to this resonance. Moreover, since
is defined in Equation (40), Figure 1 applies equally well to this resonance. Moreover, since 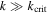 , inclination damping excites overstable librations on timescale
, inclination damping excites overstable librations on timescale 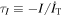 , where
, where 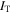 is the tidal damping rate of I.
is the tidal damping rate of I.
It is imperative that we evaluate 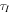 . To do so we need to understand the relation between three unit vectors, those along the spin of Mimas,
. To do so we need to understand the relation between three unit vectors, those along the spin of Mimas, 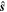 , the spin of Saturn,
, the spin of Saturn, 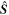 , and the orbital angular momentum of Mimas,
, and the orbital angular momentum of Mimas, 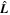 . Tidal friction drives
. Tidal friction drives  to a Cassini state on a timescale comparable to that over which it causes the satellite to spin synchronously with its mean motion (Colombo 1966; Ward 1975), a mere instant relative to the age of the solar system. In a Cassini state, the three unit vectors defined above lie in a plane. In addition to the orbital inclination,
to a Cassini state on a timescale comparable to that over which it causes the satellite to spin synchronously with its mean motion (Colombo 1966; Ward 1975), a mere instant relative to the age of the solar system. In a Cassini state, the three unit vectors defined above lie in a plane. In addition to the orbital inclination, 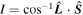 , the state is defined by the obliquity, the angle between the satellite's spin and its orbit normal,
, the state is defined by the obliquity, the angle between the satellite's spin and its orbit normal, 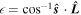 . For small values of I and
. For small values of I and  , the ratio of these angles (Colombo 1966)
, the ratio of these angles (Colombo 1966)
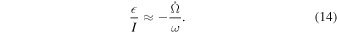
In the above, 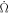 is the rate of nodal precession on the planet's equator plane which mainly arises from the planet's oblateness (Murray & Dermott 1999),
is the rate of nodal precession on the planet's equator plane which mainly arises from the planet's oblateness (Murray & Dermott 1999),
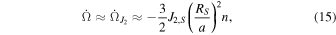
where 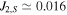 and
and  are Saturn's quadrupole coefficient and radius, and
are Saturn's quadrupole coefficient and radius, and 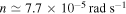 and
and  are Mimas's orbital mean motion and semimajor axis (Seidelmann 1992). Also, ω is the rate that the spin axis of Mimas would precess about the orbit normal if the later maintained a fixed orientation in inertial space (Ward 1975);
are Mimas's orbital mean motion and semimajor axis (Seidelmann 1992). Also, ω is the rate that the spin axis of Mimas would precess about the orbit normal if the later maintained a fixed orientation in inertial space (Ward 1975);
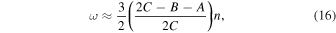
where  are the principal moments of inertia of Mimas. Mimas is tidally stretched along the axis joining it to Saturn and flattened by its spin. Its low mean density,
are the principal moments of inertia of Mimas. Mimas is tidally stretched along the axis joining it to Saturn and flattened by its spin. Its low mean density, 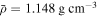 , implies a small rocky core that contributes little to its mass and less to its polar moment of inertia. Thus in estimating its principal moments of inertial, it is reasonable to approximate Mimas by a body of uniform density. It is more questionable whether a body of its size has relaxed to near hydrostatic equilibrium. Making these two assumptions, it is a straightforward exercise to derive the relations
, implies a small rocky core that contributes little to its mass and less to its polar moment of inertia. Thus in estimating its principal moments of inertial, it is reasonable to approximate Mimas by a body of uniform density. It is more questionable whether a body of its size has relaxed to near hydrostatic equilibrium. Making these two assumptions, it is a straightforward exercise to derive the relations
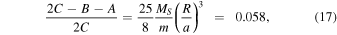
and

Substituting Equations (17) and (18) into Equation (14), we arrive at
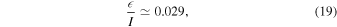
which implies 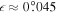 given
given 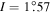 (Seidelmann 1992). Thus it appears that the spin of Mimas is closely aligned with the normal to its orbit. Probably this explains why astrometry has been unable to determine the obliquity,
(Seidelmann 1992). Thus it appears that the spin of Mimas is closely aligned with the normal to its orbit. Probably this explains why astrometry has been unable to determine the obliquity,  , although it has revealed an amplitude of
, although it has revealed an amplitude of 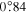 for Mimas's physical libration which implies
for Mimas's physical libration which implies 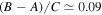 (Tajeddine et al. 2014). As a sanity check, we compare this value with 0.069 predicted by Equation (18). The agreement is satisfactory although we note that according to Tajeddine et al. (2014), the difference between a more accurate model calculation for
(Tajeddine et al. 2014). As a sanity check, we compare this value with 0.069 predicted by Equation (18). The agreement is satisfactory although we note that according to Tajeddine et al. (2014), the difference between a more accurate model calculation for 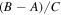 and the value deduced from the physical libration hints that Mimas may have an ocean that comes within
and the value deduced from the physical libration hints that Mimas may have an ocean that comes within 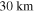 of its surface and reduces C by decoupling the interior from the external ice shell.
of its surface and reduces C by decoupling the interior from the external ice shell.
Next we consider tides raised on Mimas by Saturn. Absent dissipation, the tidal bulge would peak at the sub-Saturn point and the point diametrically opposite to it. Because Mimas has a finite obliquity, the tidal bulge oscillates across the equator at frequency n. Time varying strains dissipate energy and as a result damp orbital inclination on timescale 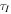 where
where
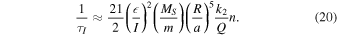
In the above, we have simply multiplied the standard expression for 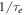 by the small quantity
by the small quantity 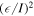 . Because time varying strains are
. Because time varying strains are 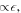 they dissipate energy at a rate
they dissipate energy at a rate 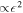 . An inclined orbit has has an excess of orbital energy relative to an equatorial orbit possessing an identical component angular momentum oriented parallel to the planet's spin. This excess energy is ∝I2, therefore
. An inclined orbit has has an excess of orbital energy relative to an equatorial orbit possessing an identical component angular momentum oriented parallel to the planet's spin. This excess energy is ∝I2, therefore 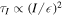 . For any reasonable choice of parameters,
. For any reasonable choice of parameters, 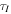 exceeds
exceeds 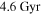 , the age of the solar system. Consequently, although
, the age of the solar system. Consequently, although  , the libration of ϕ is not due to overstability. Sinclair (1972) attributes it to the evolution of the initial inclination, Ii, following capture as Mimas evolved deeper into resonance. We agree. Sinclair estimated a capture probability of
, the libration of ϕ is not due to overstability. Sinclair (1972) attributes it to the evolution of the initial inclination, Ii, following capture as Mimas evolved deeper into resonance. We agree. Sinclair estimated a capture probability of 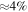 , whereas employing more modern methods (Borderies & Goldreich 1984), we find 6% with capture taking place at
, whereas employing more modern methods (Borderies & Goldreich 1984), we find 6% with capture taking place at 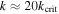 when
when 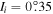 . These values at capture are deduced from the conservation of the adiabatic invariant,
. These values at capture are deduced from the conservation of the adiabatic invariant,  , as the MMR evolves and translate to the current libration amplitude,
, as the MMR evolves and translate to the current libration amplitude,  , and current orbital inclination,
, and current orbital inclination, 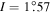 .
.
Mima's orbital eccentricity, 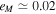 , is much larger than its orbital inclination, Ii, prior to formation of the Mimas–Tethys MMR. Meyer & Wisdom (2008) calculations show that Mimas might have been captured in an eccentricity-type MMR with Enceladus or Dione, experienced overstable librations, and then escaped before entering its current resonance with Tethys. Such a scenario might account for its current eccentricity. Related discussion is given in Section 6.2.
, is much larger than its orbital inclination, Ii, prior to formation of the Mimas–Tethys MMR. Meyer & Wisdom (2008) calculations show that Mimas might have been captured in an eccentricity-type MMR with Enceladus or Dione, experienced overstable librations, and then escaped before entering its current resonance with Tethys. Such a scenario might account for its current eccentricity. Related discussion is given in Section 6.2.
4.2. Titan–Hyperion
Titan and Hyperion are partners in a 4:3 e'-MMR with resonant argument 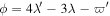 . This type of MMR is shown to be stable in the subsection titled "stability of equilibrium" in Appendix
. This type of MMR is shown to be stable in the subsection titled "stability of equilibrium" in Appendix
For many years, the origin of this MMR was a puzzle (Peale 1978) because the tidal torque arising from Titan's equilibrium tide in Saturn seemed incapable of driving a significant outward migration of Titan. However, the enhanced outward migration rates reported by Lainey et al. (2015), although they did not mention Titan, makes it reasonable to assume that the outward migration of Titan may have led to the formation of its MMR with Hyperion.
Tidal damping of Hyperion's orbital eccentricity is utterly negligible so libration of the resonant argument does not result from overstability. Instead it is a fossil of Hyperion's free eccentricity,  , at the time of MMR capture. Currently
, at the time of MMR capture. Currently  . Growth to the current e' takes about
. Growth to the current e' takes about 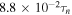 according to Equations (7) and (46). Since Titan is hardly affected by Hyperion, its mean motion has decreased by
according to Equations (7) and (46). Since Titan is hardly affected by Hyperion, its mean motion has decreased by 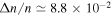 during the age of the MMR.
during the age of the MMR.
5. RESONANCE LOCK
Up to this point, our discussion has been based on a conventional tidal torque whose magnitude is independent of whether the satellite under consideration is participating in an MMR. Both equilibrium tides and dynamic tides can give rise to conventional tidal torques. Resonance lock involves a dynamic tide whose frequency in the planet's rest frame, 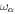 , is locked to that of the satellite's mean motion, n, according to (Fuller et al. 2016)
, is locked to that of the satellite's mean motion, n, according to (Fuller et al. 2016)
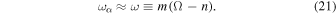
Here, ω is the tidal excitation frequency in the planet's rest frame, m the mode's azimuthal wave number, and Ω the planet's spin frequency. Now suppose that as the planet evolves, 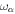 increases on timescale
increases on timescale 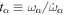 . Then resonance lock forces the satellite to migrate such that,
. Then resonance lock forces the satellite to migrate such that,
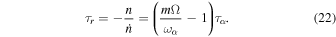
Here we implicitly assume that Ω does not vary.
Note that 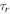 is entirely controlled by Saturn. For a satellite migrating independently, resonance lock implies a tidal torque,
is entirely controlled by Saturn. For a satellite migrating independently, resonance lock implies a tidal torque, 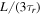 , where L is the orbital angular momentum of the satellite. Suppose the satellite is captured into an MMR with an outer satellite. Subsequently, to maintain the MMR, angular momentum is transferred from the inner to the outer satellite. Thus the outer satellite exerts a negative torque on the inner satellite, pushing it deeper into resonance lock, i.e., the frequency mismatch,
, where L is the orbital angular momentum of the satellite. Suppose the satellite is captured into an MMR with an outer satellite. Subsequently, to maintain the MMR, angular momentum is transferred from the inner to the outer satellite. Thus the outer satellite exerts a negative torque on the inner satellite, pushing it deeper into resonance lock, i.e., the frequency mismatch, 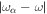 , decreases. Ultimately,
, decreases. Ultimately, 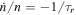 is restored for both inner and outer satellites and the tidal torque on the inner satellite increases to
is restored for both inner and outer satellites and the tidal torque on the inner satellite increases to 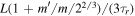 .17
.17
The key difference between the conventional tidal torque and that due to resonance lock is that the former provides a constant torque, whereas the latter maintains a constant migration rate.18
More precisely, the conventional tide contributes a term, 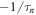 , to the total
, to the total 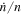 , whereas the torque from resonance lock determines the total net
, whereas the torque from resonance lock determines the total net 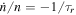 . We have to acknowledge that constant
. We have to acknowledge that constant 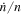 stems from an oversimplified model for resonance lock. In reality, it takes a finite time for resonance lock to adjust the tidal torque, and
stems from an oversimplified model for resonance lock. In reality, it takes a finite time for resonance lock to adjust the tidal torque, and  is not constant during that time interval. Presumably, the timescale for the orbital evolution is much longer than the adjustment time for resonance lock. However, adjustment may involve a significant variation of the dynamics. For example, a resonance lock may be overstable or be broken (Burkart et al. 2014). It may cause the critical argument of a MMR to librate if the adjustment time is similar to the libration period around the stable fixed point,
is not constant during that time interval. Presumably, the timescale for the orbital evolution is much longer than the adjustment time for resonance lock. However, adjustment may involve a significant variation of the dynamics. For example, a resonance lock may be overstable or be broken (Burkart et al. 2014). It may cause the critical argument of a MMR to librate if the adjustment time is similar to the libration period around the stable fixed point, 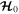 . Unfortunately, lack of knowledge about the interior of Saturn limits our ability to investigate these possibilities.
. Unfortunately, lack of knowledge about the interior of Saturn limits our ability to investigate these possibilities.
Resonance lock is appealing because under simple assumptions it naturally leads to migration rates consistent with those measured by Lainey et al. (2015). Moreover, it predicts a similar migration timescale, 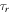 , independent of mass and semimajor axis, for each satellite experiencing resonance lock. Several consequences of resonance lock are explored below. It is our hope that future investigations may ultimately reveal whether resonance lock is a reality.
, independent of mass and semimajor axis, for each satellite experiencing resonance lock. Several consequences of resonance lock are explored below. It is our hope that future investigations may ultimately reveal whether resonance lock is a reality.
Below we discuss the influence of resonance lock on eccentricity type MMRs under the simplified assumption,  . Four consequences are briefly described. It is implicit in each that these are relative changes that would occur if the tidal torque involved resonance lock as opposed to being of conventional form. Related derivations, if any, are provided in Appendix
. Four consequences are briefly described. It is implicit in each that these are relative changes that would occur if the tidal torque involved resonance lock as opposed to being of conventional form. Related derivations, if any, are provided in Appendix
- 1.As Enceladus migrates deeper into the 2:1 MMR with Dione, its eccentricity grows faster, leading to more rapid internal heating, reduced conductive losses, and quicker internal melting of its ice shell.
- 2.
- 3.Both e- and e'-MMRs are stable at equilibrium as shown in Appendix
D . These results are of limited utility because they are derived for satellites that remain locked in MMR and have their internal structure unchanged up to .
. - 4.More rapid orbital migration for satellites with large orbits opens the possibility that Titan's 4:3 MMR with Hyperion formed by tidally driven convergent migration.
6. SUMMARY AND DISCUSSION
We classify satellite MMRs in the solar system into two groups according to their depths in resonance. One group comprises Mimas–Tethys and Titan–Hyperion. Each pair is deep in resonance and its critical argument, ϕ, exhibits a large libration. Inclination damping of Mimas and eccentricity damping of Hyperion are much too weak to affect libration dynamics. Therefore, these large librations are fossils of resonance formation. The other group includes Enceladus–Dione, Io–Europa, and Europa–Ganymede. Currently these MMRs are too shallow in resonance for a separatrix to appear. Dissipation associated with periodic tides the planet raises in the satellites acts to damp librations of the resonant arguments.
Both Enceladus and Io exhibit unmistakable signs of tidal heating. It is doubtful whether tidal heating at their current eccentricities can match their observed heat outputs. Either or both might be in the cooling phase of a limit cycle as suggested in Section 3.1.
After completion of most of the research reported in our paper, Fuller et al. (2016) proposed resonance lock to account for the unexpectedly fast migration rates reported by Lainey et al. (2015). We summarize the influence of resonance lock on the dynamics of MMR in Section 5. Tidal torques based on resonance lock would not alter our major conclusions. However, they do offer several advantages over conventional tidal torques in addition to providing a natural fit to the orbital expansion rates of Saturn's satellites. First, they do not require the satellites to have formed much later than Saturn (Lainey et al. 2015). Second, they raise the possibility that the Titan–Hyperion MMR formed by convergent tidal migration. Third, they make the formation of the internal ocean of Enceladus much easier.
6.1. Torque Comparison
Lainey et al. (2012) analyze more than a century of astrometric data to determine the orbital evolution of Saturn's satellites Mimas through Rhea. They reach two surprising conclusions. The semimajor axes are changing about an order of magnitude faster than previously expected. Surprisingly, the orbit of Mimas is shrinking although those of the others are expanding. Recently, Lainey et al. (2015) combine results from their individual groups and reach conclusions similar to those in Lainey et al. (2012). But Mimas's inward migration is no longer discussed. Below we speculate about how the otherwise impressive investigation in Lainey et al. (2012) might have slipped up on this particular point.
According to Equation (28), the evolution of Mimas's mean motion should satisfy,
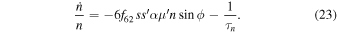
where the first and second terms on the rhs arise from the resonant torque by Tethys and tidal torque from Saturn. The argument, ϕ, librates between −97° and 97° with period 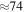 years. At a time when
years. At a time when  , the torque from Tethys exceeds that from Saturn by a factor
, the torque from Tethys exceeds that from Saturn by a factor 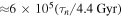 . Over a time span
. Over a time span  , the time-average
, the time-average 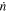 is negative and controlled by Saturn's tidal torque. However, the time span of the data in Lainey et al. (2012) is only slightly above a century. Thus the
is negative and controlled by Saturn's tidal torque. However, the time span of the data in Lainey et al. (2012) is only slightly above a century. Thus the 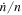 they deduced,
they deduced, 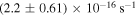 , might have been corrupted by Tethys's torque.
, might have been corrupted by Tethys's torque.
Enceladus's mean motion is similarly affected by the torque from Dione. For this MMR, ϕ librates between −1 5 and 1
5 and 1 5 with a period of
5 with a period of 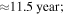
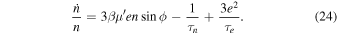
The effect of eccentricity damping on 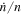 is an extra complication. Neglecting this, we find the ratio of the maximum resonant torque from Dione to the tidal torque to be
is an extra complication. Neglecting this, we find the ratio of the maximum resonant torque from Dione to the tidal torque to be 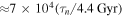 . However, in this case the libration period is much shorter than the time spanned by the astrometric data in Lainey et al. (2012, 2015) so determination of
. However, in this case the libration period is much shorter than the time spanned by the astrometric data in Lainey et al. (2012, 2015) so determination of 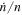 for Enceladus may not be adversely influenced by the torque from Dione.
for Enceladus may not be adversely influenced by the torque from Dione.
6.2. Vestiges of MMRs Past
It is likely that the orbits of some satellites exhibit traces of their participation in extinct MMRs.
Mimas's orbital eccentricity, 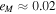 , is a prime example (Seidelmann 1992). Dermott et al. (1988) proposed that temporary capture into resonance can pump up eccentricity or inclination. Meyer & Wisdom (2008) suggested that Mimas's eccentricity might result from the past participation by Mimas in a 3:1 MMR with Dione or a 3:2 MMR with Enceladus. For
, is a prime example (Seidelmann 1992). Dermott et al. (1988) proposed that temporary capture into resonance can pump up eccentricity or inclination. Meyer & Wisdom (2008) suggested that Mimas's eccentricity might result from the past participation by Mimas in a 3:1 MMR with Dione or a 3:2 MMR with Enceladus. For 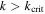 , there is a door leading to passage through the MMR and librational instability due to eccentricity damping can open it. As already mentioned in Section 4, the inclination of Tethys might have been excited by the Tethys–Dione 4:6 inclination-type MMR.
, there is a door leading to passage through the MMR and librational instability due to eccentricity damping can open it. As already mentioned in Section 4, the inclination of Tethys might have been excited by the Tethys–Dione 4:6 inclination-type MMR.
MMRs that excite eccentricity result in tidal heating that may cause internal melting. Thermal activity of Enceladus, Io, and Europa are outstanding examples of tidal heating in current resonances. It is less certain but plausible that Mimas has an internal ocean that reduces the apparent polar moment of inertia as deduced from the amplitude of its physical libration (Tajeddine et al. 2014). This could be a consequence of its involvement with the MMRs mentioned in the preceding paragraph.
If the expansion rates for the orbits of Saturn's satellites determined by Lainey et al. (2015) are correct, the frequency at which satellites entered and escaped from MMRs must have been much greater than previously imagined. Maximum rates of tidal heating associated with eccentricity type MMRs would also have been greatly enhanced. Thus more satellites are likely to possess internal oceans.
Consider the putative ocean of Mimas. Tajeddine et al. (2014) estimate that its surface lies below 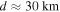 of ice. Given the thermal diffusivity of ice,
of ice. Given the thermal diffusivity of ice, 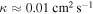 , an ocean of this depth would retreat after
, an ocean of this depth would retreat after 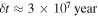 . We also estimate the timescale for eccentricity damping,
. We also estimate the timescale for eccentricity damping, 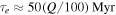 , from a model of Mimas consisting of an ocean sandwiched between a core with
, from a model of Mimas consisting of an ocean sandwiched between a core with  and a ice shell of thickness
and a ice shell of thickness  chosen to match the mean density
chosen to match the mean density 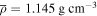 . These require Mimas to have escaped from a MMR with either Enceladus or Dione no longer than a few times
. These require Mimas to have escaped from a MMR with either Enceladus or Dione no longer than a few times 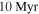 ago. At present, the Mimas–Tethys resonance
ago. At present, the Mimas–Tethys resonance 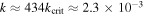 . Therefore, Mimas has been in the MMR with Tethys for
. Therefore, Mimas has been in the MMR with Tethys for
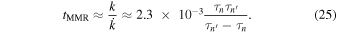
Convergent migration requires  so the minimum value of
so the minimum value of  . Minimum
. Minimum 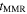 is short enough such that Mimas's orbit probably suffered at most modest eccentricity damping during the time it has spent in resonance with Tethys.
is short enough such that Mimas's orbit probably suffered at most modest eccentricity damping during the time it has spent in resonance with Tethys.
There is an alternative scenario for the unexpectedly large physical libration of Mimas that does not involve an internal ocean. Perhaps Mimas has a nonhydrostatic shape which enhances 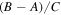 above its hydrostatic value (Tajeddine et al. 2014). We estimate
above its hydrostatic value (Tajeddine et al. 2014). We estimate  for a solid Mimas, a value consistent with the persistence of Mimas's orbital eccentricity even with the slow migration rate traditionally adopted.
for a solid Mimas, a value consistent with the persistence of Mimas's orbital eccentricity even with the slow migration rate traditionally adopted.
We thank the anonymous referee who provided valuable comments and questions, which helped us to greatly improve the paper. We thank Katherine Deck for alerting us to differences in librational stability between e- and e'-type MMRs (Deck & Batygin 2015) and Eugene Chiang for helpful comments on our presentation.
APPENDIX A: SATELLITE PARAMETERS
In this section, we provide all numeric parameters employed in this paper in Table 3.
APPENDIX B: MIMAS-TETHYS 4:2 
In this section we derive the constant of motion, k, and the Hamiltonian, 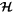 , for the Mimas–Tethys 4:2 mixed
, for the Mimas–Tethys 4:2 mixed 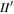 MMR starting from the linearized equations of motion. Relevant disturbing functions read
MMR starting from the linearized equations of motion. Relevant disturbing functions read
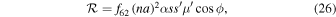

with resonant argument, 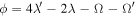 and numerical coefficient,
and numerical coefficient,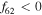 (Murray & Dermott 1999). Other symbols follow conventional definitions: λ, mean longitude, Ω, longitude of ascending node, n, mean motion, a, semimajor axis, I, inclination,
(Murray & Dermott 1999). Other symbols follow conventional definitions: λ, mean longitude, Ω, longitude of ascending node, n, mean motion, a, semimajor axis, I, inclination,  ,
,  , mass ratio of satellite to planet, and
, mass ratio of satellite to planet, and  . Equations governing the evolution of the orbital elements take the form
. Equations governing the evolution of the orbital elements take the form
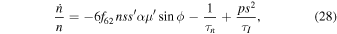
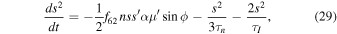
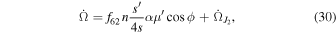

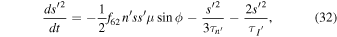

where 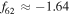 . Inclination damping reduces the orbital energy of a satellite while conserving the component of its orbital angular momentum perpendicular to the equatorial plane of Saturn, i.e.,
. Inclination damping reduces the orbital energy of a satellite while conserving the component of its orbital angular momentum perpendicular to the equatorial plane of Saturn, i.e., 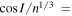 constant, yielding p = 12 in Equations (28) and (31).21
constant, yielding p = 12 in Equations (28) and (31).21
We use the lower index "Res" to label change rates due to MMR. For example, 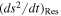 refers to the first term on the right-hand side of Equation (29). Note that
refers to the first term on the right-hand side of Equation (29). Note that 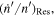
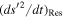 and
and 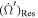 are all smaller a factor
are all smaller a factor  than corresponding rates for the inner satellite. Therefore, we neglect them since resonance dynamics mainly affects the inner body. Considering only resonance terms, we find
than corresponding rates for the inner satellite. Therefore, we neglect them since resonance dynamics mainly affects the inner body. Considering only resonance terms, we find
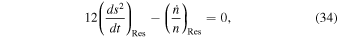
which yields a constant of motion in resonance dynamics,22
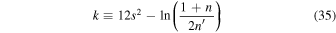
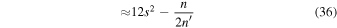
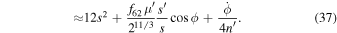
In the last line of the above equation, we employ 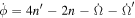 , neglect secular precessions,
, neglect secular precessions, 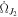 and
and 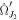 , set
, set  and
and 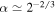 . We further neglect,
. We further neglect, 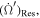 because it is proportional to μ and
because it is proportional to μ and  .
.
The Hamiltonian, 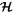 , provides a second constant of motion;
, provides a second constant of motion;
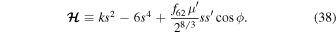
Equations of motion follow as 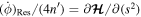 and
and 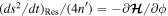 . Level curves of
. Level curves of  undergo a topological change as k crosses
undergo a topological change as k crosses
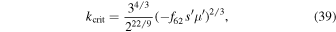
with corresponding critical inclination,
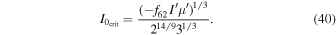
Currently,  and
and 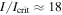 .
.
Dissipative terms in  and
and 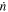 impose variations on both k and
impose variations on both k and 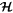 . Thus
. Thus
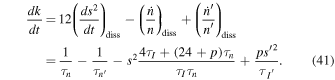

APPENDIX C: FIRST-ORDER e'-MMRS
Expressions for k and 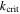 have been defined in the main text all e-MMRs listed in Table 1. However, the Io–Europa and Titan–Hyperion MMRs are
have been defined in the main text all e-MMRs listed in Table 1. However, the Io–Europa and Titan–Hyperion MMRs are 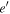 -MMRs which share the feature that the outer satellite's eccentricity is perturbed by the inner satellite. Here we treat the perturbed satellite as a test particle. This is an excellent approximation for Titan–Hyperion, but a crude one for Io–Europa. But our discussion of Io–Europa is mainly conceptual so it is insensitive to the accuracy of the approximation.
-MMRs which share the feature that the outer satellite's eccentricity is perturbed by the inner satellite. Here we treat the perturbed satellite as a test particle. This is an excellent approximation for Titan–Hyperion, but a crude one for Io–Europa. But our discussion of Io–Europa is mainly conceptual so it is insensitive to the accuracy of the approximation.
For the MMR involving Io and Europa with argument 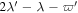 ,
,

where 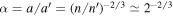 and
and 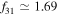 ,
,
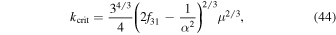
and
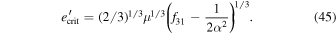
For the MMR involving Titan and Hyperion with argument  ,
,
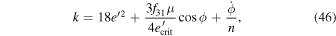
where 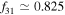 ,
,

and
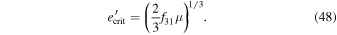
C.1. Stability of First-order e'-MMRs
This subsection is devoted to investigating the stability of first order 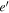 -MMRs under the action of conventional tidal torques. Previously, Goldreich & Schlichting (2014) showed that eccentricity damping could lead to the escape from first-order e-MMRs provided
-MMRs under the action of conventional tidal torques. Previously, Goldreich & Schlichting (2014) showed that eccentricity damping could lead to the escape from first-order e-MMRs provided 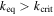 . This result is obtained in the limit that the separation of the e-MMR from the
. This result is obtained in the limit that the separation of the e-MMR from the 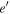 -MMR is sufficient so that the latter may be neglected. Delisle et al. (2015) and Deck & Batygin (2015) study the stability of MMRs in which the e- and
-MMR is sufficient so that the latter may be neglected. Delisle et al. (2015) and Deck & Batygin (2015) study the stability of MMRs in which the e- and  -MMRs strongly overlap. They find stability in the limit that
-MMRs strongly overlap. They find stability in the limit that 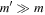 which suggests that isolated
which suggests that isolated 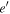 -MMRs are stable. In what follows, we provide support for this suggestion.
-MMRs are stable. In what follows, we provide support for this suggestion.
C.2. Definitions of  and
and 
Consider an isolated  first-order MMR. Disturbing functions for inner and outer satellites read
first-order MMR. Disturbing functions for inner and outer satellites read
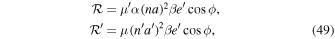
where 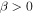 ,
, 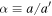 , and
, and 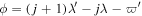 . These yield equations of motion
. These yield equations of motion
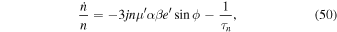

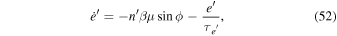
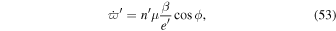
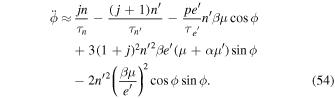
The value of p depends on the mechanism for eccentricity damping. We comment on appropriate choices at the end of this section. We exclude 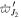 from the expression for
from the expression for 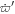 because it does not affect the resonance dynamics. Its only role is to determine the exact location for the e'-MMR. Given that
because it does not affect the resonance dynamics. Its only role is to determine the exact location for the e'-MMR. Given that 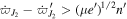 23
, i.e., the separation of the e- and e'-MMRs is larger than the width of the resonance, the e'-MMR can be treated independently from the e-MMR. Below, we also omit
23
, i.e., the separation of the e- and e'-MMRs is larger than the width of the resonance, the e'-MMR can be treated independently from the e-MMR. Below, we also omit 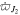 in the interest of brevity. Terms involving ϕ in Equations (50)–(53) are due to the resonance dynamics.
in the interest of brevity. Terms involving ϕ in Equations (50)–(53) are due to the resonance dynamics.
Absent dissipation, ϕ librates around 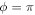 ,
, 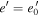 with frequency
with frequency
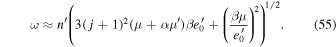
Observing that,
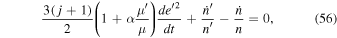
we define the constant of motion,
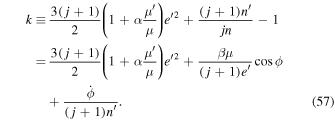
With conjugate coordinate and momentum, ϕ and 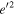 , it follows that
, it follows that
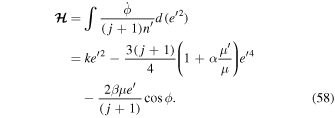
Hamiltonian equations then yield the equations of motion,
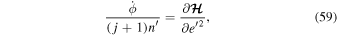
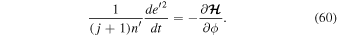
The topology of the phase space is similar to that of an e-MMR, except that the maximum of 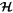 is located at
is located at 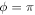 instead of
instead of  .
.
C.3. Stability of Equilibrium
Now we demonstrate that e' MMRs are usually stable. Define
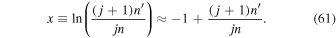
In terms of ϕ, x and e', the equations of motion take the form
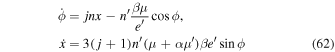
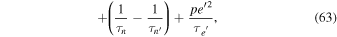
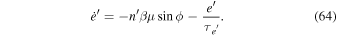
Equilibrium is at  , where
, where
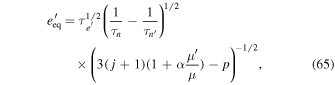
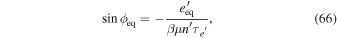
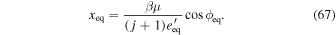
Expanding the right-hand sides of Equations (62)–(64) to first order in 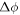 ,
, 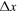 and
and 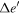 yields
yields

where  is a real 3 × 3 matrix. This system has three eigenvalues, a complex conjugate pair and a real one. The real part of the complex eigenvalues is
is a real 3 × 3 matrix. This system has three eigenvalues, a complex conjugate pair and a real one. The real part of the complex eigenvalues is
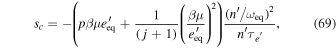
and the real eigenvalue is
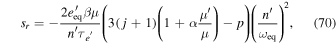
with
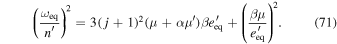
Recall that 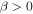 as claimed just after Equation (49). For tidal damping of eccentricity, p = 3; for disk induced damping of eccentricity,
as claimed just after Equation (49). For tidal damping of eccentricity, p = 3; for disk induced damping of eccentricity,  (Tanaka & Ward 2004). Therefore, both sc and sr are negative, i.e., the e'-MMR is usually stable.
(Tanaka & Ward 2004). Therefore, both sc and sr are negative, i.e., the e'-MMR is usually stable.
APPENDIX D: RESONANCE LOCK
In this section, we analyze e- and e'-MMRs assuming that resonance lock forces the inner satellite to migrate outward at a constant rate,
Comparing Equations (73) and (50), we see that resonance lock determines the total migration rate,  , instead of just contributing a term to it.
, instead of just contributing a term to it.
Since the resonance lock changes the format of the Equation for 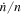 , it is worth checking the stability of the e- and e'-MMRs in the case of resonance lock. To remind the reader, under the conventional tidal torque, Goldreich & Schlichting (2014) find that e-type MMRs can be overstable, and Appendix C.3 shows that e'-MMRs are stable.
, it is worth checking the stability of the e- and e'-MMRs in the case of resonance lock. To remind the reader, under the conventional tidal torque, Goldreich & Schlichting (2014) find that e-type MMRs can be overstable, and Appendix C.3 shows that e'-MMRs are stable.
We now prove that with resonance lock, both e- and e'-MMRs are stable. To make the analysis simple without losing generality, we assume that the inner satellite is in resonance lock with some oscillation mode in Saturn while the outer satellite is not. Thus we neglect the tidal torque on the outer satellite although, in principle, there must be a tidal torque on the outer satellite due to e.g., the equilibrium tides. However, if resonance lock of the inner satellite dominates convergent migration between inner and outer satellites, we can neglect the tidal torque on the outer satellite.
D.1. Stability of e-MMR in Resonance Lock
The equations of motion are
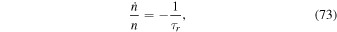



where  ,
,  is a coefficient of order unity and
is a coefficient of order unity and 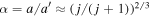 . Defining
. Defining
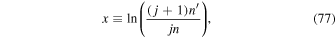
the equilibrium state is at
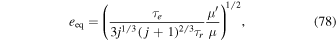

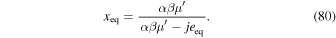
Small oscillations around the equilibrium state have three eigenfrequencies.24 One eigenfrequency is real, the other two are complex conjugates. The real eigenfrequency and the real part of the complex eigenfrequencies are respectively,

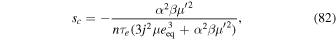
which are both negative, indicating that the equilibrium is stable. Recall that Goldreich & Schlichting (2014) found the e-MMR to be overstable for conventional tidal torques.25
Another difference between conventional tidal torques and those based on resonance lock is that for the latter, eeq is enhanced by a factor 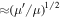 with respect to eeq for the former (Goldreich & Schlichting 2014).26
Consequently, the width of the e-MMR at the equilibrium eccentricity is enhanced by
with respect to eeq for the former (Goldreich & Schlichting 2014).26
Consequently, the width of the e-MMR at the equilibrium eccentricity is enhanced by 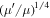 . Should this enhanced width lead to resonance overlap with the e'-MMR, chaos and escape from the e-MMR might ensue (Tittemore & Wisdom 1988, 1990; Malhotra & Dermott 1990).27
. Should this enhanced width lead to resonance overlap with the e'-MMR, chaos and escape from the e-MMR might ensue (Tittemore & Wisdom 1988, 1990; Malhotra & Dermott 1990).27
D.2. Stability of e'-MMR in Resonance Lock
The equations of motion are
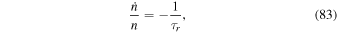
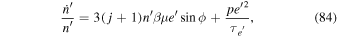
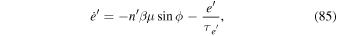
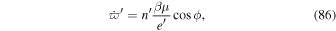
where 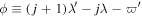 , β is a positive coefficient of order of unity, and
, β is a positive coefficient of order of unity, and 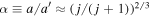 . Adopting the same definition for x as that in Equation (77). The equilibrium state is at
. Adopting the same definition for x as that in Equation (77). The equilibrium state is at
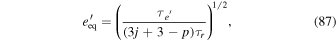
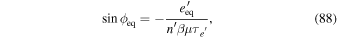
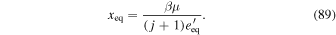
Comparison Equations (87) and (65) reveals that, like for e-MMR, the resonance lock also enhances the equilibrium eccentricity for the e'-MMR by a similar factor 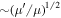 . The oscillation around this equilibrium has three eigenfrequencies. The real eigenfrequency and the real part of the complex eigenfrequencies are respectively,
. The oscillation around this equilibrium has three eigenfrequencies. The real eigenfrequency and the real part of the complex eigenfrequencies are respectively,
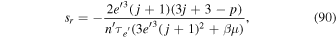

The values of p are discussed in the paragraph after Equation (71). We see that for the usual values of p both sr and sc are negative, and thus the e'-MMR is stable.
Footnotes
- 3
Peale (1978) discusses the origin of the Titan–Hyperion MMR.
- 4
The introduction of Tittemore & Wisdom (1988) has a good discussion about the criterion for MMR overlap. Refer to this paper and the references therein.
- 5
In fact, the orbital angular momentum exchanges with the satellite's spin angular momentum but the latter is tiny in comparison to the former.
- 6
Here
 is the outer satellite's mean motion and E and L are the orbital energy and angular momentum per unit mass of the inner satellite.
is the outer satellite's mean motion and E and L are the orbital energy and angular momentum per unit mass of the inner satellite. - 7
 is the contribution from secular terms to the rate of precession.
is the contribution from secular terms to the rate of precession. - 8
For
 , the additional fixed points bifurcate from the inflection point at
, the additional fixed points bifurcate from the inflection point at  .
. - 9
Here we no longer treat the inner satellite as a test particle.
- 10
We do not provide an explicit form for
 but note that our discussion assumes a conventional tidal torque.
but note that our discussion assumes a conventional tidal torque. - 11
We provide a derivation of
 for the
for the  type MMR in Appendix B. The derivation for Equation (7) is similar.
type MMR in Appendix B. The derivation for Equation (7) is similar. - 12
Evidence comes from volcanoes on Io, magnetic induction by Europa, and geysers on Enceladus.
- 13
Quantities pertaining to Io, Europa, and Ganymede carry subscripts 1, 2, and 3, respectively.
- 14
Tidal heating rate is
 .
. - 15
In fact, they can be measured with respect to an arbitrary plane, but the equatorial plane of Saturn is a convenient choice.
- 16
Mimas and Tethys will only encounter the
 MMR if they escape from the current
MMR if they escape from the current  MMR.
MMR. - 17
Provided no tidal torque acts directly on the outer satellite. This torque is derived by employing
 ,
,  ,
,  , and
, and  as
as  .
. - 18
By "constant" here, we mean unchanging on times much shorter than the evolution time of the planet–satellite system.
- 19
- 20
By itself, MMR overlap cannot cause escape because the motion is reversible unless a dissipative process such as tidal migration or eccentricity damping is present.
- 21
Eccentricity damping would contribute an additional migration rate,
 , but since e does not enter in the resonance dynamics, we ignore it.
, but since e does not enter in the resonance dynamics, we ignore it. - 22
Constant k arises because
 is an ignorable coordinate. Full planar dynamics of two satellites involves four degrees of freedom, corresponding to four independent angles, λ,
is an ignorable coordinate. Full planar dynamics of two satellites involves four degrees of freedom, corresponding to four independent angles, λ,  , Ω and
, Ω and  . Tethys is barely affected by Mimas because it is much more massive. This reduces the four degrees of freedom to two. Resonant argument
. Tethys is barely affected by Mimas because it is much more massive. This reduces the four degrees of freedom to two. Resonant argument  implies that λ and Ω always appear in the combination
implies that λ and Ω always appear in the combination  , which further reduces the degrees of freedom from two to one.
, which further reduces the degrees of freedom from two to one. - 23
For Enceladus and Dione,
 , much larger than
, much larger than  . Refer to Tittemore & Wisdom (1988) for a discussion on the criterion for MMR overlap.
. Refer to Tittemore & Wisdom (1988) for a discussion on the criterion for MMR overlap. - 24
The imaginary part of the eigenfrequency corresponds to oscillation; the real part, if positive (negative), corresponds to exponential growth (damping).
- 25
- 26
- 27
By itself, MMR overlap cannot cause escape because Hamiltonian motion is reversible. However, escape is a possibility in the presence of a dissipative process, such as tidal migration or eccentricity damping.