ABSTRACT
In the early, disk-embedded phase of evolution of terrestrial planets, a protoplanetary core can accumulate gas from the circumstellar disk into a planetary envelope. In order to relate the accumulation and structure of this primordial atmosphere to the thermal evolution of the planetary core, we calculated atmosphere models characterized by the surface temperature of the core. We considered cores with masses between 0.1 and 5 M⊕ situated in the habitable zone around a solar-like star. The time-dependent simulations in 1D-spherical symmetry include the hydrodynamics equations, gray radiative transport, and convective energy transport. Using an implicit time integration scheme, we can use large time steps and and thus efficiently cover evolutionary timescales. Our results show that planetary atmospheres, when considered with reference to a fixed core temperature, are not necessarily stable, and multiple solutions may exist for one core temperature. As the structure and properties of nebula-embedded planetary atmospheres are an inherently time-dependent problem, we calculated estimates for the amount of primordial atmosphere by simulating the accretion process of disk gas onto planetary cores and the subsequent evolution of the embedded atmospheres. The temperature of the planetary core is thereby determined from the computation of the internal energy budget of the core. For cores more massive than about one Earth mass, we obtain that a comparatively short duration of the disk-embedded phase (∼105 years) is sufficient for the accumulation of significant amounts of hydrogen atmosphere that are unlikely to be removed by later atmospheric escape processes.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
In the early evolution of planetary systems, solid bodies form within the disk from the coagulation of dust and ice and hence initially reside embedded in the gas of the circumstellar disk. The processes responsible for the growth of the solid bodies from centimeter size up to the size of planetesimals and planetary embryos are not well understood (Morbidelli et al. 2009; Johansen et al. 2014, p. 547). However, if one accepts the core-accretion scenario for the formation of gas planets (Perri & Cameron 1974; Mizuno 1980), massive protoplanetary cores (several 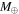 ) have to exist already at an early stage of evolution of the protoplanetary disk. Since the growth of gas planets by gas accretion takes considerable time (on the order of megayears, e.g., Hubickyj et al. 2005), not much shorter than the overall lifetime of the disk, the formation of the cores of gas planets has to be a comparatively fast process.
) have to exist already at an early stage of evolution of the protoplanetary disk. Since the growth of gas planets by gas accretion takes considerable time (on the order of megayears, e.g., Hubickyj et al. 2005), not much shorter than the overall lifetime of the disk, the formation of the cores of gas planets has to be a comparatively fast process.
In the standard formation scenario of the terrestrial planets in the solar system (e.g., Raymond et al. 2014, p. 595), the planetary embryos only grow to about the size of Mars in the nebula-embedded phase and gain their final masses after the evaporation of the gas disk from collisions over a period of about 100 Myr. The reason for this dichotomy in planetary embryo size in the gas disk between the inner and the outer disk region is not entirely clear (Raymond et al. 2014, p. 595), though the existence of water ice in the disk (snow line) is a likely factor. This scenario gets more complicated when planetary migration is considered, for which angular momentum exchange with the gaseous disk is an important driver (Armitage 2010).
For this study, however, we adopt the working hypothesis that planetary cores with masses between 0.1 and 5 M⊕ exist in the inner disk early enough to be embedded in the disk gas for a significant time. This assumption is supported by the measured masses and radii of exoplanets, pointing to low average densities and extended H/He envelopes. Statistics of exoplanets indicate that also most of the small-radius planets, that is, the most Earth-like sample among the detected exoplanets, are not rocky but possess an extended gaseous envelope (Rogers 2015). This suggests that the cores of these planets must have formed early enough to be able to accumulate a primordial envelope from the disk gas.
Planetary cores begin to accumulate gas gravitationally into an atmosphere once they become sufficiently massive that their gravitational potential becomes relevant compared to the local enthalpy of the surrounding disk nebula gas. Therefore, depending on the disk environment, embedded planetary cores beyond about Moon to Mars size can be expected to possess significant gaseous envelopes.
1.1. Modeling of Primordial Planetary Atmospheres
For the numerical description of planetary atmospheres, some assumptions and simplifications of the physical scenario and the geometry of the problem can be adopted.
First, the Hill radius RHill defines the sphere where the gravitational potential of the planet dominates over the influence of the central host star (e.g., Mizuno et al. 1978):
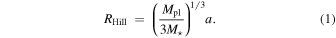
Here, Mpl and M⋆ are the masses of the planet and of the host star, respectively, and a is the semimajor axis of the planet. The Hill radius, by specifying the gravitational sphere of influence, gives the largest possible spatial extension of the planetary atmosphere, and for radii with 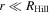 the gravitational field can be well approximated in spherical symmetry.
the gravitational field can be well approximated in spherical symmetry.
Another important consideration is the vertical thickness of the protoplanetary disk. The vertical structure of the disk is essentially determined by hydrostatic equilibrium and can be quantified from the pressure scale height Hp of the vertical density stratification. A reasonable approximation of an embedded planetary atmosphere in spherical symmetry thus requires that the vertical pressure scale height of the disk is larger than the spatial extent of the atmosphere.
Combining these two criteria, we assume in this study that  throughout, justifying a spherical symmetric description. Spherical symmetry also implies that the effect of the angular momentum of the gas flow with respect to the planetary core is neglected.
throughout, justifying a spherical symmetric description. Spherical symmetry also implies that the effect of the angular momentum of the gas flow with respect to the planetary core is neglected.
Apart from the geometry, it is also possible to simplify the physical description of the problem. The full time-dependent physical scenario can be simplified by considering only stationary solutions, skipping the time derivatives in the equation of motion and in the equation of energy. The former corresponds to the assumption of dynamic (i.e., hydrostatic) equilibrium, and the latter corresponds to the adoption of thermal equilibrium. Such stationary models are the simplest way to study the structure of planetary atmospheres. While these simplifications are probably justified during some parts of the planetary evolution, the thermal relaxation timescale (Kelvin–Helmholtz timescale) can become significant for massive atmospheres, and dynamical processes can also have long relaxation timescales compared to evolutionary timescales of the planetary system (Stökl et al. 2015).
In spherical geometry and in the stationary limit, the structure of planetary atmospheres is described by the well-known stellar structure equations, and with the assumption of suitable boundary conditions for the planetary core and the surrounding protoplanetary nebula, these equations can be readily integrated. Such stationary models of disk-accumulated atmospheres around terrestrial planets have been calculated by Hayashi et al. (1979), Nakazawa et al. (1985), and Rafikov (2006) based on analytically prescribed dust opacities, and by Ikoma & Genda (2006) using realistic data for the equation of state and for dust and gas opacities.
For this study, we employ a radiation hydrodynamics scheme to compute time-dependent, that is, nonstationary, models of planetary atmospheres. A similar scheme has been used by Wuchterl (1991a, 1991b) to study the dynamic behavior of a planetary envelope with a critical core mass, i.e., at the verge of self-gravitational instability. However, Wuchterl (1991a, 1991b) did not investigate less-massive cores (as in the present study) and used this scheme for short-duration dynamical phases only and did not attempt to cover the gas-accumulation phase.
1.1.1. Planetary Luminosity and Accretion of Planetesimals
The condition of thermal equilibrium, in the absence of energy sources and sinks within the atmosphere, corresponds to a radially constant energy flux. The construction of a stationary atmosphere model therefore requires the specification of a planetary luminosity. It is a common approach to associate the planetary luminosity with the energy generated by the impact of a stream of accreted planetesimals onto the surface of the planetary core (Hayashi et al. 1979). This scenario provides a plausible source of the planetary luminosity, but in turn requires the specification of the accretion rate of planetesimals. Unfortunately, the accretion rate of planetesimals onto a protoplanetary core is a poorly constrained quantity. A rough estimate can be made from the mass of the core and the lifetime of a protoplanetary disk, which is typically a few megayears (Haisch et al. 2001; Hillenbrand 2005). However, this averaged rate might not be representative for the later stages when planetary atmospheres are accumulated.
The size and material strength of the planetesimals also enter the problem because, depending on the amount of atmosphere, small or fragile planetesimals will be unable to penetrate the deep atmosphere to reach the surface of the planetary core but dissipate their kinetic energy already in the outer, optically thin part of the atmosphere. Therefore, only sufficiently strong and massive planetesimals can be considered to contribute to the planetary luminosity in the approximation of a stationary (constant-flux) atmosphere. On the other hand, the impact frequency of very massive planetesimals will be very low. At some point, this will contradict the basic assumptions of a stationary and spherical symmetric model of a continuous and spatially evenly distributed planetary luminosity. The conjunction of planetary luminosity and planetesimal accretion therefore not only depends on the assumption of a sufficient accretion rate, but also on a suitable strength and size distribution of the planetesimals.
In this study, we replace the identification of the accretion rate as the source of the luminosity with a characterization of the planetary atmosphere based on the surface temperature of the planetary core. The surface temperature of the core is linked to its thermal capacity and therefore establishes more plausibly a steady boundary condition for stationary atmosphere models than the inherently discontinuous accretion luminosity.
A detailed description of the interior physics of the planetary core, such as mantle differentiation, magma ocean solidification, phase transitions of the mantle material, outgassing of volatiles, convective transport, and heat conduction, is beyond the scope of this work. For the time-dependent evolution simulations, we therefore calculate the surface temperature using a simple integral heat capacity for the planetary core.
This approach of an internal energy balance for the core still allows the inclusion of an accretion luminosity at the core surface or in the atmospheric structure; however, for simplicity and clarity, we assume for the present study that the formation of the planetary core has been completed and no further accretion of planetesimals occurs. The heating effect of planetesimal accretion on the atmosphere models and the interaction with the decelerating and disintegrating planetesimals are the subjects of a forthcoming paper. The first atmospheric evolution simulations, including the calculation of the trajectory of infalling planetesimals, indicate that for reasonable assumptions (modest average size and material strength of planetesimals) the atmospheric evolution scenario does not change qualitatively.
The paper is structured as follows. Section 2 presents stationary atmosphere models with a constant surface temperature of the core. The stability of such atmospheres with a constant core temperature is studied in time-dependent calculations in Section 3. Time-dependent simulations of the accumulation and evolution of nebula-attached atmospheres, including a thermal energy balance of the core, are covered in Section 4. Finally, a discussion and summary are presented in Section 5.
2. STATIONARY MODELS
To set the stage for the time-dependent evolution calculations, we computed a grid of stationary atmosphere models characterized by the surface temperature of the core, exploring a parameter space in surface temperature, planetary luminosity, and core mass.
The stationary models are computed with the initial model integrator of the TAPIR code (short for The Adaptive, Implicit RHD code), solving the hydrostatic structure equations in 1D-spherical symmetry. The thermal structure of the atmosphere is determined by radiative and convective energy transport. The latter is included in the form of the stationary limit of the turbulent convection model used in the time-dependent simulations. The atmosphere models span from the surface of the planetary core up to the Hill radius, where the atmospheric model is attached to the surrounding disk medium. Focusing on potentially habitable planets, we assume for the conditions in the ambient disk a constant temperature of 200 K, corresponding to an Earth-like orbit around a solar-type star. The gas density is set to ρ = 5 × 10−10 g cm−3 in accordance with the minimum-mass planetary nebula (Hayashi 1981) at 1 au.
Both the disk and the planetary atmosphere are assumed to have a homogeneous solar composition. We use the equation of state by Saumon et al. (1995) and opacity data from Freedman et al. (2008) for the gas and from Semenov et al. (2003) for the dust. The amount of dust is specified by the dust-depletion factor, f, which gives the amount of dust in a gaseous medium relative to the equilibrium amount of dust for the local density and temperature. For protoplanetary disks and planetary envelopes, the dust-depletion factor is usually set to values f < 1 to allow for depletion from the formation of large solid bodies, settling and radial drift of dust in the disk, and dust settling (rain-out) in planetary atmospheres. In our models, we use a constant dust-depletion factor of f = 0.01 throughout. The radius of the planetary core is determined from a mean density of 5.5 g cm−3, corresponding to an Earth-like composition.
In order to relate the core-temperature-based atmosphere models to the usual luminosity-based models, we cover a parameter range in surface temperature, planetary luminosity, and core mass with a series of stationary models with core masses between 0.1 and 5 M⊕. Figure 1 illustrates the planetary luminosity and the surface pressure of the stationary models as a function of the surface temperature of the core.
Figure 1. Planetary luminosity (upper panel) and surface gas pressure (lower panel) as a function of core surface temperature for stationary atmosphere models with core masses, as labeled, between 0.1 M⊕ and 5 M⊕. The gray shaded area marks the region where self-gravity precludes the existence of hydrostatic solutions.
Download figure:
Standard image High-resolution imageIn general, the stationary models are analogous to those presented in Stökl et al. (2015) and are consistent with the results from Ikoma & Genda (2006), allowing for the numerical differences, in particular data for dust and gas opacities and the different implementation of the outer boundary condition.
The lower ends of the lines in Figure 1 reflect the limit of gravitational collapse (gray shaded areas). Below that limit, self-gravity precludes the existence of hydrostatic atmosphere solutions.
The model sequences in Figure 1 illustrate that, within some range, multiple solutions exist for one fixed surface temperature. This multiplicity corresponds to different temperature and density structures of the models and also has been found by Ikoma & Genda (2006). This is a different mechanism than the multiplicity described by Pečnik & Wuchterl (2005), which is caused by self-gravity. Depending on the model parameters and temperature range, we could find up to five stationary solutions that are compatible with one and the same core surface temperature. An important factor for producing this diversity is the feature-rich dust opacity—connected to the formation and evaporation of separate dust species—which dominates the total opacity in large parts of the envelope.
The main point of interest is the multiplicity in the large S-shaped curve of the lines in the center and lower part of the panels in Figure 1. The more complicated features in the upper (high-luminosity) part (e.g., for the 2 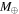 core) are less relevant because they concern hot and thin envelopes, called "uniform" solutions in the isothermal classification scheme of Pečnik & Wuchterl (2005), and do not resemble gravitationally bound atmospheres in the conventional sense. At these high luminosities, the numerical domain is entirely filled with hot and thin gas up to the Hill radius, where the envelope is confined by the invariable outer boundary conditions of T = 200 K and ρ = 5 × 10−10 g cm−3. In this case, the invariable outer boundary condition is, however, an inconsistent numerical scenario as it is based on the assumption of an unperturbed disk environment in thermal equilibrium, which is certainly invalid for these high luminosities. Nevertheless, in Figure 1 we have included models over the full luminosity range for completeness.
core) are less relevant because they concern hot and thin envelopes, called "uniform" solutions in the isothermal classification scheme of Pečnik & Wuchterl (2005), and do not resemble gravitationally bound atmospheres in the conventional sense. At these high luminosities, the numerical domain is entirely filled with hot and thin gas up to the Hill radius, where the envelope is confined by the invariable outer boundary conditions of T = 200 K and ρ = 5 × 10−10 g cm−3. In this case, the invariable outer boundary condition is, however, an inconsistent numerical scenario as it is based on the assumption of an unperturbed disk environment in thermal equilibrium, which is certainly invalid for these high luminosities. Nevertheless, in Figure 1 we have included models over the full luminosity range for completeness.
A particularly noteworthy aspect in the luminosity curves (in the upper panel of Figure 1) are the sections of negative slope 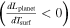 , meaning that the luminosity of the planet decreases for a rising core surface temperature. To investigate the dynamical stability of the atmospheres on these negative slopes when considered on top of a core with a fixed surface temperature, we computed time-dependent simulations of these atmospheres by employing a constant-temperature inner boundary condition.
, meaning that the luminosity of the planet decreases for a rising core surface temperature. To investigate the dynamical stability of the atmospheres on these negative slopes when considered on top of a core with a fixed surface temperature, we computed time-dependent simulations of these atmospheres by employing a constant-temperature inner boundary condition.
3. TIME-DEPENDENT SIMULATIONS WITH CONSTANT Tsurf
For the time-dependent simulations, the TAPIR code uses an implicit time integration scheme and thus allows the efficient integration of the dynamical evolution over long periods in time. The physical equations consist of the hydrodynamics equations (equation of continuity, equation of motion, and equation of internal energy) and the equations of gray radiative transport in the moment description (radiation energy equation and radiation flux equation). Convective transport is included in the form of a turbulent convective energy equation following Kuhfuß (1987) and Wuchterl & Feuchtinger (1998). Solving the Poisson equation for self-gravity leads to an equation summing up the mass within a radius R (i.e., m(R)). The TAPIR code also features an adaptive grid equation (Dorfi & Drury 1987) that continuously redistributes a fixed number of grid points according to the resolution requirements of the evolving solution. A more detailed description of the equations and the physical and numerical parameters is given in Stökl et al. (2015).
The physical equations are discretized in finite volumes on a staggered mesh in 1D-spherical symmetry. All models presented in this paper consist of 500 radial grid points. Advected quantities are calculated using the second-order van Leer slope limiter. Consequentially, the discretization uses a five-point stencil, leading to a Jacobian with a banded structure of two off-diagonal rows of nonzero entries. The boundary conditions are implemented in two (according to the five-point stencil) ghost cells both at the inner and outer boundary.
The full set of equations is solved with an implicit scheme, which repeatedly computes corrections to the set of variables from the inversion of the Jacobi matrix until a relative accuracy of 10−5 is achieved. The time step of an implicit time-integration method is not limited by the Courant–Friedrichs–Lewy condition. For a near-stationary flow—which applies, most of the time, to the gas accretion flow from the disk into the planetary envelope—it is therefore possible to use large time steps and to cover efficiently evolutionary timescales. If, of course, the flow pattern changes on a shorter timescale, the time steps have to be reduced accordingly.
Time step control is based on the number of iterations required for a single time step. Keeping that number small guarantees that the changes per time step remain close to the linear slope, and, consequentially, the temporal discretization errors remain small.
Spatial accuracy is independent from temporal discretization and only depends on the spatial resolution (i.e., number of grid points and adaptive grid equation) and on the advection scheme.
The methodical approach of the hydrodynamical calculations is very similar to that described in Wuchterl (1991a), although the discretized equations differ in many aspects, such as the advection scheme, convective transport, and boundary conditions.
The numerical scenario of the dynamical simulations is equivalent to that of the stationary models: at the Hill radius, constant outer boundary conditions of ρ = 5 × 10−10 g cm−3 and T = 200 K represent a stationary environment in the habitable zone of the disk. The outer boundary is open for radiation and fluid flow. The luminosity and gas transport over the outer boundary result from the local solution of the radiation flux equation and the equation of motion, respectively. In a first set of simulation runs, set up to investigate the stability properties of planetary atmospheres, we started from stationary solutions and used the temperature of the atmosphere at the surface of the planetary core as a constant inner boundary condition. Numerically, this is implemented by fixing the radiation energy density in the innermost cell of the physical domain. For the constant core-temperature simulations, the deep atmosphere is always optically thick, and the gas energy is therefore tightly coupled to the radiation field via the local opacity.
There is no prescribed luminosity at the inner boundary, and the luminosity of the atmosphere results from the radiative and convective energy transport according to the temperature gradient in the atmosphere. Hence, the physical inner boundary conditions are changed from a constant luminosity in the stationary models to a constant core surface temperature description.
3.1. Results
For most models in our grid of stationary models, the time-dependent calculations demonstrate that the envelopes are in fact dynamically stable and return to their initial configuration after a perturbation. In these cases, the boundary conditions directly, though not uniquely (as discussed above), determine the atmospheric structure. Here in particular, the boundary conditions are expressed through 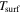 and Mcore at the inner boundary and ρ and T at the outer boundary. Therefore, a numerical simulation starting from an arbitrary initial configuration (e.g., spatially constant ρ and T) will ultimately converge to the stable solution, or one of the stable solutions in the case of multiplicity, provided it does not enter self-gravitational collapse during that evolution.
and Mcore at the inner boundary and ρ and T at the outer boundary. Therefore, a numerical simulation starting from an arbitrary initial configuration (e.g., spatially constant ρ and T) will ultimately converge to the stable solution, or one of the stable solutions in the case of multiplicity, provided it does not enter self-gravitational collapse during that evolution.
In Figure 1, we have illustrated that, within a certain parameter range, multiple stationary solutions exist for one surface temperature. Figure 2 focuses on the relevant range for the model series with a core mass of 0.6 M⊕. The results of the time-dependent simulations now show that, from these multiple solutions, only those in the upper and lower branches are stable, while the solutions in the branch with  are unstable. In the simulation, an unstable atmospheric solution (green dot in Figure 2) evolves, depending on the initial numerical perturbation, toward either the upper branch or the lower branch (indicated by dashed lines). Finally, the atmosphere settles to the corresponding stationary solutions on the stable branches for the same core temperature (blue and red dots).
are unstable. In the simulation, an unstable atmospheric solution (green dot in Figure 2) evolves, depending on the initial numerical perturbation, toward either the upper branch or the lower branch (indicated by dashed lines). Finally, the atmosphere settles to the corresponding stationary solutions on the stable branches for the same core temperature (blue and red dots).
Figure 2. Planetary luminosity and atmospheric surface pressure as a function of surface temperature for a core with 0.6 M⊕. Assuming a fixed core temperature boundary condition, an unstable atmosphere model (green dots) will evolve along the dashed lines either to the high-luminosity solution (blue dots) or the low-luminosity solution (red dots).
Download figure:
Standard image High-resolution imageThe differences between the three stationary solutions in Figure 2 for one and the same surface temperature are illustrated in Figure 3. There are two stable solutions: a thin solution with a low overall density and a high luminosity, and a dense solution characterized by a more compact structure and a low luminosity.
Figure 3. Gas density and temperature versus radius of three stationary planetary atmospheres (solid lines) for the same core temperature of 2738 K and a core mass of 0.6 M⊕. The color coding of the solid lines corresponds to the dots in Figure 2. The black, dashed lines illustrate snapshots from the dynamical evolutions starting from the unstable solution and leading, depending on the initial perturbation, either to the thin or the dense stable configuration. The numbers next to the lines give the model age in years.
Download figure:
Standard image High-resolution imageFigure 3 also illustrates snapshots from the dynamical evolutions leading from the unstable model to either of the stable configurations. Starting from the unstable state, it first takes some time before the numerical inaccuracies (or initial perturbation) grow to an amplitude that noticeably changes the envelope structure. The more accurately balanced the initial model is, the longer this growth takes. For the calculation illustrated in Figure 3, the growth time is on the order of 10 years. In order to predetermine the direction of evolution, we artificially perturbed the initial model by changing the density in the innermost cell by ±0.1%, which only marginally reduced the growth time.
In the cases where the evolution goes toward the thin configuration, the exponentially growing perturbation leads to a dynamical outflow on the dynamical timescale of about 106 s (12 days). The outflow propagates as a dynamical wave that is partially reflected at the outer boundary (see line for 11.75 years in Figure 3) and subsequently travels back and forth through the envelope with decreasing amplitude until it dies away after about four to five cycles.
If the evolution goes in the direction of the dense stable solution, the atmospheric changes happen at a much slower pace. The growth of the initial perturbation leads to an inflow of disk gas into the atmosphere that is very similar to the accumulation of atmosphere as described in Section 4. In this phase, the timescale of evolution is given by the ability of the atmosphere to assimilate and radiate off the potential energy released in the gas-accretion process. In the example illustrated in Figure 3, it takes about 30 Myr until the envelope finally settles to the dense, stable solution.
This, however, is obviously not a realistic result, as an evolution starting from an unstable stationary configuration is a purely hypothetical scenario. In the next section, we attempt to devise a more realistic setup for the accumulation and evolution of embedded primordial atmospheres.
4. TIME-DEPENDENT ATMOSPHERIC ACCRETION AND EVOLUTION SIMULATIONS
As a next step, we now replace the prescribed core surface temperature with an evolutionary scenario that relates the core surface temperature to a simple model for the internal energy budget of the planetary core. Detailed modeling of the interior physics of the core is beyond the scope of the present study; we therefore use a constant, integral heat capacity ccore for the entire core:

where 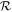 is the specific gas constant, and mmol is the mean molecular mass of the core with mmol = 30 g mol−1. The planetary core is thus assumed to undergo temperature changes uniformly throughout its structure. This does not necessarily imply an isothermal core: it can also be interpreted as a temperature structure with fixed gradients, like the adiabatic gradient in a convective magma ocean.
is the specific gas constant, and mmol is the mean molecular mass of the core with mmol = 30 g mol−1. The planetary core is thus assumed to undergo temperature changes uniformly throughout its structure. This does not necessarily imply an isothermal core: it can also be interpreted as a temperature structure with fixed gradients, like the adiabatic gradient in a convective magma ocean.
The formalism of an integral heat capacity implicitly assumes efficient energy transport in the interior of the core, as compared to transport in the atmosphere. The planetary luminosity is thus determined solely from the energy transport through the atmosphere.
Considering the high temperatures at the base of the atmospheric models—above 2000 K except for the least-massive cores—it seems plausible that the planetary cores possess deep magma oceans and molten interiors. Solomatov (2000, pp. 323–338) gives a number of estimates that can be used to constrain the efficiency of convective transport in a planetary magma ocean and arrives at a maximum convective flux of about 109 erg s−1 cm−2. This corresponds to a planetary luminosity of about 5 × 1027 erg s−1 for an Earth-size planet. Some of our models, in particular in the upper part of our grid of stationary models (Figure 1) and in the initial high-luminosity phase in the time-dependent simulations (see below), show core luminosities beyond that value. The high luminosities of these models therefore should be considered a hypothetical result that would be limited to significantly lower values by a more realistic model of energy transport within the core. Estimates from Solomatov (2000, pp. 323–338) indicate that the convective turnover timescale in a planetary magma ocean is on the order of days. Fast evolutionary changes are therefore no contradiction to the assumption of convective transport within the core.
The only energy source for the thermal budget of the core that is included in the calculations is radiogenic heat production scaled proportional to the core mass according to a value of 1021 erg s−1 for the young Earth (Stacey & Davis 2008). Other potential sources of internal energy, such as phase transitions or gravitational segregation, are neglected. For the mean density of the core, we adopted ρ = 5.5 g cm−3.
for the young Earth (Stacey & Davis 2008). Other potential sources of internal energy, such as phase transitions or gravitational segregation, are neglected. For the mean density of the core, we adopted ρ = 5.5 g cm−3.
The energy-exchange processes between the planetary core and the atmosphere (by radiation and conduction and convection) are not explicitly modeled; the surface temperature of the core is directly equated to the temperature at the base of the atmosphere. Technically, the surface temperature is implemented (as described in Section 3) via the radiation energy density in the innermost cell above the core surface. However, in this case, special attention had to be paid to ensure that gas and radiation fields near the surface remain reasonably close to radiative equilibrium at all times also for thin atmospheres.
The initial configuration for the accretion and evolution simulations is a bare, hot planetary core embedded in the homogeneous, unperturbed gas of the circumstellar disk. A planetary atmosphere only forms in the course of the dynamical simulation from the inflow of gas over the outer boundary.
In order to allow a simple correlation of the time-dependent evolution tracks with the results from stationary calculations, we adopted a hot initial temperature of the planetary core. That way, the quasi-stationary phase in the atmospheric evolution is systematically approached from the hot side. In particular, the initial temperature of the planetary core is 10,000 K in all cases, which corresponds to only a fraction of the gravitational binding energy of the core. The exact value of the initial temperature, however, is not significant. As will be seen below, the planets undergo rapid initial cooling phases; therefore, the initial temperature of the core soon becomes irrelevant for the further planetary evolution. The effect of the hot initial condition is investigated in comparative runs with cooler initial temperatures in Section 4.2.
As in Section 3, the outer boundary conditions are placed at the Hill radius and represent a stationary disk environment. The location of the outer boundary condition is not updated when the total mass, and consequently the Hill radius, increases with the growth of a massive planetary atmosphere. In order to characterize the intrinsic atmospheric evolution, the nebula conditions imposed on the outer boundary are kept constant indefinitely, irrespective of the real lifetime of the protoplanetary disk of a few megayears. In a realistic scenario, the evaporating protoplanetary disk would expose the atmosphere to the radiation and stellar wind of the host star. The high extreme ultraviolet and soft X-ray luminosity of the young host star would then produce a hot thermosphere, leading to atmospheric escape (Erkaev et al. 2013; Koskinen et al. 2013; Lammer et al. 2014).
4.1. Results
Figure 4 illustrates the evolutionary tracks of planetary atmospheres around planetary cores between 0.1 and 5 M⊕. The evolution tracks start at the right margin at Tsurf = 10,000 K and zero luminosity; the initial surface pressure is that of the unperturbed ambient nebula, corresponding to habitable zone values of T = 200 K and ρ = 5 × 10−10 g cm−3. With the onset of the simulation, very quickly a radiative flux is established, the luminosity peaks at a high level, and the core starts to cool down. The intensive radiation field heats the ambient gas and produces a thin, hot, and expanding bubble around the planetary core. This outflow depletes the gas in the computational domain compared to the unperturbed disk nebula, causing a density inversion where it joins the invariable outer boundary conditions of T = 200 K and ρ = 5 × 10−10 g cm−3, equivalent to the situation in the stationary models of luminous atmospheres, as discussed in Section 2.
Figure 4. Evolutionary tracks of the planetary luminosity and atmospheric surface pressure as a function of the surface temperature for planetary atmospheres around cores between 0.1 and 5 M⊕, as labeled. The locations of stationary models (see Figure 1) are included as small green dots. The crosses on the evolutionary tracks indicate simulation times, in years, of 1 (red), 102 (green), 104 (blue), 106 (purple), 5 × 106 (cyan), 107 (gray), and 109 (black).
Download figure:
Standard image High-resolution imageAfter the initial dynamic phase (lasting less than 1 year for all models), the evolution tracks align along the sequence of stationary models, indicating that, from that point on, the atmospheric structure is always close to the hydrostatic equilibrium.
The high luminosity in this first evolution phase implies that the planetary core cools down quickly; the initial dynamic high-luminosity phase lasts less than 100 years (green crosses) in all simulation runs. The later planetary evolution is therefore independent of the exact value of the initial core temperature. As mentioned above, the high luminosities at this phase are connected to the simple core-temperature model. Consideration of convective energy transport in the interior of the core would probably reduce the maximum luminosities to values on the order of about 1027–1028 erg s−1. The initial high-temperature, high-luminosity phase should therefore not be considered as a realistic scenario but as a numerical approach to correlate the time-dependent evolution tracks with the stationary atmosphere models in a systematic way.
Finally, when the planets have cooled down to a certain temperature—characteristic of the respective core mass—the formation of a substantial atmosphere through accumulation of disk gas sets in: disk gas flows inward over the outer boundary, the atmospheric density and mass increase, the atmosphere becomes optically thick, and consequently the planetary luminosity is much reduced. The cooling of the planetary core virtually stops at this point, as, first, the planetary luminosity is much lower and, second, the luminosity is balanced with the release of gravitational energy from the inflowing gas.
With respect to the sequence of stationary models in Figure 4, the position of the atmosphere has moved to the left along the upper branch until the model sequence bows in to the unstable branch (with 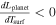 ). At this point, the model moves, essentially at constant core temperature, toward the lower stable branch, which, however, is above the limit of self-gravitational collapse only for the least-massive cores.
). At this point, the model moves, essentially at constant core temperature, toward the lower stable branch, which, however, is above the limit of self-gravitational collapse only for the least-massive cores.
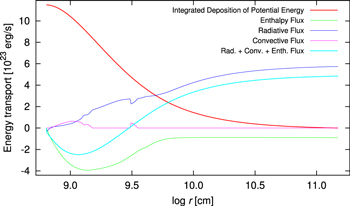
In this phase, the release of gravitational energy from the inflow of gas and the consequent contraction of the atmosphere dominates the energy balance of the atmosphere. As illustrated in Figure 5, the energy generation is broadly distributed over the atmospheric structure. In the example in Figure 5, about one-half of the total energy gained from gas accretion (∼11 × 1023 erg s−1) ends up as thermal energy in the atmosphere, while the remaining part (∼6 × 1023 erg s−1) constitutes the planetary luminosity during this stage. The energy split between atmosphere heating and luminosity is variable and depends on the model and the evolution time.
Figure 5. Contributions to energy balance in a dynamic atmosphere around a 1 M⊕ core at a simulation time of ∼5.2 × 105 years. The red line shows the integrated deposition of gravitational energy into the atmosphere. The total energy flux in the atmosphere (cyan line) essentially comprises convective transport (purple line), radiative flux (blue line), and enthalpy transported by the accretion fluid flow (green line).
Download figure:
Standard image High-resolution imageAs there is only little energy generation from gas accretion in deep atmosphere layers, the temperature stratification in this part of the atmosphere is essentially isothermal or even exhibits a small temperature inversion. Accordingly, there is no convective and, in an optically thick environment, only little radiative transport. (In Figure 5, there is a tiny inward-directed radiative flux near the surface.) In effect, these layers thus form a thermal insulation for the planetary core, and the core temperature is almost constant for large parts of the planetary evolution in the time-dependent simulations. As the phase of gas inflow and atmospheric growth lasts much longer than the initial evolution, the atmosphere remains in a narrow range of core surface temperatures for most of the time during the nebula-embedded atmospheric evolution.
In the gas-accumulation phase, the atmospheric evolution timescale becomes comparable to or larger than the evolution timescale of the protoplanetary disk. Therefore, in a realistic scenario, the further development of the planetary atmosphere would be determined by the changing nebula properties, the eventual evaporation of the disk, and irradiation from the host star. If we neglect these effects and assume an indefinitely constant disk environment, the hypothetical long-term outcomes of the evolution of the two smallest cores in Figure 4 are stationary solutions on the lower stable branch. These solutions are characterized by the luminosity provided from radiogenic energy production (which is also assumed to be indefinitely constant).
For more massive cores, there are no such stationary solutions because of the onset of self-gravitational instability for low luminosities. Therefore, when the evolution track of a growing atmosphere crosses that limit of self-gravitational stability, the atmosphere goes into a runaway collapse that would eventually lead to the formation of a gas planet.
In our simulations, we never obtained a dynamical pulsation-like behavior as described by Wuchterl (1991b) and Pečnik & Wuchterl (2007). The reason for this discrepancy is unclear.
In our calculations, the limit of runaway collapse is at about ∼0.5 M⊕, but in general this limit depends on disk properties and the physical parameterization. More important, however, are the timescales of evolution: if we consider a typical disk lifetime of a few megayears, only the most massive cores in our sample would undergo a runaway atmospheric collapse; for the less massive cores, the collapse is a purely hypothetical result because the evaporation of the protoplanetary disk would cut off the supply of gas.
The release of gravitational energy in the collapse produces a steeply rising planetary luminosity. In the evolution tracks in Figure 4, the runaway collapse appears as a marked gain in core temperature as the excessive heating of the atmosphere by the inrush of gas and the corresponding atmospheric compression are transmitted downward to the core. This heating of the core from above is a scenario where the simple, constant heat capacity model of the core particularly shows its limitations, leading to clearly unrealistic results. Generally, the numerical results for the more advanced collapse stages have to be viewed with reservations. While the numerical setup, as discussed in Section 1.1, allows a consistent, time-dependent simulation of the atmospheric evolution and gas accumulation right into the onset of the self-gravitational collapse, it does not allow an adequate description of the more advanced collapse processes. In the course of the collapse, some fundamental modeling assumptions are violated. In particular, spherical symmetry is no longer a good approximation when the atmosphere becomes large compared to the thickness of the protoplanetary disk, and for high radial velocities when the angular momentum of the flow with respect to the planetary core becomes important. The high gas accretion rate in the runaway collapse would also quickly exhaust the gas supply in the circumstellar disk (possibly opening an annular gap), and the further evolution would be determined by mass (i.e., angular momentum) transport mechanisms in the disk.
Figure 6 illustrates the total atmospheric mass as a function of time in the planetary evolution simulations with core masses between 0.1 and 5 M⊕. The upward S-curve in the lines between 10 and 100 years corresponds to the settling of the atmospheric structure into a quasi-hydrostatic configuration, as discussed above. This effect is more pronounced for more massive planetary cores.
Figure 6. Total mass of the planetary atmosphere within the Hill radius as a function of time in atmospheric evolution simulations. The lines correspond to core masses, from bottom to top, of 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1, 2, 3, 4, and 5 M⊕. The shaded area illustrates the typical lifetime of circumstellar disks, and the crosses along the time axis indicate the evolution times highlighted in Figure 4 with the same color coding. The filled circles on the lines indicate the point where the atmospheric mass equals the core mass (crossover mass).
Download figure:
Standard image High-resolution imageThen follows a prolonged smooth phase of atmospheric growth and gas accumulation (at essentially constant core temperature). Cores more massive than 0.5 M⊕ at some point enter a runaway collapse, while less massive cores eventually settle into a stationary solution. The filled circles on the lines indicate the point where the atmospheric mass equals the core mass. This crossover mass can serve as a rough estimate for the onset of gravitational instability (Bodenheimer & Pollack 1986; Ikoma et al. 2000), and in our results these points indeed approximately coincide with the beginning of the runaway collapse. The time at which the collapse occurs depends on the mass of the planetary core. A comparison with the typical lifetime of a protoplanetary disk of 1–10 Myr (gray shaded area in Figure 6) shows that only the atmospheres around the 4 M⊕ and 5 M⊕ cores will actually undergo collapse. For the less massive cores, the atmospheric growth would come to a halt once the protoplanetary disk evaporates, producing planets with extended hydrogen envelopes around a rocky core, often referred to as "mini-Neptunes."
For the more massive cores, where a comparison is possible, the gravitational accumulation of disk gas into an envelope and the onset of runaway accretion, as illustrated in Figure 6, agree qualitatively with calculations of core-collapse gas planet formation as in Ikoma et al. (2000), Ikoma & Hori (2012), or Broeg & Benz (2012). A detailed quantitative comparison, however, is not sensible because of the different physical assumptions (Jupiter versus Earth-like orbit) and numerical description, in particular the dust opacity data. As the atmospheric structure is close to a hydrostatic configuration during most of the evolution, the hydrodynamic (versus quasi-static) description does not seem to be essential for the calculation of the atmospheric accumulation timescale. During the accretion process, there is only little physical interaction between the planetary core and the atmosphere. The numerical treatment of the planetary core and its initial temperature are therefore also not crucial for the description of the atmospheric growth phase.
Table 1 compiles the evolution time up to the runaway collapse for different core masses. The growth times agree very well with those in Ikoma et al. (2000), but this might be coincidental considering the differences in the numerical description. The initial dynamic adjustment phase in our simulations does not make an appreciable difference in the long-term accretion evolution. Except for a somewhat different scaling on the time axis, our results are very similar to the curves given in Ikoma et al. (2000) for the case with constant core mass (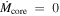 ).
).
Table 1. Duration of Atmospheric Growth up to Runaway Collapse in Atmospheric Evolution Simulations
| Mcore (M⊕) | tgrowth (years) |
|---|---|
| 5 | 3.2 × 106 |
| 4 | 5.9 × 106 |
| 3 | 1.3 × 107 |
| 2 | 3.6 × 107 |
| 1 | 2.7 × 108 |
| 0.9 | 4.1 × 108 |
| 0.6 | 6.7 × 108 |
| 0.7 | 1.2 × 109 |
| 0.6 | 2.8 × 109 |
Note. Planetary models with cores masses smaller than 0.6 M⊕ do not undergo collapse but settle toward stationary solutions.
Download table as: ASCIITypeset image
4.2. Atmospheric Accumulation onto Cores with Lower Initial Temperature
In order to verify the dependence of atmospheric growth and evolution on the initial temperature of the planetary core, we performed test runs with a lower initial core temperature of 1000 K.
Figure 7 compares the temporal evolution of atmosphere mass and core temperature for cores with 1 M⊕ and initial temperatures of 1000 K and 10,000 K (reference model). The thermal insulation of the core once an optically thick atmosphere has formed, as discussed above, suggests that the atmospheric evolution is quite similar in the more evolved stages. In fact, the curves for the atmospheric mass soon become indistinguishable after the initial dynamic phase. In the 10,000 K case, the high initial luminosity causes a steep decline of the core temperature so that it is already down to about 6500 K at the left margin of Figure 7 at t = 1 year. After the short high-luminosity phase, the core gets thermally insulated and from then on essentially remains at its characteristic temperature, in this case about 3200 K (compare Figure 4). Only later in the evolution with an increasing gas accretion rate does heating of the core from overlying atmospheric layers become important, and the core temperature starts to rise.
Figure 7. Atmospheric mass and core temperature versus time in atmosphere accumulation simulations for cores with 1 M⊕ and initial core temperatures of 10,000 and 1000 K.
Download figure:
Standard image High-resolution imageThe evolution of the atmosphere in the case of an initial core temperature of 1000 K follows the same lines except that there is no initial high-luminosity phase. Accordingly, the core remains constant at its initial temperature throughout most of the atmospheric growth phase. In this case, the heating effect from gas accretion in the late evolution toward runaway collapse is more pronounced because of the larger temperature difference between the core and the atmosphere.
The different temperature gradients above the core surface are apparent in Figure 8, which compares the structure of the atmosphere in the 10,000 and 1000 K runs at a same simulation time of ∼5.2 × 105 years. This is the same time slice as used in Figure 5 to illustrate the energy fluxes. Apart from the different temperature inversion above the core surface and a corresponding density spike, the atmosphere structures are very similar.
Figure 8. Temperature and density as a function of radius in time-dependent atmosphere calculations for cores with 1 M⊕ and initial temperatures of 10,000 and 1000 K at a simulation time of ∼5.2 × 105 years. The label "stat" refers to a stationary atmosphere with the same luminosity as in the time-dependent models.
Download figure:
Standard image High-resolution imageFor comparison, we have also included in Figure 8 a stationary atmosphere model using the same luminosity as in the time-dependent models. The relevant luminosity at the outer boundary of the time-dependent atmosphere can be read from Figure 5 (L = 4.84 × 1023 erg s−1). In the stationary model, the luminosity is necessarily assumed to be constant throughout the atmosphere.
The structure of the stationary model is in surprisingly good agreement with the time-dependent simulations. This can be understood, first, from the insensitivity of the outer envelope to the temperature of the planetary core, and, second, from the convective transport in the inner atmosphere layers, which fixes the temperature gradient close to the adiabatic value. This good agreement, however, relies on the suitable specification of the planetary luminosity for the stationary model. As can be read from Figure 4, the planetary luminosity varies by about three to four orders of magnitude during the embedded evolution phase of the planet. The consistent determination of the properties of a planetary atmosphere therefore requires consideration of the whole time-dependent problem.
5. SUMMARY AND DISCUSSION
In this paper, we explore the dynamic interaction of a terrestrial planetary core with its gaseous environment in the protoplanetary disk. The simulation runs are thus not meant to represent particular objects, nor to delineate the general evolution of terrestrial planets, but to investigate the basic mechanisms of interaction. In doing so, we have adopted a number of physical simplifications in the numerical description of the planetary core, the planetary atmosphere, and the circumstellar disk:
- 1.The internal energy budget of the planetary core is described by a very simple model. The energy transport mechanisms within the core and the energy exchange between core and atmosphere are also not explicitly modeled. Accordingly, cooling and heating of the core are only crudely described, and the planetary luminosities in the initial cooling phase of the evolution calculations are unrealistically high, which otherwise would be limited by the energy transport within the core. This means that the timescales of heating and cooling are somewhat inaccurate, though the overall physical scenario of evolution should come out essentially correct.
- 2.The conditions in the surrounding protoplanetary nebula (temperature and density) are assumed to remain constant indefinitely, regardless of the limited lifetime of the circumstellar disk. This is an intentional assumption to study the inherent timescale of the gas accretion and planetary growth without interference from the evolution and evaporation of the planetary disk. In future work, we will combine the atmospheric growth and evolution simulations with dynamic mass loss calculations triggered by disk evaporation, as presented in Stökl et al. (2015).
- 3.The time-dependent atmosphere simulations have a large number of physical and numerical parameters, such as conditions (ρ, T) in the protoplanetary nebula; the equation of state; chemical composition; dust model, dust opacities, and dust depletion factor f; Hill radius (the mass of the host star and semimajor axis of the planet); mean density of the planetary core; numerical viscosity; and convection model and parameters. The effects of some of these parameters on dynamical and stationary atmosphere models are discussed in Stökl et al. (2015). In general, the overall evolution scenario of embedded planetary atmospheres appears to be quite robust, qualitatively, while the absolute numbers and timescales are subject to the physical and numerical parameters.Despite these methodological limitations of our numerical approach, it appears that several general conclusions can be drawn from the simulation results.
- 4.The structure and properties of nebula-embedded planetary atmospheres are a time-dependent problem. For the investigated planetary cores between 0.1 and 5 M⊕, the timescale of atmospheric growth is at least of the same order of magnitude as the disk evolution timescale and much larger for the low-mass cores. This basic result complements our previous study (Stökl et al. 2015), where we have shown that the dynamic reaction timescale of a planetary atmosphere based on changes in the disk environment can also become very large.
- 5.Whether or not a planet experiences runaway growth leading to the formation of a gas planet depends on the relation between the atmospheric growth timescale and the disk lifetime. For our parameterization (disk properties, mean density of the core, dust opacities), only the cores with 4 M⊕ and 5 M⊕ accrete fast enough to go into runaway collapse within a realistic lifetime of the protoplanetary disk. Given enough time, however, much smaller cores would also eventually enter runaway collapse. From that point of view, the separation between primordial atmospheres of terrestrial planets and core-collapse formation of a gas planet is a gradual and time-dependent one.
- 6.Stationary atmosphere models, when considered with reference to a fixed core temperature (versus a planetary luminosity), are not necessarily stable, and multiple solutions may exist for one core temperature. The stability of an atmosphere can be estimated from the sign of
 in a sequence of stationary models.
in a sequence of stationary models. - 7.Starting from a high initial core temperature, the evolution tracks of the time-dependent atmosphere simulations align along the sequence of stationary models. Except for the least massive planets, the atmospheres settle at a characteristic core temperature dependent on core mass and physical parameterization. Once an optically thick atmosphere has formed, it establishes an insulation for the planetary core, and for the remainder of the atmospheric growth phase, the temperature of the core remains almost constant. Accordingly, the atmospheric structure and evolution are essentially decoupled from the particulars of the planetary core.
- 8.For most of the disk-embedded planetary evolution, the atmosphere is not in a static configuration but is characterized by gas accretion, independent of the assumed accretion rate of planetesimals. As the gas-accretion rate during this phase varies by several orders of magnitude, the numerical modeling of such planetary atmospheres depends on the time-dependent simulation of the interaction of the planetary atmosphere and the circumstellar disk.
5.1. Connection to Observations
Even though envelope growth is a time-dependent process and the final amount of atmosphere depends on the duration of the disk-embedded phase, it only takes a comparatively short period to accumulate a significant primordial atmosphere. Table 2 compiles our results for the amount of atmosphere around cores with various masses after being embedded in the disk for 104, 105, and 106 years (compare Figure 6).
Table 2. Envelope Mass Fractions fenv after Being Embedded in the Disk for 104, 105, and 106 Years
| Mcore (M⊕) | fenv in % for | ||
|---|---|---|---|
| tdisk = 104 years | tdisk = 105 years | tdisk = 106 years | |
| 0.1 | 0.12 (0) | 0.13 (0) | 0.13 (0) |
| 0.2 | 0.13 (0) | 0.16 (0) | 0.26 (0) |
| 0.3 | 0.21 (0) | 0.32 (0) | 0.58 (0) |
| 0.4 | 0.26 (0) | 0.47 (0) | 0.96 (0) |
| 0.5 | 0.32 (0) | 0.62 (0) | 1.3 (0) |
| 0.6 | 0.38 (0) | 0.77 (0) | 1.8 (0) |
| 0.7 | 0.44 (0) | 0.93 (0) | 2.2 (0.38) |
| 0.8 | 0.49 (0) | 1.1 (0) | 2.6 (1.1) |
| 0.9 | 0.55 (0) | 1.2 (0.29) | 3.0 (1.8) |
| 1 | 0.61 (0) | 1.4 (0.57) | 3.4 (2.4) |
| 2 | 1.2 (1.0) | 3.0 (2.8) | 7.9 (7.6) |
| 3 | 1.9 (1.8) | 4.8 (4.7) | 13 (13) |
| 4 | 2.7 (2.6) | 6.8 (6.7) | 20 (20) |
| 5 | 3.4 (3.4) | 8.9 (8.8) | 27 (27) |
Note. The envelope mass fraction is defined as fenv = Matm/(Matm + Mcore)). The numbers in brackets give an estimate of the envelope mass fraction that survives the atmospheric escape driven by the young host star (after 1 Gyr).
Download table as: ASCIITypeset image
Planetary cores less massive than about 0.5 M⊕ are probably unable to retain gravitationally a dense planetary envelope after the evaporation of the protoplanetary disk (Stökl et al. 2015). More massive cores are able to keep a significant fraction of their nebula-accreted atmosphere, and the final amount of atmosphere depends on the efficiency of atmospheric escape processes. Hydrodynamic atmospheric escape caused by the high soft X-ray and extreme ultraviolet (XUV) radiation of the young host star can remove on the order of about 1025 g of atmosphere gas (Erkaev et al. 2013; Lammer et al. 2014; Johnstone et al. 2015) in the habitable zone of a solar-like star. Nonthermal atmospheric escape processes, such as pickup of planetary hydrogen ions by the stellar wind, also contribute to atmosphere loss but are less important under these conditions (Kislyakova et al. 2013, 2014).
An estimate of the atmosphere that will remain after the phase of high mass loss driven by the young host stars' XUV radiation is given by the numbers in brackets in Table 2. The values were calculated by Johnstone et al. (2015), who combined a static lower atmosphere model with a hydrodynamic upper atmosphere model to derive scaling laws for the mass loss rate as a function of planetary mass, atmospheric mass, and input stellar XUV flux. Using the stellar XUV evolutionary tracks derived by Tu et al. (2015), they calculated the amount of atmosphere lost by hydrogen atmospheres with a range of planetary masses and initial atmospheric masses. The numbers given in Table 2 correspond to the assumption that the star started out its life as an average rotator.
From this estimate of the atmospheric loss, it appears that terrestrial planets with masses larger than about 1 M⊕—if they form quick enough to get embedded in the disk—can hardly avoid ending up with permanent hydrogen envelopes. These planets would therefore appear enshrouded with dense and extended hydrogen envelopes, and hence they resemble mini-Neptunes more than the terrestrial planets in the solar system.
This result is an important constraint for explaining the formation of large rocky planets (i.e., without dense hydrogen envelopes) in the habitable zone of solar-like stars. Assuming that planets such as Kepler-62e or Kepler-62f (Borucki et al. 2013) and Kepler-452b (Jenkins et al. 2015) with radii considerable larger than 1 R⊕ are indeed rocky and do not possess an extended envelope (Kaltenegger et al. 2013; Jenkins et al. 2015), one arrives at core masses of several M⊕. According to our results, such cores—and also their parent planetary embryos, depending on their mass evolution–would be quick in accumulating substantial primordial envelopes if embedded in the disk gas for any length of time. If they do, it is unlikely that they will lose their primordial atmosphere in the later evolution.
Finally, we want to highlight that this result of our study is in agreement with the observation-based statistical analysis of Rogers (2015). Rogers (2015) focuses on the mass range studied in our work and concludes that most 1.6 R⊕ exoplanets are not rocky. By analyzing the known exoplanets within this radius–mass domain and by including the sample of Kepler transiting sub-Neptunes with the Keck radial velocity follow-up, they showed that the majority of exoplanets with radii of 1.6 R⊕ and larger show an average density too low to be consistent with a pure iron and silicate composition without a gaseous envelope. More planet mass–radius measurements by satellites like CHEOPS (Broeg et al. 2013) will produce more accurate data that can be used to constrain the transition between rocky planets and planets with extended gaseous envelopes. As demonstrated in Figure 6 and Table 2, cores of about Earth mass can easily capture a large amount of primordial envelope from the nebula that is unlikely to be lost by thermal escape after the dissipation of the disk (Lammer et al. 2014; Johnstone et al. 2015).
The authors acknowledge the support by the FWF NFN project S116 "Pathways to Habitability: From Disks to Active Stars, Planets and Life," and the related FWF NFN subprojects, S 116 02-N16 "Hydrodynamics in Young Star-Disk Systems" and S116 07-N16 "Particle/Radiative Interactions with Upper Atmospheres of Planetary Bodies Under Extreme Stellar Conditions." The authors also thank the anonymous referee for the thoughtful and constructive comments.