ABSTRACT
The latest observation of HL Tau by ALMA revealed spectacular concentric dust rings in its circumstellar disk. We attempt to explain the multiple ring structure as a consequence of aggregate sintering. Sintering is known to reduce the sticking efficiency of dust aggregates and occurs at temperatures slightly below the sublimation point of the constituent material. We present a dust growth model that incorporates sintering and use it to simulate global dust evolution due to sintering, coagulation, fragmentation, and radial inward drift in a modeled HL Tau disk. We show that aggregates consisting of multiple species of volatile ices experience sintering, collisionally disrupt, and pile up at multiple locations slightly outside the snow lines of the volatiles. At wavelengths of 0.87–1.3 mm, these sintering zones appear as bright, optically thick rings with a spectral slope of  , whereas the non-sintering zones appear as darker, optically thinner rings of a spectral slope of
, whereas the non-sintering zones appear as darker, optically thinner rings of a spectral slope of  –2.5. The observational features of the sintering and non-sintering zones are consistent with those of the major bright and dark rings found in the HL Tau disk, respectively. Radial pileup and vertical settling occur simultaneously if disk turbulence is weak and if monomers constituting the aggregates are
–2.5. The observational features of the sintering and non-sintering zones are consistent with those of the major bright and dark rings found in the HL Tau disk, respectively. Radial pileup and vertical settling occur simultaneously if disk turbulence is weak and if monomers constituting the aggregates are  in radius. For the radial gas temperature profile of
in radius. For the radial gas temperature profile of  , our model perfectly reproduces the brightness temperatures of the optically thick bright rings and reproduces their orbital distances to an accuracy of
, our model perfectly reproduces the brightness temperatures of the optically thick bright rings and reproduces their orbital distances to an accuracy of  .
.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
HL Tau is a flat spectrum T Tauri star with a circumstellar disk that is very luminous at millimeter wavelengths (Beckwith et al. 1990). Although the age of HL Tau has not been well constrained, its low bolometric temperature and high mass accretion rate (e.g., White & Hillenbrand 2004), as well as the presence of an optical jet (Mundt et al. 1988) and an infalling envelope (Hayashi et al. 1993), suggest that the stellar age is likely less than 1 Myr. For these reasons, HL Tau is considered to be an ideal observational target for studying the very initial stages of disk evolution and planet formation.
The recent Long Baseline Campaign of the Atacama Large Millimeter/submillimeter Array (ALMA) provided spectacular images of the HL Tau disk (ALMA Partnership et al. 2015). ALMA resolved the disk at three millimeter wavelengths with an unprecedented spatial resolution of  at 0.87 mm. The observations revealed a pattern of multiple bright and dark rings that are remarkably symmetric with respect to the central star. The spectral index at 1 mm is ∼2 in the central emission peak and some of the bright rings, and is ∼2.3–3 in the dark rings (ALMA Partnership et al. 2015; Zhang et al. 2015). The fact that the millimeter spectral index is
at 0.87 mm. The observations revealed a pattern of multiple bright and dark rings that are remarkably symmetric with respect to the central star. The spectral index at 1 mm is ∼2 in the central emission peak and some of the bright rings, and is ∼2.3–3 in the dark rings (ALMA Partnership et al. 2015; Zhang et al. 2015). The fact that the millimeter spectral index is  in the dark, presumably optically thin rings suggests that dust grains in the HL Tau disk have already grown into aggregates whose radius is larger than a few millimeters, assuming that the aggregates are compact (Draine 2006, see Kataoka et al. 2014 for how the aggregates' porosity alters this interpretation). The observed continuum emission is best reproduced by models assuming substantial dust settling (Kwon et al. 2011, 2015; Pinte et al. 2016), implying that the large aggregates are dominant in mass and that the turbulence in the gas disk is weak. Because dust growth and settling are key processes in planet formation, understanding the origin of this axisymmetric dust structure is greatly relevant to understanding how planets form in protoplanetary disks.
in the dark, presumably optically thin rings suggests that dust grains in the HL Tau disk have already grown into aggregates whose radius is larger than a few millimeters, assuming that the aggregates are compact (Draine 2006, see Kataoka et al. 2014 for how the aggregates' porosity alters this interpretation). The observed continuum emission is best reproduced by models assuming substantial dust settling (Kwon et al. 2011, 2015; Pinte et al. 2016), implying that the large aggregates are dominant in mass and that the turbulence in the gas disk is weak. Because dust growth and settling are key processes in planet formation, understanding the origin of this axisymmetric dust structure is greatly relevant to understanding how planets form in protoplanetary disks.
There are a variety of mechanisms that can produce axisymmetric dust rings and gaps in a protoplanetary disk. One of the most common mechanisms of creating a dust ring is dust trapping at local gas pressure maxima under the action of gas drag (Whipple 1972). In a protoplanetary disk, pressure bumps may be created by disk–planet interaction (Paardekooper & Mellema 2004, 2006; Fouchet et al. 2010; Gonzalez et al. 2012; Pinilla et al. 2012; Zhu et al. 2012; Dipierro et al. 2015; Dong et al. 2015), magnetorotational instability (Johansen et al. 2009; Uribe et al. 2011), and/or steep radial variation of the disk viscosity (Kretke & Lin 2007; Dzyurkevich et al. 2010; Flock et al. 2015). Axisymmetric dust rings may also be produced by secular gravitational instability (Youdin 2011; Takahashi & Inutsuka 2014), baroclinic instability arising due to dust settling (Lorén-Aguilar & Bate 2015), or a combined effect of dust coagulation and radial drift (Laibe 2014; Gonzalez et al. 2015). Planet-carved gaps may explain the observed features of the HL Tau disk even if dust trapping at the pressure maxima is ineffective (Kanagawa et al. 2015).
Another intriguing possibility is that the multiple ring patterns of the HL Tau disk are related to the snow lines of various solid materials. Recently, Zhang et al. (2015) used a temperature profile based on a previous study (Men'shchikov et al. 1999) and showed that the major dark rings seen in the ALMA images lie close to the sublimation fronts of some main cometary volatiles, such as  and
and  . They interpreted this as being evidence of rapid particle growth by condensation, as recently predicted by Ros & Johansen (2013) for
. They interpreted this as being evidence of rapid particle growth by condensation, as recently predicted by Ros & Johansen (2013) for  ice particles. However, it is unclear whether relatively minor volatiles such as
ice particles. However, it is unclear whether relatively minor volatiles such as  and clathrates indeed accelerate dust growth.
and clathrates indeed accelerate dust growth.
In this study, we focus on another important mechanism that can affect dust growth near volatile snow lines: sintering. Sintering is the process of fusing grains together at a temperature slightly below the sublimation point. Sintered aggregates are characterized by thick joints, called necks, that connect the constituent grains (e.g., see Figures 3 and 4 of Poppe 2003; Figure 1 of Blackford 2007). A familiar example of a sintered aggregate is a ceramic material (i.e., pottery), which is an agglomerate of micron-sized clay particles fused together by sintering. Sintered aggregates are less sticky than unsintered ones because the necks prevent collision energy from being dissipated through plastic deformation. For example, unsintered dust aggregates are known to absorb much collision energy through rolling friction among constituent grains (Dominik & Tielens 1997). However, sintered aggregates are unable to lose their collision energy in this way, and therefore their collision tends to end up with bouncing, fragmentation, or erosion rather than sticking (Sirono 1999; Sirono & Ueno 2014). Thus, sintering suppresses dust growth in regions slightly outside the snow lines.
Figure 1. Upper panel: radial profiles of the brightness temperature TB of the HL Tau disk retrieved from the ALMA data (ALMA Partnership et al. 2015; see text for details). The red, green, and blue curves are for ALMA Bands 3, 6, and 7, respectively. The dashed line shows the gas temperature profile T(r) adopted in this study (Equation (1)). Lower panel: spectral index between Bands 6 and 7,  , vs. radial distance r.
, vs. radial distance r.
Download figure:
Standard image High-resolution imageThe importance of sintering in the context of protoplanetary dust growth was first pointed out by Sirono (1999), and has been studied in more detail by Sirono (2011a, 2011b) and Sirono & Ueno (2014). Sirono (1999) simulated collisions of two-dimensional sintered and unsintered aggregates (both made of  sized icy grains) with a wall, taking into account the high mechanical strength of the sintered necks. At collision velocities lower than
sized icy grains) with a wall, taking into account the high mechanical strength of the sintered necks. At collision velocities lower than  , the sintered aggregates were found to bounce off a wall, whereas the unsintered ones stuck to it. By using the same sintered neck model, Sirono & Ueno (2014) simulated collisions between two identical sintered aggregates, each of which consists of up to 104 icy grains (again of
, the sintered aggregates were found to bounce off a wall, whereas the unsintered ones stuck to it. By using the same sintered neck model, Sirono & Ueno (2014) simulated collisions between two identical sintered aggregates, each of which consists of up to 104 icy grains (again of  radius) and has a porosity of 30%–80%. They found that the aggregates erode each other rather than stick if the collision velocity is above
radius) and has a porosity of 30%–80%. They found that the aggregates erode each other rather than stick if the collision velocity is above  . This threshold is considerably lower than that for unsintered aggregates, which is around
. This threshold is considerably lower than that for unsintered aggregates, which is around  when the constituent grains are ice and
when the constituent grains are ice and  in radius (Dominik & Tielens 1997; Wada et al. 2009, 2013).
in radius (Dominik & Tielens 1997; Wada et al. 2009, 2013).
Another important fact about sintering is that it can occur at multiple locations in a protoplanetary disk, as noted by Sirono (1999, 2011b). In contrast to condensational growth as envisioned by Zhang et al. (2015), sintering requires only a small amount of volatiles because the volume of a neck is generally a small fraction of the grain volume. For example, the volume fraction is only  even if the neck radius is as large as 30% of the grain radius (Sirono 2011b). Therefore, the inclusion of
even if the neck radius is as large as 30% of the grain radius (Sirono 2011b). Therefore, the inclusion of  ice at a standard cometary abundance (∼0.2%–
ice at a standard cometary abundance (∼0.2%– Mumma & Charnley 2011) is enough to sinter the grains near the
Mumma & Charnley 2011) is enough to sinter the grains near the  snow line.
snow line.
In this study, we investigate how this "sintering barrier" against dust coagulation affects the global evolution of dust in a protoplanetary disk. We present a simple recipe to account for the change in the mechanical strength of dust aggregates due to sintering, and apply it to global simulations of dust evolution in a disk that take into account coagulation, fragmentation, and radial inward drift induced by gas drag (Adachi et al. 1976; Weidenschilling 1977). Our simulations for the first time show that sintering-induced fragmentation leads to a pile up of dust materials in the vicinity of each volatile snow line. We demonstrate that at millimeter wavelengths, these pileups can be seen as multiple bright dust rings, as observed in the HL Tau disk.
The structure of this paper is as follows. We begin by modeling the HL Tau gas disk in Section 2. Section 3 introduces our model for aggregate sintering and sublimation. Section 4 describes our simulation method, Section 5 presents the results from our fiducial simulation run, and Section 6 presents a parameter study. The validity and possible limitations of our model are discussed in Section 7. A summary is presented in Section 8.
2. DISK MODEL
We model the HL Tau protoplanetary disk as a static, axisymmetric, and vertically isothermal disk. The radial profiles of the temperature and gas density are presented in Sections 2.1 and 2.2, respectively.
2.1. Temperature Profile
We construct a radial temperature profile T(r) of the HL Tau disk based on the data of the surface brightness profiles provided by ALMA Partnership et al. (2015). We deproject the intensity maps of the disk's dust continuum at ALMA Bands 3, 6, and 7 into circularly symmetric views, assuming the disk inclination angle of  and the position angle of 138◦ (ALMA Partnership et al. 2015). We then obtain the radial profiles of the intensities Iν by azimuthally averaging the deprojected images. The upper panel of Figure 1 shows the derived radial emission profiles. Here, the intensities are expressed in terms of the Planck brightness temperature
and the position angle of 138◦ (ALMA Partnership et al. 2015). We then obtain the radial profiles of the intensities Iν by azimuthally averaging the deprojected images. The upper panel of Figure 1 shows the derived radial emission profiles. Here, the intensities are expressed in terms of the Planck brightness temperature  . Shown in the lower panel is the spectral index between Bands 6 and 7,
. Shown in the lower panel is the spectral index between Bands 6 and 7,  , where
, where  and
and  are the frequencies at Bands 6 and 7, respectively.
are the frequencies at Bands 6 and 7, respectively.
As noted by ALMA Partnership et al. (2015), the HL Tau disk has a pronounced central emission peak at  and three major bright rings at ∼20, 40, and 80 au. The central emission peak and two innermost bright rings have a spectral index of
and three major bright rings at ∼20, 40, and 80 au. The central emission peak and two innermost bright rings have a spectral index of  . In general, this indicates that the emission at these wavelengths is either optically thick, or optically thin but from dust particles larger than millimeters. The brightness temperature is equal to the gas temperature in the former case and is lower in the latter case. While Zhang et al. (2015) adopted the latter interpretation, we now pursue the former interpretation. Specifically, we assume that the Band 7 emission is optically thick and hence
. In general, this indicates that the emission at these wavelengths is either optically thick, or optically thin but from dust particles larger than millimeters. The brightness temperature is equal to the gas temperature in the former case and is lower in the latter case. While Zhang et al. (2015) adopted the latter interpretation, we now pursue the former interpretation. Specifically, we assume that the Band 7 emission is optically thick and hence  at the center, 20 au, and 40 au. The simplest profile satisfying this assumption is the single power law
at the center, 20 au, and 40 au. The simplest profile satisfying this assumption is the single power law

which is shown by the dashed line in the upper panel of Figure 1. We adopt this temperature profile in this study.
2.2. Density Structure
The density structure of the HL Tauri gas disk is unknown. Therefore, we simply assume that the gas surface density  obeys a power law with an exponential taper (Hartmann et al. 1998; Kitamura et al. 2002; Andrews et al. 2009),
obeys a power law with an exponential taper (Hartmann et al. 1998; Kitamura et al. 2002; Andrews et al. 2009),

where  and
and  are a characteristic radius and the total mass of the gas disk, respectively, and γ (
are a characteristic radius and the total mass of the gas disk, respectively, and γ ( ) is the negative slope of
) is the negative slope of  at
at  . We take
. We take  as the fiducial value but also consider
as the fiducial value but also consider  and 1.5. The dependence of our simulation results on γ will be studied in Section 6.1. The values of
and 1.5. The dependence of our simulation results on γ will be studied in Section 6.1. The values of  and
and  are fixed to
are fixed to  and
and  , respectively. The adopted disk mass is about twice the upper end of the previous mass estimates for the HL Tau disk (Guilloteau et al. 2011; Kwon et al. 2011, 2015). We assume such a massive disk because the dust mass in the disk decreases with time due to the radial drift of dust particles (see Section 5.1). Figure 2 shows the surface density profiles for
, respectively. The adopted disk mass is about twice the upper end of the previous mass estimates for the HL Tau disk (Guilloteau et al. 2011; Kwon et al. 2011, 2015). We assume such a massive disk because the dust mass in the disk decreases with time due to the radial drift of dust particles (see Section 5.1). Figure 2 shows the surface density profiles for  , 0.5, and 1.5.
, 0.5, and 1.5.
Figure 2. Radial profiles of the gas surface density  adopted in this study (Equation (2)). The solid, dotted, and dotted–dashed lines are for
adopted in this study (Equation (2)). The solid, dotted, and dotted–dashed lines are for  (fiducial), 0.5, and 1.5, respectively. The dashed line shows
(fiducial), 0.5, and 1.5, respectively. The dashed line shows  .
.
Download figure:
Standard image High-resolution imageBecause the disk is assumed to be vertically isothermal, the vertical distribution of the gas density obeys a Gaussian with the midplane value  , where
, where  is the gas scale height,
is the gas scale height,  is the sound speed, and Ω is the Keplerian frequency. The isothermal sound speed is given by
is the sound speed, and Ω is the Keplerian frequency. The isothermal sound speed is given by  , where
, where  is the Boltzmann constant and mμ is the mean molecular mass of the disk gas assumed to be
is the Boltzmann constant and mμ is the mean molecular mass of the disk gas assumed to be  . The Keplerian frequency is given by
. The Keplerian frequency is given by  , where G is the gravitational constant and M* is the stellar mass. We adopt
, where G is the gravitational constant and M* is the stellar mass. We adopt  so that the sum of the stellar and disk masses in the fiducial model,
so that the sum of the stellar and disk masses in the fiducial model,  , is within the range of the previous estimates for the HL Tau system (Beckwith et al. 1990; Sargent & Beckwith 1991; ALMA Partnership et al. 2015).
, is within the range of the previous estimates for the HL Tau system (Beckwith et al. 1990; Sargent & Beckwith 1991; ALMA Partnership et al. 2015).
We note here that the assumed disk model is marginally gravitationally stable: the Toomre stability parameter  satisfies
satisfies  at all radii for all choices of γ. This can be seen in Figure 2, where the surface density corresponding to Q = 1 is shown by the dashed line.
at all radii for all choices of γ. This can be seen in Figure 2, where the surface density corresponding to Q = 1 is shown by the dashed line.
3. SUBLIMATION AND SINTERING OF ICY DUST
We model dust in the HL Tau disk as aggregates of (sub)micron-sized grains. Each constituent grain, which we call a monomer, is assumed to be coated by an ice mantle composed of various volatile molecules (Section 3.1). The composition of the mantle at a given distance from the central star is determined using the equilibrium vapor pressure curves for the volatile species (Sections 3.2 and 3.3). The equilibrium vapor pressures also determine the rate at which the sintering of aggregates proceeds at each orbital distance (Section 3.4). The sintering rate will be used to determine the sticking efficiency of the aggregates in our dust coagulation simulations (see Section 4.4).
3.1. Volatile Composition
We assume that the volatile composition of the HL Tau disk is similar to that of comets in our solar system. We select six major cometary volatiles in addition to  and take their abundances relative to
and take their abundances relative to  to be consistent with cometary values (Mumma & Charnley 2011). The volatiles we select are ammonia (
to be consistent with cometary values (Mumma & Charnley 2011). The volatiles we select are ammonia ( ), carbon dioxide (
), carbon dioxide ( ), hydrogen sulfide (
), hydrogen sulfide ( ), ethane (
), ethane ( ), methane (
), methane ( ), and carbon monoxide (CO). We neglect another equally abundant species, methanol (
), and carbon monoxide (CO). We neglect another equally abundant species, methanol ( ), because the snow line of
), because the snow line of  is very close to that of more abundant
is very close to that of more abundant  (Sirono 2011b). Table 1 lists the abundances we adopt and the observed ranges of cometary abundances taken from Mumma & Charnley (2011).
(Sirono 2011b). Table 1 lists the abundances we adopt and the observed ranges of cometary abundances taken from Mumma & Charnley (2011).
Table 1.
Abundances of Major Cometary Volatiles Relative to  (in Percent)
(in Percent)
| Species | Cometary Valuea | Adopted Value fj |
|---|---|---|

|
100 | 100 |

|
0.2–1.4 | 1 |

|
2–30 | 10 |

|
0.12–1.4 | 1 |

|
0.1–2 | 1 |

|
0.4–1.6 | 1 |
| CO | 0.4–30 | 10 |
Note.
aMumma & Charnley (2011).Download table as: ASCIITypeset image
3.2. Equilibrium Vapor Pressures
The equilibrium vapor pressures of volatiles determine the temperatures at which sublimation and sintering occurs. In this study, we approximate the equilibrium vapor pressure for each volatile species j by the Arrhenius form

where Lj is the heat of sublimation in Kelvin and Aj is a dimensionless constant. Table 2 summarizes the values of Lj and Aj for the seven volatile species considered in this study. For  ,
,  ,
,  , and
, and  , we follow Sirono (2011b) and take the values from Table 2 of Yamamoto et al. (1983). The values for
, we follow Sirono (2011b) and take the values from Table 2 of Yamamoto et al. (1983). The values for  are derived from the analytic expression of the vapor pressure by Moses et al. (1992, see their Table III; note that we here neglect the small offset of T in their original expression). For
are derived from the analytic expression of the vapor pressure by Moses et al. (1992, see their Table III; note that we here neglect the small offset of T in their original expression). For  , we determined Lj and Aj by fitting Equation (3) to the vapor pressure data provided by (Haynes 2014, page 6–92). Figure 3 shows
, we determined Lj and Aj by fitting Equation (3) to the vapor pressure data provided by (Haynes 2014, page 6–92). Figure 3 shows  of the seven volatile species as a function of r for the temperature distribution given by Equation (1).
of the seven volatile species as a function of r for the temperature distribution given by Equation (1).
Figure 3. Equilibrium vapor pressures  (Equation (3)) of major cometary volatiles as a function of orbital distance r for the temperature profile given by Equation (1). From left to right:
(Equation (3)) of major cometary volatiles as a function of orbital distance r for the temperature profile given by Equation (1). From left to right:  (black),
(black),  (red),
(red),  (orange),
(orange),  (yellow),
(yellow),  (green),
(green),  (blue), and CO (purple). The gray curves show the partial pressures of the volatiles (dashed curve for
(blue), and CO (purple). The gray curves show the partial pressures of the volatiles (dashed curve for  , dotted–dashed curve for
, dotted–dashed curve for  and
and  , dotted curve for the other species) for the gas density profile given by Equation (2) with
, dotted curve for the other species) for the gas density profile given by Equation (2) with  and
and  . The filled circles indicate the locations of the snow lines,
. The filled circles indicate the locations of the snow lines,  .
.
Download figure:
Standard image High-resolution imageFigure 4. Sintering timescales  (Equation (6)) for major cometary volatiles as a function of orbital distance r for our HL Tau disk model. From left to right:
(Equation (6)) for major cometary volatiles as a function of orbital distance r for our HL Tau disk model. From left to right:  (black),
(black),  (red),
(red),  (orange),
(orange),  (yellow),
(yellow),  (green),
(green),  (blue), and CO (purple). Panels (a) and (b) are for monomer sizes
(blue), and CO (purple). Panels (a) and (b) are for monomer sizes  and
and  , respectively. The dashed gray curve indicates
, respectively. The dashed gray curve indicates  , which is the typical timescale for particle collision in a disk (Takeuchi & Lin 2005; Brauer et al. 2008). The filled circles indicate the locations of the snow lines,
, which is the typical timescale for particle collision in a disk (Takeuchi & Lin 2005; Brauer et al. 2008). The filled circles indicate the locations of the snow lines,  (see also Figure 3), whereas the open circles indicate the locations of the sintering lines,
(see also Figure 3), whereas the open circles indicate the locations of the sintering lines,  . Icy aggregates experience sintering in the sintering zones defined by
. Icy aggregates experience sintering in the sintering zones defined by  (horizontal bars).
(horizontal bars).
Download figure:
Standard image High-resolution imageTable 2. Vapor Pressure Parameters
| Species | Lj (K) | Aj | Ref. |
 (K) (K) |
|---|---|---|---|---|

|
6070 | 30.86 | 1 | 5463 |

|
3754 | 30.21 | 2 | 3379 |

|
3148 | 30.01 | 2 | ⋯ |

|
2860 | 27.70 | 3 | ⋯ |

|
2498 | 30.24 | 4 | 2248 |

|
1190 | 24.81 | 2 | ⋯ |
| CO | 981.8 | 26.41 | 2 | ⋯ |
References. (1) Bauer et al. (1997), (2) Yamamoto et al. (1983), (3) Haynes (2014), (4) Moses et al. (1992).
Download table as: ASCIITypeset image
Strictly speaking, the vapor pressure data given in Table 2 only apply to pure ices. In protoplanetary disks, volatiles may be trapped inside the  mantle of dust grains instead of being present as pure ices. If this is the case, the volatiles would sublimate not only at the sublimation temperatures for pure ices but also at higher temperatures where monolayer desorption from the
mantle of dust grains instead of being present as pure ices. If this is the case, the volatiles would sublimate not only at the sublimation temperatures for pure ices but also at higher temperatures where monolayer desorption from the  substrate, phase transition of
substrate, phase transition of  ice, or codesorption with the
ice, or codesorption with the  ice takes place (Collings et al. 2003, 2004; Martín-Doménech et al. 2014). However, all these high-temperature desorption processes are irrelevant to neck formation (sintering) because the desorbed molecules are unable to recondense onto grain surfaces at such high temperatures. By using the vapor pressure data for pure ices, we effectively neglect all these desorption processes.
ice takes place (Collings et al. 2003, 2004; Martín-Doménech et al. 2014). However, all these high-temperature desorption processes are irrelevant to neck formation (sintering) because the desorbed molecules are unable to recondense onto grain surfaces at such high temperatures. By using the vapor pressure data for pure ices, we effectively neglect all these desorption processes.
When estimating the locations of the snow lines, it is important to note that the vapor pressure data in the literature are subject to small but still non-negligible uncertainties. For example, the values of the sublimation energies we use for  ,
,  ,
,  , and
, and  are 10%–20% higher than those derived from the very recent temperature programmed desorption experiments by Martín-Doménech et al. (2014, see their Table 4). Luna et al. (2014) compiled the sublimation energies of major cometary volatiles from different experimental methods, and showed that the published sublimation energies have a standard deviation of 14%, 8%, 11%, and 8% for
are 10%–20% higher than those derived from the very recent temperature programmed desorption experiments by Martín-Doménech et al. (2014, see their Table 4). Luna et al. (2014) compiled the sublimation energies of major cometary volatiles from different experimental methods, and showed that the published sublimation energies have a standard deviation of 14%, 8%, 11%, and 8% for  ,
,  ,
,  , and
, and  , respectively (see their Table 2 and Figures 4 and 5). Such uncertainties might be present in the vapor pressure data for other volatiles species. As we demonstrate in Section 6.4, even a 10% uncertainty in Lj can lead to a 20%–30% uncertainty in the location of its snow line, and a better match between our simulation results and the ALMA observation can be achieved if the sublimation energies of
, respectively (see their Table 2 and Figures 4 and 5). Such uncertainties might be present in the vapor pressure data for other volatiles species. As we demonstrate in Section 6.4, even a 10% uncertainty in Lj can lead to a 20%–30% uncertainty in the location of its snow line, and a better match between our simulation results and the ALMA observation can be achieved if the sublimation energies of  ,
,  , and
, and  are taken to be 10% lower than the fiducial values. We denote these tuned sublimation energies by
are taken to be 10% lower than the fiducial values. We denote these tuned sublimation energies by  (see Table 2). For
(see Table 2). For  and
and  , the tuned sublimation energies are more consistent with the results of Martín-Doménech et al. (2014).
, the tuned sublimation energies are more consistent with the results of Martín-Doménech et al. (2014).
3.3. Snow Lines
For each volatile species j, we define the snow line as the orbit inside which the equilibrium pressure  exceeds the partial pressure Pj. Assuming that the disk gas is well mixed in the vertical direction, Pj is related to the surface number density of j-molecules in the gas phase, Nj, as
exceeds the partial pressure Pj. Assuming that the disk gas is well mixed in the vertical direction, Pj is related to the surface number density of j-molecules in the gas phase, Nj, as

In this study, we do not directly treat the evolution of Nj, but instead estimate them by assuming that the ratio between Nj and the surface number density of  molecules in the solid phase is equal to the cometary abundance fj given in Table 1. We also assume that the mass fraction of
molecules in the solid phase is equal to the cometary abundance fj given in Table 1. We also assume that the mass fraction of  ice inside the aggregates is 50%. Under these assumptions, Nj can be expressed as
ice inside the aggregates is 50%. Under these assumptions, Nj can be expressed as

The adopted relative abundances give the relations  for
for  and
and  , and
, and  for
for  ,
,  ,
,  , and
, and  . For the purpose of calculating the locations of the snow lines, the simplification made here is acceptable as a first-order approximation, because the locations of the snow lines are predominantly determined by the strong dependence of
. For the purpose of calculating the locations of the snow lines, the simplification made here is acceptable as a first-order approximation, because the locations of the snow lines are predominantly determined by the strong dependence of  on T(r) and are much less sensitive to a change in Pj.
on T(r) and are much less sensitive to a change in Pj.
To see the approximate locations of the snow lines in our HL Tau disk model, we temporarily assume the standard dust-to-gas mass ratio of  throughout the disk. The dashed, dotted–dashed, and dotted lines in Figure 3 show the partial pressure curves
throughout the disk. The dashed, dotted–dashed, and dotted lines in Figure 3 show the partial pressure curves  for the fiducial disk model (
for the fiducial disk model ( ). For each volatile species, the location of the snow line is given by the intersection of
). For each volatile species, the location of the snow line is given by the intersection of  and Pj, which is indicated by a filled circle in Figure 3. In this example, the
and Pj, which is indicated by a filled circle in Figure 3. In this example, the  snow line lies at a radial distance of 3.5 au, which is well interior to the innermost dark ring of the HL Tau disk lying at ∼ 13 au (see Figure 1). Zhang et al. (2015) suggested that the
snow line lies at a radial distance of 3.5 au, which is well interior to the innermost dark ring of the HL Tau disk lying at ∼ 13 au (see Figure 1). Zhang et al. (2015) suggested that the  snow line lies on the 13 au dark ring, assuming a higher gas temperature than ours. The snow lines of
snow line lies on the 13 au dark ring, assuming a higher gas temperature than ours. The snow lines of  ,
,  ,
,  , and
, and  are narrowly distributed over the intermediate region of 10–30 au, and those of
are narrowly distributed over the intermediate region of 10–30 au, and those of  and
and  are located in the outermost region of 100–150 au.
are located in the outermost region of 100–150 au.
3.4. Sintering Zones
Sintering is the process of neck growth, and its timescale is inversely proportional to the rate at which the neck radius increases (e.g., Swinkels & Ashby 1981). The timescale depends on the size of monomers, with larger monomers generally leading to slower sintering. In this study, we simply assume monodispersed monomers and treat their radius a0 as a free parameter (see Section 6.3 for parameter study). We only consider  because sintering is too slow to affect dust evolution in a protoplanetary disk beyond this size range (see below).
because sintering is too slow to affect dust evolution in a protoplanetary disk beyond this size range (see below).
When neck growth is driven by vapor transport of volatile j, its timescale is given by (Sirono 2011b)

where  ,
,  , and
, and  are the molecular mass, molecular volume, and surface energy of the species, respectively. The small prefactor
are the molecular mass, molecular volume, and surface energy of the species, respectively. The small prefactor  comes from the fact that the neck radius is much smaller than a0. In general,
comes from the fact that the neck radius is much smaller than a0. In general,  rapidly decreases with increasing T because
rapidly decreases with increasing T because  strongly depends on T. For species other than
strongly depends on T. For species other than  and
and  , we use the same set of
, we use the same set of  and
and  adopted by Sirono (2011b). The molecular volumes of
adopted by Sirono (2011b). The molecular volumes of  and
and  are estimated as
are estimated as  and
and  assuming that the densities of
assuming that the densities of  and
and  solids are
solids are  and
and  (Moses et al. 1992), respectively. We assume that the surface energy of
(Moses et al. 1992), respectively. We assume that the surface energy of  ice is equal to that of
ice is equal to that of  liquid:
liquid:  (Meyer 1977). For
(Meyer 1977). For  , we use
, we use  , which is the value at
, which is the value at  (Moses et al. 1992). The locations of the sintering lines discussed below are insensitive to the values of
(Moses et al. 1992). The locations of the sintering lines discussed below are insensitive to the values of  and
and  because of the strong temperature dependence of
because of the strong temperature dependence of  .
.
The necks not only grow but also are destroyed by at least two processes.
- 1.The necks evaporate when the ambient gas temperature exceeds the sublimation temperature of the volatile j that constitutes the necks. This occurs at
 , where
, where  is the orbital radius of the snow line of the volatile.
is the orbital radius of the snow line of the volatile. - 2.The necks break when the aggregate is plastically deformed by another aggregate upon collision. Unsintered aggregates are known to experience substantial plastic deformation even if the collision velocity is much below the fragmentation threshold (Dominik & Tielens 1997; Wada et al. 2008). Therefore, fully sintered aggregates form only if they do not collide with each other until the sintering is completed, i.e., only if the sintering timescale is shorter than their collision timescale, which we will denote by
 . Because
. Because  falls off rapidly toward the central star, there exists a location
falls off rapidly toward the central star, there exists a location  inside which
inside which  for a given volatile species j. In this study, we call these locations the sintering lines.
for a given volatile species j. In this study, we call these locations the sintering lines.
Taken together, each volatile species j causes aggregate sintering only inside the annulus defined by  . We call such regions the sintering zones. Our sintering zones are essentially equivalent to the "sintering regions" of Sirono (2011b).
. We call such regions the sintering zones. Our sintering zones are essentially equivalent to the "sintering regions" of Sirono (2011b).
In order to find the location of the sintering zones, one needs to estimate  . In principle, the collision time can be calculated using the size, number density, and relative speed of aggregates, as we do in our simulations (see Equation (12)). In this subsection, we avoid such detailed calculations and instead use the formula
. In principle, the collision time can be calculated using the size, number density, and relative speed of aggregates, as we do in our simulations (see Equation (12)). In this subsection, we avoid such detailed calculations and instead use the formula  , which is an approximate expression for the collision timescale of macroscopic aggregates in a turbulent disk with the dust-to-gas mass ratio of 0.01 (Takeuchi & Lin 2005; Brauer et al. 2008). This is a rough estimate (see Sato et al. 2015), but still provides a reasonable estimate for
, which is an approximate expression for the collision timescale of macroscopic aggregates in a turbulent disk with the dust-to-gas mass ratio of 0.01 (Takeuchi & Lin 2005; Brauer et al. 2008). This is a rough estimate (see Sato et al. 2015), but still provides a reasonable estimate for  because
because  is a steep function of r.
is a steep function of r.
In Figure 4, we plot the sintering timescales of the seven volatile species as a function of r for our HL Tau disk model with  . We also indicate
. We also indicate  by the dotted lines, the location of the sintering lines (
by the dotted lines, the location of the sintering lines ( ) by the open circles, and the locations of the sintering zones (
) by the open circles, and the locations of the sintering zones ( ) by the horizontal bars. We consider two different values of a0—0.1 and
) by the horizontal bars. We consider two different values of a0—0.1 and  (panels (a) and (b), respectively)—to highlight the importance of this parameter in our sintering model. For
(panels (a) and (b), respectively)—to highlight the importance of this parameter in our sintering model. For  , the width of each sintering zone is 30%–50% of
, the width of each sintering zone is 30%–50% of  , and the sintering zones of
, and the sintering zones of  ,
,  , and
, and  significantly overlap with each other. A larger a0 leads to longer sintering timescales and hence to narrower sintering zones. For
significantly overlap with each other. A larger a0 leads to longer sintering timescales and hence to narrower sintering zones. For  , the sintering zones for species other than
, the sintering zones for species other than  almost disappear. For this reason, we restrict ourselves to
almost disappear. For this reason, we restrict ourselves to  in the following sections.
in the following sections.
4. SIMULATION METHOD
As introduced in Section 1, sintering is expected to reduce the sticking efficiency of dust aggregates. In protoplanetary disks, this can occur in the sintering zones defined in Section 3.4. To study how the presence of the sintering zones affects the radial distribution of dust in a disk, we conduct global simulations of dust evolution, including sintering-induced fragmentation. In our simulations, we calculate the evolution of the surface density and representative size of icy aggregates due to coagulation and radial drift using the single-size approach (Section 4.1). The radial drift is due to aerodynamical drag by the gas disk (Adachi et al. 1976; Weidenschilling 1977), and its velocity depends on the size of the aggregates and the gas surface density (Section 4.2). We also consider turbulence in the gas disk to compute the vertical scale height and collision velocity of the aggregates (Section 4.3). The sticking efficiency of the aggregates is given as a function of their sintering timescale (Section 4.4). Based on the work of Sirono (1999) and Sirono & Ueno (2014), we assume that sintered aggregates have a lower sticking efficiency than unsintered aggregates. We do not consider a spontaneous (noncollisional) breakup of icy aggregates due to sintering (Sirono 2011a) and sublimation (Saito & Sirono 2011) near the snow lines. These effects might be important in the vicinity of the  snow line, where grains constituting the aggregates would lose a significant fraction of their volume (see Section 7.3). The aggregate internal density is fixed at
snow line, where grains constituting the aggregates would lose a significant fraction of their volume (see Section 7.3). The aggregate internal density is fixed at  , assuming a material (monomer) density of
, assuming a material (monomer) density of  and a constant aggregate porosity of 80%. Possible effects of porosity evolution will be discussed in Section 7.4.
and a constant aggregate porosity of 80%. Possible effects of porosity evolution will be discussed in Section 7.4.
The output of the simulations is then used to generate the radial profiles of dust thermal emission (Sections 4.5 and 4.6), which we will compare with the ALMA observation of the HL Tau disk in Sections 5 and 6.
4.1. The Single-size Approach for Global Dust Evolution
We simulate the global evolution of particles in a gas disk using the single-size approximation. We assume that the total solid mass at each orbital radius r is dominated by particles with a mass  . We then follow the evolution of the solid surface density
. We then follow the evolution of the solid surface density  and "representative" (mass-dominating) particle mass
and "representative" (mass-dominating) particle mass  , taking into account aggregate collision and radial drift (see Equations (7) and (8) below). The single-size approach (or mathematically speaking, moment approach) has often been used in the modeling of particle growth in planetary atmospheres (e.g., Ferrier 1994; Ormel 2014) as well as in protoplanetary disks (e.g., Kornet et al. 2001; Garaud 2007; Birnstiel et al. 2012; Estrada et al. 2015; Krijt et al. 2016, see also Appendix of Sato et al. 2015 for the mathematical background of the single-size approximation and a comparison between single-size and full-size simulations). This approach allows us to track the evolution of the mass budget of dust in a disk without using the computationally expensive Smoluchowski's coagulation equation. A drawback of this approach is that one has to assume the aggregate size distribution at each orbit whenever it is needed. In this study, we assume a power-law size distribution when we predict dust emission from the disk (see Section 4.5).
, taking into account aggregate collision and radial drift (see Equations (7) and (8) below). The single-size approach (or mathematically speaking, moment approach) has often been used in the modeling of particle growth in planetary atmospheres (e.g., Ferrier 1994; Ormel 2014) as well as in protoplanetary disks (e.g., Kornet et al. 2001; Garaud 2007; Birnstiel et al. 2012; Estrada et al. 2015; Krijt et al. 2016, see also Appendix of Sato et al. 2015 for the mathematical background of the single-size approximation and a comparison between single-size and full-size simulations). This approach allows us to track the evolution of the mass budget of dust in a disk without using the computationally expensive Smoluchowski's coagulation equation. A drawback of this approach is that one has to assume the aggregate size distribution at each orbit whenever it is needed. In this study, we assume a power-law size distribution when we predict dust emission from the disk (see Section 4.5).
Under the single-size approximation, the evolution of  and m* is described by (Ormel 2014; Sato et al. 2015)
and m* is described by (Ormel 2014; Sato et al. 2015)


where  and
and  are the radial drift velocity and mean collision time of the representative particles, respectively, and
are the radial drift velocity and mean collision time of the representative particles, respectively, and  is the change of m* upon a single aggregate collision. Equation (7) expresses the mass conservation for solids, while Equation (8) states that the growth rate of representative particles along their trajectory,
is the change of m* upon a single aggregate collision. Equation (7) expresses the mass conservation for solids, while Equation (8) states that the growth rate of representative particles along their trajectory,  , is equal to
, is equal to  . The mass change
. The mass change  is equal to m* when the collision results in pure sticking, while
is equal to m* when the collision results in pure sticking, while  when fragmentation or erosion occurs. Our Equations (7) and (8) correspond to Equations (3) and (8) of Ormel (2014), respectively, although Equation (8) of Ormel (2014) assumes
when fragmentation or erosion occurs. Our Equations (7) and (8) correspond to Equations (3) and (8) of Ormel (2014), respectively, although Equation (8) of Ormel (2014) assumes  . The expressions for
. The expressions for  ,
,  , and
, and  will be given in Sections 4.2–4.4, respectively.
will be given in Sections 4.2–4.4, respectively.
We solve Equations (7) and (8) by discretizing the radial direction into 300 logarithmically spaced binds spanning from  to
to  . The parameter sets and initial conditions used in the simulations are described in Section 4.7.
. The parameter sets and initial conditions used in the simulations are described in Section 4.7.
4.2. Radial Drift
The motion of a particle in a gas disk is characterized by the dimensionless Stokes number  , where Ω is the Keplerian frequency and
, where Ω is the Keplerian frequency and  is the particle's stopping time. When the particle radius is much smaller than the mean free path of the gas molecules in the disk, as is true for the particles in our simulations, the stopping time is given by Epstein's drag law. The Stokes number of a representative aggregate at the midplane can then be written as (Birnstiel et al. 2010)
is the particle's stopping time. When the particle radius is much smaller than the mean free path of the gas molecules in the disk, as is true for the particles in our simulations, the stopping time is given by Epstein's drag law. The Stokes number of a representative aggregate at the midplane can then be written as (Birnstiel et al. 2010)

where  and
and  are the internal density and radius of the aggregate, respectively. We use Equation (9) whenever we calculate
are the internal density and radius of the aggregate, respectively. We use Equation (9) whenever we calculate  .
.
The drift velocity  is given by (Adachi et al. 1976; Weidenschilling 1977)
is given by (Adachi et al. 1976; Weidenschilling 1977)

where

is the parameter characterizing the sub-Keplerian motion of the gas disk,  is the Keplerian velocity, and
is the Keplerian velocity, and  is the midplane gas pressure. In our disk model,
is the midplane gas pressure. In our disk model,  and therefore
and therefore  everywhere. At
everywhere. At  , we approximately have
, we approximately have  ×
×  and
and  .
.
4.3. Collision Time
We evaluate the collision term  assuming that collisions between representative aggregates dominate the evolution of m*. Under this assumption, the collision time is approximately given by
assuming that collisions between representative aggregates dominate the evolution of m*. Under this assumption, the collision time is approximately given by

where  , n*, and
, n*, and  are the collisional cross section, number density, and collision velocity of the representative aggregates, respectively. We use the midplane values for n* and
are the collisional cross section, number density, and collision velocity of the representative aggregates, respectively. We use the midplane values for n* and  . We do not consider the erosion of representative aggregates by a number of small grains (Seizinger et al. 2013; Krijt et al. 2015) because there remain uncertainties in the threshold velocity for erosive collisions as a function of the projectile mass (see Section 2.3.2 of Krijt et al. 2015).
. We do not consider the erosion of representative aggregates by a number of small grains (Seizinger et al. 2013; Krijt et al. 2015) because there remain uncertainties in the threshold velocity for erosive collisions as a function of the projectile mass (see Section 2.3.2 of Krijt et al. 2015).
To evaluate n*, we consider disk turbulence and assume that vertical settling balances with turbulent diffusion for the representative aggregates. We parameterize the strength of disk turbulence with the dimensionless parameter  , where D is the particle diffusion coefficient in the turbulence. For simplicity,
, where D is the particle diffusion coefficient in the turbulence. For simplicity,  is assumed to be independent of time and distance from the midplane, but we allow
is assumed to be independent of time and distance from the midplane, but we allow  to depend on r (see Section 4.7). Under this assumption, n* at the midplane can be written as
to depend on r (see Section 4.7). Under this assumption, n* at the midplane can be written as

where

is the scale height of the representative aggregates (Dubrulle et al. 1995; Youdin & Lithwick 2007).
The collision velocity  is given by the root sum square of the contributions from Brownian motion, gas turbulence (Ormel & Cuzzi 2007), and size-dependent drift relative to the gas disk (Adachi et al. 1976; Weidenschilling 1977). The expressions for these contributions can be found in, for example, Section 2.3.2 of Okuzumi et al. (2012). The contributions from turbulence and drift motion are functions of the Stokes numbers of two colliding aggregates,
is given by the root sum square of the contributions from Brownian motion, gas turbulence (Ormel & Cuzzi 2007), and size-dependent drift relative to the gas disk (Adachi et al. 1976; Weidenschilling 1977). The expressions for these contributions can be found in, for example, Section 2.3.2 of Okuzumi et al. (2012). The contributions from turbulence and drift motion are functions of the Stokes numbers of two colliding aggregates,  and
and  . In this study, we set
. In this study, we set  and
and  because we consider collisions between aggregates similar in size. Sato et al. (2015) and Krijt et al. (2016) have recently shown that such a choice best reproduces the results of coagulation simulations that resolve the full size distribution of the aggregates. As long as
because we consider collisions between aggregates similar in size. Sato et al. (2015) and Krijt et al. (2016) have recently shown that such a choice best reproduces the results of coagulation simulations that resolve the full size distribution of the aggregates. As long as  , the collision velocity is an increasing function of
, the collision velocity is an increasing function of  .
.
For macroscopic aggregates satisfying  , either turbulence or radial drift mostly dominates their collision velocity. For this range of
, either turbulence or radial drift mostly dominates their collision velocity. For this range of  , the collision velocities driven by turbulence and radial drift are approximately given by
, the collision velocities driven by turbulence and radial drift are approximately given by  and
and  , respectively, where we use
, respectively, where we use  and
and  (for the expression of
(for the expression of  , see Equation (28) of Ormel & Cuzzi 2007).
, see Equation (28) of Ormel & Cuzzi 2007).
4.4. Collisional Mass Gain/Loss
We denote the change in m* due to a single collision between two mass-dominating aggregates by  . Following Okuzumi & Hirose (2012), we model
. Following Okuzumi & Hirose (2012), we model  as
as

where the fragmentation threshold  characterizes the sticking efficiency of the colliding aggregates. The mass change is positive for
characterizes the sticking efficiency of the colliding aggregates. The mass change is positive for  and negative for
and negative for  as shown in Figure 5(a). Equation (15) is a fit to the data of the collision simulations for unsintered aggregates by Wada et al. (2009, their Figure 11). For sintered aggregates, Equation (15) overestimates the sticking efficiency at low collision velocities where the aggregates bounce rather than stick (Sirono 1999). However, we show in Section 7.1 that the bouncing hardly alters the evolution of m* in the sintering zone. For simplicity, we use Equation (15) for both unsintered and sintered aggregates.
as shown in Figure 5(a). Equation (15) is a fit to the data of the collision simulations for unsintered aggregates by Wada et al. (2009, their Figure 11). For sintered aggregates, Equation (15) overestimates the sticking efficiency at low collision velocities where the aggregates bounce rather than stick (Sirono 1999). However, we show in Section 7.1 that the bouncing hardly alters the evolution of m* in the sintering zone. For simplicity, we use Equation (15) for both unsintered and sintered aggregates.
Figure 5. Panel (a): growth efficiency  (Equation (15)) vs. the scaled collision velocity
(Equation (15)) vs. the scaled collision velocity  . Panel (b): catastrophic fragmentation threshold
. Panel (b): catastrophic fragmentation threshold  (Equation (16)) vs. the ratio between the collision and effective sintering timescales
(Equation (16)) vs. the ratio between the collision and effective sintering timescales  for
for  .
.
Download figure:
Standard image High-resolution imageTo account for the effect of sintering on the aggregate sticking efficiency, we model the fragmentation threshold  as
as

where

is the effective sintering timescale (see Equation (6) for the definition of the individual sintering timescale  ) and
) and  and
and  are the thresholds for unsintered and sintered aggregates, respectively. In Equation (17), the summation is taken over all solid-phase volatiles (i.e., volatiles satisfying
are the thresholds for unsintered and sintered aggregates, respectively. In Equation (17), the summation is taken over all solid-phase volatiles (i.e., volatiles satisfying  ). As described in Section 3.3, the snow line location
). As described in Section 3.3, the snow line location  for each species is calculated from the relation
for each species is calculated from the relation  with Equations (4) and (5). At
with Equations (4) and (5). At  , where all volatile ices sublimate, we exceptionally set
, where all volatile ices sublimate, we exceptionally set  to mimic the low sticking efficiency of bare silicate grains compared to (unsintered) ice-coated grains (e.g., Chokshi et al. 1993).
to mimic the low sticking efficiency of bare silicate grains compared to (unsintered) ice-coated grains (e.g., Chokshi et al. 1993).
Equation (16) is constructed so that  in the non-sintering zones (
in the non-sintering zones ( ) and
) and  in the sintering zone (
in the sintering zone ( ). Simulations of aggregate collisions suggest that
). Simulations of aggregate collisions suggest that  (Wada et al. 2009) and
(Wada et al. 2009) and  (Sirono & Ueno 2014) if the colliding aggregates are identical and made of
(Sirono & Ueno 2014) if the colliding aggregates are identical and made of  sized ice monomers. The theory of particle sticking (Johnson et al. 1971), on which the simulations by Wada et al. (2009) are based, indicates that
sized ice monomers. The theory of particle sticking (Johnson et al. 1971), on which the simulations by Wada et al. (2009) are based, indicates that  scales with the monomer size as
scales with the monomer size as  (Chokshi et al. 1993; Dominik & Tielens 1997). For
(Chokshi et al. 1993; Dominik & Tielens 1997). For  , the scaling is yet to be studied, so we simply assume the same scaling as for
, the scaling is yet to be studied, so we simply assume the same scaling as for  . We thus model
. We thus model  and
and  as
as


Figure 5(b) shows  versus
versus  for
for  .
.
4.5. Aggregate Opacity
We calculate the absorption cross section of porous aggregates using the analytic expression by Kataoka et al. (2014, their Equation (18)), which is based on Mie calculations with effective medium theory. Monomers are treated as composite spherical grains made of astronomical silicates, carbonaceous materials, and water ice with the mass abundance ratio of 2.64:3.53:5.55 (Pollack et al. 1994). We calculate the effective refractive index of the monomers using the Bruggeman mixing rule. The optical constants of silicates, carbons, and water ice are taken from Draine (2003), Zubko et al. (1996, data for ACH2 samples), and Warren (1984, data for  ), respectively. We neglect the contribution of volatiles other than
), respectively. We neglect the contribution of volatiles other than  to the monomer optical properties. The effective refractive index of porous aggregates is computed using the Maxwell–Garnett rule in which the monomers are regarded as inclusions in vacuum.
to the monomer optical properties. The effective refractive index of porous aggregates is computed using the Maxwell–Garnett rule in which the monomers are regarded as inclusions in vacuum.
Because we adopt the single-size approach, we only track the evolution of aggregates dominating the dust surface density. However, these aggregates do not necessarily dominate millimeter dust emission from a disk. While the mass-dominating aggregates are generally the largest aggregates in the population (e.g., Birnstiel et al. 2012; Okuzumi et al. 2012), smaller ones can dominate the millimeter opacity of the population when the largest aggregates are significantly larger than a millimeter in radius. In order to take into account this effect, we only assume a size distribution when we calculate dust opacities. Specifically, we assume a power-law distribution

where  is the column number density of aggregates per unit aggregate radius a (
is the column number density of aggregates per unit aggregate radius a ( ),
),  is the minimum aggregate radius, and C is the normalization constant determined by the condition
is the minimum aggregate radius, and C is the normalization constant determined by the condition  . We fix
. We fix  to be
to be  with the understanding that millimeter opacities are insensitive to the choice of
with the understanding that millimeter opacities are insensitive to the choice of  as long as
as long as  . The slope of −3.5 is based on the classical theory of fragmentation cascades (Dohnanyi 1969; Tanaka et al. 1996; see Birnstiel et al. 2011 for how the coagulation of the fragments modifies this value). Therefore, Equation (20) would overestimate the amount of fragments when the collisions between the largest aggregates (which are the source of the fragments) do not lead to their catastrophic disruption. Possible effects of this simplification are discussed in Section 7.2.
. The slope of −3.5 is based on the classical theory of fragmentation cascades (Dohnanyi 1969; Tanaka et al. 1996; see Birnstiel et al. 2011 for how the coagulation of the fragments modifies this value). Therefore, Equation (20) would overestimate the amount of fragments when the collisions between the largest aggregates (which are the source of the fragments) do not lead to their catastrophic disruption. Possible effects of this simplification are discussed in Section 7.2.
The upper panel of Figure 6 shows our dust opacities  at wavelengths
at wavelengths  , 1.3, and 2.9 mm (corresponding to ALMA Bands 7, 6, and 3, respectively) as a function of a*. Note that the opacities are expressed in units of
, 1.3, and 2.9 mm (corresponding to ALMA Bands 7, 6, and 3, respectively) as a function of a*. Note that the opacities are expressed in units of  per gram of dust. In the lower panel of Figure 6, we plot the opacity slope measured at
per gram of dust. In the lower panel of Figure 6, we plot the opacity slope measured at  –1.3 mm,
–1.3 mm,  . Our model gives
. Our model gives  at
at  and
and  in the opposite limit.
in the opposite limit.
Figure 6. Upper panel: absorption opacities  (in units of
(in units of  per gram of dust) of dust at wavelengths
per gram of dust) of dust at wavelengths  0.87, 1.3, and 2.9 mm as a function of the representative aggregate radius a. The opacities are calculated by assuming that the aggregate size distribution (not resolved in our simulation) obeys a power law
0.87, 1.3, and 2.9 mm as a function of the representative aggregate radius a. The opacities are calculated by assuming that the aggregate size distribution (not resolved in our simulation) obeys a power law  (Equation (20)). Lower panel: opacity slope at
(Equation (20)). Lower panel: opacity slope at  –1.3 mm vs. a*.
–1.3 mm vs. a*.
Download figure:
Standard image High-resolution image4.6. Dust Thermal Emission
We calculate the intensities Iν of dust thermal emission at each orbital radius r as

where  is the Planck function,
is the Planck function,

is the line of sight optical depth, and i is the disk inclination. We use  for the HL Tau disk (ALMA Partnership et al. 2015). The Planck brightness temperature
for the HL Tau disk (ALMA Partnership et al. 2015). The Planck brightness temperature  is computed by solving the equation
is computed by solving the equation  for
for  . Equation (22) assumes that the dust disk is geometrically thin (i.e., the radial distance over which
. Equation (22) assumes that the dust disk is geometrically thin (i.e., the radial distance over which  and
and  vary is longer than the dust scale height). This assumption is, however, not always satisfied in our simulations, as we discuss in detail in Section 6.3.
vary is longer than the dust scale height). This assumption is, however, not always satisfied in our simulations, as we discuss in detail in Section 6.3.
We will also use the flux density

where d is the distance to HL Tau,  and
and  are the boundaries of our computational domain (see Section 4.1), and the factor
are the boundaries of our computational domain (see Section 4.1), and the factor  accounts for the ellipticity of the disk image. In accordance with ALMA Partnership et al. (2015), we set
accounts for the ellipticity of the disk image. In accordance with ALMA Partnership et al. (2015), we set  , the standard mean distance to Taurus.
, the standard mean distance to Taurus.
When comparing our simulation results with the ALMA observation, it is useful to smooth the simulated radial emission profiles at the spatial resolution of ALMA. In this study, we do this in two steps. First, we generate projected images of our simulation snapshots assuming the disk inclination of  . For simplicity, the geometrical thickness of the disks is neglected in this process. Second, we smooth the "raw" images along their major axis using a circular Gaussian with the FWHM angular resolutions of
. For simplicity, the geometrical thickness of the disks is neglected in this process. Second, we smooth the "raw" images along their major axis using a circular Gaussian with the FWHM angular resolutions of  ,
,  , and
, and  mas for
mas for  , 1.3, and 0.87 mm, in accordance with the ALMA observation of HL Tau at Bands 3, 6, and 7, respectively (ALMA Partnership et al. 2015). Because we assume
, 1.3, and 0.87 mm, in accordance with the ALMA observation of HL Tau at Bands 3, 6, and 7, respectively (ALMA Partnership et al. 2015). Because we assume  , these angular resolutions translate into the spatial resolutions of ≈10, 3.9, and 3.3 au at Bands 3, 6, and 7, respectively.
, these angular resolutions translate into the spatial resolutions of ≈10, 3.9, and 3.3 au at Bands 3, 6, and 7, respectively.
4.7. Parameter Sets and Initial Conditions
We conduct 10 simulation runs with different sets of model parameters. Columns 1 through 4 of Table 3 list the run names and parameter choices (γ, a0,  ) for the simulation runs. Run Sa0 is our fiducial model and assumes
) for the simulation runs. Run Sa0 is our fiducial model and assumes  ,
,  , and
, and  . Model Sa0-NoSint is the same as model Sa0 but neglects sintering. Runs Sa0-Lgam and Sa0-Hgam are designed to study the dependence of the results on the gas surface density slope γ. Runs Sa0-Lalp and Sa0-Halp will be used to study how the sintering-induced ring formation scenario constrains the radial distribution of
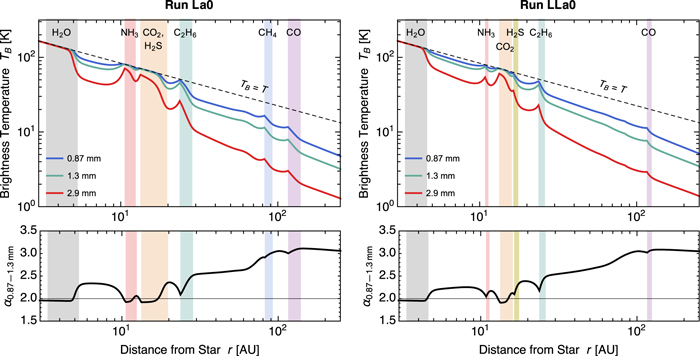
. Model Sa0-NoSint is the same as model Sa0 but neglects sintering. Runs Sa0-Lgam and Sa0-Hgam are designed to study the dependence of the results on the gas surface density slope γ. Runs Sa0-Lalp and Sa0-Halp will be used to study how the sintering-induced ring formation scenario constrains the radial distribution of  in the HL Tau disk. Runs La0 and LLa0 assume more fragile aggregates (i.e., larger a0) and weaker turbulence than in the fiducial run. As we will see, the set of a0 and
in the HL Tau disk. Runs La0 and LLa0 assume more fragile aggregates (i.e., larger a0) and weaker turbulence than in the fiducial run. As we will see, the set of a0 and  controls the degree of dust sedimentation (i.e., the geometrical thickness of the dust disk). Runs Sa0-tuned and La0-tuned are the same as runs Sa0 and La0, respectively, except that they adopt slightly lower Lj for
controls the degree of dust sedimentation (i.e., the geometrical thickness of the dust disk). Runs Sa0-tuned and La0-tuned are the same as runs Sa0 and La0, respectively, except that they adopt slightly lower Lj for  ,
,  , and
, and  (see
(see  in Table 2). These runs will be used to quantify possible uncertainties of our results that might arise from the uncertainties in the vapor pressure data.
in Table 2). These runs will be used to quantify possible uncertainties of our results that might arise from the uncertainties in the vapor pressure data.
Table 3. List of Simulation Runs
| Run | γ | a0 |

|

|
Fν (Jy) at 
|
Section | ||
|---|---|---|---|---|---|---|---|---|
| (μm) | (Myr) | 2.9 mm | 1.3 mm | 0.87 mm | ||||
| Sa0 | 1 | 0.1 |

|
0.26 | 0.070 | 0.79 | 2.2 | 5 |
| Sa0-NoSinta | 1 | 0.1 |

|
0.12 | 0.063 | 0.79 | 2.3 | 5.5 |
| Sa0-Lgam | 0.5 | 0.1 |

|
0.29 | 0.076 | 0.76 | 2.1 | 6.1 |
| Sa0-Hgam | 1.5 | 0.1 |

|
0.05 | 0.072 | 0.80 | 2.3 | 6.1 |
| Sa0-Lalp | 1 | 0.1 | 0.03 | 0.18 | 0.066 | 0.77 | 2.2 | 6.2 |
| Sa0-Halp | 1 | 0.1 | 0.1 | 0.29 | 0.075 | 0.75 | 2.1 | 6.2 |
| La0 | 1 | 1 |

|
0.41 | 0.064 | 0.78 | 2.3 | 6.3 |
| LLa0 | 1 | 4 |

|
0.45 | 0.062 | 0.80 | 2.4 | 6.3 |
| Sa0-tunedb | 1 | 0.1 |

|
0.27 | 0.068 | 0.77 | 2.2 | 6.4 |
| La0-tunedb | 1 | 1 |

|
0.41 | 0.063 | 0.79 | 2.3 | 6.4 |
Notes.
aNo sintering. bUses instead of Lj for
instead of Lj for  ,
,  , and
, and  (see Table 2).
(see Table 2).
Download table as: ASCIITypeset image
The initial conditions are given by  and
and  , where we have assumed that the dust-to-gas mass ratio of the initial disk is 0.01.
, where we have assumed that the dust-to-gas mass ratio of the initial disk is 0.01.
5. RESULTS FROM THE FIDUCIAL SIMULATION
We now present the results of our simulations in the following two sections. In this section, we particularly focus on the fiducial run Sa0 and analyze its results in detail. The dependence on model parameters will be discussed in Section 6.
5.1. Evolution of the Total Dust Mass and Flux Densities
In our simulations, the observational appearance of the disk changes with time because dust particles grow and drift inward. In particular, the millimeter emission of the disk diminishes as the particles drain onto the central star. For this reason, we select from each simulation run one snapshot that best reproduces the millimeter flux densities of the HL Tau disk reported by ALMA Partnership et al. (2015). Specifically, we calculate the relative errors between the simulated and observed flux densities at  , 1.3, and 2.9 mm as a function of time, and search for the time
, 1.3, and 2.9 mm as a function of time, and search for the time  at which the sum of the relative errors is minimized. For reference, the flux densities reported by the ALMA observation are 0.0743, 0.744, and 2.14 Jy at
at which the sum of the relative errors is minimized. For reference, the flux densities reported by the ALMA observation are 0.0743, 0.744, and 2.14 Jy at  , 1.3, and 2.9 mm (Bands 7, 6, and 3), respectively (ALMA Partnership et al. 2015).
, 1.3, and 2.9 mm (Bands 7, 6, and 3), respectively (ALMA Partnership et al. 2015).
Figure 7 illustrates such an analysis for our fiducial simulation run Sa0. This figure shows the simulated time evolution of the flux densities at the three wavelengths as well as the evolution of the total dust mass  within the computational domain. The dust mass and flux densities decrease on a timescale of
within the computational domain. The dust mass and flux densities decrease on a timescale of  , which reflects the timescale on which the dust near the disk's outer edge (which dominates
, which reflects the timescale on which the dust near the disk's outer edge (which dominates  ) grows into rapidly drifting pebbles (see, e.g., Sato et al. 2015). Comparing the flux densities from the simulation with those from the ALMA observations (shown by the dashed horizontal line segments in the lower panel of Figure 7), we find that the sum of the relative errors in the flux densities is minimized when
) grows into rapidly drifting pebbles (see, e.g., Sato et al. 2015). Comparing the flux densities from the simulation with those from the ALMA observations (shown by the dashed horizontal line segments in the lower panel of Figure 7), we find that the sum of the relative errors in the flux densities is minimized when  . At this time, the flux densities in the simulation are 0.070, 0.79, and 2.2 Jy at
. At this time, the flux densities in the simulation are 0.070, 0.79, and 2.2 Jy at  2.9, 1.3, and 0.87 mm, respectively, which is in agreement with the ALMA measurements to an accuracy of less than 6%.
2.9, 1.3, and 0.87 mm, respectively, which is in agreement with the ALMA measurements to an accuracy of less than 6%.
Figure 7. Simulated time evolution of the total dust mass  (upper panel) and flux densities Fν (lower panel) of the HL Tau disk from simulation run Sa0. The blue, green, and red solid curves in the lower panel are Fν at wavelengths
(upper panel) and flux densities Fν (lower panel) of the HL Tau disk from simulation run Sa0. The blue, green, and red solid curves in the lower panel are Fν at wavelengths  , 1.3 mm, and 2.9 mm, respectively. The dashed horizontal line segments indicate the ALMA measurements of the flux densities at these wavelengths (Bands 7, 6, and 3, respectively). The vertical dotted line indicates the time
, 1.3 mm, and 2.9 mm, respectively. The dashed horizontal line segments indicate the ALMA measurements of the flux densities at these wavelengths (Bands 7, 6, and 3, respectively). The vertical dotted line indicates the time  at which the simulated flux densities best reproduce the ALMA measurements (
at which the simulated flux densities best reproduce the ALMA measurements ( for run Sa0; see Section 5.1).
for run Sa0; see Section 5.1).
Download figure:
Standard image High-resolution imageColumns 5 through 8 of Table 3 list the values of  and
and  for all simulation runs. We find that
for all simulation runs. We find that  falls within the range 0.1–
falls within the range 0.1– . Since
. Since  may be regarded as the time after disk formation, our results are consistent with the idea that HL Tau is younger than 1 Myr. In fact, the age predicted from our simulations depends on the disk mass
may be regarded as the time after disk formation, our results are consistent with the idea that HL Tau is younger than 1 Myr. In fact, the age predicted from our simulations depends on the disk mass  assumed: a higher
assumed: a higher  leads to a larger
leads to a larger  because it takes longer for dust emission to decay to the observed level when the initial dust mass is larger. However, a disk mass much in excess of
because it takes longer for dust emission to decay to the observed level when the initial dust mass is larger. However, a disk mass much in excess of  seems to be unrealistic because the disk would then be gravitationally unstable at outer radii (see Section 2.2).
seems to be unrealistic because the disk would then be gravitationally unstable at outer radii (see Section 2.2).
5.2. Aggregate Size and Dust Surface Density
Below we fix t to be  and look at the radial distribution of dust in detail. Figures 8(a) and (b) show the radial distribution of the representative aggregate radius a* and dust surface density
and look at the radial distribution of dust in detail. Figures 8(a) and (b) show the radial distribution of the representative aggregate radius a* and dust surface density  at this time. We also show in Figure 8(c) the Stokes number
at this time. We also show in Figure 8(c) the Stokes number  of the representative aggregates, which is more directly related to their dynamics than a*. In these figures, the vertical stripes indicate the locations of the sintering zones. Here, the sintering zone of each volatile j is defined by the locations where
of the representative aggregates, which is more directly related to their dynamics than a*. In these figures, the vertical stripes indicate the locations of the sintering zones. Here, the sintering zone of each volatile j is defined by the locations where  and
and  , with the latter being equivalent to
, with the latter being equivalent to  (see Figure 8(e) for the radial distribution of
(see Figure 8(e) for the radial distribution of  and
and  ). The sintering zones of
). The sintering zones of  ,
,  , and
, and  partially overlap with each other and form a single sintering zone. The exact locations of the sintering zones are 3–6 au (
partially overlap with each other and form a single sintering zone. The exact locations of the sintering zones are 3–6 au ( ), 11–23 au (
), 11–23 au ( –
– –
– ), 24–33 au (
), 24–33 au ( ), 80–106 au (
), 80–106 au ( ), and 116–160 au (
), and 116–160 au ( ). Strictly speaking, the locations of the sintering zones are time-dependent because the volatile partial pressures Pj and aggregate collision timescale
). Strictly speaking, the locations of the sintering zones are time-dependent because the volatile partial pressures Pj and aggregate collision timescale  evolve with
evolve with  (see Equations (4), (5), and (12)). However, a comparison of Figures 4 and 8 shows that the sintering zones little migrate during this
(see Equations (4), (5), and (12)). However, a comparison of Figures 4 and 8 shows that the sintering zones little migrate during this  . This is because the locations of the sintering zones depend on the radial distribution of the gas temperature T (which is taken to be time-independent) much more strongly than on the distribution of
. This is because the locations of the sintering zones depend on the radial distribution of the gas temperature T (which is taken to be time-independent) much more strongly than on the distribution of  .
.
Figure 8. Radial distribution of the representative aggregate radius a* (panel (a)), dust surface density  (panel (b)), aggregate Stokes number
(panel (b)), aggregate Stokes number  (panel (c)), and radial inward dust flux
(panel (c)), and radial inward dust flux  (panel (d)) at time
(panel (d)) at time  from the fiducial simulation. The shaded areas mark the sintering zones defined by
from the fiducial simulation. The shaded areas mark the sintering zones defined by  (see Section 3.4 for details). Panel (e) shows the collision timescale
(see Section 3.4 for details). Panel (e) shows the collision timescale  (Equation (12); solid line) and effective sintering timescale
(Equation (12); solid line) and effective sintering timescale  (Equation (17); dashed line), while panel (f) plots the collision velocity
(Equation (17); dashed line), while panel (f) plots the collision velocity  (solid line) and fragmentation threshold
(solid line) and fragmentation threshold  (Equation (16); dashed line) for the representative aggregates.
(Equation (16); dashed line) for the representative aggregates.
Download figure:
Standard image High-resolution imageFigures 8(a) and (b) show that sintering produces a clear pattern in the radial distribution of the dust component. We see that dust aggregates in the sintering zones tend to have a high surface density and a small radius compared to those in the adjacent non-sintering zones. The small aggregate size is a direct consequence of fragmentation induced by sintering. To see this, we plot in Figure 8(f) the collision velocity  and fragmentation threshold
and fragmentation threshold  as a function of r. In the non-sintering zones, we find
as a function of r. In the non-sintering zones, we find  and
and  –
– , implying that no disruptive collisions occur for the unsintered aggregates (as we show below, the maximum size of the unsintered aggregates is determined by radial drift rather than fragmentation). In the sintering zones,
, implying that no disruptive collisions occur for the unsintered aggregates (as we show below, the maximum size of the unsintered aggregates is determined by radial drift rather than fragmentation). In the sintering zones,  is decreased to
is decreased to  and
and  is suppressed down to the same value. Since
is suppressed down to the same value. Since  is an increasing function of a* (as long as
is an increasing function of a* (as long as  ), this indicates that the sintered aggregates disrupt each other so that
), this indicates that the sintered aggregates disrupt each other so that  never exceeds
never exceeds  . The disrupted aggregates pile up there because the inward drift speed
. The disrupted aggregates pile up there because the inward drift speed  decreases with decreasing a*. These pileups provide the high surface densities in the sintering zones.
decreases with decreasing a*. These pileups provide the high surface densities in the sintering zones.
To understand the radial distribution of  and a* more quantitatively, we look at the radial inward mass flux of drifting aggregates,
and a* more quantitatively, we look at the radial inward mass flux of drifting aggregates,

The radial distribution of  is shown in Figure 8(d). The mass flux is radially constant (
is shown in Figure 8(d). The mass flux is radially constant ( ) at
) at  , which indicates that the radial dust flow in this region can be approximated by a steady flow. Such a quasi-steady dust flow is commonly realized when some mechanism like radial drift or fragmentation limits dust growth (see, e.g., Birnstiel et al. 2012; Lambrechts & Johansen 2014). Substituting
, which indicates that the radial dust flow in this region can be approximated by a steady flow. Such a quasi-steady dust flow is commonly realized when some mechanism like radial drift or fragmentation limits dust growth (see, e.g., Birnstiel et al. 2012; Lambrechts & Johansen 2014). Substituting  (
( ) into Equation (24), we obtain the relation between
) into Equation (24), we obtain the relation between  and
and  ,
,

Because  , we have
, we have  for constant
for constant  .
.
Using Equation (25) with the assumption that either radial drift or fragmentation limits dust growth, one can analytically estimate the radial distribution of  and a* in the non-sintering and sintering zones. When radial drift limits dust growth, the maximum aggregate size is determined by the condition (Okuzumi et al. 2012)
and a* in the non-sintering and sintering zones. When radial drift limits dust growth, the maximum aggregate size is determined by the condition (Okuzumi et al. 2012)

where  is the collision timescale given by Equation (12) and
is the collision timescale given by Equation (12) and

is the timescale of radial drift. Substituting  (
( ) and
) and  into Equation (13), the collision timescale can be evaluated as
into Equation (13), the collision timescale can be evaluated as

Furthermore, the collision velocity can be approximated as the root square sum of the turbulence-driven velocity  and differential radial drift velocity
and differential radial drift velocity  ,
,

where we have used the approximate expressions for  and
and  given in Section 4.3. Substituting Equations (25) and (27)–(29) into Equation (26), we obtain the equation for the maximum Stokes number in the drift-limited growth,
given in Section 4.3. Substituting Equations (25) and (27)–(29) into Equation (26), we obtain the equation for the maximum Stokes number in the drift-limited growth,

where we labeled  by the subscript "drift" to emphasize drift-limited growth. In Figure 9(c), we compare
by the subscript "drift" to emphasize drift-limited growth. In Figure 9(c), we compare  to
to  with the Stokes number directly obtained from run Sa0 at
with the Stokes number directly obtained from run Sa0 at  . We find that
. We find that  reproduces
reproduces  in the non-sintering zones, implying that radial drift limits the growth of unsintered aggregates. We are also able to estimate a* and
in the non-sintering zones, implying that radial drift limits the growth of unsintered aggregates. We are also able to estimate a* and  in the non-sintering zones by substituting
in the non-sintering zones by substituting  into
into  and Equation (25), respectively. These are shown by the dashed lines in Figures 9(a) and (b).
and Equation (25), respectively. These are shown by the dashed lines in Figures 9(a) and (b).
Figure 9. Same as panels (a)–(c) of Figure 8, but compared with the analytic estimates assuming a steady inward dust flow ( ). The dashed curves show the drift-limited solution for unsintered aggregates (labeled by "NS"), while the dotted curves show the fragmentation-limited solution of sintered aggregates (labeled by "S").
). The dashed curves show the drift-limited solution for unsintered aggregates (labeled by "NS"), while the dotted curves show the fragmentation-limited solution of sintered aggregates (labeled by "S").
Download figure:
Standard image High-resolution imageIf fragmentation limits dust growth, the maximum Stokes number is simply determined by the balance

We will denote the solution to this equation by  . If we approximate
. If we approximate  by Equation (29), Equation (31) can be rewritten as a quadratic equation for
by Equation (29), Equation (31) can be rewritten as a quadratic equation for  , and its positive root gives
, and its positive root gives

The dotted–dashed and dotted lines in Figure 9(c) show  for
for  and
and  (denoted by
(denoted by  and
and  ), respectively. We can see that
), respectively. We can see that  reproduces
reproduces  in the sintering zones, which confirms that fragmentation limits the growth of sintered aggregates. One can estimate the values of a* and
in the sintering zones, which confirms that fragmentation limits the growth of sintered aggregates. One can estimate the values of a* and  in the sintering zones by substituting
in the sintering zones by substituting  into
into  and Equation (25). These estimates are in excellent agreement with the simulation results, as shown by the dotted lines of Figures 9(a) and (b).
and Equation (25). These estimates are in excellent agreement with the simulation results, as shown by the dotted lines of Figures 9(a) and (b).
5.3. Lifetime of the Ring Patterns
It is worth mentioning at this point that the radial pattern of dust shown in Figure 8 fades out as the disk becomes depleted of dust. As the dust-to-gas mass ratio  decreases, the collision timescale
decreases, the collision timescale  of the aggregates increases, and consequently the maximum aggregate size set by radial drift (Equation (26)) decreases. The radial pattern disappears when the radial drift barrier dominates the fragmentation barrier at all r because sintering has no effect on radial drift. This is illustrated in Figure 10, where we plot the radial distribution of a* and
of the aggregates increases, and consequently the maximum aggregate size set by radial drift (Equation (26)) decreases. The radial pattern disappears when the radial drift barrier dominates the fragmentation barrier at all r because sintering has no effect on radial drift. This is illustrated in Figure 10, where we plot the radial distribution of a* and  for model Sa0 at different values of t. We find that the radial pattern present at
for model Sa0 at different values of t. We find that the radial pattern present at  has disappeared by
has disappeared by  . In this particular example,
. In this particular example,  falls below
falls below  at all r when
at all r when  . In models La0 and LLa0, which assume weaker turbulence, dust evolution is slower than in model Sa0 owing to the lower turbulence-driven collision velocity (see
. In models La0 and LLa0, which assume weaker turbulence, dust evolution is slower than in model Sa0 owing to the lower turbulence-driven collision velocity (see  in Table 3). However, even in these cases, the sintering-induced ring patterns are found to decay in 2 Myr. We note that the lifetime of the pattern would be longer for radially more extended (
in Table 3). However, even in these cases, the sintering-induced ring patterns are found to decay in 2 Myr. We note that the lifetime of the pattern would be longer for radially more extended ( ) disks, because the lifetime of dust flux in a disk generally scales with the orbital period at the disk's outer edge (Sato et al. 2015).
) disks, because the lifetime of dust flux in a disk generally scales with the orbital period at the disk's outer edge (Sato et al. 2015).
Figure 10. Radial distribution of the representative aggregate radius a (upper panel) and dust surface density  (lower panel) at
(lower panel) at  (dotted lines),
(dotted lines),  (solid lines), and
(solid lines), and  (dashed line) from simulation run Sa0.
(dashed line) from simulation run Sa0.
Download figure:
Standard image High-resolution image5.4. Optical Depths and Brightness Temperatures
We move on to the observational appearance of the sintering-induced dust rings at millimeter wavelengths. The upper left panel of Figure 11 shows the radial distribution of the line of sight optical depths  (Equation (22)) from the snapshot of run Sa0 at
(Equation (22)) from the snapshot of run Sa0 at  . We here present the optical depths at three wavelengths
. We here present the optical depths at three wavelengths  0.87, 1.3, and 2.9 mm, which correspond to ALMA Bands 7, 6, and 3, respectively.
0.87, 1.3, and 2.9 mm, which correspond to ALMA Bands 7, 6, and 3, respectively.
Figure 11. Radial distribution of the line of sight optical depths  (upper left panel), brightness temperatures
(upper left panel), brightness temperatures  (upper right panel), opacity slope
(upper right panel), opacity slope  (lower left panel), and spectral slope
(lower left panel), and spectral slope  (lower right panel) at
(lower right panel) at  from run Sa0. The blue, green, and red curves in the upper panels correspond to wavelengths
from run Sa0. The blue, green, and red curves in the upper panels correspond to wavelengths  0.87, 1.3, and 2.9 mm (ALMA Bands 7, 6, and 3), respectively. The dashed line in the upper right panel shows the gas temperature profile T in our disk model (Equation (1)). The shaded areas mark the sintering zones.
0.87, 1.3, and 2.9 mm (ALMA Bands 7, 6, and 3), respectively. The dashed line in the upper right panel shows the gas temperature profile T in our disk model (Equation (1)). The shaded areas mark the sintering zones.
Download figure:
Standard image High-resolution imageOverall, the optical depths in the sintering zones are higher than in the non-sintering zones. This mainly reflects the higher dust surface density in the sintering zones (see Figure 8(b)). The radial variation of  represents only a minor contribution to the radial variation of
represents only a minor contribution to the radial variation of  , in particular in outer regions where the representative aggregates are smaller than
, in particular in outer regions where the representative aggregates are smaller than  in radius. At
in radius. At  0.87 and 1.3 mm, the three inner sintering zones (of
0.87 and 1.3 mm, the three inner sintering zones (of  ,
,  –
– –
– , and
, and  ) are optically thick, while the two outer sintering zones (of
) are optically thick, while the two outer sintering zones (of  and
and  ) are optically thin or marginally thick. The
) are optically thin or marginally thick. The  sintering zone is much darker than the other sintering zones because the disk surface density drops at
sintering zone is much darker than the other sintering zones because the disk surface density drops at  . The non-sintering zones are optically thin or marginally thick at all three wavelengths. The opacity index at
. The non-sintering zones are optically thin or marginally thick at all three wavelengths. The opacity index at  0.87–1.3 mm,
0.87–1.3 mm, 
 is shown in the lower left panel of Figure 11. We see that
is shown in the lower left panel of Figure 11. We see that  at
at  and approaches the interstellar value ∼1.7 beyond 80 au.
and approaches the interstellar value ∼1.7 beyond 80 au.
The upper right panel of Figure 11 shows the distribution of the brightness temperatures  for the same snapshot. For comparison, we also plot the gas temperature T of our disk model given by Equation (1). We find that the three innermost sintering zones are optically thick (
for the same snapshot. For comparison, we also plot the gas temperature T of our disk model given by Equation (1). We find that the three innermost sintering zones are optically thick ( ) at
) at  0.87 and 1.3 mm.
0.87 and 1.3 mm.
An interesting observational signature of the sintering-induced rings appears in the radial variation of the spectral slope. In the lower right panel of Figure 11, we plot the spectral index at 0.87–1.3 mm, 
 , as a function of r. In the three innermost sintering zones, we have
, as a function of r. In the three innermost sintering zones, we have  because these zones are optically thick at these wavelengths. If these regions were optically thin, we would have
because these zones are optically thick at these wavelengths. If these regions were optically thin, we would have  because
because  (see the lower left panel of Figure 11). In the non-sintering zones lying at ∼6–11 au and ∼33–80 au, we obtain
(see the lower left panel of Figure 11). In the non-sintering zones lying at ∼6–11 au and ∼33–80 au, we obtain  –2.5, which is between the values in the optically thick and thin limits. This reflects the fact that the non-sintering zones are marginally thick at 0.87–1.3 mm.
–2.5, which is between the values in the optically thick and thin limits. This reflects the fact that the non-sintering zones are marginally thick at 0.87–1.3 mm.
5.5. Comparison with the ALMA Observation
Now we make more detailed comparisons between the simulation results and the ALMA observation of the HL Tau disk. We smooth the radial profiles of the intensities Iν from run Sa0 ( ) at the ALMA resolutions as described in Section 4.6. In the center panels of Figure 12, the solid lines show the radial profiles of the brightness temperatures
) at the ALMA resolutions as described in Section 4.6. In the center panels of Figure 12, the solid lines show the radial profiles of the brightness temperatures  and spectral slope
and spectral slope  obtained from the smoothed Iν. For comparison,
obtained from the smoothed Iν. For comparison,  and
and  from the raw Iν are shown by the dotted lines. The left panels show the profiles from the ALMA observations (same as Figure 1). We also show in the right panels the results from the non-sintering run Sa0-NoSint to clarify the features of the sintering-indued structures.
from the raw Iν are shown by the dotted lines. The left panels show the profiles from the ALMA observations (same as Figure 1). We also show in the right panels the results from the non-sintering run Sa0-NoSint to clarify the features of the sintering-indued structures.
Figure 12. Comparison between the ALMA observation and our fiducial model calculation Sa0. The left panels show the radial profiles of  at Bands 3, 6, and 7 and
at Bands 3, 6, and 7 and  of the HL Tau disk obtained from the ALMA observation (same as Figure 1). The center and right panels are from simulation runs Sa0 and Sa0-NoSint. The simulated profiles are obtained by smoothing the raw simulation data (dotted curves) at the ALMA resolutions (see text for details). The dashed lines show
of the HL Tau disk obtained from the ALMA observation (same as Figure 1). The center and right panels are from simulation runs Sa0 and Sa0-NoSint. The simulated profiles are obtained by smoothing the raw simulation data (dotted curves) at the ALMA resolutions (see text for details). The dashed lines show  , where T is the gas temperature given by Equation (1).
, where T is the gas temperature given by Equation (1).
Download figure:
Standard image High-resolution imageAfter smoothing, the innermost emission dip lying at 6–11 au has been partially smeared at 0.87 mm (Band 7) and 1.3 mm (Band 6). The emission dip in the smoothed images has a lower spectral slope than that in the raw images directly obtained from the simulation. This is a consequence of the frequency-dependent angular resolution: Because Band 6 has a coarser resolution than Band 7, the emission dip seen at Band 6 is more significantly buried than that seen at Band 7, resulting in a decrease in the spectral slope after smoothing. At 2.9 mm (Band 3), the radial structure of  at
at  has been significantly smoothed out.
has been significantly smoothed out.
We find that our simulation reproduces many observational features of the HL Tau disk. First, the simulation predicts a central emission peak that closely resembles the observed one. This central emission peak is associated with the  sintering zone as shown in Figure 11. The radial extent of the simulated central peak is
sintering zone as shown in Figure 11. The radial extent of the simulated central peak is  , which is comparable to
, which is comparable to  of the observed peak. The simulation perfectly reproduces the emission features of the central region: the magnitudes and radial slopes of
of the observed peak. The simulation perfectly reproduces the emission features of the central region: the magnitudes and radial slopes of  at all three ALMA Bands, and the millimeter spectral slope of
at all three ALMA Bands, and the millimeter spectral slope of  . In our simulation, the spectral slope simply reflects the high optical thickness of the central region, and has nothing to do with the optical properties of the aggregates in the region. Sintering plays an essential role in the buildup of the optically thick region; without sintering, the disk would be entirely optically thin at these bands, as shown by run Sa0-NoSint (see the right panels of Figure 12). The fact that the central emission peak has a lower intensity at Band 3 than at Bands 6 and 7 is explained as a consequence of the lower spatial resolution (
. In our simulation, the spectral slope simply reflects the high optical thickness of the central region, and has nothing to do with the optical properties of the aggregates in the region. Sintering plays an essential role in the buildup of the optically thick region; without sintering, the disk would be entirely optically thin at these bands, as shown by run Sa0-NoSint (see the right panels of Figure 12). The fact that the central emission peak has a lower intensity at Band 3 than at Bands 6 and 7 is explained as a consequence of the lower spatial resolution ( ) at Band 3 (i.e., this compact emission is underresolved at this band).
) at Band 3 (i.e., this compact emission is underresolved at this band).
The simulation also predicts two bright rings in the region of ∼10–30 au that might be identified with the two innermost bright rings of HL Tau observed at ∼20 and 40 au. In our simulation, the two emission rings are associated with the sintering zones of  –
– –
– (11–23 au) and
(11–23 au) and  (24–33 au). These rings are optically thick at Bands 6 and 7 (and therefore
(24–33 au). These rings are optically thick at Bands 6 and 7 (and therefore  ) and are optically thin at Band 3. These features are consistent with those of the two innermost bright rings of HL Tau. However, the separation of the predicted rings is much smaller than in the observed rings, as we discuss below.
) and are optically thin at Band 3. These features are consistent with those of the two innermost bright rings of HL Tau. However, the separation of the predicted rings is much smaller than in the observed rings, as we discuss below.
Farther out in the disk, the simulation predicts an optically thin emission peak at 80 au associated with  sintering. Its location coincides with the 80 au bright ring in the ALMA image of HL Tau, and its brightness temperatures agree with those of the observed ring at all three wavelengths to within a factor of two. The simulation also predicts a less pronounced peak at 120 au associated with
sintering. Its location coincides with the 80 au bright ring in the ALMA image of HL Tau, and its brightness temperatures agree with those of the observed ring at all three wavelengths to within a factor of two. The simulation also predicts a less pronounced peak at 120 au associated with  sintering. As mentioned in Section 5.4, this 120 au peak is much less pronounced than other inner peaks because this location is close to the outer edge of our modeled gas disk. Interestingly, the observed HL Tau disk also has a minor emission peak exterior to the 80 au ring (
sintering. As mentioned in Section 5.4, this 120 au peak is much less pronounced than other inner peaks because this location is close to the outer edge of our modeled gas disk. Interestingly, the observed HL Tau disk also has a minor emission peak exterior to the 80 au ring ( see ALMA Partnership et al. 2015).
see ALMA Partnership et al. 2015).
The innermost dark ring seen at 6–11 au in the simulated image is optically marginally thick and has  , which is consistent with the observed innermost dark ring at
, which is consistent with the observed innermost dark ring at  . Our simulation also explains why this innermost emission dip is much shallower at Band 3 than at Bands 6 and 7: as mentioned, this is simply because the spatial resolution at Band 3 is no high enough to distinguish the dark ring from the central emission peak.
. Our simulation also explains why this innermost emission dip is much shallower at Band 3 than at Bands 6 and 7: as mentioned, this is simply because the spatial resolution at Band 3 is no high enough to distinguish the dark ring from the central emission peak.
However, there are some discrepancies between the prediction from the fiducial model and the observation of the HL Tau disk. For example, the second innermost ring predicted by the model, which is associated with the  sintering zone, is about 10 au interior to that observed by ALMA. For this reason, the dark ring just inside the
sintering zone, is about 10 au interior to that observed by ALMA. For this reason, the dark ring just inside the  sintering zone is much narrower than the second innermost dark ring of HL Tau extending from 30 to 40 au. In addition, as we explain in detail in Section 6.3, the fiducial model predicts that dust particles are vertically well mixed in the gas disk, which seems to be inconsistent with the observations of HL Tau, suggesting that large dust particles settle to the disk midplane (Kwon et al. 2011; Pinte et al. 2016). In the following section, we examine if these discrepancies can be removed or alleviated by tuning the parameters in our model.
sintering zone is much narrower than the second innermost dark ring of HL Tau extending from 30 to 40 au. In addition, as we explain in detail in Section 6.3, the fiducial model predicts that dust particles are vertically well mixed in the gas disk, which seems to be inconsistent with the observations of HL Tau, suggesting that large dust particles settle to the disk midplane (Kwon et al. 2011; Pinte et al. 2016). In the following section, we examine if these discrepancies can be removed or alleviated by tuning the parameters in our model.
6. PARAMETER STUDY
The previous section mainly focused on our fiducial simulation (run Sa0). We here study how the simulation results depend on the model parameters.
6.1. Gas Surface Density Slope
Because the gas density distribution of the HL Tau disk is unknown, it is important to quantify how strongly our results depend on the assumption about the gas density profile. We present the results of two simulation runs—Sa0-Lgam and Sa0-Hgam—in which we change γ in Equation (2) to 0.5 and 1.5, respectively. The other parameters are unchanged form the fiducial run.
Figure 13 compares the radial profiles of the brightness temperature and spectral slope at 0.87 and 2.9 mm from these runs with those from run Sa0. The three snapshots are taken at different times but still provide similar flux densities (see Table 3) because  is defined as such. We find that the variation of γ within the range 0.5–1.5 little affects the emission properties of the disk, with the variation of
is defined as such. We find that the variation of γ within the range 0.5–1.5 little affects the emission properties of the disk, with the variation of  within a factor of 2 and the variation of
within a factor of 2 and the variation of  as small as
as small as  at all r. This is mainly because the steady-state radial distribution of the dust surface density
at all r. This is mainly because the steady-state radial distribution of the dust surface density  is insensitive to γ. If we measure the aggregate size by St, the steady-state distribution of
is insensitive to γ. If we measure the aggregate size by St, the steady-state distribution of  is determined from Equation (25) with either
is determined from Equation (25) with either  (Equation (30)) or
(Equation (30)) or  (Equation (32)). The γ dependence of the radial dust flux
(Equation (32)). The γ dependence of the radial dust flux  is weak as long as we fix
is weak as long as we fix  and
and  .
.  depends on γ only through
depends on γ only through  (for
(for  and
and  ), and its variation is small as long as we vary γ within the range 0.5–1.5. For
), and its variation is small as long as we vary γ within the range 0.5–1.5. For  , the dependence is less obvious from Equation (30), but it turns out that the weak γ dependences of
, the dependence is less obvious from Equation (30), but it turns out that the weak γ dependences of  and
and  partly cancel out in this equation.
partly cancel out in this equation.
Figure 13. Comparison between runs Sa0 (solid curves), Sa0-Lgam (dotted curves), and Sa0-Hgam (dotted–dashed curves). The upper panel shows the brightness temperatures  as a function of orbital distance r at wavelengths 0.87 mm (blue curves) and 2.9 mm (red curves) at time
as a function of orbital distance r at wavelengths 0.87 mm (blue curves) and 2.9 mm (red curves) at time  . The gas temperature profile T (Equation (1)) is shown by the dashed line. The lower panel shows the opacity index at 0.87–1.3 mm.
. The gas temperature profile T (Equation (1)) is shown by the dashed line. The lower panel shows the opacity index at 0.87–1.3 mm.
Download figure:
Standard image High-resolution image6.2. Radial Variation of Turbulence
The radial distribution of turbulence strength  is another important uncertainty in our simulations. Our fiducial model assumes
is another important uncertainty in our simulations. Our fiducial model assumes  , which gives a turbulence-driven collision velocity nearly independent of r (
, which gives a turbulence-driven collision velocity nearly independent of r ( ). In fact, a radially constant collision velocity is required in our model to simultaneously reproduce dark rings at small r and bright rings at large r.7
To demonstrate this, we consider two models in which
). In fact, a radially constant collision velocity is required in our model to simultaneously reproduce dark rings at small r and bright rings at large r.7
To demonstrate this, we consider two models in which  is fixed to 0.03 and 0.1 at all r (models Sa0-Lalp and Sa0-Halp, respectively). These values correspond to the values of
is fixed to 0.03 and 0.1 at all r (models Sa0-Lalp and Sa0-Halp, respectively). These values correspond to the values of  in the fiducial Sa0 model at
in the fiducial Sa0 model at  and
and  , respectively.
, respectively.
Figure 14 compares the result of fiducial run Sa0 with those of runs Sa0-Lalp and Sa0-Halp. We find that model Sa0-Lalp fails to produce an emission peak at  , because turbulence is too weak to cause fragmentation of sintered aggregates at that location. By contrast, model Sa0-Halp produces only shallow dips at
, because turbulence is too weak to cause fragmentation of sintered aggregates at that location. By contrast, model Sa0-Halp produces only shallow dips at  . In this high-
. In this high- model the maximum aggregate size at
model the maximum aggregate size at  is limited by turbulent fragmentation, even in the non-sintering zones. The suppressed dust growth causes a slowdown of radial drift, which acts to fill the density dips in the non-sintering zones. Thus, a model assuming a high
is limited by turbulent fragmentation, even in the non-sintering zones. The suppressed dust growth causes a slowdown of radial drift, which acts to fill the density dips in the non-sintering zones. Thus, a model assuming a high  in the outer regions and a low
in the outer regions and a low  in the inner regions best reproduces the observation of HL Tau.
in the inner regions best reproduces the observation of HL Tau.
Figure 14. Comparison between runs Sa0 (solid curves), Sa0-Lalp (dotted curves), and Sa0-Halp (dotted–dashed curves). The upper panel shows the brightness temperatures  as a function of orbital distance r at wavelengths 0.87 mm (blue curves) and 2.9 mm (red curves) at time
as a function of orbital distance r at wavelengths 0.87 mm (blue curves) and 2.9 mm (red curves) at time  . The gas temperature profile T (Equation (1)) is shown by the dashed line. The lower panel shows the opacity index at 0.87–1.3 mm.
. The gas temperature profile T (Equation (1)) is shown by the dashed line. The lower panel shows the opacity index at 0.87–1.3 mm.
Download figure:
Standard image High-resolution imageTheoretically, a  that is lower at smaller r is expected for turbulence driven by the magnetorotational instability (MRI; Balbus & Hawley 1991). Because the origin of the MRI is the coupling between the gas disk and magnetic fields, MRI turbulence tends to be weaker at locations where the ionization degree is lower. In protoplanetary disks, a lower ionization degree corresponds to a higher gas density and hence to a smaller orbital radius, because ionizing cosmic-rays or X-rays are attenuated at large column densities and recombination is faster in denser gas (e.g., Sano et al. 2000; Bai 2011).
that is lower at smaller r is expected for turbulence driven by the magnetorotational instability (MRI; Balbus & Hawley 1991). Because the origin of the MRI is the coupling between the gas disk and magnetic fields, MRI turbulence tends to be weaker at locations where the ionization degree is lower. In protoplanetary disks, a lower ionization degree corresponds to a higher gas density and hence to a smaller orbital radius, because ionizing cosmic-rays or X-rays are attenuated at large column densities and recombination is faster in denser gas (e.g., Sano et al. 2000; Bai 2011).
6.3. Monomer Size and Dust Settling
As mentioned in Section 4.6, our calculations of dust thermal emission neglect the geometrical thickness of the dust subdisk. In reality, if a dust disk has an inclination of  and a finite vertical extent
and a finite vertical extent  , then any radial structure of the disk emission is smeared out over this length scale in the direction of the minor axis of the disk image. Pinte et al. (2016) point out that the scale height of large dust particles in the HL Tau disk must be as small as
, then any radial structure of the disk emission is smeared out over this length scale in the direction of the minor axis of the disk image. Pinte et al. (2016) point out that the scale height of large dust particles in the HL Tau disk must be as small as  at
at  in order to be consistent with the well separated morphology of the bright rings observed by ALMA. Such a small dust scale height strongly indicates that dust settling has occurred in the gas disk; without settling, the dust scale height would be
in order to be consistent with the well separated morphology of the bright rings observed by ALMA. Such a small dust scale height strongly indicates that dust settling has occurred in the gas disk; without settling, the dust scale height would be  at 100 au.
at 100 au.
However, in our fiducial model, the settling of representative aggregates is severely prevented by turbulent diffusion. According to Equation (14), significant settling of dust particles ( ) requires
) requires  . This condition is not satisfied in fiducial run Sa0, because the value of
. This condition is not satisfied in fiducial run Sa0, because the value of  of the representative aggregates observed in the simulation is comparable to the value of
of the representative aggregates observed in the simulation is comparable to the value of  assumed (see Figure 8(c)). In this run,
assumed (see Figure 8(c)). In this run,  is arranged to have a high value so that aggregates disrupt and pile up in the sintering zones. If turbulence were weak, sintered aggregates would not experience disruption as long as we maintain the assumption
is arranged to have a high value so that aggregates disrupt and pile up in the sintering zones. If turbulence were weak, sintered aggregates would not experience disruption as long as we maintain the assumption  .
.
One way to reconcile sintering-induced ring formation with dust settling in our model is to assume weaker turbulence and a lower fragmentation velocity. Within our dust model, a lower value of  corresponds to a larger monomer size a0 (see Equations (18) and (19)). However, aggregates made of larger monomers tend to be sintered less slowly, as demonstrated in Section 3.4. To examine if there is a range of a0 where the aggregates can experience settling and sintering simultaneously, we performed two simulations (La0 and LLa0). In run La0, we increase a0 to
corresponds to a larger monomer size a0 (see Equations (18) and (19)). However, aggregates made of larger monomers tend to be sintered less slowly, as demonstrated in Section 3.4. To examine if there is a range of a0 where the aggregates can experience settling and sintering simultaneously, we performed two simulations (La0 and LLa0). In run La0, we increase a0 to  while lowering
while lowering  to
to  . Run LLa0 is a more extreme case of
. Run LLa0 is a more extreme case of  and
and  . The other parameters are the same as in the fiducial run Sa0.
. The other parameters are the same as in the fiducial run Sa0.
Figure 15 shows the raw radial profiles of  and the 0.87–1.3 mm spectral index at
and the 0.87–1.3 mm spectral index at  obtained from runs La0 and LLa0. The profiles after smoothing at the ALMA resolutions are shown in Figure 16. Note that we neglect the geometric thickness of the dust disk when calculating
obtained from runs La0 and LLa0. The profiles after smoothing at the ALMA resolutions are shown in Figure 16. Note that we neglect the geometric thickness of the dust disk when calculating  . Indeed, the dust disks in models La0 and LLa0 are geometrically thin, unlike in model Sa0 because turbulent diffusion is inefficient in these two models. We plot in Figure 17 the dust scale height
. Indeed, the dust disks in models La0 and LLa0 are geometrically thin, unlike in model Sa0 because turbulent diffusion is inefficient in these two models. We plot in Figure 17 the dust scale height  from Equation (14) as a function of r for the three models. At
from Equation (14) as a function of r for the three models. At  , we find
, we find  for model La0 and
for model La0 and  for model LLa0. Models Sa0, La0, and LLa0 give similar results for the radial distribution of
for model LLa0. Models Sa0, La0, and LLa0 give similar results for the radial distribution of  , particularly in inner disk regions. However, model LLa0 fails to produce an emission peak at 80 au because the
, particularly in inner disk regions. However, model LLa0 fails to produce an emission peak at 80 au because the  sintering zone completely disappears for
sintering zone completely disappears for  .
.
Figure 15. Same as the right panels of Figure 11, but for models La0 (left panels) and LLa0 (right panels).
Download figure:
Standard image High-resolution imageFigure 16. Same as Figure 12, but for models La0-tuned (center panels) and LLa0-tuned (right panels).
Download figure:
Standard image High-resolution imageFigure 17. Dust scale height Hd vs. orbital radius r at time  for runs Sa0 (black curve) and La0 (dashed curve). The dashed line shows the gas scale height
for runs Sa0 (black curve) and La0 (dashed curve). The dashed line shows the gas scale height  .
.
Download figure:
Standard image High-resolution imageIn summary, we find that dust settling gives a strong constraint on the turbulence strength and monomer grain size in the HL Tau disk. Dust settling and pile up occur simultaneously only if  and
and  . If
. If  , sintering would be too slow to provide an appreciable emission peak at
, sintering would be too slow to provide an appreciable emission peak at  . If
. If  , sintered aggregates would be disrupted only when
, sintered aggregates would be disrupted only when  , but such a strong turbulence would inhibit dust settling.
, but such a strong turbulence would inhibit dust settling.
Interestingly, the above results suggest that the grains constituting the aggregates in the HL Tau disk are considerably larger than the interstellar grains ( in radius; e.g., Mathis et al. 1977). They are also larger than the grains constituting interplanetary dust particles of presumably cometary origin (typically 0.1–0.5 μm in diameter; e.g., Rietmeijer 1993). However, such a large grain size is not excluded by previous observations of HL Tau. The near-infrared scattered light images of the envelope of HL Tau are best reproduced by models that assume the maximum particle size of more or less
in radius; e.g., Mathis et al. 1977). They are also larger than the grains constituting interplanetary dust particles of presumably cometary origin (typically 0.1–0.5 μm in diameter; e.g., Rietmeijer 1993). However, such a large grain size is not excluded by previous observations of HL Tau. The near-infrared scattered light images of the envelope of HL Tau are best reproduced by models that assume the maximum particle size of more or less  (Lucas et al. 2004; Murakawa et al. 2008). Because the scattered light probes the envelope's surface layer where coagulation is inefficient, the observed micron-sized particles might be monomers rather than aggregates.
(Lucas et al. 2004; Murakawa et al. 2008). Because the scattered light probes the envelope's surface layer where coagulation is inefficient, the observed micron-sized particles might be monomers rather than aggregates.
6.4. Sublimation Energies
As mentioned in Section 5.5, the fiducial model does not fully explain the exact locations and widths of all major HL Tau rings. For example, the innermost dark ring predicted by model Sa0 lies somewhat closer to the central star than the observed one. If we define the position of the innermost dark ring as the location where  at Band 6 is maximized, the radius of the predicted innermost dark ring (8 au) is
at Band 6 is maximized, the radius of the predicted innermost dark ring (8 au) is  % smaller than that of the observed one (13 au). Furthermore, the second innermost dark ring in model Sa0 is much narrower than that observed because the
% smaller than that of the observed one (13 au). Furthermore, the second innermost dark ring in model Sa0 is much narrower than that observed because the  snow line lies very close to the
snow line lies very close to the  sintering line. Of course, a different temperature profile would provide a different configuration of the sintering zones. However, as long as T(r) is assumed to obey a single power law, it is generally impossible to move some of the sintering zones while leaving the positions of the others unchanged. For example, a temperature profile that is slightly higher than Equation (1) would shift the
sintering line. Of course, a different temperature profile would provide a different configuration of the sintering zones. However, as long as T(r) is assumed to obey a single power law, it is generally impossible to move some of the sintering zones while leaving the positions of the others unchanged. For example, a temperature profile that is slightly higher than Equation (1) would shift the  sintering zone to 40 au, but would also shift the
sintering zone to 40 au, but would also shift the  sintering zone to 100 au. Moreover, a different T(r) would make our prediction for the brightness temperatures in the optically thick regions less good.
sintering zone to 100 au. Moreover, a different T(r) would make our prediction for the brightness temperatures in the optically thick regions less good.
However, the locations of the sintering zones depend not only on the gas temperature profile but also on the sublimation energies Lj in  . As mentioned in Section 3.2, there is typically a 10% uncertainty in the published data of Lj. In general, a 10% uncertainty in the sublimation energy causes a
. As mentioned in Section 3.2, there is typically a 10% uncertainty in the published data of Lj. In general, a 10% uncertainty in the sublimation energy causes a  uncertainty in the sublimation temperature
uncertainty in the sublimation temperature  because
because  is a function of the ratio
is a function of the ratio  . Assuming the temperature profile given by Equation (1), we have
. Assuming the temperature profile given by Equation (1), we have  and hence
and hence  , where
, where  ,
,  , and
, and  denote the uncertainties of Lj,
denote the uncertainties of Lj,  , and
, and  , respectively. Consequently, a 10% uncertainty in Lj leads to a
, respectively. Consequently, a 10% uncertainty in Lj leads to a  uncertainty in the snow line location. Such an uncertainty can be significant because the separation of the observed rings is only a fraction of their radii.
uncertainty in the snow line location. Such an uncertainty can be significant because the separation of the observed rings is only a fraction of their radii.
To demonstrate the potential importance of uncertainties in the sublimation energies, we performed two simulations (Sa0-tuned and La0-tuned). The parameters adopted in these simulations are the same as those in Sa0 and La0, respectively, except that the sublimation energies of  ,
,  , and
, and  are lowered by 10% from our baseline values (see column 5 of Table 2). According to the estimate shown previously, such modifications shift the sintering zones of these volatiles outward by
are lowered by 10% from our baseline values (see column 5 of Table 2). According to the estimate shown previously, such modifications shift the sintering zones of these volatiles outward by  . The resulting radial profiles of
. The resulting radial profiles of  and
and  before smoothing are shown in Figure 18. In model Sa0-tuned, the three innermost sintering zones are located at 4–8 au (
before smoothing are shown in Figure 18. In model Sa0-tuned, the three innermost sintering zones are located at 4–8 au ( ), 13–23 au (
), 13–23 au ( –
– –
– ), and 29–40 au (
), and 29–40 au ( ) instead of 3–6 au, 11–23 au, and 24–33 au as in model Sa0. Figure 19 shows the radial emission profiles after smoothing, which we compare with the ALMA observation. For the sake of comparison, we define the radii of the bright and dark rings by the orbital radii at which
) instead of 3–6 au, 11–23 au, and 24–33 au as in model Sa0. Figure 19 shows the radial emission profiles after smoothing, which we compare with the ALMA observation. For the sake of comparison, we define the radii of the bright and dark rings by the orbital radii at which  at Band 6 is locally maximized and minimized, respectively. Then, the radii of four innermost bright/dark rings are found to be 13, 23, 32, and 38 au for the observation, 9, 16, 24, and 30 au for model Sa0-NoSint, and 9, 15, 24, and 29 au for model La0-NoSint. Thus, model Sa0-NoSint reproduces the ring radii in the observed image to an accuracy of
at Band 6 is locally maximized and minimized, respectively. Then, the radii of four innermost bright/dark rings are found to be 13, 23, 32, and 38 au for the observation, 9, 16, 24, and 30 au for model Sa0-NoSint, and 9, 15, 24, and 29 au for model La0-NoSint. Thus, model Sa0-NoSint reproduces the ring radii in the observed image to an accuracy of  , which is about 10% better than model Sa0. Model La0-NoSint is slightly less accurate, with a maximum error of 35%, but it is still 10% better than the original model La0. Furthermore, the second innermost dark ring in these models is much wider than that in model Sa0. As a consequence, the radial distribution of
, which is about 10% better than model Sa0. Model La0-NoSint is slightly less accurate, with a maximum error of 35%, but it is still 10% better than the original model La0. Furthermore, the second innermost dark ring in these models is much wider than that in model Sa0. As a consequence, the radial distribution of  now has a clear peak structure at the position of this ring, and the peak value
now has a clear peak structure at the position of this ring, and the peak value  agrees with the observed value
agrees with the observed value  to within a relative error of 10%.
to within a relative error of 10%.
Figure 18. Same as the right panels of Figure 11, but for runs Sa0-tuned (left panels) and La0-tuned (right panels).
Download figure:
Standard image High-resolution imageFigure 19. Same as Figure 12, but for models Sa0-tuned (center panels) and La0-tuned (right panels), which adopt optimized sublimation energies for  ,
,  , and
, and  .
.
Download figure:
Standard image High-resolution imageThus, assuming sublimation energies of  ,
,  , and
, and  that are only 10% lower than the baseline values significantly improves our predictions for the radial configuration of the dust rings. Interestingly, for
that are only 10% lower than the baseline values significantly improves our predictions for the radial configuration of the dust rings. Interestingly, for  and
and  , the tuned values of the sublimation energies are more consistent with the results of recent experiments by Martín-Doménech et al. (2014; 5165 K for
, the tuned values of the sublimation energies are more consistent with the results of recent experiments by Martín-Doménech et al. (2014; 5165 K for  and 2965 K for
and 2965 K for  ) than our fiducial values. However, not all new data for sublimation energies improve our predictions. Martín-Doménech et al. (2014) also measured the sublimation energies of
) than our fiducial values. However, not all new data for sublimation energies improve our predictions. Martín-Doménech et al. (2014) also measured the sublimation energies of  and
and  , and the measured values (2605 K for
, and the measured values (2605 K for  and 890 K for
and 890 K for  ) are also lower than ours by about 10%. A 10% change in the sublimation energy of
) are also lower than ours by about 10%. A 10% change in the sublimation energy of  has little effect on the resulting ring patterns, because the
has little effect on the resulting ring patterns, because the  sintering zone partially overlaps with the sintering zones of
sintering zone partially overlaps with the sintering zones of  and
and  . A 10% decrease in the sublimation energy of
. A 10% decrease in the sublimation energy of  shifts the
shifts the  sintering zone to 143–197 au, which makes the correspondence between the CO sintering zone and the faint 97 au ring of HL Tau (see Section 5.5) less good.
sintering zone to 143–197 au, which makes the correspondence between the CO sintering zone and the faint 97 au ring of HL Tau (see Section 5.5) less good.
7. DISCUSSION
7.1. Possible Effects of Bouncing
As mentioned in the introduction, sintered aggregates tend to bounce rather than stick when they collide at a velocity below the fragmentation threshold. For example, sintered aggregates made of 0.1 μm sized icy grains bounce at  (Sirono 1999; S. Sirono 2016, in preparation). This effect was neglected in this study by simply applying Equation (15) to both sintered and unsintered aggregates. In principle, such a simplification causes an overestimate of the maximum size of aggregates in the sintering zones. However, this effect is expected to be minor because sintered aggregates grow only moderately even without the bouncing effect. To see this, we go back to the radial profile of the radius a* of the representative aggregates from run Sa0 shown in Figure 8(a). Because the radial inward flow of the aggregates is nearly stationary (see Figure 8(d)), this figure shows how the size of individual representative aggregates evolve as they move inward. We find that a* is radially constant in the
(Sirono 1999; S. Sirono 2016, in preparation). This effect was neglected in this study by simply applying Equation (15) to both sintered and unsintered aggregates. In principle, such a simplification causes an overestimate of the maximum size of aggregates in the sintering zones. However, this effect is expected to be minor because sintered aggregates grow only moderately even without the bouncing effect. To see this, we go back to the radial profile of the radius a* of the representative aggregates from run Sa0 shown in Figure 8(a). Because the radial inward flow of the aggregates is nearly stationary (see Figure 8(d)), this figure shows how the size of individual representative aggregates evolve as they move inward. We find that a* is radially constant in the  and
and  sintering zones, meaning that the aggregates do not grow at all when they go through these zones. Appreciable growth of sintered aggregates occurs only in inner regions of the
sintering zones, meaning that the aggregates do not grow at all when they go through these zones. Appreciable growth of sintered aggregates occurs only in inner regions of the  and
and  –
– –
– sintering zones. However, even at these locations, the aggregate size increases only by a factor of less than two until they reach the inner edges of the sintering zones. Therefore, we can conclude that inclusion of bouncing collisions would little change the evolution of representative aggregates in the sintering zones.
sintering zones. However, even at these locations, the aggregate size increases only by a factor of less than two until they reach the inner edges of the sintering zones. Therefore, we can conclude that inclusion of bouncing collisions would little change the evolution of representative aggregates in the sintering zones.
7.2. Limitations of the Single Size Approach
Our single-size approach (Section 4.1) relies on the assumption that the mass budget of dust at each orbital radius is dominated by a single population of aggregates having mass  . This assumption might be inadequate at the boundaries of sintering and non-sintering zones, around which two populations of aggregates of different characteristic sizes (i.e., sintered and unsintered aggregates) can coexist. However, this effect would only be important in the close vicinity of the boundaries because the sintering timescale is a steep function of r and the aggregates in our simulations do not drift faster than they collide with each other.
. This assumption might be inadequate at the boundaries of sintering and non-sintering zones, around which two populations of aggregates of different characteristic sizes (i.e., sintered and unsintered aggregates) can coexist. However, this effect would only be important in the close vicinity of the boundaries because the sintering timescale is a steep function of r and the aggregates in our simulations do not drift faster than they collide with each other.
A probably more critical limitation of the single-size approach is that one has to assume the size distribution of fragments produced by the collisions of the mass-dominating aggregates. In this study we avoided detailed modeling of the fragmentation process by assuming a simple power-law fragment size distribution (Equation (20)) independent of the collision velocity of the largest aggregates. The assumed power-law distribution would reasonably approximate the true fragment size distribution when the collisions of the mass-dominating aggregates are highly disruptive. In fact, however, unsintered aggregates in our simulations do not experience catastrophic disruption because their collision velocity is always below the catastrophic disruption threshold  . For example, our fiducial run Sa0 shows that
. For example, our fiducial run Sa0 shows that  –0.4 in the non-sintering zones, which implies that fragments would carry away only a few tens of percent of the total mass of two colliding mass-dominating aggregates in these zones. Equation (20) might also overestimate the amount of fragments from sintered aggregates because they actually bounce off, rather than fragment at low collision velocities (see Section 7.1). The preliminary results of our aggregate collision simulations (S. Sirono 2015, in preparation) show that fragments from two colliding sintered aggregates carry away only a few percent of their total mass even when
–0.4 in the non-sintering zones, which implies that fragments would carry away only a few tens of percent of the total mass of two colliding mass-dominating aggregates in these zones. Equation (20) might also overestimate the amount of fragments from sintered aggregates because they actually bounce off, rather than fragment at low collision velocities (see Section 7.1). The preliminary results of our aggregate collision simulations (S. Sirono 2015, in preparation) show that fragments from two colliding sintered aggregates carry away only a few percent of their total mass even when  .
.
Therefore, it important to assess how the predictions from our models depend on the amount of fragments assumed. We consider a fragment size distribution that is similar to Equation (20), but assumes a reduced amount of fragments in the size range  ,
,

where the factor  encapsulates the reduction of fragment production, and C is again determined by the condition
encapsulates the reduction of fragment production, and C is again determined by the condition  . We consider two values—
. We consider two values—  and 0.03—based on the estimates for unsintered and sintered aggregates mentioned above.
and 0.03—based on the estimates for unsintered and sintered aggregates mentioned above.
We now recalculate the radial profiles of  and
and  for model Sa0-tuned using Equation (33) instead of Equation (20). The results are shown in the center and right panels of Figure 20. These, together with the result for
for model Sa0-tuned using Equation (33) instead of Equation (20). The results are shown in the center and right panels of Figure 20. These, together with the result for  (the center panels in Figure 19), show that both
(the center panels in Figure 19), show that both  and
and  in the two innermost emission dips decrease as
in the two innermost emission dips decrease as  is decreased. In these inner regions, the radius a* of the largest (mass-dominating) aggregates is significantly larger than millimeters, and therefore the fragments smaller than millimeters have a non-negligible contribution to the millimeter dust opacity. In this case, the opacity index
is decreased. In these inner regions, the radius a* of the largest (mass-dominating) aggregates is significantly larger than millimeters, and therefore the fragments smaller than millimeters have a non-negligible contribution to the millimeter dust opacity. In this case, the opacity index  decreases toward zero, which is the value in the geometric optics limit, as the amount of the fragments decreases (see, e.g., Draine 2006). This explains why a lower value of
decreases toward zero, which is the value in the geometric optics limit, as the amount of the fragments decreases (see, e.g., Draine 2006). This explains why a lower value of  leads to a lower value of the spectral slope in the optically thin inner dips where the relation
leads to a lower value of the spectral slope in the optically thin inner dips where the relation  applies. In the case of
applies. In the case of  , the spectral slope in the innermost emission dip falls below two, due to the effect of the frequency-dependent angular resolution already mentioned in Section 5.5. We find that the results for
, the spectral slope in the innermost emission dip falls below two, due to the effect of the frequency-dependent angular resolution already mentioned in Section 5.5. We find that the results for  and 0.03 better reproduce the observed depths of the two innermost emission dips than the result for
and 0.03 better reproduce the observed depths of the two innermost emission dips than the result for  . However, these low-
. However, these low- models yield poorer agreement with the observed value of
models yield poorer agreement with the observed value of  in these emission dips. Varying the value of
in these emission dips. Varying the value of  within the range 0.03–1 has no effect on the predictions for
within the range 0.03–1 has no effect on the predictions for  and
and  outside the two innermost emission dips. Taken together, we cannot judge at this point which value of
outside the two innermost emission dips. Taken together, we cannot judge at this point which value of  best reproduces the observed appearance of HL Tau. In any case, the effects of assuming the lower values of
best reproduces the observed appearance of HL Tau. In any case, the effects of assuming the lower values of  are not significant as long as
are not significant as long as  is higher than 0.3, which is the value we expect for unsintered aggregates in the dark rings.
is higher than 0.3, which is the value we expect for unsintered aggregates in the dark rings.
Figure 20. Same as Figure 12, but for model Sa0-tuned with the modified fragment size distribution given by Equation (33). The center and right panels are for fragment reduction factor  (center panels) and 0.03 (right panels).
(center panels) and 0.03 (right panels).
Download figure:
Standard image High-resolution image7.3. Evolution of the Monomer Size Distribution and Possible Planetesimal Formation Near the  Sintering Zone
Sintering Zone
We have assumed that vapor transport within an aggregate, which drives sintering, does not alter the size of monomer grains. In reality, this is not true because the growth of necks must be compensated by the shrinkage of the bodies of monomers. Furthermore, if the monomers within an aggregate are not uniform in size, a small number of large monomers may grow—the phenomenon known as Ostwald ripening (see, e.g., Lifshitz & Pitaevskii 1981)—while smaller ones may completely evaporate leaving silicate grains (Kuroiwa & Sirono 2011; Sirono 2011a).8
The evolution of the monomer size distribution is negligible in the sintering zones of minor volatiles like  and
and  (as noted in the introduction, sintering can still occur because the neck volume is much smaller than the monomer volume). However, this is not the case for water ice because it constitutes more than half of the monomer volume.
(as noted in the introduction, sintering can still occur because the neck volume is much smaller than the monomer volume). However, this is not the case for water ice because it constitutes more than half of the monomer volume.
As pointed out by Kuroiwa & Sirono (2011), the evolution of the monomer size distribution due to water vapor transport would result in a decrease in the sticking efficiency of the icy aggregates. Kuroiwa & Sirono (2011) showed that water vapor transport within an aggregate produces a small number of large ice-rich monomers and a large number of small bare silicate monomers. Aggregates made of the two populations of monomers would be fragile, like sintered aggregates made of equally ice-coated grains, because the total binding energy (∝number of contacts) of the former would be determined by weak silicate–silicate contacts. These aggregates would experience catastrophic disruption and pile up near the  snow line in a similar way to sintered aggregates.
snow line in a similar way to sintered aggregates.
In addition, the evaporation of small monomers could directly result in the fragmentation of icy aggregates. Sirono (2011a) demonstrated that an aggregate made of initially submicron-sized  monomers breaks up into large detached monomers of radii ∼1–10
monomers breaks up into large detached monomers of radii ∼1–10  (see also Kuroiwa & Sirono 2011). This spontaneous breakup would also produce a pileup of dust near the
(see also Kuroiwa & Sirono 2011). This spontaneous breakup would also produce a pileup of dust near the  snow line, but the surface density contrast provided by this effect could be much more significant than that by than sintering-induced fragmentation, because the micron-sized monomers are much more strongly coupled to the disk gas than aggregates. Sirono (2011a) notes that the dust surface density in the
snow line, but the surface density contrast provided by this effect could be much more significant than that by than sintering-induced fragmentation, because the micron-sized monomers are much more strongly coupled to the disk gas than aggregates. Sirono (2011a) notes that the dust surface density in the  sintering zone can become high enough to trigger the formation of icy planetesimals via the gravitational instability (Goldreich & Ward 1973; Sekiya 1998; Youdin & Shu 2002).
sintering zone can become high enough to trigger the formation of icy planetesimals via the gravitational instability (Goldreich & Ward 1973; Sekiya 1998; Youdin & Shu 2002).
Thus, the evolution of the monomer size distribution due to vapor transport would further promote the fragmentation and accumulation of aggregates in the  sintering zone. This may not affect the observational appearance of the HL Tau disk because the
sintering zone. This may not affect the observational appearance of the HL Tau disk because the  sintering zone is already optically thick, even without the monomer size evolution. However, this could have a significant effect on planet(esimal) formation near the
sintering zone is already optically thick, even without the monomer size evolution. However, this could have a significant effect on planet(esimal) formation near the  snow line.
snow line.
7.4. Possible Effects of Porosity Evolution
We neglected the evolution of the porosity of icy aggregates by assuming the fixed aggregate internal density of  . In reality, the porosity of aggregates (much smaller than planetesimals) can vary greatly through collisions (e.g., Ormel et al. 2007; Suyama et al. 2008; Okuzumi et al. 2009), compression by gas drag (Kataoka et al. 2013a, 2013b), and condensation and sintering of
. In reality, the porosity of aggregates (much smaller than planetesimals) can vary greatly through collisions (e.g., Ormel et al. 2007; Suyama et al. 2008; Okuzumi et al. 2009), compression by gas drag (Kataoka et al. 2013a, 2013b), and condensation and sintering of  ice (again, minor volatile ices occupy only a small fraction of grain volume and are therefore negligible here). In the absence of the compaction due to condensation and sintering, the internal density of icy aggregates in protoplanetary disks can decline to as low as 10−4–10−3 g cm−3 (Okuzumi et al. 2012; Kataoka et al. 2013b).
ice (again, minor volatile ices occupy only a small fraction of grain volume and are therefore negligible here). In the absence of the compaction due to condensation and sintering, the internal density of icy aggregates in protoplanetary disks can decline to as low as 10−4–10−3 g cm−3 (Okuzumi et al. 2012; Kataoka et al. 2013b).
The porosity evolution has two important effects on the evolution of icy aggregates. First, fluffy aggregates tend to grow to the size regime where the gas drag onto the aggregates is determined by Stokes' law. This particularly occurs in the inner regions of protoplanetary disks, where the mean free path of the disk gas molecules is short. In the Stokes drag regime, the growth limit given by Equation (30) no longer applies because that limit assumes Epstein's drag law. Okuzumi et al. (2012) found that fluffy aggregates that are subject to Stokes' drag law grow fast enough to overcome the radial drift barrier. In a massive protoplanetary disk as considered in this study, icy aggregates break through the drift barrier and form icy planetesimals at  (see the bottom right panel of Kataoka et al. 2013a). Second, the millimeter absorption opacity of large porous aggregates is similar to that of small compact aggregates because
(see the bottom right panel of Kataoka et al. 2013a). Second, the millimeter absorption opacity of large porous aggregates is similar to that of small compact aggregates because  can be approximated as a function of the product
can be approximated as a function of the product  (Kataoka et al. 2014).
(Kataoka et al. 2014).
In this study, these important effects have been neglected by fixing the aggregate porosity to a relatively low value. Rapid coagulation beyond the Epstein drag regime could strongly reduce the optical depth in the non-sintering zone lying at  , where the radial drift barrier determines the maximum size of the relatively compact aggregates that we assumed in this study. This effect should be studied in detail in future work.
, where the radial drift barrier determines the maximum size of the relatively compact aggregates that we assumed in this study. This effect should be studied in detail in future work.
On the other hand, the above two effects are less important at  , where even the highly fluffy aggregates would grow within the Epstein drag regime. To show this, we first note that neither
, where even the highly fluffy aggregates would grow within the Epstein drag regime. To show this, we first note that neither  (Equation (30)) nor
(Equation (30)) nor  (Equation (32)) depends on
(Equation (32)) depends on  (note again that Epstein's law is used in the derivation of Equation (30)). This means that porosity evolution has no effect on the maximum attainable Stokes number at each r, and therefore does not change the radial distribution of
(note again that Epstein's law is used in the derivation of Equation (30)). This means that porosity evolution has no effect on the maximum attainable Stokes number at each r, and therefore does not change the radial distribution of  because the radial advection velocity vr is a function of
because the radial advection velocity vr is a function of  (see Equation (10)). Porosity evolution does not change the dust absorption opacity
(see Equation (10)). Porosity evolution does not change the dust absorption opacity  either, because the product
either, because the product  is proportional to
is proportional to  in the Epstein regime (see Equation (9)). This is a natural consequence of the fact that both the stopping time in the Epstein regime and the absorption opacity are determined by the mass-to-area ratio
in the Epstein regime (see Equation (9)). This is a natural consequence of the fact that both the stopping time in the Epstein regime and the absorption opacity are determined by the mass-to-area ratio  of the aggregates. Taken together, the radial distribution of the absorption optical depth
of the aggregates. Taken together, the radial distribution of the absorption optical depth  is independent of the aggregate porosity, as long as the aggregates grow within the Epstein drag regime.
is independent of the aggregate porosity, as long as the aggregates grow within the Epstein drag regime.
Nevertheless, porosity evolution might have some important observational consequence in the outer disk region. The millimeter continuum emission from the HL Tau disk is known to be polarized in the direction roughly perpendicular to the disk major axis at a level of 0.9% in the average degree of polarization (Stephens et al. 2014). Yang et al. (2015) and Kataoka et al. (2015b) point out that self-scattering of thermal emission by dust rings (Kataoka et al. 2015a) can explain the polarization observation. However, this mechanism produces a degree of polarization of  only when the size of the dust particles falls within a particular range. For example, if the particles are compact and their size distribution obeys our Equation (20), the self-scattering scenario is consistent with the observation only when the maximum particle size
only when the size of the dust particles falls within a particular range. For example, if the particles are compact and their size distribution obeys our Equation (20), the self-scattering scenario is consistent with the observation only when the maximum particle size  (
( in this study) is
in this study) is  (Kataoka et al. 2015b; Yang et al. 2015), which is considerably smaller than the size of mass-dominating aggregates predicted in this study. In the compact particle model, a particle size larger than a millimeter is ruled out because the scattered emission would be too weakly polarized (see also Kataoka et al. 2015a). By contrast, large but fluffy aggregates are known to produce highly polarized scattered light like constituent monomers do (Min et al. 2016), and therefore might be able to explain the polarization observation of HL Tau.
(Kataoka et al. 2015b; Yang et al. 2015), which is considerably smaller than the size of mass-dominating aggregates predicted in this study. In the compact particle model, a particle size larger than a millimeter is ruled out because the scattered emission would be too weakly polarized (see also Kataoka et al. 2015a). By contrast, large but fluffy aggregates are known to produce highly polarized scattered light like constituent monomers do (Min et al. 2016), and therefore might be able to explain the polarization observation of HL Tau.
7.5. Possible Effects of Condensation Growth
We neglected the condensation growth of ice particles near the snow lines. In fact, a recent study by Ros & Johansen (2013) has shown that condensation growth can be effective at locations slightly outside the  snow line. This effect might change our predictions for dust evolution near
snow line. This effect might change our predictions for dust evolution near  snow line because condensation dominantly takes place on the smallest particles (i.e., monomers). If condensation dominates over sintering-induced fragmentation and bouncing, the regions slightly outside the snow lines would be seen as
snow line because condensation dominantly takes place on the smallest particles (i.e., monomers). If condensation dominates over sintering-induced fragmentation and bouncing, the regions slightly outside the snow lines would be seen as  rings at millimeter wavelengths, as noted by Zhang et al. (2015). However, it is unclear whether condensation growth becomes important for volatiles less abundant than
rings at millimeter wavelengths, as noted by Zhang et al. (2015). However, it is unclear whether condensation growth becomes important for volatiles less abundant than  , like
, like  and
and  . To address this open question, we will incorporate condensation growth into our global dust evolution simulations in future work.
. To address this open question, we will incorporate condensation growth into our global dust evolution simulations in future work.
7.6. Sintering-induced Ring Formation in Other Objects?
Perhaps the strongest prediction from our model, as well as from the model of Zhang et al. (2015), is that the multiple dust rings may not be peculiar to the HL Tau disk. In principle, sintering-induced ring formation operates as long as the disk is not too depleted of dust (or not too old), the monomers are sufficiently small to cause rapid sintering, and turbulence is strong enough to cause the disruption of sintered aggregates. If these conditions are satisfied, axisymmetric dust rings emerge slightly outside the snow lines of relatively major volatiles. An intriguing object in this context is TW Hya. For this system, the CO snow line was indirectly detected at an orbital distance of ∼30 au (Qi et al. 2013), and furthermore, near-infrared scattered light images of the disk suggest the presence of two axisymmetric dust gaps at ∼80 au (Debes et al. 2013) and ∼20 au (Akiyama et al. 2015; Rapson et al. 2015). A latest ALMA observation has shown that there is also a gap in millimeter dust emission in the vicinity of the 20 au scattered light gap (Nomura et al. 2015). The gaps at 80 au and 20 au could be associated with non-sintering zones exterior to and interior to the CO sintering zone, respectively. However, it is not obvious whether our ring formation mechanism directly applies to TW Hya because this object is known to be much older than HL Tau (at least 3 Myr; Vacca & Sandell 2011). This question should also be addressed in future work.
8. CONCLUSIONS
Motivated by the recent ALMA observations of the HL Tau disk, we explored the possibility that sintering of icy dust aggregates might lead to the formation of multiple dust rings in a protoplanetary disk. Sintering is a particle fusion process that occurs when the temperature is slightly below the melting point. Sintered aggregates are generally harder but less sticky than unsintered aggregates. Therefore, if dust aggregates in a protoplanetary disk consist of various materials, their growth can be suppressed at different orbits corresponding to the sublimation fronts of different materials. This possibility was originally pointed out by Sirono (1999, 2011b), and here we have for the first time studied its effects on the global evolution of dust in a protoplanetary disk.
Following Sirono (2011b), we regard aggregates as sintered if their sintering timescale is shorter than their collision timescale (Section 3.4). This criterion defines the "sintering zones" in which one of the volatile species included in the aggregates causes sintering. The temperature profile of the HL Tau disk has been modeled based on the millimeter intensity maps provided by the ALMA observations (ALMA Partnership et al. 2015), together with the assumption that the central emission peak and inner bright rings are optically thick at 1 mm (Section 2.1, Figure 1). Based on the aggregate collision simulations by Sirono & Ueno (2014), we assumed that sintered aggregates have a maximum sticking velocity that is 60% lower than that for unsintered aggregates (Equations (18) and (19); Figure 5(a)). For both sintered and unsintered aggregates, we regarded collisions at velocities higher than the threshold disruptive (Equation (15); Figure 5(b)).
Using the aggregate sintering model described above, we simulated the global evolution of dust in the HL Tau disk for various sets of model parameters. As a first step toward more comprehensive modeling, we focused on the evolution of the mass-dominating (largest) aggregates, and assumed a power-law size distribution for smaller aggregates when we convert the simulation data into radial profiles of millimeter dust emission. Key parameters in our model are the strength of turbulence ( ), the size of monomers that constitute the aggregates (a0), and the sublimation energies of the volatiles (Lj). The monomer size is relevant here because it controls the timescale of sintering (Equation (6)) and the fragmentation strength of dust aggregates (Equations (18) and (19)).
), the size of monomers that constitute the aggregates (a0), and the sublimation energies of the volatiles (Lj). The monomer size is relevant here because it controls the timescale of sintering (Equation (6)) and the fragmentation strength of dust aggregates (Equations (18) and (19)).
Our key findings are summarized as follows.
- 1.Because dust is gradually lost to the central star owing to radial drift, the total dust mass in the disk decreases with time (Section 5.1). For the total disk mass of
 and the initial dust-to-gas mass ratio of 0.01, our HL Tau disk models best reproduce the millimeter flux densities from the ALMA observations when the disk age in the models is chosen to be 0.1–0.5 Myr. This is consistent with the general belief that HL Tau is a young (≲1 Myr) protoplanetary disk.
and the initial dust-to-gas mass ratio of 0.01, our HL Tau disk models best reproduce the millimeter flux densities from the ALMA observations when the disk age in the models is chosen to be 0.1–0.5 Myr. This is consistent with the general belief that HL Tau is a young (≲1 Myr) protoplanetary disk. - 2.Dust aggregates pile up in the sintering zones due to the combined effect of radial drift and sintering-induced fragmentation (Section 5.2). In general, aggregates grow locally until either rapid radial drift or fragmentation starts to halt their growth. After that, the aggregates start to drift toward the central star at a velocity proportional to the maximum size. Sintered aggregates have a lower maximum size and hence a lower inward drift velocity than unsintered aggregates simply because the former tend to disrupt more easily upon collision. For this reason, aggregates tend to pile up in the sintering zones.
- 3.At millimeter wavelengths, the sintering zones are seen as bright rings because the dust surface density in the sintering zones is higher than in the non-sintering zones (Section 5.4). In particular, at the wavelengths of 0.87 mm and 1.3 mm, the three innermost sintering zones (which correspond to
 ,
,  –
– –
– , and
, and  , respectively) are optically thick, producing a millimeter spectral index of
, respectively) are optically thick, producing a millimeter spectral index of  . The predicted spectral index and brightness temperatures are consistent with those of the central emission peak and the two innermost bright rings of the HL Tau disk (Section 5.5). Our model also predicts an optically thin emission peak at
. The predicted spectral index and brightness temperatures are consistent with those of the central emission peak and the two innermost bright rings of the HL Tau disk (Section 5.5). Our model also predicts an optically thin emission peak at  , which is associated with the
, which is associated with the  sintering zone, and two optically thin dark rings of a spectral slope of 2.3–2.5 at
sintering zone, and two optically thin dark rings of a spectral slope of 2.3–2.5 at  , which are associated with the two innermost non-sintering zones. These are all consistent with the ALMA observation.
, which are associated with the two innermost non-sintering zones. These are all consistent with the ALMA observation. - 4.The sintering-induced ring patterns diminish as the disk becomes depleted of dust (Section 5.3). As the dust-to-gas mass ratio decreases, aggregates collide with each other less frequently, making their maximum size more severely limited by radial drift rather than fragmentation. The sintering-induced rings disappear once radial drift dominates over fragmentation, even in the sintering zones. For a disk with a total mass of
 , the characteristic radius of 150 au, and the initial dust-to-gas mass ratio of 0.01, we find that the sintering-induced rings decay in 2 Myr. The ring patterns of HL Tau might be a sign of its youth.
, the characteristic radius of 150 au, and the initial dust-to-gas mass ratio of 0.01, we find that the sintering-induced rings decay in 2 Myr. The ring patterns of HL Tau might be a sign of its youth. - 5.Models that assume a lower turbulence parameter
 toward the central star best reproduce the multiple ring structure of HL Tau (Section 6.2). If
toward the central star best reproduce the multiple ring structure of HL Tau (Section 6.2). If  were radially constant, turbulence-driven collision velocity
were radially constant, turbulence-driven collision velocity  would increase with decreasing radial distance r. In this case, either unsintered aggregates would fragment at small r or sintered aggregates would fragment at large r. The former case does not reproduce dark rings at small r, while the latter case does not reproduce bright rings at large r. The radial dependence of
would increase with decreasing radial distance r. In this case, either unsintered aggregates would fragment at small r or sintered aggregates would fragment at large r. The former case does not reproduce dark rings at small r, while the latter case does not reproduce bright rings at large r. The radial dependence of  suggested by our model is qualitatively consistent with the predictions from magnetohydrodynamical turbulence models.
suggested by our model is qualitatively consistent with the predictions from magnetohydrodynamical turbulence models. - 6.The vertical extent of the observed dust rings places a strong constraint on the turbulence strength and monomer size assumed in our model (Section 6.3). When
 , sintering would be too slow to induce dust ring formation. When
, sintering would be too slow to induce dust ring formation. When  , disruption of sintered aggregates would require turbulence that is too strong to allow dust settling to the midplane. If the macroscopic dust particles in the HL Tau disk have already settled, as suggested by previous studies (Kwon et al. 2011; Pinte et al. 2016), disk turbulence must be moderately weak (
, disruption of sintered aggregates would require turbulence that is too strong to allow dust settling to the midplane. If the macroscopic dust particles in the HL Tau disk have already settled, as suggested by previous studies (Kwon et al. 2011; Pinte et al. 2016), disk turbulence must be moderately weak ( ) and monomers must be micron-sized (
) and monomers must be micron-sized ( ). The predicted monomer size might be consistent with the near-infrared observations of HL Tau, suggesting the presence of micron-sized grains on the surface of its circumstellar envelope (Lucas et al. 2004; Murakawa et al. 2008).
). The predicted monomer size might be consistent with the near-infrared observations of HL Tau, suggesting the presence of micron-sized grains on the surface of its circumstellar envelope (Lucas et al. 2004; Murakawa et al. 2008). - 7.The exact locations and widths of the dust rings predicted by our model are subject to uncertainties in the vapor pressure data (Section 6.4). In general, a 10% uncertainty in the sublimation energy of a volatile species causes a
 uncertainty in the predicted location of the volatile's sintering zone. We find that reducing the sublimation energies of
uncertainty in the predicted location of the volatile's sintering zone. We find that reducing the sublimation energies of  ,
,  , and
, and  by only 10% from our fiducial values significantly improves our predictions for the observational appearance of the ring structures in an inner region of the HL Tau disk. The models using the tuned sublimation energies reproduce the radial positions of the HL Tau's inner rings to an accuracy of
by only 10% from our fiducial values significantly improves our predictions for the observational appearance of the ring structures in an inner region of the HL Tau disk. The models using the tuned sublimation energies reproduce the radial positions of the HL Tau's inner rings to an accuracy of  .
.
The authors thank Neal Turner for discussions on the temperature distribution of the HL Tau disk, and Akimasa Kataoka for useful comments on the modeling of aggregate porosity. We also thank Takashi Tsukagoshi, Tetsuya Hama, Misato Fukagawa, Hideko Nomura, and Mario Flock for comments and discussions, and the anonymous referee for prompt and constructive comments. This work is supported by Grants-in-Aid for Scientific Research (nos. 23103004, 23103005, 25400447, 26287101, 15H02065) from MEXT of Japan and by the Astrobiology Center Project of National Institutes of Natural Sciences (NINS) (grant no. AB271020). This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.00015.SV. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ.
Footnotes
- 7
In most of our simulation runs, the turbulence-driven velocity is the dominant component of the aggregate collision velocity. The only exception is run LLa0, in which the turbulence-driven velocity is only slightly larger than the drift-driven velocity. In this run, radial drift and turbulence nearly equally contribute to the aggregate fragmentation.
- 8
In general, vapor tends to be transported from solid surfaces of a high positive curvature (e.g., bumps) to surfaces of a high negative curvature (e.g., dips) so that the total energy of the solid associated with surface tension is minimized (see, e.g., Blackford 2007). Sintering (neck growth) is simply driven by the high negative curvature of the necks. Ostwald ripening is the phenomenon in which large monomers with a (positive) surface curvature lower than the average surface curvature within the aggregate grow at the expense of small monomers with a curvature higher than the average.