ABSTRACT
The Ertel theorem on the vorticity along the flow of adiabatic fluids is generalized for non-adiabatic flows. Several limiting cases are analyzed and the results are applied to flows behind different hydrodynamics fronts, particularly to thermal fronts (heat and cooling fronts). An important conclusion of the present analysis is that vorticity is inherent in the condensation's (or hot spots) formation by thermal instabilities in plasma flows. Implications for several astrophysical plasmas are outlined.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
It has been well established (Mihalas & Mihalas 1984; Landau & Lifshitz 1987) that when gas dynamics equations are linearized, assuming small disturbances, a rotational and a potential mode result and they are independent of each other. If viscosity is accounted for it produces damping on the potential mode and if thermal conduction is taken into account, an additional damped thermal mode appears. When a heat/loss of energy term is taken into account in the energy equation the potential and thermal modes are strongly modified (Ibáñez 1985; Ibáñez & Sanchez 1992). However, most of the general analyses that have been made have considered the initially undisturbed fluid at rest or with a constant initial velocity 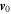 (Ytrehus & Smolderen 1982), and the potential and thermal modes have been extensively studied in different contexts. Less attention, however, has been paid to the rotational mode. Nonetheless, the importance of this mode is apparent through its connection with the onset and its sustaining of turbulence in fluids under very different physical conditions, in particular in astrophysics (Dennis & Chandran 2005; Burkert 2006; Heyer & Brunt 2006; Pan & Padoan 2009; Braun & Schmidt 2012). In fact, an important property of the vortex motion is that at the onset of the nonlinear regime it generates a potential mode that generates density irregularities even in a fluid that is initially homogeneous. The above aspect has been of crucial importance for the problem of galaxy formation (Ozernoy & Chernin 1969).
(Ytrehus & Smolderen 1982), and the potential and thermal modes have been extensively studied in different contexts. Less attention, however, has been paid to the rotational mode. Nonetheless, the importance of this mode is apparent through its connection with the onset and its sustaining of turbulence in fluids under very different physical conditions, in particular in astrophysics (Dennis & Chandran 2005; Burkert 2006; Heyer & Brunt 2006; Pan & Padoan 2009; Braun & Schmidt 2012). In fact, an important property of the vortex motion is that at the onset of the nonlinear regime it generates a potential mode that generates density irregularities even in a fluid that is initially homogeneous. The above aspect has been of crucial importance for the problem of galaxy formation (Ozernoy & Chernin 1969).
Ertel (1942) found that any moving fluid particle carries with it a constant value of the quantity 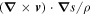 (where
(where 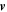 the velocity, s is the entropy per unit mass and ρ is the mass density) as far as the flow is adiabatic (Ertel theorem). At the present note the Ertel analysis will be generalized to non-adiabatic flows (Section 3), several asymptotic cases are considered (Section 4), and the implications regarding flows behind the heat and cooling waves (Zel'dovich & Pikel'ner 1969; Doroshkevich & Zel'dovich 1981; Ibáñez et al. 2005, 2006) are analyzed, (Section 5).
the velocity, s is the entropy per unit mass and ρ is the mass density) as far as the flow is adiabatic (Ertel theorem). At the present note the Ertel analysis will be generalized to non-adiabatic flows (Section 3), several asymptotic cases are considered (Section 4), and the implications regarding flows behind the heat and cooling waves (Zel'dovich & Pikel'ner 1969; Doroshkevich & Zel'dovich 1981; Ibáñez et al. 2005, 2006) are analyzed, (Section 5).
2. BASIC EQUATIONS
An optically thin and heat conducting ideal gas with a mean molecular weight μ is governed by the well-known fluid dynamics equations: equations of continuity, motion, heat transfer, and the equation of state for an ideal gas, i.e.,

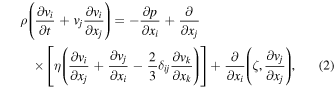
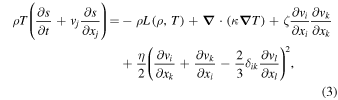
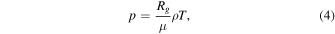
where ρ, vi, p, T, cv, Rg, η, and ζ are mass density, the ith component of the velocity, pressure, temperature, specific heat at constant volume, the universal gas constant, and the coefficients of dynamic and bulk viscosity, where the thermal conduction coefficient 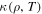 generally is weakly dependent on density but strongly dependent on temperature (Parker 1953; Spitzer 1962; Braginskii 1965).
generally is weakly dependent on density but strongly dependent on temperature (Parker 1953; Spitzer 1962; Braginskii 1965). 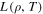 is the heat-loss function defined as the energy output minus the energy input per unit mass and time, which can be written as
is the heat-loss function defined as the energy output minus the energy input per unit mass and time, which can be written as

3. GENERALIZED ERTEL EQUATION
If one takes the curl in both sides of Equation (2) and with the help of Equations (1) and (3), as well as the definition of the substantial, or intrinsic derivative of the entropy
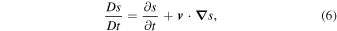
one can get the equation
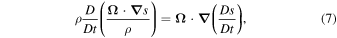
where  is the vorticity (see the
is the vorticity (see the
In the general case for inviscid flows of optically thin gases, Equation (3) can be written in the form
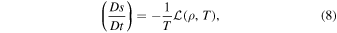
where
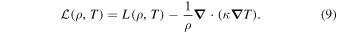
therefore, Equation (7) becomes
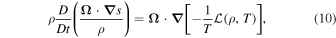
so only two terms of the change with the time of the entropy are accounted for: the heat/loss term and the thermal conduction dissipation, Equations (8) and (9).
In the adiabatic limit 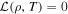 , from Equation (10), the Ertel classical result follows,
, from Equation (10), the Ertel classical result follows,
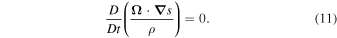
i.e., in non-isentropic flows any moving particle carries with it a constant potential vorticity 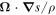 .
.
If one writes the vorticity as 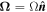 , where
, where 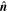 is a unit vector in a given direction, from Equation (10) it follows that
is a unit vector in a given direction, from Equation (10) it follows that
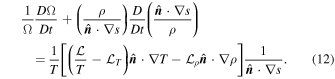
Integrating Equation (12) with time along particle paths, in the interval 0 to t one obtains
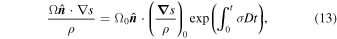
where the sub-index 0 means that the value of the respective quantity at time t = 0 and σ is identical to the right-hand side term of Equation (12), i.e.,
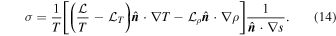
Equation (13) is the generalization of the Ertel result for non-adiabatic flows.
In general 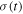 is a function of time, so one can make a Taylor expansion, i.e.,
is a function of time, so one can make a Taylor expansion, i.e.,
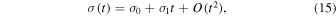
where
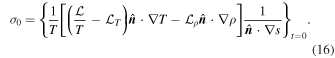
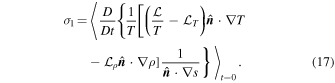
Therefore, up to the first term, Equation (13) simplifies to
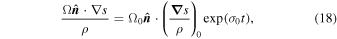
and Equation (18) holds for times such that 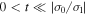 .
.
4. ASYMPTOTIC CASES
4.1. Non-isentropic Limit
For adiabatic flows (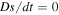 ) that are not isentropic,
) that are not isentropic,  , Equation (13) reduces to
, Equation (13) reduces to
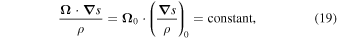
i.e., the quantity 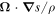 , carried along the flow by any particle, is conserved, a result first obtained by Ertel (1942).
, carried along the flow by any particle, is conserved, a result first obtained by Ertel (1942).
In the particular case of linear disturbances (for instance, ![$\sim \mathrm{exp}[i({\boldsymbol{k}}\cdot {\bf{r}}-\omega t)]$](https://content.cld.iop.org/journals/0004-637X/818/2/119/revision1/apj522147ieqn16.gif) ,
, 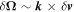 ,
, 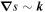 , constant = 0) Equation (19) describes an entropy-vortex wave, which, as it is well-known, becomes independent of the potential disturbances as far as the first order approximation holds (Landau & Lifshitz 1987).
, constant = 0) Equation (19) describes an entropy-vortex wave, which, as it is well-known, becomes independent of the potential disturbances as far as the first order approximation holds (Landau & Lifshitz 1987).
Without loss of generality, 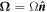 , where
, where 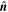 is a particular direction in space. If, for example,
is a particular direction in space. If, for example, 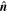 is taken along the z-axis, Equation (19) simplifies to
is taken along the z-axis, Equation (19) simplifies to
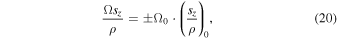
where the sub-index 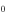 denotes values at z = 0, where
denotes values at z = 0, where 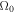 is the magnitude (
is the magnitude (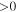 ) of the vorticity at z = 0. The signs ± correspond to vorticity in both directions on
) of the vorticity at z = 0. The signs ± correspond to vorticity in both directions on 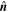 . More explicitly, Equation (20) can be written as
. More explicitly, Equation (20) can be written as

where
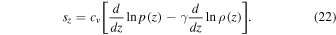
In particular, if the pressure remains constant along z,
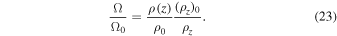
If one additionally assumes, for instance, that 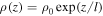 , for
, for 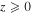 , l being the density length-scale, from Equation (23) one obtains
, l being the density length-scale, from Equation (23) one obtains
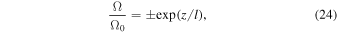
i.e., vorticity increases as density increases. This situation occurs, for example, behind hydrodynamics fronts in the relaxation layer where density increases and the flow cools down. So any clump formed behind the front with vorticity 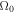 will amplify the vorticity on a length-scale
will amplify the vorticity on a length-scale 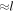 .
.
In the limiting case, when density remains constant, the vorticity 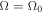 does not change along z, but nonetheless the pressure as well as the temperature decrease (or increase) with z as far as the flow is adiabatic, as it can be easily realized. The physical implications of the above results will be discussed bellow.
does not change along z, but nonetheless the pressure as well as the temperature decrease (or increase) with z as far as the flow is adiabatic, as it can be easily realized. The physical implications of the above results will be discussed bellow.
4.2. Isobaric Limit
In the isobaric limit from Equation (16) the rate 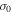 simplifies to
simplifies to
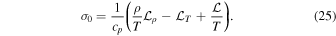
Therefore, there is an exponential growth (instability) of the vorticity in the direction 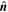 if
if
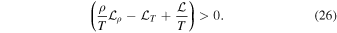
If the thermal conduction is neglected Equation (25) simplifies to
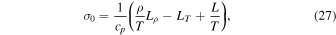
and the vorticity grows up as far as
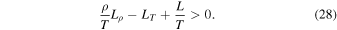
Additionally, if the flow is close to the thermal equilibrium 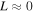 , the above criterion (28) reduces to the well-known isobaric Field (1965) criterion of instability for linear (potential) disturbances. Henceforth, in this sense, the former isobaric criterion holds for the condensational (potential) mode as well as for the entropy-vortex mode. However, the criterion (26) for an exponential increasing of the vorticity holds out the thermal equilibrium (which requires that L = 0) as far as the condition
, the above criterion (28) reduces to the well-known isobaric Field (1965) criterion of instability for linear (potential) disturbances. Henceforth, in this sense, the former isobaric criterion holds for the condensational (potential) mode as well as for the entropy-vortex mode. However, the criterion (26) for an exponential increasing of the vorticity holds out the thermal equilibrium (which requires that L = 0) as far as the condition  holds, and regardless the initial amplitude of the vorticity (
holds, and regardless the initial amplitude of the vorticity (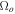 ). If thermal conduction is taken into account, Equation (25) can be written in a first approximation as
). If thermal conduction is taken into account, Equation (25) can be written in a first approximation as
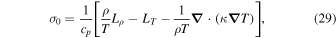
where derivative respect to T and ρ of the conductive term 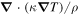 have been neglected. From Equation (29) it follows that the exponential growth is quenched by thermal conduction when
have been neglected. From Equation (29) it follows that the exponential growth is quenched by thermal conduction when
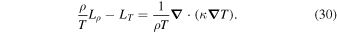
Finally, in the isochoric limit the growth rates becomes
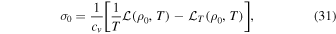
and the vorticity exponentially grows if
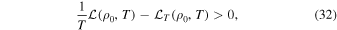
which, close to the thermal equilibrium, reduces to the linear isochoric Field's criterion 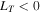 . This limit can be important during the transition from isobaric to isochoric cooling, which occurs at low temperature and over high density for perturbations at small scale-lengths (Burkert & Lin 2000), as will be discussed in the next section. It is worth remarking, however, that even at strictly constant density, vorticity may be amplified when it moves along the flow if the condition (32) is fulfilled.
. This limit can be important during the transition from isobaric to isochoric cooling, which occurs at low temperature and over high density for perturbations at small scale-lengths (Burkert & Lin 2000), as will be discussed in the next section. It is worth remarking, however, that even at strictly constant density, vorticity may be amplified when it moves along the flow if the condition (32) is fulfilled.
5. APPLICATIONS
Generally, any irreversible change of physical state of any flow implies an increase of entropy, which generates vorticity. On the other hand, a quite common phenomenon, in laboratory (Drake 1987; Stacey 1996, 1997; Stacey & Petrie 2000) as well as in astrophysical (Field 1965; Balbus & Soker 1989; Hennebelle & Pérault 1999; Burkert & Lin 2000; Koyama & Inutsuka 2002; Fukue & Kamaya 2007) plasmas, is the formation of a cold structure moving in a hot environment or vice-versa. In both of the above cases mass interchange occurs through the interface, i.e., mass evaporate from the cold face or condensates from the hot face according to the particular physical situation under consideration (Zel'dovich & Pikel'ner 1969; Cowie & McKee 1976, 1977; Silk & Norman 1977; Doroshkevich & Zel'dovich 1981). A particular property of thermal fronts is that they propagate under quasi-isobaric conditions, except by a weak change of pressure occurring just into the front. Additionally, the generation of vorticity in thermal fronts (either heat or cooling fronts) occurs regardless of the geometry of the interface. The problem is formally equivalent to the slow propagation of a flame through a burning mixture (Doroshkevich & Zel'dovich 1981; Zel'dovich et al. 1985). So, the results of Section 4.2 can be applied due to the fact that pressure is almost constant, as a first approximation. Additionally, it is unlikely that condensations originated by thermal instabilities do not contain vorticity. So, the vorticity becomes inherent to the process of condensation formation. The same conclusion follows in the case of hot spot (heat fronts) formation.
In other kinds of hydrodynamics fronts, say shock waves, the strong generation of entropy also generates vorticity in the zone where strong gradients of pressure, density, and temperature occur, but the generation and evolution of the vorticity under such conditions is outside the scope of the present paper (it will be worked out elsewhere). However, behind the strong gradients zone of a shock wave the flow tends to reach an equilibrium state (Zel'dovich & Raizer 1966) where the results obtained in Section 4. 2 make physical sense, in a first approximation. The following discussion will be address astrophysical plasmas.
From Equation (29), it follows that, close to thermal equilibrium, thermal conduction introduces a critical length-scale lF (Field scale)  (Field 1965), such that isobaric disturbances with dimensions
(Field 1965), such that isobaric disturbances with dimensions 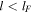 are damped by thermal conduction. This result also holds for the vorticity, i.e., vorticity at scales
are damped by thermal conduction. This result also holds for the vorticity, i.e., vorticity at scales 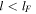 is also damped by thermal conduction in a characteristic time of the order of
is also damped by thermal conduction in a characteristic time of the order of 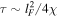 , where χ (
, where χ (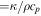 ) is the thermometric conductivity. In the opposite case the vorticity grows. Therefore, one should expect that condensations formed at scales
) is the thermometric conductivity. In the opposite case the vorticity grows. Therefore, one should expect that condensations formed at scales 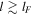 carry out vorticity. The above also explains how part of the input of thermal energy can increase the vorticity (Kritsuk & Norman 2002) as far as the condition (26) holds. Additionally, the scale-length lF should be the lower threshold value for the dimensions of the space scale of vorticity in optically thin gases as far as the viscosity can be neglected. The fact that the vorticity is damped at short scales
carry out vorticity. The above also explains how part of the input of thermal energy can increase the vorticity (Kritsuk & Norman 2002) as far as the condition (26) holds. Additionally, the scale-length lF should be the lower threshold value for the dimensions of the space scale of vorticity in optically thin gases as far as the viscosity can be neglected. The fact that the vorticity is damped at short scales 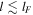 agrees with the general result that energy dissipation occurs on the smallest scales, in rotational turbulent flows (Landau & Lifshitz 1987).
agrees with the general result that energy dissipation occurs on the smallest scales, in rotational turbulent flows (Landau & Lifshitz 1987).
When a cold clump is formed by thermal instability with a vorticity  and is carried along by the gas flow, the vorticity changes as in Equation (18). Without loss of generality, assuming
and is carried along by the gas flow, the vorticity changes as in Equation (18). Without loss of generality, assuming 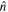 along the z-axis,
along the z-axis,
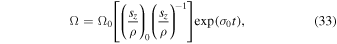
i.e., the amplitude depends on the space scale for the change of entropy as well as the rate 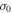 . If, for instance,
. If, for instance, 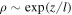 , then Equation (33) simplifies to
, then Equation (33) simplifies to
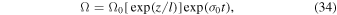
where 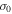 is defined by Equation (29). For a scale l that is large enough the evolution of the vorticity almost depends completely on the rate
is defined by Equation (29). For a scale l that is large enough the evolution of the vorticity almost depends completely on the rate 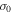 , but at a marginal state
, but at a marginal state 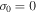 the change of the vorticity carried along the flow depends on the space change of the entropy.
the change of the vorticity carried along the flow depends on the space change of the entropy. 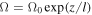 , i.e., it increases with density with the same length-scale l. The fact that at t = 0 it is assumed that
, i.e., it increases with density with the same length-scale l. The fact that at t = 0 it is assumed that 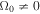 or more generally that
or more generally that ![${{\rm{\Omega }}}_{0}[{({s}_{z}/\rho )}_{0}{({s}_{z}/\rho )}^{-1}]\ne 0$](https://content.cld.iop.org/journals/0004-637X/818/2/119/revision1/apj522147ieqn54.gif) , is a condition that, in most of the physical flows, in particular where clumps are formed, holds, as was pointed out at the beginning of this section.
, is a condition that, in most of the physical flows, in particular where clumps are formed, holds, as was pointed out at the beginning of this section.
For context, a hot, completely ionized optically thin gas (the case of the atomic ISM gas) will be considered. Usually the cooling function for the above plasma is parameterized in the form
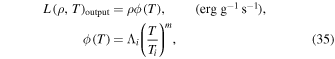
where 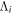 , Ti, and m are well-defined parameters, the value of which depend on the sub-range of temperatures under consideration. In particular, for plasmas with solar abundances the above values are given in Rosner et al. (1978), Vesecky et al. (1979), and Bohm-Vitense (1987).
, Ti, and m are well-defined parameters, the value of which depend on the sub-range of temperatures under consideration. In particular, for plasmas with solar abundances the above values are given in Rosner et al. (1978), Vesecky et al. (1979), and Bohm-Vitense (1987).
On the other hand, the heating function is usually assumed to have the form
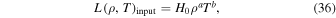
where H0, a, and b are known parameters. The particular values of these parameters characterize different physical mechanisms by which plasmas can be heated (Rosner et al. 1978; Dahlburg & Mariska 1988).
Close to the thermal equilibrium, exponential growth of the vorticity under isobaric conditions occurs as 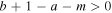 . For a constant per unit mass heating (a = 0, b = 0) the above occurs in the interval of temperature where the power of the piecewise cooling function
. For a constant per unit mass heating (a = 0, b = 0) the above occurs in the interval of temperature where the power of the piecewise cooling function 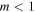 , i.e.,
, i.e., 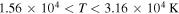 and
and 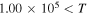
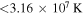 (Rosner et al. 1978; Dahlburg & Mariska 1988). Figure 1(a) is a plot of the critical value (when
(Rosner et al. 1978; Dahlburg & Mariska 1988). Figure 1(a) is a plot of the critical value (when 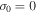 ) of lF (cm) and Figure 1(b) is the thermal relaxation time
) of lF (cm) and Figure 1(b) is the thermal relaxation time 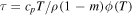 (s) as functions of temperature in the range of temperature where
(s) as functions of temperature in the range of temperature where 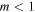 , and Figures 1(c) and (d) are the growth rate
, and Figures 1(c) and (d) are the growth rate  (s−1) as a function of
(s−1) as a function of 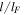 for
for 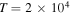 and
and 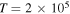 K and densities
K and densities  . The left branches (
. The left branches (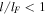 ) correspond to damped rates. For
) correspond to damped rates. For 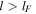 the growth rate
the growth rate 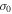 increases very fast to reach an asymptotic value for
increases very fast to reach an asymptotic value for 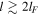 .
.
Figure 1. Figure 1(a): a plot of the critical value of the scale-length lF (cm) as a function of temperature T (K ) for a constant per unit mass heating (a = 0, b = 0, Equation (36)) in the range of temperature where  in the cooling function (Equation (35)) and the plasma is thermally unstable. Three different values of the number density n (cm−3) are shown:
in the cooling function (Equation (35)) and the plasma is thermally unstable. Three different values of the number density n (cm−3) are shown: 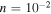 , 1 and 102. Figure 1(b): a plot of the thermal relaxation time
, 1 and 102. Figure 1(b): a plot of the thermal relaxation time 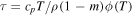 (s) as a function of temperature, in the range where
(s) as a function of temperature, in the range where 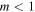 and the same values of n of Figure 1(a). Figures 1(c) and (d): growth rate
and the same values of n of Figure 1(a). Figures 1(c) and (d): growth rate  (s−1) as a function of
(s−1) as a function of 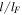 for
for 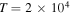 and
and  , respectively, and the same values of n of Figure 1(a). The left branches (
, respectively, and the same values of n of Figure 1(a). The left branches (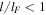 ) correspond to damped rates and the right ones correspond to unstable rates. For
) correspond to damped rates and the right ones correspond to unstable rates. For 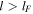 the growth rate
the growth rate 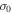 increases very fast to reach an asymptotic value for
increases very fast to reach an asymptotic value for 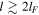 .
.
Download figure:
Standard image High-resolution imageIn homogeneous astrophysical plasmas at dimensions shorter that the Jeans length (self-gravitation is negligible) clump structures may be formed by thermal instabilities (Field 1965) or by pure dynamical effects (Chandrasekhar 1951; Ozernoy & Chernin 1969). In the former case the length-scale for inhomogeneities becomes 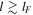 and in the last one the minimum length-scale would be determined by viscosity (Heisenberg 1947). On the other hand, and as was emphasized in Section 4.1, as far as the linear approximation is concerned, the potential and vortical modes are independent of each other. However, once the the nonlinear effects come into play these modes interact and potential motions are generated by vortical motions (Chandrasekhar 1951; Ozernoy & Chernin 1969), as can be easily realized at an order of magnitude. In fact, if vp and vv are the potential and vortical velocities and c is the sound velocity, from the motion and continuity equations one obtains
and in the last one the minimum length-scale would be determined by viscosity (Heisenberg 1947). On the other hand, and as was emphasized in Section 4.1, as far as the linear approximation is concerned, the potential and vortical modes are independent of each other. However, once the the nonlinear effects come into play these modes interact and potential motions are generated by vortical motions (Chandrasekhar 1951; Ozernoy & Chernin 1969), as can be easily realized at an order of magnitude. In fact, if vp and vv are the potential and vortical velocities and c is the sound velocity, from the motion and continuity equations one obtains
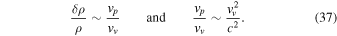
i.e., 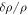 and
and 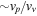 are quantities of the second order relatives to
are quantities of the second order relatives to  (vortex Mach number).
(vortex Mach number).
On the other hand, if the Taylor expansion of  is made up to the second term, instead of Equation (18) one obtains
is made up to the second term, instead of Equation (18) one obtains

where  and
and 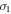 are defined by Equations (16) and (17), respectively.
are defined by Equations (16) and (17), respectively.
At this quasi-linear approximation, there are four different cases: (1) 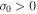 and
and 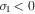 , the quantity
, the quantity 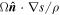 increases up to a maximum value and after becoming asymptotic decays to zero; (2)
increases up to a maximum value and after becoming asymptotic decays to zero; (2) 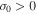 and
and  , there is a super exponential increase; (3)
, there is a super exponential increase; (3) 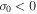 and
and 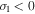 the quantity
the quantity 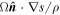 asymptotically decreases; and (4)
asymptotically decreases; and (4) 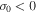 and
and 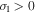 ,
, 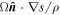 decreases first up to a minimum value and afterward increases as
decreases first up to a minimum value and afterward increases as 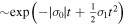 . Close to the first order marginal state
. Close to the first order marginal state 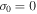 ,
, 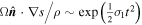 , i.e., in order to get information on the time evolution of the potential vorticity at the marginal state, one must go to the second approximation. On the other hand, when
, i.e., in order to get information on the time evolution of the potential vorticity at the marginal state, one must go to the second approximation. On the other hand, when 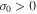 the potential vorticity of the particles flow exponentially increases and for time
the potential vorticity of the particles flow exponentially increases and for time 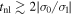 the first approximation breaks down, and accounting for the second order term in Equation (15) is required too. From the physical point of view in the isobaric case, the first order instability (
the first approximation breaks down, and accounting for the second order term in Equation (15) is required too. From the physical point of view in the isobaric case, the first order instability (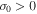 ) implies that when the temperature of flow particles decays, the density increases, as well as the the vorticity Ω along the z direction.
) implies that when the temperature of flow particles decays, the density increases, as well as the the vorticity Ω along the z direction.
Additionally, if 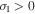 , at times
, at times 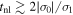 the vorticity feeds the potential velocity, as well as the fluctuation of density. In conclusion, it does not matter how small the initial vortocity is if
the vorticity feeds the potential velocity, as well as the fluctuation of density. In conclusion, it does not matter how small the initial vortocity is if 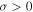 , at time tnl when the nonlinear effects appears, the vortical mode generates potential motion, which grows together with the density.
, at time tnl when the nonlinear effects appears, the vortical mode generates potential motion, which grows together with the density.
There are several additional aspects that should be addressed: (1) in case of spherical condensations, one should calculate the possible influence of the vorticity departing from the homogeneous sphere and its consequences on the mass transfer throughout the spherical cooling front. (2) If the above effect is significant for bringing the "condensation" to the verge of gravitational collapse then increasing the condensed mass close to the Jeans mass and/or lowering the Jeans limit, which is 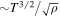 (Jeans 1929; Hunter 1962; Kegel & Traving 1976), and will therefore decrease it as temperature decreases and density increases. (3) The effect of a magnetic field on the vortical mode and on the further evolution of cold clumps (or hot spots) originated by thermal instabilities has to be examined. These problems will be considered separately.
(Jeans 1929; Hunter 1962; Kegel & Traving 1976), and will therefore decrease it as temperature decreases and density increases. (3) The effect of a magnetic field on the vortical mode and on the further evolution of cold clumps (or hot spots) originated by thermal instabilities has to be examined. These problems will be considered separately.
6. CONCLUSIONS
The Ertel theorem for adiabatic flows has been generalized for non-adiabatic flows and an expression for the potential vorticity (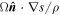 ) has been obtained (Equation (18)). In a first approximation the above quantity is
) has been obtained (Equation (18)). In a first approximation the above quantity is  , where the rate
, where the rate 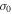 is given by Equation (16). If
is given by Equation (16). If 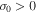 the vorticity increases with time and close to the thermal equilibrium
the vorticity increases with time and close to the thermal equilibrium 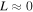 this condition is identical to the Field's instability criteria for the asymptotic cases at constant pressure or density. Therefore if cold condensations (or hot spots) are formed by thermal instabilities the vorticity is inherent to the formation process itself. At this approximation the vorticity is damped by thermal conduction at scale-lengths
this condition is identical to the Field's instability criteria for the asymptotic cases at constant pressure or density. Therefore if cold condensations (or hot spots) are formed by thermal instabilities the vorticity is inherent to the formation process itself. At this approximation the vorticity is damped by thermal conduction at scale-lengths 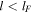 and otherwise exponentially grows to a limit value for
and otherwise exponentially grows to a limit value for 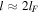 . When a fluctuation of density increases by thermal instability up to a quasi-linear regime, the vortical mode couples with the potential mode and this mode is fed by vorticity. Additionally, in the quasi-linear regime the fact that
. When a fluctuation of density increases by thermal instability up to a quasi-linear regime, the vortical mode couples with the potential mode and this mode is fed by vorticity. Additionally, in the quasi-linear regime the fact that 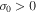 or
or 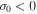 are conditions that are necessary but not sufficient for instability or stability, respectively; see case (1) and case (4) above. Thus, beyond the linear regime the exponential increase or decrease of
are conditions that are necessary but not sufficient for instability or stability, respectively; see case (1) and case (4) above. Thus, beyond the linear regime the exponential increase or decrease of 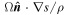 demands that
demands that 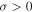 or
or 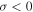 , respectively.
, respectively.
I gratefully acknowledge the anonymous referee for useful comments that helped to clarify several aspects of the present work and I thank the Departamento de Ciencias Básicas, Facultad de Ingeniería Universidad Autonoma del Caribe. This work has been supported by the Vice-Rectoría de Investigación y Transferencia, Universidad Autonóma del Caribe through project PRYINT-049 2015.
APPENDIX:
To obtain Equation (12) one must start by applying curl to both sides of the motion equation, Equation (2)
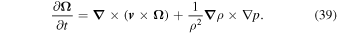
The viscous terms have been neglected because the present analysis is limited to analyzing inviscid fluids.
The entropy is a function of ρ and p, i.e., 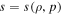 , therefore, up to the first order one may write the gradient of entropy as
, therefore, up to the first order one may write the gradient of entropy as
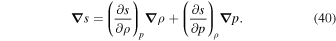
Therefore
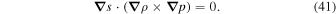
The above equation also holds in the isobaric limit because 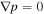 , as well as in the isochoric limit because
, as well as in the isochoric limit because 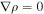 . Henceforth, from Equations (39) and (41)
. Henceforth, from Equations (39) and (41)
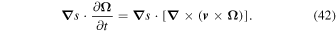
From well-known vectorial relations, Equation (42) can be written as
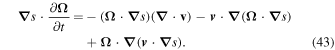
On the other hand, from Equation (8) it follows that

so the last term on the right side of Equation (43) becomes
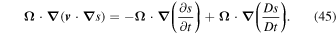
With the help of Equation (45), Equation (43) becomes
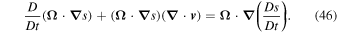
Finally, with the help of the continuity Equation (1), Equation (13) follows.




