Abstract
The tunneling probability in heavily doped 4H-SiC Schottky barrier diodes (SBDs) is analyzed based on the empirical pseudopotential method (EPM). A method of calculating the tunneling probability within the WKB approximation using the EPM electronic states of bulk 4H-SiC has been reported. In the present study, to investigate the validity of this method, the tunneling probability is calculated by connecting the incident, transmitted, and reflected wavefunctions considering the barrier potential of a SBD instead of using the WKB approximation. Comparing the calculated results with and without the WKB approximation, the difference is found to be rather small. This suggests that we can safely use the WKB approximation with the bulk electronic states, which are obtained without considering the barrier potential, when calculating the tunneling current in the heavily doped 4H-SiC SBDs.
Export citation and abstract BibTeX RIS
1. Introduction
To achieve a carbon-neutral society, further developments in semiconductor power devices are needed. Although silicon (Si) is now most widely used for power devices, the technology for Si power devices is relatively mature. 1) In this context, the use of wide-bandgap semiconductors 2–6) has been considered. Among them, silicon carbide (SiC), 7) especially 4H-SiC, is attracting attention due to both its excellent physical properties and mature device fabrication technologies. 8) It is now being studied not only as a next-generation power device material, 9–15) but also for applications other than the power devices. 16–19)
Further development of 4H-SiC devices requires the understanding of the properties of 4H-SiC. In particular, a better understanding of the tunneling effects in 4H-SiC is needed to obtain 4H-SiC ohmic contacts with lower resistance. Therefore, in this study, we consider heavily doped 4H-SiC Schottky barrier diodes (SBDs), which have a higher doping concentration than those practically used, to make the tunneling currents prominent, and perform a theoretical analysis of the tunneling effects in SBDs. Hara et al. 20) reported that smaller values of the effective mass and the barrier height than the experimental values had to be used in order to reproduce the experimental tunneling currents in SBDs. In previous studies including Ref. 20, the parabolic band approximation (PBA) is widely used, i.e. the complex bands for the tunneling probability are assumed to be parabolic. However, complex bands are inherently non-parabolic, which means that the parabolic assumption can lead to be inaccuracy of the tunneling probability.
In our previous report,
21) we calculated non-parabolic complex bands by the empirical pseudopotential method (EPM) and analyze the tunneling effects within the WKB approximation.
22) Though we found that considering the non-parabolicity of the complex bands is important when calculating the tunneling probability, there were still some concerns. One of them is the use of the WKB approximation when calculating the tunneling probability. The WKB approximation is widely used to calculate tunneling probabilities. However, the WKB approximation is derived assuming a slowly varying potential.
23) Therefore, its use for steeply varying potentials is controversial.
24) Since the barrier potential of a heavily doped 4H-SiC SBD as a function of position z, Vb(z), changes steeply especially when the reverse voltage is large, the validity of using the WKB approximation for the tunneling probability in the heavily doped 4H-SiC SBDs needs to be confirmed before calculating the reverse voltage dependence of the tunneling currents. Another is that Vb is not taken into account when calculating the complex bands; we calculated the tunneling probability using the electronic states without Vb. In this study, we investigate the validity of the previous method
21) by calculating the EPM electronic states considering Vb in the Schr dinger equation and the tunneling probability without using the WKB approximation. We then compare the calculated tunneling probabilities with the previous and experimental results.
dinger equation and the tunneling probability without using the WKB approximation. We then compare the calculated tunneling probabilities with the previous and experimental results.
This paper is divided into four sections. In Sect. 2, we describe the calculation methods used in this study. In the extended abstract, 25) we calculated the electronic states considering Vb using a periodic superlattice model. In the present study, we extend the method and derive the tunneling probability by combining the electronic states of the superlattice structure and bulk 4H-SiC. In Sect. 3, we show and analyze the calculated results. Finally, a conclusion is given in Sect. 4.
2. Theory
We first introduce the models to calculate the tunneling probability without using the WKB approximation in Sect. 2.1. In Sect. 2.2, we describe the calculation method of the electronic states with Vb. Then, the calculation methods of the tunneling probability without and with the WKB approximation are explained in Sects. 2.3–2.5.
2.1. Model
In this section, we explain the details of the calculation models for calculating the tunneling probability, T(Ez ), as a function of the kinetic energy along the transport direction and the complex bands.
Figure 1(a) shows the band diagram of a SBD we consider in this study. The vertical axis represents the energy E and the horizontal axis represents the z direction. E is defined with reference to the conduction band minimum of 4H-SiC without Vb and the origin in the z direction is the Schottky interface. The barrier potential Vb(z) includes the image force effects 26) and is assumed to be 27)
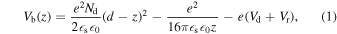
where Vr is the reverse voltage, Vd the diffusion potential, Nd the donor density, d the length of the depletion layer, and  s the relative dielectric constant of 4H-SiC. The barrier height of a SBD including the image force lowering, Φ, is expressed as
s the relative dielectric constant of 4H-SiC. The barrier height of a SBD including the image force lowering, Φ, is expressed as  where
where  is the z-coordinate at which Vb(z) has its maximum value and
is the z-coordinate at which Vb(z) has its maximum value and  is the Fermi level of the metal.
is the Fermi level of the metal.
Fig. 1. (a) The band diagram of a SBD. Φ, d,  , and
, and  , are the barrier height of the SBD including the image force lowering, the length of the depletion layer, the Fermi level of metal, and that of 4H-SiC, respectively. E is the energy and the z-axis is parallel to the 〈0001〉 direction. (b) Schematic diagram of the model to calculate the tunneling probability T. The model consists of the central Schottky barrier region, which is a 4H-SiC region with the barrier potential Vb(z), and the bulk 4H-SiC regions. (c) Schematic diagram of the periodic superlattice structure to calculate the electronic states with Vb(z). The area surrounded by the red line represents one period of the superlattice, which is the same as the Schottky barrier region in (b). The one period of the superlattice consists of multiple primitive unit cells of 4H-SiC arranged along the 〈0001〉 direction. Lsl and Lcell are the period of the superlattice and the c-axis lattice constant of 4H-SiC, respectively.
, are the barrier height of the SBD including the image force lowering, the length of the depletion layer, the Fermi level of metal, and that of 4H-SiC, respectively. E is the energy and the z-axis is parallel to the 〈0001〉 direction. (b) Schematic diagram of the model to calculate the tunneling probability T. The model consists of the central Schottky barrier region, which is a 4H-SiC region with the barrier potential Vb(z), and the bulk 4H-SiC regions. (c) Schematic diagram of the periodic superlattice structure to calculate the electronic states with Vb(z). The area surrounded by the red line represents one period of the superlattice, which is the same as the Schottky barrier region in (b). The one period of the superlattice consists of multiple primitive unit cells of 4H-SiC arranged along the 〈0001〉 direction. Lsl and Lcell are the period of the superlattice and the c-axis lattice constant of 4H-SiC, respectively.
Download figure:
Standard image High-resolution imageThe schematic diagram of the model to obtain T(Ez ) is shown in Fig. 1(b). We divide the system into three regions; the left bulk 4H-SiC region, the central Schottky barrier region with Vb(z), and the right bulk 4H-SiC region. We call the boundary between the left (right) bulk region and the central Schottky barrier region the left (right) boundary. The central region consists of several primitive unit cells of 4H-SiC along the z direction, which is the transport direction. Note that the barrier potential Vb(z) includes a constant region near each end of the central region as shown in Fig. 1. The reason for this is explained in Sect. 3.
When Nd and Vr are assumed to be 2.6 × 1018 cm−3 and 10 V, respectively, the tunneling currents at energies near the Fermi level of the metal are dominant in the whole tunneling current, and the tunneling length is at most 6 nm. Since the length of one primitive unit cell of 4H-SiC along the 〈0001〉 direction, Lcell, is about 1 nm, we can take the tunneling effects into account by cosidering the superlattice whose one period consists of 6 primitive unit cells. If the form of Vb(z) changes, the calculation can be performed in the same way by changing the period of the superlattice accordingly. We use the EPM using the plane wave expansion when calculating the complex band structures. We, therefore, consider a periodic superlattice model when calculating the electronic states with Vb(z) by periodically arranging the central Schottky barrier region of Fig. 1(b). The schematic diagram of the resulting superlattice model is shown in Fig. 1(c).
2.2. Complex band structure
The EPM electronic states 28) can be obtained by solving the following equation: 29,30)

Here Vps( r ) is a pseudopotential, Vb(z) the barrier potential, b a factor to take the non-local effects into account, φ( r ) the wavefunction, and En, k the energy eigenvalue corresponding to φn, k ( r ). Note that the subscript n, k represents the n-th smallest eigenvalue with a wave vector k . Vb(z) is ignored when calculating electronic states of bulk 4H-SiC. The potential Vps( r ) is expressed as the sum of the pseudopotentials of each Si and C atom as follows:
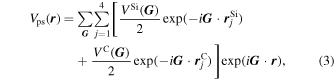
where
G
= (
G
xy
, Gz
) = (Gx
, Gy
, Gz
) is the reciprocal lattice vector, VSi(
G
) (VC(
G
)) the pseudopotential of Si (C) atom, and  (
( ) (j = 1, 2, 3, 4) the vectors representing the positions of the Si (C) atoms in a primitive unit cell. The wavefunction φn,
k
(
r
) is expressed as
) (j = 1, 2, 3, 4) the vectors representing the positions of the Si (C) atoms in a primitive unit cell. The wavefunction φn,
k
(
r
) is expressed as
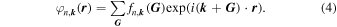
From Eqs. (3) and (4), Eq. (2) can be transformed to

where I is an identity matrix and F is given by
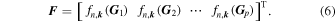
Here p is the number of plane wave bases for φn, k ( r ). The (l, j) elements of H 0 and H 1 are expressed as follows:

where k xy = (kx , ky ) is the in-plane wave vector. By solving the eigenvalue problem of Eq. (5) for a given k xy and E, we obtain a complex waevenumber kz ≡ k + i κ (both k and κ are real), from which we can construct the complex band structures. Hereafter, from the wavefunction φn, k , we omit the band index n and add the subscript E to explicitly indicate that the state is at energy E, and we refer to it as φ k ,E .
2.3. Scattering states
We calculate the scattering states by connecting the incident, transmitted, and reflected EPM wavefunctions in the model of Fig. 1(b). We first calculate the bulk wavefunction  (
( ) for the left (right) region; the wavefunction for the central region,
) for the left (right) region; the wavefunction for the central region,  , is calculated within the superlattice model of Fig. 1(c). The scattering wavefunctions associated with an incident wave
, is calculated within the superlattice model of Fig. 1(c). The scattering wavefunctions associated with an incident wave  having a real wave vector
k
inc from the left are then expanded by
having a real wave vector
k
inc from the left are then expanded by  (α = L, C, R):
(α = L, C, R):
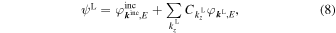
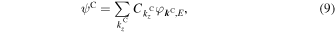
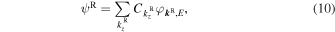
where  is a expansion coefficient. Now, considering the condition that ψL and ψC are continuous at the left boundary, the following equations have to be satisfied for any x and y,
is a expansion coefficient. Now, considering the condition that ψL and ψC are continuous at the left boundary, the following equations have to be satisfied for any x and y,
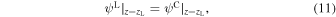
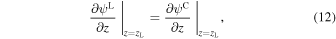
where z = zL (=0) is the boundary between the left and the central region. By Fourier transforming in xy-plane, these equations can be written as
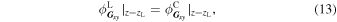
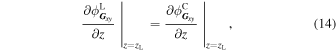
where  and
and  are the Fourier components of ψL and ψC, respectively. From Eqs. (8) and (9),
are the Fourier components of ψL and ψC, respectively. From Eqs. (8) and (9),  and
and  can be written as
can be written as
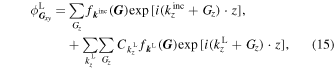
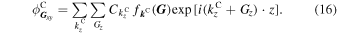
In the same way, for ψC and ψR to be continuous at the right boundary at z = zR (=Lsl), the following boundary conditions have to be satisfied for any G xy ,
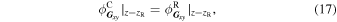
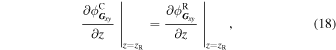
where
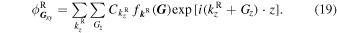
Solving Eqs. (13), (14), (17), and (18) for every
G
xy
results in making the wavefunction continuous in the whole region. As a result, we can determine the transmission wavefunction ψR corresponding to an incident wavefunction  in the left bulk region.
in the left bulk region.
2.4. Probability current density
Probability current density Jz is expressed as 31,32)
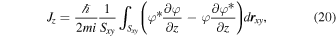
where Sxy
is the area in the plane perpendicular to the transport direction, m = bm0, and
r
xy
= (x, y). The wavefunction of an incident wave in bulk 4H-SiC  is expressed as
is expressed as
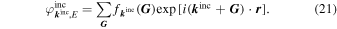
Substituting Eq. (21) into Eq. (20), the probability current density associated with  is given by
is given by

Using Eq. (10), the probability current density associated with ψR is given by
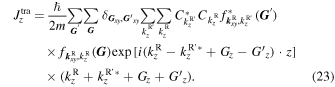
The tunneling probability for the kinetic energy along the transport direction is then obtained from the ratio of the probability current densities of the incident and transmitted waves as
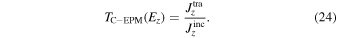
Here, Ez = E − Exy with Exy being the kinetic energy correspondng to k xy in the considered band structure. We call this method connecting wavefunction approach in the C-EPM. This method does not use the WKB approximation.
2.5. WKB approximation
For comparison, we calculate the tunneling probabilities within the WKB approximation. The WKB tunneling probability using the electronic states in bulk 4H-SiC by the B-EPM is given by
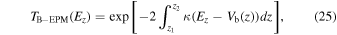
where z1 and z2 are the classical turning points. The damping factor κ is obtained from the complex band structure of bulk 4H-SiC. When using the PBA, the tunneling probability is expressed as
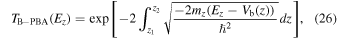
where mz is the effective mass of bulk 4H-SiC along the transport direction. We call this method bulk PBA (B-PBA).
3. Results and discussion
In this section, the calculated complex band structures and tunneling probabilities are presented. As in our previous study,
21) we consider a SBD whose donor density Nd and barrier height without the image force effects are 2.6 × 1018 cm−3 and 1.46 eV, respectively. The parameters for the pseudopotentials and the material parameters of 4H-SiC are also the same as those in our previous study.
21) In the present study,
k
xy
is assumed to be that at the M point in bulk 4H-SiC. Note that we set the cut-off of
G
to  for φn,
k
(
r
) in the C-EPM,
for φn,
k
(
r
) in the C-EPM,  for φn,
k
(
r
) in the B-EPM, and
for φn,
k
(
r
) in the B-EPM, and  for Vps(
r
) , where a0 is the a-axis lattice constant of 4H-SiC (a0 = 0.308 051 nm
33)). The length of one period of the superlattice Lsl is set to be 6Lcell, where the c-axis lattice constant Lcell is 1.008 480 nm.
33) The minimum barrier potential,
for Vps(
r
) , where a0 is the a-axis lattice constant of 4H-SiC (a0 = 0.308 051 nm
33)). The length of one period of the superlattice Lsl is set to be 6Lcell, where the c-axis lattice constant Lcell is 1.008 480 nm.
33) The minimum barrier potential,  , [see Fig. 1(c)] is set to
, [see Fig. 1(c)] is set to  .
.
Figure 2 shows the complex band structures of bulk 4H-SiC by the EPM (blue dotted line) and those by the PBA (red line). As shown in Fig. 2, there is a forbidden region within the conduction band of bulk 4H-SiC along the transport direction. To prevent the electron injection to this forbidden region, we introduce the constant potential region of Vb(z) as shown in Fig. 1.
Fig. 2. Complex band structure of bulk 4H-SiC by the B-EPM (blue dotted line) and B-PBA (red line) for Vb(z) = 0. The right and left panels show the real and the complex bands, respectively. The shaded area represents a forbidden region within the conduction band.
Download figure:
Standard image High-resolution imageFigure 3 shows the energy dependence of the tunneling probabilities by the B-EPM, the B-PBA, and the C-EPM. The calculation results obtained by fitting to reproduce the experimental tunneling currents 20) with the B-PBA are also shown with a black dotted line as pseudo-experimental results. Note that TC-EPM(z) corresponds to the tunneling probabilities for the lower conduction band passing through k = E = 0 in Fig. 2. We see that TC-EPM(z) as well as TB-EPM(z) overestimates the experimental results 20) because of considering the non-parabolicity of the complex bands as we mentioned in our previous study. 21) It should be noted that considering the effect of k xy on TB-EPM(z) leads to improving the reproduction of the experimental result 20) by the EPM. The C-EPM results generally agree with the B-EPM results, but there are some large deviations at a few energy points such as E ≃ −1.46 eV and −1.37 eV. To understand the origin of this phenomena, we plot the complex band structure of the superlattice in Fig. 4. We find some flat real bands appearing, which implies that the resonant tunneling occurs at these energies. The peaks in TC-EPM(z) coincide with the energies where the resonant tunneling occurs in the superlattice structure. These peaks may be a numerical artifact and could be removed. Apart from these peaks, we see that there is not significant difference between TC-EPM(Ez ) and TB-EPM(Ez ). This suggests that we can safely use the WKB approximation with electronic states without considering the barrier potential when calculating the tunneling current in the heavily doped 4H-SiC SBDs.
Fig. 3. The energy dependence of the tunneling probabilities by the B-EPM (blue solid line), B-PBA (red dashed line), and C-EPM (green dots). The experimental results (black dotted line) are obtained by fitting to reproduce the experimental results 20) by calculation within the PBA. Nd and Vr are the donor density and the reverse voltage, respectively. Note that T(Ez ) is calculated in fine energy intervals near the resonant energies of the superlattice. The area between the two vertical gray dashed lines represents the energy region of the allowed band.
Download figure:
Standard image High-resolution imageFig. 4. Complex band structure for the superlattice structure along the transport direction. The in-plane wave vector k xy is assumed to be that at the M point in bulk 4H-SiC.
Download figure:
Standard image High-resolution imageHere, according to Ref. 24, the condition for the approximate tunneling probability by the WKB approximation and the exact probability to have the similar functional forms is that  is sufficiently large, where Δz and
is sufficiently large, where Δz and  are the length of the barrier potential and the mean barrier height, respectively. This corresponds to the tunneling probability T ≪ 1. In the present model, Δz is at least about 4 nm and Φ is larger than 1 eV, leading to T of at most 10−6. This means that T ≪ 1 holds, i.e. the condition is considered to be satisfied. Hence, the present result that it is reasonable to use the WKB approximation for the considered barrier potential is consistent with the discussion in Ref. 24.
are the length of the barrier potential and the mean barrier height, respectively. This corresponds to the tunneling probability T ≪ 1. In the present model, Δz is at least about 4 nm and Φ is larger than 1 eV, leading to T of at most 10−6. This means that T ≪ 1 holds, i.e. the condition is considered to be satisfied. Hence, the present result that it is reasonable to use the WKB approximation for the considered barrier potential is consistent with the discussion in Ref. 24.
Finally, we comment on the possible causes of the discrepancy between our calculation and the experimental results. First, in our model, the electronic states in bulk 4H-SiC are used for those in metals, which could lead to the overestimation of the tunneling probability. Moreover, the barrier potential Vb(z) is simply kept constant at both ends of the Schottky barrier, which may lead to deviations from the actual electronic states. The scatterings, such as electron-phonon scattering, may also influence both the electronic states and transport phenomena. To obtain a definite answer, we have to take all these effects into account.
4. Conclusion
The tunneling probability of heavily doped 4H-SiC SBDs is calculated without using the WKB approximation. First, we calculate the complex bands of bulk 4H-SiC and those of a periodic superlattice model with the barrier potential by the EPM. Then, by making the wavefunctions continuous in the whole region, we determine the transmission wave for a given incident wave and obtain the tunneling probability using the probability current densities for the transmission and incident waves. Comparing the calculated tunneling probability with that by the WKB approximation, we find that there is not much difference between them. These results suggest that we can safely use the WKB approximation with the bulk 4H-SiC electronic states when calculating the tunneling current in the heavily doped 4H-SiC SBDs.
Acknowledgments
This work was supported by JSPS KAKENHI Grant No. JP21H05003.





