Abstract
We discuss chiral structures in self-organizing, artificial, and biological materials. A review of experimental studies and recent advances in the localization of light in chiral structures is given. The behavior of polarized resonant modes in such structures is examined using the example of a one-dimensional photonic crystal containing liquid crystal materials. The anomalous spectral shifts of transmission peaks are interpreted as the contribution of the geometric phase caused by the twisting of the layers of the liquid crystal. The optical Tamm state localized at the boundary between chiral and nonchiral mirrors in the form of a cholesteric layer and a polarization-preserving anisotropic mirror is analytically and numerically described. Considerable attention is paid to the presentation of the properties of localized optical modes in the cholesteric with a resonant metal-dielectric nanocomposite. New possibilities for controlling the properties of the photonic structure are noted, due to the combination of the dispersion of the resonant medium and the intrinsic dispersion of the cholesteric. Attention is focused on controlled hybrid modes in the cholesteric structure formed by the coupling of localized modes. Possible applications and further ways of developing the concept of chiral photonic structures are deliberated.
Export citation and abstract BibTeX RIS
1. Introduction
The term chirality is derived from the Greek word for hand, χειρ, to define mirror symmetry breaking. Both an optical material (in the case of bianisotropy) and a structure with rotational-translational symmetry (e.g., a spatial helix) can be chiral. In this review, we confine ourselves to considering structurally chiral media, i.e., anisotropic media with a rotating optical axis. In the case of performing uniform periodic rotations, such media are referred to as helicoidal or spiral (helical) [1].
Symmetry is a key characteristic considered when designing optical properties. Symmetries can be considered in the order of their violation as the medium departs from a homogeneous state possessing all spatial and temporal symmetries. In photonics, it is usual to speak about crystallographic (translational, reflectional, and rotational) symmetries. Of special interest are structures with periodically varying dielectric properties at the wavelength scale, such as photonic crystals (PCs) [2].
Everyday events in our surrounding world are frequently characterized by disparity in the interaction between two material entities: matter and light (electromagnetic waves). In most cases a linear approximation can adequately describe the situation, the low-energy field having practically no effect on material properties. On the contrary, the matter imposes its structure, symmetrical and topological properties on the field. Constructive interference of periodically recurring reflections (the Bragg effect) gives rise to reflection bands in the transmitted light spectrum. In the case of infinite PCs, such intervals are frequently called photonic band gaps or stop-bands. The anisotropy of chiral photonic structures accounts for the differences among polarized radiation spectra. In a helical photonic structure, the stop-band is manifested only for one circular polarization corresponding to the sign of the helicoid twist [3–5]. Structural defects (point, linear, surface, and bulk defects) are responsible for localization of electromagnetic waves. A localized mode is defined as a bunch of light energy. The language of band structure and dispersion equations of solid state physics is naturally transferred into the description of PC properties. Photonics is peculiar in that typical structures are made mostly by top-down methods, as a rule with a small number of periods. This accounts for edge effects that could be disregarded if the number of periods were greater. Under real conditions, the spatial limitation of photonic structures [6] and dissipation (extinction in the material) results in a localized mode manifesting itself in the form of resonance in the stop-band to which a spectral line of finite width corresponds. The respective concentration of light energy is the secondary photonic structure composed of photons themselves rather than atoms, providing a basis for the formation of new classes of miniature optical elements, such as photonic crystals [2, 7] and metasurfaces [8, 9], and thereby contributing to the further development of photonics as the science of the technological application of matter–light interactions [10]. It encompasses a wide range of research, from optoelectronics and information transmission [11] to display technologies [12], from ultrahigh-resolution imaging [13] to optical cloaking [14], from photovoltaics [15] to photosynthesis and biological photonic structures [16–18]. What had recently been considered impossible has now turned into workable technologies and services. Recent advances in nanoscience and nanotechnologies made optical frequencies as readily accessible as radiofrequencies and photonic devices highly competitive with radioequipment in terms of hardware components. Constituent elements of photonic engineering, photonic structures, are optical media inhomogeneous at the wavelength scale in which traditional materials are combined with alternative ones exhibiting record-breaking optical properties [19].
Sustainable interest in chiral photonic structures is due to their physical characteristics, their important role in biological systems, and a great variety of applications. Much attention is given in the literature to investigations of the properties of localized modes in chiral photonic structures and their unusual optical manifestations. Localized optical states together with chirality serve as unifying elements in the systems considered in the present review focused on spectral and polarization properties of certain photonic structures that lack mirror symmetry. New polarization properties in localized resonant modes are described for such chiral structures associated with manifestations of the Mauguin effect, optical activity, selective Bragg reflection, and the geometric phase. Special attention is focused on the properties of helical structures, widespread in self-organizing and biological materials, where they play an important role in coloration, photosynthesis, and plant protection from UV radiation. The optical Tamm state localized at the boundary between chiral and nonchiral mirrors in the form of a cholesteric layer and a polarization-preserving anisotropic mirror is described. Equal attention is paid to the properties of localized optical modes in cholesterics with resonant metal-dielectric inclusions. Novel opportunities opening up for the effective control of spectral properties of resonant PC structures due to the combination of cholesteric intrinsic dispersion and resonant medium dispersion are outlined. Controlled hybrid modes in the cholesteric structure formed by the coupling of localized modes are described.
2. Chiral structures
2.1. Chiral structures in self-organizing and biological materials
Chiral molecules arranged in several layers give rise to the structural chirality of optical materials. They create a helical periodicity like that produced by a twisted thread laid in a few rows. In this case, different orientations of a single anisotropic material alternate, and no alternation of several different materials is required. The addition of an odd number changes parity. This rule holds for mirror parity too (as shown by Yu P Solov'ev in Ref. [20]). A nonchiral object acquires this property as it comes in contact with a chiral one. Chirality fills up a space through all means of interaction (mechanical, quantum-chemical, electromagnetic).
Light localized on such periodicity also acquires chiral properties. Diffraction occurs along a smooth gradient formed by the rotating optical axis rather than at sharp interfaces between materials with different impedances determined by a permittivity tensor. The wave impedance, i.e., the ratio of complex amplitudes of electric and magnetic field, remains constant across the structure. For a diffracting eigenwave, field strength vectors create, at any fixed moment of time, an exponentially narrowing helicoid with the same pitch as in a helicoid of the photonic structure, λ = p (Fig. 1). It is noteworthy that the space period for such a wave is preserved, despite frequency variation. A wave for which the strength of the electric field is directed along the axis with the minimal refractive index n− corresponds to the upper frequency limit. The frequency can be written in the form ω+ = 2πc/n−p, as in the case of light in a homogeneous medium. A gradual decrease in light frequency leads to screw pitch elongation for circular polarization in a free space. However, such lengthening is compensated by rotation: the field strength helicoid rotates toward the optical axis with a high refractive index, while the screw pitch remains unaltered. When the strength is oriented along the optical axis with the highest refractive index n+, the lower limit of the band gap is reached. Here, ω− = 2πc/n+p. Further compensation of the lengthening becomes impossible, and the wave ceases to diffract.
Figure 1. (Color online.) In a helicoidal structure, circular Bragg diffraction forms a diffracting standing wave with the same helix pitch as in the structure's helicoid, λ = p. The cholesteric director is shown in blue and green colors, electric field strength in red and yellow. The angle between them does not change with depth; however, it rotates as the light frequency varies and thereby compensates the change in wavelength.
Download figure:
Standard imageIn other words, frequency variations cause the optical density to change, while the wavelength remains unaltered. The spatial periodicity imposes itself on the temporal one. This conclusion goes beyond the framework of the concepts of structures from isotropic materials with constant optical density; therefore, it is more convenient to describe waves in terms of frequencies than in terms of wavelengths. In the case of a helicoid structure, the description of an electromagnetic field in terms of wavelengths is preferred [21] (see Section 3.1.2. for details).
In animate nature, chiral structures can be formed in a self-organization process following the bottom-up principle. The same is true for liquid crystals (LCs) [22]. Chiral LCs include cholesteric LCs (chiral nematic LCs), the blue phase of chiral LCs, smectic C*, and widely tunable heliconical structures [23].
Natural colors develop in two ways: chemically (by pigment utilization) and structurally (based on layered media and diffraction gratings). Nonpigmentary structural coloration is characterized by the iridescence produced by light scattered from variably sloping surfaces. Keratinous structures impart bright structural color to birds' feathers (peacock, magpie), squamate reptiles' skin (snakes, lizards, chameleons), and mammalian hair (water vole, mole); the calcareous aragonite of mollusks is responsible for the brilliancy of the nacre and the pearl; chitin in the butterfly's wing scales causes iridescence of certain species (Morpho amathonte, Urania moth), as it does in the shining integument of various beetles, such as the sacred scarab (Scarabaeus sacer), the rose chafer (Cetonia aurata), and the golden ground beetle (Carabus auratus) [16]. Some of these structures possess optical anisotropy and chirality. The possibility of maintaining periodicity using a homogeneous material assures considerable savings for wildlife [24–29]. The formation of hard chitin and cellulose structures resembles the self-organization of chiral liquid-crystalline structures in that induration occurs slowly due to minimization of free energy in the course of chiral ordering [24]. Possible functions of such structures include thermoregulation, mimicry, and intra-species communication. A change in the spatial period of the structure results in the alteration of its color [30]. Gradual variation of the period broadens the stop-band spectrum [31, 32]. Because a helicoidal structure reflects only one of the two circular polarizations of light, reflection of nonpolarized light is less than 50%. The total reflection of nonpolarized light is assured by both the combination of oppositely twisted helicoidal structures [33] and the placement of the half-wave phase plate between unidirectionally twisted helicoid structures [27]. The latter option finds implementation in chiral chitinous structures where the left sign of the helicoid is preferable. Figure 2 shows Chrysina resplendens, a golden scarab beetle found in South America [29], and the micrograph of a fragment of its reflecting integument composed of left-twisted chitinous structures separated by untwisted layers functioning as a half-wave phase plate. Such structure can reflect more than half of the nonpolarized light [26].
Figure 2. (Color online.) (a) Chrysina resplendens, a representative of lamellicorn beetles (Scarabaeoidea), native to South America, (b) TEM micrograph of a fragment of the oblique section through the reflecting integument (cuticle) including the unidirectional layer (u) and the adjacent helicoidal regions (h1, h2). The parabolic pattern is typical of oblique sections through the helicoidal cuticle [34]. The pattern direction does not change above or below the unidirectional layer, which suggests conservation of twist direction. The period of the structure (helicoid half-pitch) is indicated by the black bar. Left-circularly polarized light is reflected by the first layer, right-circularly polarized light penetrates into the second layer (the half-wave plate) and is converted into left-circularly polarized light; it is reflected by the third layer and again undergoes transformation into right-circularly polarized light on the way back. The photo of the beetle and the micrograph are borrowed from Ref. [29].
Download figure:
Standard imageCellulose nanocrystals find numerous applications [35]. Cellulose-based structures in a plant leaf provide a good illustration of chirality. For example, leaves of young plants Danaea nodosa are known to form chiral cellulose structures with a pitch p ∼ 320 nm (Fig. 3), which for the refractive index of 1.53 produces iridescence in the form of blue-green reflection near the wavelength λ = np = 490 nm [24, 36, 37]. A similar chiral structure and its reflection spectra are found in spikemoss (Selaginella willdenowii) [38] and fruits of the tropical Pollia condensata plant from west Africa [39]. These structures are supposed to protect plants from UV radiation and stimulate their photosynthetic activity. The former ability manifests itself for the wavelengths corresponding to the stop-band of the structure. Blue leaves of Begonia pavonina were shown to recover after light irradiation faster than green ones [36, 40]. The mountain flower edelweiss is at high risk of UV-induced mutations and its reproductive tissues need protection [41]. An analogous protective function can be ensured by absorption of UV radiation in pigments [36, 42]. Another potential function of such structures is to promote photosynthesis. The leaves of certain plants growing in shaded areas focus light by microlenses [43, 44]. Focusing is possible by the planar chiral layer of an anisotropic material in the form of a cycloidal diffraction wave plate [45, 46], a so-called Fresnel lens [47], or a geometric phase lens [48] which can also be present in biological subjects [49]. The lenses focus light by altering the wave front curvature. Both convex and concave lenses change the curvature as a result of different phase incursion at parts differing in thickness. Although flat lenses are uniformly thick over the entire area, their differently oriented anisotropic layers can induce different geometric phases of the wave (see Section 3.1.1 for details). Plant cell walls vary in thickness from 100 nm to 1 μm and, unlike those in animal tissues, provide rigidity and shape to the cell. Moreover, they change the properties of light penetrating into the cell owing to the presence of cellulose fibers of various structures [50], surprisingly similar to the structure of a flat geometric phase lens.
Figure 3. (Color online.) Opalescent blue leaf of the fern Danaea nodosa growing in shaded areas of tropical rainforests (Central America). (a) Its iridescent young leaves gradually become green with advancing age. (b) The color of the leaves is due to Bragg reflection from the chiral structures in many-layer outer walls of the leaf cells. (From Ref. [36]).
Download figure:
Standard imageLight can be concentrated not only transversely to the direction of propagation as in lenses but also in the longitudinal direction as in optical resonators. Such resonators can be formed by layered structures in plant cells; they are also supposed to be involved in photosynthesis [17, 18].
2.2. Artificial chiral structures
Cholesteric liquid crystals (CLCs) are one-dimensional photonic crystals with unique properties, such as a wide transparency region, strong nonlinearity, and high sensitivity to external fields [1, 22]. A change in temperature, application of electromagnetic fields or mechanical stresses can significantly alter the cholesteric helix pitch, position, and width of the band gap. CLCs are qualitatively different from other types of LCs, because they possess reflection which is caused by diffraction and is polarization-selective. CLCs have a photonic band gap (stop-band) for light propagating along the helical axis with circular polarization coincident with the cholesteric helix twist. Reflection of light of such polarization from a cholesteric does not change the sign of light wave polarization. Radiation with opposite circular polarization does not undergo diffraction reflection and passes through the medium virtually unaltered.
Helical ordering is the most common and well-known form of chiral structures in the form of a one-dimensional anisotropic photonic crystal with periodicity along a single spatial coordinate. The structure along the remaining two coordinates can be regarded as uniform. Such nano- and microstructures are formed in a self-organization process based on the bottom-up nanotechnology. In this sense, the industry of chiral liquid crystals is a nature-like technology, even if the majority of synthetic liquid crystals are highly poisonous, unlike natural ones. The industry of LC displays began from the twisted-nematic optical shutter technology for which chirality of the structure is of fundamental importance. At present, this technology is supplemented by in-plane switching (IPS) and multidomain vertical alignment (MVA) [12]. Helical structures, including sculptured thin films [5], can be manufactured by top-down nanotechnology. Since such structures are made to be instantly hard, they are untunable but more resistant to variations in temperature and some other parameters and easier to configure (e.g., creating a defect or pitch gradient).
A cycloidal diffraction wave plate (Fig. 4) holds a special place among one-dimensional structures other than helical ones. Such structures can collect light like lenses [46]. The plate is formed by a nematic LC by means of photo-orientation on the surface [45, 51, 52], which opens the way for control and rearrangement of the diffraction pattern or hologram.
Figure 4. Model of optical axis modulation in (a) a CLC and (b) a cycloidal diffraction wave plate. Local orientation of the optical axis is represented by line segments. The system of coordinates is chosen so that the x and y axes are in the plane of the substrate, while the z axis is directed normally to it. (From Ref. [51].)
Download figure:
Standard imageTwo-dimensional chiral structures are represented by diffraction gratings, wave plates, and metasurfaces periodic in two directions of their plane and restricted in the third dimension. Diffraction wave plates can be created by changing light polarization and photo-orientation. Another method of fabricating such structures makes use of electro-hydrodynamic instability [53, 54] (also producing fingerprint structures) by oblique ordering of uniformly lying helix CLC [55].
The blue phase of CLCs for which temperature-stable materials have been found recently with the use of polymer networks is of special interest among 3D periodic chiral structures. One more example of such structures is gyroid, a three-dimensionally structured film with zero curvature at each point [56]. The gyroid structure was described mathematically in 1970. Thereafter, it was synthesized and discovered in butterfly wings. Photonic topological insulators have been proposed based on three-dimensionally structured bianisotropic materials [57].
Finally, one more class of anisotropic structures (colloids and nanocomposites based on oriented nonspherical metal particles) finds application in medicine for the diagnosis and treatment of neoplasms [58]. Worthy of special note are applications that will become possible using chiral metamaterials [59]. An important contribution to terahertz electronics has come with the advent of the first artificial molecules with chirality rapidly switched from a right-handed to a left-handed orientation by a beam of light. [60]. The terahertz range is of great scientific and practical interest, because it includes vibrational and rotational spectra of complex organic molecules, e.g., DNA.
3. Optical fields
3.1. Peculiarities of optical field distribution in chiral structures
3.1.1. Polarization and geometric phase
Anisotropy and chirality of photonic structures give rise to altered polarization of light propagating in them. A notable specific feature related to polarization in chiral structures is the geometric (topological) phase [61]. The geometric phase is defined as the phase acquired when an oscillatory system travels along a closed trajectory in the parameter space. The notion of a geometric phase, first introduced in optics [62, 63] and mechanics [64], presently includes, in addition, various phenomena of quantum and relativistic physics [65, 66].
In recent years, photonics has experienced another spike of interest in topological ideas [67, 68] due to the popularity of the graphene model and the topological insulator concept [69], on the one hand, and progress in optical technologies, on the other hand. For example, recently in the polarization optics the 3D structure of the light polarization field with nontrivial topology was measured directly [70].
The geometric phase in a twisted nematic not only allows explanation of polarization phenomena [71] but is also employed to design wave fronts using so-called Pancharatnam–Berry-phase optical elements [45, 72]. The geometric phase can be manipulated regardless of the total phase, which allows it to be used for shifting frequencies in modulators by adding the phase plate mechanical rotation frequency to the field frequency [73–75]; also, switching with the use of a ferroelectric LC is possible [76]. The authors of Ref. [77] proposed a waveguide in which a geometric phase is used instead of the refractive index gradient for total internal reflection.
A simple example of a geometric phase in polarization optics is provided by the QHQ-device depicted in Fig. 5. A full-wave phase plate (b, c, d) having a vertical axis is placed between parallel polarizers (a, e) turned 45° with respect to the vertical plane. The plate is split into two quarter-wave parts (b, d) and the half-wave part at the center (c). The incident radiation passing through the polarizer (a) becomes linearly polarized. The quarter-wave plate (b) makes polarization circular. The half-wave plate (c) changes the sign of circular polarization. Then, inverse transformation takes place. The quarter-wave plate (d) makes light linearly polarized again, after which it passes unobstructed through the polarizer (e) and leaves it. The central half-wave plate (c) can rotate in its plane, and the phase of the passing circular radiation is essentially determined by optical axis rotation. Evidently, for vertical and horizontal positions of the optical axis (0 and π/2) the phase of the outgoing radiation differs by π. Generally speaking, the change in the radiation phase corresponds to the double angle of rotation. The above qualitative considerations can be justified by the rigorous quantitative description in the algebraic language of Jones matrices and geometric language of the Poincaré sphere [61, 75].
Figure 5. QHQ-device consists of two linear polarizers (a) and (e), two quarter-wave Q-plates (b) and (d), and one half-wave H-plate (c). A turn of the H-plate through an arbitrary angle does not affect polarization of outgoing radiation but changes its phase by a double rotation angle. (From Ref. [75].)
Download figure:
Standard imageIf the position of the optical axis is neither vertical nor horizontal, the QHQ-device becomes chiral. Mirror reflection of the QHQ-device with polarizers corresponds to the right-left circular polarization conversion. The chirality of the structure and the optical field changes while the sign of the geometric phase remains unaltered. In other words, the geometric phase in this case is even with respect to chirality sign, i.e., it has the same sign for right- and left-hand structures. A more complicated case of the nonadiabatic geometric phase also even with respect to chirality sign is described in Section 3.2.2. On the other hand, chirality of the optical field can be altered without changing structure chirality by turning both polarizes through 90° and changing right- to left-handedness of circular polarization. In this case, the geometric phase is odd with respect to the structure chirality sign, i.e., it has different signs for right- and left-hand turns of the half-wave plate.
For polar holography and a polarization diffraction grating (Fig. 4b), phase control is more common than light transmission control (what is meant here is the geometric phase determined by a change in polarization in an anisotropic medium rather than the dynamic phase depending on the medium thickness).
3.1.2. Peculiarities of optical field distribution in helical structures.
Let us turn to a mathematical description of light propagation in a helical structure confining ourselves to the case of normal incidence of the light propagating along the z axis of the helicoid. The Maxwell's equation in optics is usually written at permeability μ = 1:

The wave is described by vector E of complex amplitudes for electric field components in orthogonal directions x and y. Projection  of the permittivity tensor
of the permittivity tensor  onto the xy plane in the cholesteric depth z has the form
onto the xy plane in the cholesteric depth z has the form
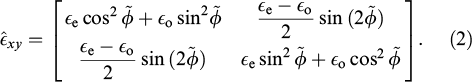
Here, the optical axis coincident with the cholesteric director is described by the twist angle  measured from the x axis toward the y axis; p is the helix pitch. Positive and negative pitches correspond to right- and left-handed helicoids, respectively.
measured from the x axis toward the y axis; p is the helix pitch. Positive and negative pitches correspond to right- and left-handed helicoids, respectively.
To find the simplest solution, the symmetry between electric and magnetic field intensities needs to be restored and permeability  taken into consideration. The explicitly written magnetic field strength H increases the field vector dimensionality from 2 to 4:
taken into consideration. The explicitly written magnetic field strength H increases the field vector dimensionality from 2 to 4:

Accordingly, the order of the differential equation is reduced from second to first. Suppose that the principal axes of the magnetic and electric permeability tensors coincide. This assumption makes possible a transition to the orthonormal basis u, ν, z uniformly rotating together with the cholesteric director, so that the u axis always goes along the director:

In the Berreman method [78], Maxwell's equations in a stationary case take a form more general than Eqn (1):

Matrix  for the rotating basis formulated in [79, 80] can be reduced as follows:
for the rotating basis formulated in [79, 80] can be reduced as follows:

where  is the dimensionless wavelength,
is the dimensionless wavelength,  is the dimensionless coordinate, and λ0 is the wavelength in a vacuum. There are different units for electric and magnetic strengths in the SI system; therefore, they have to be normalized via the vacuum impedance
is the dimensionless coordinate, and λ0 is the wavelength in a vacuum. There are different units for electric and magnetic strengths in the SI system; therefore, they have to be normalized via the vacuum impedance  . The differential transfer matrix
. The differential transfer matrix  can be just as well written in the nonrotating basis [78, 81].
can be just as well written in the nonrotating basis [78, 81].
Four normal waves correspond to Eqn (3). They are determined by the eigenvalues of matrix  having the sense of refractive indices n. The respective eigenvectors of matrix
having the sense of refractive indices n. The respective eigenvectors of matrix  have the sense of polarizations J0. Based on the helicoid axis reversal symmetry, these four normal waves can be classified as two pairs of counter-directed waves. In each pair, the wave with a larger refractive index has a lower phase velocity. This wave will be called slow and the other wave fast:
have the sense of polarizations J0. Based on the helicoid axis reversal symmetry, these four normal waves can be classified as two pairs of counter-directed waves. In each pair, the wave with a larger refractive index has a lower phase velocity. This wave will be called slow and the other wave fast:

Substituting the solution for  into Eqn (3) yields
into Eqn (3) yields

where  is the unit matrix and superscript '+' in
is the unit matrix and superscript '+' in  is omitted. The refractive indices are as follows:
is omitted. The refractive indices are as follows:
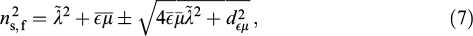
where d μ = (
μ = ( eμo –
eμo –  oμe)/2 is the antisymmetry of permittivities, and the overbar defines the arithmetic mean over ordinary and extraordinary permittivities:
oμe)/2 is the antisymmetry of permittivities, and the overbar defines the arithmetic mean over ordinary and extraordinary permittivities:
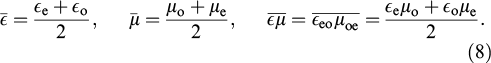
The scale invariance of Maxwell's equations (3) and normalization of material parameters (see Supplement in [80]) reduce the structure to two crucial parameters: electric and magnetic anisotropies

Consider the case of equal anisotropies δ = δμ. The clarity and elegance of this single-parametric set of structures should compensate the difficulty of their physical realization in the optical range for the reader [82]. Dispersion equation (7) is simplified due to the symmetry of permittivities d
= δμ. The clarity and elegance of this single-parametric set of structures should compensate the difficulty of their physical realization in the optical range for the reader [82]. Dispersion equation (7) is simplified due to the symmetry of permittivities d μ = 0:
μ = 0:

Without further loss of generality, we assume the normalization  . Then,
. Then,  . In other words, the permittivity is normalized to the geometric mean of
. In other words, the permittivity is normalized to the geometric mean of  o and
o and  e:
e:  , the arithmetic mean being not less than unity. The second term in the right-hand part of the dispersion equation becomes squared anisotropy
, the arithmetic mean being not less than unity. The second term in the right-hand part of the dispersion equation becomes squared anisotropy  . Anisotropy here is akin to the standard deviation of permittivities:
. Anisotropy here is akin to the standard deviation of permittivities:

The dispersion curve of Eqn (11) is a hyperbola, and pure imaginary values give rise to an exact circle in the stop-band. Dispersion equation (11) can be written for both the refractive index and the wave vector:
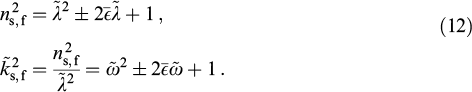
This symmetry of  and
and  dispersions appears to have been noticed for the first time in Ref. [21]. It indicates the symmetry of longwave and shortwave limits (Fig. 6). In the longwave limit, the medium is homogeneous, and a manifestation of anisotropy reduces to polarization rotation opposite to the helix twist. The negative optical activity ceases as the situation comes close to the static field case
dispersions appears to have been noticed for the first time in Ref. [21]. It indicates the symmetry of longwave and shortwave limits (Fig. 6). In the longwave limit, the medium is homogeneous, and a manifestation of anisotropy reduces to polarization rotation opposite to the helix twist. The negative optical activity ceases as the situation comes close to the static field case  . It is not identical with natural optical activity, since normal waves are not purely circular [83]. In the shortwave limit
. It is not identical with natural optical activity, since normal waves are not purely circular [83]. In the shortwave limit  , the symmetric positive optical activity is supported by the Mauguin waveguide regime. Violation of the equal anisotropies condition, δ
, the symmetric positive optical activity is supported by the Mauguin waveguide regime. Violation of the equal anisotropies condition, δ ≠ δμ, breaks symmetry, as shown by the dashed lines in Fig. 6. Ordinary and extraordinary waves can then be distinguished in the high-frequency limit equivalent to helix untwisting. Both positive and negative optical activities of a helicoidal medium can be described either in the algebraic language of Jones matrices or in the geometric language of Mauguin's rolling cone [83–85].
≠ δμ, breaks symmetry, as shown by the dashed lines in Fig. 6. Ordinary and extraordinary waves can then be distinguished in the high-frequency limit equivalent to helix untwisting. Both positive and negative optical activities of a helicoidal medium can be described either in the algebraic language of Jones matrices or in the geometric language of Mauguin's rolling cone [83–85].
Figure 6. (Color online.) Symmetry of dispersion curves. (a) Wavelength  as a function of refractive index |nf, s|. (b) Frequency
as a function of refractive index |nf, s|. (b) Frequency  as a function of wave number
as a function of wave number  . The blue curve denotes a fast wave, the purple curve a slow wave. The solid line refers to the solution of dispersion equations (12) for
. The blue curve denotes a fast wave, the purple curve a slow wave. The solid line refers to the solution of dispersion equations (12) for  e = μe = 3/2,
e = μe = 3/2,  o = μo = 2/3, δ
o = μo = 2/3, δ = δμ. The semicircle is a diffracting wave for which the refractive index acquires purely imaginary values |nf| = Im (nf). The Mauguin regime,
= δμ. The semicircle is a diffracting wave for which the refractive index acquires purely imaginary values |nf| = Im (nf). The Mauguin regime,  , is symmetric to the homogenization regime, ω ⪡ 2π. The dashed line is the solution of dispersion equation (7) for
, is symmetric to the homogenization regime, ω ⪡ 2π. The dashed line is the solution of dispersion equation (7) for  o = 2/3,
o = 2/3,  e = 3/2, μe = μo = 1. The symmetry is broken.
e = 3/2, μe = μo = 1. The symmetry is broken.
Download figure:
Standard imageFigure 7. Chiral anisotropic medium placed in a resonator with nonchiral mirrors.
Download figure:
Standard imageFigure 8. (A) Photonic band gap of a PC–LC structure for light with polarization transverse to the predominant direction of LC molecules. Solid line — experiment, dotted line — theory. Bottom: an extended scale showing four transmittance peaks. (B) Calculated transmission spectrum of nonpolarized light depending on the twist-cell voltage. Black color corresponds to transmission. Ovals encircle areas of avoided crossing between T-mode no. 69 and L-modes nos (a) 74, (b) 73, (c) 72, (d) 71, and (e) 70. Dashed lines separate four conditional voltage ranges exhibiting different types of mode behavior.
Download figure:
Standard imageThus, it is possible to classify effects of a helical photonic structure on optical fields by grouping phenomena into three classes according to the ratio of light wavelength λ inside the structure and helix pitch p:
- λ < p — negative optical activity, polarization rotation opposite to the helix twist;
- λ > p — positive optical activity, Mauguin's effect, linearly polarized light is adiabatically controlled by the helix twist;
- λ = p — equality is conserved within the frequency range
 for an incident circularly polarized wave with the sign coincident with the helix twist sign; selective volume reflection (Bragg circular diffraction) takes place.
for an incident circularly polarized wave with the sign coincident with the helix twist sign; selective volume reflection (Bragg circular diffraction) takes place.
Let us focus on the circular Bragg diffraction at λ = p. The refractive index nf for a fast wave acquires purely imaginary values. This is the case when the phase velocity becomes infinite and the group velocity meaningless. It would be reasonable here to write dispersion equation (11) in the form of a trigonometric identity where a certain angle χ ∈ [0,π/2] acts instead of the wavelength:
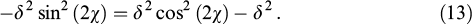
This means that at the wavelength

the refractive index of the fast wave nf = iδ sin (2χ) describes full reflection in the bulk cholesteric. This wave is conventionally called a diffracting wave [1]. The spatial form of the diffracting wave shown in Fig. 1 can be derived from the nontrivial solvability of Eqn (6). It can be shown as in [21] that both the incident and the reflected waves have circular polarization with the sign coinciding with the helix twist sign. At a fixed point in space, intensity vectors of the incident and reflected waves rotate in opposite directions. The phase difference between them is 2χ. For a superposition of these waves, the electric and magnetic fields are oriented at the same angle -χ to the optical axis of the helical structure. The problem of polarization is closely related to that of the absence of nodes and antinodes in such a standing wave (see Fig. 9 below).
Figure 9. Local field intensity in the defect L-mode, i.e., the squared amplitude of the electric field strength. Calculating the mode number encounters difficulties, because standing wave nodes are smeared out. Parameters are the same as in Fig. 8; the thickness of the defect is diminished five-fold for clarity.
Download figure:
Standard imageThe selectivity of reflection of only one of the two circular polarizations is compensated by the enhanced reflective power compared with that of a scalar (nonchiral) Bragg reflector consisting of a few layers of isotropic materials. The measure of reflectivity is radius r of the semicircle in Fig. 6. This dimensionless radius with the sense of the extinction coefficient determines not only the depth of the stop-band but also its width. It makes an exponential contribution to the Q-value and the laser oscillation threshold of resonators. In the case of equal anisotropies, this radius (in accordance with Eqn (10)) is equal to the anisotropy: r μ = δ. In the absence of magnetic anisotropy, e.g., in a cholesteric, the circle undergoes deformation proportional to electric anisotropy, and its radius decreases by roughly half, r
μ = δ. In the absence of magnetic anisotropy, e.g., in a cholesteric, the circle undergoes deformation proportional to electric anisotropy, and its radius decreases by roughly half, r ≈ δ/2. The reflective power of a scalar Bragg reflector is optimal when optical paths in the layers are of equal length, and each alternating layer holds a quarter-wavelength. In this case, the stop-band width is given by expression [86]:
≈ δ/2. The reflective power of a scalar Bragg reflector is optimal when optical paths in the layers are of equal length, and each alternating layer holds a quarter-wavelength. In this case, the stop-band width is given by expression [86]:
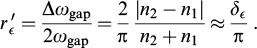
This means that at equal periods and contrasts of the refraction index, the frequency interval of reflection of a scalar structure is π/2 times narrower than in a cholesteric, while the thickness of the entire structure needed for a fixed light reflection value at the frequency in the stop-band center becomes greater. Two factors in this comparison are of importance. First, a helical structure in the sense of permittivity tensor (2) considered in two orthogonal projections on planes xz and yz represents two sinusoidal profiles displaced by the quarter-pitch of a helicoid relative to each other. Both profiles independently contribute to the reflection of the diffracting wave. It doubles the reflective power and quantitatively compensates for reflection of only half of the polarized light by the helical structure. For a scalar reflector with the sinusoidal profile,  . Second, the reflectivity of the stepwise profile of the alternating layers at equal anisotropies is stronger than that of the sinusoidal profile,
. Second, the reflectivity of the stepwise profile of the alternating layers at equal anisotropies is stronger than that of the sinusoidal profile,  , because the first term of Fourier expansion of the stepwise profile has an anisotropy amplitude 4/π times that of the stepwise profile itself. A reflector consisting of two similarly thick helical structures with opposite chirality signs reflects arbitrarily polarized light as efficiently as the beetle integument shown in Fig. 2. Its reflective power with respect to the thickness is similar to that of the scalar reflector with the sinusoidal profile and twice that with respect to the width.
, because the first term of Fourier expansion of the stepwise profile has an anisotropy amplitude 4/π times that of the stepwise profile itself. A reflector consisting of two similarly thick helical structures with opposite chirality signs reflects arbitrarily polarized light as efficiently as the beetle integument shown in Fig. 2. Its reflective power with respect to the thickness is similar to that of the scalar reflector with the sinusoidal profile and twice that with respect to the width.
A variety of complicated problems can be addressed based on the simplest models. Dispersion equation (12) for a helical structure gives dispersion curves in the form of conical sections. Such an exact solution can be compared with another possible analytical solution for the case of a step-index profile. Here, the dispersion curve of the Rytov equation [87] only roughly corresponds to a parabola (see Section 6 in [86]). The solution proposed by Abeles [88, 89] comes from joining the Rayleigh waves at the interfaces and raising the respective matrix to the power through the Chebyshev identity. The simplicity of helical symmetry is attributable to the smoothness, as opposed to discreteness of crystal translational symmetry. The solution of dispersion equation (7) for cholesterics is in excellent agreement with the measured transmission [90] and luminescence [91] spectra. The discovery of this solution has a remarkable history [92–95]. The author of [96] treats it as a paradigmatic case. It is poorly known and as a rule rarely mentioned in classical studies on wave physics in one-dimensional periodic and layered media [97, 98]. Many authors confine themselves to the generality of the Hill scalar equation
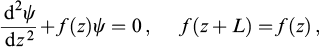
the simplest case of which is the Mathieu equation for harmonic potential f(z) = cos (kz) that has no analytical solution [99].
3.2. Localized modes in chiral structures with nonchiral mirrors
The simplest example of light localization is a standing wave that needs only a flat wave source and a mirror on its propagation path to appear. In the case of two plane-parallel mirrors of a Fabry–Perot resonator, part of the standing wave is confined inside the resonator cavity. As a matter of fact, to localize light within part of the space it needs to be surrounded by mirrors. The present section is focused on structures for which mirrors remain nonchiral (conventional), but the region of localization contains chiral material (Fig. 7). We shall consider a one-dimensional structure in the form of a Fabry–Perot resonator containing an anisotropic material with the rotating optical axis.
Of special interest is the study of an LC placed inside a Fabry–Perot resonator where the easy LC control by low electric voltages is combined with the high resolution power of the device. This allows controlling the main characteristics of the passing light, including transmission [100–103], phase [104], and polarization [105]. The last property is usually controlled in the adiabatic Mauguin's waveguide regime [84] in the twist layer of a nematic LC (twist-cell). The twist-nematic Fabry–Perot resonator described in [106] used for the purpose is referred to as a twist-resonator below.
The principal method for modeling the twist-resonator is the formalism of complex vectors and matrices of dimension 2 developed by Jones [107]. The Chebyshev ratio for raising matrices to power as proposed by Abeles [88, 89] was successfully used for both layered and anisotropic media [108–110]. As a rule, it is sufficient to describe the eigenwave (optical mode) that keeps its shape as it passes through the medium. A set of eigenwaves is characterized by eigenvectors and eigenvalues of Jones matrices. A different approach to finding eigenwaves is the solution of a system of ordinary differential equations like Riccati equations [111–113]. In the framework of the coupled mode theory and mode analysis, this approach is equivalent to the matrix approach [10].
Taking account of anisotropic reflection in the bulk of LC allowed generalizing the formalism to matrices of dimension 4 [78, 114, 115]. That kind of generalization is necessary for such media as chiral LCs [116–119], thin twist-cells, and other media with sharp variations of dielectric characteristics at the wavelength scale [120–123]. However, a few dozen wavelengths as a rule fall on the twist-cell length, and permittivity changes gradually; therefore, the Jones formalism ensures a good approximation. It was used to describe the behavior of the twist-resonator at high [106] and low [113, 124] strengths. The relationship between these two limiting cases is described in [125] and generalized in [126]. Another approach to the solution to this problem consists in the replacement of the many-layer medium with a homogeneous anisotropic plate [127]. An independent method represented in [84, 128] makes use of a different mathematical apparatus, namely the group theory and phase space. Moreover, the twist-resonator can be regarded as an anisotropic defect of a one-dimensional photonic crystal [129–132] that can be made from a liquid crystalline material [133, 134].
To detect an optical response, it is necessary to know the LC orientation. To the best of our knowledge, this problem has no general analytical solution for a twisted structure under an electric voltage, even in a one-dimensional case. Simulation of experimental spectra requires a numerical solution [135]. In this case, unlike that of a cell with an LC oriented in a single plane [136], the twist causes coupling between optical modes and is apparent in the observed spectra as their avoided crossing. The description of mode number by the number of standing wave antinodes becomes problematic, because there are no antidotes in circularly polarized standing waves [135, 137]. Reference [138] proposes a method to eliminate mode coupling with the use of anisotropic mirrors. An original theoretical solution of the paradox related to the jump of the mode number due to the binding on the mirror is reported in [124].
The validity of an analytical description of the twist-resonator structure unaffected by electric voltage was confirmed experimentally in [85, 135]. The first result of the LC optical axis twist is the coupling between o and e traveling eigenmodes that makes them elliptically polarized. However, the radiation of these modes leaving the resonator is practically linearly polarized [139]. The second unobvious result that follows from the theory concerns the direction of the spectral shift of transmission peaks associated with LC structure twisting. It is proposed to interpret the shift as a nonadiabatic geometric phase incursion during wave passage through the optical resonator. Observation of a spectral shift encounters difficulty due to the presence of four oppositely directed and orthogonally polarized optical waves in the twist-resonator. The positive feedback condition describes the total spectral shift, taking into consideration different types of coupling between these waves. One is LC twisting and the corresponding spectral shift of twisting. Another is coupling of modes reflected from mirrors and the respective spectral shift of reflection that needs to be taken into account and distinguished from the basic effect. The third is reflection (diffraction) in the bulk of the twisted LC deemed insignificant in the approach in question. The setting of the experiment reported in [85] rules out an appreciable influence of parasitic factors other than twisting and reflection on the shift. The available theoretical and experimental data are discussed in greater detail below.
3.2.1. Two series of polarized localized modes
Let us consider a Fabry–Perot resonator consisting of two flat mirrors (see Fig. 7) with their reflecting surfaces facing each other and oriented in the xy plane. The surfaces cross the z axis at points 0 and L. A nematic LC (nematic) is placed between the mirrors. The unit vector of the predominant direction of LC molecules is called the LC director. In the twisted state, the nematic layer is split into plane-parallel sublayers. The director in each sublayer is constant but turns in passing from one sublayer to another. It is supposed that there are no external orienting fields and the twist is uniform, i.e., the director uniformly rotates clockwise in the layer plane. In Fig. 7, the full angle of twist is 80°, but further consideration holds equally well for an arbitrary angle.
The field of the LC director determines the local permittivity tensor at all points of the medium. The axis of extraordinary permittivity coincides with the LC director. Let us consider a nematic with positive uniaxial anisotropy. The ordinary and extraordinary refractive indices correspond (in terms of phase velocity) to slow and fast waves, respectively; they equal ne, o = n ± δn.
Experimental and theoretical studies of defect modes in nematic-filled nonchiral resonators in electric and magnetic fields are reported in [140]. Two series of transmission bands are distinguished in the spectrum. They correspond to the modes in which light polarization is either transverse or parallel to the predominant direction of LC molecules; these are ordinary and extraordinary modes, o- and e-modes, respectively. Application of the external field leads to the inclination of liquid crystal molecules localized far from the boundaries. E-modes undergo essential displacement in fields exceeding the Fréedericksz threshold, while o-modes do not change their position. Twisting of the predominant direction of nematic LC molecules in the PC layer plane creates coupling between defective o- and e-modes. Normal modes can be referred to as L-modes, virtually longitudinal with respect to the predominant direction of the molecules and T-modes almost transverse to it. The situation is complicated by the fact that normal modes change polarization from linear to elliptical, and o-modes become also displaced under effect of the external field.
To calculate the LC structure in a twist-cell under voltage, the variational free energy minimization method was employed. It proved difficult to come to the analytical solution for deformation under the influence of electric voltage. Therefore, the numerical method of minimizing free energy through gradient descent was used. To simulate a spectrum, the following parameters of the structure were chosen: ITO film (nITO = 1.88858 + 0.006 i, dITO = 140 nm), glass substrate (nsub = 1.45), orientant (nPVA = 1.515, dPVA = 1000 nm), defective layer filled with 5CB LC (n|| = 1.701 + 3.9 × 10−4 i, n⊥ = 1.536 + 3.9 × 10−4 i, d = 10815 nm). The thickness of the defective layer does not strictly correspond to the spacer thickness and is found from the distance between spectral peaks (intermode spacing). Materials of the alternating layers were zirconium dioxide (ZrO2) and silicon dioxide (SiO2).
Figure 8A presents an experimental light transmission spectrum for the case of a polarizer oriented across the rubbing direction of the nearest substrate. It shows a second series of minor peaks, besides the main one. There is good agreement between theoretical and observed spectra. Although extinction of materials was considered in the calculations, the spectral peaks turned out to be higher than in experiment due to the weak light scattering by structural inhomogeneities and other imperfections inherent in experimental procedures, including tolerance limits for manufacturing multilayer structures.
Figure 8B presents a calculated transmission spectrum of nonpolarized radiation at the long-wavelength wing of the photonic band gap under increasing cell voltage. The spectrum gives evidence of four stages in the displacement of transmission peaks.
I. 0 < U < UC = 0.78 V. Position of defect modes remains unaltered at voltages below the Fréedericksz threshold.
II. 0.78 V < U < 1.1 V. L-mode peaks move toward shorter wavelengths if the Fréedericksz threshold is slightly exceeded, but the position of T-modes remains virtually unaltered, because the refractive index for them does not change because of molecule inclination.
III. 1.1 V < U < 1.6 V. At high voltages, the middle layer of LC molecules inclines along the light propagation axis. It decreases the medium anisotropy, upsets the Mauguin regime, and enhances the ellipticity of polarization. The coupling of L- and T-modes increases upon reflection from the mirrors. Mode repulsion (avoided crossing) is augmented. Solid ovals in Fig. 8B outline areas where transmission peaks are pushed apart; dashed ovals mark regions of crossing between weakly coupled modes of the same parity. Each avoided crossing changes the mode number by one: +1 for T and −1 for L. In the general case, simple identification of the mode number as the number of standing wave antinodes is inapplicable to elliptically polarized resonant modes, because standing wave nodes are smeared out by the interference of counter-propagating elliptical waves of the same sign (Fig. 9).
IV. 1.6 V < U. At a voltage of twice the Fréedericksz threshold, the middle layer of LC molecules acquires an almost homeotropic orientation along the rotation axis. The molecules cannot create a torque. Therefore, the central layer eliminates the adhesion of near-surface LC layers. Each half of an LC layer returns to its orientation plane. Molecules in the left and right parts of the defect are oriented in horizontal and vertical planes, respectively. L- and T-modes merge and become polarization-degenerate. This regime is called polarization-independent. The refractive index goes down, as the voltage and LC inclination into the homeotropic state increase, while mode doublets move into the short-wavelength region toward the position of the untwisted homeotropic mode with linear polarization. It is shown in Section 3.2.2 that a mode with the same number has an even shorter wavelength at zero voltage.
Let us consider the field in an L-mode localized at the defect (see Fig. 9). Standing wave nodes and antinodes cancel each other out in the center of the defect due to ellipticity of counter-propagating traveling waves that form a standing wave. For example, two counterpropagating waves with identical circular polarization do not have nodes [137].
Table. Complications introduced by taking account of wave coupling.
| Anisotropic medium | Homogeneous | Twisted | Twisted in resonator |
|---|---|---|---|
| Eigenwaves | o (ordinary) e (extraordinary) | to, te | ro, re |
| Eigenpolarization | Linear | Elliptic | Linear at the boundaries, elliptical in the bulk |
The phenomenon under study has a great potential for applications, such as controlling the structures with sharp optical properties and high-precision measurements in excellent agreement with numerical calculations. In addition to purely optical applications, it makes possible highly accurate characteristic of such LC parameters as viscosity and elasticity coefficients.
3.2.2. Nonadiabatic geometric phase and anomalously shifted wavelength of localized modes.
The geometric phase manifests itself in the transmission spectra of chiral structures via the phase matching condition that describes the total spectral shift taking into account various types of wave coupling. One of them of special interest in the present report is LC twisting and its respective spectral shift. Another is mode coupling associated with reflection from mirrors and the corresponding spectral shift of reflection. Wave couplings are responsible for the transition from simple to more complicated wave types listed in the table below and shown in Fig. 10.
Figure 10. Eigenwaves considered at various stages of anisotropy. Polarizations at (a) z = 0 and (b) z = L for φ = 80°.
Download figure:
Standard image(1) The simplest class of eigenwaves comprises o- and e-waves propagating without a change in polarization in a homogeneous anisotropic medium with a constant direction of the optical axis. These waves are characterized by linear polarization either along or across the optical axis.
(2) Twisting of the optical axis causes coupling between o- and e-waves via nondiagonal components of the permittivity tensor. A new class of eigenwaves is represented by to- and te-waves [110]. These waves have elliptical polarization. Ellipticity of polarization is conserved; the principal axes of the ellipse are directed along and across the optical axis.
(3) Resonator mirrors create a coupling between to-, te-waves by changing the sign of ellipticity upon reflection. The right-hand polarized waves become left-hand polarized and vice versa. The third class of eigenwaves consists of ro-, re-waves. These are standing waves localized in the resonator. They have variable elliptical polarization. The principal axes of the ellipse deviate from directions along and across the optical axis. It is remarkable that ro-, re-waves on the mirrors have linear polarization [124, 125]. Their polarization is conserved during reflection. T-, L-modes in Fig. 8 can be regarded with a good accuracy as ro-, re-modes.
The table can be generalized to the case of anisotropic reflection from the mirrors by taking account of the phase difference between the reflected o- and e-components of the field. Anisotropy of reflection takes place even for mirrors from an isotropic material, because the medium inside the resonator is anisotropic. Therefore, polarization of the light leaving the resonator is no longer linear. However, the difference from linearity is as a rule insignificant, which accounts for the lack of its experimental observations [139]. The breaking of spatial symmetry of the twist-cell also contributes to the deviation from linear polarization [126].
Let us introduce the mean phase σ = nk0L, anisotropy phase (angle) δ = δk L, and twist angle φ, where k0 = ω/c is the wave vector modulus in a vacuum, δk = δnk0. Then, the total traveling wave phase is

where υ is the twisted anisotropy phase. This expression is called the Mauguin formula [84]. Dividing both parts by k0L yields effective refractive indices of the twisted medium:
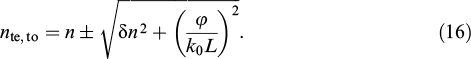
The ellipticity parameter tan Θ = φ/δ reflects the smoothness of twisting relative to the anisotropy value. It corresponds to the adiabaticity parameter of the process known as Mauguin's waveguide regime. The smaller Θ is, the smoother the twisting and the closer the eigenwave polarization to the linear one.
The phase incursion for a cycle in the resonator is equal to the 2ρ angle,

Figure 11a shows dispersion curves of te- and to-waves for φ = π/2 and φ = 0. The o-mode number No = (σ – δ})/2π = 2L/λo plotted along the y-axis is proportional to light field frequency. The phase incursion on the x-axis is the wave vector multiplied by the resonator length. Figure 11a, unlike Fig. 6, shows no splitting of the to-wave branch corresponding to the stop-band of a cholesteric LC for φ = π/2 and σ = υ at point B. The splitting stays beyond the framework of the model because Eqn (15) disregards reflection in the bulk of the LC.
Figure 11. (Color online.) Dispersion curves. The abscissa is the phase incursion proportional to the wave vector kte, toL = σ ± υ. Ordinate axis shows the number of the o-mode proportional to the wave frequency No = 2L/λo. Blue color represents o-, to-, ro-waves, green color e-, te-, re-waves. Calculation parameters: φ = π/2, δn/n = 0.3. (a) No resonator, Eqn (15). Points O and T indicate the third mode frequency for the o-wave and to-wave, respectively. Splitting at point B is not shown. (b) In resonator, Eqn (18). Points T and R correspond to mode 3 frequency for to-wave and ro-wave, respectively. G1 and G2 are Gooch–Terry minima, sin υ = 0; G3/2 is Gooch–Terry maximum, sin υ = ± 1.
Download figure:
Standard imageThe dotted lines corresponding to the phases of o- and e-waves of an untwisted structure, υ(φ = 0) = δ, are straight, since frequency dispersion of the materials is not taken into consideration. Points O and T mark the third mode frequency for o- and to-waves. In such a numeration, the o-mode with the zero number corresponds to point B.
Figure 11b presents the dispersion curves of re- and ro-waves obtained by matching phase (17):
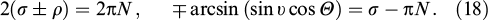
Let us find the spectral shift of the twisted structure relative to the untwisted one and consider the o-wave without loss of generality:
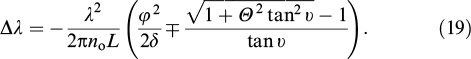
The second term can be neglected far from Gooch–Terry maxima [85, 111], which yields a corollary of the Mauguin formula (15):
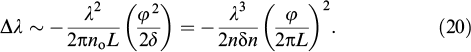
Let us proceed from eigenwave frequency dispersion to the wave shape, phase, and polarization changing with variation of the twist-layer depth [113, 125]. Figure 12 shows smooth shift trajectories of various polarizations of the waves penetrating deep into the twisted layer. The space, the points of which unambiguously correspond to light polarization ellipses, is usually mapped on a sphere of unit radius called a Poincaré sphere. To study right-hand twisted to- and ro-waves, it is convenient to map right-hand polarization on the upper hemisphere of the Poincaré sphere as in Refs [10, 112] but not on the lower one as in [61, 110, 141]. Figure 12b presents a cylindrical projection of polarization trajectories. The ro-wave polarization trajectory RR' is a spherical trochoid. It describes the trajectory of the point rigidly bound to a cone rolling over the plane. Mauguin described such a cone rolling slip-free along the 'equator' of the Poincaré sphere [84]. Geometric calculations related to this cone are termed the Mauguin–Poincaré rolling cone method. It allows the Mauguin formula (15) to be treated as the Pythagorean theorem for the addition of orthogonal components of the cone angular velocity.
Figure 12. (Color online.) (a) Poincaré sphere and (b) part of its cylindrical projection. Angles Φ = 2φ = 0°, 90°, 180°, 270° correspond to y, x – y, x, x + y directions, respectively. Rotation trajectories for φ = 80°: OO' — linear polarizations on the Poincaré sphere 'equator' corresponding to o-wave, TT' — to-wave trajectory on Poincaré sphere parallel of latitude Θ, RR' — ro-wave trajectory, a spherical trochoid. The parameters correspond to the rightmost peak in Fig. 13a, λ = 579.1 nm.
Download figure:
Standard imageParallel displacement of a geometric object over a curved surface results in its rotation about its own axis. A classical example is Foucault's pendulum, whose plane of swing is rotated by the diurnal rotation of the Earth. Similarly, the parallel transfer of polarization over the curved surface of a Poincaré sphere causes state phase incursion, called the geometric phase. This phase originates from a global geometric characteristic (transfer trajectory) and is independent of local characteristics, such as velocity of the state traveling along the trajectory. In the context of polarization optics, the following 'geometric' formula holds for closed trajectories:

where β is the geometric phase, and Ω is the area enclosed by the trajectory on the Poincaré sphere. A rigorous proof with the use of the Stokes theorem is provided by D N Klyshko in Ref. [61]. To recall, the 'geometric' formula corresponds to the Gauss–Bonnet theorem and can be understood as the addition of spherical excesses of triangles making up the enclosed area.
Reference [85] demonstrates the direct relationship between geometric formula (21) and Mauguin's formula (15). Here, only the Aharonov–Anandan nonadiabatic phase corresponding to eigenwave ellipticity works [142, 143]. This minor contribution from the geometric phase should be distinguished from the geometric phase in the zeroth-order adiabatic approximation responsible for the phase jump by π in a cell twisted through π radians.
To simulate experimental spectra (Fig. 13a), zirconium dioxide (ZrO2) and silicon dioxide (SiO2) were used as materials for alternating layers (just as in Fig. 8). The thickness of layers making up dielectric mirrors was 83 nm for SiO2 and 66 nm for ZrO2. ITO thickness was 117 nm and nITO = 1.88858 + 0.006 i, taking into account absorption; for the glass substrate, nsub = 1.45. Polyvinyl alcohol with a diffraction index of 1.515 served as the orientant with a layer thickness of 300 and 600 nm, the difference being due to different LC orientations at the mirrors. For MBBA crystals, n|| = 1.737 + 3.9 × 10−4 i and n⊥ = 1.549 + 3.9 × 10−4 i. The thickness of the nematic LC layer was 7980 nm, and the angle of twist φ = 80°.
Figure 13. (Color online.) (a) o-polarized spectrum and (b) spectral shift of transmission peaks. (•) — experimental values, (°) — calculated values found by direct numerical simulation, solid line — formula (19), dashed line — corollary of the Mauguin formula without regard for the resonator (20). Magnified fragments of (c) experimental and (d) theoretical transmission spectra of untwisted (homeoplanar, h-planar) and twisted structures. Twisting shifts transmission peaks to the short-wavelength region.
Download figure:
Standard imageFigure 13b demonstrates experimental and theoretical values of spectral shifts of the transmission peaks. Good agreement is observed for all 14 peaks. The measured spectral shift is proportional to the third power of the wavelength, in conformity with the Mauguin formula without regard for the resonator (20).
The shift related to the optical axis twist considered in this section can be observed directly without polarizers, and the desired measuring accuracy is ensured by the use of a resonator. The proposed experimental design ensures the absence of serious disturbing interferences during transition to the twisted structure. In this scheme, however, the untwisted structure retains a constant refractive index for the o-wave alone. The respective shift of the e-wave can be measured under the experimental conditions with a transition from a twisted to a planar structure that could be observed with the use of a photo-orientant with reversible intermolecular bonds.
This approach takes into account the spectral shift due to mode coupling associated with twisting and reflection from mirrors. The shift is described analytically and detected in experiment in twist-structures free of deformation by the external field. Generalization of the Mauguin–Poincaré rolling cone method made it possible to solve the problem geometrically; it was independently confirmed using Jones's [107] and Berreman's [78] matrix formalisms.
The method shows that the twist-related spectral shift in question characterizes the twisted layer rather than the whole resonator, which serves only to facilitate measurement. Indeed, the twisted layer produces no peaks. What, then, actually does shift as the layer twists? Evidently, the phase of the eigenwave leaving the twisted layer does, which suggests a change in the effective refraction index. The optical length of the resonator is not the sole characteristic from which it can be deduced. For example, polarization diffraction gratings are highly susceptible to the magnitude of the effective refractive index and make experimental verification of the described phenomenon possible.
The assumption of intermediate optical response determining the medium response interval n|| > neff > n⊥ has been formulated. However, despite its self-evidence, this assumption can be invalid. In the case of a twisted nematic LC, this fact is explained as the contribution from the geometric phase. It is a nonlocal characteristic; therefore, neff must not be treated as  , where εeff is a certain local response of the material. On the contrary, neff should be understood in the sense of phase incursion neff 2πL/λ. In addition, the pictorial representation of the geometric phase is given in the form of the region enclosed by the trajectory on the Poincaré sphere, with spectral shifts related to the areas of a spherical rectangle and triangle. The observed spectral shift exists not only in the twist-nematic LC but also in any other twisted anisotropic medium.
, where εeff is a certain local response of the material. On the contrary, neff should be understood in the sense of phase incursion neff 2πL/λ. In addition, the pictorial representation of the geometric phase is given in the form of the region enclosed by the trajectory on the Poincaré sphere, with spectral shifts related to the areas of a spherical rectangle and triangle. The observed spectral shift exists not only in the twist-nematic LC but also in any other twisted anisotropic medium.
Finally, it should be noted that in the case in question,as in the example of the QHQ-device discussed in Section 3.1.1, the nonadiabatic correction for the geometric phase is unrelated to the chirality sign of the structure, i.e., it has the same sign for right- and left-hand twisted structures.
3.3. Localized modes in structures with chiral mirrors, surface waves
Let us now consider the case of chiral mirrors when both localized mode properties and the fact of localization are conditioned by chirality. To begin with, we turn to the principle of light reflection by chiral mirrors. If the optical axis sharply turns, the light undergoes reflection and diffraction at the boundary [144]. In the case of gradual rotation, the well apparent boundary disappears [81, 93, 95, 145], and the action of the permittivity gradient on light can be interpreted in the wave representation by generalizing the Snellius and Fresnel laws to diffraction phenomena that just as well contribute to reflection and diffraction in the bulk medium. Such reflection becomes essential for the helical structures discussed in Section 3.1.2.
Let us consider two chiral mirrors. In a one-dimensional case, the region of localization can be represented as a 'gap' between helicoidal structure sections following one another, i.e., its defect. This analog of the Fabry–Perot resonator has a few defect modes, i.e., localized optical states usually corresponding to a whole number of half-waves fitting in the cavity. Anisotropy of the cholesteric and the defect accounts for some peculiarities of polarization [146–152], including a defect of twisting that lacks an intermediate layer and has zero length [153, 154]. Its thorough theoretical [79, 80, 155, 156] and experimental [133, 153, 157, 158] investigation involving a chiral layer containing less than one helicoid pitch [54, 100, 135, 159–161] gave rise to a discussion on the polarization and relaxation time of localized states [162, 163]. Theoretically, infinite relaxation time is possible only in the presence of permeability anisotropy [21]. Reference [82] gives evidence of the existence of plasmonic-photonic structures with such properties. It is impossible to correlate electric and magnetic strengths at the boundary in the absence of magnetic anisotropy [80], and an endless increase in the cholesteric thickness does not provide an infinite Q-factor. Saturation of the quality factor with increasing cholesteric thickness changes the circular polarization of the outgoing radiation from co-directed to oppositely directed. This polarization crossover [154] is known as the Kopp–Genack effect [164].
A twist defect is the imperfection of the twisting of a helical structure with zero thickness. The absence of a resonator layer makes it different from nonchiral resonators. The spatial field distribution is represented by two waves exponentially decreasing in opposite directions; it does not have a flat top and resembles a surface wave or can also be regarded as two mirrors facing each other with a common reflecting surface [165]. Similarly to a surface wave, the twist defect generates a single spectral resonance. The mode localized at the twist defect differs from the surface wave at the cholesteric-isotropic dielectric interface in that the latter is observed only at angles ensuring total internal reflection [166–168], whereas a twist defect imposes no limitation on the incidence angle of the exciting wave. A surface wave in nonchiral structures is known which is unrestricted by total internal reflection — it is the optical Tamm state (OTS) [169–171]. The OTS is an analog of the electronic Tamm state at the superlattice boundary, and its dispersion lies above the light cone described by the straight line k = ω/c [172]. Such state can be excited even normally to the surface without energy transfer along it, which is convenient for applications. The natural question arises as to whether there is an OTS at the cholesteric–metal interface on which light is incident normally. Two factors should be kept in mind. The first is cholesteric semi-transparency due to circular Bragg diffraction; the second is polarization instability caused by alternation of circular polarizations: reflection from the cholesteric does not alter the circular polarization sign, but that from the metal does [173]. Such an alternation is akin to traffic lights forbidding movement across the cholesteric for a wave with coincident circular polarization and permitting movement after the wave is reflected by the metal [119]. Variation of polarization is compensated by virtue of an additional anisotropic layer producing a series of localized states with nontrivial polarization properties [174–176]. Various combinations with two mirrors were thoroughly investigated and proposed for practical applications [100, 116, 135, 161, 173]. The energy density of such states can increase near a mirror, but they are localized in the bulk of the additional layer rather than on its surface. The additional layer is not necessary when a handedness-preserving mirror is used [163, 177-179]. Such a mirror can preserve not only the chirality sign but also the ellipticity value of the incident radiation. This specific case can be referred to as a polarization-preserving anisotropic mirror [179]. Otherwise, it can be defined as a half-wave reflection phase plate [180]. The state localized at the boundary between such a mirror and the cholesteric has been described and called the chiral optical Tamm state [160]. A recent publication reports an experimental observation of this state at the cholesteric-metasurface interface [181].
Let us construct the chiral OTS by the Berreman numerical method [78] considering a right-hand twisted cholesteric LC with anisotropy δ = 0.2 and normalized helical pitch  as the chiral medium. The layer thickness equals five helicoid pitches, and the substrate is a nanocomposite of silver spheroids flattened out in the x direction and placed in the matrix with a refractive index equaling the mean refractive index of a cholesteric LC. The use of the Maxwell-Garnett formula (30) allows choosing nanocomposite parameters such that no = (1 + i) × 10, ne = (1 + i)/20 at a given frequency in the visible wavelength range. The condition
as the chiral medium. The layer thickness equals five helicoid pitches, and the substrate is a nanocomposite of silver spheroids flattened out in the x direction and placed in the matrix with a refractive index equaling the mean refractive index of a cholesteric LC. The use of the Maxwell-Garnett formula (30) allows choosing nanocomposite parameters such that no = (1 + i) × 10, ne = (1 + i)/20 at a given frequency in the visible wavelength range. The condition  ensures the antiphase amplitude reflection coefficients of the substrate:
ensures the antiphase amplitude reflection coefficients of the substrate:  , Re (re) = −Re (ro). As a result, incident and reflected light polarizations are matched.
, Re (re) = −Re (ro). As a result, incident and reflected light polarizations are matched.
Figure 14a shows the OTS in the form of local field intensity depending on the distance to the boundary. The local intensity is normalized to that of the OTS-exciting wave. Radiation has left-hand circular polarization, falls from the right, and penetrates the boundary from the chiral medium. The leftward traveling wave B contains an OTS-exciting wave and is therefore more intense than the right-propagating wave A re-reflected from the substrate. To make the figure less cumbersome, we do not show total local intensity |A + B|2, which is almost 7 times that of an OTS-exciting wave near the boundary.
Figure 14. (a) Local field intensity depending on the distance to the boundary. Thick solid line — schematic of optical axis orientation in the substrate (straight section) and in the chiral medium (sinusoidal projection onto the x-axis). (b) Field stitching at the boundary. Solid and dashed arrows denote electric and magnetic field strength vectors, respectively. The field in the chiral medium is presented in the form of circular waves incident on (B) and reflected from (A) the boundary. The field in the anisotropic medium is decomposed into extraordinary (x) and ordinary (y) waves.
Download figure:
Standard imageFigure 14b explains the condition for field joining at the boundary. Polarization ellipse of the resulting field is stretched out in the x direction for both electric and magnetic strengths. In the chiral medium, its major semi-axis is proportional to the sum of amplitudes |A| + |B|, and the minor one to the difference |A| – |B|. In the substrate, the electric field is stretched in an extraordinary wave, and the magnetic field in an ordinary one. The equality of the aspect ratio of the ellipse in the chiral medium and the substrate yields

Figure 15 presents the spectrum of reflection from the boundary for right-hand circularly polarized light normally incident on the boundary from a right-hand twisted chiral medium. Gradual rotation of the mirrors shifts the OTS frequency as far as the edges of the band gap. When optical axes coincide, the OTS is localized at the high-frequency edge of the band gap. For angle φ = π/4, the most pronounced dip in reflectance occurs in the middle of the band. For the exciting light of right-hand circular polarization, reflection in the dip amounts to 90% (the red cross in Fig. 15), and for left-hand circularly polarized light to 45% (Fig. 14a). The angle φ = π/4 is due to the fact that the maximum gradient of the refractive index in a chiral medium takes place at the angle π/4 to the optical axis, and the electric field oriented in this direction experiences strong volume reflection. When the optical axes are mutually perpendicular, OTS moves to the low-frequency edge of the band gap. There is no reflection dip at angles higher than π/2.
Figure 15. (Color online.) Reflection spectrum of the boundary at different angles φ between the optical axes at the boundary. Blue dashed lines show the edges of the photonic band gap. The solid red line represents the analytical dependence. The red cross at φ = π/4 corresponds to the parameters of Fig. 14a.
Download figure:
Standard imageTo describe the part of the chiral OTS located in a cholesteric, the mathematical description from Section 3.1.2 is used. In the absence of magnetic anisotropy, the directions of electric and magnetic polarizations are given by angles χE and χH:
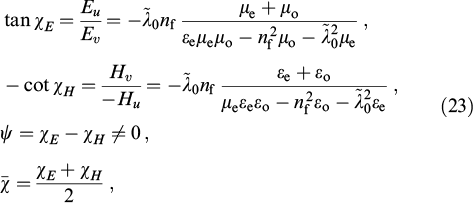
where the refractive index nf should be substituted from dispersion equation (7).
The eigenfrequency of the state is determined by the angle  :
:
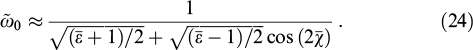
Even in the case of an anisotropic mirror ideally preserving polarization, the nonzero angle ψ between the directions of electric and magnetic polarizations gives rise to the appearance of a nonlocal component in the chiral OTS [80]; the state becomes a resonant one and acquires finite relaxation time τψ:

Let us consider now a layer of a cholesteric LC having finite thickness L confined by the medium with permittivity  . The corresponding relaxation time
. The corresponding relaxation time

The equality of relaxation times yields the critical coupling condition. The coupling manifests itself in the Kopp–Genack crossover: a rise in the thickness of the chiral LC changes the circular polarization sign of radiation leaving the chiral OTS. Equating expressions for relaxation times (25) and (26) leads to the analytical expression for the crossover thickness apparently first derived in Ref. [21]:

To clarify the physical phenomenon, we shall use, besides the analytical expressions obtained and numerical calculations, an approximate analytical method, namely the time-domain coupled mode theory [182]. This theory allows describing the field in resonators coupled to waveguides. The spatial structure of the localized mode is not considered here. Essentially the same method going back to the solution to the quantum-mechanical scattering problem by Lippmann and Schwinger [183] is employed to describe open resonators. It should be distinguished from the spatial coupled-mode theory widely used in chiral LC optics. Equations of this theory describe coupled amplitudes of propagating waves. Both approaches are based on the notion of coupled modes [184].
In a right-hand twisted helicoid, the right-hand circular reflection amplitude of the same chirality is given by the formula
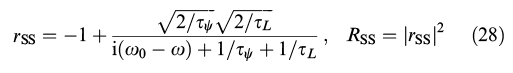
(Fig. 16). This equation describes the spectral dip in the form of the Lorentz contour with the full width at half-maximum (FWHM):

It is sufficient to describe spectral manifestations of the state in terms of the time-domain coupled mode theory.
Figure 16. (Color online.) (a) Reflection spectrum, Eqn (28). Maximum reflectance dip corresponds to the critical coupling condition — the equality of relaxation times (25) and (26). (b) The width of the spectral dip, Eqn (29). Line width saturation with increasing thickness of the cholesteric layer. The straight lines cross at the cholesteric thickness associated with a change in polarization of radiation leaving the chiral OTS. It corresponds to the Kopp–Genack effect [154]. The twist pitch of cholesteric LC p = 1 μm, LC anisotropy δε = 0.1.
Download figure:
Standard imageThe chiral OTS is localized at a boundary of strictly zero thickness and exponentially decreases on both sides. Unlike for media consisting of isotropic layers, there are no difficulties in finding the edge of the structure, because chiral structures have smooth screw symmetry and can be regarded, in this sense, as homogeneous. The geometric phase of a running wave that crosses the boundary is determined by the mirror rotation angle in the boundary plane, which ensures the uniqueness of the frequency at which the phases are matched, making the found state radically different from the series of states corresponding to the spectrum of a nonchiral resonator.
3.4. Spectral and polarization properties of a cholesteric liquid crystal having a defective nanocomposite layer with resonant dispersion
This section deals with spectral and polarization properties of chiral photonic crystals containing nanocomposite materials with resonant frequency dispersion.
3.4.1. Types of defects and localized modes in a cholesteric.
The introduction of different types of defects into the structure of an ideal CLC gives rise to narrow transmission bands in the PC band gaps corresponding to localized defect modes. There are a few methods to induce photonic defect modes in CLCs, e.g., using a thin layer of a homogeneous isotropic [149] or homogeneous anisotropic substance inserted between two CLC layers [185, 186], a twist defect (jump in the rotation angle of the cholesteric helix) [133, 153, 154], or a defect caused by a local change in the CLC helix pitch [134, 150, 187]. Reference [149] was the first to report the use of numerical analysis for the study of defect modes in CLCs as materials with photonic band gaps. One of the elucidated optical effects associated with a defect in the form of a thin layer of an isotropic dielectric placed between cholesteric layers is the induction of defect modes in the CLC stop-band for both circular polarizations of normally incident light. An analytical approach to the theory of optical defect modes in CLCs with an isotropic defective layer was developed in Ref. [152] in the framework of a model allowing the exclusion of polarization mixing and deriving the equation for light with only diffracting polarization. Defect modes induced in CLCs by a twist defect, i.e., a sharp turn of the director around the cholesteric axis at the interface between two CLCs, were analyzed analytically in [155, 188]. Light propagation in CLCs containing a combined defect formed by the dielectric layer and a twist defect at the interface between dielectric and CLC layers was investigated in [156, 189]. The localized modes in CLCs, like defect modes in scalar periodically layered media, can be used to produce narrow-band tunable filters [189], amplifiers of polarization plane rotation [190], polarization azimuthal stabilizers [191], and other devices. Low-threshold lasing in CLCs is a subject of extensive research [192]. There are two possibilities for such oscillation, one at the edge of the band gap [193] and the other in the defect mode [185], the lasing threshold in the latter case usually being lower, because the mode frequency is closer to the center of the stop-band, reflection from the CLC layers is stronger, and photonic state density is higher [194].
Nowadays, limitations imposed on the optical properties of natural materials are being successfully overcome due to replacing them with metamaterials. Of special interest are composite media containing metallic nanoparticles used to design nanostructured metal-dielectric photonic crystals and their application for the development of new approaches to light control. Resonance of effective permittivity has been predicted for nanocomposites made of spherical metal nanoparticles dispersed in a transparent matrix [195, 196]. Both the position and the width of the resonance region in the visible wavelength range depend on nanoparticle size and concentration. Effective characteristics of a nanocomposite consisting of metallic nanoparticles suspended in a dielectric matrix are formed by virtue of plasmon resonance of nanoparticles and can acquire unique values in the optical range that are lacking in natural materials. An example is provided by the real part of the effective refractive index, which can be much higher or lower than unity and can even vanish [195, 197–199].
A combination of resonant medium dispersion and intrinsic dispersion of a photonic crystal opens up promising prospects for controlling the spectral and optical properties of photonic crystals [200–210].
3.4.2. Model of the effective resonant medium
To describe nanocomposite materials containing various inclusions, effective medium theories, such as the Maxwell-Garnett and Bruggeman theories, were developed together with approaches to the derivation of formulas for these models [211–216]. Let us consider the simplest case in which the defective layer is a dielectric with metallic inclusions spherical in shape. The effective permittivity of the nanocomposite layer εmix is defined by the Maxwell-Garnett equation finding wide application for considering matrix media when the matrix material contains dispersed isolated inclusions of a minor volume fraction,
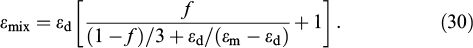
Here, f is the filling factor, i.e., a nanoparticle fraction in the matrix, εd and εm (ω) are permittivities of the matrix and the material of the nanoparticles, respectively, and ω is the radiation frequency. The effective medium models make use of the quasi-static approximation with the applicability condition given by the smallness of the size of nanoparticles and the distance between them in comparison with the optical wavelength in the medium. The nanoparticle size is significantly smaller than the field penetration depth in the material. The permittivity of the metal from which nanoparticles are made is found using the Drude approximation:

where ε0 is a constant taking account of contributions from inter-band transitions, ωp is the plasma frequency, and γ is the quantity inverse to electron relaxation time. For metal nanoballs suspended in a transparent optical glass, ε0 = 5, ωp = 9.6 eV, γ = 0.02 eV [217], εd = 2.56.
Disregarding the minor factor γ2 yields the resonant frequency depending on characteristics of the starting materials and concentration of the dispersed phase f:
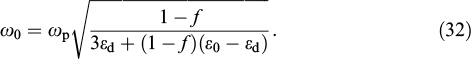
Figure 17 presents the dispersion dependence of nanocomposite permittivity for two filling factor values: f = 0.02, 0.1. It follows that frequency ω0 corresponding to resonance in the defective layer shifts into the long wavelength spectral region. The half-width of the resonance curve  changes insignificantly, but the
changes insignificantly, but the  curve undergoes a well apparent modification, and the frequency range within which the nanocomposite behaves as a metal expands at
curve undergoes a well apparent modification, and the frequency range within which the nanocomposite behaves as a metal expands at  .
.
Figure 17. Wavelength dependence of the imaginary  (dashed curve) and real
(dashed curve) and real  (solid curve) parts of effective permittivity of the nanocomposite εmix. The filling factor f = 0.02 (a), 0.1 (b).
(solid curve) parts of effective permittivity of the nanocomposite εmix. The filling factor f = 0.02 (a), 0.1 (b).
Download figure:
Standard image3.4.3. Control of spectral properties in a cholesteric with a defective nanocomposite layer.
The structure of interest consists of two identical layers of an ideal right-hand twisted CLC separated by a nanocomposite defect layer (Fig. 18). The cholesteric length is 10P, where P = 275 mm is the crystal helix pitch, and the thickness of the defective layer d = 5P/7. The medium outside the cholesteric is isotropic and has the refractive index n = (no + ne)/2, where no = 1.4 and ne = 1.6 are ordinary and extraordinary CLC refractive indices, respectively. Such a choice of an external medium results in weak Fresnel reflection from the cholesteric surface and interference bands from boundary surfaces. The numerical analysis of spectral properties and the field distribution in the sample was performed using the Berreman transfer matrix method [78], making possible the quantitative characteristic of light propagation in a CLC with a structural defect [218]. The equation describing propagation of light with frequency ω along the z-axis has the form

where Ψ(z) = (Ex,Hy,Ey,−Hx)T, and Δ(z) is the Berreman matrix [78] depending on the dielectric function and the incident wave vector.
Figure 18. Diagram of cholesteric structure with a defect.
Download figure:
Standard imageFigure 19 shows the primary (f = 0) transmission spectrum under the normal incidence of a light beam on the cholesteric having a structural defect in the form of a dielectric plate. Similar to Ref. [149], the figure demonstrates peaks in the cholesteric stop-band corresponding to CLC defect modes induced for both circular polarizations of normally incident light. Moreover, the defect modes have the same wavelength and similar transmissivity characteristics at this wavelength.
Figure 19. Transmission spectrum for waves with right-hand (solid line) and left-hand (dashed line) circular polarizations, θ = 0°. The filling factor f = 0.
Download figure:
Standard imageIf the filling factor is nonzero and the nanocomposite resonance frequency ω0 coincides with the defect mode frequency, the latter splits. Manifestation of the splitting effect in transmission, reflection, and absorption spectra is illustrated in Fig. 20. The difference from frequency splitting of two coupled oscillators consists in the presence of more than two modes in the reflection spectrum. It follows from Fig. 20a that due to the splitting defect modes possess equal wavelength for right-hand and left-hand circular polarizations but different transmission in the peak center. Calculations show that splitting increases with increasing volume fraction of nanoballs in the composite, as it does in a scalar PC with the resonant defect layer of nanocomposite [205]. The reflection and absorption spectra (Fig. 20b, c) are characterized by a strong dependence of reflection and absorption coefficients on the direction of incident light circular polarization. The appearance of the spectral region forbidden for both polarizations after splitting of the defect modes (Fig. 20a) is related in first and foremost to strong reflection and absorption of right-hand and left-hand circularly polarized waves (Fig. 20b,c).
Figure 20. (a) Transmission T, (b) reflection R, and (c) absorption A spectra for waves with right-hand (solid line) and left-hand (dashed line) circular polarization, θ = 0°. The filling factor f = 0.02.
Download figure:
Standard imageFigure 21 illustrates spatial distributions of the electric field in defect modes with the wavelength λ = 435.8 nm (Fig. 20a). Field localization most strikingly manifests itself in the region commensurate with the wavelength for the mode corresponding to right-hand diffracting polarization. New features in the transmission spectrum appear as a consequence of variation of the light incidence angle θ. The CLC band gap shifts to the short-wavelength region as θ increases, in accordance with the Bragg condition; simultaneously, the long-wavelength edge of the stop-band becomes displaced toward the resonance frequency ω0 of the defective layer. At θ = 26° (Fig. 22a), the short-wavelength peak corresponding to the defect mode disappears from the stop-band, and only the long-wavelength peak of defect modes corresponding to right- and left-hand circular polarizations remains. Importantly, the resonance frequency ω0 at this angle happens to be close to the long-wavelength boundary of the stop-band. Mixing of the resonant mode with the photonic modes leads to the splitting of the band gap, i.e., separation of the additional transparency band corresponding to diffracting polarization from the long-wavelength edge and the appearance of the frequency band gap in the vicinity of ω0 for the waves of both polarizations due largely to field absorption in the nanocomposite layer. As the angle of incidence θ increases further, the resonance frequency ω0 is detected in the continuous transmission spectrum, and the resulting resonance situation gives rise to an additional band gap in the transmission spectrum (Fig. 22b).
Figure 21. Distribution of the squared electric field modulus for λ = 435.8 nm (Fig. 20a), f = 0.02 for defect modes with T = 0.3 (a), 0.76 (b).
Download figure:
Standard imageFigure 22. Transmission spectra for different angles of incidence: θ = 26° (a), 30° (b). Solid and dashed lines for light with right- and left-hand circular polarizations, respectively. The filling factor f = 0.01.
Download figure:
Standard imageAnalogous effects can be realized in a different way, such as a change in the cholesteric helix pitch. Indeed, an increase in the helix pitch, e.g., by temperature variation, causes the displacement of the band gap into the long-wavelength region. In this case, mixing of the resonant mode with photonic modes results in the splitting of the stop-band (Fig. 23a) and the appearance of the band gap in the continuous spectrum (Fig. 23b).
Figure 23. Transmission spectra for different helix pitches: P = 305 nm (a), 320 nm (b). Solid and dashed lines for the right- and left-hand circularly polarized waves, respectively. The filling factor f = 0.01.
Download figure:
Standard imageThe described resonance splitting may be helpful for explaining photosynthetic phenomena [17]. The chirality of photonic structures involved in photosynthesis is evidenced by the helical configuration of hydrogen bonds [219, 220]. An advantage of chiral structures for photosynthesis stems from their high reflectivity compared to that of a scalar Bragg reflector of the same thickness and refractive index contrast responsible for the higher Q-factor of the resonator. A detailed comparison is presented in Section 3.1.2. Another advantage is the self-organization and tunability of chiral structures.
3.5. Controlled hybrid modes in a bounded cholesteric liquid crystal with a twist defect
Recent years have witnessed considerable interest in hybrid mode formation due to the coupling of different resonances in scalar photonic crystals. Hybridization of Tamm plasmon-polaritons with modes of other types is the subject of especially extensive research that includes interaction with exciton modes [169, 221–223], surface plasmon-polaritons [224–226], and microresonant modes [223, 227]. A description of hybrid modes reveals new specific features in chiral photonic crystals, absent in scalar PCs, due to their unique polarization properties and high sensitivity to external fields [174, 175, 228]. The possibility of an optical localized state in a CLC–quarter-wave phase plate–metallic film system has been demonstrated. The necessity to use the phase plate arises from polarization peculiarities of light reflection from CLCs and metal. The field is localized in such a system with a maximum at the phase plate–metal interface. The role of the phase plate can be performed either by an additional CLC layer with opposite twisting [176] or a planar anisotropic defect in a CLC [187, 189].
Let us consider coupling between CLC defect modes and localized modes. The former are induced by a twist defect in the crystal structure.
3.5.1. Description of the model
The study system is presented in Fig. 24. It consists of a right-hand twisted cholesteric liquid crystal with a structural twist defect, a quarter-wave phase plate, and a metal film.
Figure 24. Schematic representation of a cholesteric with twist defect–phase plate–metal structure [176, 228].
Download figure:
Standard imageThe following CLC parameters were used for modeling: ordinary and extraordinary refractive indices ne = 1.71 and no = 1.54, respectively, helix pitch p = 0.4 μm. These parameters correspond to the mixture of the chiral center (Merck, S-811) and the nematic liquid crystal (Merck, E44) [229]. For the given CLC, the band center is at the wavelength λ0 = 650 nm. The CLC length is 4 μm. The center of the layer contains a twist defect with the same integer number of pitches on its right and left sides. The magnitude of the twist defect is given by angle α. It is assumed that rotation of the CLC layer occurs in a clockwise direction and observation is carried out in the direction of light propagation.
Let us assume in addition that CLC refractive indices ne and no are equal to the respective indices of the phase plate. The thickness of the quarter-wave plate d = λ0/4(ne – no) = 0.96 μm. The structure is surrounded by a medium with the refractive index equaling the mean CLC refractive index next = (ne + no)/2. The thickness of the metallic film dm = 50 nm; its permittivity is given in the form of the Drude approximation (31).
The simplest way to implement the proposed structure is to use polymer cholesteric elastomers instead of liquid ones [230]. Experiments [133, 231] revealed twist defect-induced photonic defect modes in such cholesteric materials. The twist defect can be caused by rotation of one part of the elastomer about the axis with respect to the other part, so that the helix undergoes a break in the continuous change of its director. The spectral properties of such materials, similarly to those of usual CLCs, can be modified by various impacts [176, 228]. The combination of a quarter-wave plate with a metallic film can be replaced with a polarization-preserving mirror, as proposed in Ref. [160].
3.5.2. Hybrid modes and their spectral manifestation.
Calculations of transmission spectra and field strength distribution in the structure were based on the transfer matrix method for calculating layered anisotropic structures [78].
Figure 25a presents a calculated transmission spectrum of the structure at the varied twist-defect angle α for the right-hand circular polarization of incident light. Calculations were performed for the case of rotation of the first CLC layer when the second layer bordering the phase plate remained motionless. In the absence of a twist defect (α = 0), the spectrum exhibited only one peak, corresponding to the localized mode at a wavelength of 643 nm. A rise in α caused a shift of the peak of the defect mode to the long-wavelength region. At α = 1.38 rad, the wavelengths of both peaks coincided, and the resonance frequency was split. The split peaks occurred at the wavelengths of 637 and 649 nm, respectively (see the inset in Fig. 25a). In the case of α variation, the spectrum demonstrated the avoided crossing characteristic of hybrid states.
Figure 25. (Color online.) Transmittance of the structure (see Fig. 24) as a function of the twist-defect angle α for (a) right-hand and (b) left-hand circular polarizations of incident light. The first CLC layer rotates, while the CLC layer bordering the phase plate is motionless. The inset shows the transmission spectrum at α = 1.38. Resonance wavelengths correspond to the localized and defect modes of CLCs, respectively.
Download figure:
Standard imageThe white dashed line in Fig. 25a shows the position of the resonance wavelength for a CLC containing a twist defect [156],
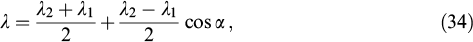
where λ2 and λ1 are the longwave and shortwave boundaries of the CLC band gap. The thickness of the CLC being only 4 μm, its band gap is wider than pno < λ < pne; therefore, λ2 – λ1 ≠ p(ne – no). This fact was used to plot the white dashed line in Fig. 25a.
The incident left-hand circularly polarized light produced a different spectrum (Fig. 25b). It did not contain the transmission peak corresponding to the CLC defect mode, the cause being the weak dip typical of the spectrum of light with nondiffracting circular polarization (see above). Splitting occurred when there was a coincidence of peak frequencies corresponding to the localized mode and the defect mode of the CLC.
Figure 26 demonstrates the spatial distribution of squared electric field modulus |E|2(z) for a wavelength of 649 nm at α = 1.38 rad and two circular polarizations of incident light. In both cases, the field is localized on the twist defect and the phase plate–metal interface. However, localization is much more pronounced for the right-hand circularly polarized light. A similar distribution pattern |E|2(z) is observed for the 637 nm wavelength.
Figure 26. (Color online.) Spatial distribution of the squared electric field modulus for a wavelength of 649 nm.
Download figure:
Standard imageVariation in the helix pitch under the influence of external factors makes possible efficient tuning of the CLC transmission spectrum. The structure transmission spectrum (see Fig. 24) was calculated for different CLC helix pitches (Fig. 27).
Figure 27. (Color online.) Transmission spectrum of the structure (see Fig. 24) as a function of the CLC helix pitch. The white dashed line shows the CLC defect mode peak position calculated from formula (35); α = 1.38 rad.
Download figure:
Standard imageThe condition for the existence of optical localized modes has the form

If CLC and phase plate parameters are substantially different and the ratio is not fulfilled, there are no optical states localized at the phase plate–metal interface. Therefore, the spectrum has a single peak corresponding to the CLC defect mode at a helix pitch significantly different from 400 nm.
Variation in the phase plate thickness changes the structure's transmission spectrum. The properties of a structure containing a phase plate of thickness d' = 5d = 4.8 μm were considered. The quarter-wave plate remained unaltered with respect to the wavelength λ0 = 650 nm and birefringence of 0.17. The spectrum contained a few peaks corresponding to the localized modes of the CLC–phase plate–metal system. Variation in the twist defect allows the transmission spectrum of the structure of interest to be tuned (Fig. 28).
Figure 28. (Color online.) Transmittance of the structure (see Fig. 24) as a function of the twist defect angle for right-hand circular polarization of incident light. The first CLC layer rotates, while the CLC layer bordering the phase plate is motionless. The white dashed line shows the CLC defect mode peak position calculated from formula (35); d' = 5d.
Download figure:
Standard image4. Conclusion
We have analyzed the main approaches to solving the fundamental problem of interaction between light with right-hand and left-hand circular polarization and photonic structures lacking mirror symmetry. Chiral structures are characterized by the Mauguin effect, optical activity, Bragg's selective reflection, and geometric phase. New polarization properties associated with these phenomena in localized resonant modes have been revealed.
Considerable attention is given to the helical structure inherent in self-organizing and biological materials as exemplified by a cholesteric liquid crystal. Due to translational-rotational symmetry, helical structures exhibit spatial periodicity and can selectively reflect circularly polarized light within a wavelength range close to the structure period. Such chiral reflection can result in light localization in the surface, resonant, and hybrid modes. These states are characterized by high polarization sensitivity; therefore, their appearance imposes certain conditions on the structure parameters. The problem of light localization between chiral and nonchiral mirrors has a nontrivial solution. Recommendations are provided for designing such localized states, including correlation of the phase and polarization, as well as balancing couplings between the localized states and relaxation channels.
We have revealed a number of important peculiarities in the spectral properties of a CLC with a structural defect related first and foremost to the resonant character of nanocomposite effective permittivity and its essential dependence on the filling factor. Worthy of special note is splitting of the frequencies of defect modes induced for both circular polarizations of radiation incident on the sample in the transmission, absorption, and reflection spectra.
Ample opportunities appear to open up for efficient control of transmission spectra of a CLC with a defect by varying the angle of light incidence on the cholesteric or by altering the helix pitch under the influence of external fields. There are such values of the angle of incidence or helix pitch at which the resonance frequency of a nanocomposite happens to be close to the boundary of the CLC band gap, which accounts for the appearance of an additional transparency band for waves with diffracting polarization or an additional stop-band for waves having two circular polarizations.
The existence is documented of hybrid optical modes that are formed by a CLC defect mode and localized modes of the CLC structure. The defect mode is excited by a twist defect in the cholesteric structure. The possibility of transmission spectrum tuning by varying the twist-defect angle and the CLC helix pitch is documented. The described chirality effects are of importance for designing new-generation photonic polarization devices, such as lenses, prisms, resonators, filters, relays, tunable diffraction gratings, and holograms. A spectacular example of such optical devices is provided by LC displays, which have successfully competed for many decades not only with cathode ray tube screens but also with new technologies of plasma displays, OLED displays, quantum dot displays, and energy-saving technologies of electronic paper. Another promising avenue of research is focused on a better understanding of biophotonic phenomena in a wide area encompassing a variety of topics, from the efficiency of chiral biological structures for pigmentation and photosynthesis to mechanisms of visual and analog perception. The class of natural and synthetic structurally chiral optical materials is rapidly expanding. New chemical compounds, mixtures, and nanocomposites demonstrate record-breaking anisotropic optical responses and tuning rates. On the whole, consideration of the totality of materials and structures in this review is expected to contribute to control flexibility and ease and reliability of production.































