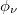Abstract
We explore the phenomenon of flux-driven circular current in a mesoscopic conducting ring where site energies are modulated in the cosine form following the well-known Aubry-André-Harper (AAH) model. Due to unique and diverse characteristic features of AAH potential several atypical features of persistent current are found, associated with the electron filling and AAH phase factor. Finally, a transition from a conducting phase to an insulating one upon the variation of AAH modulation strength is discussed by studying Drude weight. Our analysis might be useful to examine the magnetic response of any other similar class of aperiodic lattices.
Export citation and abstract BibTeX RIS
Introduction
During the early 80s Büttiker, Imry and Landauer first proposed [1] that a non-decaying circular current can be generated in a metallic ring provided the required conditions are satisfied. If such a ring is threaded by a magnetic flux ϕ, commonly referred to as Aharonov-Bohm (AB) flux, then it carries a net circular current which does not drop to zero even if the flux is removed [1]. This is the so-called flux-driven persistent current in a conducting mesoscopic ring. Soon after this proposal, interest among the researchers has grown up very rapidly and after the pioneering experiment done by Levy and co-workers [2] the phenomenon of persistent current came into a realization. No doubt a wealth of literature knowledge has been developed [3–25] to illustrate this phenomenon exploring several interesting features, but few issues still exist and those are not clearly explained in an understandable way. For instance, the appearance of half flux-quantum ( , where
, where  describes the flux-quantum) periodicity is not so clear. It is well known that persistent current shows
describes the flux-quantum) periodicity is not so clear. It is well known that persistent current shows 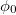 periodicity, but for some specific cases
periodicity, but for some specific cases  periodicity, instead of
periodicity, instead of  , is obtained and the physics behind it is not well mentioned. Few groups [5,11] have shown that
, is obtained and the physics behind it is not well mentioned. Few groups [5,11] have shown that  periodicity can be noticed only if ensemble averages of the currents are taken into account, but no proper justification is available yet for getting this
periodicity can be noticed only if ensemble averages of the currents are taken into account, but no proper justification is available yet for getting this 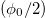 periodic currents for a single configuration, i.e., in the absence of such averaging process. As an example we would like to note that an ordered half-filled ring exhibits
periodic currents for a single configuration, i.e., in the absence of such averaging process. As an example we would like to note that an ordered half-filled ring exhibits 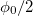 periodicity, and this cannot be explained with the usual physical arguments. As long as the filling factor is changed, current gets back to its
periodicity, and this cannot be explained with the usual physical arguments. As long as the filling factor is changed, current gets back to its  periodicity. The other long standing debatable question is associated with the measured current amplitudes and the theoretical estimates. The estimated current amplitude is always very small (sometimes even two orders of magnitude smaller) compared to the measured currents. Several attempts have been made [16,19–21] to resolve it, and definitely much progress has been done, but further probing is always required for better understanding the issue. Thus, the phenomenon of flux-driven persistent current is still a very active field of research.
periodicity. The other long standing debatable question is associated with the measured current amplitudes and the theoretical estimates. The estimated current amplitude is always very small (sometimes even two orders of magnitude smaller) compared to the measured currents. Several attempts have been made [16,19–21] to resolve it, and definitely much progress has been done, but further probing is always required for better understanding the issue. Thus, the phenomenon of flux-driven persistent current is still a very active field of research.
The present work is not devoted to remove the controversial facts described above, rather we investigate other important aspects which have not been clearly illuminated so far. The works involving circular current in disordered systems are mostly confined within fully "uncorrelated" (random) disordered lattices, and very few works are available where some specific aperiodic lattices have been considered [3,10,20,26–31]. On the other hand, to the best of our knowledge, no attempt has been made to explore persistent current in an AB loop where site potentials are modulated in the "cosine" form following the AAH model. Due to unique and extraordinary diverse natures of AAH potentials, different non-trivial signatures are obtained in the context of electronic localization and other related issues, as put forward in several works [32–37]. The recent breakthroughs in nanoscience have already revealed the designing mechanism of getting a system with this kind of potential in several ways, and various realizations of AAH model like diagonal, off-diagonal and even generalized version have been explored [33,34]. It has been verified that the AAH potential contains an arbitrary phase, the so-called AAH phase, and it has a significant impact to modulate the characteristic features [33,34]. This phase can be regulated externally with a suitable setup [34,35], which essentially yields tunable physical properties. Thus, non-trivial and tunable flux-driven circular current can be expected in an AB ring where site potentials are described in the form of AAH model, and in the present work, we essentially focus on that. The specific dependences of AAH potential, its strength and the phase factor associated with this potential on circular current in a 1D ring are critically investigated. Finally, a transition from a conducting phase to an insulating one is also discussed by varying the AAH strength. It is done by calculating the Drude weight [38–42], a standard prescription to describe localization properties in isolated (not connected with external baths) systems. Our analysis may open a new platform in analyzing magneto-transport phenomena in AAH systems.
AAH ring and theoretical formulation
Let us begin with fig. 1, where a mesoscopic ring, threaded by an AB flux ϕ, is shown. In presence of ϕ (measured in units of  ), a net circular current is established in the ring which does not dissipate even if the flux is withdrawn. To describe this quantum system we use a tight-binding (TB) framework, and under nearest-neighbor hopping (NNH) approximation the TB Hamiltonian of the ring for non-interacting electrons can be written as a sum
), a net circular current is established in the ring which does not dissipate even if the flux is withdrawn. To describe this quantum system we use a tight-binding (TB) framework, and under nearest-neighbor hopping (NNH) approximation the TB Hamiltonian of the ring for non-interacting electrons can be written as a sum  , where
, where 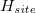 and
and 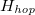 are associated with the site energy and hopping of electrons at neighboring sites. In terms of the fermionic operators cn and
are associated with the site energy and hopping of electrons at neighboring sites. In terms of the fermionic operators cn and  we can express the sub-Hamiltonians
we can express the sub-Hamiltonians  and
and 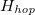 as
as

and

The TB parameters 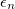 and t correspond to the on-site energy and NNH integral, respectively. The factor θ arises due to the magnetic flux ϕ threaded by the ring, and for a N-site ring it becomes
and t correspond to the on-site energy and NNH integral, respectively. The factor θ arises due to the magnetic flux ϕ threaded by the ring, and for a N-site ring it becomes 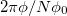 . As already mentioned, in the present work we consider a diagonal AAH ring where site energies are modulated in a "deterministic" way, aiming to have non-trivial signatures compared to the traditional "uncorrelated" random disordered rings. Moreover, there is a finite possibility to regulate the AAH phase externally [34,35], yielding a tunable energy spectrum which therefore directly affects the magneto-transport properties. In addition, it is important to note that designing of a ring that maps directly a random disordered model is quite difficult, while the AAH ring can be formed with advanced nanotechnology and some proposals have already been made along this direction [43,44]. Thus, emerging features in current are definitely expected in AAH rings. The AAH modulation included in the site energies is taken in the standard cosine form [34,35] following the relation
. As already mentioned, in the present work we consider a diagonal AAH ring where site energies are modulated in a "deterministic" way, aiming to have non-trivial signatures compared to the traditional "uncorrelated" random disordered rings. Moreover, there is a finite possibility to regulate the AAH phase externally [34,35], yielding a tunable energy spectrum which therefore directly affects the magneto-transport properties. In addition, it is important to note that designing of a ring that maps directly a random disordered model is quite difficult, while the AAH ring can be formed with advanced nanotechnology and some proposals have already been made along this direction [43,44]. Thus, emerging features in current are definitely expected in AAH rings. The AAH modulation included in the site energies is taken in the standard cosine form [34,35] following the relation

where W gives modulation strength, 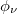 denotes the AAH phase, and b is an irrational number. In literature, the common choice of b is [45]
denotes the AAH phase, and b is an irrational number. In literature, the common choice of b is [45] 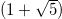 /2, called golden mean, though any other "irrational" number can also be taken into account. The purpose is that we need to make the site energies deterministic incommensurate ones. For W = 0, the ring becomes a perfect one.
/2, called golden mean, though any other "irrational" number can also be taken into account. The purpose is that we need to make the site energies deterministic incommensurate ones. For W = 0, the ring becomes a perfect one.
Fig. 1: 1D AB ring where different lattice sites (colored balls) are subjected to AAH potential.
Download figure:
Standard imageThis is all about the ring Hamiltonian for which we discuss the phenomenon of flux-driven circular current. To calculate the current first we need to determine the discrete energy eigenvalues, and we find them by exactly diagonalizing the TB Hamiltonian. For an N-site ring, N energy eigenvalues appear which are labeled as 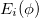 . Once
. Once 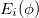 's are available, the ground state energy,
's are available, the ground state energy, 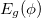 , of the system at absolute zero temperature is computed by taking the sum of the lowest Ne energy levels, where Ne represents the total number of electrons in the ring system. Mathematically it becomes
, of the system at absolute zero temperature is computed by taking the sum of the lowest Ne energy levels, where Ne represents the total number of electrons in the ring system. Mathematically it becomes

Taking the first-order derivative of 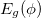 with respect to ϕ, we compute the net persistent current. It is defined as [3]
with respect to ϕ, we compute the net persistent current. It is defined as [3]

This is the standard prescription of determining flux-driven circular current in an isolated loop. The above equation suggests that the magnitude and sign of the current fully depend on the variation of 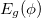 with flux ϕ. Thus, the critical analysis of
with flux ϕ. Thus, the critical analysis of 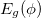 is the foremost requirement to have a complete idea of circular current. Since Ne is directly involved in
is the foremost requirement to have a complete idea of circular current. Since Ne is directly involved in 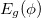 , we are expecting non-trivial signatures in current with Ne in AAH ring due to its spectral peculiarity. The detailed picture will be understood from our numerical results in the forthcoming section.
, we are expecting non-trivial signatures in current with Ne in AAH ring due to its spectral peculiarity. The detailed picture will be understood from our numerical results in the forthcoming section.
Finally, we describe the conducting properties and the phase transition from conducting phase to the insulating one by means of the Drude weight [38–42] D. Conventionally it is defined as a part of the frequency dependent conductivity [38–40]

where 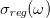 is a regular function of ω, and D is the Drude weight which is the zeroth component of electrical conductivity. More specifically we can say that D describes the DC conductivity, which is commonly used to separate between the metallic and insulating phases. As originally pointed out by Kohn [40], D can be calculated from the ground state energy by taking its second-order derivative in the limit
is a regular function of ω, and D is the Drude weight which is the zeroth component of electrical conductivity. More specifically we can say that D describes the DC conductivity, which is commonly used to separate between the metallic and insulating phases. As originally pointed out by Kohn [40], D can be calculated from the ground state energy by taking its second-order derivative in the limit 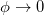 . Mathematically it (D) can be expressed as [41]
. Mathematically it (D) can be expressed as [41]

For a detailed analysis see refs. [38,39], where Scalapino and his group have elaborately described the criteria to get metallic or insulating phase. For the metallic phase D becomes finite, while  for the insulating one [38–40].
for the insulating one [38–40].
Results and discussion
The primary aim of our analysis is to address the interplay between the strange AAH potential and electron filling on flux-driven circular current. Along with this, the attention is also given to explore the critical roles of the modulation strength, AAH phase and ring size on persistent current.
Now, before presenting the results, let us mention the values of the physical parameters which are kept constant throughout the computations. We set the irrational number  which is most commonly used in the literature (see ref. [45] and the references therein), as already stated earlier, and since the AAH modulation is introduced only in site energies to make the system a diagonal AAH one, we keep the NNH integral t uniform [33,45]. We set
which is most commonly used in the literature (see ref. [45] and the references therein), as already stated earlier, and since the AAH modulation is introduced only in site energies to make the system a diagonal AAH one, we keep the NNH integral t uniform [33,45]. We set 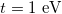 [35,45], and measure all the energies in unit of t. Here we make a valid approximation by setting the system temperature to zero, as the average energy level spacing is too large (due to small ring size) compared to the thermal energy kBT (kB, the Boltzmann constant).
[35,45], and measure all the energies in unit of t. Here we make a valid approximation by setting the system temperature to zero, as the average energy level spacing is too large (due to small ring size) compared to the thermal energy kBT (kB, the Boltzmann constant).
Spectral features
To understand the precise role of AAH potentials on flux-driven circular current, the spectral properties (characteristics of energy eigenspectrum) of the physical system are undoubtedly required, and in this sub-section we focus on that.
We start with fig. 2, where the dependence of energy eigenvalues on the AAH phase 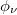 is shown. At a first glance it is seen that the energy eigenvalues almost merge into three bands, like what we get in other quasi-periodic systems, and the energy levels associated with these bands are very less affected by the phase
is shown. At a first glance it is seen that the energy eigenvalues almost merge into three bands, like what we get in other quasi-periodic systems, and the energy levels associated with these bands are very less affected by the phase 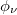 . On the other hand, some other energy levels which appear between the bands are reasonably influenced by this AAH phase. Thus, a mixture of two different kinds of energy levels is obtained, and as a result of this finite phase dependence on current is naturally expected. It becomes more clear from our further discussion.
. On the other hand, some other energy levels which appear between the bands are reasonably influenced by this AAH phase. Thus, a mixture of two different kinds of energy levels is obtained, and as a result of this finite phase dependence on current is naturally expected. It becomes more clear from our further discussion.
Fig. 2: Energy eigenvalues as a function of AAH phase  for a 20 site ring. Here we choose the AAH modulation strength W = 1 and AB flux
for a 20 site ring. Here we choose the AAH modulation strength W = 1 and AB flux 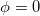 .
.
Download figure:
Standard imageFigure 3 describes the variation of individual energy levels as a function of magnetic flux ϕ. To visualize the specific role of AAH potential, here we plot the energy levels of an AAH ring for three different values of W (figs. 3(a)–(c)) along with the perfect ring fig. 3(d). In the presence of AAH modulation, the energy spectrum is broken into three bands which are separated by finite gaps, while no such gap appears for the perfect ring 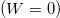 . Several noteworthy features are noticed by comparing the slopes of distinct energy levels for the three different strengths of W. When W = 1, all the energy levels have finite variation with flux ϕ (fig. 3(a)), which indicates that all the energy eigenstates can carry finite current, and depending on the slopes of these states we get the sign of the currents. Now, for the energy levels which are situated well inside the band, the slope is relatively higher compared to the states located near the band edges, and it gives an important signature towards filling dependent current. With increasing W, the slope of the states gradually decreases which means that they are getting localized, and from the spectrum fig. 3(b) it is clearly seen that the localization starts from the band edges. When the modulation strength is reasonably high, all the states are almost flat with respect to ϕ (fig. 3(c)), and under this situation no current will be obtained. It is well known that for a 1D system where on-site energies are modulated in the cosine form (viz., diagonal AAH system), a phase transition from a conducting phase to the insulating one takes place at the critical modulation strength
. Several noteworthy features are noticed by comparing the slopes of distinct energy levels for the three different strengths of W. When W = 1, all the energy levels have finite variation with flux ϕ (fig. 3(a)), which indicates that all the energy eigenstates can carry finite current, and depending on the slopes of these states we get the sign of the currents. Now, for the energy levels which are situated well inside the band, the slope is relatively higher compared to the states located near the band edges, and it gives an important signature towards filling dependent current. With increasing W, the slope of the states gradually decreases which means that they are getting localized, and from the spectrum fig. 3(b) it is clearly seen that the localization starts from the band edges. When the modulation strength is reasonably high, all the states are almost flat with respect to ϕ (fig. 3(c)), and under this situation no current will be obtained. It is well known that for a 1D system where on-site energies are modulated in the cosine form (viz., diagonal AAH system), a phase transition from a conducting phase to the insulating one takes place at the critical modulation strength 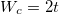 [45,46]. Below this critical point (W < Wc) all the states are extended in nature, while they are absolutely localized when W > Wc. The "absolute localization" for W > Wc takes place only in the asymptotic limit
[45,46]. Below this critical point (W < Wc) all the states are extended in nature, while they are absolutely localized when W > Wc. The "absolute localization" for W > Wc takes place only in the asymptotic limit  , and we here do not consider that limit as persistent current is a mesoscopic phenomenon, where N is finite (small). For the perfect ring, we get intersecting energy levels [3] and each of them provides a finite variation with ϕ (fig. 3(d)).
, and we here do not consider that limit as persistent current is a mesoscopic phenomenon, where N is finite (small). For the perfect ring, we get intersecting energy levels [3] and each of them provides a finite variation with ϕ (fig. 3(d)).
Fig. 3: (a)–(c) Energy eigenvalues as a function of AB flux ϕ for an AAH ring with W = 1, 1.5 and 2.5, respectively. To understand AAH effect on the energy levels, an energy spectrum is given in (d) without including any AAH factor. The other parameters are N = 16 and 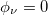 .
.
Download figure:
Standard imageFrom the information of individual energy levels, finally we determine the ground state energy 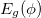 for a fixed number of electrons Ne, to get the net persistent current (see eq. (5)). A finite effect of
for a fixed number of electrons Ne, to get the net persistent current (see eq. (5)). A finite effect of 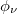 on the ground state energy is clearly reflected from the curves shown in fig. 4(a). On the other hand, each of these curves provides a smaller variation with AB flux ϕ compared to the perfect ring (fig. 4(b)), which thus suggests much smaller current in the AAH ring than in the perfect one.
on the ground state energy is clearly reflected from the curves shown in fig. 4(a). On the other hand, each of these curves provides a smaller variation with AB flux ϕ compared to the perfect ring (fig. 4(b)), which thus suggests much smaller current in the AAH ring than in the perfect one.
Fig. 4: Ground state energy as a function of AB flux ϕ for (a) AAH ring 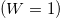 and (b) perfect ring
and (b) perfect ring 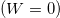 . The red, green and blue lines in (a) correspond to
. The red, green and blue lines in (a) correspond to 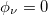 ,
, 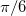 and
and 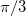 , respectively. Here we set N = 30 and
, respectively. Here we set N = 30 and 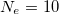 .
.
Download figure:
Standard imageCharacteristics of circular current
From the information of the above spectral features now we analyze the characteristic features of flux-driven circular current under different input conditions.
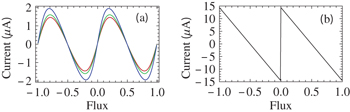
Figure 5 describes the variation of current with AB flux ϕ where the current of an AAH ring along with the current of a perfect ring are shown to visualize the precise AAH effect. In the absence of AAH modulation, current shows a saw-tooth–like behavior providing a sharp transition at 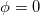 (fig. 5(b)), following the sudden change in slope in
(fig. 5(b)), following the sudden change in slope in 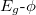 curve across this flux (fig. 4(b)). But, as long as the AAH modulation is introduced, such sudden jump completely disappears and the current varies smoothly (fig. 5(a)). This is solely due to the smooth dependence (viz., without any sharp crossing) of Eg on ϕ, as is evident from fig. 4(a). Along with this, we also get much reduced current (an order of magnitude smaller) compared to the perfect ring. This is because of the electronic localization due to scattering of electrons at non-uniform site potentials, satisfying the above-mentioned energy-flux nature. Finally, the dependence of
curve across this flux (fig. 4(b)). But, as long as the AAH modulation is introduced, such sudden jump completely disappears and the current varies smoothly (fig. 5(a)). This is solely due to the smooth dependence (viz., without any sharp crossing) of Eg on ϕ, as is evident from fig. 4(a). Along with this, we also get much reduced current (an order of magnitude smaller) compared to the perfect ring. This is because of the electronic localization due to scattering of electrons at non-uniform site potentials, satisfying the above-mentioned energy-flux nature. Finally, the dependence of 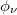 in ground state energy is also clearly reflected in persistent current as given in fig. 5(a). With the change of
in ground state energy is also clearly reflected in persistent current as given in fig. 5(a). With the change of 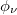 , site energies are modified according to eq. (2), which results in a finite variation in ground state energy, and hence the current. This picture gives a clear indication that the current can be regulated externally by controlling the phase factor
, site energies are modified according to eq. (2), which results in a finite variation in ground state energy, and hence the current. This picture gives a clear indication that the current can be regulated externally by controlling the phase factor 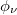 , and this is one of the primary requirements of this study.
, and this is one of the primary requirements of this study.
Fig. 5: Persistent current as a function of AB flux ϕ for (a) AAH ring  and (b) perfect ring
and (b) perfect ring  . The red, green and blue lines in (a) correspond to
. The red, green and blue lines in (a) correspond to 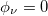 ,
,  and
and  , respectively. Here we set N = 30 and
, respectively. Here we set N = 30 and 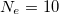 .
.
Download figure:
Standard imageNow, in order to see the dependence of the current on the total number of electrons Ne, in fig. 6 we present the current-flux characteristics at three different values of Ne which are represented by three colored curves. The results of both the AAH and perfect rings are presented to understand the contrasting nature of current. The saw-tooth behavior with large amplitude in the perfect case is already established. But the fact is that here all the current amplitudes are comparable to each other for these three cases of Ne. On the other hand, a large mismatch between the current amplitudes takes places in the case of AAH ring. For two different values of 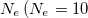 and 14) currents are quite comparable to each other (red and blue lines in fig. 6), while for the other
and 14) currents are quite comparable to each other (red and blue lines in fig. 6), while for the other 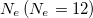 , the current almost vanishes (green line in fig. 6). This high degree of reduction in current at a particular filling in the AAH ring is because of the peculiar nature of energy band spectrum where both the conducting and almost zero conducting states are mixed, unlike the perfect ring or uncorrelated "random" disordered one. For this
, the current almost vanishes (green line in fig. 6). This high degree of reduction in current at a particular filling in the AAH ring is because of the peculiar nature of energy band spectrum where both the conducting and almost zero conducting states are mixed, unlike the perfect ring or uncorrelated "random" disordered one. For this 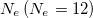 , almost zero variation of Eg takes places with flux ϕ yielding a vanishing current. A more clear picture of it can be understood from our forthcoming analysis.
, almost zero variation of Eg takes places with flux ϕ yielding a vanishing current. A more clear picture of it can be understood from our forthcoming analysis.
Fig. 6: (a) Current as a function of ϕ at three specific values of Ne for the AAH ring with W = 1 and  . (b) The results are shown for the perfect ring
. (b) The results are shown for the perfect ring  . The red, green and blue curves represent
. The red, green and blue curves represent 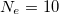 , 12 and 14, respectively. Here we choose N = 30.
, 12 and 14, respectively. Here we choose N = 30.
Download figure:
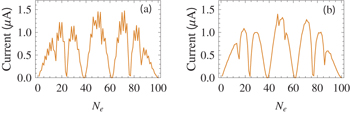
Standard imageFigure 6 generates an obvious question, i.e., how will the current vary if the total number of electrons is changed systematically from its minimum value 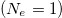 to the maximum
to the maximum 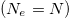 one? The answer is given in fig. 7, where the variation of current at two different flux values are shown. The pattern is very interesting. Here we get a strong oscillatory behavior with Ne. In both these two cases of ϕ, we find that the current almost drops to zero at some specific values of Ne resulting in an insulating phase, while for the other filling factors finite currents are obtained. For any other ϕ, we also get the identical
one? The answer is given in fig. 7, where the variation of current at two different flux values are shown. The pattern is very interesting. Here we get a strong oscillatory behavior with Ne. In both these two cases of ϕ, we find that the current almost drops to zero at some specific values of Ne resulting in an insulating phase, while for the other filling factors finite currents are obtained. For any other ϕ, we also get the identical  picture which we confirm through our detailed investigation. Now, it is important to know what is special about these specific values of Ne, for instance
picture which we confirm through our detailed investigation. Now, it is important to know what is special about these specific values of Ne, for instance 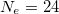 , 38, 62 and 76, where current shows a sharp dip. To explore it, let us look into the spectra presented in fig. 8, where the ground state energy and the corresponding current as a function of flux ϕ are shown. Clearly we notice that almost zero deviation in Eg with ϕ occurs which thus generates vanishingly small currents in the ring. On the other hand, for other Ne (not shown in fig. 8), Eg has finite slope with ϕ, and accordingly finite currents are obtained. All these issues are due to the existence of both finite and almost vanishing current carrying states. Thus, from the
, 38, 62 and 76, where current shows a sharp dip. To explore it, let us look into the spectra presented in fig. 8, where the ground state energy and the corresponding current as a function of flux ϕ are shown. Clearly we notice that almost zero deviation in Eg with ϕ occurs which thus generates vanishingly small currents in the ring. On the other hand, for other Ne (not shown in fig. 8), Eg has finite slope with ϕ, and accordingly finite currents are obtained. All these issues are due to the existence of both finite and almost vanishing current carrying states. Thus, from the 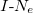 spectrum (fig. 7) we can claim that the AAH ring can be utilized as a high-to-low conducting switching device and vice versa by regulating the filling factor.
spectrum (fig. 7) we can claim that the AAH ring can be utilized as a high-to-low conducting switching device and vice versa by regulating the filling factor.
Fig. 7: Absolute persistent current as a function of Ne for a 100-site AAH ring with W = 1 and 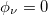 , where (a) and (b) correspond to
, where (a) and (b) correspond to 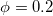 and 0.25, respectively.
and 0.25, respectively.
Download figure:
Standard imageFig. 8: Ground state energy and persistent current as a function of ϕ for four different Ne considering the identical ring as taken in fig. 7, where the red, green, blue and black lines represent 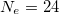 , 38, 62 and 76, respectively. It is quite difficult to distinguish the colored curves as they almost overlap with each other.
, 38, 62 and 76, respectively. It is quite difficult to distinguish the colored curves as they almost overlap with each other.
Download figure:
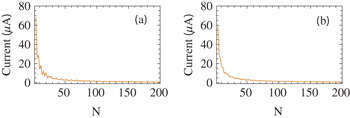
Standard imageFor the sake of completeness, now we discuss the dependence of ring size N on persistent current. The results are presented in fig. 9. As expected, current amplitude gradually decreases with N, and it eventually drops to zero in the asymptotic limit. Thus, the phenomenon of persistent current is no longer visible when 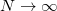 since it is a mesoscopic phenomenon.
since it is a mesoscopic phenomenon.
Fig. 9: Absolute persistent current as a function of N, by varying N from 4 to 200 taking the interval 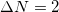 , where (a) and (b) correspond to
, where (a) and (b) correspond to 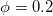 and 0.25, respectively. Here we take W = 1 and
and 0.25, respectively. Here we take W = 1 and  .
.
Download figure:
Standard imageNear-zero field magnetic response
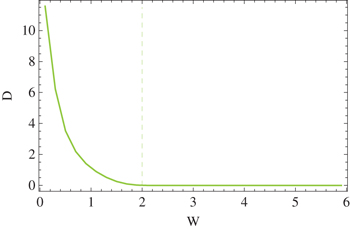
Finally, we reveal the conducting behavior of the AAH ring and its dependence on the modulation strength W. As already mentioned, the conducting nature can be estimated in a simpler way by calculating the Drude weight D, in which a second-order derivative of ground state energy in the limit 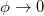 is taken into account (see eq. (7)). Figure 10 depicts the variation of D as a function of W for a 200 site AAH ring in the half-filled band case. It shows that D gradually decreases with W, and at the critical point
is taken into account (see eq. (7)). Figure 10 depicts the variation of D as a function of W for a 200 site AAH ring in the half-filled band case. It shows that D gradually decreases with W, and at the critical point 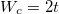 (in our calculation we set t = 1) it (D) drops almost to zero (exactly vanishing nature is obtained only when
(in our calculation we set t = 1) it (D) drops almost to zero (exactly vanishing nature is obtained only when  ). Thus, for W < 2t we get the conducting phase since D is finite, while for the other range where W > 2t the insulating phase
). Thus, for W < 2t we get the conducting phase since D is finite, while for the other range where W > 2t the insulating phase 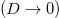 is obtained. This phase transition at the critical point
is obtained. This phase transition at the critical point 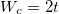 is fully consistent with the earlier analysis [45,46]. The
is fully consistent with the earlier analysis [45,46]. The  spectrum shown in fig. 10 is computed for
spectrum shown in fig. 10 is computed for  , though the nature of this spectrum and the transition point remain unchanged for any other choices of
, though the nature of this spectrum and the transition point remain unchanged for any other choices of 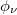 which we confirm through our detailed numerical analysis.
which we confirm through our detailed numerical analysis.
Fig. 10: Drude weight as a function of W for a 200 site ring in the half-filled band case. The dashed vertical line describes the critical point where the transition from the conducting to insulating phase takes place. Here we set 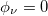 .
.
Download figure:
Standard imageClosing remarks and outlook
To conclude, in the present work we explore the phenomenon of flux-driven circular current in an AB conducting ring where site energies are modulated in the cosine form following the well-known AAH model. A TB framework is given to describe the quantum system where spectral features are obtained by exactly diagonalizing the TB Hamiltonian, and the circular current is computed by the conventional derivative method. Several interesting features emerge which are summarized as follows.
- i)The AAH ring exhibits fractal-like energy bands and gaps. Most of the energy levels are almost independent with respect to the AAH phase
 , while the other energy levels are strongly influenced by this phase. These later states give a possibility to have externally controlled circular current.
, while the other energy levels are strongly influenced by this phase. These later states give a possibility to have externally controlled circular current. - ii)A mixture of both conducting and almost zero conducting states appear, which produce a strong filling dependent current. At some specific values of Ne almost vanishing current is obtained, while for other Ne reasonably large current is generated. This phenomenon can be utilized to get high-to-low conducting switching action and vice versa.
- iii)Finally, a transition from conducting to insulating phase is described by studying magnetic response in the zero field limit.
Future prospects and open questions: Our analysis may be extended further in a conducting ring where a similar kind of modulation can be included in NNH integrals together with site energies, and the interplay between these two modulations may provide some interesting new results. The role of electron-electron interaction along with these modulations will be another important study. We shall focus on these issues in our forthcoming work.
Acknowledgments
SKM acknowledges the financial support of DST-SERB, Government of India under Project File No.: EMR/2017/000504.