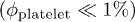Abstract
The transport of cells and substances in dense suspensions like blood heavily depends on the microstructure and the dynamics arising from their interactions with red blood cells (RBCs). Computer simulations are used to probe into the detailed transport-related characteristics of a blood-like suspension, for a wide range of volume fractions and shear rates. The shear-induced diffusion of RBCs does not follow the established linear scaling with shear rate for higher volume fractions. The properties directly related to RBC deformability —stretching and flow orientation— are not sufficient to explain this departure according to the model of Breedveld, pointing to the dominance of collective effects in the suspension. A cluster size analysis confirms that collective effects dominate high volume fractions, as the mean cluster size is above 2 and the number of "free RBCs" is significantly decreased in denser suspensions. The mean duration of RBC contacts in clusters is increased in the high volume fraction and shear rate cases, showing that these clusters live longer.
Export citation and abstract BibTeX RIS

Published by the EPLA under the terms of the Creative Commons Attribution 3.0 License (CC-BY). Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.
Introduction
In dilute suspensions of hard spheres, the collision of two isolated spheres in the Stokes regime is symmetric and reversible. In the absence of long-range interactions diffusion arises from the collision of three or more particles [1,2] or due to surface roughness [3]. However, the collision of two or more elastic particles, such as red blood cells (RBCs), can alone give rise to diffusive behavior at long times [4–6]. Pair collisions of RBCs have been studied under a variety of conditions [7–9], as well as the shear-induced diffusion of RBCs in dilute systems [10], yet the mechanism behind the transport of deformable particles in dense suspensions has received less attention and is not yet fully understood. The hydrodynamic interactions of blood components like platelets, white blood cells and micro-/nano-particles with RBCs determine their distribution inside the blood vessels as well as the efficacy of drug-delivery systems [11,12] and are an active research topic [12–14].
Recently, Gross et al. [15] proposed a connection between viscosity and diffusion in such systems using kinetic arguments, obtaining good agreement with their simulation results. The range of validity for this relation has not been identified. In this letter we present results from simulations of a blood-like suspension in a shear-flow environment, focusing on the shear-induced diffusion from the perspective of the micro-structure and the collective effects, employing a wide range of shear rates and volume fractions.
Methods
We employ the combined immersed-boundary lattice-Boltzmann method (IB-LBM) in two dimensions [16]. Fluid is simulated with LBM using the D2Q9 LBGK scheme, while RBCs are represented as closed deformable biconcave membranes with a diameter  and a thickness
and a thickness 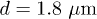 . The membrane of an RBC consists of 26 neighboring vertices connected by Hookean springs and enhanced with bending resistance. In addition, forces that ensure the conservation of area (2D equivalent of volume) and that consider the cell-cell interactions are specified. This model has been used and validated in previous studies [16,17].
. The membrane of an RBC consists of 26 neighboring vertices connected by Hookean springs and enhanced with bending resistance. In addition, forces that ensure the conservation of area (2D equivalent of volume) and that consider the cell-cell interactions are specified. This model has been used and validated in previous studies [16,17].
Simulations are performed in a Lees-Edwards periodic boundary conditions (LEbc) domain, providing an unbounded type of shear flow and avoiding wall-induced migration [18]. The size of the domain was set to  and the flow profile has the form
and the flow profile has the form  with
with  . The kinematic viscosity of the fluid is
. The kinematic viscosity of the fluid is 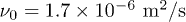 and the density
and the density  , close to that of blood plasma [19]. The LB relaxation time is set to
, close to that of blood plasma [19]. The LB relaxation time is set to 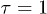 and the lattice constant to
and the lattice constant to 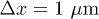 , yielding a timestep
, yielding a timestep  . Inner and outer viscosities and densities are equal, while a soft repulsive force is used to prevent overlap. The form of the repulsive force is
. Inner and outer viscosities and densities are equal, while a soft repulsive force is used to prevent overlap. The form of the repulsive force is  , where h is the gap between surface points,
, where h is the gap between surface points, 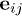 the connecting vector and
the connecting vector and 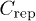 a constant set to 0.05 in lattice units. The force becomes zero for distances larger than
a constant set to 0.05 in lattice units. The force becomes zero for distances larger than  . Similar power-law forces have been used by [20,21].
. Similar power-law forces have been used by [20,21].
The shear rates studied range from 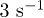 to
to  and the volume fractions from
and the volume fractions from 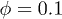 to 0.5, yielding an absolute number of RBCs of 1600 to 8000, respectively. In all cases the simulation time was
to 0.5, yielding an absolute number of RBCs of 1600 to 8000, respectively. In all cases the simulation time was 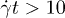 with a typical duration of
with a typical duration of 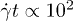 , sufficient to measure the transport properties of RBCs. A constant number of platelets is present in the system as part of a larger study regarding their transport in channel and shear flows, but due to their low relative numbers (
, sufficient to measure the transport properties of RBCs. A constant number of platelets is present in the system as part of a larger study regarding their transport in channel and shear flows, but due to their low relative numbers (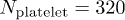 with
with 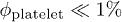 ) and small size, their contribution to viscosity and diffusion is insignificant (diffusion data not shown). The particle Reynolds number
) and small size, their contribution to viscosity and diffusion is insignificant (diffusion data not shown). The particle Reynolds number 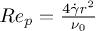 ranges from
ranges from  to
to 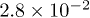 for
for 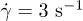 to
to 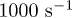 , respectively. Thermal fluctuations are neglected in our study, since the thermal Péclet number
, respectively. Thermal fluctuations are neglected in our study, since the thermal Péclet number 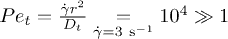 .
.
Performing a reliable analysis of the transport of RBCs requires sufficiently large domain sizes and shear strains [22], which leads to very long simulation times, especially in the lower shear rate regimes. It is common to rescale the timestep of the simulation according to the capillary number 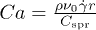 , where
, where  is the elastic modulus of the cell. IB-LBM [15,23] and dissipative particle dynamics (DPD) [24,25] studies have followed this approach, motivated by the assumption that the shear elasticity provides the most dominant contribution to the suspension stress. Such scaling, however, deprives the timescales defined by the particle Reynolds number, lubrication, and interparticle forces from an appropriate scaling. Lubrication and interparticle forces dominate dense suspensions, where the gap between particles becomes comparable to the extents of these forces [15,26]. In contrast to these earlier studies we avoid such scaling because in our opinion this contributes to a consistent and well-defined model.
is the elastic modulus of the cell. IB-LBM [15,23] and dissipative particle dynamics (DPD) [24,25] studies have followed this approach, motivated by the assumption that the shear elasticity provides the most dominant contribution to the suspension stress. Such scaling, however, deprives the timescales defined by the particle Reynolds number, lubrication, and interparticle forces from an appropriate scaling. Lubrication and interparticle forces dominate dense suspensions, where the gap between particles becomes comparable to the extents of these forces [15,26]. In contrast to these earlier studies we avoid such scaling because in our opinion this contributes to a consistent and well-defined model.
Results and discussion
As with blood, this suspension exhibits a shear-thinning behavior: its viscosity decreases when subjected to shear strain. In all simulations RBCs were randomly positioned in the LEbc domain and the relative apparent viscosity was computed using Batchelor's method [27]. In low volume fractions  the fluid is Newtonian1
and the effective viscosity of the suspension
the fluid is Newtonian1
and the effective viscosity of the suspension 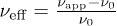 remains relatively constant for all the examined shear rates (fig. 1 and inset). The suspension starts exhibiting non-Newtonian characteristics for
remains relatively constant for all the examined shear rates (fig. 1 and inset). The suspension starts exhibiting non-Newtonian characteristics for 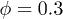 and strong shear-thinning behavior in high volume fractions,
and strong shear-thinning behavior in high volume fractions, 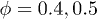 .
.
Fig. 1: (Color online) Effective viscosity 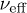 with respect to shear rate
with respect to shear rate 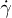 . Relative viscosity
. Relative viscosity 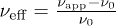 , where
, where 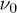 is the viscosity of the solvent and
is the viscosity of the solvent and 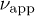 the apparent viscosity. The fluid exhibits shear thinning in higher volume fractions and is Newtonian in the lower ones. Inset: magnification in log-linear scale.
the apparent viscosity. The fluid exhibits shear thinning in higher volume fractions and is Newtonian in the lower ones. Inset: magnification in log-linear scale.
Download figure:
Standard imageAs the mean particle distance decreases with increasing ϕ, RBCs interact more frequently and the effective volume of the RBCs appears to be practically larger for  and 0.5, due to the extent of the repulsive force [28]. The shear thinning observed is an effect of both repulsion and deformability [26,29].
and 0.5, due to the extent of the repulsive force [28]. The shear thinning observed is an effect of both repulsion and deformability [26,29].
Shear-induced diffusion is the result of excluded-volume effects [1]. Neighboring particles are displaced from their initial streamlines when passing each other, thus leading to net post-collisional displacements, as opposed to the reversible two-particle collisions in the Stokes flow. Breedveld et al. [1] suggested that the diffusion tensor of a hard-sphere suspension should scale linearly with 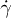 as
as

where  is a dimensionless symmetric tensor. The arguments are based on a dimensional analysis, in which the only relevant dimensions are the particle radius r as the lengthscale, and
is a dimensionless symmetric tensor. The arguments are based on a dimensional analysis, in which the only relevant dimensions are the particle radius r as the lengthscale, and 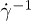 as the timescale, considering the shear-induced character of the process. Equation (1) is widely used to describe the diffusion of RBCs and platelets with advection-diffusion models [30–32].
as the timescale, considering the shear-induced character of the process. Equation (1) is widely used to describe the diffusion of RBCs and platelets with advection-diffusion models [30–32].
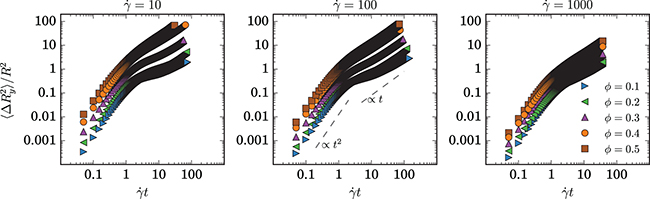
We measure diffusion in the shear-gradient direction Dy from the mean square displacement (MSD) as 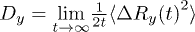 , where
, where 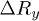 is the displacement in the y-direction. It is well known that in non-Brownian suspensions MSD typically exhibits two distinct regimes: over short shear strains
is the displacement in the y-direction. It is well known that in non-Brownian suspensions MSD typically exhibits two distinct regimes: over short shear strains 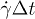 the velocity of a particle is self-correlated leading to a super-diffusive quadratic behavior
the velocity of a particle is self-correlated leading to a super-diffusive quadratic behavior  (ballistic regime) and at large shear strains to the diffusive regime
(ballistic regime) and at large shear strains to the diffusive regime 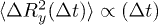 , where the interactions of particles have lead to decorrelation [15]. This behavior is also observed in our model as shown in fig. 2. It is consequential that the duration of the simulations has to span a sufficient number of shear strains
, where the interactions of particles have lead to decorrelation [15]. This behavior is also observed in our model as shown in fig. 2. It is consequential that the duration of the simulations has to span a sufficient number of shear strains 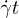 , until the ballistic regime is exceeded and MSD is well into the diffusive regime.
, until the ballistic regime is exceeded and MSD is well into the diffusive regime.
Fig. 2: (Color online) Mean square displacement in the shear-gradient direction 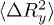 normalized with the effective radius of an RBC
normalized with the effective radius of an RBC  . Two regimes are clear: the ballistic where
. Two regimes are clear: the ballistic where 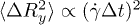 and the diffusive where
and the diffusive where 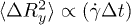 .
.
Download figure:
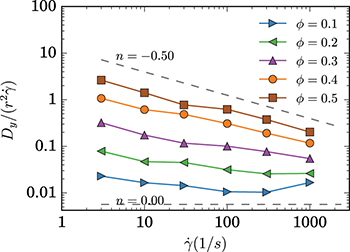
Standard imageAs shown in fig. 3, 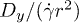 is increasing with ϕ, with diffusion following the linear scaling with
is increasing with ϕ, with diffusion following the linear scaling with  in low volume fractions. Contrary to the predictions of (1)
in low volume fractions. Contrary to the predictions of (1) 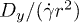 scales with
scales with  for higher volume fractions.
for higher volume fractions.
Fig. 3: (Color online) Diffusion along the shear gradient direction Dy in units of 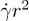 (equivalent to the inverse Peclet number
(equivalent to the inverse Peclet number  ), with respect to volume fraction and shear rate. Dy was calculated from the mean square displacement.
), with respect to volume fraction and shear rate. Dy was calculated from the mean square displacement.
Download figure:
Standard imageGross et al. [15] made a similar observation for three-dimensional suspension of deformable particles in Couette flow. Using kinetic and scaling arguments, they established a connection between viscosity ν and diffusivity D in which  in the Newtonian regime, where q indicates the scaling of the viscosity with respect to the capillary number
in the Newtonian regime, where q indicates the scaling of the viscosity with respect to the capillary number  , and
, and 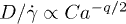 in the shear-thinning regime. While for the Newtonian cases this connection holds, for the shear-thinning regime our simulations do not confirm their findings, in which
in the shear-thinning regime. While for the Newtonian cases this connection holds, for the shear-thinning regime our simulations do not confirm their findings, in which  and not
and not 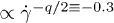 . The difference in the dimensionality of the problem, in the form of missing shear elasticity and reduced mobility, may explain partly the differences in our results. However, the same arguments and assumptions hold in 2D and since Gross et al. do not employ relations or theorems that involve dimensionality, like the equipartition theorem, the explanation should be sought in their assumptions. One of the principal assumptions of the study was that the shear-elasticity provides the most dominant contribution to the suspension stress, rendering capillary number the only relevant quantity under examination. This assumption disregards the contribution of interparticle forces, which is substantial at high volume fractions and can, alone, induce shear thinning even in hard-sphere suspensions [26]. With proper comparison, the shift between our results and Gross et al. [15] could be explained in terms of differences in the resolution and the reach of the repulsive force, highlighting the role of the interparticle force in high volume fractions.
. The difference in the dimensionality of the problem, in the form of missing shear elasticity and reduced mobility, may explain partly the differences in our results. However, the same arguments and assumptions hold in 2D and since Gross et al. do not employ relations or theorems that involve dimensionality, like the equipartition theorem, the explanation should be sought in their assumptions. One of the principal assumptions of the study was that the shear-elasticity provides the most dominant contribution to the suspension stress, rendering capillary number the only relevant quantity under examination. This assumption disregards the contribution of interparticle forces, which is substantial at high volume fractions and can, alone, induce shear thinning even in hard-sphere suspensions [26]. With proper comparison, the shift between our results and Gross et al. [15] could be explained in terms of differences in the resolution and the reach of the repulsive force, highlighting the role of the interparticle force in high volume fractions.
The deviation of diffusion from the linear scaling with the shear rate requires further investigation. Looking into the other parameters of eq. (1), only the radius r is possible to be dependent on  . Since RBCs are deformable, which stretch and tank-tread under shear [33], it is reasonable to associate stretch and angle of orientation of RBCs with a shear-dependent increase in the collisional cross-section, rendering
. Since RBCs are deformable, which stretch and tank-tread under shear [33], it is reasonable to associate stretch and angle of orientation of RBCs with a shear-dependent increase in the collisional cross-section, rendering  . A decrease in the collisional cross-section results in smaller post-collisional migrations and eventually to smaller values of diffusion. However, our data do not support this assumption. Even though an increase of the average orientation angle 〈θ〉 is measured (fig. 4(a)), there is no notable difference with respect to the shear rate. The average maximum diameter of an RBC
. A decrease in the collisional cross-section results in smaller post-collisional migrations and eventually to smaller values of diffusion. However, our data do not support this assumption. Even though an increase of the average orientation angle 〈θ〉 is measured (fig. 4(a)), there is no notable difference with respect to the shear rate. The average maximum diameter of an RBC 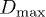 , defined as the maximum distance between any two surface points (SPs) of an RBC, shows that cells are stretched in all cases of high shear rates and in high volume fractions (fig. 4(b)). The increase in high shear rates is an effect of the shear forces and the deformability of the RBCs, while the latter can be attributed to the interparticle force and the decreasing mean gap with increasing volume fraction. The collisional cross-section
, defined as the maximum distance between any two surface points (SPs) of an RBC, shows that cells are stretched in all cases of high shear rates and in high volume fractions (fig. 4(b)). The increase in high shear rates is an effect of the shear forces and the deformability of the RBCs, while the latter can be attributed to the interparticle force and the decreasing mean gap with increasing volume fraction. The collisional cross-section  is computed by integrating
is computed by integrating 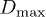 over all angles
over all angles 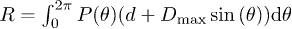 , where
, where 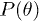 is the distribution of angles and d the RBC thickness. The collisional cross-section R is almost independent of
is the distribution of angles and d the RBC thickness. The collisional cross-section R is almost independent of 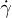 , slightly decreasing with
, slightly decreasing with  for
for 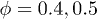 , as the fittings of fig. 4(c) show. This change of
, as the fittings of fig. 4(c) show. This change of 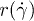 is not sufficient to explain the non-linear scaling of diffusion in high volume fractions. These results demonstrate that pair collisions, which drive diffusion in dilute systems, are not the principal mechanism for dense systems and higher-order collisions and collective effects should be taken into account.
is not sufficient to explain the non-linear scaling of diffusion in high volume fractions. These results demonstrate that pair collisions, which drive diffusion in dilute systems, are not the principal mechanism for dense systems and higher-order collisions and collective effects should be taken into account.
Fig. 4: (Color online) (a) Average orientation angle 〈θ〉 and standard deviation of the angle (inset) as a function of volume fraction for several values of the shear rate; (b) average diameter of an RBC  as a function of shear rate.
as a function of shear rate.  is defined as the average maximum distance between the surface points of an RBC. (c) Collisional cross-section R, the fittings to
is defined as the average maximum distance between the surface points of an RBC. (c) Collisional cross-section R, the fittings to  are also shown for
are also shown for  and 0.5. For
and 0.5. For 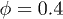 and 0.5 we obtain
and 0.5 we obtain  and
and  , respectively.
, respectively.
Download figure:
Standard imageThe pair distribution function 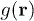 (PDF) describes the microstructure from the perspective of the spatial arrangement of particles. It expresses the probability of finding particles at distance r from a reference particle normalized by the number concentration of the suspension [34] (fig. 5). In the dilute case, where particle interactions are less frequent,
(PDF) describes the microstructure from the perspective of the spatial arrangement of particles. It expresses the probability of finding particles at distance r from a reference particle normalized by the number concentration of the suspension [34] (fig. 5). In the dilute case, where particle interactions are less frequent,  has a uniform distribution lacking local maxima. Local maxima develop close to the small RBC radius for larger ϕ, while the distinguishable ripples indicate rouleux-like structures. The second peak close the large RBC diameter
has a uniform distribution lacking local maxima. Local maxima develop close to the small RBC radius for larger ϕ, while the distinguishable ripples indicate rouleux-like structures. The second peak close the large RBC diameter 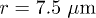 indicates that neighboring RBCs are often aligned in the flow. RBCs appear stretched at higher shear rates of
indicates that neighboring RBCs are often aligned in the flow. RBCs appear stretched at higher shear rates of 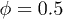 (fig. 4(b)).
(fig. 4(b)).
Fig. 5: Two-dimensional pair distribution function 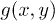 , as calculated from the distances between the centers of the particles. Lighter gray corresponds to higher probability, units of distance are in μm and the color scale is per subplot. RBCs are deformable with a biconcave shape and can have neighboring particles at distances shorter than their larger diameter, which explains the blurred RBC shape, contrary to hard spheres where the spherical shape is clearly visible in PDF plots. An asymmetry and a preferred orientation with increasing shear rate and volume fraction can be distinguished.
, as calculated from the distances between the centers of the particles. Lighter gray corresponds to higher probability, units of distance are in μm and the color scale is per subplot. RBCs are deformable with a biconcave shape and can have neighboring particles at distances shorter than their larger diameter, which explains the blurred RBC shape, contrary to hard spheres where the spherical shape is clearly visible in PDF plots. An asymmetry and a preferred orientation with increasing shear rate and volume fraction can be distinguished.
Download figure:
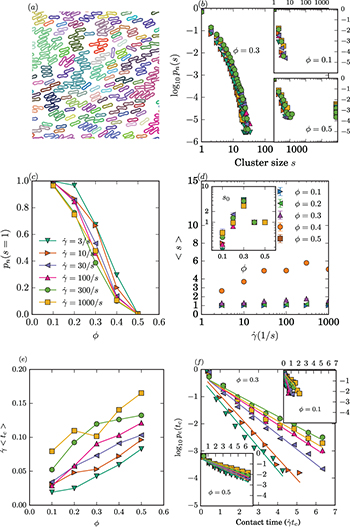
Standard imageThe formation of RBC clusters is a key finding that is extracted from the pair distribution function. These clusters are different from the hydro-clusters of hard-sphere suspensions as studied by Brady and Bossis [35], owing to the repulsive interparticle force keeping RBCs separated and preserving a lubrication layer. We perform a cluster size analysis to obtain a quantitative estimate on collective effects of the suspension and the RBC-RBC interactions.
Two RBCs are considered "in contact" and belong to the same cluster when the distance between two of their surface points (SPs) is less than a cutoff distance  , defined as the peak of the SP-SP distance distribution. The collection of RBCs that are in contact forms a cluster and the number of particles in one cluster defines the size s of the cluster. Figure 6(a) shows a snapshot of the simulation, coloring the RBCs belonging to the same cluster. The total number of clusters with size s at time t is denoted as
, defined as the peak of the SP-SP distance distribution. The collection of RBCs that are in contact forms a cluster and the number of particles in one cluster defines the size s of the cluster. Figure 6(a) shows a snapshot of the simulation, coloring the RBCs belonging to the same cluster. The total number of clusters with size s at time t is denoted as 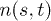 . The average number of clusters n(s) is obtained over a time period T, and is defined as
. The average number of clusters n(s) is obtained over a time period T, and is defined as  [36], with
[36], with 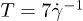 being several times larger than the correlation time
being several times larger than the correlation time 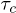 extracted from the velocity autocorrelation function and long enough to capture the duration of RBC contacts. The quantity we are interested in is the cluster size distribution
extracted from the velocity autocorrelation function and long enough to capture the duration of RBC contacts. The quantity we are interested in is the cluster size distribution  .
.
Fig. 6: (Color online) (a) Detail from simulation  and
and  . RBCs belonging to the same cluster have the same color. Platelets are not shown. (b) Cluster size s distribution with respect to shear rate
. RBCs belonging to the same cluster have the same color. Platelets are not shown. (b) Cluster size s distribution with respect to shear rate  for
for 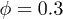 (main) and
(main) and 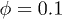 and 0.5 (insets). (c) Percentage of single RBCs
and 0.5 (insets). (c) Percentage of single RBCs 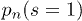 (RBCs not belonging to a cluster). (d) Average cluster size
(RBCs not belonging to a cluster). (d) Average cluster size 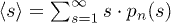 with respect to shear rate (main) and typical cluster size s0 (inset) obtained from fitting cluster distribution to
with respect to shear rate (main) and typical cluster size s0 (inset) obtained from fitting cluster distribution to 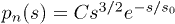 . A hyper-cluster dominates
. A hyper-cluster dominates 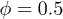 , with
, with 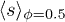 and being many times larger than
and being many times larger than  , is not visible within the range plotted. (e) Mean duration
, is not visible within the range plotted. (e) Mean duration  of a contact between two RBCs and (f) distribution of contact durations between two RBCs, along with their respective fits to an exponential distribution. Symbol notation is shown in (c) and applies to all plots except for the main figure of panel (d).
of a contact between two RBCs and (f) distribution of contact durations between two RBCs, along with their respective fits to an exponential distribution. Symbol notation is shown in (c) and applies to all plots except for the main figure of panel (d).
Download figure:
Standard imageFigure 6(b) shows the cluster size distribution  . Cluster sizes s > 1 are not frequent for volume fraction
. Cluster sizes s > 1 are not frequent for volume fraction 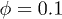 (dilute case), signifying that pair collisions are more frequent than three- (or multi-) particle collisions as they are expressed by
(dilute case), signifying that pair collisions are more frequent than three- (or multi-) particle collisions as they are expressed by 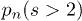 , being 10 times less frequent than
, being 10 times less frequent than  . The maximum cluster size
. The maximum cluster size 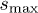 remains well under 10 for all dilute cases.
remains well under 10 for all dilute cases.
For 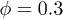 and 0.5
and 0.5  is higher indicating multi-particle collisions and collective motion. The extreme case of
is higher indicating multi-particle collisions and collective motion. The extreme case of 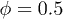 indicates that one big cluster dominates the flow. With the mean gap being comparable to
indicates that one big cluster dominates the flow. With the mean gap being comparable to  though, it is highly unlikely that it is a finite-size effect which will change by increasing the domain size.
though, it is highly unlikely that it is a finite-size effect which will change by increasing the domain size.
The percentage of "free" RBCs  is decreasing with ϕ and only slightly depends of the shear rate, as shown in fig. 6(a). For the same ϕ, higher
is decreasing with ϕ and only slightly depends of the shear rate, as shown in fig. 6(a). For the same ϕ, higher 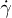 result in lower single-cell percentages, revealing higher-order collisions. The average cluster size
result in lower single-cell percentages, revealing higher-order collisions. The average cluster size 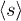 is a way to measure the order of RBC collisions. Figure 6(d) shows that
is a way to measure the order of RBC collisions. Figure 6(d) shows that 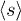 remains close to 1 for
remains close to 1 for  and 0.2, a slight increase with
and 0.2, a slight increase with 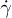 is observed for
is observed for  , while
, while  is increasing with
is increasing with  , hinting on many-particle collisions. Case
, hinting on many-particle collisions. Case 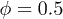 is dominated by a hyper-cluster resulting in very large values for
is dominated by a hyper-cluster resulting in very large values for 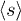 .
.
An attempt to fit the data to the kinetic clustering model (KCM) using non-linear least squares and obtain a typical cluster size s0 is shown in fig. 6(d). KCM was developed by Raiskinmäki et al. [37] using kinetic arguments to study the basic mechanisms of shear thickening in particulate suspensions. The cluster size distribution of KCM follows a Poissonian,  , with s0 denoting a typical cluster size and was also used by Ding and Aidun [36] to uncover a universal scaling relation for the cluster size distribution, independently of particle shape and concentration. The typical cluster size is increasing with ϕ, until the fitting algorithm fails, due to the appearance of big clusters in
, with s0 denoting a typical cluster size and was also used by Ding and Aidun [36] to uncover a universal scaling relation for the cluster size distribution, independently of particle shape and concentration. The typical cluster size is increasing with ϕ, until the fitting algorithm fails, due to the appearance of big clusters in  in the form of tails. For
in the form of tails. For 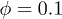 , the typical cluster size is below 1 RBC, in which due the sporadic interaction of RBCs s0 is underestimated.
, the typical cluster size is below 1 RBC, in which due the sporadic interaction of RBCs s0 is underestimated.
The duration of a contact tc is defined as the maximum time interval in which the distance of any of the surface points between a pair of RBCs, remains under 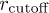 . If two RBCs escape this distance, ts is stored and a new measurement starts. The mean duration
. If two RBCs escape this distance, ts is stored and a new measurement starts. The mean duration  of a contact is increasing with ϕ and
of a contact is increasing with ϕ and 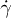 (fig. 6(e)), showing that in these cases clusters live longer. The duration distribution
(fig. 6(e)), showing that in these cases clusters live longer. The duration distribution  (fig. 6(f)) appears to follow an exponential distribution describing the time between events in a Poisson process, which seems to be in agreement with the KCM approach. Since the suspension is governed mostly by two-particle collisions for
(fig. 6(f)) appears to follow an exponential distribution describing the time between events in a Poisson process, which seems to be in agreement with the KCM approach. Since the suspension is governed mostly by two-particle collisions for 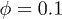 , the extent of
, the extent of  indicates the duration of a collision in the dilute limit, where approximately after
indicates the duration of a collision in the dilute limit, where approximately after 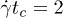 , none of the pair contacts has survived. For larger hematocrits, however, the distribution is more widespread, indicating that more than two-particle collisions are present and sustain a "bond" for larger times.
, none of the pair contacts has survived. For larger hematocrits, however, the distribution is more widespread, indicating that more than two-particle collisions are present and sustain a "bond" for larger times.
Conclusions
In this letter we have investigated the transport of RBCs in a shear-flow environment. The shear-induced diffusion of the suspension exhibits a departure from the linear scaling with the shear rate, resulting in a less efficient mixing. This result is important due to the wide use of the linear scaling model in coarse-grained models using the advection diffusion equation [30–32]. The analysis provided by Gross et al. [15] with similar findings for a similar system, is not confirmed by our results. The decrease of the normalized diffusivity  due to a potential decrease in collisional cross-section, is by itself not enough to explain this departure, indicating that pair collisions are not the driving mechanism behind transport in dense suspensions as collective effects are taking place. A cluster analysis shows that multi-particle collisions resulting in collective effects dominate higher-hematocrit simulations. For future work a parametric study covering various interparticle forces and elastic moduli would be enlightening regarding the mixing of RBCs.
due to a potential decrease in collisional cross-section, is by itself not enough to explain this departure, indicating that pair collisions are not the driving mechanism behind transport in dense suspensions as collective effects are taking place. A cluster analysis shows that multi-particle collisions resulting in collective effects dominate higher-hematocrit simulations. For future work a parametric study covering various interparticle forces and elastic moduli would be enlightening regarding the mixing of RBCs.
Acknowledgments
This research received funding from the European Union, 7th Framework Programme under grant agreement No. 26996 (THROMBUS). Author AGH acknowledges partial financial support by the Russian Scientific Foundation, grant No. 14-11-00826. We thank Profs. P. M. A. Sloot, G. E. Karniadakis and D. Bonn for fruitful discussions.
Additional remark: Nine movies (hmt10yd1e1.mp4, hmt10yd1e2.mp4, hmt10yd1e3.mp4, hmt30yd1e1.mp4, hmt30yd1e2.mp4, hmt30yd1e3.mp4, hmt50yd1e1.mp4, hmt50yd1e2.mp4, hmt50yd1e3.mp4) from our simulations visualizing the motion of RBCs were added as supplementary material.
Footnotes
- 1
Case
 contains only platelet-like particles in very low volume fractions
contains only platelet-like particles in very low volume fractions 
Supplementary video hmt10yd1e1 (5.78 MB mp4)
Supplementary video hmt10yd1e2 (5.3 MB mp4)
Supplementary video hmt10yd1e3 (4.65 MB mp4)
Supplementary video hmt30yd1e1 (5.91 MB mp4)
Supplementary video hmt30yd1e2 (5.93 MB mp4)
Supplementary video hmt30yd1e3 (5.75 MB mp4)
Supplementary video hmt50yd1e1 (5.02 MB mp4)