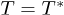Abstract
It is well established that at early times, long before the time of radiation-matter density equality, the universe could have been well described by a spatially flat, radiation only model. In this article we consider the whole primeval universe, as a first approach, as a black-body radiation system in an n-dimensional Euclidean space. We propose that the (3 + 1)-dimensional nature of the universe could be the result of a thermodynamic selection principle stemming from the second law of thermodynamics. In regard to the three spatial dimensions we suggest that they were chosen by means of the minimization of the Helmholtz free energy per hypervolume unit following possibly a kind of broken symmetry process, while the time dimension, as is well known, is related with the principle of increment of entropy for closed systems: the so-called arrow of time.
Export citation and abstract BibTeX RIS
Introduction
The question of why space is 3-dimensional goes back to ancient Greece [1]. In modern times this question was first raised by Kant in 1746 [2]. Later, Ehrenfest in 1917 by means of the stable orbits argument showed that n = 3 [3]. In 1983, Barrow brought forward a very interesting approach to the dimensionality problem [1]. Since then, many authors have worked on this problem extended to the case (3 + 1). Such is the case of Brandenberger and Vafa [4], that in 1989 proposed a natural mechanism for explaining why there are 3 large space dimensions in the context of string gas cosmology [4,5]. Regarding the (3 + 1) problem, Tegmark published an enlightening article summarized through his fig. 1 [6]. For a deeper discussion on this issue one can also see among others the following works [6–9].
Since the works by Kaluza and Klein [10,11], many proposals about universe models with dimensionality different from three have been published [4,5,10–25]. Remarkably this has been the case of results stemming from the string, D-branes and gauge theories [4,5,18–24]. However, nowadays we only have evidence for a universe with three space and one time dimensions.
In 1989, Landsberg and De Vos [12] proposed a spatial n-dimensional generalization of the Planck distribution, the Wien displacement, and the Stefan-Boltzmann laws for black-body radiation (BBR) for a zero curvature space. Later, Menon and Agrawal [13] modified the n-dimensional Stefan-Boltzmann constant found by Landsberg and De Vos by using the appropriate spin-degeneracy factor of the photon without affecting the normalized Planck spectrum given by Landsberg and De Vos. Shortly thereafter, Barrow and Hawthorne investigated the behavior of matter and radiation in thermal equilibrium in an n-dimensional space in the early universe, in particular they calculated the number of particles N, the pressure p and the energy density u [14]. More recently, Gonzalez-Ayala et al. [26] calculated several thermodynamic potentials for BBR such as the Helmholtz potential F, the enthalpy H, the Gibbs potential G and the entropy S by means of the generalized Planck distribution for an n-dimensional Euclidean space. Moreover, they calculated the corresponding densities per hypervolume unit for these potentials; that is f, h, g and s, respectively. They display in the region of very high temperatures (of the order of Planck's temperature TP) a convex behavior [26]. Temperatures as high as 1032 K are only possible in very early times in the evolution of the universe. It is known that this period was dominated by energy in the form of radiation and it is possible to consider a flat universe which is compatible with observations [27,28]. Thus, considering the whole primeval universe as a black-body radiation system in an Euclidean space is in principle a reasonable approach [29].
The critical energy density at the Planck epoch (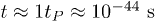 , one Planck time) [30,31] was around
, one Planck time) [30,31] was around 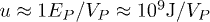 (a Planck energy in a Planck volume) and the temperature around
(a Planck energy in a Planck volume) and the temperature around 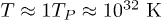 . In particular, the temperature and energy density obtained when the minimum of the Helmholtz density is located at n = 3 are surprisingly close to those values indicating a possible connection between these critical points and the subsequent processes that led to (or the conditions that fixed) the known 3-dimensional character of space. This is not in contradiction with extensively studied models aiming to explain this characteristic. For example, according to string theories at some point (at the end of the Planck epoch) the rest of the dimensions collapsed (or they simply stayed at the same size) and only the 3-dimensional space grew bigger [27,32]. The remaining question is: Why did only 3 dimensions expand? Or what kind of conditions fixed the space dimensionality to 3? If our universe was born with the thermodynamic laws included, then, thermodynamic analysis could give us a clue that a maximum or a minimum criteria might have been fulfilled at the earliest period of its evolution. The conditions of energy and temperature in that epoch were probably suitable to maximize some kind of thermodynamic function. In addition, in times very close to the Big Bang within the Planck scale, it is believed that the realm of string theory [32] or loop quantum gravity (LQG) [33–35] is found, where relativistic quantum gravity effects can be very important.
. In particular, the temperature and energy density obtained when the minimum of the Helmholtz density is located at n = 3 are surprisingly close to those values indicating a possible connection between these critical points and the subsequent processes that led to (or the conditions that fixed) the known 3-dimensional character of space. This is not in contradiction with extensively studied models aiming to explain this characteristic. For example, according to string theories at some point (at the end of the Planck epoch) the rest of the dimensions collapsed (or they simply stayed at the same size) and only the 3-dimensional space grew bigger [27,32]. The remaining question is: Why did only 3 dimensions expand? Or what kind of conditions fixed the space dimensionality to 3? If our universe was born with the thermodynamic laws included, then, thermodynamic analysis could give us a clue that a maximum or a minimum criteria might have been fulfilled at the earliest period of its evolution. The conditions of energy and temperature in that epoch were probably suitable to maximize some kind of thermodynamic function. In addition, in times very close to the Big Bang within the Planck scale, it is believed that the realm of string theory [32] or loop quantum gravity (LQG) [33–35] is found, where relativistic quantum gravity effects can be very important.
In the present work we analyze some thermodynamic properties of a universe dominated only by radiation within a flat spatial geometry (specifically an n-dimensional Euclidean space), filled with BBR. As was shown in [26], in the region of very high temperatures and low dimensionality the internal energy density u and the entropy density s show in the first place (as n increases and for an isothermal process) a local maximum and then a local minimum while in the Helmholtz free-energy density first a local minimum and then a local maximum, being the Helmholtz potential density the first function that presents a critical point. Remarkably, the form of the isotherms is reminiscent of those found in first-order phase transitions in gas state equations of the van der Waals type (see fig. 2). Starting at Planck temperature TP, the density  finds a saddle point at
finds a saddle point at 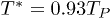 , and the other two densities (u and s) present extreme points after this value. If n is considered as an integer, the first maximum of
, and the other two densities (u and s) present extreme points after this value. If n is considered as an integer, the first maximum of 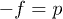 vs. n (being p the pressure) is located at n = 3. According to this model, for any later moment, after the time corresponding to
vs. n (being p the pressure) is located at n = 3. According to this model, for any later moment, after the time corresponding to 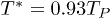 , the spatial dimension n = 3 remained "frozen" due to 2nd-law arguments. Before this point, for all
, the spatial dimension n = 3 remained "frozen" due to 2nd-law arguments. Before this point, for all 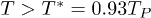 , any transition of n is permitted (where there is no conflict with proposals of the type of string theories [32] or the type of the so-called vanishing dimensions models [15–17], for example). This kind of thermodynamic behavior offers a possible starting point for determining the (3 + 1)-dimensional nature of the space-time. Considerations on the applicability of this approach has been presented in [26].
, any transition of n is permitted (where there is no conflict with proposals of the type of string theories [32] or the type of the so-called vanishing dimensions models [15–17], for example). This kind of thermodynamic behavior offers a possible starting point for determining the (3 + 1)-dimensional nature of the space-time. Considerations on the applicability of this approach has been presented in [26].
Black-body radiation in an n-dimensional space
For a black body in an n-dimensional space it is known [12–14,26,36,37] that the number of modes per unit frequency interval  is
is
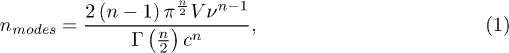
where V is the hypervolume and n the dimensionality of the space. The number  of photons in the frequency interval ν to
of photons in the frequency interval ν to 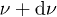 is
is

Integration over all frequencies of 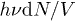 gives the energy density (per hypervolume unit)
gives the energy density (per hypervolume unit) 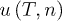 , which is [14,26]
, which is [14,26]
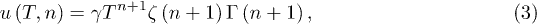
where 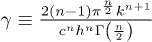 , and
, and 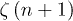 and
and 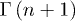 are, respectively, the Riemann zeta function and the gamma function evaluated in n + 1. The Helmholtz function F, the entropy S, the pressure p and the Gibbs free energy G are given by the following expressions [26]:
are, respectively, the Riemann zeta function and the gamma function evaluated in n + 1. The Helmholtz function F, the entropy S, the pressure p and the Gibbs free energy G are given by the following expressions [26]:

respectively. Since the negative of the Helmholtz potential density will become very important in our analysis, the complete form will be given as
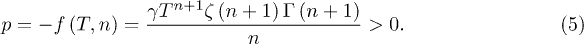
The corresponding thermodynamic potential densities are immediately obtained by dividing each quantity in eq. (4) by the hypervolume V (except for the pressure p). All these results agree with the well-known 3-dimensional cases [38].
Critical points
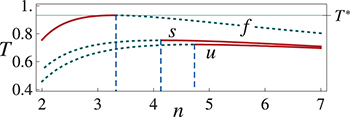
In fig. 1 the critical points of 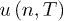 ,
, 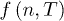 and
and 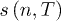 with respect to the dimension n are shown. These critical points can be minima, maxima or saddle points. For each function there is a certain critical temperature
with respect to the dimension n are shown. These critical points can be minima, maxima or saddle points. For each function there is a certain critical temperature 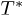 at which for any
at which for any 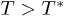 there are no more extreme points of the corresponding thermodynamic potential density. The region of transition between such convexities (from maxima to minima or vice versa) occurs at dimensionalities in the interval from 3 to 5 and at nearly the Planck temperature. In each case (see fig. 1) the boundary between the maxima and the minima is the saddle point corresponding to the unique temperature
there are no more extreme points of the corresponding thermodynamic potential density. The region of transition between such convexities (from maxima to minima or vice versa) occurs at dimensionalities in the interval from 3 to 5 and at nearly the Planck temperature. In each case (see fig. 1) the boundary between the maxima and the minima is the saddle point corresponding to the unique temperature 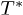 . By decreasing the temperature from
. By decreasing the temperature from 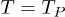 , the first function that reaches a critical point is
, the first function that reaches a critical point is 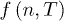 which occurs at the isotherm
which occurs at the isotherm 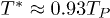 . For temperatures below this value there are maxima and minima of the Helmholtz density function and it is possible to talk about thermodynamic optimization criteria. That being said, the first function to optimize was the Helmholtz free energy density and it occurs in a region near the value n = 3. This might not be a mere coincidence as will be pointed out later. The separations between the regions of maxima and minima for
. For temperatures below this value there are maxima and minima of the Helmholtz density function and it is possible to talk about thermodynamic optimization criteria. That being said, the first function to optimize was the Helmholtz free energy density and it occurs in a region near the value n = 3. This might not be a mere coincidence as will be pointed out later. The separations between the regions of maxima and minima for 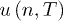 ,
, 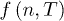 and
and 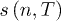 are well defined (see fig. 1 and it is also summarized in table 1 of ref. [26]). In fig. 2 we depict the isotherm curves corresponding to the negative of the Helmholtz potential density
are well defined (see fig. 1 and it is also summarized in table 1 of ref. [26]). In fig. 2 we depict the isotherm curves corresponding to the negative of the Helmholtz potential density 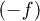 . In fact, from fig. 1, as the temperature decreases from
. In fact, from fig. 1, as the temperature decreases from  to zero, the first potential that reaches a critical point (a saddle point) is
to zero, the first potential that reaches a critical point (a saddle point) is 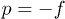 . The first isotherm that reaches a critical point is
. The first isotherm that reaches a critical point is 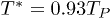 . Between
. Between 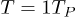 and
and 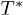 , or even for higher temperatures than TP there are no other critical points. After this moment, for temperatures in the interval from
, or even for higher temperatures than TP there are no other critical points. After this moment, for temperatures in the interval from 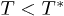 to T = 0, there is always first a maximum and then a minimum of this function. This kind of behavior resembles the form of the isotherms of a gas-liquid phase transition (see, for example, fig. 1.2(a) of ref. [39] for a p vs. ρ plane, being ρ the density). As is well known, the critical isotherm (CI) corresponds to a saddle point which divides the pressure-volume plane into two regions: above CI, the transitions do not occur and below CI, the transitions are permitted. However, as we shall see in the present case, in the region below the critical isotherm
to T = 0, there is always first a maximum and then a minimum of this function. This kind of behavior resembles the form of the isotherms of a gas-liquid phase transition (see, for example, fig. 1.2(a) of ref. [39] for a p vs. ρ plane, being ρ the density). As is well known, the critical isotherm (CI) corresponds to a saddle point which divides the pressure-volume plane into two regions: above CI, the transitions do not occur and below CI, the transitions are permitted. However, as we shall see in the present case, in the region below the critical isotherm 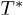 restrictions imposed by the 2nd law appear and transitions between dimensions are forbidden. With this in mind, in fig. 2 we can see the isotherms as possible transitions of the space dimensionality. Remarkably, the graphics p vs. n in fig. 2 and p vs. ρ in fig. 1.2(a) from ref. [39] are very similar. As asserted by Callen [40], a variety of important thermodynamic properties are linked to the broken symmetry origin of thermodynamic coordinates. For example, in the transition from a gas (high symmetrical phase) with no intrinsic value of the volume to a condensed phase, as a solid, the volume of the solid has a broken symmetry origin as a thermodynamic variable [40]. It is very suggestive to observe that in fig. 2, when the BBR-system goes from highly symmetrical states
restrictions imposed by the 2nd law appear and transitions between dimensions are forbidden. With this in mind, in fig. 2 we can see the isotherms as possible transitions of the space dimensionality. Remarkably, the graphics p vs. n in fig. 2 and p vs. ρ in fig. 1.2(a) from ref. [39] are very similar. As asserted by Callen [40], a variety of important thermodynamic properties are linked to the broken symmetry origin of thermodynamic coordinates. For example, in the transition from a gas (high symmetrical phase) with no intrinsic value of the volume to a condensed phase, as a solid, the volume of the solid has a broken symmetry origin as a thermodynamic variable [40]. It is very suggestive to observe that in fig. 2, when the BBR-system goes from highly symmetrical states 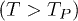 to the first saddle point at
to the first saddle point at 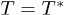 for
for 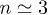 , probably a breaking of symmetry has occurred. Evidently, this idea must be taken as a conjecture.
, probably a breaking of symmetry has occurred. Evidently, this idea must be taken as a conjecture.
Fig. 1: (Colour online) 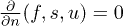 (T in Planck units). The red continuous lines are the minima and the dotted lines are the maxima of f, s and u. The blue vertical dashed lines are located at the unique saddle point of each potential.
(T in Planck units). The red continuous lines are the minima and the dotted lines are the maxima of f, s and u. The blue vertical dashed lines are located at the unique saddle point of each potential.
Download figure:
Standard imageFig. 2: (Colour online) The thin continuous lines are the isothermal processes, and the thick black line shows the critical points. The highest extreme point corresponds to the saddle point located at the isotherm 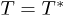 (T in Planck units), above it there are no more extreme points.
(T in Planck units), above it there are no more extreme points.
Download figure:
Standard imageThe critical isotherm 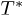 in fig. 2 divides the plane p vs. n into two regions; above
in fig. 2 divides the plane p vs. n into two regions; above 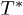 there are no restrictions over any particular value of n. However, as mentioned before, below
there are no restrictions over any particular value of n. However, as mentioned before, below  there will be restrictions on transitions from
there will be restrictions on transitions from 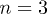 to any other dimensionality.
to any other dimensionality.
Possible restrictions on dimensionality changes
A well-known theorem derived from the 2nd law linked with the Helmholtz potential F is the Helmholtz potential minimum principle [41]. This theorem implies that for isothermal processes

where the equality is fulfilled by reversible processes. This phase-transition–like1
approach to dimensionality suggests an important role to the statement, "the particular phase that is realized in Nature for a given set of independent variables is the one with the lowest free energy" [42]. Let us consider a hypercube with volume 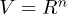 as the black-body system, where R is the length of the edge. The above equation can be expressed as
as the black-body system, where R is the length of the edge. The above equation can be expressed as
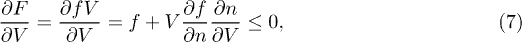
where it has been used the consideration that  . Then,
. Then,

In this way, the important role of the quantity 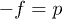 appearing in fig. 2 is clear. In an adiabatic expansion (no heat exchange between the universe and the "exterior"), the condition showed in [26] is
appearing in fig. 2 is clear. In an adiabatic expansion (no heat exchange between the universe and the "exterior"), the condition showed in [26] is 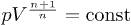 . By using eq. (3) and the expression for p in eq. (4), the adiabatic condition for two different moments is
. By using eq. (3) and the expression for p in eq. (4), the adiabatic condition for two different moments is

where R0 and T0 are some initial conditions that, in our case, are very near the Planck epoch and 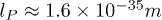 is the Planck length. This is a result that agrees with typical treatments in cosmology (see, for example, [30]). Then, eq. (8) is now (in Planck units)
is the Planck length. This is a result that agrees with typical treatments in cosmology (see, for example, [30]). Then, eq. (8) is now (in Planck units)

The difference between the thick (black) line in fig. 2 and the restriction given by eq. (10) (red dotted line in fig. 2) is very small. According to eq. (10) for an isothermal process the region below the dotted line is prohibited. In the region where 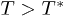 when
when 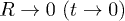 then T → ∞, which is related with an initial singularity for any value of n. As mentioned before, the first objective function reaching an extreme point was
then T → ∞, which is related with an initial singularity for any value of n. As mentioned before, the first objective function reaching an extreme point was 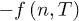 , but, is it an adequate quantity to optimize? Notice that when the internal energy is minimized it is possible to have an infinite number of configurations, some with more order than others for the same value of the energy. On the other hand, by maximizing the entropy it is possible to obtain an endless number of energetic configurations, thus, by themselves neither the maxima nor the minima of s and u, respectively, determine an advantageous and unambiguous objective function. This is not the case for
, but, is it an adequate quantity to optimize? Notice that when the internal energy is minimized it is possible to have an infinite number of configurations, some with more order than others for the same value of the energy. On the other hand, by maximizing the entropy it is possible to obtain an endless number of energetic configurations, thus, by themselves neither the maxima nor the minima of s and u, respectively, determine an advantageous and unambiguous objective function. This is not the case for 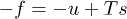 , which gives a kind of trade off between entropy (organization) and energetic content, and this could be indeed a more meaningful optimization criterion [42]. When maximized, it offers the better compromise between large entropy and low energy. Let us recall that in stability analysis for closed systems, the stability points are found in the maximum value of entropy or in minimum-energy configurations. Each one on their own does not establish an optimum criterion, because a restriction over u (or s) allows an infinite number of configurations of s (or u, respectively). Then, the minimum of the Helmholtz free energy gives a good commitment between the organization of a system and its energetic content. In the scenario where the universe cools down through an adiabatic free expansion, the first potential whose optimization is reached is the
, which gives a kind of trade off between entropy (organization) and energetic content, and this could be indeed a more meaningful optimization criterion [42]. When maximized, it offers the better compromise between large entropy and low energy. Let us recall that in stability analysis for closed systems, the stability points are found in the maximum value of entropy or in minimum-energy configurations. Each one on their own does not establish an optimum criterion, because a restriction over u (or s) allows an infinite number of configurations of s (or u, respectively). Then, the minimum of the Helmholtz free energy gives a good commitment between the organization of a system and its energetic content. In the scenario where the universe cools down through an adiabatic free expansion, the first potential whose optimization is reached is the 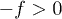 function. The first maximum appears at n = 3. The only isotherm with a saddle point (
function. The first maximum appears at n = 3. The only isotherm with a saddle point (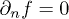 and
and  ) is that with
) is that with 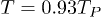 , which could have fixed globally or locally the dimensionality of the black-body system to n = 3. After this point, the adiabatic cooling process continues due to the expansion. Nevertheless, any isothermal dimensionality "phase" transition is forbidden as soon as the temperature diminishes, because for small times
, which could have fixed globally or locally the dimensionality of the black-body system to n = 3. After this point, the adiabatic cooling process continues due to the expansion. Nevertheless, any isothermal dimensionality "phase" transition is forbidden as soon as the temperature diminishes, because for small times 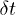 afterwards, the change from n = 3 to any other value of n is inside the forbidden zone. It is possible to see in fig. 1 that the saddle point of
afterwards, the change from n = 3 to any other value of n is inside the forbidden zone. It is possible to see in fig. 1 that the saddle point of  is not located exactly at n = 3. This could be a consequence of having a simplified model. This is not the unique drawback of the simplified approach here presented. As a matter of fact, our model without quantum corrections has an important problem with the applicability of statistical mechanics concepts at very early times of the universe evolution near the Planck epoch. For example, at a temperature
is not located exactly at n = 3. This could be a consequence of having a simplified model. This is not the unique drawback of the simplified approach here presented. As a matter of fact, our model without quantum corrections has an important problem with the applicability of statistical mechanics concepts at very early times of the universe evolution near the Planck epoch. For example, at a temperature  , the number of photons is
, the number of photons is 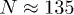 for n = 3.
for n = 3.
Additional problems arise when the evolution of the universe is considered. One of the key problems of this approach appears when the size of the universe is considered to be finite, curved space or non-trivial topology. Let us recall that the above equations are built by considering an infinite Euclidean space. It is accepted that the physics inside of the horizon distance dh is the same; however, in some theories the size of the universe is not restricted to the horizon distance. In inflationary cosmology the inflation process trusts in the fact that there exists a region beyond the initial horizon distance where physics works in the same way that it does inside of the physical causality region. In this way, considering a spherical volume with radius dh might work as a first inferior bound for the statistics of the black-body radiation system here discussed. The size of the horizon distance may be treated by extrapolating the validity of the Einstein equations to a time near the end of the Planck era. Then, the corresponding fluid equation in an n-dimensional space reads as

Since the evolution of the the scale factor from the Friedmann equation for a spatially flat universe (see [26]) is

it leads to a dependence of the temperature of the radiation-dominated universe with time and the scale factor:

being
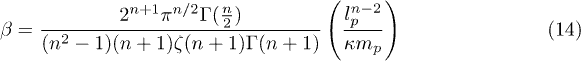
where κ is related with the n-dimensional gravitational constant Gn (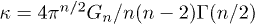 ; see [43]) or to the Planck length in 3 dimensions (
; see [43]) or to the Planck length in 3 dimensions (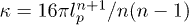 ; see [44]). If the causal region of the universe is considered as dh, there is an upper limit for the wavelength of photons inside the horizon
; see [44]). If the causal region of the universe is considered as dh, there is an upper limit for the wavelength of photons inside the horizon  and then a minimum frequency
and then a minimum frequency 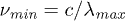 , as a consequence, the dimensionless constants that describe the black-body radiation are modified [26]. For example, for n = 3 and
, as a consequence, the dimensionless constants that describe the black-body radiation are modified [26]. For example, for n = 3 and 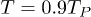 the factor that appears in the Stefan-Boltzmann law should be reduced by 10−3 when the lower limit of the corresponding integrals is considered. However, for
the factor that appears in the Stefan-Boltzmann law should be reduced by 10−3 when the lower limit of the corresponding integrals is considered. However, for 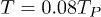 , for example, the constants are different in approximately 5% [26]. For higher values of n the difference between the integrals are even smaller [26]. Taking into account the LQG corrections (see below) the number of photons at
, for example, the constants are different in approximately 5% [26]. For higher values of n the difference between the integrals are even smaller [26]. Taking into account the LQG corrections (see below) the number of photons at 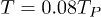 are
are 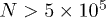 and N > 1034 for n = 9. Nevertheless, it should be noted that a more complete analysis should be made in order to include further effects of the evolution of the universe near the Planck epoch, such as a possible variable speed of light or the quantum effects motivated by of loop quantum cosmology theory, for example.
and N > 1034 for n = 9. Nevertheless, it should be noted that a more complete analysis should be made in order to include further effects of the evolution of the universe near the Planck epoch, such as a possible variable speed of light or the quantum effects motivated by of loop quantum cosmology theory, for example.
Modifications stemming from loop quantum cosmology
A first approach to the possible consequences of the quantum gravity effects in the black-body radiation in the very early universe may be included by incorporating the modified dispersion relation [33–35] that comes from LQG. The modified Helmholtz free-energy density f in this case (see [26]) is
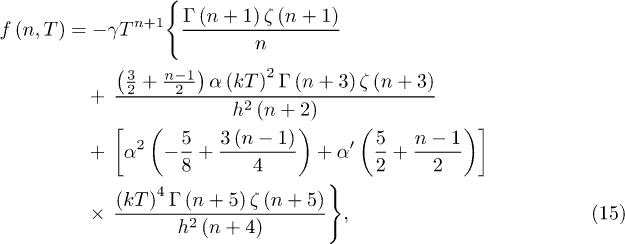
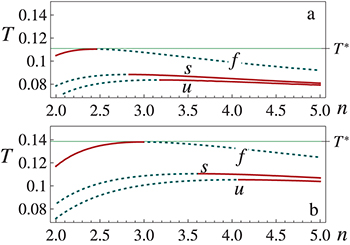
where α and 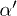 take different values depending on the details of the quantum gravity candidates. The value at which the saddle point occurs depends on these parameters. In fig. 3, there is depicted the analysis of maxima and minima for the Helmholtz potential density incorporating these corrections. A similar analysis of critical points reveals that the corresponding saddle point
take different values depending on the details of the quantum gravity candidates. The value at which the saddle point occurs depends on these parameters. In fig. 3, there is depicted the analysis of maxima and minima for the Helmholtz potential density incorporating these corrections. A similar analysis of critical points reveals that the corresponding saddle point 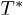 decreases by one order of magnitude. The critical points in this case are located in a narrower interval than in the non-LQG modified model (see fig. 1). In the first case of fig. 3 the critical points of f, u and s are very close to n = 3 (closer than n = 2 or n = 4). Conceptually, an optimization of the three functions at the same dimensionality would be relevant (if not desirable) in the analysis of possible phase transitions and stability. The possibility of finding a couple of values of α and
decreases by one order of magnitude. The critical points in this case are located in a narrower interval than in the non-LQG modified model (see fig. 1). In the first case of fig. 3 the critical points of f, u and s are very close to n = 3 (closer than n = 2 or n = 4). Conceptually, an optimization of the three functions at the same dimensionality would be relevant (if not desirable) in the analysis of possible phase transitions and stability. The possibility of finding a couple of values of α and 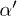 that optimize at the same time the three functions in n = 3 and its physical relevance might be an interesting issue for further analysis, which might also be related with the selection of a suitable LQG model candidate. In particular, for
that optimize at the same time the three functions in n = 3 and its physical relevance might be an interesting issue for further analysis, which might also be related with the selection of a suitable LQG model candidate. In particular, for 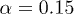 and
and 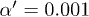 (see fig. 3(b)),
(see fig. 3(b)), 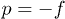 reaches its saddle point at n = 3.
reaches its saddle point at n = 3.
Fig. 3: (Colour online) Maxima (dotted lines) and minima (continuous lines) of f incorporating LQG corrections. In (a) the cases 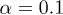 and
and  (which reproduce the curves of the spectral energy density shown in [35]) the saddle point of f is located at
(which reproduce the curves of the spectral energy density shown in [35]) the saddle point of f is located at 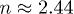 . In (b)
. In (b)  and
and 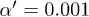 the saddle point of f is at
the saddle point of f is at 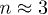 .
.
Download figure:
Standard imageConclusions
It has been proposed a model based on simple suppositions to study scenarios that put the space dimensionality n = 3 as a convenient candidate to optimize a thermodynamic quantity: the Helmholtz potential density; that is, the pressure of the BBR-system. After picking this value, later isothermal transitions are prohibited by 2nd-law restrictions and the dimensionality remains "frozen" at n = 3. Regarding the 1 in (3 + 1)-dimensionality, it is generally accepted that the arrow of time is imposed by the principle of entropy increment for closed systems. Thus, it is possible that the laws of thermodynamics are responsible for the selection of the dimensionality of the universe by means of a phase-transition–like process analogous to those caused by symmetry breaking processes. We believe that the present simplified approach to the (3 + 1)-dimensionality problem may give clues for further analysis that takes into account more detailed theories of the early universe.
Acknowledgments
We want to acknowledge partial support from COFAA-SIP-EDI-IPN and SNI-CONACYT, México.
Footnotes
- 1
Evidently, we have not strong reasons to assert that changes in dimensionality are true phase transitions. We only remark certain similarities between them. For example, if we define response coefficients analog to compressibility,
 , and volumetric expansion,
, and volumetric expansion,  , they diverge to infinite at
, they diverge to infinite at  .
.