Abstract
The dielectric and thermal properties of a typical antiferroelectric (AFE) material are investigated by minimising numerically the free energy as given by the Kittel model of AFEs. The phase line of second-order phase transitions in the  phase diagram is shown to change to a first-order line at the tricritical point T3cp, E3cp. The static dielectric susceptibility and the electrocaloric (EC) effect are calculated as a function of temperature and the applied electric field E. It is found that in a given range of electric fields and temperatures the EC effect has negative values but generally becomes positive above the AFE ordering temperature T0. The dielectric susceptibility shows characteristic peaks at the phase transitions between the field-induced polar and the AFE antipolar phase, and diverges at the tricritical point. We present experimental results for a negative EC effect, which have been obtained by direct EC measurements in PbZrO3 ceramics, and agree qualitatively with the above model.
phase diagram is shown to change to a first-order line at the tricritical point T3cp, E3cp. The static dielectric susceptibility and the electrocaloric (EC) effect are calculated as a function of temperature and the applied electric field E. It is found that in a given range of electric fields and temperatures the EC effect has negative values but generally becomes positive above the AFE ordering temperature T0. The dielectric susceptibility shows characteristic peaks at the phase transitions between the field-induced polar and the AFE antipolar phase, and diverges at the tricritical point. We present experimental results for a negative EC effect, which have been obtained by direct EC measurements in PbZrO3 ceramics, and agree qualitatively with the above model.
Export citation and abstract BibTeX RIS
Introduction
The electrocaloric (EC) effect is defined as the temperature change  occurring in a system after the application or removal of an external electric field under adiabatic conditions. Recent theoretical [1] and experimental [2–4] studies in various bulk and thin-film systems revealed the co-existence of the normal
occurring in a system after the application or removal of an external electric field under adiabatic conditions. Recent theoretical [1] and experimental [2–4] studies in various bulk and thin-film systems revealed the co-existence of the normal  and anomalous (or negative)
and anomalous (or negative) 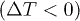 EC effect under field application. Earlier, Peräntie et al. [5] observed a negative EC effect in
EC effect under field application. Earlier, Peräntie et al. [5] observed a negative EC effect in  -oriented PMN-28PT in a narrow temperature range below
-oriented PMN-28PT in a narrow temperature range below  . It has been argued [3] that the anomalous EC effect appears when the applied electric field is not collinear with the dielectric polarisation of the material. Specifically, a negative EC effect is expected if there is a transition between two states of the system, where the lower-temperature state has a smaller polarisation than the higher-temperature state. Thus the field may increase the amount of disorder in the dipolar subsystem, leading to a lower value of the dipolar entropy and hence a negative
. It has been argued [3] that the anomalous EC effect appears when the applied electric field is not collinear with the dielectric polarisation of the material. Specifically, a negative EC effect is expected if there is a transition between two states of the system, where the lower-temperature state has a smaller polarisation than the higher-temperature state. Thus the field may increase the amount of disorder in the dipolar subsystem, leading to a lower value of the dipolar entropy and hence a negative  . An analogous effect is known to exist in antiferromagnets [6]. It is expected that a combination of the normal and anomalous EC materials could be used in practical applications such as cooling devices [7,8].
. An analogous effect is known to exist in antiferromagnets [6]. It is expected that a combination of the normal and anomalous EC materials could be used in practical applications such as cooling devices [7,8].
Antiferroelectrics (AFEs) undergo a phase transition in zero electric field into an ordered antiferroelectric phase at the AFE Curie temperature Tc, characterised by the order parameter Ps representing a staggered polarisation. In contrast to normal ferroelectric (FE) systems, the field-induced macroscopic polarisation  in the AFE phase may increase with increasing temperature, leading to a negative EC response [2,3]. Thus AFEs represent a relatively simple model system which provides a possibility to understand the physical mechanism of the negative EC effect on a semi-phenomenological level.
in the AFE phase may increase with increasing temperature, leading to a negative EC response [2,3]. Thus AFEs represent a relatively simple model system which provides a possibility to understand the physical mechanism of the negative EC effect on a semi-phenomenological level.
In this paper we write down the free energy function of a typical bulk AFE system within the framework of the generic Kittel model [9–11] and calculate numerically the field and temperature dependence of the macroscopic polarisation 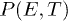 , from which the dipolar entropy change and the EC effect can be derived. To test the predictions of the Kittel model we have carried out direct ECE measurements in PbZrO3 ceramics, which had been characterised as an AFE system by Shirane et al. already back in 1951 [12]. Our experiments evidence a negative EC effect in a broad temperature range below the AFE transition temperature, which had not been reported earlier in the literature. Thus we feel that PbZrO3 might be an appropriate system in which to investigate simultaneously the mechanism of antiferroelectricity and a negative EC effect, which are currently of considerable interest both theoretically and experimentally [1–5].
, from which the dipolar entropy change and the EC effect can be derived. To test the predictions of the Kittel model we have carried out direct ECE measurements in PbZrO3 ceramics, which had been characterised as an AFE system by Shirane et al. already back in 1951 [12]. Our experiments evidence a negative EC effect in a broad temperature range below the AFE transition temperature, which had not been reported earlier in the literature. Thus we feel that PbZrO3 might be an appropriate system in which to investigate simultaneously the mechanism of antiferroelectricity and a negative EC effect, which are currently of considerable interest both theoretically and experimentally [1–5].
Kittel model of antiferroelectrics
In analogy to the EC effect in ferroelectrics [13] we consider the case where an electric field E is applied at the initial temperature T1 under adiabatic conditions and subsequently the system reaches the final temperature T2. The entropy of the system is assumed to be the sum of the phonon contribution Sph plus a dipolar entropy  , i.e.,
, i.e.,

The condition that the change of the total entropy S should be zero leads to the relation [13]
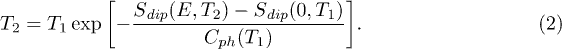
Here Cph is the heat capacity of the phonon subsystem, which is assumed to have a weak temperature dependence on the interval  . By contrast, the dipolar specific heat can vary strongly in the same interval, however, it is in principle contained in the change of the dipolar entropy and should thus not be added to Cph in the denominator.
. By contrast, the dipolar specific heat can vary strongly in the same interval, however, it is in principle contained in the change of the dipolar entropy and should thus not be added to Cph in the denominator.
The EC temperature change is given by  and can be calculated by solving the self-consistent equation (2) for T2. The dipolar entropy
and can be calculated by solving the self-consistent equation (2) for T2. The dipolar entropy  is derived from the Kittel free energy density for an AFE system [9–11,14,15]
is derived from the Kittel free energy density for an AFE system [9–11,14,15]
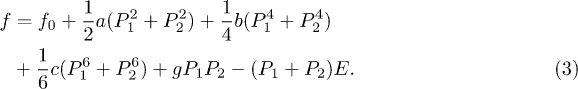
For simplicity we consider the uniaxial case with P1 and P2 representing the polarisation components for the two sublattices 1 and 2, respectively. Here a, b, c are the Landau-type expansion coefficients for each sublattice, and g is the AFE coupling strength [9]. We write [9–11,15]

where T0 is the paraelectric-to-antiferroelectric transition temperature in zero field. In dimensionless units we shall then set 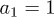 ,
,  ,
,  , and
, and 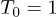 . In eq. (3) we have included the 6-th order terms in order to facilitate the comparison with the ferroelectric case
. In eq. (3) we have included the 6-th order terms in order to facilitate the comparison with the ferroelectric case  discussed earlier [13] and with the case b < 0 describing a first-order transition [9,16].
discussed earlier [13] and with the case b < 0 describing a first-order transition [9,16].
The physical polarisation P and the staggered polarisation Ps, which plays the role of the order parameter, are given by
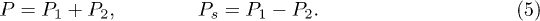
In thermodynamic equilibrium, the minimum of the free energy 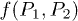 calls for
calls for  . This leads to the relations
. This leads to the relations


In general, for a given value of E the solutions of these equations may contain several branches including some metastable states. In order to focus on the stable states only, we shall avoid solving eqs. (6) but instead calculate  and
and  directly by minimising the free energy (3) by means of a suitable numerical routine. We shall select
directly by minimising the free energy (3) by means of a suitable numerical routine. We shall select  and
and  so that
so that  and
and  . It can be checked by evaluating the Hessian of
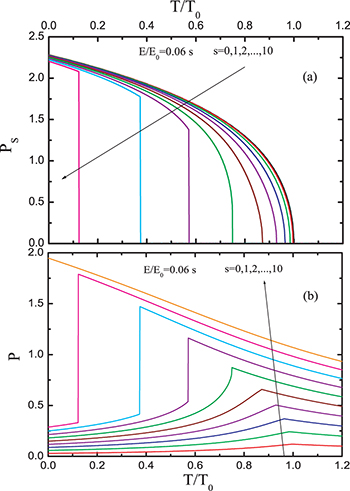
. It can be checked by evaluating the Hessian of  that all solutions P1, P2 obtained in this way are stable. In fig. 1(a) we plot the order parameter
that all solutions P1, P2 obtained in this way are stable. In fig. 1(a) we plot the order parameter  and in fig. 1(b) the total polarisation
and in fig. 1(b) the total polarisation  . For E = 0 the system undergoes a second-order transition from paraelectric to the AFE phase with non-zero order parameter
. For E = 0 the system undergoes a second-order transition from paraelectric to the AFE phase with non-zero order parameter  at the AFE ordering temperature
at the AFE ordering temperature  . As E is increased, the transition is shifted to lower temperatures and reaches a tricritical point at the tricritical temperature
. As E is increased, the transition is shifted to lower temperatures and reaches a tricritical point at the tricritical temperature  and tricritical field
and tricritical field 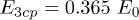 , where E0 is arbitrarily chosen as the critical field of the analogous ferroelectric model with g = 0 and b < 0 [13], i.e.,
, where E0 is arbitrarily chosen as the critical field of the analogous ferroelectric model with g = 0 and b < 0 [13], i.e., 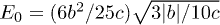 . For fields larger than
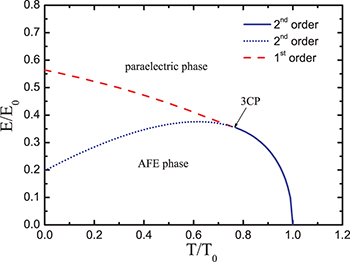
. For fields larger than  , the order parameter Ps is zero at all temperatures. For E > E3cp and T < T3cp, the transition from the paraelectric (or field-induced polar phase [15]) to the AFE (or antipolar [15]) phase is of the first order. The corresponding phase diagram is shown in fig. 2. The solid line represents the line of second-order phase transitions, which is derived from the condition that the derivative
, the order parameter Ps is zero at all temperatures. For E > E3cp and T < T3cp, the transition from the paraelectric (or field-induced polar phase [15]) to the AFE (or antipolar [15]) phase is of the first order. The corresponding phase diagram is shown in fig. 2. The solid line represents the line of second-order phase transitions, which is derived from the condition that the derivative  should diverge at the AFE transition. From eqs. (6) with
should diverge at the AFE transition. From eqs. (6) with 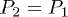 above the line and
above the line and  below, we find the equation for the critical value of P1c at the transition
below, we find the equation for the critical value of P1c at the transition
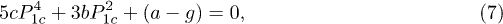
which is trivially solved. The critical field is then

A formal solution of this equation exists for all 0 < T < T0; however, only for T > T3cp it corresponds to a true phase transition line (solid line in fig. 2), whereas below T3cp it lies in the metastable regime (dotted line). The line of first-order transitions for  (dashed line) has been determined numerically from the positions of the jumps of
(dashed line) has been determined numerically from the positions of the jumps of  (see fig. 1(a)).
(see fig. 1(a)).
Fig. 1: (Colour on-line) Numerical results for the AFE order parameter  or staggered polarisation (a) and the dielectric polarisation
or staggered polarisation (a) and the dielectric polarisation 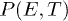 (b).
(b).
Download figure:
Standard imageFig. 2: (Colour on-line)  phase diagram of an antiferroelectric obtained numerically by minimising the free energy (3). Solid and dotted lines represent lines of second-order transitions in the stable and metastable region, respectively. Dashed line: line of first-order transitions, which joins the second-order lines at the tricritical point 3CP.
phase diagram of an antiferroelectric obtained numerically by minimising the free energy (3). Solid and dotted lines represent lines of second-order transitions in the stable and metastable region, respectively. Dashed line: line of first-order transitions, which joins the second-order lines at the tricritical point 3CP.
Download figure:
Standard imageThe dielectric susceptibility is defined as  and can be derived from eqs. (5) and (6). The result is
and can be derived from eqs. (5) and (6). The result is

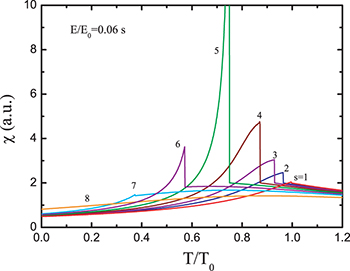
Here  . Numerically, we find that for non-zero fields
. Numerically, we find that for non-zero fields  exhibits a discontinuity on crossing the phase transition line (solid lines in fig. 2) and diverges at the tricritical point from below (see fig. 3). For E = 0,
exhibits a discontinuity on crossing the phase transition line (solid lines in fig. 2) and diverges at the tricritical point from below (see fig. 3). For E = 0,  has a cusp at
has a cusp at  (see the inset of fig. 5).
(see the inset of fig. 5).
Fig. 3: (Colour on-line) Dielectric susceptibility for the AFE Kittel model at  , which is found to diverge at the tricritical point
, which is found to diverge at the tricritical point  and
and  .
.
Download figure:
Standard imageEC effect: theory and experiment
The dipolar entropy is derived from eq. (3), namely, ![$S_{\textit{dip}}=-[\partial(f-f_0)/\partial T]_E$](https://content.cld.iop.org/journals/0295-5075/107/1/17002/revision1/epl16357ieqn53.gif) , and is given by
, and is given by

To calculate the electrocaloric temperature change  we insert the above expression for
we insert the above expression for  into eq. (2) with
into eq. (2) with 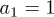 and find
and find
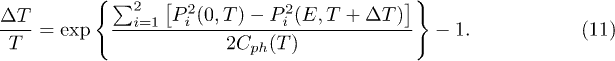
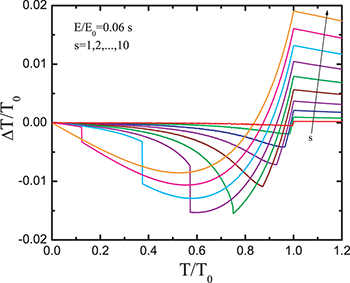
This is a self-consistent equation for  as a function of E and T, which can be solved by iteration or by some other suitable method [13]. The results are shown in fig. 4 for
as a function of E and T, which can be solved by iteration or by some other suitable method [13]. The results are shown in fig. 4 for  and a set of field values in the range
and a set of field values in the range  . For non-zero fields and T < T0 the EC effect is negative, i.e.,
. For non-zero fields and T < T0 the EC effect is negative, i.e.,  in a broad range of temperatures and fields. The maximum value of
in a broad range of temperatures and fields. The maximum value of  occurs at the tricritical point T3cp, E3cp. For T > T0 the EC effect is always positive and it decreases with the temperature in a manner similar to normal ferroelectrics [13]. From the experimental point of view, it is of special interest to investigate the EC in antiferroelectric systems in the range of temperatures and fields where a negative EC effect occurs.
occurs at the tricritical point T3cp, E3cp. For T > T0 the EC effect is always positive and it decreases with the temperature in a manner similar to normal ferroelectrics [13]. From the experimental point of view, it is of special interest to investigate the EC in antiferroelectric systems in the range of temperatures and fields where a negative EC effect occurs.
Fig. 4: (Colour on-line) The EC temperature change 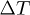 (in arbitrary units) calculated from the AFE model as a function of the initial temperature T and applied field E.
(in arbitrary units) calculated from the AFE model as a function of the initial temperature T and applied field E.
Download figure:
Standard imageThe main prediction of the above analysis based on the Kittel model for AFE systems is the occurrence of a negative EC effect in a broad temperature range below the AFE Curie temperature T0 (fig. 4). It should be noted, however, that the Kittel model is now believed to be rather trivial and thus unable to describe in detail all the properties of real AFE systems such as single crystal PbZrO3 (PZ) [17,18]. For example, it has been reported that the AFE phase of PZ below  shows weak transient ferroelectricity in a temperature range of 20 K [18]; however, it has further been suggested that the FE phase might be defect induced and thus not present in pure crystals [19]. On the other hand, it has long been known that a FE phase between the paraelectric and the AFE phase appears in PbZrO3 ceramics doped with a small amount of Ba [20].
shows weak transient ferroelectricity in a temperature range of 20 K [18]; however, it has further been suggested that the FE phase might be defect induced and thus not present in pure crystals [19]. On the other hand, it has long been known that a FE phase between the paraelectric and the AFE phase appears in PbZrO3 ceramics doped with a small amount of Ba [20].
In order to test the predictions of the above model, we have investigated experimentally the EC effect in PbZrO3 ceramics (PZ). The ceramic powder was prepared by solid-state synthesis using PbO (Sigma, 99.9% purity, 211907) and ZrO2 (TZ-0, Tosoh) as precursos. The powders were mixed in a stochiometric ratio, homogenized in a planetary mill and calcined twice in alumina crucibles at  for 2 hours with intermediate milling. The sample was then sintered for 2 hours at
for 2 hours with intermediate milling. The sample was then sintered for 2 hours at  using the pressure-assisted sintering technique and a uniaxial pressure of 24.5 MPa. During sintering the sample was embedded into a packing powder of the same composition in order to prevent the evaporation of PbO. The density after the sintering was
using the pressure-assisted sintering technique and a uniaxial pressure of 24.5 MPa. During sintering the sample was embedded into a packing powder of the same composition in order to prevent the evaporation of PbO. The density after the sintering was  , as determined by the Archimedes method. The phase purity of the sample was confirmed by X-ray diffraction, whereby the structure was identified as orthorhombic, as previously reported by others [21]. The sintered sample was cut, ground to final thickness of about
, as determined by the Archimedes method. The phase purity of the sample was confirmed by X-ray diffraction, whereby the structure was identified as orthorhombic, as previously reported by others [21]. The sintered sample was cut, ground to final thickness of about  , and sputter-coated with gold electrodes. Finally, the sample was annealed to relax any internal stresses, possibly induced during the preparation procedure.
, and sputter-coated with gold electrodes. Finally, the sample was annealed to relax any internal stresses, possibly induced during the preparation procedure.
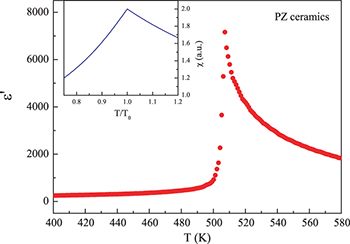
From the dielectric measurements, the AFE transition temperature in PZ was found at  and no FE phase was observed on heating the system starting from temperatures far below T0 (see fig. 5). It seems that any FE phase that might exist in the individual grains is smeared out in the ceramic sample, whereas the AFE transition temperature T0 is not affected by averaging over the grain orientations [12].
and no FE phase was observed on heating the system starting from temperatures far below T0 (see fig. 5). It seems that any FE phase that might exist in the individual grains is smeared out in the ceramic sample, whereas the AFE transition temperature T0 is not affected by averaging over the grain orientations [12].
Fig. 5: (Colour on-line) Real part of the dielectric permittivity of PZ ceramics measured in zero bias field at a frequency 1 MHz, showing a cusp at  , corresponding to the AFE transition temperature T0. Inset: static dielectric susceptibility of the AFE Kittel model in zero bias field.
, corresponding to the AFE transition temperature T0. Inset: static dielectric susceptibility of the AFE Kittel model in zero bias field.
Download figure:
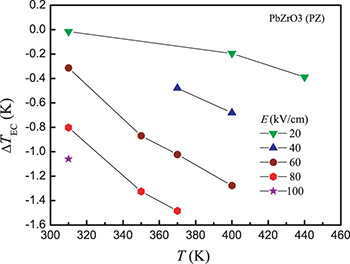
Standard imageThe EC temperature changes were measured by a specially made high-resolution calorimeter [22,23], allowing a precise temperature stabilisation (within 0.1 K) as well as high-resolution measurements of the EC temperature changes induced by an external field E [24]. In fig. 6 a typical EC response of an AFE material, i.e., the negative EC effect is shown. The results for the EC temperature change 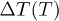 in PZ ceramics are plotted in fig. 7 for a discrete set of applied fields E in the temperature range
in PZ ceramics are plotted in fig. 7 for a discrete set of applied fields E in the temperature range 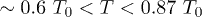 , and agree qualitatively with the calculated behaviour of
, and agree qualitatively with the calculated behaviour of  displayed in fig. 4. Since the largest observed value of
displayed in fig. 4. Since the largest observed value of 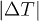 in PZ is found for
in PZ is found for  , we can tentatively assume that this corresponds to the tricritical field
, we can tentatively assume that this corresponds to the tricritical field 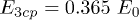 , giving an estimate for the parameter E0 in PZ, i.e.,
, giving an estimate for the parameter E0 in PZ, i.e.,  .
.
Fig. 6: (Colour on-line) Typical EC signal as a function of time, measured in the antiferroelectric PZ ceramics by a small bead thermistor.
Download figure:
Standard imageFig. 7: (Colour on-line) The EC temperature change  in PZ ceramics as a function of temperature for different electric field amplitudes, measured by direct experimental technique described in ref. [24].
in PZ ceramics as a function of temperature for different electric field amplitudes, measured by direct experimental technique described in ref. [24].
Download figure:
Standard imageConclusions
The predictions of the generic Kittel model of antiferroelectrics are in qualitative agreement with the experimental data for the negative electrocaloric effect in PbZrO3 ceramics, obtained from direct measurements of the EC temperature change in this system. Another prediction is the occurrence of a tricritical point at some special values of the electric field and temperature, which has not been investigated in detail so far. Obviously, in spite of its apparent simplicity, the model seems capable of describing the basic mechanism of antiferroelectricity in PZ and related perovskites, and could probably be extended to include an intermediate ferroelectric phase occurring, for example, in barium-doped PZ.
Acknowledgments
This work was supported by the Slovenian Research Agency under programmes P1-0044, P1-0125, and P2-0105, and by the NAMASTE Centre of Excellence.