Phonon drag thermopower in graphene in equipartition regime

The transport properties of graphene have been attracting considerable interest in recent years [1–4]. A study was performed on the electrical [5, 6] and thermal conductivity [7–10], thermomagnetic effects [11] and electrical phenomena generated by irradiation [12, 13].

Particularly promising for the field of applications appear to be experimental [14–18] and theoretical [19–24] studies of the thermoelectric properties of graphene. The high electrical conductivity combined with a significant Seebeck coefficient (thermoelectromotive force or thermopower), provide a basis for expecting graphene to reveal a fairly high thermoelectric figure of merit. Scattering from phonons is essential for the evolvement of electron transport in graphene [5, 6, 25–28]. Thus, in graphene, as in other sp² carbon materials [29–33], one can envisage the amplification of thermoelectric effects as a result of the phonon drag effect discovered in 1946 by Gurevich [34].

We calculate the electric current generated by phonon drag in the presence of a temperature gradient in a graphene sample, obtain the corresponding contribution to the Seebeck coefficient and compare it with the contribution of diffusion to thermopower.

The conditions chosen for the calculations are the most favorable for the experimental observation of the effect of electron drag by phonons. The assumptions accepted for the sample and external conditions in the system are as follows. We consider electrons near the Dirac point having an idealized linear dispersion law E_k = ℏv_F k (the Fermi velocity v_F  ≈ 10⁸ cm s⁻¹). The Fermi level ε_F in the system is assumed to be much higher than the temperature, opening the way to the application of the degenerate electron gas approximation, which implies monopolar conduction. The condition of the onset of degeneracy defines the upper limit of temperature below which this theory is applicable. The absolute value of the electron wave vector k near the Fermi level will be denoted in what follows by k_F . We are going to consider a free-standing graphene monolayer and take into account the contribution of the intrinsic acoustic in-plane (LA and TA) phonons only, which correlates with previous studies [25] of the mechanisms underlying electron relaxation in graphene. The dispersion law of such lattice vibrations is given by ℏω_ph(q) = ℏqv_s, where the sound velocity is v_s ∼ 2·10⁶ cm s⁻¹.

On the other hand, it is assumed that the temperature is high enough to maintain an equipartition (EP) regime of electron-phonon interaction, in which the numbers of occupation of the phonon modes contributing to the drag effect are larger than 1. The phonons interacting with electrons have a wave vector on the order of k_F and energy ℏv_sk_F .

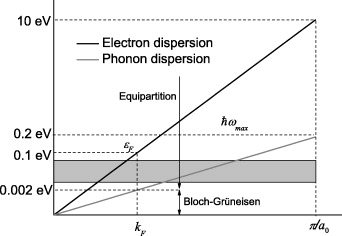
In the case of high temperatures, the equilibrium distribution function for phonon mode occupation numbers transforms into N⁽⁰⁾_ph(q) = T/ℏω_ph(q) for both phonon emission and absorption processes. This defines the lower temperature limit of applicability of the theory developed. Only the contribution from acoustic phonons is considered, and, hence, the occupation numbers of optical phonons must be small. This condition specifies the second upper limit in temperature for the theory developed. Figure 1 demonstrates all characteristic energies, wave vectors and velocities related to the problem being analyzed. We readily see that in actual fact the above conditions are satisfied by the very broad temperature range, including room temperature. Finally, we neglect the reverse influence of the electron subsystem of the crystal on its phonon subsystem.

Zoom In Zoom Out Reset image size

The Fermi energy of graphene ε_F is known to be related [2] with carrier concentration n_s as 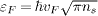$\varepsilon _F=\hbar v_F \sqrt {\pi n_s}$. In transistor-based electronic devices the concentration is controlled by properly varying the gate voltage and is determined by the capacity of the structure. These parameters are measured in an experiment. Through them can be expressed all the results obtained. Doping is another way to control the Fermi level in graphene [35].

A temperature gradient in the sample produces a directed phonon flow (the so-called "phonon wind"). The behavior of the phonon system in the presence of a temperature gradient can be described in the relaxation time approximation with the Boltzmann kinetic equation. The kinetic equation describing the correction N⁽¹⁾_ph(q) = N_ph(q) − N⁽⁰⁾_ph(q) to the equilibrium distribution function for phonon mode occupation numbers in the presence of temperature gradient reads as

$$\begin{equation} v_s \frac{\bm{q}}{q} \frac{\partial N^{(0)}_{ph}({\bm{q}})}{\partial T} k_B \nabla T = -\frac{N^{(1)}_{ph}({\bm{q}})}{\tau_{ph}({\bm{q}})}, \end{equation} \tag{ 1 }$$

and, hence, the correction itself can be written as

$$\begin{equation} N^{(1)}_{ph}({\bm{q}}) =- \frac{\tau_{ph}({\bm{q}})k_B}{\hbar q^2}({\bm{q}} \nabla T), \end{equation} \tag{ 2 }$$

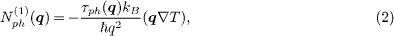
where τ_ph(q) is the relaxation time of phonon with wave vector q.

Here the relaxation time should be taken for the in-plane acoustic phonons with a wave vector magnitude from 0 to 2k_F . Within the temperature range treated in this letter, phonon scattering from point defects and sample edges are dominant mechanisms [7, 8, 19, 20]. For a sample 2 μm in size and with the same concentration of point defects as observed in ref. [7], scattering from edges dominates over that from point defects. The relaxation time for edge scattering can be estimated as the ratio of the minimum linear size of the sample L (de facto mean free path) to the sound velocity v_s. For the corresponding time for a 2 μm sample one obtains 100 ps, and it does not depend on the magnitude of the phonon wave vector q for in-plane phonons, thus permitting us to write simply in what follows τ_ph.

Thermal conductivity of graphene reaches the value of 5000 Wm⁻¹ K⁻¹ [3, 4, 7, 8]. In a general case, the relaxation time of phonons that generates the drag effect cannot be straightly connected with the thermal conductivity of the sample because the phonons from the whole Brillouin zone, the phonons from other branches and other mechanisms of phonon scattering (including the three-phonon Normal and Umklapp processes at the temperature higher than 300 K) define the total thermal conductivity of the sample.

However, the value of the relaxation time of the phonons generating the drag effect can be connected with the low-temperature (T < 30 K) thermal conductivity of the sample. It is known that the thermal conductivity of graphene at low temperatures is provided by ZA phonons and corresponding relaxation mechanism is scattering on the edges of the sample. The dispersion relation of ZA phonons is quadratic [7]: ω_ZA(q) = Kq², where K = 3.13·10⁻³ cm² s⁻¹ [36]. The relation (9) from [7] after the substitution the relaxation time τ_ZA(q) = L/v_ZA(q) and some algebra connects the phonon mean free path L and thermal conductivity κ:

$$\begin{equation} \kappa = 0.35\frac{k_B^{5/2}T^{3/2}}{K^{1/2}h\hbar^{3/2}}L, \end{equation} \tag{ 3 }$$

where h ∼ 0.35 nm estimates the thickness of graphene layer [8]. This expression gives approximately 900 Wm⁻¹ K⁻¹ for the sample with L = 2 μm at 50 K.

The rate of electron transitions from a state with wave vector k into a state with wave vector k' = k + q driven by scattering from a phonon with wave vector q (involving absorption or emission of one acoustic phonon) is described by the "Fermi golden rule":

$$\begin{eqnarray} W_{{\bm{k}} \rightarrow {\bm{k}} + {\bm{q}}}^{em,abs} &=& \frac{2 \pi}{\hbar} \frac{N_{ph}({\bm{q}})}{v_F \omega_{ph}({\bm{q}})} |M_{e\hbox{-}ph}({\bm{q}})|^2\nonumber\\ & &\times\frac{S}{N_u M} \delta \left( k^\prime - k \pm \frac{\omega_{ph} ({\bm{q}})}{v_F} \right), \end{eqnarray} \tag{ 4 }$$

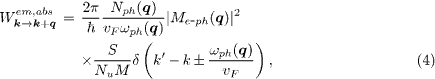
where M_e−ph(q) is the matrix element of electron scattering from a phonon specifying the magnitude of electron-phonon interaction, M is the carbon atom mass, S the sample area, and N_u is the number of elementary cells in the sample. The combination of the three last quantities can be expressed through the surface density of graphene ρ = 6.5·10⁻⁸ g cm⁻² and the lattice constant a₀ = 2.46 Å.

For long-wavelength acoustic phonons the modulus of the matrix element depends on the phonon wave vector and the scattering angle θ_k+q,k as $M_{e\hbox{-}ph}({\bm {q}})=Dq \frac {1}{2} (1+\cos (\theta _{{\bm {k}} + {\bm {q}}, {\bm {k}}} ))$ [25, 27, 37]. The term in brackets suppresses electron backscattering [25]. In the case of completely isotropic electron scattering, M_e−ph(q) = Dq, the phonon drag thermopower would increase fourfold. The quantity D can be estimated as 16 eV. Note that this value is very close to the combination ℏv_F 2π/a₀, which permits the estimation of the graphene electron bands.

Should a more accurate expression for the matrix element M_e−ph as a function of the wave vectors of electrons and phonons be required, it can be readily derived through the deformation potential precisely calculated in ref. [28].

In the first order of the perturbation theory the contribution to the drag comes from 4 types of electron transitions, which correspond to the coming and leaving of electrons into the state with wave vector k following absorption and emission of a phonon with wave vector q. The rate of variation of the electron distribution function mediated by interaction with phonons can be represented in the following equation in full form in the standard way through the phonon collision integral [38]:

$$\begin{eqnarray} \left(\frac{\partial}{\partial t} f({\bm{k}}) \right)_{ph}\!\!&\!=\!&\!- \int\!\!{\frac{{\rm d} {\bm{q}}}{4 \pi^2}} \left[W_{{\bm{k}} \rightarrow {\bm{k}}+{\bm{q}}}^{abs}f^{(0)}(\varepsilon_{{\bm{k}}}) \left(1\!-\!f^{(0)}(\varepsilon_{{\bm{k}} + {\bm{q}}}) \right)\right.\nonumber\\ & &\left.+ W_{{\bm{k}} \rightarrow {\bm{k}} - {\bm{q}}}^{em}f^{(0)}(\varepsilon_{{\bm{k}}}) \left(1 - f^{(0)}(\varepsilon_{{\bm{k}} - {\bm{q}}}) \right) \right. \nonumber\\ & &-\left. W_{{\bm{k}} - {\bm{q}} \rightarrow {\bm{k}}}^{abs}f^{(0)}(\varepsilon_{{\bm{k}} - {\bm{q}}}) \left(1 - f^{(0)}(\varepsilon_{{\bm{k}}}) \right)\right.\nonumber\\ & &\left.- W_{{\bm{k}} + {\bm{q}} \rightarrow {\bm{k}}}^{em}f^{(0)}(\varepsilon_{{\bm{k}} + {\bm{q}}}) \left(1 - f^{(0)}(\varepsilon_{{\bm{k}}}) \right) \right]. \end{eqnarray} \tag{ 5 }$$

In eq. (5) f⁽⁰⁾(ε_k) is the equilibrium distribution function of electrons with a chemical potential depending on ε_F and temperature. At low temperatures, the chemical potential can be assumed equal to ε_F , and the correction accounting for temperature variation may be neglected. Integration is run over the phonon wave vector q over the whole Brillouin zone. Scattering from acoustic phonons does not initiate interband and intervalley transitions and variation of the electron spin.

Obviously enough, an equilibrium distribution function describes randomized phonons, and drag is mediated only by the nonequilibrium term N⁽¹⁾_ph which should be substituted from (2) into (4), and further, into (5). v_F being approximately 50 times larger than v_s, electrons scatter from phonons in an almost elastic way. The energy conservation law is fundamentally important in including into (5) the distribution function of electrons before and after their scattering from a phonon [38]. One can set

$$\begin{equation} f^{(0)}({\bm{k}} + {\bm{q}}) = f^{(0)}({\bm{k}} ) \pm \frac{\partial f^{0}(\varepsilon)}{\partial \varepsilon}\hbar \omega_{ph}({\bm{q}}). \end{equation} \tag{ 6 }$$

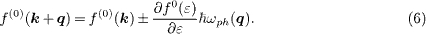
The " + " sign identifies here the absorption of a quantum of sound, and the " − " sign, the emission. Conversely, integrating in angle, one can set

$$\begin{equation} \delta \left( k^\prime - k \pm \frac{\omega_{ph} ({\bm{q}})}{v_F} \right) \approx \frac{1}{q}\delta \left( \cos{\theta_{{\bm{k}}, {\bm{q}}} + \frac{q}{2k}} \right), \end{equation} \tag{ 7 }$$

which corresponds to neglecting the phonon energy when considering scattering. As a result, the interaction with a phonon flux transforms the collision integral to

$$\begin{equation} \left(\frac{\partial}{\partial t} f({\bm{k}}) \right)_{ph} = v_F \frac{{\bm{k}}}{k} k_B\nabla T G_{ph}(k) \frac{\partial f^{(0)}}{\partial \varepsilon}, \end{equation} \tag{ 8 }$$

where the dimensionless parameter is introduced,

$$\begin{equation} G_{ph}(k)=\frac{S}{2M N_u} \frac{D^2}{\hbar^3 v_F^4} \frac{L}{v_s} \varepsilon^2(k). \end{equation} \tag{ 9 }$$

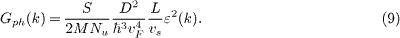
We readily see that the phonon collision integral includes the quantity $\frac {\partial f^{(0)}}{\partial \varepsilon }$ and a scalar product of the electron wave vector k by the vector describing the external factor ∇T. Hence, the phonon collision integral can be interpreted as a field term of the Boltzmann kinetic equation. This makes possible the calculation of the nonequilibrium term f⁽¹⁾(k) for the electron distribution function f⁽⁰⁾(ε_k) in the relaxation time approximation by the straightforward multiplication of the right-hand part of relation (8) by the electron transport relaxation time τ(ε_k).

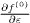One can now calculate the electric current, as well as the current j generated by the external electric field. In the derivation of the current ${\bm {j}} =\frac {e}{\pi ^2} \int {{\mathrm { d}}{\bm {k}}\, {\bm {v}}_{{\bm {k}}} f^{(1)}({\bm {k}})}$, the first approximation (delta-function approximation) in relation (6) for $\frac {\partial f^{(0)}}{\partial \varepsilon }$ will be already sufficient. The final expression for the contribution provided by the phonon drag to thermopower looks as

$$\begin{equation} S_{ph}=\frac{ \pi^4}{2e} \frac{k_B\hbar}{M a_0^2}\frac{L}{v_s} \left( \frac{D}{\hbar v_F \pi / a_0} \right)^2 \left( \frac{\varepsilon_F}{\hbar v_F \pi / a_0} \right)^2. \end{equation} \tag{ 10 }$$

The transport electron relaxation time cancels when the current is divided by the electrical conductivity of the sample.

The most remarkable feature in the relation obtained is that it does not contain an explicit dependence of thermopower on temperature, which argues with [23]. The obtained relation correlates with the observation that only a directed phonon flux (phonon wind) contributes to thermopower; now, in accordance with relation (2), this flux is proportional to temperature gradient and does not depend directly on the temperature itself.

The non-dimensional factor 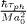$\frac {\hbar \tau _{ph}}{M a_0^2}$ in relation (10) is close in magnitude to 8, and the ratio 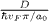$\frac {D}{\hbar v_F \pi / a_0}$ approaches 2.

The obtained phonon drag thermopower should be compared with the well-known formula (see, for instance, relation (4) from ref. [21]) of diffusion thermopower in graphene:

$$\begin{equation} S_{d} = \frac{\pi^2}{3e} \frac{k_B^2T}{\varepsilon_F}. \end{equation} \tag{ 11 }$$

In the case of a degenerate electron gas, the diffusion thermoelectric current turns out to be zero in the first approximation for 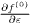$\frac {\partial f^{(0)}}{\partial \varepsilon }$. Taking the second term in the Sommerfeld expansion results in the proportionality to T/ε_F , which appears in (11). This expression for the diffusion factor in the thermopower in graphene correlates with the Mott formula and coincides with that developed for metals [39] and graphite [32]. To bring the result in compliance with the mechanism of carrier scattering in a particular sample, one has naturally to introduce a factor of order unity.

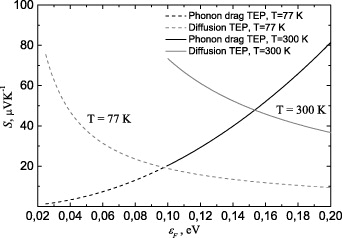
Figure 2 plots the dependences of the contribution to thermopower due to electron drag by phonons and of the contribution to thermopower due to diffusion, as functions of the Fermi level, which were calculated by relations (10) and (11), respectively.

Zoom In Zoom Out Reset image size

In most of the available relevant publications [10, 14–17] thermoelectric properties of graphene find a straightforward interpretation in terms of the Mott formula. No phonon drag was observed in these studies. Small deviations from the Mott formula were recorded, however, at low temperatures. These deviations should most probably be assigned only to a decrease of the measurement accuracy. Only the data reported in ref. [10] may be interpreted as reflecting saturation of thermopower with decreasing temperature. Finally, several graphs in ref. [16] suggest the growth of thermopower with increasing Fermi level.

The first reason for the phonon drag effect becoming suppressed could be the reverse effect exerted by electrons on the phonon system, accompanied by the corresponding decrease of the phonon relaxation time [38] The second possible factor could be the effect of the substrate, which may likewise reduce the phonon mean free paths. Intrinsic phonons of graphene may be expected to become scattered from phonons of the substrate or from substrate irregularities. For instance, the limitation of the electron mobility caused by the phonons from the substrate was indicated in [40]. Molecular-dynamics modeling [41] yields a value of about 5 ps for the relaxation time of long-wavelength acoustic phonons in 4 × 4 nm² graphene sheets on a SiO₂ substrate. For a free-standing sample, the relaxation time of such phonons turned out to be about 10 times larger, approaching in magnitude the value of 100 ps used in this study. Nevertheless, it appears pertinent to note that the interaction of mechanically exfoliated graphene with the substrate is assigned to weak van der Waals forces [42, 43]. The substrate, in particular, does not affect the shape of the Raman spectra [44], which are very sensitive probes of the vibrational characteristics of a crystal.

A calculation was made of the phonon drag contribution to thermopower in graphene in the Bloch-Grüneisen (BG) temperature regime[19]. The BG regime specifies the case where temperature is not high enough to drive excitation of phonons with a wave vector on the order of the characteristic electron wave vector. The Seebeck coefficient in this case is proportional to T³, the situation coinciding with the case of graphite [32]. To realize the BG regime in graphene, however, the temperatures should be at their lowest limit. As already mentioned, in the case of a degenerate electron gas phonons interacting with electrons of energy on the order of ε_F ∼ 0.1 eV have a temperature of about 20 K. The very noticeable predictions of thermopower enhancement are made for graphene with a band gap opened for both diffusion [24] and phonon drag contributions [20].

As was mentioned above, the phonons that generate the drag of electrons are a very small part of the excited phonons that define thermal conductivity. In theory it allows to manipulate the thermal conductivity and the phonon drag thermopower separately. We suggest that the phonon drag thermopower is defined by the scattering of phonons on the edges of the sample. Thermal conductivity can also rise nearly up to the room temperature with the increase of the size. But due to the relation ZT = σTS²/κ for the thermoelectric figure of merit it will grow with the increase of the sample size linearly or even faster. The problem of the thermal conductivity reduction is complicated because making samples with point defects, placing samples onto the substrate or increasing ambient temperature will reduce both the electrical and the thermal conductivity of the sample and these effects should be considered simultaneously. Thereby tuning the size of the sample seems to be the straightest way of improving graphene thermoelectrical properties.

The quality of graphene samples prepared is improving continuously [2, 45, 46]. As demonstrated in this study, in a high-quality sample with a large phonon mean free path, which probably correlates with high thermal conductivity, at temperatures of the environment from liquid nitrogen to room temperature, and at a high Fermi level one may expect the contribution to thermopower due to phonon drag to dominate over the diffusion-associated one, and a sharp increase of the Seebeck coefficient and thermoelectric figure of merit.

We are deeply grateful to M. M. Glazov for support and fruitful discussions. Our thanks are due to A. Ya. Vul' and A. T. Dideykin for their interest in this work. This study was supported by a grant for young scientists of the Dynasty foundation. Partial support was provided by the Russian Ministry of Education and Science (projects 8683).