Abstract
Understanding the generation of intrinsic rotation in tokamak plasmas is crucial for future fusion reactors such as ITER. We proposed a new mechanism named turbulent acceleration for the origin of the intrinsic parallel rotation based on gyrokinetic theory. The turbulent acceleration acts as a local source or sink of parallel rotation, i.e., volume force, which is different from the divergence of residual stress, i.e., surface force. However, the order of magnitude of turbulent acceleration can be comparable to that of the divergence of residual stress for electrostatic ion temperature gradient (ITG) turbulence. A possible theoretical explanation for the experimental observation of electron cyclotron heating induced decrease of co-current rotation was also proposed via comparison between the turbulent acceleration driven by ITG turbulence and that driven by collisionless trapped electron mode turbulence. We also extended this theory to electromagnetic ITG turbulence and investigated the electromagnetic effects on intrinsic parallel rotation drive. Finally, we demonstrated that the presence of turbulent acceleration does not conflict with momentum conservation.
Export citation and abstract BibTeX RIS
1. Introduction
The intrinsic rotation can be generated by a self-organization process in turbulent atmosphere. This phenomenon is widely discovered in nature, such as the planetary atmosphere [1], solar tachocline [2], as well as in laboratory, such as the intrinsic rotation in tokamak plasmas [3]. The intrinsic rotation in tokamak plasmas has been extensively studied for decades since rotation is helpful for stabilizing magnetohydrodynamic (MHD) instabilities such as resistive wall modes [4, 5] and neoclassical tearing modes [6], and plays an important role in improving plasma confinement by suppressing micro-turbulence [7–9]. In addition, another idea to control tokamak plasma turbulence via artificial intelligence techniques with using artificial neutral networks was also proposed recently [10–12].
What the mechanisms account for the intrinsic rotation drive is still an open question. We proposed a new mechanism named turbulent acceleration for the intrinsic parallel rotation drive by electrostatic ion temperature gradient (ITG) turbulence [13]. The turbulent acceleration cannot be written as a divergence of stress term, which is different from the physics of residual stress, and so acts as a local source or sink. In other words, the turbulent acceleration is an effective volume-force, while the divergence of residual stress is a kind of surface-force. We also proposed a possible theoretical explanation for the experimental observation of electron cyclotron heating (ECH) induced decrease of co-current core toroidal rotation via the comparison between the turbulent acceleration driven by ITG turbulence and that driven by collisionless trapped electron mode (CTEM) turbulence [14]. Then, we extended our theory to electromagnetic ITG turbulence and found the importance of electromagnetic effects on intrinsic parallel rotation drive [15]. Finally, we demonstrated that the conserved quantity corresponding to axisymmetry is the total canonical momentum or total momentum carried by both particles and electromagnetic fields, and the presence of turbulent acceleration does not imply its confliction with momentum conservation [16].
The rest of this paper is organized as follows. In section 2, the new mechanism named turbulent acceleration for electrostatic ITG turbulence and the comparison of turbulent acceleration between ITG turbulence and CTEM turbulence are presented. Then, an extension to electromagnetic ITG turbulence and some discussions on relevant experiments are given in section 3. The relationship between the turbulent acceleration and the momentum conservation law is clarified in section 4. Finally, we make a summary and discuss our future work in section 5.
2. Turbulent acceleration driven by electrostatic turbulence
2.1. Electrostatic ITG turbulence
Starting from the conservative form of the nonlinear electrostatic gyrokinetic equation in the continuity form [17]
with gyrocenter equations of motion
and
Here,  is the gyrocenter distribution function,
is the gyrocenter distribution function,  is the gyrocenter magnetic moment and
is the gyrocenter magnetic moment and  is the parallel velocity of ions' gyrocenter,
is the parallel velocity of ions' gyrocenter, 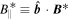 is the Jacobian of the transformation from particle phase space to the gyrocenter phase space with
is the Jacobian of the transformation from particle phase space to the gyrocenter phase space with 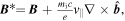 and
and 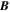 is the equilibrium magnetic field with
is the equilibrium magnetic field with 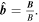
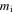 is the ion mass,
is the ion mass, 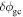 is the gyrocenter electric potential fluctuation, and
is the gyrocenter electric potential fluctuation, and 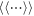 denotes gyroaveraging. In the following, we denote
denotes gyroaveraging. In the following, we denote 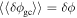 since a long wavelength approximation
since a long wavelength approximation 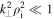 is used, where
is used, where  is the perpendicular wave number and
is the perpendicular wave number and 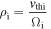 is the ion Larmor radius with
is the ion Larmor radius with  being the ion thermal velocity and
being the ion thermal velocity and 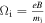 being the ion cyclotron frequency. In this paper, the index
being the ion cyclotron frequency. In this paper, the index  refers to the components parallel to the equilibrium magnetic field, and the index
refers to the components parallel to the equilibrium magnetic field, and the index 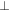 refers to the components perpendicular to the equilibrium magnetic field. Note that the usual experimentally measured quantity is the ion parallel flow velocity rather than the ion parallel momentum density, so we focus on the mean parallel flow velocity equation. By taking the zeroth order and the first order moments of equation (1), decoupling the density from momentum density equation and taking flux average of parallel flow equation, we can finally obtain the evolution equation of the mean parallel flow velocity [13]
refers to the components perpendicular to the equilibrium magnetic field. Note that the usual experimentally measured quantity is the ion parallel flow velocity rather than the ion parallel momentum density, so we focus on the mean parallel flow velocity equation. By taking the zeroth order and the first order moments of equation (1), decoupling the density from momentum density equation and taking flux average of parallel flow equation, we can finally obtain the evolution equation of the mean parallel flow velocity [13]
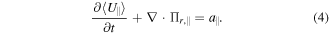
Here, 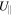 is the ion parallel flow velocity and
is the ion parallel flow velocity and  denotes flux average.
denotes flux average. 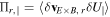 is the usual parallel Reynolds stress with
is the usual parallel Reynolds stress with 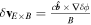 being the fluctuating
being the fluctuating  drift velocity and
drift velocity and 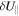 being the parallel flow fluctuation, which consists of three terms including diffusion, convection, and residual stress
being the parallel flow fluctuation, which consists of three terms including diffusion, convection, and residual stress  The parallel Reynolds stress has been intensively investigated [18, 19],
The parallel Reynolds stress has been intensively investigated [18, 19], 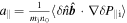 is the turbulent acceleration with
is the turbulent acceleration with 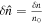 being the normalized density fluctuation and
being the normalized density fluctuation and 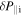 being the ion pressure fluctuation with
being the ion pressure fluctuation with 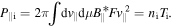 The turbulent acceleration cannot be written as a divergence of the parallel Reynolds stress, and plays a role of local source/sink of parallel rotation. Its existence does not depend on the magnetic geometry and it is independent of the mean parallel velocity or the gradient of mean parallel velocity. Therefore, it is a new candidate mechanism for the origin of intrinsic rotation.
The turbulent acceleration cannot be written as a divergence of the parallel Reynolds stress, and plays a role of local source/sink of parallel rotation. Its existence does not depend on the magnetic geometry and it is independent of the mean parallel velocity or the gradient of mean parallel velocity. Therefore, it is a new candidate mechanism for the origin of intrinsic rotation.
For electrostatic ITG turbulence, an adiabatic electron response is assumed, i.e., 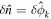 with
with 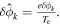 By linearizing the ion pressure equation we can obtain the ion pressure fluctuation
By linearizing the ion pressure equation we can obtain the ion pressure fluctuation
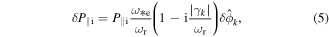
where 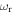 and
and 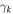 are real frequency and linear growth rate, respectively. Then, a quasilinear expression for the turbulent acceleration can be written as [13]
are real frequency and linear growth rate, respectively. Then, a quasilinear expression for the turbulent acceleration can be written as [13]
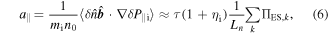
where 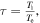
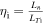 with
with 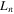 being the density gradient scale length and
being the density gradient scale length and 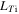 being the ITG scale length.
being the ITG scale length.  is electrostatic residual stress which is consistent with previous result [19],
is electrostatic residual stress which is consistent with previous result [19], 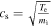 is the ion acoustic velocity and
is the ion acoustic velocity and  By taking the parallel symmetry breaking induced by intensity gradient [19], i.e.,
By taking the parallel symmetry breaking induced by intensity gradient [19], i.e., 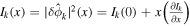 and
and 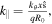 where
where 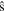 is the magnetic shear,
is the magnetic shear, 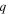 is the safety factor,
is the safety factor, 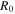 is the major radius,
is the major radius, 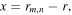 with
with 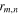 being the radial location of the resonant surface, we can obtain the turbulent acceleration
being the radial location of the resonant surface, we can obtain the turbulent acceleration
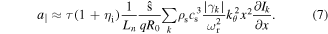
It is obvious that the turbulent acceleration can provide a co-current intrinsic rotation drive for positive magnetic shear 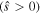 and positive intensity gradient
and positive intensity gradient 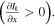 For convenience of comparison, the divergence of the residual stress obtained in [19] is written as
For convenience of comparison, the divergence of the residual stress obtained in [19] is written as

Here, 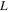 is the scale length of the radial variation of the residual stress. Thus, the ratio of the turbulent acceleration to the divergence of the residual stress is
is the scale length of the radial variation of the residual stress. Thus, the ratio of the turbulent acceleration to the divergence of the residual stress is  which means the turbulent acceleration can be comparable to the divergence of the residual stress, depending upon
which means the turbulent acceleration can be comparable to the divergence of the residual stress, depending upon 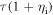 and
and 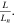 Hence, the new mechanism of turbulent acceleration is qualitatively different from the usual Reynolds stress, but it is quantitatively comparable to the divergence of residual stress.
Hence, the new mechanism of turbulent acceleration is qualitatively different from the usual Reynolds stress, but it is quantitatively comparable to the divergence of residual stress.
2.2. Electrostatic CTEM turbulence
For CTEM turbulence, by using quasi-neutrality condition, the ion gyrocenter density fluctuation can be approximated by the electron density fluctuation without considering finite Larmor radius effects, which is consist of adiabatic response and non-adiabatic response, i.e., 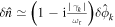 [14]. There is no phase shift between the density fluctuation and the ion pressure fluctuation (equation (5)), so the turbulent acceleration vanishes [14], i.e.,
[14]. There is no phase shift between the density fluctuation and the ion pressure fluctuation (equation (5)), so the turbulent acceleration vanishes [14], i.e., 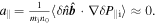 This is different from the ITG case as mentioned above where the turbulent acceleration can provide co-current intrinsic rotation drive, and its order of magnitude can be comparable to that of the divergence of residual stress. We also note that the residual stress driven by CTEM turbulence is an outward flux of co-current rotation for positive magnetic shear
This is different from the ITG case as mentioned above where the turbulent acceleration can provide co-current intrinsic rotation drive, and its order of magnitude can be comparable to that of the divergence of residual stress. We also note that the residual stress driven by CTEM turbulence is an outward flux of co-current rotation for positive magnetic shear 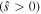 and positive intensity gradient
and positive intensity gradient 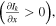 leading to flattening of co-current rotation or an increment of counter-current rotation [14]. Therefore, the turbulence mode transition from ITG to CTEM may result in a reduction of co-current rotation. This is because the co-current turbulent acceleration for ITG turbulence vanishes for CTEM turbulence, and the divergence residual stress for CTEM turbulence provides counter-current rotation drive. This may offer a theoretical explanation for the experimental observation of co-current core toroidal rotation reduction in co-current neutral beam injection heated L-mode [20] and H-mode plasmas [21, 22] with ECH turning on.
leading to flattening of co-current rotation or an increment of counter-current rotation [14]. Therefore, the turbulence mode transition from ITG to CTEM may result in a reduction of co-current rotation. This is because the co-current turbulent acceleration for ITG turbulence vanishes for CTEM turbulence, and the divergence residual stress for CTEM turbulence provides counter-current rotation drive. This may offer a theoretical explanation for the experimental observation of co-current core toroidal rotation reduction in co-current neutral beam injection heated L-mode [20] and H-mode plasmas [21, 22] with ECH turning on.
Conversely, the turbulence mode transition from CTEM to ITG can lead to increase of co-current rotation. This is qualitatively consistent with the experimental observation in TCV tokamak where the toroidal rotation inverts its sign spontaneously from the counter-current to co-current direction after electron density exceeding a well-defined threshold [23]. The turbulence mode transition from TEM to ITG occurs at the transition from linear Ohmic confinement to saturated Ohmic confinement during the density ramp up. The phenomena of rotation reversal were also observed in Alcator C-Mod tokamak [24, 25], but the direction of rotation reversal is from co-current to counter-current. The difference between the experimental observation from TCV and that from Alcator C-Mod may result from the different boundary condition with limiter configuration in TCV and divertor configuration in Alcator C-Mod, which has not been well understood yet.
3. Intrinsic rotation drive by electromagnetic ITG turbulence
For electromagnetic turbulence, the shear component of magnetic perturbation, i.e., 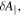 is considered [15]. Starting from the nonlinear electromagnetic gyrokinetic equation with gyrocenter equations of motion in the symplectic formulation (i.e.,
is considered [15]. Starting from the nonlinear electromagnetic gyrokinetic equation with gyrocenter equations of motion in the symplectic formulation (i.e., 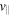 representation)
representation)
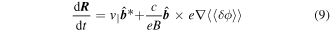
and
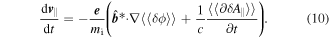
Here, uniform equilibrium magnetic field 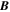 is assumed.
is assumed. 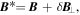
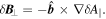
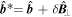 with
with 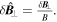 By taking the process similar to electrostatic case, we can obtain the mean field equation of the parallel flow velocity
By taking the process similar to electrostatic case, we can obtain the mean field equation of the parallel flow velocity
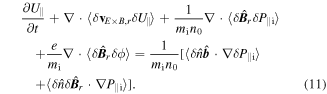
Here, 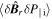 is known as the kinetic stress [26, 27] and it is somewhat analogous to the kinetic dynamo physics which is a transport process of electron parallel momentum (current) [27, 28]. The kinetic stress was experimentally identified to drive the intrinsic parallel plasma flow in MST [26].
is known as the kinetic stress [26, 27] and it is somewhat analogous to the kinetic dynamo physics which is a transport process of electron parallel momentum (current) [27, 28]. The kinetic stress was experimentally identified to drive the intrinsic parallel plasma flow in MST [26]. 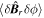 is the cross Maxwell stress, which was also presented in [29]. Both kinetic stress and cross Maxwell stress are surface force since they enter the parallel flow equation via their divergence. This is similar to the usual Reynolds stress
is the cross Maxwell stress, which was also presented in [29]. Both kinetic stress and cross Maxwell stress are surface force since they enter the parallel flow equation via their divergence. This is similar to the usual Reynolds stress 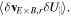 While, the turbulent acceleration on the right hand side of equation (11) is an effective volume-force, because it cannot be recast into the divergence of stress term.
While, the turbulent acceleration on the right hand side of equation (11) is an effective volume-force, because it cannot be recast into the divergence of stress term. 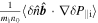 is the turbulent acceleration driven by parallel gradient of ion pressure fluctuation, which has been investigated for electrostatic turbulence as mentioned above.
is the turbulent acceleration driven by parallel gradient of ion pressure fluctuation, which has been investigated for electrostatic turbulence as mentioned above. 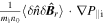 is a new turbulent acceleration related to the correlation between density and magnetic fluctuations and the equilibrium ion pressure gradient as well. Combining these two terms, the total electromagnetic turbulent acceleration can be rewritten as
is a new turbulent acceleration related to the correlation between density and magnetic fluctuations and the equilibrium ion pressure gradient as well. Combining these two terms, the total electromagnetic turbulent acceleration can be rewritten as  which represents the correlation between density fluctuation and perturbed pressure gradient along the total magnetic field.
which represents the correlation between density fluctuation and perturbed pressure gradient along the total magnetic field.
Quasilinear estimates of all the intrinsic rotation drive can be calculated for the typical parameters of the pedestal top region on DIII-D where the dominant instability is electromagnetic ITG turbulence [30]. The total stress force can be written as
and the total turbulent acceleration is

Here,  is the scale length of the radial variation of the stresses and
is the scale length of the radial variation of the stresses and  is the electrostatic residual stress mentioned in section 2.1.
is the electrostatic residual stress mentioned in section 2.1.  for the typical parameters of the pedestal top region on DIII-D with
for the typical parameters of the pedestal top region on DIII-D with  and the terms related to
and the terms related to  come from electromagnetic effects. From equations (12) and (13), we can see that the electromagnetic effects can reduce the electrostatic stress force and even reverse it, but enhance the turbulent acceleration, and the total turbulent acceleration is comparable to the total stress force. Therefore, taking into account the electromagnetic effects and the turbulent acceleration is important for more accurate understanding and prediction of intrinsic rotation in pedestal region.
come from electromagnetic effects. From equations (12) and (13), we can see that the electromagnetic effects can reduce the electrostatic stress force and even reverse it, but enhance the turbulent acceleration, and the total turbulent acceleration is comparable to the total stress force. Therefore, taking into account the electromagnetic effects and the turbulent acceleration is important for more accurate understanding and prediction of intrinsic rotation in pedestal region.
Now, we discuss some possible relevant experimental observations. In the MST, the kinetic stress related to density fluctuations 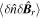 was directly measured [26], so the turbulent acceleration related to the kinetic stress (i.e.,
was directly measured [26], so the turbulent acceleration related to the kinetic stress (i.e., 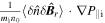 ) can be also easily obtained there. This turbulent acceleration
) can be also easily obtained there. This turbulent acceleration 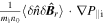 can provide counter-current rotation drive for normal ion pressure profile
can provide counter-current rotation drive for normal ion pressure profile 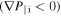 and positive kinetic stress. Taking this turbulent acceleration into account in the intrinsic flow drive of MST will lead to the reversal point of flow drive closer to that of the plasma parallel flow [26], which may result in better agreement between the intrinsic flow drive and the observed parallel flow profile.
and positive kinetic stress. Taking this turbulent acceleration into account in the intrinsic flow drive of MST will lead to the reversal point of flow drive closer to that of the plasma parallel flow [26], which may result in better agreement between the intrinsic flow drive and the observed parallel flow profile.
4. Turbulent acceleration and momentum conservation
As mentioned above, turbulent acceleration is obtained by decoupling density from the gyrocenter parallel momentum density equation and then taking flux average of flow velocity, i.e.,

Besides, there is an alternative method to derive the mean parallel flow velocity equation by taking flux average of the gyrocenter parallel momentum density first, and then decoupling flow velocity and density as follows
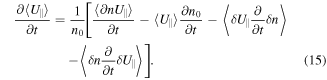
Through equations (14) and (15), we can obtain the same mean field equation of the parallel flow velocity (i.e., equation (11)) regardless of the sequence of taking flux average and decoupling the parallel flow from parallel momentum density [16]. Therefore, the presence of the turbulent acceleration does not result from regrouping terms as one may wonder.
By taking summation of gyrocenter momentum density equation over both species and using quasi-neutrality condition for electron density 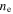 and ion gyrocenter density
and ion gyrocenter density 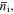 i.e.,
i.e., 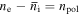 with
with 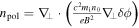 being ion polarization density, we can obtain the gyrocenter momentum conservation equation after some algebra [16]
being ion polarization density, we can obtain the gyrocenter momentum conservation equation after some algebra [16]
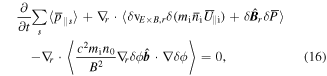
where s includes ions and electrons,  =
=  with
with 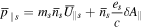 being the gyrocenter canonical parallel momentum of one species including the ordinary gyrocenter kinematic momentum and the gyrocenter magnetic vector momentum. The ordinary kinematic momentum carried by electrons was neglected because of small electron mass as compared to ion mass
being the gyrocenter canonical parallel momentum of one species including the ordinary gyrocenter kinematic momentum and the gyrocenter magnetic vector momentum. The ordinary kinematic momentum carried by electrons was neglected because of small electron mass as compared to ion mass 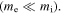
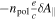 is the total gyrocenter magnetic vector momentum resulting from the ion polarization density
is the total gyrocenter magnetic vector momentum resulting from the ion polarization density  Then, we obtain the conservation equation of the total gyrocenter canonical parallel momentum carried by ions and electrons. The terms under the divergence are radial flux of the ion gyrocenter parallel kinematic momentum, total kinetic stress and electric Maxwell stress, respectively. By using the relationship between total gyrocenter magnetic vector momentum and the electromagnetic fields momentum
Then, we obtain the conservation equation of the total gyrocenter canonical parallel momentum carried by ions and electrons. The terms under the divergence are radial flux of the ion gyrocenter parallel kinematic momentum, total kinetic stress and electric Maxwell stress, respectively. By using the relationship between total gyrocenter magnetic vector momentum and the electromagnetic fields momentum
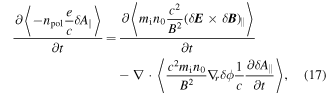
equation (16) can be rewritten as
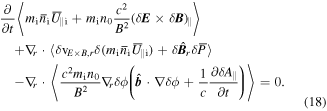
This is another conservative format of momentum which is the total gyrocenter parallel momentum density including the ion gyrocenter kinematic momentum and electromagnetic fields momentum. The pieces under the divergence are radial flux of the ion gyrocenter kinematic momentum, total kinetic stress, and electric Maxwell stress including both parallel electrostatic field and inductive electric field.
These two gyrocenter momentum conservation equations mentioned above (i.e., equations (16) and (18)) are equivalent. We can see that the conserved quantity can be either the total gyrocenter parallel canonical momentum carried by both species or the total gyrocenter parallel momentum including the ion gyrocenter kinematic momentum and the electromagnetic fields momentum, but not the ion parallel kinematic momentum or the ion parallel flow velocity. Hence, the turbulent acceleration-the local source or sink of the mean ion parallel flow does not imply that the momentum conservations is broken [16].
5. Summary and discussions
A new mechanism for the origin of intrinsic rotation named turbulent acceleration has been discovered. It cannot be written as a divergence of stress term and acts as the local source or sink of parallel rotation. The order of magnitude of turbulent acceleration is comparable to that of the divergence of residual stress which is also thought to be the origin of intrinsic rotation in previous works. Therefore, the turbulent acceleration is significant for intrinsic rotation. The co-current acceleration driven by electrostatic ITG turbulence vanishes after mode transition to CTEM turbulence, which qualitatively agrees with experimental observations. An extension to electromagnetic ITG turbulence has also been investigated, showing that the electromagnetic effects are important for both stress force and turbulent acceleration. We have derived two equivalent equations of momentum conservation and discussed the conserved quantity corresponding to the axisymmetry of tokamak plasmas. We clarified that the turbulent acceleration does not contradict with momentum conservation law.
Our ongoing work is extending to toroidal geometry, such as considering kinetic ballooning mode, which is the dominant electromagnetic mode in the peaked gradient region of DIII-D pedestal plasmas [30]. Moreover, inspired by the investigation of intrinsic rotation (which is mainly carried by ions) driven by turbulence, we are also working on the intrinsic non-inductive current (which is mainly carried by electrons) driven by turbulence. This could be also important for tokamak performance, since the modification of current profile may affect the confinement and a variety of MHD instabilities.
Acknowledgments
These works are supported by National Natural Science Foundation of China (NSFC) under Contract Nos. 11675059 and 11305071, and the Ministry of Science and Technology of China under Contract No. 2013GB112002.


