ABSTRACT
Here we report on the significant role of a so far overlooked dynamical aspect, namely, a secular resonance between the dwarf planet Ceres and other asteroids. We demonstrate that this type of secular resonance can be the dominant dynamical factor in certain regions of the main asteroid belt. Specifically, we performed a dynamical analysis of the asteroids belonging to the (1726) Hoffmeister family. To identify which dynamical mechanisms are actually at work in this part of the main asteroid belt, i.e., to isolate the main perturber(s), we study the evolution of this family in time. The study is accomplished using numerical integrations of test particles performed within different dynamical models. The obtained results reveal that the post-impact evolution of the Hoffmeister asteroid family is a direct consequence of the nodal secular resonance with Ceres. This leads us to the conclusion that similar effects must exist in other parts of the asteroid belt. In this respect, the obtained results shed light on an important and entirely new aspect of the long-term dynamics of small bodies. Ceres' fingerprint in asteroid dynamics, expressed through the discovered secular resonance effect, completely changes our understanding of the way in which perturbations by Ceres-like objects affect the orbits of nearby bodies.
1. INTRODUCTION
Orbital resonances exist everywhere in the solar system, and play an essential role in the dynamics of small bodies. The synergy of fast and slow orbital angles produces a great assortment of resonant phenomena (Dermott & Murray 1981; Williams & Faulkner 1981; Milani & Knežević 1994; Nesvorný & Morbidelli 1998). Over the years numerous methods and models have been developed to interpret the complex dynamical environment of the main asteroid belt. It is well known that this region is sculpted by a web of mean-motion and secular resonances coupled with subtle non-gravitational forces (Gladman et al. 1997; Farinella & Vokrouhlický 1999; Bottke et al. 2006; Minton & Malhotra 2010; Novaković et al. 2010b). The implications of these effects on a large number of examples with unique dynamical characteristics have already been successfully described by existing dynamical models. It is, however, still not possible to explain or predict all the dynamics of the main asteroid belt.
There are two general types of orbital resonances in the solar system. The most intuitive type, referred to as mean-motion resonances, occurs when the orbital periods of an asteroid and of a perturber are nearly commensurate. The second type, called secular resonance, concerns slowly varying angles like the longitude of perihelion or the longitude of the ascending node.
Secular resonances may play a significant role in the long-term dynamical stability of a planetary system (Laskar 1989; Knežević et al. 1991; Michel & Froeschlé 1997), however until now studies related to the dynamics of small solar system objects considered only planets as important perturbers.
The role of the most massive asteroids in the asteroid dynamics is generally assumed to be small, and in most cases it is neglected. Still, it is known that perturbations arising from the most massive asteroids could be important in some situations. Being located relatively close to each other, the most important interaction between the most massive and the rest of the asteroids intuitively occurs during their mutual close encounters. The long-term effects of these encounters have been studied by many authors, typically aiming to explain the evolution of asteroid families (Nesvorný et al. 2002; Carruba et al. 2003, 2013; Novaković et al. 2010a; Delisle & Laskar 2012). Moreover, it was demonstrated by Christou & Wiegert (2012) that there are populations of asteroids in the 1/1 mean motion resonances with the two most massive objects in the main belt, namely, (1) Ceres and (4) Vesta.
Nevertheless, the importance of massive asteroids for secular dynamics and long-term chaotic diffusion is generally accepted to be negligible; thus, it has never been studied. In this paper, we show that this paradigm not only lacks justification, but it is actually incorrect. The results obtained here reveal that a nodal secular resonance with (1) Ceres, namely, , plays a key role in the dynamics of asteroids belonging to the Hoffmeister family.
2. METHODS AND RESULTS
The motivation for our work comes from the unusual shape of the Hoffmeister asteroid family (Milani et al. 2014) when projected on the proper orbital semimajor axis ap versus sine of proper orbital inclination plane (Figure 1). The distribution of family members as seen in this plane clearly suggests different dynamical evolution for the two parts of the family delimited in terms of semimajor axis. The part located at AU is dispersed, and seems to undergo significant evolution in inclination, contrary to that at AU, which looks much more condensed and practically shows no similar evolution. Our goal here is to reveal the mechanism responsible for the observed asymmetry.
Figure 1. Hoffmeister family in the space of proper orbital semimajor axis vs. sine of proper orbital inclination. Note the strange shape of the family in this plane, in particular the large dispersion in the sin(ip) direction of the part located at semimajor axis less than about 2.78 AU (denoted by a shaded area in this figure).
Download figure:
Standard image High-resolution imageAnalyzing the region around the Hoffmeister family we found a few potentially important dynamical mechanisms. The family is delimited in terms of semimajor axis by two mean motion resonances, the 3J-1S-1 three body resonance with Jupiter and Saturn at 2.752 AU, and the 5/2 J mean-motion resonance with Jupiter at 2.82 AU. Moreover, the region is crossed by the secular resonance, with g, s, and being the secular frequencies of the asteroid's and Saturn's orbits.
2.1. Numerical Simulations
2.1.1. Dynamical Model
To identify which ones, if any, among the different possible dynamical mechanisms are actually at work here, we performed a set of numerical integrations. For this purpose we employed the ORBIT9 integrator embedded in the multipurpose OrbFit package.4 The dynamical model includes the gravitational effects of the Sun and the four outer planets, from Jupiter to Neptune. It also accounts for the Yarkovsky thermal effect, a subtle non-gravitational force due to the recoil force of anisotropically emitted thermal radiation by a rotating body (Bottke et al. 2006), causing mainly a secular drift in the semimajor axis. The indirect effect of the inner planets is accounted for by applying a barycentric correction to the initial conditions.
Our simulations follow the long-term orbital evolution of test particles initially distributed randomly inside an ellipse determined by the Gauss equations. This ellipse corresponds to the dispersion of the Hoffmeister family members immediately after the breakup event, assuming an isotropic ejection of the fragments from the parent body.
The total number of particles used is 1678, the same as the number of asteroids we currently identified as members of the family. The family membership is determined utilizing the hierarchical clustering method and standard metric as proposed by Zappala et al. (1990).
For simplicity, the Yarkovsky effect is approximated in terms of a pure along-track acceleration, inducing on average the same semimajor axis drift speed as predicted from theory.5
Assuming an isotropic distribution of spin axes in space, to each particle we randomly assign a value from the interval , where is the estimated maximum of the semimajor axis drift speed due to the Yarkovsky force. The value of is determined using a model of the Yarkovsky effect developed by Vokrouhlický (1998, 1999), and assuming thermal parameters appropriate for regolith-covered C-type objects. In particular, we adopt values of = = 1300 for the surface and bulk densities (Carry 2012), Γ = 250 for the surface thermal inertia (Delbó & Tanga 2009), and  = 0.95 for the thermal emissivity parameter. In this way we found that for a body of D = 1 km in diameter is about AU Myr−1. Next, we select sizes of the test particles equal to sizes of the Hoffmeister family members, estimated using their absolute magnitudes provided by AstDys database6
, and geometric albedo of pv = 0.047 (Masiero et al. 2011). Finally, since the Yarkovsky effect scales as , the particle sizes are then used to calculate corresponding values of for each particle by scaling from the reference value for objects of D = 1 km.
= 0.95 for the thermal emissivity parameter. In this way we found that for a body of D = 1 km in diameter is about AU Myr−1. Next, we select sizes of the test particles equal to sizes of the Hoffmeister family members, estimated using their absolute magnitudes provided by AstDys database6
, and geometric albedo of pv = 0.047 (Masiero et al. 2011). Finally, since the Yarkovsky effect scales as , the particle sizes are then used to calculate corresponding values of for each particle by scaling from the reference value for objects of D = 1 km.
The orbits of the test particles are propagated for 300 Myr, which is a rough estimate of the age of the Hoffmeister family (Nesvorný et al. 2005; Spoto et al. 2015). Time series of mean orbital elements7 are produced using on-line digital filtering (Carpino et al. 1987). Then, for each particle we compute the synthetic proper elements (Knežević & Milani 2000) for consecutive intervals of 10 Myr. This allows us to study the evolution of the family in the space of proper orbital elements.
If our first dynamical model were complete we should be able to reproduce the current shape of the family. However, we found that the shape cannot be reproduced with the afore described model. In particular, in these simulations we observed only a dispersion of the semimajor axis caused by the Yarkovsky effect, but no evolution in inclination (Figure 2). This implies that neither mean-motion nor secular resonances involving the major outer planets are responsible for the strange shape of the Hoffmeister family.
Figure 2. Evolution of the Hoffmeister family in the space of proper orbital elements. The three panels show the distribution of the test particles after 5, 15, and 145 Myr of the evolution, from top to bottom, respectively. The orange dots represent the evolution of the particles within the dynamical model that includes the four giant planets, from Jupiter to Neptune, and accounts for the Yarkovsky effect. The dark green dots show the evolution when Ceres is added to the previous model. The vertical dashed lines mark the locations of mean motion resonances. The inclined blue lines denote the position of the secular resonance; the solid line refers to the center, and the dashed line refers to the approximate lower border of this resonance. Finally, the red dashed lines mark the approximate position of the secular resonance with Ceres. These plots clearly show very different dynamical evolutions of particles, depending whether or not Ceres is considered as a perturbing body. While after 5 Myr the two distributions are still quite similar, after 15 Myr a remarkable difference is visible, with green dots evolving along the resonance. The last snapshot corresponds to the distribution of the green dots after 145 Myr, very similar to the distribution of the real Hoffmeister's family members, indicating that this resonance is responsible for the strange shape of the family.
Download figure:
Standard image High-resolution imageIn order to clarify the situation we turned our attention to the inner planets, and their possible role in the evolution of the family. For a representative sample of about 200 test particles we repeated the above described simulations using a model with seven planets (from Venus to Neptune), which also includes the Yarkovsky thermal force. However, the seven-planet model did not give any different results, which remain practically the same as the one obtained within the model with the four outer planets only. Thus, obviously there is still something missing in the dynamical model.
2.1.2. Extended Dynamical Model
Being left with almost no other option, we turn our attention to asteroid (1) Ceres. Having a proper orbital semimajor axis of 2.767 AU, and therefore being inside the range covered by the family members, it seems to be the only remaining candidate. Hence, we again numerically integrated the same test particles, using the four-planet dynamical model but this time also including Ceres as a perturbing body.8
These new simulations already after about 150 Myr very nearly matched the current spreading of the family in the semimajor axis versus inclination plane, clearly implicating Ceres as the culprit for what we see today. The striking feature observed in these runs is a fast dispersion of orbital inclinations for objects with semimajor axis of about 2.78 AU. After 15 Myr of evolution the spread in sine of inclination is 3 times larger than the initial one, as can be seen in the middle panel in Figure 2.
2.1.3. Mechanism of Ceres Perturbations
The fact that the main perturber is Ceres raises a very important question. What is the exact mechanism by which Ceres is perturbing the members of the Hoffmeister family to such a high degree? The current paradigm suggests this may be the result of close encounters, or it might be the consequence of the 1/1 mean motion resonance with Ceres. However, our simulations undoubtedly show that none of these two mechanisms could explain the evolution of the family. Actually, we found that most of the evolution is taking place within a narrow range of the semimajor axis. However, this range does not correspond to the location of the 1/1 resonance with Ceres, neither is there any reason for close encounters to affect only objects within this specific range of semimajor axes. Moreover, it is very unlikely that these two effects would primarily affect orbital inclinations. Finally, regardless of the mechanism, such a large perturbation on asteroids caused by Ceres has never been observed in the asteroid belt. This situation motivates us to test some other mechanisms which are at work in this region, despite generally being accepted to be negligible. These are the secular resonances with asteroid Ceres.
Analyzing the secular frequencies of the Hoffmeister family members we immediately notice that some of these are very close to the nodal frequency of Ceres ( arcsec yr−1). This is an interesting fact because the secular resonances involving the nodal frequencies are known to affect mainly the orbital inclination.
To better understand the reasons for the dispersion in inclination, and to determine the possible role of the secular resonance with Ceres, we pick a few particles that experienced significant changes in inclination during our numerical simulations, and analyzed their behavior in more detail. This analysis identified a mechanism responsible for the evolution of orbital inclinations, revealing a completely new role of Ceres in asteroid dynamics.
As an illustration, in Figure 3 we show the evolution of one test particle. This particle was initially located at a semimajor axis of 2.788 AU, with its Yarkovsky induced drift set to be negative, forcing it to move toward the Sun. After about 65 Myr this particle enters the region where the fast dispersion in orbital inclination has been observed. During the time spent in this area, the particle's inclination has experienced a fast increase, with the average value jumping from about 4 4–4
4–4 9.
9.
Figure 3. Time evolution of the critical angle of the secular resonance (top) and the mean inclination (bottom) for one of the test particles. The correspondence of the time periods in which the critical angle is librating and the mean inclination is rapidly increasing (marked in both panels by the shaded area) clearly reveals the importance of the secular resonance with Ceres in asteroid dynamics in this part of the main asteroid belt. The solid black line shows the average of the mean inclination to better appreciate the evolution.
Download figure:
Standard image High-resolution imageLet us recall here that a resonance occurs when the corresponding critical angle librates.9 In the case of the secular resonance the critical angle is , where Ω and are the longitude of the ascending node of an asteroid and Ceres, respectively. Clearly, as can be seen in Figure 3, the period of increase in inclination exactly corresponds to the period of libration of the critical angle of the secular resonance. This correlation is a direct proof that this resonance is responsible for the evolution and observed spread in the orbital inclination for asteroids belonging to the Hoffmeister asteroid family. In Figure 2 we plotted the location of the resonance.
Though our numerical simulations clearly show that passing through the resonance may cause significant changes in orbital inclination, we further investigated the mechanism. A key to understanding the observed behavior are the cyclic oscillations in inclination for objects trapped inside this resonance (see Figure 4). In the scenario with the Yarkovsky effect included in the model, some of the objects are reaching the border of the while steadily drifting in semimajor axis, and enter it at random value of the inclination cycle. During the time spent inside the resonance their inclination is continuously repeating the cycles. However, as the semimajor axis is evolving due to the Yarkovsky effect, the objects must sooner or later reach the other border of the , and subsequently exit from the resonance. As the exit also happens at a random value of the inclination cycle, the values of orbital inclination with which bodies enter the cycle typically differ from those with which they exit. In this way the resonance changes the inclination of objects that cross it. Certainly, this mechanism would not work without the Yarkovsky effect.
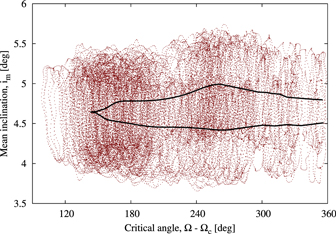
Figure 4. Variation of the mean orbital inclination im vs. the critical angle for the same test particle as shown in Figure 3. Note, however, that only the time interval when this particle is inside the resonance is shown, i.e., from about 66 to 85 Myr. During this time span, the inclination of the particle undergoes cyclic variations with two different periods. The first mode of these oscillations (red points) has a very short period of about 38 kyr; if averaged out, it reveals the second, long-period one (denoted by the black line), with a period of about 25 Myr. Note that the long period is actually associated with the libration of the critical angle. A similar situation was also observed for secular resonances with the major planets (see, e.g., Froeschlé et al. 1991).
Download figure:
Standard image High-resolution imageInterestingly, this process is very similar to the one observed inside another relatively weak secular resonance, namely, the , which affects members of the Koronis asteroid family (Bottke et al. 2001).
It is also worth mentioning that although passage across the secular resonance could result in a very fast change in orbital inclination, the total changes are limited and could not exceed the maximal variations. The amplitude of variations in orbital inclination is not the same for all objects, but it is generally similar to the one shown in Figure 4.
Moreover, we have found that our test particles typically spend 15–30 Myr inside the , before being moved outside by the Yarkovsky effect. Thus, as a libration period is very long (about 40 Myr), most of the particles spend less than one librating cycle inside this resonance (Figure 3).
Finally, let us re-examine the role of for the members of the Hoffmeister family. The results presented above clearly indicate that without Ceres in the model, the does not affect the family. Still, with Ceres included in the dynamical model may only affect a limited number of members. Our analysis has shown that about 5% of family members could reach this resonance after their inclination is pumped-up, at least a bit, by the resonance (see Figure 2). The orbital inclination of these objects is then additionally dispersed by , being the main reason for the slightly different distributions toward high and low inclinations. Moreover, although the analysis along this line is beyond the scope of the Letter, we noticed that the resonance also slightly affects the orbital eccentricity of family members.
Nevertheless, the role of the in the dynamical evolution of the Hoffmaister family members is minor compared to the role of the secular resonance. Thus, the evolution of the family is almost completely determined by the combined effect of the resonance and the Yarkovsky effect, and would be practically the same even if the is not that close.
3. CONCLUSIONS
This is the first time compelling evidence for orbital evolution of small bodies caused by a secular resonance with an asteroid has been found. We prove that the post-impact transformation of the Hoffmeister asteroid family is a direct consequence of the nodal secular resonance with Ceres. This result has very important repercussions for our view of how Ceres-size bodies affect the dynamics of nearby objects, and opens new possibilities to study such effects in the main asteroid belt and beyond. Examples include the dynamics of specific asteroid populations, the early phases of planetary formation, and extra-solar debris disks.
The authors would like to thank Aaron Rosengren for his comments and suggestions on the manuscript. This work has been supported by the European Union [FP7/2007-2013], project: STARDUST-the Asteroid and Space Debris Network. B.N. and Z.K. also acknowledge support by the Ministry of Education, Science and Technological Development of the Republic of Serbia, Project 176011. Numerical simulations were run on the PARADOX-III cluster hosted by the Scientific Computing Laboratory of the Institute of Physics Belgrade.
Footnotes
- 4
Available from http://adams.dm.unipi.it/orbfit/.
- 5
This model of the net Yarkovsky force is a reasonable approximation over short timescales, but may not be accurate enough in the long term, because the spin axis or the rotational period may change. The spin evolution of an asteroid not subject to collisions is expected to be dominated by the Yarkovsky–O'Keefe–Radzievskii–Paddack (YORP) effect (see, e.g., Rubincam 2000). The models predict that YORP torques may evolve bodies toward asymptotic rotational states (Čapek & Vokrouhlický 2004), or could cause reshaping that would significantly increase the time over which objects can preserve their sense of rotation (Cotto-Figueroa et al. 2015). This has implications for the Yarkovsky effect; however, the constant Yarkovsky drift we used here represents the long-term average of this effect. Regardless of the actual behavior of any single body, the average drift rate should be nearly constant for a large enough statistical sample.
- 6
- 7
The mean orbital elements are obtained by removal of the short-periodic perturbations from the instantaneous osculating elements.
- 8
In these simulations, for the mass of Ceres we used a value of , as estimated by Baer et al. (2011).
- 9
A libration is the oscillation of an angle around a fixed point, contrary to the circulation when the angle cycles over all values from 0° to 360°.