ABSTRACT
The plasma emission is the radiation mechanism responsible for solar type II and type III radio bursts. The first theory of plasma emission was put forth in the 1950s, but the rigorous demonstration of the process based upon first principles had been lacking. The present Letter reports the first complete numerical solution of electromagnetic weak turbulence equations. It is shown that the fundamental emission is dominant and unless the beam speed is substantially higher than the electron thermal speed, the harmonic emission is not likely to be generated. The present findings may be useful for validating reduced models and for interpreting particle-in-cell simulations.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Partial conversion of electrostatic wave energy to transverse electromagnetic (EM) wave energy during the late nonlinear stage of the bump-on-tail instability is called the plasma emission process, and the resultant radiation emission occurs at the plasma frequency and/or its harmonic(s). It is believed that the plasma emission is responsible for the solar type II and type III radio bursts (McLean & Labrum 1985; Goldman 1983; Melrose 1986). According to the standard theoretical paradigm, based upon the first theory proposed in the 1950s (Ginzburg & Zheleznyakov 1958), an electron beam interacting with the background plasma excites Langmuir (L) waves via the bump-on-tail instability, followed by nonlinear processes of wave decay and scattering, eventually leading to the generation of EM radiation.
Such an elaborate process can, in principle, be demonstrated on the basis of EM weak turbulence theory—the fundamental equations thereof and their derivation can be found, e.g., in (Yoon 2006; Yoon et al. 2012; Ziebell et al. 2014b). Indeed, over the past several decades, the physics of plasma emission was discussed within the framework of reduced or partial EM weak turbulence theory (McLean & Labrum 1985; Goldman 1983; Melrose 1986; Robinson & Cairns 1998a, 1998b, 1998c; Li et al. 2008a, 2008b, 2009). However, the complete numerical solution of the entire set of EM weak turbulence equations has not been done hitherto. Instead, various approximations and simplifications have been made, which include the assumption of saturated wave amplitudes, predetermination of certain nonlinear processes being the most important, reduction of the equations to one-dimensional (1D) models, etc.
The above comments are not meant to diminish the value of reduced theories, however, as some of these theories, especially those of Li et al. (2008a, 2008b, 2009) and Schmidt & Cairns (2014), have advanced to the point where simple, yet reliable, plasma emission models are incorporated into macroscopic models so as to yield global-kinetic models with predictive capabilities. Nevertheless, since reduced models are based upon various assumptions, it is difficult to quantify the validity of such approaches unless there exists a benchmark full numerical solution. The present Letter reports the first ever complete numerical solutions of the EM weak turbulence equations in the presence of a beam, and the ensuing plasma emission. On the basis of the present results, detailed verification of various approximate theories can be done, but such a task is not the immediate focus of the present work.
One of the outstanding problems in the theory of plasma emission is whether the radiation is at the plasma frequency (fundamental emission) or at the first harmonic of the plasma frequency (harmonic emission). Reduced theories cannot determine the relative importance of the two emission bands.
Before we proceed, it should be mentioned that a handful of authors carried out direct EM particle-in-cell (PIC) simulations in order to characterize the nonlinear behavior of the plasma emission process (Kasaba et al. 2001; Rhee et al. 2009a, 2009b). The present full solution of EM weak turbulence equations is complementary to PIC simulation efforts.
2. THEORETICAL FORMULATION
The wave intensities for plasma normal modes are defined by their electric field energy. For longitudinal modes, the intensities 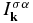 for α = L, S, where L and S stand for Langmuir and ion sound, respectively, are defined by
for α = L, S, where L and S stand for Langmuir and ion sound, respectively, are defined by
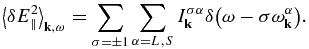
The transverse mode T has both electric and magnetic fields, but it is sufficient to define the spectral wave intensity in terms of electric field,
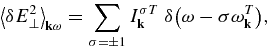
as the magnetic field intensity is trivially given by 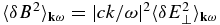 . The linear dispersion relations for electrostatic (Langmuir L and ion-sound S) and transverse EM (T) modes are given by
. The linear dispersion relations for electrostatic (Langmuir L and ion-sound S) and transverse EM (T) modes are given by
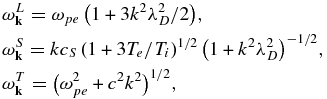
where ωpe = (4πnee2/me)1/2 is the plasma frequency, ne, e, and me being the electron number density, unit electric charge, and electron mass, respectively, λD = [Te/(4πnee2)]1/2 is the Debye length, Te and Ti are electron and ion temperatures, respectively, and cS = (Te/mi)1/2 represents the ion-sound speed, mi being the ion (proton) mass. The L mode wave kinetic equation is given by
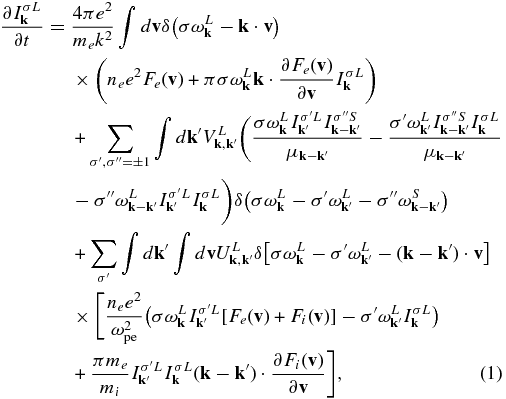
where

The first velocity integral term on the right-hand side of Equation (1) that contains the resonance factor 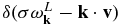 (i.e., linear wave-particle interaction) represents the spontaneous and induced emissions of L waves, which are essentially quasilinear processes; the second k'-integral term dictated by the three-wave resonance condition
(i.e., linear wave-particle interaction) represents the spontaneous and induced emissions of L waves, which are essentially quasilinear processes; the second k'-integral term dictated by the three-wave resonance condition 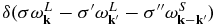 (nonlinear three-wave interaction) represents the decay/coalescence involving L mode with another L mode and an S mode; the double integral term ∫dv∫dk'⋅⋅⋅ dictated by the nonlinear wave-particle resonance condition
(nonlinear three-wave interaction) represents the decay/coalescence involving L mode with another L mode and an S mode; the double integral term ∫dv∫dk'⋅⋅⋅ dictated by the nonlinear wave-particle resonance condition ![$\delta [\sigma \omega _{\bf k}^L-\sigma ^{\prime }\omega _{{\bf k}^{\prime }}^L -({\bf k}-{\bf k}^{\prime })\cdot {\bf v}]$](https://content.cld.iop.org/journals/2041-8205/795/2/L32/revision1/apjl503632ieqn5.gif) represents the spontaneous and induced scattering processes involving two Langmuir waves and the particles.
represents the spontaneous and induced scattering processes involving two Langmuir waves and the particles.
For the ion-sound mode, α = S, the wave kinetic equation is given by
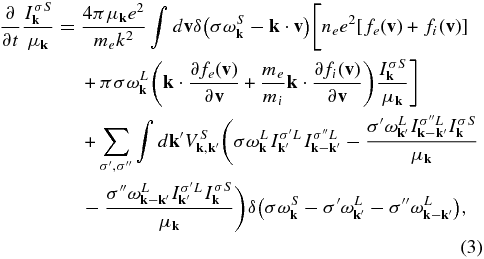
where
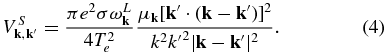
The first velocity integral term on the right-hand side of Equation (3) that contains the resonance factor  represents the spontaneous and induced emissions of S waves. The k'-integral term dictated by the three-wave resonance condition
represents the spontaneous and induced emissions of S waves. The k'-integral term dictated by the three-wave resonance condition  corresponds to the decay/coalescence involving S mode with two L modes.
corresponds to the decay/coalescence involving S mode with two L modes.
For the transverse mode T, the wave kinetic equation is given by
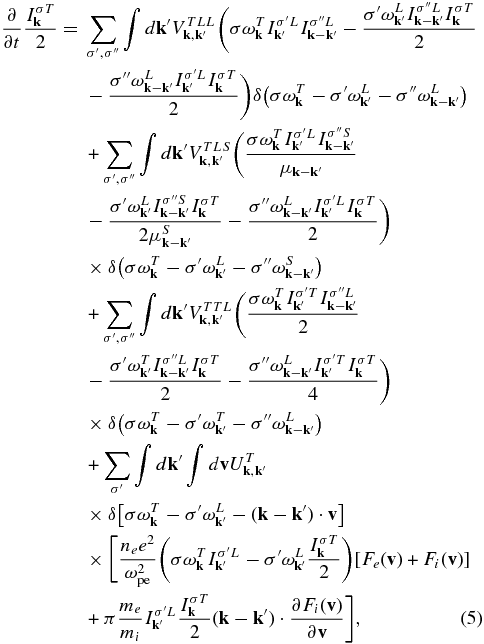
where the elements of the interaction matrix are
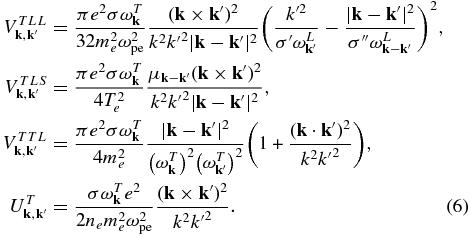
The first k'-integral terms in Equation (5) dictated by the three-wave resonance condition 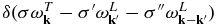 represents the coalescence of two L modes into a T mode at the second harmonic plasma frequency. This process is responsible for the harmonic emission (T↔L + L). The next k' integrals associated with the factor
represents the coalescence of two L modes into a T mode at the second harmonic plasma frequency. This process is responsible for the harmonic emission (T↔L + L). The next k' integrals associated with the factor  describe the merging of L and S modes into a T mode at the fundamental plasma frequency. This is one of the processes responsible for the fundamental emission (T↔L + S). The third k' integrals with
describe the merging of L and S modes into a T mode at the fundamental plasma frequency. This is one of the processes responsible for the fundamental emission (T↔L + S). The third k' integrals with 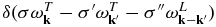 depict the merging of a T mode and an L mode into the next higher harmonic T mode. This process, known as the incoherent Raman scattering, is responsible for generating higher-harmonic plasma emission (T↔T + L). The double integral term ∫dv∫dk'⋅⋅⋅ dictated by the nonlinear wave-particle resonance condition
depict the merging of a T mode and an L mode into the next higher harmonic T mode. This process, known as the incoherent Raman scattering, is responsible for generating higher-harmonic plasma emission (T↔T + L). The double integral term ∫dv∫dk'⋅⋅⋅ dictated by the nonlinear wave-particle resonance condition ![$\delta [\sigma \omega _{\bf k}^T-\sigma ^{\prime }\omega _{{\bf k}^{\prime }}^L -({\bf k}-{\bf k}^{\prime })\cdot {\bf v}]$](https://content.cld.iop.org/journals/2041-8205/795/2/L32/revision1/apjl503632ieqn11.gif) represents spontaneous and induced scattering processes involving T and L modes and the particles, largely dominated by thermal protons (T↔p + L), but also electrons (T↔e + L). This process represents an alternative mechanism for the fundamental emission.
represents spontaneous and induced scattering processes involving T and L modes and the particles, largely dominated by thermal protons (T↔p + L), but also electrons (T↔e + L). This process represents an alternative mechanism for the fundamental emission.
Finally, the formal particle kinetic equation is given by
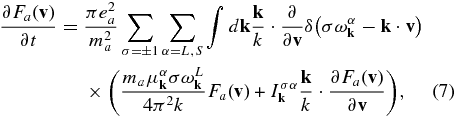
where a = i, e stands for ions and electrons, respectively, and 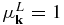 and
and 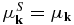 .
.
3. NUMERICAL ANALYSIS
We developed a sophisticated numerical routine termed the EM weak turbulence simulation code to solve the complete set of Equations (1)–(7) in a self-consistent manner. It adopts the normalized time, ωpet, dimensionless wave frequency and wave vector, ω/ωpe and kvth/ωpe, where vth corresponds to the thermal speed associated with the background electrons, and dimensionless velocity vector, v/vth. The spectral wave intensity is defined by

where  ,
,  , as noted before,
, as noted before, 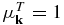 , and
, and ![$g=1/[2^{3/2}(4\pi)^2n_e\lambda _D^3]$](https://content.cld.iop.org/journals/2041-8205/795/2/L32/revision1/apjl503632ieqn17.gif) is related to the customary plasma parameter,
is related to the customary plasma parameter, 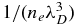 , which is taken to be 5 × 10−3. Of course, in the actual heliospheric environment, this number should be much smaller, on the order of 10−8 or so, but we adopted an unrealistically high value of the plasma parameter in order to facilitate the numerical procedure, since a realistically small number would bring the initial wave level to a tiny value, delaying the linear growth, and therefore the overall evolution.
, which is taken to be 5 × 10−3. Of course, in the actual heliospheric environment, this number should be much smaller, on the order of 10−8 or so, but we adopted an unrealistically high value of the plasma parameter in order to facilitate the numerical procedure, since a realistically small number would bring the initial wave level to a tiny value, delaying the linear growth, and therefore the overall evolution.
We solved the complete set of equations for initial configuration in which the ions are considered stationary and distributed according to the thermal equilibrium model with temperature Ti, and the electrons are composed of an isotropic thermal background plus a Gaussian distribution of a streaming component. The initial drift speed of the beam is denoted by Vb, and the temperature of the background electrons are designated by Te. The ratio of the beam electron density nb and the background electron density n0 is assumed to be nb/n0 = 10−3, and the beam is assumed to propagate in the z direction. The Gaussian thermal spread associated with the beam is taken to be the same as that of the background electron thermal speed, and we assume that the ion-to-electron temperature ratio is Ti/Te = 1/7. The discretized time step for numerical computation is chosen as  , and we use two-dimensional (2D) velocity and wave number space, −12 < (vx/vth, vz/vth) < 12, where vth = (2T/me)1/2 is the electron thermal speed, and 0 < (kxvth/ωpe, kzvth/ωpe) < 0.6. We carried out a 2D numerical analysis since the plasma emission cannot take place in a 1D system. It should be noted that the present 2D approach captures all the necessary physics, and may be largely equivalent to a fully three-dimensional situation with a cylindrical symmetry. Finally, in the present EM weak turbulence theory, the ratio of electron thermal speed to the speed of light in vacuo must be prescribed. For the present purpose, we consider
, and we use two-dimensional (2D) velocity and wave number space, −12 < (vx/vth, vz/vth) < 12, where vth = (2T/me)1/2 is the electron thermal speed, and 0 < (kxvth/ωpe, kzvth/ωpe) < 0.6. We carried out a 2D numerical analysis since the plasma emission cannot take place in a 1D system. It should be noted that the present 2D approach captures all the necessary physics, and may be largely equivalent to a fully three-dimensional situation with a cylindrical symmetry. Finally, in the present EM weak turbulence theory, the ratio of electron thermal speed to the speed of light in vacuo must be prescribed. For the present purpose, we consider  . In the low corona of the Sun, the typical electron thermal energy is ∼102 eV; thus, the present choice is approximately equal to the coronal value.
. In the low corona of the Sun, the typical electron thermal energy is ∼102 eV; thus, the present choice is approximately equal to the coronal value.
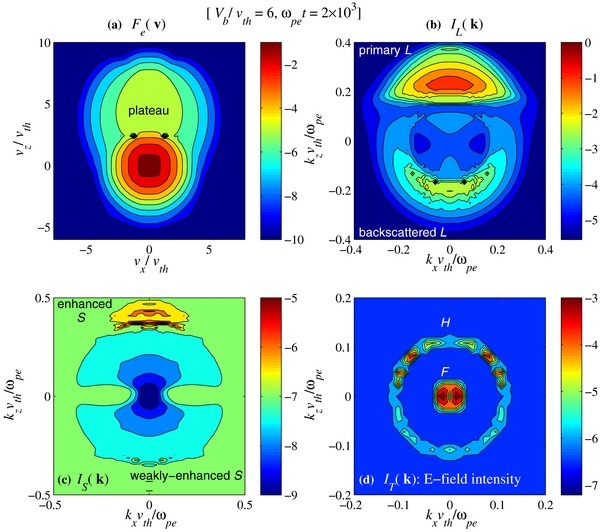
In Figure 1, we showcase a typical numerical result. For this case, we considered the initial beam speed Vb/vth = 6, and have numerically integrated the complete equations up to the normalized time step ωpet = 2 × 103. The description can be found in the figure caption. The electron distribution function shown in Figure 1(a) features a broad range of velocity-space plateau in the velocity space initially occupied by a beam, which is a result of quasilinear diffusion. The Langmuir turbulence spectrum in Figure 1(b) shows an enhanced forward-propagating component (the primary L), which is the result of initial bump-on-tail instability, and the backscattered component, which is the result of combined three-wave decay and nonlinear wave-particle interaction. Note that the morphology of the 2D L mode spectrum compares favorably with the simulated spectrum—see, e.g., Figure 2 of Rhee et al. (2009b). Nonlinear decay processes generate the ion-sound mode by decay instability, as indicated in Figure 1(c) by the "enhanced" and "weakly enhanced" range of 2D k space. Panel (d) of Figure 1 is the transverse EM mode spectrum. We plot the electric field intensity associated with the radiation, IT(k). The small k (or long wavelength) regime corresponds to the fundamental (F) emission near ωpe, while the outer ring corresponds to the harmonic (H) emission with frequency in the vicinity of 2ωpe. In short, the present Letter reports the first ever theoretical demonstration of F/H pair emission starting from the beam-plasma instability, by allowing all the relevant nonlinear processes to operate. This is in contrast to other related works, e.g., (Li et al. 2008a, 2008b, 2009), where simplified approaches are taken at the outset. Our rigorous numerical solutions are comparable to the full PIC simulations (Kasaba et al. 2001; Rhee et al. 2009a, 2009b), and indeed we find that the comparison with simulation results is favorable. For instance, the present Figure 1(d) can be compared against the simulated radiation spectral pattern, e.g., Figures 3 and 4 of Rhee et al. (2009b). Upon visual inspection of the present Figure 1(d) and the simulated radiation pattern, it is quite obvious that the agreement is excellent. This shows that the present weak turbulence simulation is a reliable research tool for quantitative investigations of plasma emission phenomena, yet it is computationally much more efficient when compared with the full PIC code scheme.
Figure 1. Panel (a) depicts the electron distribution function Fe vs. vx/vth and vz/vth; panel (b) shows the Langmuir wave spectral intensity IL(k) vs. kxvth/ωpe and kzvth/ωpe; panel (c) plots the wave spectral intensity corresponding to the ion-sound mode, IS(k); and panel (d) is the transverse mode electric field spectrum IT(k). The above results are at normalized time ωpet = 2 × 103, with the initial condition Vb/vth = 6. Other input parameters are described in the text.
Download figure:
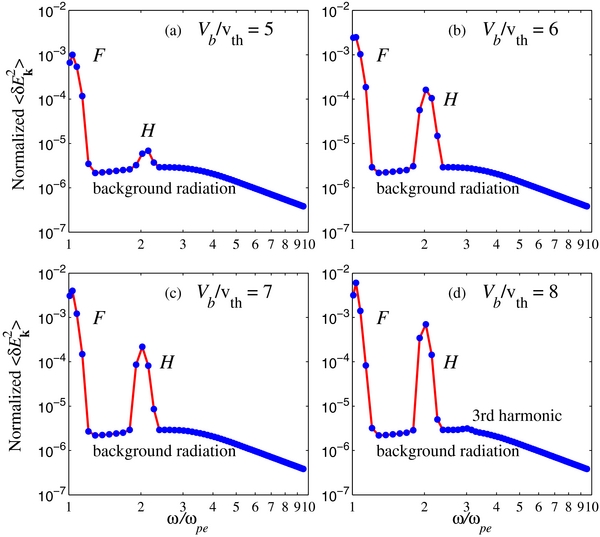
Standard image High-resolution imageWe have repeated the self-consistent calculations for other parameters, but in Figure 2, we choose to show the angle-averaged electric field spectrum (in normalized form) versus the frequency ω/ωpe, for four different initial beam speeds, while other input parameters are held constant as in Figure 1. For Vb/vth = 5, Figure 2 shows that the F emission completely dominates over H emission, but as the normalized beam speed increases to Vb/vth = 6 we observe that the H component becomes more apparent. Proceeding to higher beam velocities, one can discern that the H component becomes progressively more intense, but it never becomes higher than the F component. Note that for the case of Vb/vth = 8, there is a small, barely visible, enhancement at the third harmonic, ω ≃ 3ωpe. This is the result of the incoherent Raman process, T↔T + L, that generates higher harmonics. However, as one can see, the third-harmonic peak is extremely low so that, in general, higher harmonic plasma emission is not expected to be a common feature, which is consistent with observations. Also note that the transverse EM radiation at the plasma frequency and its harmonic takes place over a background level, as indicated in Figure 2. The theory of the background radiation for isotropic plasma in the absence of the beam was recently put forth by the present authors (Ziebell et al. 2014a), and it is supported by results obtained from PIC simulations (Ziebell et al. 2014b). It is this background level of radiation that partially hides the harmonic emission peak in the case of Vb/vth = 5. The theory of background radiation (Ziebell et al. 2014b) is based upon the nonlinear wave-particle interaction, which some reduced theories have ignored at the outset (Li et al. 2008a, 2008b, 2009). Judging from Figure 2(a), under certain conditions, one might obtain false H emission if one does not take the background radiation into account.
Figure 2. Panel (a) shows the normalized electric field intensity 〈δE2(k)〉 vs. normalized frequency ω/ωpe for initial beam speed Vb/vth = 5; panel (b) corresponds to Vb/vth = 6; panel (c) corresponds to Vb/vth = 7; and panel (d) is the case of high beam speed, Vb/vth = 8. The above results are for normalized time ωpet = 2 × 103.
Download figure:
Standard image High-resolution image4. FINAL REMARKS
To summarize, despite many decades of theoretical research on the plasma emission, the actual numerical solution of the equations of EM weak turbulence theory that forms the basis of the plasma emission had not been available in the literature. In the absence of exact numerical solution, it is difficult to quantitatively verify the validity of various approximate models. The present Letter reports the first ever complete numerical solution of electromagnetic weak turbulence equations with which, the validity of various approximate theories (Li et al. 2008a, 2008b, 2009; Schmidt & Cairns 2014) can be tested, and it may also be employed to interpret the PIC simulations (Kasaba et al. 2001; Rhee et al. 2009a, 2009b). However, such a task is beyond the scope of the present work. One of the most interesting findings according to our complete numerical solutions is that the plasma emission must be dominated by the fundamental emission, and that the presence of harmonic emission may imply high average beam velocities. In fact, weak harmonic emission may be obscured by the background EM emission, which implies that if our numerical example is the norm, then most of the plasma emission has to take place at the fundamental plasma frequency. We should caution that this conclusion is based upon the weak turbulence paradigm. Alternative models of plasma emission, e.g., one that is based upon the concept of strong turbulence (Robinson, 1997), are not the focus of the present Letter.
This work has been partially supported by the Brazilian agencies CNPq and FAPERGS. P.H.Y. acknowledges NSF grant AGS1242331 and the BK21 plus grant from the National Research Foundation (NRF) of the Republic of Korea.