Abstract
We introduce a new family of nondiffracting full Poincaré beams based on a superposition of nondiffracting Mathieu beams, which we call the Mathieu–Poincaré beams (MPBs). We studied the polarization structure of the MPBs and how it is traced on the Poincaré sphere, and found that the first region mapping the Poincaré sphere is contained within an ellipse of circular polarization of constant size for all beam orders m for a given semi-focal distance and as expected a higher order 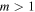 beam covers the Poincaré sphere m-fold in a nonuniform way given the noncircular symmetry of the Mathieu beams. Finally, we looked into the polarization singularities along the inter-focal line and observed that the all
beam covers the Poincaré sphere m-fold in a nonuniform way given the noncircular symmetry of the Mathieu beams. Finally, we looked into the polarization singularities along the inter-focal line and observed that the all  -points have a star (lemon) morphology for even (odd) beam order m when we used positive helical Mathieu beams to synthesize the MPBs, and that this relationship is reversed when we switched to a negative helical Mathieu beam.
-points have a star (lemon) morphology for even (odd) beam order m when we used positive helical Mathieu beams to synthesize the MPBs, and that this relationship is reversed when we switched to a negative helical Mathieu beam.
Export citation and abstract BibTeX RIS
1. Introduction
By itself, the polarization ellipse is an excellent way to visualize polarized light. However, except for the degenerate polarization states, it is impossible to determine the orientation and ellipticity angles by viewing the polarization ellipse without additional information. Hence, the Stokes parameters have played a central role in the description and measurement of optical polarization for many years. The projection of the Stokes parameters onto a sphere to represent polarized light, the Poincaré sphere, is a useful way to visualize polarization states. In such a sphere, all linear polarization states lie on the equator, while the left (positive) and right (negative) circular polarization states are located at the north and south poles, respectively. Elliptically polarized states are represented everywhere else on the surface of the Poincaré sphere. Since a single point on the Poincaré sphere represents a single unique state of polarization, optical beams with uniform polarization can be said to be entirely contained in such a point on the surface of the sphere regardless of their transverse intensity distribution.
On the other hand, optical beams which have a spatial mode that correlates spatial coordinates with states of polarization can not be mapped into a single point on the Poincaré sphere, hence they are called Poincaré beams. The state of polarization may vary along one coordinate, such as radial and azimuthal vector beams [1], or it may depend on the two transverse coordinates. The second case, where the state of polarization varies in both coordinates in such a way that the beam has all states of polarization as represented on the Poincaré sphere, is known as a full Poincaré (FP) beam [2–5]. FP beams are usually built from a superposition of Laguerre–Gauss beams [6], and more recently using nondiffracting Bessel beams [7].
Poincaré beams are of particular interest to the optical community because they contain so-called polarization singularities. These are points in space, surfaces and lines in three-dimensions, lines and points in two-dimensions, where there are dislocations of the electromagnetic field [8–10]. The research on polarization singularities was first introduced by Nye [11, 12] and Hajnal [13], and more recently they have been studied by methods such as propagating light through inhomogeneous birefringent media [14, 15], and by synthesizing Poincaré beams via superposition of both vortex and vector beams [16–19].
In this work we introduce a new family of nondiffracting FP beam based on a superposition of nondiffracting Mathieu beams, namely a Mathieu–Poincaré beam (MPB). We study the polarization structure of the MPBs and how it is traced on the surface of the Poincaré sphere. Since the MPBs span an infinite number of Poincaré spheres, we concentrate on the first mapping region surrounding the propagation axis of the beams. Finally, we look into the polarization singularities found in the polarization structure of the beams and how their morphology changes as a function of the beam parameters. To the best of our knowledge, this is the first time a family of elliptic full Poincaré beams have been studied, and the behavior of the number and morphology of polarization singularities as a function of the order and helicity of the beams has been characterized.
2. Nondiffracting MPBs
In order to define the MPBs, we first briefly describe the nondiffracting Mathieu beams to introduce notation. Nondiffracting Mathieu beams are one of the fundamental families of nondiffracting beams [20–22]. Mathieu beams occur when we solve the Helmholtz equation in elliptic cylindrical coordinates (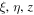 ), where ξ and η are the radial and angular elliptic coordinates respectively, and z is the propagation axis. Solving the Helmholtz equation yields two linearly independent solutions of the first kind, which are given by
), where ξ and η are the radial and angular elliptic coordinates respectively, and z is the propagation axis. Solving the Helmholtz equation yields two linearly independent solutions of the first kind, which are given by

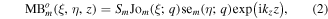
where m is the order of the Mathieu beam, 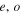 stand for even and odd respectively, Jem(.) and Cem(.) are the even radial and angular Mathieu functions, Jom(.) and sem(.) are the odd radial and angular Mathieu functions, Cm and Sm are balancing constants needed to ensure both modes carry equal power,
stand for even and odd respectively, Jem(.) and Cem(.) are the even radial and angular Mathieu functions, Jom(.) and sem(.) are the odd radial and angular Mathieu functions, Cm and Sm are balancing constants needed to ensure both modes carry equal power, 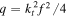 is a continuous parameter which controls the ellipticity of the beam, f is the semi-focal distance, and kt and kz are the transverse and longitudinal components of the wave vector
is a continuous parameter which controls the ellipticity of the beam, f is the semi-focal distance, and kt and kz are the transverse and longitudinal components of the wave vector 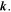 For even Mathieu beams
For even Mathieu beams  whereas
whereas  for odd Mathieu beams. From this point on we omit the propagation term
for odd Mathieu beams. From this point on we omit the propagation term 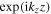 since it only introduces a global phase on the beams.
since it only introduces a global phase on the beams.
Neither of these solutions are able to transfer orbital angular momentum (OAM), but combining (1) and (2) we can construct helical Mathieu beams which actually can transfer OAM,
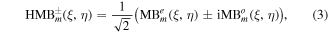
where the +(−) superscript denotes positive (negative) phase rotation. Given the possible values of the order m for even and odd Mathieu beams, helical Mathieu beams can only exist for orders 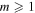 [23, 24].
[23, 24].
We define a nondiffracting MPB as a superposition of two nondiffracting helical Mathieu beams of different orders on two orthogonal polarizations. For this work we fix the order of one of the beams to zero, making it an even Mathieu beam, and we write the MPB as
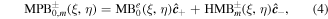
where 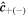 is the unit vector for positive (negative) circular polarization. We use the circular polarization basis
is the unit vector for positive (negative) circular polarization. We use the circular polarization basis 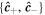 since regular and Bessel FP beams built with it constitute perfect stereographic projections of the Poincaré sphere which fix the position of one of the poles of the sphere, i.e. a C-point polarization singularity, to the origin of the transverse plane. Although using the linear polarization basis
since regular and Bessel FP beams built with it constitute perfect stereographic projections of the Poincaré sphere which fix the position of one of the poles of the sphere, i.e. a C-point polarization singularity, to the origin of the transverse plane. Although using the linear polarization basis  is also a stereographic projection of the Poincaré sphere, the position of the poles of circular polarization are off-axis, and rotate around the beam axis during propagation for regular FP beams [4].
is also a stereographic projection of the Poincaré sphere, the position of the poles of circular polarization are off-axis, and rotate around the beam axis during propagation for regular FP beams [4].
Figure 1 shows the intensity of the first two orders of nondiffracting MPBs for semi-focal distances 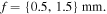 For all the intensities shown fixed the wavelength to
For all the intensities shown fixed the wavelength to  and
and  which gives us values of
which gives us values of 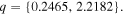 Since the parameter q depends on the square of both kt and f, we fix the values of λ and kt throughout this work and only vary the semi-focal distance whenever we wish to change the ellipticity of the beams. We can clearly see in figure 1 that reducing the semi-focal distance makes the beam distribution more circular and when
Since the parameter q depends on the square of both kt and f, we fix the values of λ and kt throughout this work and only vary the semi-focal distance whenever we wish to change the ellipticity of the beams. We can clearly see in figure 1 that reducing the semi-focal distance makes the beam distribution more circular and when 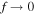 the MPBs tend to the Bessel–Poincaré beams [23]. On the other hand, for larger semi-focal distances the beam becomes more elliptic. The intensity distribution of the MPB does not vary when switching from a 'positive' to a 'negative' helical Mathieu beam in the superposition to synthesize the MPB, hence we keep the ± superscript on the beams in figure 1.
the MPBs tend to the Bessel–Poincaré beams [23]. On the other hand, for larger semi-focal distances the beam becomes more elliptic. The intensity distribution of the MPB does not vary when switching from a 'positive' to a 'negative' helical Mathieu beam in the superposition to synthesize the MPB, hence we keep the ± superscript on the beams in figure 1.
Figure 1. Intensity of nondiffracting Mathieu–Poincaré beams of orders m = 1 (left) and m = 2 (right) with semi-focal distances 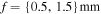 for
for 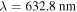 and
and 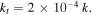
Download figure:
Standard image High-resolution imageGiven its infinite transverse profile, a MPB spans an infinite number of Poincaré spheres. However, we focus on the first region of m-fold mapping of the Poincaré sphere, which occurs from the origin of the transverse plane up to the first line of negative circular polarization. Figure 2 shows the transverse distribution of the polarization ellipse for MPBs with orders 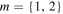 on the left and right columns, and semi-focal distances and values of q of
on the left and right columns, and semi-focal distances and values of q of 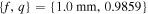 and
and 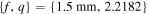 on the top and bottom row respectively. In figure 2 the polarization ellipses with positive helicity are shown in red, whereas the ones with negative helicity are green. The
on the top and bottom row respectively. In figure 2 the polarization ellipses with positive helicity are shown in red, whereas the ones with negative helicity are green. The  and
and 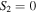 are plotted in yellow and magenta respectively, and the black lines represent the
are plotted in yellow and magenta respectively, and the black lines represent the 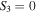 lines of linear polarization. Furthermore, the line of negative circular polarization (
lines of linear polarization. Furthermore, the line of negative circular polarization (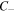 ) is an ellipse of magenta and yellow, and we can see from figure 2 that the size of the ellipse remains constant for a given value of the semi-focal distance f regardless of the order m of the MPB.
) is an ellipse of magenta and yellow, and we can see from figure 2 that the size of the ellipse remains constant for a given value of the semi-focal distance f regardless of the order m of the MPB.
Figure 2. Polarization ellipses for MPB of orders m = 1 (left column) and m = 2 (right column) for semi-focal distances of 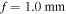 and q = 0.9859 (top row) and
and q = 0.9859 (top row) and 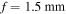 and q = 2.2182 (bottom row). Polarization ellipses of positive (negative) helicity are shown in red (green), lines of linear polarization (
and q = 2.2182 (bottom row). Polarization ellipses of positive (negative) helicity are shown in red (green), lines of linear polarization ( ) are shown in black, lines with
) are shown in black, lines with  are shown in yellow, and lines with
are shown in yellow, and lines with  are shown in magenta.
are shown in magenta.
Download figure:
Standard image High-resolution imageFor a MPB of order m, the polarization structure within the 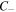 ellipse maps the Poincaré sphere m times, albeit in a nonuniform way given the noncircular symmetry of Mathieu beams. Figures 3 and 4 show how the
ellipse maps the Poincaré sphere m times, albeit in a nonuniform way given the noncircular symmetry of Mathieu beams. Figures 3 and 4 show how the 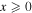 region within the
region within the 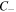 ellipse, given by elliptic coordinates
ellipse, given by elliptic coordinates 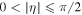 and
and  is mapped on the Poincaré sphere for first- and second-order MPBs respectively. We can see that the hyperbolae
is mapped on the Poincaré sphere for first- and second-order MPBs respectively. We can see that the hyperbolae 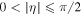 represent petals on the
represent petals on the 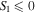 hemisphere of the Poincaré sphere, and the y-axis (
hemisphere of the Poincaré sphere, and the y-axis ( ) traces the meridian line on the
) traces the meridian line on the  plane for m = 1 and a 'petal' collapsed into a segment of the meridian line on the
plane for m = 1 and a 'petal' collapsed into a segment of the meridian line on the 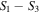 plane for m = 2, which in turn shows that for m = 2 the
plane for m = 2, which in turn shows that for m = 2 the 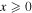 half-plane actually covers the complete Poincaré sphere.
half-plane actually covers the complete Poincaré sphere.
Figure 3. Poincaré sphere with traces corresponding to the hyperbolae of constant η for  (red) and ellipses of constant ξ for
(red) and ellipses of constant ξ for 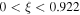 (green). The value
(green). The value 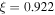 is the ellipse of negative circular polarization in figure 2 for m = 1,
is the ellipse of negative circular polarization in figure 2 for m = 1, 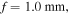 and q = 0.9859.
and q = 0.9859.
Download figure:
Standard image High-resolution imageFigures 3 and 4 also show how the ellipses of constant ξ are mapped onto the Poincaré sphere. For m = 1, the ellipses of constant ξ trace closed lines which resemble a partially open clam shell or bear trap, which have a reflection symmetry with the  plane. However, once
plane. However, once 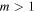 that reflection symmetry is lost, as seen in figure 4. Furthermore, this nonsymmetric tracing of the constant-ξ ellipses are evidence of the nonuniform mapping of the Poincaré sphere for
that reflection symmetry is lost, as seen in figure 4. Furthermore, this nonsymmetric tracing of the constant-ξ ellipses are evidence of the nonuniform mapping of the Poincaré sphere for  MPBs, i.e. there are regions of the sphere which are over-sampled due to the noncircular symmetry of Mathieu beams. As we mentioned earlier, for semi-focal distance
MPBs, i.e. there are regions of the sphere which are over-sampled due to the noncircular symmetry of Mathieu beams. As we mentioned earlier, for semi-focal distance 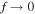 the MPBs tend to the Bessel–Poincaré beams, and the mapping on the Poincaré sphere change accordingly. The hyperbolae of constant elliptic angle η become radial lines of constant cylindrical angle ϕ and the lines traced on the sphere change from the petals to meridians. Similarly, the ellipses of constant ξ become circles of constant cylindrical radius r, and the lines traced on the sphere change from the ones shown in figures 3 and 4 to circles of latitude which are parallel to the equator plane.
the MPBs tend to the Bessel–Poincaré beams, and the mapping on the Poincaré sphere change accordingly. The hyperbolae of constant elliptic angle η become radial lines of constant cylindrical angle ϕ and the lines traced on the sphere change from the petals to meridians. Similarly, the ellipses of constant ξ become circles of constant cylindrical radius r, and the lines traced on the sphere change from the ones shown in figures 3 and 4 to circles of latitude which are parallel to the equator plane.
Figure 4. Poincaré sphere with traces corresponding to the hyperbolae of constant η for 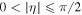 (red) and ellipses of constant ξ for
(red) and ellipses of constant ξ for 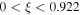 (green). The value
(green). The value 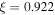 is the ellipse of negative circular polarization in figure 2 for m = 2,
is the ellipse of negative circular polarization in figure 2 for m = 2, 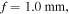 and q = 0.9859.
and q = 0.9859.
Download figure:
Standard image High-resolution image3. Polarization singularities
There are two types of singularities in transverse polarization fields: points along which the polarization is purely circular (C-points) and lines on which the polarization is purely linear (L-lines). By definition, C-points are located where the orientation of the polarization ellipse is undefined and can be found at points where the Stokes parameters 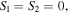 whereas L-lines appear when the handedness of the polarization ellipse becomes undefined and occur when
whereas L-lines appear when the handedness of the polarization ellipse becomes undefined and occur when 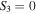 [25]. Furthermore, C-points can be classified into three different types of morphologies: star, lemon, and monstar. The classification depends on the number of straight lines that terminates on a given C-point; if there are three lines terminating on a C-point, then it can be a star or a monstar, whereas for only one line the C-point is deemed a lemon [11, 26, 27]. We can distinguish between stars and lemons or monstars, by calculating the quantities
[25]. Furthermore, C-points can be classified into three different types of morphologies: star, lemon, and monstar. The classification depends on the number of straight lines that terminates on a given C-point; if there are three lines terminating on a C-point, then it can be a star or a monstar, whereas for only one line the C-point is deemed a lemon [11, 26, 27]. We can distinguish between stars and lemons or monstars, by calculating the quantities
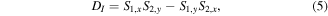
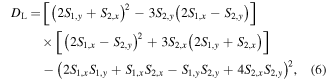
where the 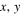 subscripts denote partial spatial derivatives. If
subscripts denote partial spatial derivatives. If  then the singularity is a star, whereas if
then the singularity is a star, whereas if 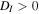 it can either be a monstar or a lemon. Furthermore, if
it can either be a monstar or a lemon. Furthermore, if 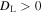 the singularity is a star or monstar, and if
the singularity is a star or monstar, and if 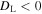 then it is a lemon. Combining these two criteria, it is easy to identify whether a C-point is a star, monstar, or lemon.
then it is a lemon. Combining these two criteria, it is easy to identify whether a C-point is a star, monstar, or lemon.
As we mentioned before, figure 2 shows the transverse structure of polarization ellipses for the MPBs of order 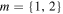 and semi-focal distances
and semi-focal distances 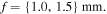 Given that the lines
Given that the lines 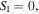
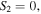 and
and 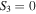 are also plotted, we can identify the position of both L-lines and C-points. We can easily see that the helicity of the polarization ellipse changes when going through a line of linear polarization, going from positive helicity near the center of the beam to negative helicity right outside the L-line. Furthermore, as we move away from the L-line, we encounter an ellipse of negative circular polarization shown in figure 2 as an ellipse of magenta and yellow dashed lines. As we noted earlier, the area inside this
are also plotted, we can identify the position of both L-lines and C-points. We can easily see that the helicity of the polarization ellipse changes when going through a line of linear polarization, going from positive helicity near the center of the beam to negative helicity right outside the L-line. Furthermore, as we move away from the L-line, we encounter an ellipse of negative circular polarization shown in figure 2 as an ellipse of magenta and yellow dashed lines. As we noted earlier, the area inside this 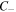 ellipse consists of the first m-fold mapping of the Poincaré sphere. Also, from figure 2 we can clearly identify the positive C-points (
ellipse consists of the first m-fold mapping of the Poincaré sphere. Also, from figure 2 we can clearly identify the positive C-points (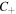 -points) by observing the intersections between the
-points) by observing the intersections between the 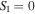 (yellow) and
(yellow) and 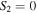 (magenta) lines. For m = 1 we find a single
(magenta) lines. For m = 1 we find a single 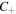 -point in the center of the beam, whereas for m = 2 there are two
-point in the center of the beam, whereas for m = 2 there are two 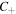 -points surrounding the propagation axis along the inter-focal line. It is straightforward to conclude that for an mth-order MPB we will find
-points surrounding the propagation axis along the inter-focal line. It is straightforward to conclude that for an mth-order MPB we will find 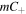 -points contained within the inter-focal line, i.e. they are always positioned within the
-points contained within the inter-focal line, i.e. they are always positioned within the 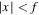 line.
line.
Now that we have identified the singularities of circular polarization along the inter-focal line, we must determine whether they are stars, monstars, or lemons. Figure 5 shows the polarization streamlines for MPBs of orders 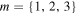 constructed with both positive and negative helical Mathieu beams in the
constructed with both positive and negative helical Mathieu beams in the 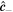 polarization. Note that when using a positive helical Mathieu beam, MPBs of odd order
polarization. Note that when using a positive helical Mathieu beam, MPBs of odd order 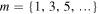 will have m star
will have m star 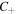 -points along the inter-focal line, whereas beams of even order
-points along the inter-focal line, whereas beams of even order 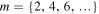 will have m lemon
will have m lemon 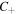 -points. However, if we were to use a negative helical Mathieu beam to synthesize the MPB, the situation is reversed: beams with odd order m will generate m lemon
-points. However, if we were to use a negative helical Mathieu beam to synthesize the MPB, the situation is reversed: beams with odd order m will generate m lemon 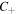 -points, and beams with even order m will have m star
-points, and beams with even order m will have m star 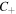 -points.
-points.
Figure 5. Polarization streamlines in the inter-focal area for positive (left column) and negative (right column) helical Mathieu beams in the Mathieu–Poincaré beams, for orders 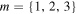 and a semi-focal distance of
and a semi-focal distance of 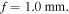
Download figure:
Standard image High-resolution image4. Conclusions
In this work we introduced the nondiffracting MPBs as a new family of nondiffracting beams with spatially inhomogeneous polarization structures which span all the polarization states on the Poincaré sphere. We studied their polarization structure and found that the first region which maps the Poincaré sphere is delimited by an ellipse of negative circular polarization. Furthermore, such ellipse retains its size for different orders of the MPB so long as the semi-focal distance is kept constant. In addition to this, we observed that the 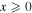 area within the
area within the  ellipse corresponds to the
ellipse corresponds to the 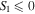 hemisphere on the Poincaré sphere for m = 1, and that for increasing values of the order m the polarization structure within the
hemisphere on the Poincaré sphere for m = 1, and that for increasing values of the order m the polarization structure within the 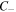 ellipse traces the sphere m-fold in a nonuniform way. Finally, we looked into the polarization singularities which occur within this first m-fold mapping region, and our most significant result is that for MPBs of order m we find exactly
ellipse traces the sphere m-fold in a nonuniform way. Finally, we looked into the polarization singularities which occur within this first m-fold mapping region, and our most significant result is that for MPBs of order m we find exactly 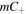 -points along the inter-focal line, and the type of singularity depends on the parity of the order and whether we used positive or negative helical Mathieu beams, which is summarized in table 1.
-points along the inter-focal line, and the type of singularity depends on the parity of the order and whether we used positive or negative helical Mathieu beams, which is summarized in table 1.
Table 1.
Summary of the morphology of the 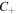 -points found along the inter-focal line in MPBs for
-points found along the inter-focal line in MPBs for 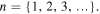
| Morphology | ||
|---|---|---|
| Order |

|
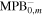
|
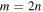
|
Lemons | Stars |

|
Stars | Lemons |
Acknowledgments
We acknowledge support from the Consejo Nacional de Ciencia y Tecnología (Grant 182005), and from the Tecnológico de Monterrey (Grant D01008).






