Abstract
We investigate the transient non-Markovian dynamics of quantum nonlocality for a pair of two-level atoms coupled to a common thermal-squeezed environment. We use Bell-CHSH inequality, steering inequality, and entanglement as theoretical tools to investigate the nonlocality dynamics. We see significant differences between the non-Markovian nonlocality dynamics and its Markovian counterpart. We mainly focus on quantum steering nonlocality which has gained much interest recently. An enhanced quantum nonlocality is shown through the violation of steering inequality and entanglement in the non-Markovian regime of the structured environment. A close correspondence is shown between steering nonlocality and entanglement dynamics.
Export citation and abstract BibTeX RIS
1. Introduction
Nonlocality has been recognized as a mystifying feature of quantum mechanics since the early days of the theory, stimulating discussions and debate that started with the argument of Einstein, Podolsky and Rosen (EPR) in 1935 [1]. In 1964, Bell proposed the famous Bell's inequality to experimentally test quantum nonlocality [2]. Experiments have successfully demonstrated the violations of Bell's inequality [3, 4], affirming the incompatibility of quantum mechanics and local hidden variable (LHV) theory. Recently, an inequality called steering inequality was proposed to illustrate quantum nonlocality [5, 6]. Steering is a form of quantum nonlocality that is closely related to the famous EPR paradox that ignited the ongoing discussions of quantum correlations. EPR steering has been experimentally tested recently [7, 8]; it has been investigated and utilized as a method to characterize nonlocality for two-qubit systems [9–13]. Three distinct types of nonlocal correlations are manifested in the literature, namely, Bell nonlocality, EPR steerability, and entanglement [5, 6]. Bell nonlocality is the strongest among the three; violation of Bell's inequality suggests the non-existence of a local hidden variable model. Whereas EPR steering indicates that the correlations cannot be described by a local hidden state model. In fact, within the hierarchy of nonlocal correlations, quantum entanglement belongs to the lower end, and EPR steering occupies an intermediate position between Bell nonlocality and entanglement. Entanglement was formally defined by Werner [14] who distinguished it from Bell nonlocality. Entanglement has received lot of attention due to its fundamental role in quantum information and quantum computation. Various criteria and measures for entanglement and subsequent experimental detection have appeared in the literature [15, 16].
We use Bell-CHSH inequality [2, 17], steering inequality (steerability) [5] and entanglement [14] as a combined tool to examine the nonlocal properties of a bipartite open quantum system. In particular, we examine the nonlocality dynamics of a two-qubit system under the decoherence in a common thermal-squeezed environment. Violation of Bell's inequality and EPR steering inequality is associated with the presence of nonlocal correlations in the quantum system which inevitably interacts with its surrounding environment (reservoirs) and the correlation is lost in general due to this unavoidable interaction. A total system plus environment evolves under a unitary evolution; non-unitary evolution of the reduced density matrix of the system can be obtained through the partial trace of the total density matrix [18–21]. Some approximations are often made in the derivation of a master equation to obtain the reduced density matrix. Born approximation assumes weak coupling strength between the system and environment to justify a perturbative approach. Markov (memoryless) approximation assumes the correlation time of the reservoir to be very short compared to the typical system response time. Under this situation reservoir correlation functions are δ-correlated in time [18–21]. The prototype of the Markov process [18–21], which completely ignores the memory effects between the system and its environments, is widely used in the study of an open quantum system and quantum optics. However, in view of many real physical systems, a large variety of analytical methods have been developed to treat non-Markovian (memory) dynamics [22–30] which prohibits the use of the Markov approximation. The non-Markovian effects are crucial in general at low temperatures when the characteristic time scale of the system dynamics becomes comparable with the reservoir correlation time, or if the environment is structured with a particular spectral density. It is important to mention here that non-Markovianity can be used as a resource in the new quantum technologies. It was shown [31] that perfect teleportation can be achieved in the presence of dephasing noise under nonlocal memory effects; non-Markovianity is a useful resource for generating steady-state entanglement [26]. The non-Markovian dynamics is also useful for quantum key distribution [32], for increasing the channel capacity [33], for quantum metrology [27, 34], and non-Markovianity can also allow an increase in extractable work [35].
Recently, important steps towards the development of a general consistent theory of non-Markovian quantum dynamics have been made and several measures have been proposed which try to define the border between Markovian and non-Markovian quantum evolution in open system dynamics. Different measures of non-Markovianity are proposed in the literature to quantify memory effects in open systems, based on the reverse flow of information between the system and the environment [23, 25, 36, 37], divisibility of the dynamical map [22, 29, 38, 39], quantum entanglement [24, 40–42], quantum Fisher information [43–46], mutual information [47–50], geometrical characterization [51] and quantum channel capacity [33]. The non-Markovianity has also been investigated in continuous variable Gaussian systems [51–55]. Here, we consider a measure of non-Markovianity in terms of the trace distance between a pair of quantum states [23, 25, 36, 37]. Our main aim here is to investigate the Markov and non-Markovian dynamics of quantum nonlocality based on EPR steering and compare it with Wootters entanglement dynamics [56] for a pair of two-level atoms coupled to a common thermal-squeezed environment. We show that the non-Markovian memory effect plays an important role in the dynamics of nonlocal correlations. We observe an enhanced nonlocality through EPR steering and entanglement with a multiple cycle of revival dynamics in a suitably tuned non-Markovian regime of the squeezed environment. One of the motivations of this study is that several proposals have already been made in the literature to physically realize a squeezed reservoir [57–60].
2. Model and quantum master equation
We consider a pair of two-level atoms coupled to a common thermal-squeezed environment. The total Hamiltonian can be written as

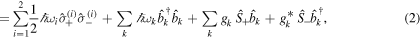
where HS is the free Hamiltonian of a pair of two-level systems, HE is the free Hamiltonian of the thermal field represented by the bosonic environment, and HI describes the interaction Hamiltonian between the system and the environment. Here 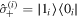 , and
, and 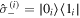 , where
, where 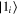 and
and 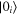 are up and down states of the ith qubit, and
are up and down states of the ith qubit, and 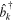 and
and 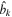 are the creation and the annihilation operators on the bosonic environment Hilbert space, and
are the creation and the annihilation operators on the bosonic environment Hilbert space, and  are the frequency of the kth environmental oscillator. Here
are the frequency of the kth environmental oscillator. Here 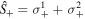 and
and 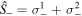 are collective raising and lowering operators for the two-qubit system, respectively, and gk are the coupling strength between the system and the environment. For simplicity, we assume two identical qubits having the same natural frequency, i.e.
are collective raising and lowering operators for the two-qubit system, respectively, and gk are the coupling strength between the system and the environment. For simplicity, we assume two identical qubits having the same natural frequency, i.e. 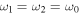 . We consider factorized initial system-environment state
. We consider factorized initial system-environment state 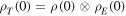 where
where
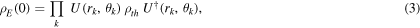

and
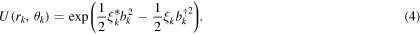
We assumed that the initial state of the bath was a squeezed thermal state. Here 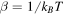 with
with 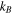 being the Boltzmann constant and T being the temperature, and we have introduced the unitary squeeze operator
being the Boltzmann constant and T being the temperature, and we have introduced the unitary squeeze operator 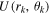 with
with 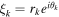 [21, 61]. The reduced density operator of the system can be obtained from the density operator of the total system by tracing over the environmental degrees of freedom
[21, 61]. The reduced density operator of the system can be obtained from the density operator of the total system by tracing over the environmental degrees of freedom ![$\rho (t)={{\rm{\Tr }}}_{E}\,[{\rho }_{T}(t)]$](https://content.cld.iop.org/journals/1751-8121/49/39/395302/revision1/jpaaa3277ieqn16.gif) . The total density operator is governed by the quantum evolution,
. The total density operator is governed by the quantum evolution, 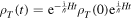 . One can obtain a time-convolutionless non-Markovian master equation for the two-atom reduced density matrix
. One can obtain a time-convolutionless non-Markovian master equation for the two-atom reduced density matrix 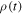 , valid to second order in the system-environment interaction strength under the Born approximation [62, 63]
, valid to second order in the system-environment interaction strength under the Born approximation [62, 63]
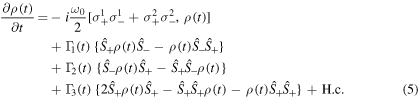
The time dependent coefficients appearing in the master equation are given by
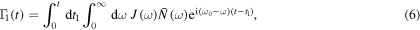
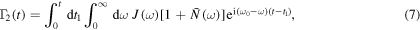
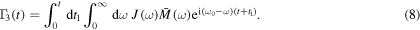
where
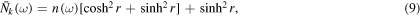
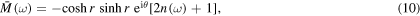
and ![$n(\omega )=1/[\exp (\beta {\hslash }\omega )-1]$](https://content.cld.iop.org/journals/1751-8121/49/39/395302/revision1/jpaaa3277ieqn19.gif) is the Planck distribution, r is the frequency independent resonant squeezing parameter and θ is the resonant phase of the squeezed reservoir. The master equation (5) is a time-local and convolutionless differential equation. The memory effect of the non-Markovian environment is taken into account by the time-dependent coefficients
is the Planck distribution, r is the frequency independent resonant squeezing parameter and θ is the resonant phase of the squeezed reservoir. The master equation (5) is a time-local and convolutionless differential equation. The memory effect of the non-Markovian environment is taken into account by the time-dependent coefficients 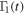 ,
, 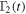 , and
, and 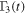 . To calculate these time-dependent coefficients in equations (6)–(8), we need to consider the spectral density to characterize the structured environment. Here we consider an Ohmic spectral density [64]
. To calculate these time-dependent coefficients in equations (6)–(8), we need to consider the spectral density to characterize the structured environment. Here we consider an Ohmic spectral density [64]

where γ is the coupling strength between the system and environment and Λ is the cutoff frequency. Given the spectral density 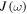 , the non-Markovian memory effect is fully characterized by the time-dependent correlation functions. The non-Markovian characteristics of the open quantum system is contained in the time-dependent coefficients (6)–(8) appearing in the master equation. The Markov master equation can be recovered from the non-Markov master equation (5) under an appropriate limit when the correlation time of the reservoir is very short compared to a typical system response time. Under this situation the upper limit of the time integrals in equations (6)–(8) can be taken as
, the non-Markovian memory effect is fully characterized by the time-dependent correlation functions. The non-Markovian characteristics of the open quantum system is contained in the time-dependent coefficients (6)–(8) appearing in the master equation. The Markov master equation can be recovered from the non-Markov master equation (5) under an appropriate limit when the correlation time of the reservoir is very short compared to a typical system response time. Under this situation the upper limit of the time integrals in equations (6)–(8) can be taken as  . For a finite temperature the Markovian case under a wide band limit (
. For a finite temperature the Markovian case under a wide band limit (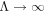 ), the time-dependent coefficients in the master equation (5) become time-independent:
), the time-dependent coefficients in the master equation (5) become time-independent: 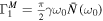 ,
, 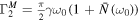 , and
, and 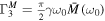 .
.
3. Nonlocality dynamics
Quantum nonlocality is demonstrated experimentally through the Bell-CHSH inequality [2, 17] and steering inequality [5, 6]. The Bell operator associated with the CHSH inequality has the following form [65]
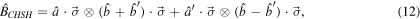
where 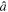 ,
, 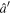 ,
, 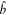 ,
, 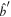 are unit vectors, and
are unit vectors, and 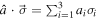 where
where 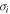 is the standard Pauli matrix. The Bell kernel associated with the CHSH inequality is given by the expectation value of the Bell-CHSH operator
is the standard Pauli matrix. The Bell kernel associated with the CHSH inequality is given by the expectation value of the Bell-CHSH operator

where ρ is the density matrix of the composite two-qubit system. The maximal mean value of the Bell-CHSH inequality or Bell kernel is given by [65]
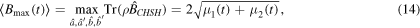
with 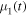 and
and 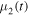 being the two largest eigenvalues for the matrix
being the two largest eigenvalues for the matrix 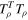 , where
, where 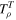 is the transpose of
is the transpose of 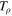 . The elements of the correlation tensor matrix
. The elements of the correlation tensor matrix 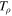 are given by
are given by

where 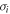 and
and 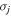 are the standard Pauli matrices with
are the standard Pauli matrices with 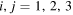 and ρ is the density matrix of the composite two-qubit system. When
and ρ is the density matrix of the composite two-qubit system. When 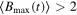 , the Bell inequality is violated, indicating the failure of the LHV model, which means that the quantum coherence dynamics for this composite system has nonlocal correlations or quantum entanglement.
, the Bell inequality is violated, indicating the failure of the LHV model, which means that the quantum coherence dynamics for this composite system has nonlocal correlations or quantum entanglement.
Next, we consider the steering inequality [5–13] to investigate the quantum nonlocality. Quantum steering is the ability to remotely prepare different quantum states by using entangled pairs as a resource. EPR steering was formulated in terms of a task in which Alice sends a quantum system to Bob [5], with the goal of convincing Bob that she is sending him one part of an entangled state, as opposed to a state chosen from some ensemble. It was argued in [5] that EPR steering is thus demonstrated by the nonexistence of a local hidden state (LHS) model for their measurement outcomes. A temporal steering inequality was formulated very recently [12]. If the correlation observed by Alice and Bob can be described by the conditional probability distribution  with
with 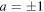 , and
, and 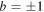 , the steering inequality is given by
, the steering inequality is given by

where
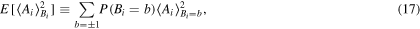
with 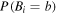 the probability of the measurement result of qubit-B, and
the probability of the measurement result of qubit-B, and
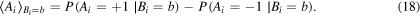
is the average expectation value of qubit-A conditioned on the outcome of qubit-B, measuring the amount that Bob's results steer her outcomes (see the appendix ,
, 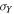 ,
, 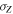 ) on qubit-A and qubit-B. The steering inequality is violated when
) on qubit-A and qubit-B. The steering inequality is violated when 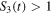 indicating the failure of the LHS model to describe the correlation between the two qubits, which means that the quantum dynamics shows evidence of nonlocal correlations [5].
indicating the failure of the LHS model to describe the correlation between the two qubits, which means that the quantum dynamics shows evidence of nonlocal correlations [5].
We finally calculate the Wootters entanglement measure [56], the concurrence C(t), defined for the time-evolved two-qubit density matrix 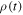 as
as

where 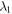 ,
, 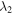 ,
, 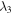 ,
, 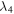 are the eigenvalues of the matrix
are the eigenvalues of the matrix 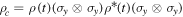 in descending order. The non-Markovian master equation (5) is solved numerically to obtain the time evolution of the density matrix.
in descending order. The non-Markovian master equation (5) is solved numerically to obtain the time evolution of the density matrix.
4. Numerical results
We numerically investigate the time evolution of the Bell kernel 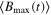 , steering inequality
, steering inequality  , and entanglement concurrence C(t) according to equations (14), (16), and (19) respectively. To investigate the nonlocality dynamics under a squeezed reservoir, we consider the initial state of the environment to be a squeezed thermal state (3) and the initial 2-qubit state is chosen as the Werner-like (WL) state [66] given by
, and entanglement concurrence C(t) according to equations (14), (16), and (19) respectively. To investigate the nonlocality dynamics under a squeezed reservoir, we consider the initial state of the environment to be a squeezed thermal state (3) and the initial 2-qubit state is chosen as the Werner-like (WL) state [66] given by
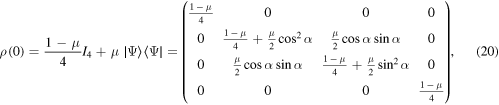
where μ is the purity parameter, I4 is the 4 × 4 identity matrix, 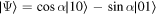 are Bell-like states and the parameter α is called the degree of entanglement. For
are Bell-like states and the parameter α is called the degree of entanglement. For 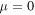 , the WL state becomes a maximally mixed state, while for
, the WL state becomes a maximally mixed state, while for  , it reduces to the Bell-like state
, it reduces to the Bell-like state  . First, we consider the simplest case
. First, we consider the simplest case  with
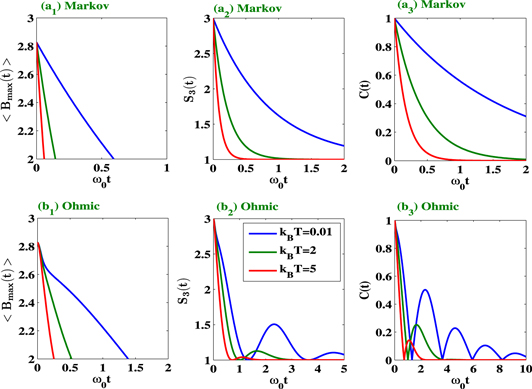
with 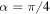 . In figure 1, we show the temperature dependence of the nonlocality dynamics through the Bell kernel, steering inequality, and concurrence in the Markov and non-Markov regime. The temperature plays a role through
. In figure 1, we show the temperature dependence of the nonlocality dynamics through the Bell kernel, steering inequality, and concurrence in the Markov and non-Markov regime. The temperature plays a role through 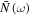 and
and 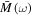 given by (9) and (10). The temperature dependence of the Markovian nonlocality dynamics is shown in figures 1(a1), (a2) and (a3). The temperature dependent non-Markovian nonlocality dynamics is shown in figures 1(b1), (b2), and (b3) with varying temperature
given by (9) and (10). The temperature dependence of the Markovian nonlocality dynamics is shown in figures 1(a1), (a2) and (a3). The temperature dependent non-Markovian nonlocality dynamics is shown in figures 1(b1), (b2), and (b3) with varying temperature 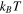 . For simplicity, we consider an Ohmic spectral density (11) for the environment. In the Markovian case, we see similar dynamics of Bell-nonlocality, EPR-steering and concurrence, namely a monotonous decay of nonlocality, the decay rate is enhanced with increasing temperature (see figures 1(a1), (a2), and (a3)). The non-Markovian dynamics of quantum coherence and hence the nonlocality of the 2-qubit system can be controlled with suitable choices of the environment spectral density by varying the cutoff frequency Λ, s and coupling strength γ in equation (11). In figure 1, we see a long-lived and enhanced dynamics of quantum violation of steering inequality and entanglement at low-temperatures for non-Markovian environments (see figures 1(b2), (b3)). The revival dynamics of quantum nonlocality and entanglement is caused by the non-Markovian memory effect at low temperature.
. For simplicity, we consider an Ohmic spectral density (11) for the environment. In the Markovian case, we see similar dynamics of Bell-nonlocality, EPR-steering and concurrence, namely a monotonous decay of nonlocality, the decay rate is enhanced with increasing temperature (see figures 1(a1), (a2), and (a3)). The non-Markovian dynamics of quantum coherence and hence the nonlocality of the 2-qubit system can be controlled with suitable choices of the environment spectral density by varying the cutoff frequency Λ, s and coupling strength γ in equation (11). In figure 1, we see a long-lived and enhanced dynamics of quantum violation of steering inequality and entanglement at low-temperatures for non-Markovian environments (see figures 1(b2), (b3)). The revival dynamics of quantum nonlocality and entanglement is caused by the non-Markovian memory effect at low temperature.
Figure 1. We plot the dynamics of Bell kernel 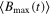 , steering parameter
, steering parameter 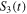 , and concurrence C(t) (entanglement measure) in (a1, a2, a3) for the Markov case and (b1, b2, b3) for non-Markovian case for Ohmic spectral density (11) of the environment. We consider three different temperatures
, and concurrence C(t) (entanglement measure) in (a1, a2, a3) for the Markov case and (b1, b2, b3) for non-Markovian case for Ohmic spectral density (11) of the environment. We consider three different temperatures 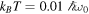 (blue curves),
(blue curves), 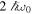 (green curves), and
(green curves), and 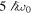 (red curves). The other parameters are taken as
(red curves). The other parameters are taken as  ,
, 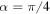 ,
, 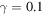 , r = 0.31,
, r = 0.31,  , and
, and 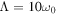 .
.
Download figure:
Standard image High-resolution imageNext, we consider the more general class of WL states given by equation (20) with 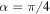 . In figure 2, we show this initial state dependence of the nonlocality dynamics through Bell-nonlocality (14), the steering inequality (16) and entanglement measured by concurrence (19) in Markov and the non-Markovian regime. We again consider an Ohmic spectral density (11) and the environmental temperature is fixed at
. In figure 2, we show this initial state dependence of the nonlocality dynamics through Bell-nonlocality (14), the steering inequality (16) and entanglement measured by concurrence (19) in Markov and the non-Markovian regime. We again consider an Ohmic spectral density (11) and the environmental temperature is fixed at 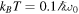 . In figure 2, we show the dynamics of nonlocality as a function of the parameter μ in both the Markov and non-Markov regime. In the Markov case, we find that the area of entanglement dynamics is larger than the Bell-nonlocality area and the area of EPR steering violation. When
. In figure 2, we show the dynamics of nonlocality as a function of the parameter μ in both the Markov and non-Markov regime. In the Markov case, we find that the area of entanglement dynamics is larger than the Bell-nonlocality area and the area of EPR steering violation. When 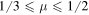 , Bell-nonlocality and EPR steering is not violated, while quantum entanglement still exists. However, as
, Bell-nonlocality and EPR steering is not violated, while quantum entanglement still exists. However, as 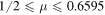 , Bell-nonlocality shows up, and the EPR steering is also violated. We observe an enhanced nonlocality through EPR steering and an entanglement with a multiple cycle of revival dynamics for a suitably tuned non-Markovian environment. For
, Bell-nonlocality shows up, and the EPR steering is also violated. We observe an enhanced nonlocality through EPR steering and an entanglement with a multiple cycle of revival dynamics for a suitably tuned non-Markovian environment. For  , we observe a long-time quantum violation of the Bell-nonlocality, steering inequality, and entanglement even if t approaches to larger values. These enhanced oscillatory behaviors of nonlocality dynamics in the non-Markov case arise due to the memory effect of the environment.
, we observe a long-time quantum violation of the Bell-nonlocality, steering inequality, and entanglement even if t approaches to larger values. These enhanced oscillatory behaviors of nonlocality dynamics in the non-Markov case arise due to the memory effect of the environment.
Figure 2. We plot the dynamics of Bell kernel 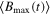 , steering parameter
, steering parameter 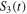 , and concurrence C(t) (entanglement measure) in (a1, b1, c1) for the Markov and (a2, b2, c2) for the non-Markov case. The temperature of the environment is fixed at
, and concurrence C(t) (entanglement measure) in (a1, b1, c1) for the Markov and (a2, b2, c2) for the non-Markov case. The temperature of the environment is fixed at 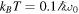 . The other parameters are taken as
. The other parameters are taken as 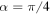 ,
, 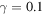 , r = 0.1,
, r = 0.1, 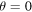 , and
, and  .
.
Download figure:
Standard image High-resolution imageIn figure 3, we separately show the dynamics of nonlocality through Bell-nonlocality (14), EPR steering (16), and entanglement measured by concurrence (19) in the non-Markov regime as a function of initial state parameter α. We consider the case 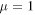 for which the WL state reduces to the Bell-like state
for which the WL state reduces to the Bell-like state 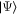 . We also consider Ohmic spectral density (11). The bath temperature is fixed at
. We also consider Ohmic spectral density (11). The bath temperature is fixed at 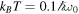 . In figures 3(a1), (b1) and (c1), we show the dynamics of nonlocality through EPR steering (in the non-Markovian regime) as a function of initial state parameter α. For
. In figures 3(a1), (b1) and (c1), we show the dynamics of nonlocality through EPR steering (in the non-Markovian regime) as a function of initial state parameter α. For 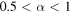 , Bell-nonlocality and steering nonlocality persists for a longer time—the same is true for the entanglement. These enhanced oscillatory behaviors of nonlocality dynamics arise due to the memory effect of the environment.
, Bell-nonlocality and steering nonlocality persists for a longer time—the same is true for the entanglement. These enhanced oscillatory behaviors of nonlocality dynamics arise due to the memory effect of the environment.
Figure 3. The nonlocality dynamics is shown as a function of initial state parameter α. We draw a contour plot in (a1) for the Bell kernel 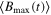 , (b1) for steering parameter
, (b1) for steering parameter 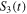 and (c1) for concurrence C(t) for the Markov case and non-Markov case with Ohmic environment. The other parameters are taken as
and (c1) for concurrence C(t) for the Markov case and non-Markov case with Ohmic environment. The other parameters are taken as 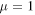 ,
, 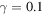 , r = 0.31,
, r = 0.31, 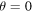 ,
, 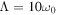 , and
, and  .
.
Download figure:
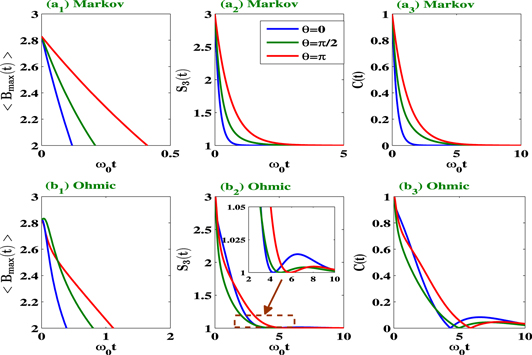
Standard image High-resolution imageIn figures 4 and 5, we investigate the effect of variation of the squeezing parameters (r and θ) on the nonlocality dynamics. It is clear from equations (6)–(8) that one can control the time dependent correlation functions 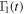 ,
, 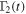 , and
, and 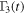 by choosing the parameters r and θ. Hence the non-Markovian evolution of the 2-qubit system is controlled by these parameters. Both
by choosing the parameters r and θ. Hence the non-Markovian evolution of the 2-qubit system is controlled by these parameters. Both 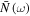 and
and 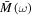 in equations (9) and (10) depend on r, whereas the parameter θ only controls
in equations (9) and (10) depend on r, whereas the parameter θ only controls 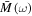 . In figure 4, we examine the nonlocality dynamics through the Bell kernel
. In figure 4, we examine the nonlocality dynamics through the Bell kernel 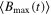 , EPR steering parameter
, EPR steering parameter 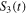 and concurrence C(t) for the Markov and non-Markov environment where we mainly focus on the r-dependence of the dynamics with a fixed value of θ. On the other hand, figure 5 reveals the θ-dependence of the nonlocality dynamics. In figure 4(a1), (a2), (a3), we see a monotonous decay of Bell, steering nonlocality, and entanglement for the Markovian case; the decay rate is enhanced with increasing r. The revival of nonlocality is observed for non-Markovian environments (see figures 4(b2), (b3)), the nonlocality is enhanced in general for smaller values of r. The θ-dependence of the nonlocality dynamics is shown in figure 5 for Markov and non-Markovian environments. Clearly, both the Markov and non-Markov dynamics of nonlocality are influenced by the parameter θ. The Bell-nonlocality shows a monotonic decay behavior with the reservoir parameters, whereas we see a long-lived oscillatory dynamics of quantum violation of steering inequality and entanglement for the non-Markovian environment (figures 4(b2), (b3) and 5(b2), (b3)). These enhanced oscillatory behaviors of nonlocality dynamics arise due to the memory effect of the environment which is discussed next with respect to figure 6. The non-Markovian nonlocality dynamics can be controlled by a proper choice of the structured environment that controls the time-dependent decay rates in equations (6)–(8). It is important to point out that the dynamical map given by the time-convolutionless non-Markovian master equation (5) is always positive for the given choice of parameters. We have numerically checked that all eigenvalues of the time-evolved density matrix
and concurrence C(t) for the Markov and non-Markov environment where we mainly focus on the r-dependence of the dynamics with a fixed value of θ. On the other hand, figure 5 reveals the θ-dependence of the nonlocality dynamics. In figure 4(a1), (a2), (a3), we see a monotonous decay of Bell, steering nonlocality, and entanglement for the Markovian case; the decay rate is enhanced with increasing r. The revival of nonlocality is observed for non-Markovian environments (see figures 4(b2), (b3)), the nonlocality is enhanced in general for smaller values of r. The θ-dependence of the nonlocality dynamics is shown in figure 5 for Markov and non-Markovian environments. Clearly, both the Markov and non-Markov dynamics of nonlocality are influenced by the parameter θ. The Bell-nonlocality shows a monotonic decay behavior with the reservoir parameters, whereas we see a long-lived oscillatory dynamics of quantum violation of steering inequality and entanglement for the non-Markovian environment (figures 4(b2), (b3) and 5(b2), (b3)). These enhanced oscillatory behaviors of nonlocality dynamics arise due to the memory effect of the environment which is discussed next with respect to figure 6. The non-Markovian nonlocality dynamics can be controlled by a proper choice of the structured environment that controls the time-dependent decay rates in equations (6)–(8). It is important to point out that the dynamical map given by the time-convolutionless non-Markovian master equation (5) is always positive for the given choice of parameters. We have numerically checked that all eigenvalues of the time-evolved density matrix 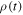 remain positive at any given time t. We have done this consistency check related to the properties of the two-qubit reduced density matrix
remain positive at any given time t. We have done this consistency check related to the properties of the two-qubit reduced density matrix 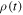 corresponding to a general class of initial states given by equation (20) with varying parameters μ and α.
corresponding to a general class of initial states given by equation (20) with varying parameters μ and α.
Figure 4. We show the nonlocality dynamics through the Bell kernel 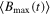 , the EPR steering parameter
, the EPR steering parameter 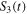 and concurrence C(t) (entanglement measure) in (a1, a2, a3) for Markov and (b1, b2, b3) for non-Markov cases. We consider three different squeeze parameters r = 0 (blue curves), r = 0.6 (green curves), and r = 1 (red curves). The values of the other parameters are
and concurrence C(t) (entanglement measure) in (a1, a2, a3) for Markov and (b1, b2, b3) for non-Markov cases. We consider three different squeeze parameters r = 0 (blue curves), r = 0.6 (green curves), and r = 1 (red curves). The values of the other parameters are  ,
,  ,
, 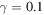 ,
, 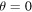 ,
, 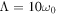 , and
, and 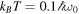 .
.
Download figure:
Standard image High-resolution imageFigure 5. We plot the dynamics Bell kernel 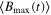 , the steering parameter
, the steering parameter 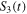 and concurrence C(t) (entanglement measure) in (a1, a2, a3) for Markov and (b1, b2, b3) for non-Markov cases. We consider three different squeeze parameters
and concurrence C(t) (entanglement measure) in (a1, a2, a3) for Markov and (b1, b2, b3) for non-Markov cases. We consider three different squeeze parameters 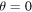 (blue curves),
(blue curves), 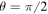 (green curves), and
(green curves), and 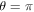 (red curves). The values of the other parameters are
(red curves). The values of the other parameters are 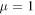 ,
, 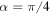 ,
, 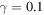 , r = 0.31,
, r = 0.31, 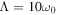 , and
, and 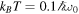 .
.
Download figure:
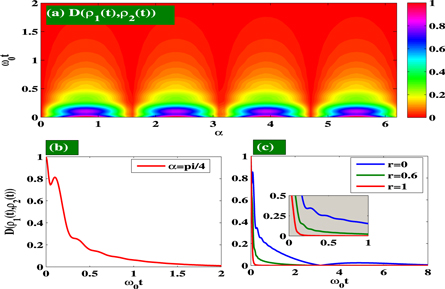
Standard image High-resolution imageFigure 6. (a) We plot the dynamics of the trace distance (21) as a function of the initial state parameter α with Ohmic bath. The values of the other parameters are 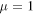 ,
, 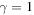 , r = 0,
, r = 0, 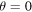 ,
, 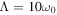 , and
, and 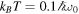 . (b) We plot the dynamics of the trace distance for a maximally entangled pair with
. (b) We plot the dynamics of the trace distance for a maximally entangled pair with 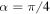 . The values of the other parameters are
. The values of the other parameters are 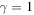 , r = 0,
, r = 0, 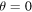 ,
, 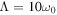 , and
, and 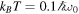 . (c) We show the dynamics of the trace distance for a pair of maximally entangled states
. (c) We show the dynamics of the trace distance for a pair of maximally entangled states 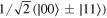 with an Ohmic bath. We consider three different values of the squeezed parameter: r = 0 (blue curves), r = 0.6 (green curves), and r = 1 (red curves) in the non-Markovian regime. The values of the other parameters are
with an Ohmic bath. We consider three different values of the squeezed parameter: r = 0 (blue curves), r = 0.6 (green curves), and r = 1 (red curves) in the non-Markovian regime. The values of the other parameters are  ,
, 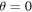 ,
, 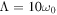 , and
, and 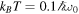 .
.
Download figure:
Standard image High-resolution imageTo describe the non-Markovian features of the environment, we consider a particular approach of quantum non-Markovianity based on the idea of information exchange between the open system and its environment [23, 25, 36, 37]. The key quantity in this approach is the trace distance 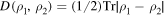 (distinguishability) between a pair of quantum states
(distinguishability) between a pair of quantum states 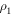 and
and 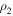 of the system. Markov processes try to continuously reduce the distinguishability of physical states indicating a flow of information from the open system to its environment. An increase of
of the system. Markov processes try to continuously reduce the distinguishability of physical states indicating a flow of information from the open system to its environment. An increase of 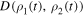 under a quantum process is interpreted as a reversed flow of information from the environment back to the open system, owing to the non-Markovian memory effect. We consider a pair of two-qubit initial states in the form
under a quantum process is interpreted as a reversed flow of information from the environment back to the open system, owing to the non-Markovian memory effect. We consider a pair of two-qubit initial states in the form

where 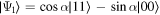 and
and 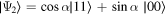 . In figure 6(a), we show the non-Markovian behavior of the dynamics as a function of the initial state parameter α. The contour plot of figure 6(a) shows the revival dynamics of trace distance (21) for particular periodic values of α. An enhanced non-Markovian feature is observed when the initial state pair is close to the maximally entangled states (
. In figure 6(a), we show the non-Markovian behavior of the dynamics as a function of the initial state parameter α. The contour plot of figure 6(a) shows the revival dynamics of trace distance (21) for particular periodic values of α. An enhanced non-Markovian feature is observed when the initial state pair is close to the maximally entangled states (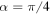 ). Also, the maximum revival of trace distance occurs for the non-Markovian case. In figure 6(b), we separately show the revival dynamics of the trace distance for a pair of maximally entangled states (
). Also, the maximum revival of trace distance occurs for the non-Markovian case. In figure 6(b), we separately show the revival dynamics of the trace distance for a pair of maximally entangled states (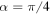 ). In figure 6(b), we see that the trace distance decays and then it revives again in the short-time regime; finally the trace distance approaches to zero at large time. It is important to note that an increase of the trace distance implies a reversed flow of information from the environment back to the open system. In figure 6(c), we investigate the influence of squeezing parameter r on non-Markovian dynamics characterized by the trace distance. We show the dynamics of the trace distance
). In figure 6(b), we see that the trace distance decays and then it revives again in the short-time regime; finally the trace distance approaches to zero at large time. It is important to note that an increase of the trace distance implies a reversed flow of information from the environment back to the open system. In figure 6(c), we investigate the influence of squeezing parameter r on non-Markovian dynamics characterized by the trace distance. We show the dynamics of the trace distance 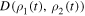 for a pair of maximally entangled states
for a pair of maximally entangled states 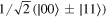 with
with 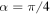 . The revival of the trace distance in finite time is observed for Ohmic environments; the non-Markovianity is enhanced in general for smaller values of r. It is clear from equations (6)–(8) that one can control the time dependent correlation functions
. The revival of the trace distance in finite time is observed for Ohmic environments; the non-Markovianity is enhanced in general for smaller values of r. It is clear from equations (6)–(8) that one can control the time dependent correlation functions 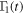 ,
, 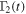 , and
, and 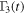 by choosing the parameters r. Figure 6 essentially demonstrates the quantum nonlocal memory effect [67–69].
by choosing the parameters r. Figure 6 essentially demonstrates the quantum nonlocal memory effect [67–69].
5. Conclusion
In summary, we investigate both the Markov and non-Markov dynamics of nonlocal correlations of a two-qubit system interacting with a common squeezed reservoir at finite temperature. We use Bell-CHSH inequality, EPR steering inequality and entanglement as a combined tool to investigate the nonlocal properties of the system. We see an enhanced long-time dynamics of nonlocality in the non-Markovian regime of the environment. In particular, the dynamics of nonlocality in a different time scale crucially depends on the initial temperature of the environment and the initial state of the system. The nonlocality dynamics shows multiple cycles of revival in the non-Markovian regime when memory effect plays an important role for the structured environment. This is established through a particular approach of non-Markovianity based on trace distance. One can control the nonlocality dynamics with a suitable choice of environmental spectral density. The memory effect on the nonlocality dynamics can also be tuned through the squeezing parameters of the environment.
Acknowledgments
We thank Chi-Fong Ai and Jin-Yu Wu for their assistance. PWC thanks Shin-Liang Chen for useful comments and discussions. PWC would also like to acknowledge the support from the Division of Physics, Institute of Nuclear Energy Research, Taiwan. MMA acknowledges the support from the Ministry of Science and Technology of Taiwan.
Appendix.: Details about the steering inequality
To obtain the steering inequality, one can first measure the state ρ in the Z-basis. The probability that Bob obtains the outcome ±1 is given by

where
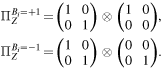
After Bob's measurement, the state ρ changes to 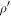 , where
, where

Now, for this new state 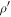 , the probability that Alice obtains ±1 is
, the probability that Alice obtains ±1 is
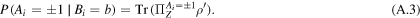
Then one can evaluate equations (17) and (18) using 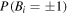 and
and  given by equations (A.1) and (A.3). One can then repeat the same procedure by replacing
given by equations (A.1) and (A.3). One can then repeat the same procedure by replacing 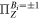 ,
, 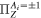 with
with  ,
,  and
and 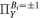 ,
, 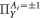 , to calculate S3 in three mutually unbiased bases given by equation (16).
, to calculate S3 in three mutually unbiased bases given by equation (16).