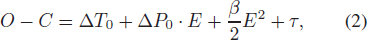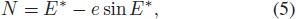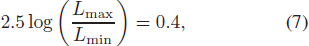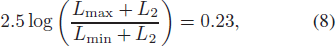Abstract
We present 145 times of light maximum for high amplitude δ Scuti star BO Lyn based on several sky surveys (CRTS, DASCH, NSVS, OMC and SuperWASP) and our photometric observations. Combining with the data in literature, a total of 179 times of light maximum are used to analyze the O − C diagram of BO Lyn. We find that it can be described by an upward parabolic component and a periodic variation with a period of 34.5 ± 0.1 yr. The latter could be caused by the light travel time effect as a result of an additional companion orbiting in a highly elliptical orbit (e = 0.64 ± 0.03). Our study indicates that the companion's luminosity cannot be ignored, and it should be a late A-type main-sequence star. The long-term period change of BO Lyn is also detected, and its value, 1.52 ± 0.26 × 10−3 d Myr−1, is consistent with evolutionary models. We suggest that more spectroscopic and photometric observations are needed in the future to confirm the nature of the BO Lyn system.
1. Introduction
δ Scuti variables are one type of variable star, with a short pulsation period, situated in the Classical Cepheid instability strip on the main sequence or moving away from the main sequence (Breger 2000). Their members, having V amplitudes greater than 0.3 mag, are known as high amplitude δ Scuti stars (HADS). Some authors have also suggested that the limit should be relaxed to ΔV > 0.1 mag (Solano & Fernley 1997). Observations and research on the associated stellar pulsations and oscillations can provide valuable information about the interior properties of these stars and hence can be applied to test the theory of stellar structure and evolution (Christensen-Dalsgaard 2003). Moreover, the pulsations also can be used as probes to detect the companions of these stars, and the corresponding technique is the Observed–Calculated method (O – C method, Sterken 2005), which is also known as the timing method. Actually, many δ Scuti stars, especially HADS, have been discovered existing in binary ormultiple systems by using different methods (Zhou 2010; Liakos & Niarchos 2017), and the O − C method is a powerful tool for deriving their orbital elements (e.g. SZ Lyn, Paparo et al. 1988, Li & Qian 2013; CY Aqr, Fu & Sterken 2003; BL Cam, Fauvaud et al. 2006, 2010; KZ Hya, Fu et al. 2008; DY Peg, Li & Qian 2010; DW Psc, Qian et al. 2015). Moreover, this method also plays an important role in the field of other variable stars, such as eclipsing binaries (Yuan, Şenavcι & Qian 2016; Liao et al. 2016) and cataclysmic variables (Han et al. 2016, 2017).
BO Lyncis (BO Lyn, α2000 = 08h43m01.2s, δ2000 = 40°59'51.8'', ⟨V⟩ = 11.955, ΔV = 0.23, Sp: A5V. A8V) was discovered to be a δ Scuti variable by Kinman et al. (1994). After a comprehensive investigation, Kinman (1998) pointed out that the properties of BO Lyn revealed that it is a member of the old disk population. Period analysis of BO Lyn was performed by Hintz et al. (2005). They used a parabola to fit the O − C diagram, and identified a period decrease of −1.5 × 10−10 d d−1 or −0.056 d Myr−1. However, based on new observations, Peña et al. (2016) found that the O − C curves show a sinusoidal behavior which could be caused by the light travel time effect (LiTE), and they provided a new linear ephemeris
To investigate the pulsation period change of BO Lyn, we collect and determine its times of light maximum, and study the O – C diagram with a single-Keplerian fit. Sections 2 and 3 describe the observations and O − C analysis. We present the discussion and conclusion in Section 4.
2. Observations and Data Collection
BO Lyn was observed by the 60 cm and 1m telescopes administered by Yunnan Observatories in China on four nights in February and March 2017. The two telescopes were equipped with a PIXIS: 2048B detector and Andor DW436 CCD camera, respectively. Two standard Johnson-Cousin Bessel filters, V and R bands, were used in the observations, and the exposure times ranged from 10 to 50 s, depending on the weather, diameters of the telescopes and filters. The comparison star was TYC 2985-390-1 (08:42:39.9 + 40:59:48.3, V = 10.91) and the check star was UCAC4 655-051112 (08:43:05.74 +40:59:41.06, V = 13.56). The light curves from the four nights and corresponding information (e.g. telescopes, exposure times) are displayed in Figure 1. Based on our observations, we determined 10 times of light maximum by fitting a cubic polynomial to each observed peak.
Fig. 1 The observed light curves of BO Lyn from the four nights. In each panel, the information about telescopes, exposure times and filters is given.
Download figure:
Standard imageActually, BO Lyn was observed by several sky surveys, and the most important one in this context should be the Digital Access to a Sky Century @ Harvard (DASCH) project, which provides digitized images for a century of coverage (Grindlay et al. 2009). Even though the light curves have lower time resolutions and higher uncertainties (∼0.1 mag) than other surveys, reliable times of light maximum can be determined by the appropriate methods and can provide useful information on more than 100 yr time scales (Liška et al. 2016). The other surveys also include NSVS (Woźniak et al. 2004), OMC1, CRTS (Drake et al. 2009) and SuperWASP (SWASP, Pollacco et al. 2006; Butters et al. 2010), and based on these data, we determined more than one hundred new times of light maximum for BO Lyn. The detection method is similar to those described in Li & Qian (2014), but the difference is that the orders of the Fourier polynomials are 1 (DASCH, NSVS and CRTS) or 3 (OMC and SWASP), depending on the time resolutions of the data from different surveys. It is worth mentioning that different orders applied to different data sets would introduce systematic deviations into the times of light maximum. Using the SWASP data as a test sample, we find that the two times of light maximum determined by different Fourier polynomials (orders 1 and 3) differ by 0.0025 d on average.
Based on our observations, the sky surveys and literature, we collected 179 times of light maximum in total for BO Lyn; DASCH allows our data to span more than 100 yr (about 120 yr). Table 1 lists the corresponding times of lightmaximumobtained fromour work. The data which have been given by Peña et al. (2016) were not listed repeatedly.
Table 1. The 145 new available times of light maximum for BO Lyn obtained from sky surveys and our observations.
| H JD. 2400000+ | Error | Ref. | HJD. 2400000+ | Error | Ref. | HJD. 2400000+ | Error | Ref. |
|---|---|---|---|---|---|---|---|---|
| 13760.2929 | 0.0025 | DASCH | 53502.1121 | 0.0025 | OMC | 54167.2002 | 0.0007 | SWASP |
| 16460.8560 | 0.0025 | DASCH | 53672.8648 | 0.0020 | SWASP | 54168.1303 | 0.0028 | SWASP |
| 17767.3116 | 0.0029 | DASCH | 53751.3774 | 0.0031 | CRTS | 54169.1595 | 0.0009 | SWASP |
| 19222.3066 | 0.0030 | DASCH | 54067.3966 | 0.0010 | SWASP | 54170.1851 | 0.0004 | SWASP |
| 20379.2094 | 0.0026 | DASCH | 54068.3286 | 0.0013 | SWASP | 54171.2140 | 0.0006 | SWASP |
| 21520.7015 | 0.0027 | DASCH | 54069.3570 | 0.0009 | SWASP | 54193.6178 | 0.0006 | SWASP |
| 23275.8407 | 0.0025 | DASCH | 54072.9042 | 0.0011 | SWASP | 54195.1107 | 0.0007 | SWASP |
| 24629.6375 | 0.0040 | DASCH | 54075.3336 | 0.0014 | SWASP | 54432.3353 | 0.0006 | SWASP |
| 25440.8248 | 0.0034 | DASCH | 54079.9029 | 0.0007 | SWASP | 54438.3102 | 0.0007 | SWASP |
| 26039.7154 | 0.0038 | DASCH | 54084.3887 | 0.0008 | SWASP | 54439.3395 | 0.0007 | SWASP |
| 26776.6734 | 0.0029 | DASCH | 54085.4155 | 0.0012 | SWASP | 54494.4159 | 0.0013 | CRTS |
| 27343.1491 | 0.0029 | DASCH | 54088.8714 | 0.0007 | SWASP | 54502.2588 | 0.0006 | SWASP |
| 27860.2601 | 0.0049 | DASCH | 54092.4178 | 0.0006 | SWASP | 54503.1928 | 0.0004 | SWASP |
| 28391.1927 | 0.0062 | DASCH | 54093.9102 | 0.0009 | SWASP | 54524.1095 | 0.0005 | SWASP |
| 28797.2064 | 0.0048 | DASCH | 54096.9020 | 0.0007 | SWASP | 54525.1369 | 0.0008 | SWASP |
| 29162.1376 | 0.0027 | DASCH | 54099.4208 | 0.0012 | SWASP | 54526.1605 | 0.0005 | SWASP |
| 29488.3310 | 0.0028 | DASCH | 54100.3534 | 0.0008 | SWASP | 54527.1866 | 0.0005 | SWASP |
| 29816.2891 | 0.0037 | DASCH | 54101.3824 | 0.0009 | SWASP | 54529.1480 | 0.0009 | SWASP |
| 30199.1492 | 0.0035 | DASCH | 54110.8088 | 0.0011 | SWASP | 54531.1091 | 0.0013 | SWASP |
| 30766.6708 | 0.0030 | DASCH | 54113.3303 | 0.0009 | SWASP | 54532.1372 | 0.0006 | SWASP |
| 31452.7645 | 0.0055 | DASCH | 54115.2899 | 0.0009 | SWASP | 54534.1884 | 0.0004 | SWASP |
| 32246.2383 | 0.0032 | DASCH | 54117.7152 | 0.0010 | SWASP | 54536.1498 | 0.0005 | SWASP |
| 41048.1150 | 0.0035 | DASCH | 54119.8626 | 0.0006 | SWASP | 54537.0828 | 0.0006 | SWASP |
| 42793.8356 | 0.0026 | DASCH | 54121.3569 | 0.0008 | SWASP | 54538.5776 | 0.0007 | SWASP |
| 44100.3907 | 0.0028 | DASCH | 54122.2918 | 0.0008 | SWASP | 54540.0685 | 0.0013 | SWASP |
| 45357.8433 | 0.0028 | DASCH | 54123.3171 | 0.0008 | SWASP | 54541.0017 | 0.0015 | SWASP |
| 46156.9983 | 0.0031 | DASCH | 54138.1625 | 0.0005 | SWASP | 54543.0581 | 0.0008 | SWASP |
| 47049.1344 | 0.0029 | DASCH | 54140.2187 | 0.0007 | SWASP | 54545.1099 | 0.0016 | SWASP |
| 51276.5843 | 0.0009 | NSVS | 54141.2435 | 0.0008 | SWASP | 54554.0746 | 0.0005 | SWASP |
| 51283.1173 | 0.0010 | NSVS | 54142.2686 | 0.0009 | SWASP | 54555.1024 | 0.0008 | SWASP |
| 51480.7519 | 0.0010 | NSVS | 54143.2985 | 0.0008 | SWASP | 54556.1281 | 0.0005 | SWASP |
| 51499.7988 | 0.0008 | NSVS | 54144.7896 | 0.0012 | SWASP | 54558.0931 | 0.0006 | SWASP |
| 51510.2582 | 0.0010 | NSVS | 54146.2852 | 0.0006 | SWASP | 54865.4268 | 0.0087 | CRTS |
| 51519.2193 | 0.0012 | NSVS | 54147.2212 | 0.0009 | SWASP | 55227.6586 | 0.0029 | CRTS |
| 51531.7281 | 0.0016 | NSVS | 54148.1553 | 0.0026 | SWASP | 55592.2297 | 0.0037 | CRTS |
| 51545.7330 | 0.0009 | NSVS | 54149.1799 | 0.0010 | SWASP | 55998.7099 | 0.0055 | CRTS |
| 51552.1718 | 0.0009 | NSVS | 54150.2072 | 0.0005 | SWASP | 56330.2302 | 0.0033 | CRTS |
| 51555.7177 | 0.0018 | NSVS | 54151.7011 | 0.0004 | SWASP | 57802.1240 | 0.0003 | R |
| 51558.3305 | 0.0020 | NSVS | 54153.1955 | 0.0005 | SWASP | 57802.1246 | 0.0003 | V |
| 51566.1755 | 0.0019 | NSVS | 54154.2210 | 0.0006 | SWASP | 57802.2171 | 0.0004 | R |
| 51573.1793 | 0.0014 | NSVS | 54155.2474 | 0.0006 | SWASP | 57802.2174 | 0.0004 | V |
| 51576.6309 | 0.0011 | NSVS | 54156.1786 | 0.0005 | SWASP | 57804.2735 | 0.0004 | V |
| 51580.1811 | 0.0025 | NSVS | 54157.2061 | 0.0005 | SWASP | 57804.2741 | 0.0007 | R |
| 51586.1586 | 0.0026 | NSVS | 54158.1400 | 0.0009 | SWASP | 57816.0356 | 0.0003 | V |
| 51595.6799 | 0.0028 | NSVS | 54160.8510 | 0.0021 | CRTS | 57816.0357 | 0.0004 | R |
| 51602.3080 | 0.0015 | NSVS | 54161.1296 | 0.0008 | SWASP | 57820.0514 | 0.0003 | V |
| 51606.1343 | 0.0013 | NSVS | 54164.1173 | 0.0011 | SWASP | 57820.0521 | 0.0003 | R |
| 51612.2024 | 0.0014 | NSVS | 54165.1398 | 0.0014 | SWASP | |||
| 53275.8116 | 0.0026 | SWASP | 54166.1685 | 0.0009 | SWASP |
Notes: References: R and V are the bands used in our observations.
Based on our observations, the sky surveys and literature, we collected 179 times of light maximum in total for BO Lyn; DASCH allows our data to span more than 100 yr (about 120 yr). Table 1 lists the corresponding times of lightmaximumobtained fromour work. The data which have been given by Peña et al. (2016) were not listed repeatedly.
Figure 2 presents the O – C diagram, from which the cyclic variations can been seen clearly. The linear ephemeris used in Figure 2 is Equation (1), which was published by Peñna et al. (2016).
Fig. 2 O – C diagram of BO Lyn using the ephemeris in Eq. (1). The periodic variation can be seen clearly.
Download figure:
Standard image3. O – C Analysis
We hypothesize that variations in the O – C diagram are caused by the long-term period change and by LiTE of a companion in a highly elliptical orbit (model 1)
and
where Δ T0 and Δ P0 are the correction values to the initial epoch and pulsation period respectively, β is the linear change of the pulsation period (d cycle−1) and τ represents the periodic change caused by the LiTE effect. Equation (3) was first given by Irwin (1952), where A = a1 sin i/c is the projected semi-major axis expressed in d (day); e is the eccentricity; ν is the true anomaly; ω is the longitude of the periastron passage in the plane of the orbit; and E* in Equation (4) is the eccentric anomaly.
The connection between E* and the mean anomaly N is
and
PB is the orbital period of the binary system; t is the time of light maximum; T is the time of passage through the periastron. A detailed description can be referenced in Li & Qian (2010).
Table 2 lists the results of the fit and Figure 3 shows the corresponding O – C diagram. The solid line in the upper panel of Figure 3 refers to the combination of a parabola and the cyclic change due to the LiTE. The parabola means that the pulsation period is increasing linearly. The orbital period of BO Lyn is PB = 12611 ± 36 d ≃ 34.53 ± 0.10 yr, which is longer than the result given by Peña et al. (2016). However, combining with the parabola, they can describe the O – C curves very well. In the middle panel, the quadratic term has been subtracted, and the periodic variation τ can be seen more clearly. The residuals after removing all the variations are displayed in the bottom panel, from which it can be seen that no change can be traced for the later O – C points (those E > −10 000). However, there is a bump at E ∼ −20 000 in the residuals. Noticing that the corresponding O – C points obtained from DASCH have the highest errors, we tend to think that the variation is not real.
Fig. 3 Upper panel: O – C diagrams of BO Lyn using the ephemeris of Eq. (1); the solid line shows the fit exhibiting an upward parabolic variation and the cyclic change due to the LiTE; Middle panel: only the cyclic change τ is plotted for better visualization; Bottom panel: Residual O – C diagram for BO Lyn. In all panels, error bars are only shown for the data with errors, and it should be mentioned that some error bars are smaller than the symbols.
Download figure:
Standard imageTable 2. The pulsation and orbital elements of BO Lyn. f(M) is the mass function of the companion and K is the velocity semi-amplitude in km s−1. In model 2, the value of β is set as zero.
| Parameter | Model 1 | Model 2 |
|---|---|---|
| T0[cor] | 2447933.7821 ± 0.0008 | 2447933.7838 ± 0.0009 |
| P0[cor] (d) | 0.093358251 ± 0.000000007 | 0.093358215 ± 0.000000007 |
| β (d cycle−1) | (3.89 ± 0.66) × 10−13 | 0 (fixed) |
| β (d Myr−1) | (1.52 ± 0.26) × 10−3 | 0 (fixed) |
| A (d) | 0.0300 ± 0.0011 | 0.0299 ± 0.0013 |
| a1 sin i (au) | 5.19 ± 0.18 | 5.17 ± 0.22 |
| e | 0.64 ± 0.03 | 0.67 ± 0.04 |
| ω (°) | 185.5 ± 3.1 | 191.1 ± 3.1 |
| PB (d) | 12611 ± 36 | 12494 ± 44 |
| PB (yr) | 34.53 ± 0.10 | 34.21 ± 0.12 |
| T | 2452047.5 ± 94.0 | 2452146.2 ± 130.5 |
| f(M) (M⊙) | 0.117 ± 0.013 | 0.118 ± 0.015 |
| K (km s−1) | 5.85 ± 0.29 | 6.09 ± 0.38 |
In some analyses, the O – C data span is not long enough, so the long-term period change β can be ignored (Qian et al. 2015). We fit the data without the period change (β = 0; model 2). The third column of Table 2 lists the corresponding results, and Figure 4 shows the O – C diagram. An F-test (a statistical test which is often used when comparing statistical models that have been fitted to a data set, see Li & Qian 2013 and the references therein for more details) indicates that there are no significant differences between model 1 and model 2. But noting that the latter has larger errors, we are inclined to believe that model 1 is better than model 2.
Fig. 4 Upper panel: O – C diagrams of BO Lyn using the ephemeris of Eq. (1); the solid line shows the fit based on a revised linear ephemeris and the cyclic change due to the LiTE; Middle panel: only the cyclic change τ is plotted for a better visualization; Bottom panel: Residual O – C diagram for BO Lyn. The descriptions of the symbols and error bars are the same as those in Fig. 3.
Download figure:
Standard imageIn the above analysis, all the weights of data points are the same. But in many analyses of other similar cases, the weights are usually set as 1/δ2, where δ values are the errors in the data. Adopting this approach, we fit the data again, and find that there is no significant change in the parameter results. It should be mentioned that some data points did not include errors, and we assumed that their errors are equal to the average error (0.00154 d). However, as we mentioned in Section 2, different detection methods can introduce systematic deviations to the times of light maximum (∼0.0025 d). Taking this into account, we decreased the O – C points obtained from DASCH, NSVS and CRTS by 0.0025 d and re-fit the O – C curves. The resulting parameter values were consistent with the previous results in the error range. Noting that the values of deviations are one order of magnitude smaller than that of A (∼0.03 d), it can be expected that their influences on the O – C diagram are minimal.
4. Discussion and Conclusions
Using the [m1]-[c1] diagram, Peña et al. (2016) suggested that the spectral type of BO Lyn varies between A5V–A8V. For an A5V star, its mass and absolute magnitude MV are 1.86 M⊙ and 2.0 respectively, and for an A8V star, they are 1.66 M⊙ and 2.4 (Adelman 2004). In the following discussion, we adopt the mean values, assuming that the mass and absolute magnitude of BO Lyn are M1 = 1.76 M⊙ and ⟨MV⟩ = 2.2 respectively. Using the mass function, we can calculate the mass of the companion M2. When the inclination of the binary system i = 90°, the companion's mass of BO Lyn is 0.95±0.30 M⊙, and the distance between the companion and the pulsating star at periastron is about 5.3 ± 0.5 au. This is similar to the situation of the SX Phoenicis star KZ Hya. Fu et al. (2008) found that it has a companion with a lower limit on mass of 0.83 M⊙. After checking the b – y value and spectroscopic data, they concluded that the companion should be a degenerate companion, like a white dwarf, neutron star or black hole. The color index b – y at the time of light minimum of BO Lyn is 0.231 (at HJD 2457401.9509, see table 6 in Peña et al. 2016). If the companion were a late type main sequence star with high inclination, the combined color index b – y should be larger than the observed value (Fu et al. 2008). Hence, this possibility can be excluded, and the companion could be an A or F type main sequence star or a degenerate star with low luminosity. If the companion were the former, its luminosity cannot be ignored, and it would decrease the observed amplitude of the pulsating star. From the spectral type (A5V-A8V, Peña et al. 2016), the amplitude of BO Lyn should be about 0.4 (= 2.4 – 2.0), but the observed V amplitude is ΔV = 0.23 mag, which is smaller than that of most other HADS stars. From the following equations:
and
where Lmax = 13.6 L⊙ and Lmin = 9.4 L⊙ (obtained from absolute magnitudes, which are the luminosities of a pulsating star at light maximum and minimum), we can calculate the luminosity of the companion to be L2 ≃ 8.4 L⊙. This value indicates that the companion should be a late A-type main sequence star with a mass of 1.67 M⊙ (Drilling & Landolt 2000). Moreover, the corresponding inclination i is around 42°.
The companion would also cause the systematic shift in mean radial velocities. Using Equation (8) in Li & Qian (2014), we can calculate the velocity semi-amplitude K = 5.89 ± 0.30 kms−1. Kinman (1998) obtained three radial velocities of BO Lyn in February 1995. Based on these data, they found a velocity amplitude of 19 km s−1 and a mean radial velocity of 30 ± 2 km s−1. From our calculation, the mean radial velocity of BO Lyn in recent years should increase about 2 km s−1. However, this calculation only works when the companion is a degenerate star with low luminosity. If the companion is a late A-type star, its luminosity cannot be ignored, and it can be expected that we would see double lines in the spectra of the BO Lyn system. In order to acquire more conclusive evidence for the companion, we suggest that high temporal and spectral resolution spectroscopic observations are needed in the future.
Stellar evolution theories predict that the pulsation periods of δ Scuti stars should increase with time. However, because not only the evolution, but also other mechanisms (e.g. LiTE) would influence the pulsation periods, making the patterns in O – C diagrams more complicated. Hintz et al. (2005) provided a value of period decrease for BO Lyn, −0.056 dMyr−1. But their results, based on a short range study, were only seeing part of the orbit, and not long-term period changes. In our analysis, we determined an increase in the period at a rate of dP/dt = 3.89 × 10−13 d cycle−1, or 1.52 × 10−3 dMyr−1. This result, based on the data spanning a longer time scale, can describe the O – C curves well by accounting for the periodic variation. Moreover, both the positive direction and the order of magnitude of period change are consistent with the value computed from evolutionary models (Breger & Pamyatnykh 1998; Breger 2000). Noting that model 2, which fixes β as zero, also gives reliable results, maybe the high amplitude periodic variation in the O – C diagramaffects the accuracy of measurements related to the long-term period change. To confirm this, more photometric observations are also needed in the future to verify these changes.
We adopted 179 times of light maximum covering more than 100 yr to study the behavior of the pulsation period of BO Lyn. Variations in the O – C diagram show a secular increase in the pulsation period with a rate of dP/dt = 3.89 × 10−13 d cycle−1 and a perturbation caused by a companion star. The corresponding orbital eccentricity e is 0.64 and the orbital period PB is about 34.5 yr. Assuming the mass of BO Lyn is 1.76 M⊙, the lower limit on the companion's mass (M2) is obtained as 0.95 M⊙. We find that the observed full amplitude (ΔV = 0.23) is smaller than the amplitude corresponding to spectral type A5V–A8V, which means that the luminosity of the companion should not be ignored. By calculation, the companion should be a late A-typemainsequence star, and the corresponding orbital inclination i is about 42°. We also suggest that high-resolution spectroscopic observations and more photometric observations are needed to check the nature of the companion and the long-termperiod change of BO Lyn. In this work, historical sky surveys play an important role. Valuable information can be determined from them, which can then be used to study the nature of stars.
Acknowledgements
This paper makes use of data from the first public release of the WASP data (Butters et al. 2010) as provided by theWASP consortium and services at the NASA Exoplanet Archive. This effort is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. Data from the OMC Archive at CAB (INTA-CSIC) are pre-processed by ISDC. The DASCH project at Harvard is grateful for partial support from NSF grants AST-0407380, AST-0909073 and AST-1313370.
This work is partly supported by the West Light Foundation of Chinese Academy of Sciences; the National Natural Science Foundation of China (Nos. 11325315 and 11573063), the Yunnan Natural Science Foundation (Nos. 2013FB084, 2014FB187 and 2017FA001) and the Strategic Priority Research Program "The Emergence of Cosmological Structures" of the Chinese Academy of Sciences (Grant No. XDB09010202). The authors thank Profs. M. Zejda and Z. Mikulášek for their presentation on those sky surveys, and also thank the referee for helpful suggestions.