Abstract
We outline a theory for the Aharonov–Bohm effect in a novel type of quantum ring, namely the quadratic Gauss quantum ring, here for brevity called the Gauss ring. A Gauss ring is a one-dimensional nonperiodic lattice with sites at z = zj = jnd with j ∈ {0, 1, 2, ⋯ , s + 1} (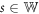 ), n ≥ 2 (
), n ≥ 2 (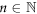 ), and d the underlying period wrapped into a ring-shaped geometry. Here we discuss the electronic spectrum of quadratic Gauss rings (n = 2, s ∈ {0, 1, 2, ⋯ , 5, 6, 7}), and show that the spectrum can be described using theoretical tools recently devised to provide an understanding of the Gauss chain [D S Citrin (2023) Phys. Rev. B 107, 235 144]. We then consider the effect on the electronic states of a magnetic flux Φ threading the Gauss ring and show that the effect of the flux is to select specific electronic states from a periodic chain whose supercells are finite-length Gauss chains thus relating the states in the Gauss quantum ring with those in a periodic Gauss chain.
), and d the underlying period wrapped into a ring-shaped geometry. Here we discuss the electronic spectrum of quadratic Gauss rings (n = 2, s ∈ {0, 1, 2, ⋯ , 5, 6, 7}), and show that the spectrum can be described using theoretical tools recently devised to provide an understanding of the Gauss chain [D S Citrin (2023) Phys. Rev. B 107, 235 144]. We then consider the effect on the electronic states of a magnetic flux Φ threading the Gauss ring and show that the effect of the flux is to select specific electronic states from a periodic chain whose supercells are finite-length Gauss chains thus relating the states in the Gauss quantum ring with those in a periodic Gauss chain.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
A quantum ring is a quasi-one-dimensional material fashioned into a ring-shaped geometry. Such structures are of interest in part due to the Aharonov–Bohm (A-B) effect [1], where it was shown that the energy of an electron in a ring threaded by magnetic flux Φ is affected by the flux, even if there is no flux through portions of the structure in which there is nonzero probability density to find the electron. The A-B effect leads to persistent currents [2] and oscillation of the energy with Φ [3, 4]. The A-B effect has been observed in numerous experiments, notably in metal and semiconductor quantum rings [5–16]. Subsequently, evidence of the A-B effect was seen in optical experiments and also led to interest in the excitonic A-B effect [17–22]. Many-body effects, not discussed in the present work, are reviewed in [23].
In a quantum ring the electron wavefunctions must be single-valued, i.e. in going 2π in angle ϕ around the ring, the value of the wavefunction must match that where one starts. (Our discussion leaves out the Zeeman splitting associated with the electron spin's interaction with the magnetic field. This effect is additive in the absence of significant spin-orbit interaction and is smaller in typical cases than energy shifts due to the A-B effect.) In the absence of any additional potential in the ring, this gives one-dimensional eigenstates 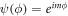 with
with 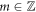 of energy at zero magnetic flux
of energy at zero magnetic flux 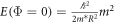 where m* is the electron effective mass and R is the quantum-ring radius. (The presence of a potential will result in energy eigenstates mixing various values of m.) In the A-B effect in a quantum ring, the energy eigenstates preserve the form ψ(ϕ), but modify the energy eigenvalues to
where m* is the electron effective mass and R is the quantum-ring radius. (The presence of a potential will result in energy eigenstates mixing various values of m.) In the A-B effect in a quantum ring, the energy eigenstates preserve the form ψ(ϕ), but modify the energy eigenvalues to 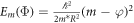 where φ = Φ/Φ0 and Φ0 = hc/e is the quantum of magnetic flux. These states contribute to the persistent currents I = ∂Em
(Φ)/∂Φ of the single-particle states. Our aim in this study is to engineer a potential around a quantum ring to attain a degree of control over the energy eigenvalues and persistent currents based on a one-dimensional quasiperiodic lattice.
where φ = Φ/Φ0 and Φ0 = hc/e is the quantum of magnetic flux. These states contribute to the persistent currents I = ∂Em
(Φ)/∂Φ of the single-particle states. Our aim in this study is to engineer a potential around a quantum ring to attain a degree of control over the energy eigenvalues and persistent currents based on a one-dimensional quasiperiodic lattice.
In recent work we have studied quadratic Gauss chains (GC) [24–28] in which lattice sites are located on the z axis at z = zj
= jn
d with 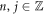 , n = 2, and d the underlying lattice constant. The name Gauss is attached to these chains due to the central rôle played in the theory by Gauss sums [24, 26, 28, 29]. Quasiperiodic lattices have been of great interest for a number of reasons. First, such structures in some cases exhibit properties intermediate between periodic and random lattices. As such, quasiperiodic lattices may show exotic behavior with regard to their spectra and localized versus delocalized states, scaling on physical properties with chain length, in the process shedding light on the nature of these effects in more familiar periodic and random lattices. GCs in particular have properties distinct from other quasiperiodic chains heretofore investigated [30–33]. Reference [25] characterized the delocalized-state spectrum in closed form; it was found to be singular-continuous with candidate delocalized states at freespace wavevectors k, i.e. between quadratic sites, such that
, n = 2, and d the underlying lattice constant. The name Gauss is attached to these chains due to the central rôle played in the theory by Gauss sums [24, 26, 28, 29]. Quasiperiodic lattices have been of great interest for a number of reasons. First, such structures in some cases exhibit properties intermediate between periodic and random lattices. As such, quasiperiodic lattices may show exotic behavior with regard to their spectra and localized versus delocalized states, scaling on physical properties with chain length, in the process shedding light on the nature of these effects in more familiar periodic and random lattices. GCs in particular have properties distinct from other quasiperiodic chains heretofore investigated [30–33]. Reference [25] characterized the delocalized-state spectrum in closed form; it was found to be singular-continuous with candidate delocalized states at freespace wavevectors k, i.e. between quadratic sites, such that  is a rational number. The delocailized-state spectrum has been shown to consist of a hierarchy of minibands and gaps. For absolute value of the onsite potential parameter λ exceeding a k-dependent value, most states become localized, but some continue as delocalized for arbitrarily large ∣λ∣ [25]. This behavior is due to a hidden symmetry of the GC and can be seen from the transfer matrix, which is periodic with its period depending on wavevector k, even though the GC itself is nonperiodic [26]. That is, the transfer matrix for the GC is surprisingly periodic with a k-dependent period where k is the free-electron wavevector between scattering sites of the GC [25]. Moreover, the structure factor and delocalized-state spectrum of the GC is related to theta functions and Gauss sums, indicating its inherent number-theoretic interest [24, 26, 28].
is a rational number. The delocailized-state spectrum has been shown to consist of a hierarchy of minibands and gaps. For absolute value of the onsite potential parameter λ exceeding a k-dependent value, most states become localized, but some continue as delocalized for arbitrarily large ∣λ∣ [25]. This behavior is due to a hidden symmetry of the GC and can be seen from the transfer matrix, which is periodic with its period depending on wavevector k, even though the GC itself is nonperiodic [26]. That is, the transfer matrix for the GC is surprisingly periodic with a k-dependent period where k is the free-electron wavevector between scattering sites of the GC [25]. Moreover, the structure factor and delocalized-state spectrum of the GC is related to theta functions and Gauss sums, indicating its inherent number-theoretic interest [24, 26, 28].
Here we study a quadratic GC wrapped upon itself into a quantum ring as in figure 1, calling it a Gauss ring (GR), and explore the flux-dependent properties of the electronic states. Our aim is to establish a theoretical approach to the A-B effect in such structures. We consider a purely one-dimensional GR of negligible width and assume that Φ entirely threads the GR. The GR is formed from a GC in which the j = 0 and 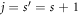 sites coïncide. Thus, the GR is composed of
sites coïncide. Thus, the GR is composed of 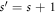 sites, with j ∈ {0, 1, 2, ⋯ , s − 2, s − 1, s}. (It will be convenient at times to employ
sites, with j ∈ {0, 1, 2, ⋯ , s − 2, s − 1, s}. (It will be convenient at times to employ  rather than s.) This is equivalent to considering an
rather than s.) This is equivalent to considering an  -site GC (recalling we start with the j = 0 site) with onsite Dirac δ-function potentials at zj
= j2
d subject to Born-von Karman boundary conditions within a Kronig-Penney model. By way of approaching the problem of the GR, we will first consider the electronic structure of an infinite chain composed of a periodic sequence of
-site GC (recalling we start with the j = 0 site) with onsite Dirac δ-function potentials at zj
= j2
d subject to Born-von Karman boundary conditions within a Kronig-Penney model. By way of approaching the problem of the GR, we will first consider the electronic structure of an infinite chain composed of a periodic sequence of 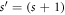 -site GCs, i.e. a superlattice (SL) whose supercell is a
-site GCs, i.e. a superlattice (SL) whose supercell is a 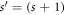 -site GC. We call this a GC SL. We then proceed to the GR. It is shown that the electronic states in the GR are a subset of those in the GC SL where the states are selected in effect by Φ; 2π
φ plays the rôle of
-site GC. We call this a GC SL. We then proceed to the GR. It is shown that the electronic states in the GR are a subset of those in the GC SL where the states are selected in effect by Φ; 2π
φ plays the rôle of 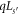 where
where 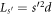 is the supercell length in the GC SL or the circumference of the GR and ℏ
q is the quasimomentum in the GC SL. There have been a few investigations of chains of coupled quantum rings where the properties from ring to ring are modulated by a Fibonacci sequence [34, 35]. We are unaware of any previous work in which the potential itself in circumnavigating a quantum ring is quasiperiodic. In our case, GRs will be seen to exhibit highly complex spectra due to the underlying GC structure, and such complexity sets in for rather low GC order.
is the supercell length in the GC SL or the circumference of the GR and ℏ
q is the quasimomentum in the GC SL. There have been a few investigations of chains of coupled quantum rings where the properties from ring to ring are modulated by a Fibonacci sequence [34, 35]. We are unaware of any previous work in which the potential itself in circumnavigating a quantum ring is quasiperiodic. In our case, GRs will be seen to exhibit highly complex spectra due to the underlying GC structure, and such complexity sets in for rather low GC order.
Figure 1. An 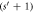 -site QC that will be formed into an
-site QC that will be formed into an 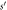 -site GR by identifying the j = 0 with the
-site GR by identifying the j = 0 with the 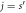 site. (The actual number of sites in the GC shown is
site. (The actual number of sites in the GC shown is  and in the GR
and in the GR  .) Index
.) Index 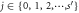 labels GC sites at z = zj
= j2
d along the ring. Due to Born-von Karman boundary conditions in the ring, the wavefunction of an electron satisfies
labels GC sites at z = zj
= j2
d along the ring. Due to Born-von Karman boundary conditions in the ring, the wavefunction of an electron satisfies  where
where 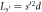 is the circumference of the GR.
is the circumference of the GR.
Download figure:
Standard image High-resolution image2. Theory
We begin by describing an electron in a chain; below we impose appropriate boundary conditions to results in the GC SL or the GR. Let the Hamiltonian be
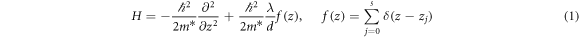
with m* the effective mass and λ the onsite potential strength (λ < 0 attractive). We do not account for the curvature of the ring or the transverse confinement, and treat the problem purely in one dimension. Therefore, we consider the GC SL or GR to be described by a one-dimensional Kronig-Penney model with Dirac δ-function potentials. Hereon, we take d = 1 and call the distance measured along the GC or around the GR circumference z, rather than employ the angle ϕ in the latter case. To minimize the number of parameters, we define the normalized Hamiltonian 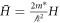 giving the Schrödinger equation
giving the Schrödinger equation 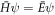 with
with 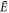 an eigenvalue of
an eigenvalue of 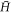 and ψ the eigenfunction. For the GC SL composed of many
and ψ the eigenfunction. For the GC SL composed of many 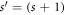 -site GCs, we require that the Bloch theorem
-site GCs, we require that the Bloch theorem 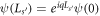 holds where
holds where  in the length of the supercell and ℏ
q is the quasimomentum. Born-von Karman boundary conditions
in the length of the supercell and ℏ
q is the quasimomentum. Born-von Karman boundary conditions 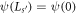 will later be imposed on the GR.
will later be imposed on the GR.
The electronic states are conveniently described using a transfer-matrix approach. To proceed, we will need to know how a wavefunction is affected by crossing a site of the GC or GR. Consider the wavefunction at fixed energy  between sites zj−1 < z < zj
. Because between sites the potential vanishes, the wavefunction must be that of a free particle,
between sites zj−1 < z < zj
. Because between sites the potential vanishes, the wavefunction must be that of a free particle,
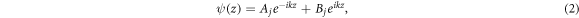
with 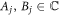 as yet undetermined. Given that ψ is continuous, we integrate the Schrödinger equation from zj
−
as yet undetermined. Given that ψ is continuous, we integrate the Schrödinger equation from zj
−  to zj
+
to zj
+  in the limit
in the limit  → 0, to give the conditions
→ 0, to give the conditions

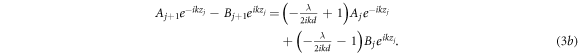
We can recast this in matrix form as
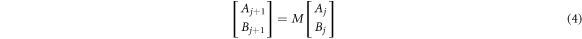
with

the transfer matrix across site 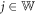 . The transfer matrix from just after the site at zj
to just before zj+1 is
. The transfer matrix from just after the site at zj
to just before zj+1 is
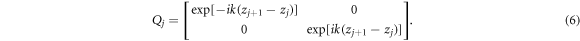
Consequently, the transfer matrix Ts
for 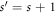 sites with
sites with  is
is
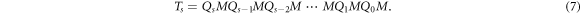
Note that the 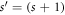 -site GC is of length
-site GC is of length 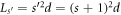 .
.
Consider now forming a chain that is a periodic sequence of 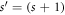 -site GCs, i.e. a GC SL. Its transfer matrix is thus ⋯Ts
Ts
Ts
Ts
⋯ . Now, Qj
and M are unimodular, and thus so is Ts
and indeed so is Ts
raised to any natural-number power. By the Bloch theorem,
-site GCs, i.e. a GC SL. Its transfer matrix is thus ⋯Ts
Ts
Ts
Ts
⋯ . Now, Qj
and M are unimodular, and thus so is Ts
and indeed so is Ts
raised to any natural-number power. By the Bloch theorem, 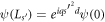 with ℏ
q the quasimomentum, which in terms of transfer matrices means the eigenvalues ξ± of Ts
for a given
with ℏ
q the quasimomentum, which in terms of transfer matrices means the eigenvalues ξ± of Ts
for a given 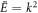 corresponding to delocalized states satisfy ξ+
ξ− = 1 or more conveniently from a computational standpoint
corresponding to delocalized states satisfy ξ+
ξ− = 1 or more conveniently from a computational standpoint
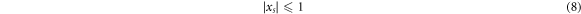
where  . For the
. For the 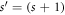 -site GR, however,
-site GR, however, 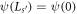 , whence we require in that case xs
= 1.
, whence we require in that case xs
= 1.
Before considering the GR, it will be helpful to understand an important point about the hidden symmetry of the infinite GC. One can show [25] that for ∣xs
∣ ≤ 1 we necessarily have 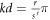 with
with 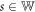 and
and 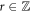 for candidate delocalized states in the infinite GC. In the present study, we first consider the GC SL.
for candidate delocalized states in the infinite GC. In the present study, we first consider the GC SL.
We now focus on the A-B effect [1] of GRs in the presence of a magnetic flux Φ threading the GR. In this case, the Hamiltonian of equation (1) is replaced with
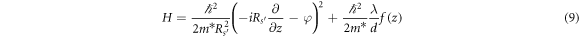
where 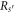 is the GR radius,
is the GR radius, 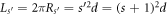 is the circumference of the
is the circumference of the 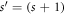 -site GR, and φ = Φ/Φ0 with Φ the magnetic flux and Φ0 = hc/e the flux quantum. For zj
< z < zj+1, the potential term in H does not appear and we have
-site GR, and φ = Φ/Φ0 with Φ the magnetic flux and Φ0 = hc/e the flux quantum. For zj
< z < zj+1, the potential term in H does not appear and we have
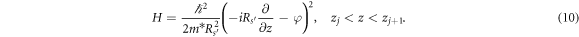
In this region, the (positive-energy) eigenstates of H can be written
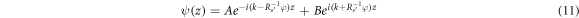
where A and B are coefficients to be determined. It is easily verified that the expression above for ψ(z) is indeed an eigenfunction of H with eigenvalue 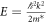 or
or 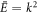 . Note that ψ(z) depends explicitly on Φ, but also implicitly on Φ as the allowed values of k depend on Φ. The energy eigenvalues
. Note that ψ(z) depends explicitly on Φ, but also implicitly on Φ as the allowed values of k depend on Φ. The energy eigenvalues 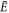 likewise depend on Φ.
likewise depend on Φ.
In the context of the transfer-matrix approach, let 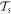 be the transfer matrix around the
be the transfer matrix around the 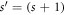 -site GR in the presence of Φ. To obtain
-site GR in the presence of Φ. To obtain 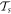 from Ts
, note that we need to replace Qj
by
from Ts
, note that we need to replace Qj
by }{Q}_{j}$](https://content.cld.iop.org/journals/1402-4896/99/2/025914/revision3/psad17adieqn58.gif) . We therefore have for the transfer matrix around the GR in the presence of Φ,
. We therefore have for the transfer matrix around the GR in the presence of Φ,
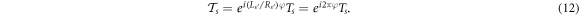
Born-von Karman boundary conditions hold when the energy eigenvalues 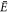 –or equivalently k–satisfy
–or equivalently k–satisfy
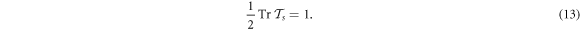
One finds by inspection of equation (12) that the spectrum is periodic in Φ with period Φ0.
The electronic states of the GR are a subset of those of the GC SL. Compare equation (8) for the GC SL with equation (13) for the GR, respectively:

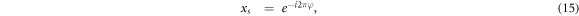
where we have slightly rearranged equation (15) for the GR using equation (12). These are twisted boundary conditions. Clearly, the solutions of equation (15) are a subset of those of equation (14) where φ in essence specifies the subset selected. In other words, varying Φ in the GR enables one to selectively explore electronic states in the GC SL. In effect, 2π
φ in the GR plays the rôle of 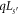 in the GC SL with q the crystal momentum.
in the GC SL with q the crystal momentum.
3. Results
In this section we start by considering the GC SL composed of supercells consisting of  -site GCs, i.e. of period
-site GCs, i.e. of period 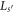 . In this case, the delocalized states are determined by ∣xs
∣ ≤ 1. In an infinite QC, the candidate delocalized states (they can become localized for ∣λ∣ above a k-dependent value) have kd/π a rational number [25]. As shown in [26], this is because for
. In this case, the delocalized states are determined by ∣xs
∣ ≤ 1. In an infinite QC, the candidate delocalized states (they can become localized for ∣λ∣ above a k-dependent value) have kd/π a rational number [25]. As shown in [26], this is because for 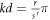 , we can write the transfer matrix for the infinite GC as a product of repeated factors of Ts
. For the GC SL with each period consisting of an
, we can write the transfer matrix for the infinite GC as a product of repeated factors of Ts
. For the GC SL with each period consisting of an 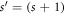 -site GC considered here, this restriction on k is lifted; however, we shall see a vestige of the effect related to the infinite GC just mentioned.
-site GC considered here, this restriction on k is lifted; however, we shall see a vestige of the effect related to the infinite GC just mentioned.
Figure 2 shows the values of kd for delocalized states for various values of λ in the GC SL with each period 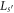 an
an 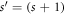 -site GC. Recall, k is a surrogate for normalized energy
-site GC. Recall, k is a surrogate for normalized energy 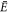 via
via 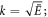 we do not show states for
we do not show states for 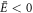 (kd imaginary) for λ < 0. Results are shown for s ∈ {0, 1, 2, ⋯ ,5, 6, 7}, i.e.
(kd imaginary) for λ < 0. Results are shown for s ∈ {0, 1, 2, ⋯ ,5, 6, 7}, i.e. 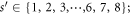 in each case, the first panel is for negative values of λ while the second for positive λ. For a given λ, the horizontal black lines show allowed values of kd for delocalized states, i.e. bands, while the white areas correspond to localized states, i.e. bandgaps. Of course bands and bandgaps also exist for values of λ between those shown. The case s = 0 in figure 2(a) and (b) treats a periodic lattice whose unit cell consists of a single quadratic site with a freespace interval of length d, and thus the lattice constant is L1 = d. We see a lower (upper) bandedge at kd = m
π with
in each case, the first panel is for negative values of λ while the second for positive λ. For a given λ, the horizontal black lines show allowed values of kd for delocalized states, i.e. bands, while the white areas correspond to localized states, i.e. bandgaps. Of course bands and bandgaps also exist for values of λ between those shown. The case s = 0 in figure 2(a) and (b) treats a periodic lattice whose unit cell consists of a single quadratic site with a freespace interval of length d, and thus the lattice constant is L1 = d. We see a lower (upper) bandedge at kd = m
π with 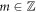 for λ < 0 (λ > 0). For s ≥ 1, bandgaps originate at
for λ < 0 (λ > 0). For s ≥ 1, bandgaps originate at 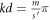 near λ = 0. For λ < 0 (λ > 0) there are two types of lower (upper) bandedges. The positions of those at kd = 2m
π or kd = m
π for s even or odd are independent of λ, while the other lower (upper) bandedges trend toward lower (higher) kd as λ decreases (increases). As s increases, the bandwidths and bandgaps become narrower in kd. (Note, simultaneous with an increase in s is an increase in the GC SL period
near λ = 0. For λ < 0 (λ > 0) there are two types of lower (upper) bandedges. The positions of those at kd = 2m
π or kd = m
π for s even or odd are independent of λ, while the other lower (upper) bandedges trend toward lower (higher) kd as λ decreases (increases). As s increases, the bandwidths and bandgaps become narrower in kd. (Note, simultaneous with an increase in s is an increase in the GC SL period 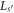 .) Also, as bands narrow for higher s, some bands narrow to the point that they are no longer clearly visible in the plots; nonetheless, they persist as ∣λ∣ increases. As one proceeds from bandgap to bandgap, the bandedge states alternate such that
.) Also, as bands narrow for higher s, some bands narrow to the point that they are no longer clearly visible in the plots; nonetheless, they persist as ∣λ∣ increases. As one proceeds from bandgap to bandgap, the bandedge states alternate such that 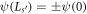 . This will mean that only half the bandedge states seen in figure 2 will serve as states of the GR where only
. This will mean that only half the bandedge states seen in figure 2 will serve as states of the GR where only 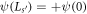 satisfies the Born-von Karman boundary conditions.
satisfies the Born-von Karman boundary conditions.
Figure 2. Delocalized states of the periodic QC with 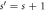 sites per period
sites per period 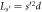 as a function of kd and λ for various s. The states satisfy ∣xs
∣ ≤ 1.
as a function of kd and λ for various s. The states satisfy ∣xs
∣ ≤ 1.
Download figure:
Standard image High-resolution imageWe now turn to the 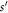 -site GR for Φ = 0 where the states satisfy the Born-von Karman boundary conditions, or in other words
-site GR for Φ = 0 where the states satisfy the Born-von Karman boundary conditions, or in other words 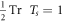 . In figure 3 are plotted the GR states as functions of kd for various λ and s. The states shown correspond to half the bandedge states seen in figure 2, namely those for which
. In figure 3 are plotted the GR states as functions of kd for various λ and s. The states shown correspond to half the bandedge states seen in figure 2, namely those for which 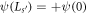 , but not those for which
, but not those for which 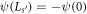 . At λ = 0, the values of k are given by
. At λ = 0, the values of k are given by 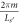 as expected. Many of the trends noted concerning figure 2 apply here as well. We also note that as s increases, the plots of the λ-dependent spectra resembles the stack structures computed in [25]. By s = 7, a stack structure emerges. The λ-independent bandedges in the case of figure 2 here translate into GR states whose energies are independent of λ.
as expected. Many of the trends noted concerning figure 2 apply here as well. We also note that as s increases, the plots of the λ-dependent spectra resembles the stack structures computed in [25]. By s = 7, a stack structure emerges. The λ-independent bandedges in the case of figure 2 here translate into GR states whose energies are independent of λ.
Figure 3. States of the GR as a function of kd and λ for various s. The states shown satisfy xs
= 1 and thus obey Born-von Karman boundary conditions at z = 0 and  at zero magnetic flux Φ = 0.
at zero magnetic flux Φ = 0.
Download figure:
Standard image High-resolution imageWhy the λ-independence of some GR states? Consider states varying as 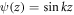 or
or  around the GR where z is the coördinate around the GR circumference. Clearly, at λ = 0, all states apart from kd = 0 are two-fold degenerate. Increasing ∣λ∣ from zero breaks this degeneracy. Those states whose energies
around the GR where z is the coördinate around the GR circumference. Clearly, at λ = 0, all states apart from kd = 0 are two-fold degenerate. Increasing ∣λ∣ from zero breaks this degeneracy. Those states whose energies 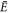 and hence kd are independent of λ vary as
and hence kd are independent of λ vary as 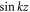 with kd = 2m
π or kd = m
π for s even or odd. In these cases, ψ(z) has nodes at the locations of the quadratic sites, and thus
with kd = 2m
π or kd = m
π for s even or odd. In these cases, ψ(z) has nodes at the locations of the quadratic sites, and thus 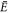 is independent of λ. The
is independent of λ. The 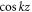 -like states for these values of kd in a perturbation picture sample the quadratic sites, and thus their energies depend on λ.
-like states for these values of kd in a perturbation picture sample the quadratic sites, and thus their energies depend on λ.
Finally, we consider the magnetic-flux dependence of the energy eigenvalues. In figure 4 are shown the GR states for a  GR for various values of φ = Φ/Φ0. The value
GR for various values of φ = Φ/Φ0. The value  is merely chosen to illustrate the general properties discussed below. The energy eigenvalues are obtained by solving equation (13). Note that the energy eigenvalues are periodic in φ with period 1 as expected. Starting at φ = 0 in figures 4(a) and (b), as we saw as in figure 3(c) and (d) which are identical with figures 4(a) and (b), that the values of kd are equally spaced at λ = 0 as is well known. The presence of the quadratic sites perturbs the energy eigenvalues, showing up as nonequispaced kd as ∣λ∣ increases from 0. As φ increases from 0, the degeneracies at λ = 0 are broken, with the degeneracy at λ = 0 eventually restored at φ = 0.5, though the kd values for λ ≠ 0 differ for φ = 0 and 0.5. States whose energies are λ-independent at φ = 0 no longer enjoy this property. Further increasing φ again leads to breaking the λ = 0 degeneracy, which is again restored at φ = 1, which is identical with the case φ = 0. In addition, the energy eigenvalues are even in φ; noting the periodicity in φ, compare, say, figures 4(c) and (o) or (d) and (p). We note that it is easy to verify from the plots that the states for the GR are a subset of those for the GC SL selected by φ.
is merely chosen to illustrate the general properties discussed below. The energy eigenvalues are obtained by solving equation (13). Note that the energy eigenvalues are periodic in φ with period 1 as expected. Starting at φ = 0 in figures 4(a) and (b), as we saw as in figure 3(c) and (d) which are identical with figures 4(a) and (b), that the values of kd are equally spaced at λ = 0 as is well known. The presence of the quadratic sites perturbs the energy eigenvalues, showing up as nonequispaced kd as ∣λ∣ increases from 0. As φ increases from 0, the degeneracies at λ = 0 are broken, with the degeneracy at λ = 0 eventually restored at φ = 0.5, though the kd values for λ ≠ 0 differ for φ = 0 and 0.5. States whose energies are λ-independent at φ = 0 no longer enjoy this property. Further increasing φ again leads to breaking the λ = 0 degeneracy, which is again restored at φ = 1, which is identical with the case φ = 0. In addition, the energy eigenvalues are even in φ; noting the periodicity in φ, compare, say, figures 4(c) and (o) or (d) and (p). We note that it is easy to verify from the plots that the states for the GR are a subset of those for the GC SL selected by φ.
Figure 4. States of the GR as a function of kd and λ for s = 1 and various φ = Φ/Φ0. The states shown satisfy  and thus obey Born-von Karman boundary conditions at z = 0 and
and thus obey Born-von Karman boundary conditions at z = 0 and 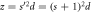 in the presence of magnetic flux Φ threading the GR.
in the presence of magnetic flux Φ threading the GR.
Download figure:
Standard image High-resolution image4. Conclusions
We have presented a theoretical sketch of the electronic structure of GRs based on the recently introduced GC [24, 25]. We have computed the electronic states in the GC SL and in the GR using a transfer-matrix approach based on a Kronig-Penney model with Dirac δ-function site potentials and allowing for a magnetic flux Φ threading the GR. We explore the effects of varying the GR circumference 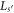 , the strength of the quadratic-site potential parameter λ, and of the magnetic flux Φ threading the GR. As λ and Φ are varied, complex behavior of the energy eigenvalues of the states is revealed. It is shown that the states in the GR are subsets of those in the GC SL selected by Φ. In essence, in the GR 2π
φ plays the rôle of
, the strength of the quadratic-site potential parameter λ, and of the magnetic flux Φ threading the GR. As λ and Φ are varied, complex behavior of the energy eigenvalues of the states is revealed. It is shown that the states in the GR are subsets of those in the GC SL selected by Φ. In essence, in the GR 2π
φ plays the rôle of 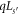 in the GC SL. The approach is easily adapted to allow for other potentials characterized by a finite set of Dirac δ-functions. The GR potential provides an additional control over the energy eigenvalues in the GR as Φ is varied and over the persistent currents of the single-particle states.
in the GC SL. The approach is easily adapted to allow for other potentials characterized by a finite set of Dirac δ-functions. The GR potential provides an additional control over the energy eigenvalues in the GR as Φ is varied and over the persistent currents of the single-particle states.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Funding
This work was supported in part by the support of Conseil Régional Grand Est.





