Abstract
We predict the existence of high frequency modes in the interference pattern of two condensates made of fermionic-atom dimers. These modes, which result from fermion exchanges between condensates, constitute a striking signature of the dimer composite nature. From the 2-coboson spatial correlation function, that we derive analytically, and the Shiva diagrams that visualize many-body effects specific to composite bosons, we identify the physical origin of these high frequency modes and determine the conditions to see them experimentally by using bound fermionic-atom pairs trapped on optical lattice sites. The dimer granularity which appears in these modes comes from Pauli blocking that prevents two dimers to be located at the same lattice site.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
All particles consisting of an even number of fermions are boson-like. Although this property merely derives from a mathematical fact—the particle creation operators commute—the boson-like nature of the particles bears a strong consequence: they must undergo Bose–Einstein condensation (BEC). This physical effect has been observed for dilute gases of ultracold bosonic atoms [1–4], decades after Einstein predicted it. An oscillatory behavior showing the condensate coherence has also been observed in the interference pattern of two condensates of bosonic atoms [5–8].
The fact that boson-like particles are made of fermions shows up in nontrivial ways. This composite nature mathematically appears through the commutator of their destruction and creation operators, ![${\left[{{ \mathcal B }}_{i},{{ \mathcal B }}_{j}^{\dagger }\right]}_{-}\,={\delta }_{i,j}-{D}_{i,j}$](https://content.cld.iop.org/journals/1367-2630/21/4/043041/revision2/njpab0cc6ieqn1.gif) . While this commutator reduces to the delta term for elementary bosons, the Di, j operator is responsible for fermion exchanges with other particles [9, 10]. Although these exchanges are commonly neglected, the composite bosons (cobosons) then reducing to point-like structureless elementary bosons, they can have significant consequences. The study of the particle composite nature in the field of semiconductor excitons was pioneered by Keldysh and Kozlov [11] as early as 1968.
. While this commutator reduces to the delta term for elementary bosons, the Di, j operator is responsible for fermion exchanges with other particles [9, 10]. Although these exchanges are commonly neglected, the composite bosons (cobosons) then reducing to point-like structureless elementary bosons, they can have significant consequences. The study of the particle composite nature in the field of semiconductor excitons was pioneered by Keldysh and Kozlov [11] as early as 1968.
In a gas, the coboson centers of mass are delocalized over the system volume LD, where D is the space dimension, while fermion exchanges occur over the coboson volume aBD, where aB is its Bohr radius. So, many-body effects induced by fermion exchanges between N cobosons are controlled by the dimensionless parameter
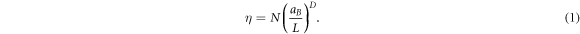
This leads us to conclude that the particle composite nature can only have significant consequences for a dense gas at the scale of the coboson size6 . Sizeable η's are difficult to reach for cold atoms due to the very small atom size; yet a 6Li2 dimer condensate with density reaching 0.3 on the dimer–dimer scattering length scale has been reported [13].
By contrast, in the case of semiconductor Wannier excitons, with size two orders of magnitude larger than typical atoms, values of η as large as 1, or even larger, are easy to reach—although for such large η's, excitons dissociate into an electron–hole plasma. The Wannier exciton composite nature has been shown to have a significant impact on the physics of excited semiconductors. Among its noticeable consequences, we can cite the exciton optical Stark effect [14–16] and the coexistence of dark and bright condensates [17, 18] that results [19] from the coupling, through fermion exchange, between bright excitons with spin ±1 and dark excitons with spin ±2.
It has been shown from the study of Wannier excitons, Frenkel excitons and Cooper pairs [10], that the dimensionless parameter which rules composite boson many-body effects physically corresponds to η = N / Nmax, where Nmax is the number of cobosons that the sample can accommodate. For Wannier excitons, this number is (L/aB)3, because for a higher number, excitons overlap and dissociate into an electron–hole plasma. In the case of Frenkel excitons, made of on-site excitations in a periodic lattice, Nmax is the number Ns of lattice sites in the sample at hand.
As a result, a more controllable platform to get sizable η is not to use a gas but an optical lattice, as previously considered to study Hong-Ou-Mandel-like interferences [20]. Indeed, dense samples in which each lattice potential well traps a single dimer have already been made, with η ∼ 0.4 for 40K2 fermionic-atom dimers [21], and η ∼ 0.5 or 0.8 for 87Rb2 [22] or 133Cs2 [23] bosonic-atom dimers. In the case of heteronuclear dimers, dense optical lattice samples of RbCs [24] and KRb [25, 26] have also been reported. These studies open an exciting route in the field of cold atoms, toward studying the rich yet essentially unexplored world of many-body effects resulting from dimensionless fermion (or boson) exchanges, that is, exchanges occurring between quantum particles in the absence of energy-like particle-particle interaction.
Motivated by the pioneering studies of condensate coherence properties in the case of bosonic atoms [5–8], we here investigate the effect of the particle composite nature on the interference pattern of two condensates made of fermionic-atom dimers. We first give arguments to find their signature in the spatial correlation function; next, we provide hints on how this function can be analytically derived, and finally we discuss the relevant limits.
To do it, we consider N pairs of fermionic atoms, α and β, in different hyperfine states, these atoms being trapped in an optical lattice having Ns sites. Their Hamiltonian reads as [20]
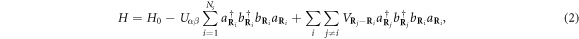
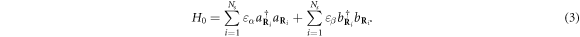
The H0 eigenstates for one fermionic-atom pair are  with energy εα + εβ, where
with energy εα + εβ, where  denotes the vacuum. The energy levels, (εα, εβ), depend on the optical lattice potential. The strength of the atom–atom attractive potential, Uαβ > 0, can be varied through Feshbach resonance, allowing a control on the spatial extension aB of a bound pair. For large Uαβ attraction, the lowest-energy subspace reduces to the Ns states,
denotes the vacuum. The energy levels, (εα, εβ), depend on the optical lattice potential. The strength of the atom–atom attractive potential, Uαβ > 0, can be varied through Feshbach resonance, allowing a control on the spatial extension aB of a bound pair. For large Uαβ attraction, the lowest-energy subspace reduces to the Ns states,  , with energy
, with energy  , each lattice site
, each lattice site  possibly hosting one bound pair, with creation operator
possibly hosting one bound pair, with creation operator  . These pairs are structureless when the lattice period, which is equal to half the optical laser wavelength λ, is large compared to the relative-motion extension aB of a bound pair. This inequality,
. These pairs are structureless when the lattice period, which is equal to half the optical laser wavelength λ, is large compared to the relative-motion extension aB of a bound pair. This inequality,  , can be easily fulfilled in optical lattice experiments, as in the case of 40K2 dimers [21].
, can be easily fulfilled in optical lattice experiments, as in the case of 40K2 dimers [21].
The third term of equation (2) describes inter-site interaction. Its  strength can be changed by changing the laser intensity which is proportional to the lattice potential depth V0. Due to this inter-site interaction, bound fermionic-atom pairs delocalize over the whole lattice. To justify our consideration of one bound pair per lattice site at most, the inter-site interaction has to be small compared to the on-site repulsion. This condition can be achieved when the lattice potential depth V0 is large compared to the recoil energy
strength can be changed by changing the laser intensity which is proportional to the lattice potential depth V0. Due to this inter-site interaction, bound fermionic-atom pairs delocalize over the whole lattice. To justify our consideration of one bound pair per lattice site at most, the inter-site interaction has to be small compared to the on-site repulsion. This condition can be achieved when the lattice potential depth V0 is large compared to the recoil energy  , with
, with  and ma the atom mass, as previously shown in the case of elementary bosons [27].
and ma the atom mass, as previously shown in the case of elementary bosons [27].
In the following, we shall refer to fermionic atoms simply as fermions, and refer to delocalized bound pairs as dimers. The dimer creation operators

with a distribution which is flat,  , in the large lattice limit. As the dimer spatial extension aB is essentially zero, it cannot enter the dimensionless parameter that controls many-body effects. Instead, this dimensionless parameter for N dimers in an optical lattice having Ns sites reads, like for Frenkel excitons [10, 28, 29], as
, in the large lattice limit. As the dimer spatial extension aB is essentially zero, it cannot enter the dimensionless parameter that controls many-body effects. Instead, this dimensionless parameter for N dimers in an optical lattice having Ns sites reads, like for Frenkel excitons [10, 28, 29], as
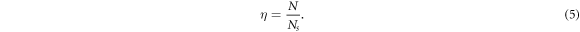
To produce two condensates made from such dimers, we propose to first prepare a single condensate in an optical lattice having a lattice spacing equal to a few hundreds of nanometers, depending on the laser wavelength. Then, we ramp up a potential barrier in the middle of the lattice using an external field in order to split this condensate into two spatially separated condensates, which are ultimately let to interfere, and we measure the correlation function. The potential barrier in the middle of the experimental setup can be produced by imposing another optical lattice with a much larger lattice spacing. Lattice spacing of the order of a hundred micrometers has been experimentally produced [30] by using two near-infrared laser beams with λ wavelength intersecting at a small angle θ, the lattice spacing being equal to  . For nearly collimated beams, that is, for θ ∼ 0, the lattice spacing can become very large, of the order of hundreds of micrometers.
. For nearly collimated beams, that is, for θ ∼ 0, the lattice spacing can become very large, of the order of hundreds of micrometers.
We predict that, compared to elementary bosons, the interference pattern has additional high frequency modes that come from fermion exchanges between condensates. These interferences constitute a striking signature of the dimer composite nature. As these additional modes are many-body in essence, a sizeable η is required to observe them. This is why previous experiments performed with two rather dilute condensates made of small bosonic atoms like rubidium [5] or sodium [6–8], with momenta  and
and  , have only seen interferences ruled by the momentum difference,
, have only seen interferences ruled by the momentum difference,  . Such interferences can be obtained by taking the bosonic atoms as elementary bosons [31–33]. The higher frequency modes we predict come from fermion exchanges involving more than one dimer from each of the two
. Such interferences can be obtained by taking the bosonic atoms as elementary bosons [31–33]. The higher frequency modes we predict come from fermion exchanges involving more than one dimer from each of the two  and
and  condensates. They can produce momentum differences
condensates. They can produce momentum differences  with
with  : the m = 2 mode appears when at least one fermion exchange in each condensate enters into play; so, its amplitude is η2 smaller than the m = 1 mode. Fermion exchanges also affect the m = (0,1) modes present for elementary bosons, but only through η corrections in their prefactors.
: the m = 2 mode appears when at least one fermion exchange in each condensate enters into play; so, its amplitude is η2 smaller than the m = 1 mode. Fermion exchanges also affect the m = (0,1) modes present for elementary bosons, but only through η corrections in their prefactors.
2. Physics of the problem
In this section, we use simple physical arguments to understand the form of the interference pattern resulting from the collision of two dimer condensates. An appropriate way to derive this interference pattern is through the dimer–dimer spatial correlation function

the two-condensate state made of N dimers of momentum  and
and  dimers of momentum
dimers of momentum  reading as
reading as
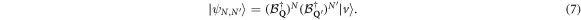
Taking  and
and  makes the physics easier to grasp.
makes the physics easier to grasp.
Let us first deal without fermion exchanges, which corresponds to taking the dimers as elementary bosons. The operator  destroys one of the
destroys one of the  dimers of the
dimers of the  state at the
state at the  site. Let this destroyed dimer have a momentum
site. Let this destroyed dimer have a momentum  . If
. If  also destroys a
also destroys a  dimer, these two detections generate a N(N − 1) factor from the number of ways to choose the two
dimer, these two detections generate a N(N − 1) factor from the number of ways to choose the two  dimers among N. Due to momentum conservation in the
dimers among N. Due to momentum conservation in the  numerator,
numerator,  and
and  must recreate two
must recreate two  dimers. The associated phase factors
dimers. The associated phase factors  and
and  to detect a
to detect a  dimer at
dimer at  then cancel; same at
then cancel; same at  . So, the term in N(N − 1) does not bring any oscillatory contribution to
. So, the term in N(N − 1) does not bring any oscillatory contribution to  (figure 1(a)). In the same way, no oscillation occurs if two
(figure 1(a)). In the same way, no oscillation occurs if two  dimers (figure 1(b)) or one
dimers (figure 1(b)) or one  dimer and one
dimer and one  dimer (figure 1(c)) are destroyed and recreated at the same site, their counting factor being, respectively,
dimer (figure 1(c)) are destroyed and recreated at the same site, their counting factor being, respectively,  and
and  , the 2 coming from detecting the
, the 2 coming from detecting the  dimer at
dimer at  or at
or at  . So, we end up with a contribution to
. So, we end up with a contribution to  equal to
equal to
Figure 1. Correlation function  defined in equation (6), in the absence of fermion exchanges. A dimer is destroyed and recreated from the same fermion pair at the same position with same momentum (a, b, c) or with different momenta (d), the total momentum being conserved. The oscillatory
defined in equation (6), in the absence of fermion exchanges. A dimer is destroyed and recreated from the same fermion pair at the same position with same momentum (a, b, c) or with different momenta (d), the total momentum being conserved. The oscillatory  term of equation (9) comes from (d). In Shiva diagrams, a coboson dimer is represented by a double line, the solid and dashed lines representing its two different fermionic atoms. See [34] for a detailed description of Shiva diagrams.
term of equation (9) comes from (d). In Shiva diagrams, a coboson dimer is represented by a double line, the solid and dashed lines representing its two different fermionic atoms. See [34] for a detailed description of Shiva diagrams.
Download figure:
Standard image High-resolution imageFor an oscillatory term to appear in the correlation function, the dimers destroyed and recreated at the  site must have different momenta (figure 1(d)). The term in which
site must have different momenta (figure 1(d)). The term in which  destroys a
destroys a  dimer and
dimer and  recreates a
recreates a  dimer brings a factor
dimer brings a factor  with a
with a  prefactor coming from the number of ways to choose these
prefactor coming from the number of ways to choose these  dimers. To conserve momentum,
dimers. To conserve momentum,  then has to destroy a
then has to destroy a  dimer and
dimer and  to create a
to create a  dimer, which brings a factor
dimer, which brings a factor  . So, we end up with a contribution to
. So, we end up with a contribution to  equal to
equal to

where  . This leads to the m = 1 mode previously found for elementary bosons. Indeed, when
. This leads to the m = 1 mode previously found for elementary bosons. Indeed, when  and
and  , the spatial correlation function for elementary bosons corresponds to
, the spatial correlation function for elementary bosons corresponds to
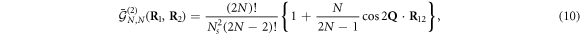
as first given in [31]. For completeness, we rederive in appendix A the n-particle correlation function for free elementary bosons using a different approach. The amplitudes of the m = (0, 1) terms both scale as  and no other mode exists in the case of elementary bosons.
and no other mode exists in the case of elementary bosons.
The dimer composite nature brings a far richer physics because  can destroy any two fermions. These two fermions can simply be the ones of the
can destroy any two fermions. These two fermions can simply be the ones of the  or
or  pair in
pair in  . Or, since identical fermions are indistinguishable, they can also be any pair resulting from fermion exchanges in the
. Or, since identical fermions are indistinguishable, they can also be any pair resulting from fermion exchanges in the  state. As exchanges conserve momentum, fermion exchange inside the
state. As exchanges conserve momentum, fermion exchange inside the  condensate does not change the momentum of the dimer detected at
condensate does not change the momentum of the dimer detected at  site, as shown in the Shiva diagram of figure 2a. So, this does not bring any oscillatory contribution. However, as each fermion exchange brings a 1/Ns factor, this term appears with a prefactor equal to
site, as shown in the Shiva diagram of figure 2a. So, this does not bring any oscillatory contribution. However, as each fermion exchange brings a 1/Ns factor, this term appears with a prefactor equal to
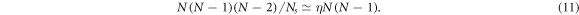
It thus is η times smaller that the leading N(N − 1) term obtained in the absence of fermion exchange, shown in figure 1(a).
Figure 2. Shiva diagrams for fermion exchanges: (a) exchanges within the  condensate do not change the momentum of the dimer detected at
condensate do not change the momentum of the dimer detected at  so, they do not lead to oscillatory terms. (b, c) Exchanges involving the two condensates can lead to dimers detected at the same site having momentum differences
so, they do not lead to oscillatory terms. (b, c) Exchanges involving the two condensates can lead to dimers detected at the same site having momentum differences  , with m = 1 as in (b), or m = 2 as in (c). Modes with
, with m = 1 as in (b), or m = 2 as in (c). Modes with  are the signature of the dimer composite nature we predict.
are the signature of the dimer composite nature we predict.
Download figure:
Standard image High-resolution imageBy contrast, fermion exchanges between the  and
and  condensates can lead to terms in which the detected dimers have a momentum difference equal to
condensates can lead to terms in which the detected dimers have a momentum difference equal to  , with m = 1 as in figure 2(b), m = 2 as in figure 2(c), and m ≥ 3 for exchanges involving more dimers from each condensate. The term corresponding to the Shiva diagram of figure 2(b) produces the same
, with m = 1 as in figure 2(b), m = 2 as in figure 2(c), and m ≥ 3 for exchanges involving more dimers from each condensate. The term corresponding to the Shiva diagram of figure 2(b) produces the same  oscillatory term as the one of equation (9), but its prefactor
oscillatory term as the one of equation (9), but its prefactor
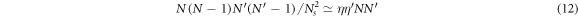
is  times smaller due to the two exchanges it contains. More generally, the m = 1 terms in which fermion exchanges enter bring density-dependent corrections to the amplitude of the interference terms already present for elementary bosons.
times smaller due to the two exchanges it contains. More generally, the m = 1 terms in which fermion exchanges enter bring density-dependent corrections to the amplitude of the interference terms already present for elementary bosons.
Momentum changes  with m ≥ 2 are a definite signature of the condensate composite nature because they generate new oscillatory modes. The
with m ≥ 2 are a definite signature of the condensate composite nature because they generate new oscillatory modes. The  momentum change in figure 2(c) produces a
momentum change in figure 2(c) produces a  contribution. This m = 2 term has four exchanges, but two sums over
contribution. This m = 2 term has four exchanges, but two sums over  and
and  which cancel two Ns factors coming from exchanges; so, it also appears with a prefactor
which cancel two Ns factors coming from exchanges; so, it also appears with a prefactor  . Note that in order to produce these higher modes, similar exchanges must occur in the
. Note that in order to produce these higher modes, similar exchanges must occur in the  and the
and the  condensates; so, m cannot be larger than
condensates; so, m cannot be larger than  .
.
Last but not least, the fact that two identical fermions cannot be at the same site must hold sway over the possibility of seeing two dimers at the same site. Indeed,  imposes
imposes  . So,
. So,  must cancel for
must cancel for  .
.
All this shows that fermion exchanges inside each condensate and between the two condensates change the interference pattern compared to that obtained with elementary bosons in three ways:
- (i)the amplitudes of the elementary-boson terms have many-body corrections reading in powers of densities, η and

- (ii)higher oscillatory modes in
 with
with  up to
up to  appear, with ever weaker amplitudes;
appear, with ever weaker amplitudes; - (iii)a dip at the scale of the optical lattice constant exists for
 .
.
The spatial correlation function for fermionic-atom dimers thus has to read
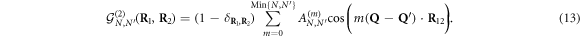
The amplitudes of the m = (0, 1) modes are equal to the elementary-boson values within density corrections coming from fermion exchanges, namely  and
and  . The larger number of exchanges required for the m = 2 mode appears in its amplitude which scales as
. The larger number of exchanges required for the m = 2 mode appears in its amplitude which scales as  within density corrections. And so on for larger m.
within density corrections. And so on for larger m.
3. Theoretical approach
For dimers characterized by a single quantum index  , as dimers in an optical lattice, it is possible to perform an exact calculation of the n-coboson spatial correlation function,
, as dimers in an optical lattice, it is possible to perform an exact calculation of the n-coboson spatial correlation function,  , in spite of the tricky fermion exchanges that occur not only within each condensate, but also between the
, in spite of the tricky fermion exchanges that occur not only within each condensate, but also between the  and
and  condensates—from which the most interesting physics arises. To do it, we have developed an original procedure in which
condensates—from which the most interesting physics arises. To do it, we have developed an original procedure in which  is written in terms of the generalized coherent states
is written in terms of the generalized coherent states  where
where  are complex scalars, as explained in appendix B. Using it, we can obtain
are complex scalars, as explained in appendix B. Using it, we can obtain  analytically for arbitrary n. As its expression is extremely complicated, even for n = 2, we shall here only discuss two limiting cases that best illustrate the involved physics, and refer the interested readers to appendix B for the general form.
analytically for arbitrary n. As its expression is extremely complicated, even for n = 2, we shall here only discuss two limiting cases that best illustrate the involved physics, and refer the interested readers to appendix B for the general form.
4. Analytical results for limiting cases
For n = 1, the function  stays equal to its elementary-boson value,
stays equal to its elementary-boson value,  , which physically corresponds to the total dimer density of the two condensates at the scale of the lattice site number Ns. This result follows from the fact that (i)
, which physically corresponds to the total dimer density of the two condensates at the scale of the lattice site number Ns. This result follows from the fact that (i)  does not depend on
does not depend on  , and (ii) the mean value of the number operator
, and (ii) the mean value of the number operator  in the
in the  state is equal to the total dimer number,
state is equal to the total dimer number,  .
.
To grasp how fermion exchanges affect the interference pattern of two condensates, let us consider the simplest case in which the predicted m = 2 oscillatory mode exists, that is  . The explicit expression of the spatial correlation function then reads (see equation (B.28))
. The explicit expression of the spatial correlation function then reads (see equation (B.28))
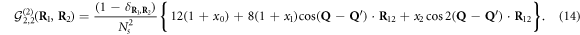
The changes from the elementary-boson result given in equation (10), induced by exchanges, appear in the xi's, as illustrated in figure 3. They read  , and
, and  . The F2,2 factor, equal to
. The F2,2 factor, equal to  , comes from the norm,
, comes from the norm,  , of the
, of the  state given in equation (B.26). Fermion exchanges like the one of figure 2(a) give the 1/Ns term of x0; the one of figure 2(b) gives the
state given in equation (B.26). Fermion exchanges like the one of figure 2(a) give the 1/Ns term of x0; the one of figure 2(b) gives the  term of x1; the one of figure 2(c) gives the x2 prefactor of the m = 2 term. Figure 3 shows the resulting correlation function for Ns = 5, from which we clearly see the next-to-lowest oscillatory mode, and the singularity at
term of x1; the one of figure 2(c) gives the x2 prefactor of the m = 2 term. Figure 3 shows the resulting correlation function for Ns = 5, from which we clearly see the next-to-lowest oscillatory mode, and the singularity at  .
.
Figure 3. Spatial correlation function  for
for  and
and  cobosons when Ns = 5 (red circles, equation (14)). For periodic lattice, the red circles correspond to the set of values for
cobosons when Ns = 5 (red circles, equation (14)). For periodic lattice, the red circles correspond to the set of values for  . The blue circles correspond to elementary bosons (equation (10)). The curves are plotted by taking
. The blue circles correspond to elementary bosons (equation (10)). The curves are plotted by taking  continuous to guide the eye. The inset shows each term in equation (14).
continuous to guide the eye. The inset shows each term in equation (14).
Download figure:
Standard image High-resolution imageSo far, we have considered bound fermion pair  with no relative-motion extension. Pauli blocking then appears in the strongest way by forbidding two dimers to be at the same site through the
with no relative-motion extension. Pauli blocking then appears in the strongest way by forbidding two dimers to be at the same site through the  prefactor in equation (13). In reality, physical dimers are trapped in lattice potential wells with finite depth and width; so they have a finite spatial extension. This physically broadens the effect of Pauli blocking and transforms the singular dip of equation (13) into a smooth dip (see figure 3). However, such dimer granularity must not affect the interference pattern at larger scale. Interestingly, a similar dip feature has been found for elementary bosons with hardcore repulsion [35].
prefactor in equation (13). In reality, physical dimers are trapped in lattice potential wells with finite depth and width; so they have a finite spatial extension. This physically broadens the effect of Pauli blocking and transforms the singular dip of equation (13) into a smooth dip (see figure 3). However, such dimer granularity must not affect the interference pattern at larger scale. Interestingly, a similar dip feature has been found for elementary bosons with hardcore repulsion [35].
5. Conclusion
In this work, we address the commonly bypassed consequences of the particle composite nature in cold-atom physics, by considering the interference pattern of two condensates made of dimers. We predict the existence of additional high frequency modes, in contrast to a unique low-frequency mode existing when the particle composite nature is neglected. With the help of analytical calculations and Shiva diagrams that visualize composite boson many-body effects, we evidence that these high modes come from dimensionless fermion exchanges between condensates. Being many-body in essence, the amplitude of these high modes depends on density; therefore, their observation requires rather dense condensates, that is, sizeable many-body parameter η, as possibly obtained by using optical lattices. In addition, Pauli blocking between the particle fermionic components produces a dip in the interference pattern that constitutes another signature of the dimer granularity.
Just like the composite nature of semiconductor excitons has revealed a breadth of remarkable effects, we anticipate cold-atom systems to provide a novel, fully controllable playground to investigate further in depth the very unique many-body effects that result from dimensionless fermion exchanges, that is, exchange in the absence of fermion-fermion interaction. Recent optical lattices already reach densities high enough for these new many-body effects to be observable, including the signatures we here predict.
Acknowledgments
SYS and MC acknowledge support from OBELIX from the French Agency for Research (ANR-15-CE30-0020). AC thanks Geza Giedke for insightful comments.
Appendix A.: Elementary bosons
Elementary boson operators obey the commutation relations ![${[{\bar{B}}_{{\bf{Q}}^{\prime} }^{\dagger },{\bar{B}}_{{\bf{Q}}}^{\dagger }]}_{-}=0$](https://content.cld.iop.org/journals/1367-2630/21/4/043041/revision2/njpab0cc6ieqn140.gif) and
and ![${[{\bar{B}}_{{\bf{Q}}^{\prime} },{\bar{B}}_{{\bf{Q}}}^{\dagger }]}_{-}={\delta }_{{\bf{Q}}^{\prime} {\bf{Q}}};$](https://content.cld.iop.org/journals/1367-2630/21/4/043041/revision2/njpab0cc6ieqn141.gif) so, by iteration,
so, by iteration,
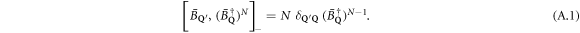
This commutator immediately gives the normalization factor of the state  as
as  where
where  denotes the vacuum, and with a little more work, the value of
denotes the vacuum, and with a little more work, the value of
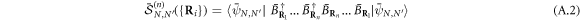
with  , that enters the n-particle spatial correlation function
, that enters the n-particle spatial correlation function
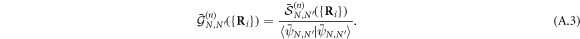
The  -space and
-space and  -space creation operators are linked through
-space creation operators are linked through  for continuous
for continuous  in a finite volume LD, with LD replaced by Ns for a discrete lattice of Ns sites located at
in a finite volume LD, with LD replaced by Ns for a discrete lattice of Ns sites located at  .
.
In this work, we propose an original procedure to evaluate the spatial correlation function (A.3). Although this procedure might appear as overcomplicated for elementary bosons, it allows handling more complex cobosons in an exact way. We introduce a generalized elementary-boson coherent state
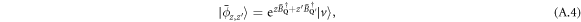
where  are complex scalars. The residue theorem gives the two-condensate state
are complex scalars. The residue theorem gives the two-condensate state  as
as
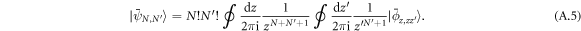
Turning from  to
to  allows controlling the total number
allows controlling the total number  of bosons with momentum
of bosons with momentum  and
and  through z, and the number
through z, and the number  of
of  bosons through
bosons through  . This will later on facilitate expansion in the boson density through z factors.
. This will later on facilitate expansion in the boson density through z factors.
We note that the only part of  that gives a non-zero contribution when projected over
that gives a non-zero contribution when projected over  is the one that has the same particle number and momentum, i.e.
is the one that has the same particle number and momentum, i.e.  itself. This remark helps seeing that
itself. This remark helps seeing that
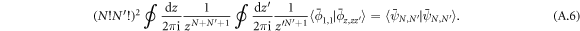
In the same way, equation (A.2) can be rewritten as
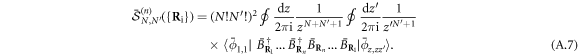
The trick now is to calculate the above scalar product by using commutators in real space instead of momentum space as in equation (A.1). We first note that  is eigenstate of the
is eigenstate of the  operator
operator
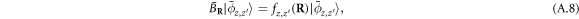
with the eigenvalue  . So, we readily find
. So, we readily find
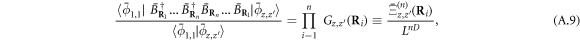
with  . The major advantage of this new procedure is to avoid enforcing momentum conservation at each commutation step; instead, the relevant momentum-conserving processes are selected at the very end only, directly through
. The major advantage of this new procedure is to avoid enforcing momentum conservation at each commutation step; instead, the relevant momentum-conserving processes are selected at the very end only, directly through  : indeed, for n = 1, equation (A.9) readily gives
: indeed, for n = 1, equation (A.9) readily gives  , in which the term that converses momentum is
, in which the term that converses momentum is  , so that
, so that  must reduce to
must reduce to  . In the same way,
. In the same way,  for n = 2 is equal to
for n = 2 is equal to 
 for n = 3 it is equal to
for n = 3 it is equal to 
 , and so on... The above results used for the scalar product in equation (A.7) give, with the help of equation (A.6), the first n-particle correlation functions for free elementary bosons as
, and so on... The above results used for the scalar product in equation (A.7) give, with the help of equation (A.6), the first n-particle correlation functions for free elementary bosons as
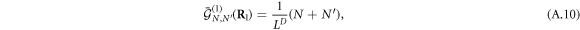
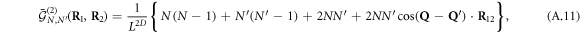
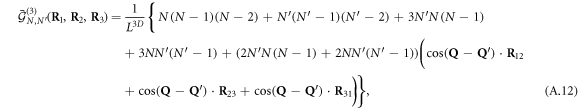
with LD replaced by Ns in the case of discrete  's.
's.
The 1-particle function  physically corresponds to the total density of the
physically corresponds to the total density of the  and
and  elementary bosons in the sample volume LD, while the other results evidence that the collision of two elementary-boson condensates leads to wave-like interference patterns associated with the momentum difference
elementary bosons in the sample volume LD, while the other results evidence that the collision of two elementary-boson condensates leads to wave-like interference patterns associated with the momentum difference  . This pattern can be observed by measuring the n-particle correlation function
. This pattern can be observed by measuring the n-particle correlation function  for n ≥ 2. The expression of this correlation function for
for n ≥ 2. The expression of this correlation function for  and
and  has already been reported in [31].
has already been reported in [31].
It can be of interest to note that the quantity
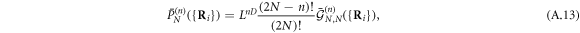
corresponds to the probability of detecting n bosons located at  in the
in the  condensate, as suggested in [31]: Indeed,
condensate, as suggested in [31]: Indeed,  while the
while the  's are linked by
's are linked by
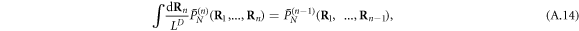
as physically required for probabilities. In the case of composite bosons, the correlation functions have additional terms induced by the fermion exchanges that prevent such identification.
Appendix B.: Composite bosons: fermionic-atom dimers
We now consider an optical lattice of Ns sites, each site possibly hosting a bound pair of different fermionic atoms, with creation operator  . Due to inter-site interaction, the resulting coboson dimer creation operators read
. Due to inter-site interaction, the resulting coboson dimer creation operators read  , with
, with  . They obey the commutation relations
. They obey the commutation relations
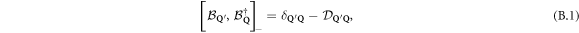
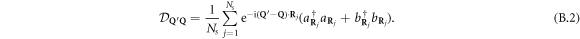
As usual [10], the deviation-from-boson operator  generates the dimensionless Pauli scatterings
generates the dimensionless Pauli scatterings  responsible for fermion exchanges between cobosons. In the case of the single-index cobosons we here consider, they reduce to
responsible for fermion exchanges between cobosons. In the case of the single-index cobosons we here consider, they reduce to
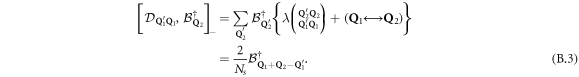
The correlation function for detecting n dimers for the state  reads as
reads as  with
with
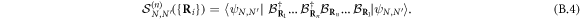
Here also, we introduce the generalized composite-boson coherent state  . As for elementary bosons, we can rewrite equation (B.4) as
. As for elementary bosons, we can rewrite equation (B.4) as
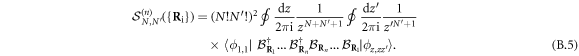
The procedure is essentially the same as for elementary bosons, equations (A.5), (A.6), (A.7) staying valid for cobosons. Momentum conservation at each commutation is even more cumbersome due to additional fermion exchanges, which are many-body in nature. This is why working with commutators in real space is really advantageous.
It will appear as convenient to first note that the deviation-from-boson operator  leads to
leads to
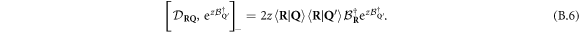
In the same way
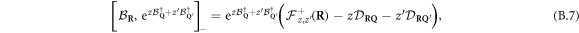
with
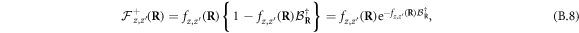
since  .
.
The above two commutators are obtained from iteration of the coboson commutation relations in momentum space, equations (B.1), (B.3), namely
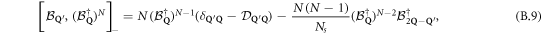
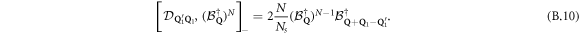
equation (B.7) then gives
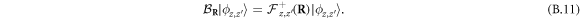
The curly bracket in equation (B.8), absent for elementary bosons (see equation (A.8)), results from fermion exchanges occurring within the  state. It makes
state. It makes  not an eigenstate of the fermion pair operator
not an eigenstate of the fermion pair operator  . In the same way, we find
. In the same way, we find
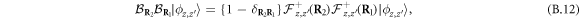
the curly bracket coming from Pauli blocking as  when
when  and so on...
and so on...
The major advantage of using commutators in real space is that  readily gives zero for
readily gives zero for  whenever it appears. Equations (B.8), (B.11) then give
whenever it appears. Equations (B.8), (B.11) then give
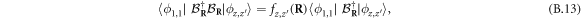
while for  , equation (B.12) gives
, equation (B.12) gives
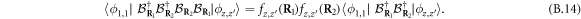
More generally,  reduces for different
reduces for different  's to
's to
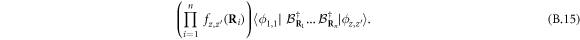
If we now use equation (B.11) for  , we end with
, we end with
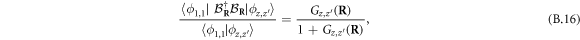
and more generally
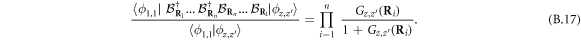
This result can also be obtained from the definition of the state  and the relation
and the relation  , so that
, so that
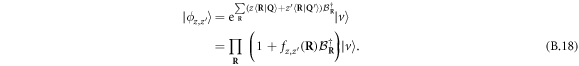
Comparing the result for coboson dimers (B.17) with that for elementary bosons (A.9), we can trace the denominator in the RHS of equation (B.17) back to the curly bracket of  given in equation (B.8).
given in equation (B.8).
Let us now focus on the correlation functions for one and two dimers. Extension to multiple dimers is straightforward. As for elementary bosons, the relevant momentum-conserving processes are selected from
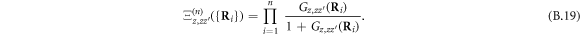
We first expand in z, which is easy to do by noting that  . For n = 1, this gives
. For n = 1, this gives
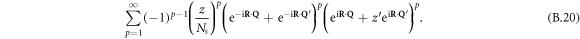
Selecting momentum-conserving processes yields
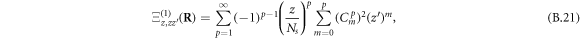
where Cpm denotes the binomial coefficient  . Similarly, for n = 2, we find
. Similarly, for n = 2, we find
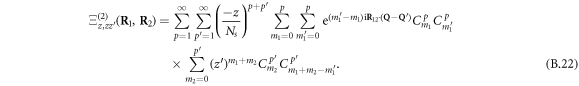
To go further and obtain the spatial correlation function, we need the normalization factor  . This quantity is quite tricky to derive from a naive expansion, because fermion exchange not only occurs between dimers carrying same momentum but also between dimers carrying different momenta. The same procedure, that is, equation (A.6) rewritten for dimers, gives
. This quantity is quite tricky to derive from a naive expansion, because fermion exchange not only occurs between dimers carrying same momentum but also between dimers carrying different momenta. The same procedure, that is, equation (A.6) rewritten for dimers, gives
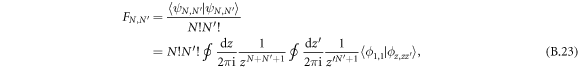
which also reads, through an integration by part over z, as
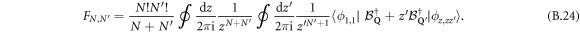
This quantity is best calculated from commutators in real space through  . We then find
. We then find
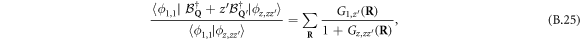
as obtained by using equation (B.11). The above sum over  has the effect of selecting momentum-conserving processes, as obtained through an z expansion similar to the one performed in equation (B.20). Equation (B.24) then leads to
has the effect of selecting momentum-conserving processes, as obtained through an z expansion similar to the one performed in equation (B.20). Equation (B.24) then leads to
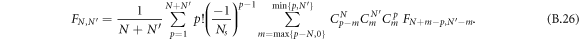
This equation provides an efficient iteration to obtain high  terms, starting from F0,0 = 1. The first ones read
terms, starting from F0,0 = 1. The first ones read
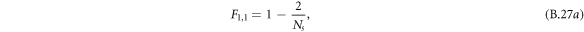


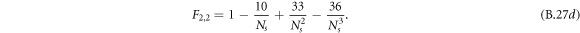
The 1-dimer function follows from equation (B.21) divided by the norm of the  state, as obtained from equation (B.26). We find that it simply reduces to the dimer density, namely
state, as obtained from equation (B.26). We find that it simply reduces to the dimer density, namely  , as obtained for elementary bosons. The physical reason for not having any correction is that it fundamentally deals with detecting a single dimer.
, as obtained for elementary bosons. The physical reason for not having any correction is that it fundamentally deals with detecting a single dimer.
The 2-dimer correlation function is modified by terms stemming from fermion exchanges. For n = 2, the result already is quite complicated
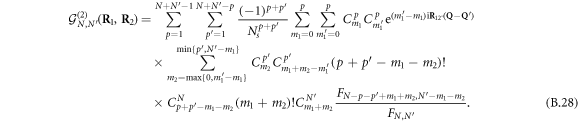
When  , it reduces to
, it reduces to
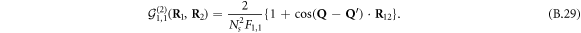
From the general form (B.28), we see that interferences in  with
with  do exist for
do exist for  . The explicit result for
. The explicit result for  is given in equation (14).
is given in equation (14).
Footnotes
- 6
Note that this composite nature also appears at the two-body level, through a significant reduction of the dimer–dimer scattering length by the repeated effective coboson–coboson interaction in which fermion exchange plays a key role [12].











