Normal projected entangled pair states generating the same state

Tensor Networks (TNs) provide us with very efficient ways of describing quantum states in discrete systems. They are particularly useful to describe ground [1] and thermal equilibrium states [1, 2] of local Hamiltonians, or to describe exotic phases of matter [3, 4]. The most prominent examples are matrix product states [5, 6] (MPS), which portray one-dimensional systems, and their higher-dimensional generalization, projected entangled pair states [7] (PEPS). Their simplicity and special properties makes them very practical in numerical computations [8–11], as well as in the characterization and classification of a variety of scenarios and phenomena. This includes, for instance, the characterization of symmetry protected phases in spin [12–14] and fermionic [15] chains, or topological order [4, 16, 17] in two dimensions, lattice gauge theories [18, 19], unitary evolutions [20, 21], one-way quantum computing [7, 22, 23], or quantum tomography [24].

TN states can be defined on arbitrary lattices. They are generated by a set of tensors, $\{{A}_{n}\}$, which are assigned to each vertex and are contracted according to the geometry of the lattice. For regular lattices, the generated states are translationally invariant (TI) if all the tensors are the same. A key feature of general TNs is that two different sets of tensors may generate the same TN state. This occurs, for instance, when they are related by a (so-called) gauge transformation; that is, when the tensors of one set are related to the other by matrix multiplication of the indices that are contracted, so that those matrices cancel with each other once they are contracted. Let us illustrate this with MPS. There, the tensors A_n have rank three: one of the indices corresponds to the physical index, and the other two to the virtual ones that are contracted in order to generate the state. For a given value of the physical index, i, the tensors are just matrices, ${A}_{n}^{i}$. Obviously, the tensors B_n, with ${B}_{n}^{i}={X}_{n}{A}_{n}^{i}{X}_{n+1}^{-1},$ generate the same state as the tensors A_n, where X_n are arbitrary non-singular matrices. One of the fundamental questions in the description of TNs is precisely if this is the only thing that can happen. That is, if two sets of tensors generate the same state, must they be related by a gauge transformation? This question is crucial in many of the applications of TNs. For instance, when the answer is affirmative, it gives rise to a canonical form of describing MPS [5, 25, 26]. Or, more importantly, it characterizes the tensors generating states with certain global or local (gauge) symmetries [27, 28]. The reason is very simple: if a state is symmetric it means that an operation leaves it invariant; however, in general, it will change the tensors, so that the resulting ones should be related to the original ones by a gauge transformation. This implies that symmetries in the quantum states can be captured by symmetries in the tensors. This question is also decisive in many other situations dealing with string order [29], topological order [17], renormalization [30], or time evolution [21]. Theorems answering such fundamental questions about the structure of TNs are typically referred to as fundamental theorems.

Proving a fundamental theorem for the most general TN is impossible: even for two tensors generating TI 2D PEPS in an N × N lattice, there cannot exist an algorithm to decide whether they will generate the same state for all N or not [31]. It is therefore necessary to impose restrictions to the TN (both on the geometry of the lattice as well as on the properties of the defining tensors). So far, most of the fundamental theorems concern MPS. They have been proven for TI states [30, 32] as long as the two tensors generate the same state for any size of the lattice. They have also been proven for not necessarily TI states for a fixed (but large enough) system size for a restricted class of tensors [33]. This class includes injective tensors, that can be inverted by just acting on the physical index, i.e. there exists another tensor, ${A}^{-1}$, such that

$$\begin{eqnarray*}&&\displaystyle \sum _{i}{A}_{\alpha ,\beta }^{i}{({A}^{-1})}_{\alpha ^{\prime} ,\beta ^{\prime} }^{i}={\delta }_{\alpha ,\alpha ^{\prime} }{\delta }_{\beta ,\beta ^{\prime} },\end{eqnarray*}$$

as well as normal tensors, that become injective after blocking a few sites. For 2D PEPS such theorems only exist for restricted (but generic) classes of tensors: for normal tensors [33] and semi-injective tensors [34]. These theorems require only a fixed (but large enough) system size. The proof techniques, however, exploit the lattice structure in a fundamental way and thus do not generalize to other geometries.

In this paper we prove the fundamental theorem for normal (and thus also injective) PEPS in arbitrary lattices (geometries and dimensions). We obtain that if two sets of such tensors generate the same state, then they must be related by a gauge transformation. This generalizes the previous results as follows. First, we relax the condition of an existence of a sequence of TNs (required in e.g. [30]) so that our results hold for a fixed (but large enough) size. The required system size is smaller than in [33]. Second, the TNs considered here do not need to be TI, which is important when applying the results to local gauge symmetries. Third, the results hold for any geometry (including, for instance, three dimensions or hyperbolic, as it is used in the constructions of AdS/CFT correspondence [35, 36]). Additionally, we show that if a TI PEPS defined in a regular lattice is normal although the tensors are different in different sites, then there exists a TI PEPS description with the same bond dimension and where the tensors at every site are the same. Furthermore, the proof presented here uses a new technique: even though it relies on a reduction to the MPS case, this reduction is done in a local way instead of 'slicing' a PEPS into an MPS along one dimension.

In this section we define non-translational invariant injective MPS. We show that two such MPS generate the same state if and only if the generating tensors are related with a gauge transformation (if the MPS contains at least three sites). This extends the previously known results as here we consider (i) a fixed system size and (ii) non-translational invariant MPS with closed boundary conditions.

A non-translational invariant MPS on n particles is a state

$$\begin{eqnarray*}&&| {\rm{\Psi }}\rangle =\displaystyle \sum _{i}\mathrm{Tr}\{{A}_{1}^{{i}_{1}}{A}_{2}^{{i}_{2}}...{A}_{n}^{{i}_{n}}\}| {i}_{1}...{i}_{n}\rangle ,\end{eqnarray*}$$

where each i_k runs through a basis of the (finite dimensional) Hilbert space associated to the kth particle and each ${A}_{k}^{{i}_{k}}$ is a ${D}_{k}\times {D}_{k+1}$ matrix (${D}_{n+1}={D}_{1}$). From now on, we will use graphical notation: each tensor is depicted by a dot with lines attached to it. The lines correspond to the different indices of the tensor; joining the lines correspond to contraction of indices. For example, a scalar is represented by a single dot with no lines joining to it, a vector is represented by a dot with a single line attached to it, a matrix by a dot with two lines attached to it:

the scalar product of two vectors, the action of a matrix on a vector and a matrix element can be written as

In this notation, the MPS $| {\rm{\Psi }}\rangle$ is written as

An injective MPS is an MPS where every tensor—if considered as a map from the virtual level to the physical one—is injective, i.e.

This is equivalent to the tensor A_i admitting a one-sided inverse ${A}_{i}^{-1}$:

Notice that this immediately shows that the contraction of two injective MPS tensors is again injective; the inverse of the obtained tensor is proportional to the contraction of the inverses of the individual tensors:

where D is the dimension of the vector space assigned to the index connecting the tensors A₁ and A₂.

In the rest of this section, we prove the two main lemmas leading to the fundamental theorem. We also illustrate how to use them by deriving the fundamental theorem for non-translational invariant MPS. In the following, we consider two injective TNs generating the same state; the defining tensors of the two TNs are labeled by A_i and B_i. The first lemma assigns a special gauge transformation to each edge of one of the TNs; the second lemma shows that once these gauges are absorbed into the tensors B_i, the resulting tensors are equal to A_i.

Lemma 1. Suppose $A,B$ are two injective, non-translational invariant MPS on three sites that generate the same state. Then for every edge and for every matrix $X$ there is a matrix $Y$ such that

Moreover, $X$ and $Y$ have the same dimension and there is an invertible matrix $Z$ such that $Y={Z}^{-1}\ {XZ}$. This $Z$ is uniquely defined up to multiplication with a constant.

This lemma will be used to assign a local gauge transformation to all edges on one of two TNs generating the same state. These local gauges will then be incorporated into the defining tensors; doing so will lead to two TNs where inserting any matrix X on any bond simultaneously in the two networks gives two new states that are still equal.

The proof of lemma 1 is based on the observation that any local operation on the virtual level can be realized by a physical one on either of the neighboring particles; and vice versa, two physical operations on neighboring particles that transform the state the same way correspond to a virtual operation on the bond connecting the two particles. Given two TNs generating the same state, this correspondence establishes an isomorphism between the algebra of virtual operations. The basis change realizing this isomorphism is the local gauge relating the two tensors.

Before proceeding to the proof, notice that due to injectivity of the tensors, if

then ${X}_{1}={X}_{2}$.

Proof of lemma 1. Consider now a deformation of the TN by inserting a matrix X on one of the bonds. This deformation can be realized by physical operations acting on either of the two neighboring particles:

with

Notice that the mappings $X\mapsto {O}_{1}$ and $X\mapsto {O}_{2}^{T}$ are algebra homomorphisms⁵ . These mappings do not depend on A₃.

Consider now the converse: two physical operations on neighboring particles that transform the MPS to the same state:

Inverting B₂ and B₃, we arrive to

for some matrix W, where D₂₃ is the dimension of the vector space on the edge $(2,3)$. Similarly, inverting B₁ and B₃, we arrive to

for some matrix V. Therefore

and thus by injectivity, V = W. Therefore

and the maps ${O}_{1}\mapsto W$ and ${O}_{2}^{T}\mapsto W$ are uniquely defined and are algebra homomorphisms.

Consider now two three-particle, non-translational invariant injective MPS generating the same state:

Deform the MPS on the lhs by inserting a matrix X on one of the bonds. By the above arguments, this deformation is equivalent to any of the two physical operations:

As the MPS defined by the A and B tensors is the same state, these physical operators also satisfy

and thus, by equation (4), for every X there is a matrix Y such that

Due to injectivity of the B tensors, the mapping $X\mapsto Y$ is uniquely defined. Due to injectivity of the A tensors, it is an injective map. As the argument is symmetric with respect of the exchange of the A and B tensors, it also has to be surjective (for every Y there is a corresponding X), and therefore the map $X\mapsto Y$ is a bijection (one-to-one mapping). Moreover, it is clear from the construction that it is an algebra homomorphism, as both $X\mapsto {O}_{1}$ and ${O}_{1}\mapsto Y$ are algebra homomorphisms. Therefore the mapping $X\mapsto Y$ is an algebra isomorphism. As X (and Y) can be any matrix on the bond, this means that the bond dimensions on the lhs and the rhs are the same and that $Y={{ZXZ}}^{-1}$ for some invertible Z and this Z is uniquely defined (up to a multiplicative constant).□

Lemma 2. Let ${A}_{1},{A}_{2}$ and ${B}_{1},{B}_{2}$ be injective MPS tensors. Suppose that for all $X$ and $Y$

Then ${A}_{1}=\lambda {B}_{1}$ and ${A}_{2}={\lambda }^{-1}{B}_{2}$ for some constant $\lambda$.

Proof. From the first equation, as X can be any matrix

Similarly, from the second equation

Therefore, applying ${A}_{2}^{-1}$ to both equations, we get that

for some matrices Z and W. Applying the inverse of B₁, we conclude that both Z and W are proportional to identity and hence ${A}_{1}=\lambda {B}_{1}$. Similarly ${A}_{2}=\mu {B}_{2}$ for some other constant μ and $\mu =1/\lambda$. □

In the following, we show how to use these lemmas for injective MPS to prove the fundamental theorem. This is a special case of the next section, and only presented to explain the ideas.

Theorem 1. Let the tensors ${A}_{i}$ and ${B}_{i}$ define two injective, non-translational invariant MPS on at least three particles. Suppose they generate the same state:

Then there are invertible matrices Z_i (${i}=1,\,\ldots ,\,n+1,{{Z}}_{{i}+1}={{Z}}_{1}$) such that

Moreover, the gauges Z_i are unique up to a multiplicative constant.

Proof. First let us choose any edge, for example the edge $(1,2)$. Let us block the tensors ${A}_{3},...{A}_{n}$ (and ${B}_{3},...{B}_{n}$) into one tensor:

As injectivity is preserved under blocking, both a and b are injective tensors. With this notation, the MPS can be written as a non-translational invariant MPS on three sites:

Therefore lemma 1 can be applied leading to a gauge transform Z₂ on the edge $(1,2)$ that, for all X with $Y={Z}_{2}^{-1}{{XZ}}_{2}$, satisfies

The lemma can be applied to all edges leading to gauge Z_i on the edge $(i-1,i)$. After incorporating these gauges into the tensor B_i:

we arrive at two MPS with the property that on every bond for every matrix X

In particular

Let us now block the MPS into a two partite MPS:

with

After this blocking, the requirements of lemma 2 are satisfied, therefore ${A}_{1}={\lambda }_{1}{\tilde{B}}_{1}$. Similarly for all i, ${A}_{i}={\lambda }_{i}{\tilde{B}}_{i}$ and ${\prod }_{i}{\lambda }_{i}=1$. Notice that these ${\lambda }_{i}$ can be sequentially absorbed into the gauges Z_i in equation (5). □

Notice that if the two MPS are translational invariant, i.e. the tensors at each vertex are the same, then the gauges relating them are also translational invariant (up to a constant), as

which can be seen by inverting the tensor A. We conclude therefore that

Corollary 1. Let the tensors $A$ and $B$ define two injective, translational invariant MPS on $n\geqslant 3$ particles. Suppose they generate the same state:

Then there is an invertible matrix $Z$ and a constant $\lambda \in {\mathbb{C}},{\lambda }^{n}=1$, such that

Moreover, the gauge $Z$ is unique up to a multiplicative constant.

In general, PEPS can be defined on any graph (no double edges are allowed, but there are extra edges attached to every vertex that is associated to a physical particle). The state corresponding to the PEPS is obtained by placing tensors on each vertex and contracting all indices corresponding to the edges of the graph. An example of a TN is depicted below:

This definition includes TNs such as MPS, 2D PEPS and higher-dimensional PEPS. It also includes PEPS defined on arbitrary lattices, such as hyperbolic lattices used in the AdS/CFT correspondence [35, 36].

We say that the TN is injective if all tensors interpreted as maps from the virtual space to the physical one are injective. This is equivalent to the tensor having a one-sided inverse, as in the MPS case. Similar to the MPS case, the contraction of two injective tensors results in an injective tensor.

One can group particles of the PEPS together treating them as one bigger particle. This regrouping can naturally be reflected in PEPS. In particular, we will block TNs to a three particle MPS as follows. Choose one edge of the PEPS and group together all vertices except the endpoints of the edge. This regrouped tensor together with the two endpoints of the edge forms a three-partite MPS as illustrated below; notice that the resulting MPS is injective:

Consider now two injective PEPS defined on the same graph that generate the same state:

After blocking to MPS as described above, we arrive at two injective MPS generating the same state; hence lemma 1 can be applied. This establishes a gauge transformation on the edge $(1,5)$ of the original PEPS. Similar regrouping can be done around every edge; applying then lemma 1 results in a gauge transformation assigned to every edge. Define now the tensors ${\tilde{B}}_{i}$ by absorbing these gauges into the tensors B_i. For the resulting PEPS, we have that for every edge and matrix X

To conclude that ${A}_{i}={\lambda }_{i}{\tilde{B}}_{i}$, we will need to use a more general version of lemma 2:

Lemma 3. Let ${A}_{1},{A}_{2}$ and ${B}_{1},{B}_{2}$ be injective tensors. Suppose for all $X$ on all edges

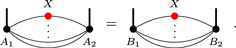
Then ${A}_{1}=\lambda {B}_{1}$ and ${A}_{2}={\lambda }^{-1}{B}_{2}$ for some constant λ.

Proof. W.l.o.g. suppose that there are three lines connecting the tensors. Similar to the proof of lemma 2, if equation (9) holds for all X, then

Applying now the inverse of A₂, we conclude that

Inverting B₁ we conclude that the gauges $Z,U,W$ satisfy

$$\begin{eqnarray*}&&\displaystyle \sum _{i}\mathrm{Id}\otimes {Z}_{i}^{(1)}\otimes {Z}_{i}^{(2)}=\displaystyle \sum _{i}{U}_{i}^{(1)}\otimes {U}_{i}^{(2)}\otimes \mathrm{Id}=\displaystyle \sum _{i}{W}_{i}^{(1)}\otimes \mathrm{Id}\otimes {W}_{i}^{(2)},\end{eqnarray*}$$

where we have written

$$\begin{eqnarray*}\begin{array}{rcl}Z & = & \displaystyle \sum _{i}{Z}_{i}^{(1)}\otimes {Z}_{i}^{(2)}\\ U & = & \displaystyle \sum _{i}{U}_{i}^{(1)}\otimes {U}_{i}^{(2)}\\ W & = & \displaystyle \sum _{i}{W}_{i}^{(1)}\otimes {W}_{i}^{(2)}.\end{array}\end{eqnarray*}$$

Therefore all three gauges are proportional to the identity and thus ${A}_{1}=\lambda {B}_{1}$. Similarly we get ${A}_{2}=1/\lambda {B}_{2}$. □

Let us now block the PEPS in equation (8) into two injective tensors: select one tensor and block all the others into another injective tensor. These PEPS now satisfy the requirements of lemma 3 and thus for all $i,{A}_{i}={\lambda }_{i}{\tilde{B}}_{i}$ for some constant ${\lambda }_{i}$, giving the fundamental theorem for general injective PEPS (the constants ${\lambda }_{i}$ can be incorporated into the gauge transformations):

Theorem 2. Two injective PEPS —defined on a graph that does not contain double edges and self-loops—generate the same state if and only if the generating tensors are related with a local gauge. These gauges are unique up to a multiplicative constant.

As the defining graph cannot contain double edges and self-loops, the theorem is applicable for MPS of size N only if $N\geqslant 3$, and for 2D PEPS of size N × M only if both $N\geqslant 3$ and $M\geqslant 3$. As an illustration of the theorem, for the two PEPS in equation (7) there are matrices ${Z}_{12},{Z}_{23},{Z}_{34},{Z}_{45},{Z}_{51}$ and Z₂₅ such that

We call a PEPS normal, if blocking tensors in certain regions results in injective tensors. To derive the fundamental theorem for this kind of PEPS, we use the same arguments as above after blocking tensors to injective ones. This technique requires that the system is big enough to allow for blocking. This proof technique presented here is not optimal in the required system size; we describe a proof technique giving tighter bounds in appendix. For simplicity, we present the proof for a TI normal PEPS on a square lattice, but it can easily be generalized to the non-TI case on any geometry.

Before proceeding to the proof, we need the following lemma:

Lemma 4. The union of two injective regions is injective.

Proof. Let A and B be two injective regions. W.l.o.g. the TN can be blocked as follows (missing edges do not change the proof):

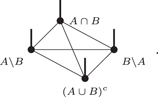
Notice that $A\cup B=(A\setminus B)\cup (A\cap B)\cup (B\setminus A)$. Let X now be a tensor such that

As the region $A=(A\setminus B)\cup (A\cap B)$ is injective

Plugging back the tensor over the region $A\cap B$,

Finally, the region $B=(A\cap B)\cup (B\setminus A)$ is injective, hence inverting the tensor over that region gives

which means that the region $A\cup B$ is injective. □

For example, if in a TI 2D PEPS every 2 × 3 and 3 × 2 region is injective, then the following regions:

are unions of smaller injective regions, and they are thus injective. Similarly, if the size of the PEPS is at least 5 × 6, then the region T depicted below is injective:

In the following we prove the fundamental theorem for a normal TI 2D PEPS. In particular, we prove it in detail for the case where every region of size 2 × 3 and 3 × 2 is injective as in the examples above. Then, we generalize the proof for any normal PEPS that is big enough to allow the necessary blockings.

Theorem 3. Let $A$ and $B$ be two normal 2D PEPS tensors such that every 2 × 3 and 3 × 2 region is injective. Suppose they generate the same state on some region $n\times m$ with $n,m\geqslant 7$. Then $A$ and $B$ are related to each other with a gauge transformation:

with ${\lambda }^{n\cdot m}=1$ and $X,Y$ invertible matrices. $X$ and $Y$ are unique up to a multiplicative constant.

Proof. Let us block the TN into three injective parts around an edge. This can be done with e.g. the following choice of regions:

where A₁ corresponds to the red region, A₂ to the blue one and A₃ to the rest. The region A₃ is injective as long as the size of the PEPS is at least 5 × 7. Therefore a 7 × 7 PEPS can be blocked to injective three partite MPS around every edge (including the vertical edges that require a PEPS size at least 7 × 5). Therefore lemma 1 can be applied giving a gauge transformation on every edge. Due to translation invariance, these gauges are described by the same matrix X (Y) on all horizontal (vertical) edges.

Define now $\tilde{B}$ by incorporating the local gauges into the tensors B, such as in the injective case:

The two PEPS tensors A and $\tilde{B}$ generate the same state. Moreover, inserting a matrix Z on any bond of the first PEPS gives the same state as inserting the same matrix Z on the corresponding bond of the second PEPS. Remember that lemma 4 implies that both

are injective regions and notice that the two regions differ in a single site. Moreover, if the PEPS is at least 5 × 5, their complement regions R^c and S^c are also injective. Let us denote the tensor on region R as A_R (${\tilde{B}}_{R}$) and on region S as A_S (${\tilde{B}}_{S}$). Then, by lemma 3, ${A}_{R}\propto {\tilde{B}}_{R}$ and ${A}_{S}\propto {\tilde{B}}_{S}$. This can be represented as

Applying the inverse of ${A}_{R}\propto {\tilde{B}}_{R}$ on the two ends of the equation, we get that the tensors A and $\tilde{B}$ are proportional.□

The above proof can be repeated for any PEPS as long as it is possible to block into injective regions as required by lemmas 1 and 3. This leads to the fundamental theorem of normal PEPS:

Theorem 4. Suppose two normal PEPS generating the same state satisfy the following:

• they can be blocked into three partite injective MPS around every edge,
• and for every site, there are injective regions with their complements also being injective that differ only in the given site.

Then the defining tensors are related with a local gauge. Moreover, the gauges are unique up to a multiplicative constant.

Notice that this statement holds for a fixed system size (which is big enough to allow blocking into injective MPS), and translational invariance is not required. In case of a translational invariant system, the gauges are also translational invariant (if the proportionality constants are not absorbed into the gauges). In the following we present some special cases. For non-TI MPS, the statement reads as

Corollary 2. Let ${\{{A}_{i}\}}_{i=1}^{n}$ and ${\{{B}_{i}\}}_{i=1}^{n}$ two normal MPS on $n\geqslant 3L$ sites with the property that blocking any $L$ consecutive sites results in an injective tensor. Suppose they generate the same state:

Then there are invertible matrices Z_i (for $i=1...n,n+1\equiv 1$) such that for all $i=1...n$

Moreover, the gauges ${Z}_{i}$ are unique up to a multiplicative constant.

In appendix we strengthen the statement to include system sizes $n\geqslant 2L+1$. For TI MPS, the statement reads as

Corollary 3. Let $A$ and $B$ be two normal TI MPS on $n\geqslant 3L$ sites with the property that blocking $L$ consecutive sites results in an injective tensor. Suppose they generate the same state:

Then there is an invertible matrix $Z$ and a constant $\lambda$ with ${\lambda }^{n}=1$ such that

Moreover the gauge $Z$ is unique up to a multiplicative constant.

$n\geqslant 2L+1$

Corollary 4. Let $A$ and $B$ be two normal 2D PEPS tensors such that every $L\times K$ region is injective. Suppose they generate the same state on some region $n\times m$ with $n\geqslant 3L$ and $m\geqslant 3K$. Then $A$ and $B$ are related to each other with a gauge:

with ${\lambda }^{n\cdot m}=1$ and $X,Y$ invertible matrices. Moreover these matrices $X,Y$ are unique up to a multiplicative constant.

In appendix we strengthen the statement to include system sizes $n\geqslant 2L+1$ and $m\geqslant 2K+1$. Similar statements can be made for the non-TI case as well as for other situations, including PEPS in 3 and higher dimensions, other lattices (e.g. triangular, honeycomb, Kagome), and other geometries (e.g. hyperbolic, as it is used in the AdS/CFT constructions [35, 36]).

Furthermore, the results hold for general TNs as well (including tensors that do not have physical index), provided that the TN satisfies the conditions in theorem 4. An example for TNs that contain tensors without physical index is the class of tree tensor network states [37]. For this particular class, our proof method works, thus given two normal or injective TTNs generating the same state, the generating tensors are related to each other by local gauges. A sufficient criterion for a binary TTN being normal is that the tensors are of minimal bond dimension [38]. MERA [11] is an other class of TNs that contain tensors without physical index. For this class, however, we did not find a simple way to block to three-partite injective MPS due to the particular geometry of the network. Therefore, our proof method is not directly applicable for MERA.

In this section we show how the above results can be applied in different scenarios. In particular, we consider local (gauge) and global symmetries as well as translation symmetry of TN states. These operations have the particular property that they leave the TN structure of the state invariant (including the injectivity property of the defining tensors), therefore checking for such symmetries is equivalent to comparing two TN states. In the case of local symmetries it is crucial that the presented method does not rely on the translation invariance of the describing tensors.

Consider a normal TN on n particles describing a state $| {\rm{\Psi }}\rangle$. Suppose $| {\rm{\Psi }}\rangle$ admits a global symmetry: ${U}^{\otimes n}{\rm{\Psi }}={\rm{\Psi }}$. Then, if the TN satisfies the conditions in theorem 4, the symmetry operators acting on the individual tensors is the same as acting with gauge transformations on the virtual level. For example, in TI MPS, this is reflected as:

with ${\lambda }^{n}=1$. Similar statements are true in the non-TI case (in which case the gauges might be different on every edge) and for any geometry. If the state admits a whole symmetry group, the gauges form a projective representation of that group on every bond.

Consider now a local (gauge) symmetry in a normal TN. If the symmetry is strictly one-local, it leaves each tensor invariant. As an illustration, for MPS, if

then

as looking at the rest of the tensors, we conclude that all gauges are the identity. For two-local symmetries, if

then

Here, if the state is symmetric under a whole group of unitaries, then the gauge Z forms a linear representation of that group. Similar statements can be obtained for three-local symmetries as well as for any geometry provided that the TN satisfies the conditions in theorem 4.

Consider now translation symmetry. We prove that a TI state (defined on a regular lattice) that has a normal PEPS description also has a TI PEPS description with the same bond dimension. This holds, for instance, for injective and normal 2D PEPS and MPS. Below we provide the proof for injective MPS, but the proof can easily be extended to the other cases as well.

Corollary 5. Let the tensors ${A}_{i}$ define an injective MPS such that the resulting state is translational invariant. Then all bond dimensions are the same and the state has a TI MPS description with an injective tensor $B$ that has the same bond dimension.

Proof. Translational invariance means

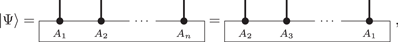
thus, by theorem 1, there are invertible matrices Z_i such that for all i ($n+1\equiv 1$)

Therefore all tensors can be expressed with the help of the first tensor (A₁) together with some invertible matrices acting on the virtual dimensions of the tensor:

with

$$\begin{eqnarray*}\begin{array}{rcl}{L}_{i} & = & {Z}_{1}{Z}_{2}...{Z}_{i-1},\\ {R}_{i} & = & {Z}_{2}{Z}_{3}...{Z}_{i}.\end{array}\end{eqnarray*}$$

As ${R}_{i}{L}_{i+1}^{-1}={Z}_{1}^{-1}$ for all i, substituting A_i as in equation (10), the state can be written as

where we have used that ${A}_{n+1}\equiv {A}_{1}$ and thus ${R}_{n+1}={L}_{n+1}=1$, which means that ${R}_{n}={Z}_{2}...{Z}_{n}={Z}_{1}^{-1}$. This means that the state admits a TI MPS description with the tensor

□

The corresponding statement for injective 2D PEPS is

Corollary 6. Let the tensors ${A}_{(i,j)}$ define an injective 2D PEPS such that the resulting state is translational invariant. Then all vertical (resp. all horizontal) bond dimensions are the same and the state has a TI 2D PEPS description with an injective tensor $B$ that has the same bond dimension.

In this paper we have shown the 'fundamental theorem' for injective and normal PEPS: two such TNs generate the same state if and only if the defining tensors are related with a local gauge. Moreover, the gauges relating the two set of tensors are uniquely defined up to a multiplicative constant. This result holds for a fixed (but large enough) system size. It is valid for any geometry, TI and non-TI setting, including 1D (MPS), 2D PEPS, higher-dimensional PEPS, and other lattice geometries such as the honeycomb lattice, the Kagome lattice, tree tensors networks, and the hyperbolic lattice used in the AdS/CFT correspondence. The proof method, however, is not applicable for some other classes of tensors networks. These TNs include MERA, where we did not find a simple way to apply lemma 1 due to the particular geometry of the network, or TNs describing topological order, where the presence of virtual symmetries prevent the tensors to be normal.

We thank Barbara Kraus, David Sauerwein, Erez Zohar and Ilya Kull for inspiring conversations.

JGR and DPG acknowledge financial support from MINECO (grant MTM2014-54240-P), Comunidad de Madrid (grant QUITEMAD+CM, ref. S2013/ICE-2801), and Severo Ochoa project SEV-2015-556.

This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme through the ERC Starting Grant WASCOSYS (No. 636201), the ERC Consolidator Grant GAPS (No. 648913), and the ERC Advanced Grant QENOCOBA (No. 742102).

In section 4 we have shown that two normal TNs generate the same state if and only if the generating tensors are related with a gauge transformation. In the proof, we have blocked tensors to injective tensors. This proof is not optimal in the system size. For example, consider an MPS on five sites

where the blocking of any two consecutive tensors:

is injective. The proof in section 4 does not work for this case as this MPS cannot be blocked to a three-partite injective MPS (as it is too short). Here we prove a more size-efficient variant of lemma 1 for this situation.

Lemma 4 implies that any region of at least size two is also injective. Now, similar to the injective case, for every edge and every matrix X and Y, if

then X = Y.

Consider now any virtual operation X on a given edge:

This operation can also be realized by three different two-local physical operators:

with

Notice that both $X\mapsto {O}_{1}$ and $X\mapsto {O}_{3}^{T}$ are algebra homomorphisms, but the map $X\mapsto {O}_{2}$ not necessarily. Conversely:

Lemma 5. Suppose that the state $| {\rm{\Psi }}^{\prime} \rangle$ can be written as

Then there is a virtual operation X on the bond $(2,3)$ such that

moreover

and the maps ${O}_{1}\mapsto X$ and ${O}_{3}^{T}\mapsto X$ are uniquely defined and are algebra homomorphisms.

Proof. Invert the injective tensor on the region 45. We get

Similarly, inverting the tensor on the region 51, we get

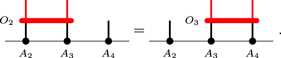
Therefore, plugging A₄ on the right side in equation (A2) and A₁ on the left side in equation (A3), we get

Comparing the two ends of the equation, similar to equation (3), we get that

Finally X = Y by comparing the states they generate. These relations define X uniquely and by composition, the maps ${O}_{1}\mapsto X$ and ${O}_{3}\mapsto {X}^{T}$ are algebra homomorphisms. □

Notice that similar to the injective case, this leads to

Corollary 7. Let $A$ and $B$ be two normal TI MPS on $n\geqslant 2L+1$ sites with the property that blocking $L$ consecutive sites results in an injective tensor. Suppose they generate the same state:

Then there is an invertible matrix Z and a constant λ with ${\lambda }^{n}=1$ such that

Moreover the gauge $Z$ is unique up to a multiplicative constant.

The arguments in lemma 5 can be applied for 2D PEPS as well. In the TI setting, this leads to

Corollary 8. Let $A$ and $B$ be two normal 2D PEPS tensors such that every $L\times K$ region is injective. Suppose they generate the same state on some region $n\times m$ with $n\geqslant 2L+1$ and $m\geqslant 2K+1$. Then $A$ and $B$ are related to each other with a gauge:

with ${\lambda }^{n\cdot m}=1$ and $X,Y$ invertible matrices. Moreover these matrices $X,Y$ are unique up to a multiplicative constant.

Sketch of proof. We only need to prove a statement similar to lemma 5. For that, notice that a virtual operation on a given bond can be interpreted as a physical operation on any of the following four regions (in the case of $K=L=2$):

We need to prove that conversely, any four physical operators on the above regions that transforms the PEPS into the same state means that the transformation can equally be done with a virtual operation on the highlighted edge. The system size required to compare any two consecutive regions is only 5 × 5 (and in general, $(2L+1)\times (2K+1)$). Therefore, similar to lemma 5

with open boundaries. Compare now the first and the last expression in the above equation. One can add two-two tensors in the upper left and lower right corner and invert the resulting regions, leading to

This results in the desired virtual operation on the highlighted edge. The rest of the proof is the same as the proof of theorem 3. □