Interaction of an Archimedean spiral structure with orbital angular momentum light

The phase properties of a light beam can be characterized by its polarization state, which is connected to the spin angular momentum (SAM) of light, denoted by its handedness s = ±1. An additional phase can be superimposed, which leads to a helical wavefront, such that these light beams are also called twisted light. The additional phase can be identified as OAM of the light beam and is quantified by the integer number ℓ. Considering applications in quantum information technologies, it should be noted that in contrast to the SAM s, which is restricted to two values, the OAM ℓin principle can take infinite values. In the extreme limit, a single photon carrying OAM can be created, which can be used for quantum phenomena like entanglement [32]. For the mathematical description of twisted light beams different approaches exist, which differs in the radial profile, for example Laguerre–Gaussian [33], Bessel function [34], and others [35], where we here consider Bessel beams, because they are exact solutions of Maxwell equations [36]. The vector potential of a monochromatic Bessel beam with frequency ω propagating along the z-axis with the wavevector q_z in Cartesian coordinates {x, y, z} is given by ${\bf{A}}({\bf{r}},t)=({A}_{x}{{\bf{e}}}_{x}+{A}_{y}{{\bf{e}}}_{y}+{A}_{z}{{\bf{e}}}_{z})\exp [-{\rm{i}}(\omega t-{q}_{z}z)]$ with the components [30, 34, 37]:

$$\begin{eqnarray}&&{A}_{x}({\bf{r}},t)={A}_{0}{J}_{{\ell }}({q}_{r}r)\exp ({\rm{i}}{\ell }\varphi ),\end{eqnarray} \tag{ 1 }$$

$$\begin{eqnarray}&&{A}_{y}({\bf{r}},t)={{\rm{i}}{s}{A}}_{0}{J}_{{\ell }}({q}_{r}r)\exp ({\rm{i}}{\ell }\varphi ),\end{eqnarray} \tag{ 2 }$$

$$\begin{eqnarray}&&{A}_{z}({\bf{r}},t)=-{\rm{i}}{s}\displaystyle \frac{{q}_{r}}{{q}_{z}}{A}_{0}{J}_{{\ell }+s}({q}_{r}r)\exp ({\rm{i}}({\ell }+s)\varphi ),\end{eqnarray} \tag{ 3 }$$

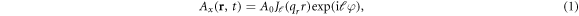
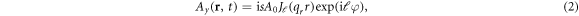
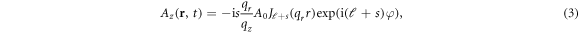
with the radius 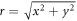$r=\sqrt{{x}^{2}+{y}^{2}}$, the azimuthal angle 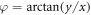$\varphi =\arctan (y/x)$, the wavevector in the transversal plane q_r and the amplitude A₀. 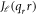${J}_{{\ell }}({q}_{r}r)$ is the Bessel function of order ℓ. From the vector potential the electric field can be readily derived via ${\bf{E}}=-\partial {\bf{A}}/\partial t$.

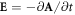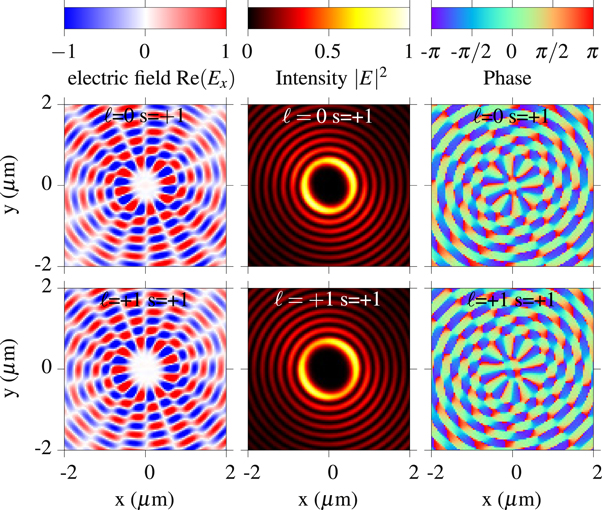
The two quantum numbers ℓof OAM and s of SAM are strongly intertwined. In particular, it leads to the distinction of two classes of OAM light: the parallel class for ℓand s having the same sign and the anti-parallel class for ℓand s having opposite sign [30]. The field patterns in the two classes are topologically different and also do not evolve into each other in time. A snapshot of the electric field for the two classes is shown exemplarily in figure 1(c) for OAM with ℓ = +1, s = +1 (parallel class) and 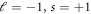${\ell }=-1,s=+1$ (anti-parallel class). The field patterns of light in the parallel class are characterized by a saddle point in the middle and a two-fold symmetry. The field patterns in the anti-parallel class are radially symmetric and in time will cycle through radially and azimuthally polarized fields [29, 30].

Zoom In Zoom Out Reset image size

The interaction of OAM light with matter leads to many new effects ranging from unusual transition in single particles like molecules or semiconductor quantum dots [30, 38–41] to applications as tweezers in biology [42, 43]. Due to the non-trivial spatial structure of the OAM light, the OAM-light–matter interaction has to be treated with care [30, 44]. To describe the interaction of OAM light with a plasmonic nanostructure, we perform numerical simulation using the boundary element method [45].

The characteristics of an Archimedean spiral is that its radius increases when making a rotation. For a single rotation the increase in radius is given by

$$\begin{eqnarray}&&r(\varphi )={r}_{0}+\tilde{d}\,\displaystyle \frac{\varphi }{2\pi },\end{eqnarray} \tag{ 4 }$$

where r₀ is the starting radius and after one rotation the radius has increased by the distance 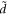$\tilde{d}$. A similar structure is given by dividing a single rotation into m elements, where the distance between the starting point of the one element and the end point of the other element is given by the distance d, such that the increase in radius for each element r_m is given by

$$\begin{eqnarray}&&{r}_{m}(\varphi )={r}_{0}+\displaystyle \frac{d\,\mathrm{mod}(m\varphi ,2\pi )}{2\pi }\,\end{eqnarray} \tag{ 5 }$$

with mod being the modulus function giving the remainder of the division of 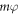$m\varphi$ by 2π. A sketch of the segmented spiral is shown in figure 1(a). In a planar system, where all the waves propagate within a 2D plane, an Archimedean spiral can generate a vortex, because each wave travelling from a point of the structure to the centre collects a phase, which is proportional to the distance of an infinitesimal curved small element of the structure to the centre. Overall, all phase retardations result in a spiral phase profile along a circle around the centre [2, 3]. For the generation of vortices in planar systems, it can be shown that both the single spiral and the segmented spiral induce a similar phase relation if 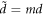$\tilde{d}={md}$ [2]. However, due to the reduced curvature, the segmented spiral has reduced losses [8], hence we will also consider the segmented spiral here. Note that the number of segments m is also called topological charge of the spiral and is a geometrical property of the structure [2, 4–6, 8, 11, 24, 46].

Here, we will consider a segmented Archimedean spiral consisting of m = 4 segments and each arm of the spiral is made of a bent nanorod. In some sense this is the positive analogue to the grooved Archimedean spirals fabricated in gold surface. We assume the spirals are made of gold nanorods with a radial cross-section of 40 nm diameter surrounded by air. We also compare this to a more realistic set-up where the structure is embedded into a medium with an effective refractive index of n = 1.5, which mimics a glass substrate and a coverage with a polymer. Such structures are widely used in nanoplasmonics and have the advantage of avoiding scattering effects at the air/glass surface [47, 48]. The dielectric function of gold is taken from experimental data [49]. We then excite the gold structure with an external light field as described above and consider the scattered electric fields.

For the grooved spiral in a metal system, it was found that a vortex of SPPs is generated, when the distance d between the parts of the segmented spiral agrees with the wavelength of the propagating SPP [2, 7, 8]. Transferring this concept to light waves in air and considering an optical wavelength of λ_opt = 800 nm, we set the distance to d = λ_opt. We assume a structure which holds several wavelengths and we choose its radius to r₀ = 18 μm. The structure is illuminated by a light beam travelling from the bottom along positive z-direction impinging on the plasmonic structure lying in the z = 0-plane. The centre of the spiral is aligned with the beam axis. The transverse wavevector q_r of the excitation field is chosen such that the maximum of the Bessel function is at r₀ as sketched in figure 1(b). For the zero-order Bessel function the value is chosen to 0.6 at r₀, to achieve similar intensity to the higher order Bessel beams.

We start with an excitation of the Archimedean spiral with plane wave light, i.e. with ℓ = 0 and circular polarization of s = ±1. The top row in figure 2 shows the scattered electric field within the z = 0-plane in an area of 2 μm around the centre as indicated by the red box in figure 1(a). From left to right we present the real part of the electric field patterns for s = +1, the intensity for s = +1 and the phases for s = ±1. The field pattern given by Re(E_x) is rotationally-symmetric around the z-axis and has a vortex with vanishing amplitude in the centre. We find four minima and four maxima along the azimuthal direction. The corresponding y-components of the electric field (not shown here) looks the same, but rotated. The field pattern for s = −1 is analogue for Re(E_x) and differs only in the sign of Re(E_y). The intensity of the electric field, defined as 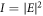$I=| E{| }^{2}$ including both real and imaginary parts, has a pattern of concentric rings. Note that the intensity can also be obtained by integration over one period of the real parts of the fields. Again, the intensity for s = −1 is the same. In agreement with the four maxima and minima in the fields, the phase exhibits four phase jumps. Note that the phase is defined as the angle ϑ between the x- and y-component of the electric field with 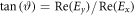$\tan (\vartheta )={\rm{Re}}({E}_{y})/{\rm{Re}}({E}_{x})$. For the two polarizations s = ±1 the rotation direction of the phase is inverted. When going clockwise on a circle around the vortex, the phase increases from −π to +π for s = +1, while it decreases for s = −1. This leads to the conclusion that the handedness of polarization remains in the scattered fields. These findings are a clear evidence that the Archimedean spiral structure generates a vortex with the topological charge v = 4 in the scattered optical field.

Zoom In Zoom Out Reset image size

For experimental investigations of the observed effect, we take an Archimedean spiral structure surrounded by an effective medium with a refractive index of n = 1.5. To fulfil the conditions for vortex generation, the distance between the spiral segments is reduced to the effective wavelength in the medium with 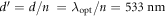$d^{\prime} =d/n\,={\lambda }_{{\rm{opt}}}/n=533\,\mathrm{nm}$. The corresponding figure is shown in figure 2 (bottom row). We find that the same effects appear, but now all wavelengths are scaled with the refractive index n of the medium. Accordingly, the distance between the rings in the scattered field get smaller as seen in figure 2.

Next, we consider an excitation with an OAM light beam with ℓ = ±1, ±2 as well as different polarizations s = ±1. The different rows in figure 3 display the fields for excitation with varying OAM ℓ = ±1, ±2. The two columns correspond to the different signs of polarization s = ±1. Let us look first at an excitation with positive polarization s = +1 (left) and an OAM light beam with ℓ = +1 in the first row and ℓ = −1 in the second row. Again, we find a vortex in the centre of the spiral, but the number of maxima has change to 5 for ℓ = +1 and to 3 for ℓ = −1. In agreement with the number of maxima, the phase shows 5 and 3 jumps, respectively. Hence, the topological charge of the vortex is v = 5 and v = 3, accordingly. This indicates that the topological charge of the vortex v in a m segmented Archimedean spiral can be calculated by

$$\begin{eqnarray}&&v=| m+{\ell }| .\end{eqnarray} \tag{ 6 }$$

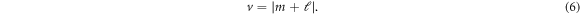
The validity of the equation is confirmed, when considering an excitation with ℓ = ±2 in the lowest two rows. Here we find a vortex with v = 4 + 2 = 6 for an excitation with ℓ = 2, displaying 6 maxima in the electric field component and 6 phase jumps, and a vortex with v = 4 − 2 = 2, with 2 maxima in the electric field component and 2 phase jumps, for an excitation with ℓ = −2. While we find that the OAM of the exciting fields strongly determines the topological charge of the vortex, the polarization s has been kept constant so far. Given that the polarization strongly determines the electric field patterns of the OAM light and is strongly intertwined with the OAM of the light, we now consider the influence of polarization by changing its value to s = −1 in the right column of figure 3. The amplitude profiles stay the same for both polarization s = ±1 only the phase rotation direction is inverted as discussed for non OAM light. This confirms that equation (6) does only depend on the value of OAM and not on the polarization of the excitation. We remark that we have also checked the validity of equation (6) with Archimedean spiral structures having m = 3 and m = 5 (not shown).

Zoom In Zoom Out Reset image size

The mechanism behind the vortex generation for the optical fields can be understood by considering the metallic spiral as a (perfect) electric conductor. As such the spiral structure describes a boundary condition problem for which the solutions are given by the vortex fields. Adding to that the conditions of the exciting beam given in equations (1) and (2), this explains the dependence of the vortex number on ℓ, but not on s. These equations clearly show that the OAM ℓ gives an additional spatial phase, which has to be taken into account for the boundary conditions, while the polarization s does not. On the other hand, when only looking at the longitudinal component of the electric field E_z, i.e. along the propagation direction (not shown), the field distribution goes with ℓ + s (see equation (3)) and accordingly the generated vortex is of the order of m + ℓ + s. However, the generated longitudinal component is orders of magnitude weaker than the transversal components, hence this effect is not seen in the total fields.

The mechanism for the optical fields is slightly different to the vortex formation of SPP on metallic surfaces. For the SPPs the grooves in the surface act as a source of SPPs and the vortex formation can be described by an interference pattern of waves running inside the spiral with the correct phase [2, 3, 5, 7]. A similar equation for the vortex number has also been found [2, 4, 6, 11, 24, 46]. In the SPP case the vortex manifests in the electric field perpendicular to the surface, while with our positive structure we obtain a vortex in the transverse components of the electric field. For both cases, the unique geometry of the Archimedean spiral leads to an interference pattern such that a vortex is generated.

The condition to create a vortex for the micrometer-sized spiral is d = λ_opt = 800 nm. For an excitation with light having a wavelength slightly above and below 800 nm, where this condition is not met anymore, no vortex will form, but rather an irregular pattern appears. To achieve a vortex for a different wavelength, the distance at the edges has to be adjusted. However, it is interesting to see what happens, if we excite the spiral with d = 800 nm with half the wavelength, i.e. with λ = 400 nm. Expecting a similar behaviour of the spiral like a waveguide, this should lead to an excitation of a higher order mode. The corresponding results are shown in figure 4 for an excitation with ℓ = 0, s = 1 and with OAM light having ℓ = +1, s = +1. In the middle of the spiral, we again find that a vortex is formed, but the vortex number is different: for ℓ = 0 the vortex number is v = 8 and for ℓ = +1 the vortex number is v = 9. This can be summarized by rule

$$\begin{eqnarray}&&v=| 2m+{\ell }| .\end{eqnarray} \tag{ 7 }$$

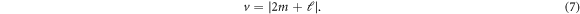
In other words, an excitation with half the wavelength leads to the excitation of a higher order mode, while the OAM ℓjust imposes the same phase relation and therefore just enters as before. We note that a small amplitude at the centre appears, which we attribute to an influence of the z-component and the finite discretization. We conclude that the vortex number v does not only depend on the segments of the spiral and the phase properties of the exciting light, but also on the wavelength of the exciting light.

Zoom In Zoom Out Reset image size

Seeing that the Archimedean spiral can be used to generate optical vortices, it is natural to ask whether such structures also have a strong optical response regarding plasmonic resonances. To this end, we consider a nanometer-sized Archimedean spiral, where localized surface plasmon resonances are expected to dominate the optical response [48]. For rotationally arranged nanoantennas, the resonances induced by OAM light can be very different to an excitation with plane waves and the resonance behaviour strongly depends on both the OAM and polarization of the light beams [29]. In particular, dark modes (i.e. modes which cannot be excited by plane waves) can be driven by OAM light. For the plasmonic resonance of a system, the size of the structure is typically a fraction of the wavelength with a rule of thumb being that the size of a nanorod should be around half the wavelength of the exciting field. Therefore, we now consider a nanostructure with a radius of r₀ = 100 nm and a distance d = 80 nm between the segments. We illuminate the structure with an OAM light beam having a ratio of the wavevectors q_r/q_z = 0.1. In contrast to the micrometer-sized structure, we do not expect a vortex generation as the response is dominated by the near-field.

To classify the bright modes of the system, figure 5(a) shows the scattering cross-section as a function of the wavelength for an excitation with circularly polarized light having ℓ = 0. We find that the scattering cross-section exhibits two resonances, which we label A and B, at λ_A = 1000 nm and λ_B = 640 nm, respectively. In figure 5(c) the corresponding surface charge distribution is displayed. At resonance A, the surface charge of only two out of the four elements shows a dipolar character with a positive charge at one end and a negative charge at the other end, while the other two elements exhibit a uniform surface charge. Note that the surface charge is displayed for just one snapshot in time. The behaviour of the surface charge distributions can be explained by the field patterns of the excitation field: at a given time all field lines are pointing in the same direction just as for plane waves with circular polarization. Supposing that each element can be approximated by a dipole, only the two rods whose dipole moments are in line with the excitation field get excited. The other two elements, which are perpendicularly aligned, remain nearly unaffected. This leads to the excitation of the bright mode A.

Zoom In Zoom Out Reset image size

Looking at its surface charges the resonance B can be clearly identified as a higher order mode. We find two nodes within the surface charge of each element and the two ends of the elements have the same sign of charge. Also here only two elements are affected due to the homogeneous orientation of the field patterns. Because resonance B is excited by plane waves, we classify it as a bright mode. The excitation of resonance B is possible under normal incidence, because the rod is bent such that the symmetry is slightly broken [47, 50].

In figure 5(b) the scattering cross-section for an excitation with OAM light having ℓ = ±1 and s = ±1 is displayed. We find that three different resonances are excited. At λ_B = 640 nm the resonance B is excited, while the resonance A is not found. Instead two new resonances C and D are excited at λ_C = 935 nm and λ_D = 1170 nm. Indeed, the surface charges corresponding to these modes are qualitatively different to resonance A. At resonance C we find that all four elements have a dipolar character and at the ends of two different segments at r₀ and r₀ + d the same sign is found. At resonance D again all four elements have a dipolar character, but the ends of neighbouring elements have different signs of surface charge. The energetic positioning of the modes A, C and D can be reasoned within a hybridization model [29, 51], where two rods with the same surface charges repel each other like in an anti-bonding mode and accordingly have a higher energy (and shorter wavelength), while two rods with the different surface charges attract each other like in bonding mode and have a lower energy (and larger wavelength).

The two resonances C and D are not equally excited by the four OAM light beams. Resonance C is excited by OAM light with ℓ = +1, s = +1 and ℓ = −1, s = −1, i.e., by beams of the parallel class. On the other hand, resonance D is excited by beams of the anti-parallel class having ℓ = +1, s = −1 and ℓ = −1, s = +1. This difference can be explained by the different field patterns of the two classes shown in figure 1(c). In the parallel class the field patterns have a saddle point in the middle exhibiting a two-fold symmetry reflecting the two-fold symmetry of resonance C. In contrast, in the anti-parallel class the field patterns cycle though radially and azimuthally polarized fields giving rise to the azimuthal symmetry found in the surface charges of resonance D. There is also a difference in intensity between the two classes for resonance B, showing a dichroistic behaviour with the parallel class being more intense than the anti-parallel class [52].

The difference in modes C and D to mode A are further visible in the far-field radiation patterns which are shown in figure 5(d). The radiation pattern consists of the real part of the product of the radial unit vector 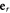${{\bf{e}}}_{r}$ with the electric E and magnetic field B on a surface of a sphere in the far-field, i.e. R ∝ $\mathrm{Re}[{{\bf{e}}}_{r}\cdot ({\bf{E}}\times {{\bf{B}}}^{* })]$. The radius at each point of this sphere is scaled with the amplitude of R encoded also in the colour. For mode A most of the power is radiated in z-direction upwards and downwards, which agrees with the Poynting vector for plane waves pointing along the propagation direction. This radiation pattern has a typical dipole character with two wings. Mode C offers a completely different behaviour. Most of the power is radiated in the transversal plane showing four wings being characteristic of a quadrupolar field. The small asymmetry in the radiation pattern can be explained by deviation in charge distribution from a perfect quadrupole such that an additional small dipole contributes. The radiation of mode D lies also in the transverse plane, but shows an azimuthal shape, i.e. a higher order mode, corresponding to the azimuthal surface charge distribution. The radiation patterns underline the finding that different resonance modes of the Archimedean spiral are excited by OAM light.

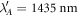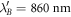The same behaviour of the resonances is found, when the spiral structure is embedded into a glass/polymer medium with refractive index n = 1.5. The only quantitative change is that the resonances red-shift. In the embedded structure the dipole resonances are found at ${\lambda }_{A}^{{\prime} }=1435\,\mathrm{nm}$ and ${\lambda }_{B}^{{\prime} }=860\,\mathrm{nm}$, while the resonance excited by OAM light lie at 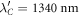${\lambda }_{C}^{{\prime} }=1340\,\mathrm{nm}$ and ${\lambda }_{D}^{{\prime} }=1690\,\mathrm{nm}$. In addition to the surrounding medium, the position of the resonances can be tuned by changing the geometry of the system, like length of the rods or the gap d between the segments [53].

By changing the number of segments of the Archimedean spiral, a similar behaviour of the resonances is expected. We have performed calculations for m = 3 and m = 5 (not shown), which exhibit the same features as m = 4. For the excitation with plane waves, a bright mode of type A can be identified and also higher order modes of type B appear. When excited with OAM light, the bright mode A vanishes in favour of mode C and D. In particular, the azimuthally polarized mode D, where the ends of neighbouring elements have different signs of the surface charge, will be excited at every geometry. For mode C the behaviour is more complicated, because due to symmetry neighbouring elements cannot always have same sign. For odd spiral numbers the lack of symmetry is compensated by single elements having temporarily zero surface charge. Nonetheless a similar mode type C is excited.