Abstract
We propose a one-step scheme for driving many atoms into a NOON state. In this scheme, two cavities are coupled to each other through the photon-hopping interaction and each cavity contains N four-level atoms. The 2N atoms are driven into a NOON state via a phase-shift which depends on the collective atomic excitations. Interestingly, the time of generating the NOON state is independent of the atom number, i.e., it is unchanged with the increasing of the atom number. Also, our scheme is insensitive to cavity decay and can effectively suppress atomic spontaneous emission.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Entanglement is always of great interest for fundamental studies of quantum mechanics. Recently, of particular interest are NOON states [1–3], between two modes a and b with the form 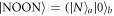
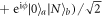 (ϕ is arbitrary phase and N = 1, 2, 3...), which are widely applied in quantum lithography [3, 4], quantum metrology [5, 6], quantum imaging [7], and quantum information processing [8, 9]. Many schemes have been proposed for generating photonic NOON states [10–18], however, most of them are based on the step-by-step strategy that means the time of generating NOON states will increase with increasing photon-number. On the other hand, atoms as important and excellent media, draw a great deal of attention [19–22] due to their various applications in quantum information and quantum metrology [23–26]. In particular, the systems including many atoms are extensively used for quantum state engineering in quantum information processing, such as spin-squeezed states [27–29] and entangled states [30, 31].
(ϕ is arbitrary phase and N = 1, 2, 3...), which are widely applied in quantum lithography [3, 4], quantum metrology [5, 6], quantum imaging [7], and quantum information processing [8, 9]. Many schemes have been proposed for generating photonic NOON states [10–18], however, most of them are based on the step-by-step strategy that means the time of generating NOON states will increase with increasing photon-number. On the other hand, atoms as important and excellent media, draw a great deal of attention [19–22] due to their various applications in quantum information and quantum metrology [23–26]. In particular, the systems including many atoms are extensively used for quantum state engineering in quantum information processing, such as spin-squeezed states [27–29] and entangled states [30, 31].
In recent years, the generation of atomic NOON state attracts a lot of attention. For example, a scheme for creating NOON states of the quasi-momentum of ultra-cold atoms is proposed in the system where the condensed atoms trapped in an optical potential of three sites in a ring configuration [32]. A heralded generation of an atomic NOON state in motion-sensitive SW interferometer is demonstrated and the second order NOON state is generated experimentally [33]. In the strong-coupling regime, a scheme is proposed for the production of NOON state in the cavity-QED system where two cavity modes interact with an ensemble of atoms, and the atomic NOON state is generated by the adiabatic evolution and the simple local operations [34]. Additionally, a two-steps protocol for creating a NOON state of repulsively interacting Bose atoms in the double-well potential is proposed [35]. However, most of these schemes need more than one-step or the projective measurements. Therefore, it is important and valuable to investigate the generation of atomic NOON state based on the one-step strategy.
Coupled cavities, as a promising platform in quantum information processing and quantum simulation, have attracted a lot of attention [36–38]. The coupled-cavity systems promise to overcome the difficulty of individual addressability existing in a single cavity [39], which can be experimentally implemented in many systems [40–42]. And many schemes of generating quantum states have been proposed in the coupled-cavity systems [43–45]. In single cavity, a scheme of generating Greenberger–Horne–Zeilinger atomic state has been proposed, which is insensitive to cavity decay [46]. However, atomic spontaneous emission has a strong effect on the state generation, because the atomic excited states are populated during the whole generation process. Here, we propose a one-step scheme for driving many atoms into a NOON state, where 2N atoms are separately trapped in two cavities coupled with the photon-hopping interaction. In our scheme, the atomic ground states are used to engineer the NOON state, and the atomic excited states are hardly excited due to the large detunings. Thus atomic spontaneous emission can be effectively suppressed.
2. The model
We consider two cavities coupled with the photon-hopping interaction, each of which contains N identical four-level atoms. Each four-level atom has two excited states and two ground states with the corresponding energies 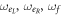 , and ωg (see figure 1). The transition
, and ωg (see figure 1). The transition  is coupled to a cavity mode with the strength gi and the transition
is coupled to a cavity mode with the strength gi and the transition 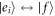 is driven by a classical field with the strength Ωi (i = L, R). In experiment, superconducting transmission line resonators coupled to multi-level atoms are an alternative candidate for realizing the system [47]. In the coupled transmission line resonators system, the resonators can be coupled at both ends, which form a small capacitance and thereby enable photon-hopping between the adjacent resonators [48, 49]. The Hamiltonian of the atom-cavity system is given by
is driven by a classical field with the strength Ωi (i = L, R). In experiment, superconducting transmission line resonators coupled to multi-level atoms are an alternative candidate for realizing the system [47]. In the coupled transmission line resonators system, the resonators can be coupled at both ends, which form a small capacitance and thereby enable photon-hopping between the adjacent resonators [48, 49]. The Hamiltonian of the atom-cavity system is given by
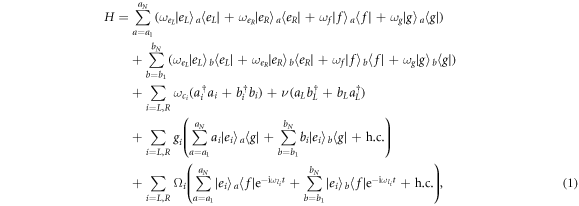
where 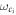 and
and 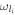 are the frequencies of cavity mode and classical field (i = L, R), respectively. ν is the photon-hopping strength between the two cavities. Applying the transform
are the frequencies of cavity mode and classical field (i = L, R), respectively. ν is the photon-hopping strength between the two cavities. Applying the transform

and transforming the Hamiltonian into the interaction picture, we obtain
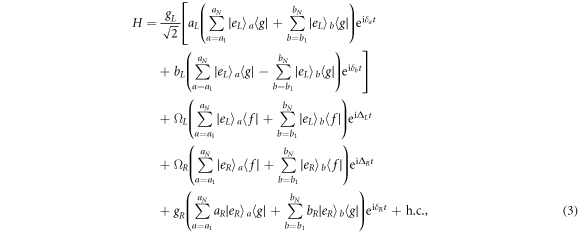
where 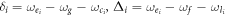 , δa = δL − ν, and δb = δL + ν (i = L, R). For large detunings with
, δa = δL − ν, and δb = δL + ν (i = L, R). For large detunings with
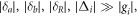
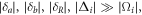
we can adiabatically eliminate the atomic excited states and obtain the following Hamiltonian [28]
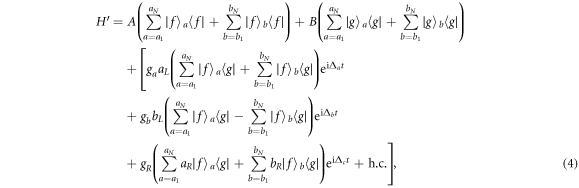
where 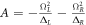 ,
, 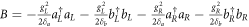 ,
, 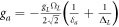 ,
, 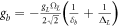 ,
,  , Δa = δa − ΔL, Δb = δb − ΔL, and Δc = δR − ΔR. The first and second terms describe the Stark shift of classical field, and the third and fourth terms describe the photon-number dependent Stark shift. We can neglect the first and second terms by choosing the parameters ΔL = −ΔR and ΩL = ΩR. The third and fourth terms can also be neglected, because the cavity modes are always in the vacuum state. Hence, the Hamiltonian (4) reduces to
, Δa = δa − ΔL, Δb = δb − ΔL, and Δc = δR − ΔR. The first and second terms describe the Stark shift of classical field, and the third and fourth terms describe the photon-number dependent Stark shift. We can neglect the first and second terms by choosing the parameters ΔL = −ΔR and ΩL = ΩR. The third and fourth terms can also be neglected, because the cavity modes are always in the vacuum state. Hence, the Hamiltonian (4) reduces to
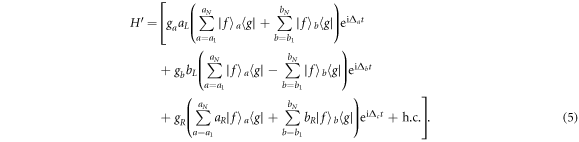
The Hamiltonian (5) describes an effective two-level atom model. In the model, two cavities coupled with the photon-hopping interaction, each of which contains N identical two-level atoms. The transition 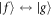 is coupled to the two cavity modes. Therefore, the four-level atoms can be replaced with two-level atoms in our scheme. We further assume the large detuning condition
is coupled to the two cavity modes. Therefore, the four-level atoms can be replaced with two-level atoms in our scheme. We further assume the large detuning condition
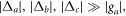
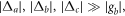
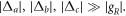
Initially, the cavity modes are in the vacuum state, and they are only virtually excited due the large detuning condition. Thus the cavity modes will be always in the vacuum state. By adiabatically eliminating the cavity modes, we obtain the following effective atomic Hamiltonian
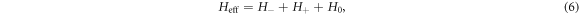
where
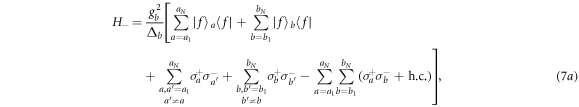
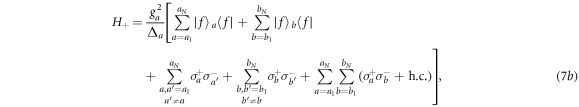
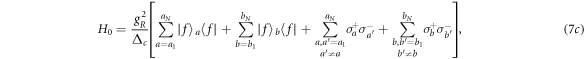
where  is the lowering operator of the atom i and
is the lowering operator of the atom i and 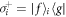 is the raising operator of the atom i (i = a1, b1..., aN, bN). H− is the desired Hamiltonian which can drive the atoms into a NOON state. However, the undesired Hamiltonian H+ will disturb the NOON state generation. Hence, we introduce two extra cavity modes aR and bR to eliminate the effect of the Hamiltonian H+. The two extra cavity modes lead to the Hamiltonian H0. By setting gL = gR = ΩL = ΩR = g and δR = −δa, we obtain
is the raising operator of the atom i (i = a1, b1..., aN, bN). H− is the desired Hamiltonian which can drive the atoms into a NOON state. However, the undesired Hamiltonian H+ will disturb the NOON state generation. Hence, we introduce two extra cavity modes aR and bR to eliminate the effect of the Hamiltonian H+. The two extra cavity modes lead to the Hamiltonian H0. By setting gL = gR = ΩL = ΩR = g and δR = −δa, we obtain
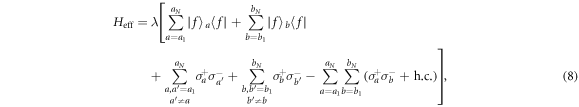
where 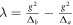 is the effective coupling strength.
is the effective coupling strength.
Figure 1. The energy level diagram of the four-level atoms.
Download figure:
Standard image High-resolution imageNext, we consider the time evolution of the atom-cavity system under the effective Hamiltonian Heff. In cavity a and b, all N atoms are initially prepared in the coherent spin states ![${[{(1/\sqrt{2})(| g\rangle +{\rm{i}}| f\rangle )}_{a}]}^{\otimes N}$](https://content.cld.iop.org/journals/1367-2630/20/9/093019/revision2/njpaadf9eieqn18.gif) and
and ![${[{(1/\sqrt{2})(| g\rangle -{\rm{i}}| f\rangle )}_{b}]}^{\otimes N}$](https://content.cld.iop.org/journals/1367-2630/20/9/093019/revision2/njpaadf9eieqn19.gif) , respectively. The initial state of the total system can be expressed as follows:
, respectively. The initial state of the total system can be expressed as follows:
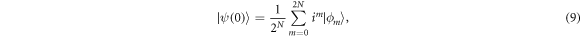
where  is the sum of all
is the sum of all  terms with m atoms in excited states and
terms with m atoms in excited states and 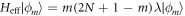 [46]. After the evolution time τ = π/(2λ), the state is given by
[46]. After the evolution time τ = π/(2λ), the state is given by
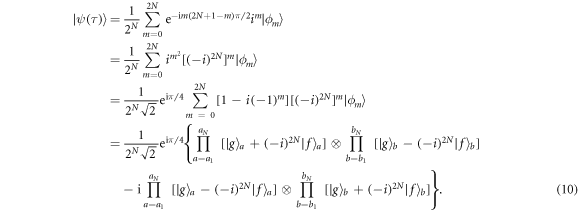
In analogy to the photonic number state, we define the number state for the atoms in cavity a and b as follows:
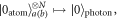

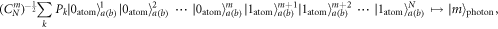

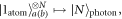
where ![$| {0}_{\mathrm{atom}}{\rangle }_{a(b)}\equiv \tfrac{1}{\sqrt{{2}^{N}}}{[| g\rangle -{(-{i})}^{2N}| e\rangle ]}_{a(b)}$](https://content.cld.iop.org/journals/1367-2630/20/9/093019/revision2/njpaadf9eieqn23.gif) ,
, ![$| {1}_{\mathrm{atom}}{\rangle }_{a(b)}\equiv \tfrac{1}{\sqrt{{2}^{N}}}{[| g\rangle +{(-{i})}^{2N}| e\rangle ]}_{a(b)}$](https://content.cld.iop.org/journals/1367-2630/20/9/093019/revision2/njpaadf9eieqn24.gif) , and {Pk} represents the set of all distinct permutations of the atoms. Therefore, the generated atomic state
, and {Pk} represents the set of all distinct permutations of the atoms. Therefore, the generated atomic state 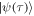 can be written as a NOON state as follows:
can be written as a NOON state as follows:
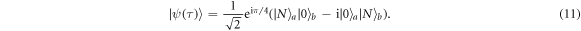
From the above derivation, we know that the time of state generation τ is just a function of the effective coupling strength λ, and the effective coupling is independent of the atom number. Thus, the generation time τ is independent of the atom number N, i.e., the time of generating the NOON state is unchanged with increasing the atom number.
3. The NOON state of four atoms
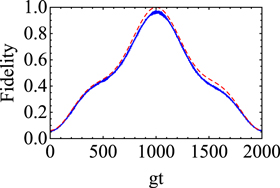
As an example, we generate the NOON state of four atoms and discuss the effect of dissipation. We first check the validity of the effective Hamiltonian 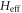 . Figure 2 illustrates the time evolution of fidelity under the effective and the original Hamiltonians, where the parameters are chosen as
. Figure 2 illustrates the time evolution of fidelity under the effective and the original Hamiltonians, where the parameters are chosen as 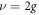 and
and  . It shows that the time evolution of the fidelity under the effective Hamiltonian agrees well with that under the original Hamiltonian, which exemplify the validity of the effective Hamiltonian Heff. As shown above, the generation time of NOON state is independent of the atom number N, which only depends on the effective coupled strength λ. Thus, we consider the effects of the system parameters on the generation time τ. Without loss of generality, we assume that
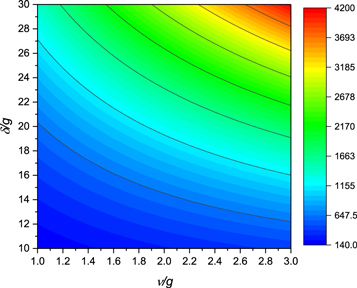
. It shows that the time evolution of the fidelity under the effective Hamiltonian agrees well with that under the original Hamiltonian, which exemplify the validity of the effective Hamiltonian Heff. As shown above, the generation time of NOON state is independent of the atom number N, which only depends on the effective coupled strength λ. Thus, we consider the effects of the system parameters on the generation time τ. Without loss of generality, we assume that 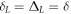 . In figure 3, we plot the generation time τ versus the detuning δ and the photon-hopping strength ν. The generation time τ increases with increasing the detuning δ and the photon-hopping strength ν. In other words, the less detuning and photon-hopping strength lead to the short generation time. However, the less detuning and photon-hopping strength will reduce validity of the effective Hamiltonian. Therefore, while ensuring the validity of the effective Hamiltonian, decreasing the detuning δ and the photon-hopping strength ν is a good way for shortening the generation time.
. In figure 3, we plot the generation time τ versus the detuning δ and the photon-hopping strength ν. The generation time τ increases with increasing the detuning δ and the photon-hopping strength ν. In other words, the less detuning and photon-hopping strength lead to the short generation time. However, the less detuning and photon-hopping strength will reduce validity of the effective Hamiltonian. Therefore, while ensuring the validity of the effective Hamiltonian, decreasing the detuning δ and the photon-hopping strength ν is a good way for shortening the generation time.
Figure 2. The time evolution of fidelity under the effective and the original Hamiltonians, where the parameters are chosen as 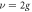 and
and 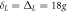 .
.
Download figure:
Standard image High-resolution imageFigure 3. The generation time τ versus the detuning δ and the photon-hopping coupling strength ν.
Download figure:
Standard image High-resolution imageNext, we investigate the effects of cavity decay and atomic spontaneous emission. We numerically simulate the evolution of our system by using the effective master equation:
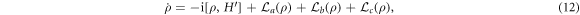
where ρ is the effective density matrix and 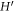 is the effective Hamiltonian (4).
is the effective Hamiltonian (4). 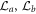 and
and 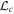 are the Lindblad terms, which describe the effects of cavity decay and atomic spontaneous emission. The expressions of the Lindblad terms and the validity of the effective master equation are shown in appendix. Figure 4 shows the fidelity of the NOON state versus the cavity decay rate κ and the atomic spontaneous emission rate γ. When cavity decay is the dominant dissipation, the fidelity decreases very slowly with increasing the cavity decay rate κ. Since the cavity modes are initially in the vacuum state and only excited virtually, they will be always in the vacuum state throughout the generation process. Therefore, the fidelity is insensitive to cavity decay. When atomic spontaneous emission plays a dominant role, the fidelity decreases from 0.97 to 0.84 with increasing the atomic spontaneous emission rate γ. When γ−1 is greater than 165 g−1, the fidelity is greater than 0.9. In our scheme, each atom is initially prepared in a superposition state between two ground states. During the whole generation process, the atomic excited states are hardly excited due to the large detunings. Thus, atomic spontaneous emission can be effectively suppressed.
are the Lindblad terms, which describe the effects of cavity decay and atomic spontaneous emission. The expressions of the Lindblad terms and the validity of the effective master equation are shown in appendix. Figure 4 shows the fidelity of the NOON state versus the cavity decay rate κ and the atomic spontaneous emission rate γ. When cavity decay is the dominant dissipation, the fidelity decreases very slowly with increasing the cavity decay rate κ. Since the cavity modes are initially in the vacuum state and only excited virtually, they will be always in the vacuum state throughout the generation process. Therefore, the fidelity is insensitive to cavity decay. When atomic spontaneous emission plays a dominant role, the fidelity decreases from 0.97 to 0.84 with increasing the atomic spontaneous emission rate γ. When γ−1 is greater than 165 g−1, the fidelity is greater than 0.9. In our scheme, each atom is initially prepared in a superposition state between two ground states. During the whole generation process, the atomic excited states are hardly excited due to the large detunings. Thus, atomic spontaneous emission can be effectively suppressed.
Figure 4. The fidelity versus the cavity decay rate κ and the atomic spontaneous emission rate γ, where the parameters are chosen as 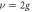 and
and 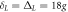 . The blue dashed line corresponds to the fidelity of the two-level atoms in the presence of atomic spontaneous emission, and the parameters are chosen as
. The blue dashed line corresponds to the fidelity of the two-level atoms in the presence of atomic spontaneous emission, and the parameters are chosen as 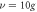 and
and 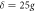 .
.
Download figure:
Standard image High-resolution imageIn addition, the fidelity in the presence of cavity decay is higher than that in the presence of atomic spontaneous emission. It is probably because the atomic excited states and cavity modes are unavoidably populated, even though they have been adiabatically eliminated due to the large detunings. Atomic spontaneous emission has more dissipative paths than cavity decay, thus atomic spontaneous emission has a stronger effect on the fidelity than cavity decay. As shown in section 2, two-level atoms can also be used for the NOON state generation by similar approach. In the case of using two-level atoms, however, the atomic excited states are always populated during the whole generation process. The populations of excited states will keep decreasing due to the effect of atomic spontaneous emission. As a result, the fidelity of two-level atoms is much lower than that of four-level atoms in the presence of atomic spontaneous emission (see figure 4).
At last, we give a brief discussion about the experimental implementation. The multi-level configuration can be realized by Rb atoms and Rydberg atoms. The coupled superconducting stripline microwave resonators [50] and the coupled toroidal micro-resonators [51] are appropriate candidates for our scheme. For example, the parameters can be chosen as: g ∼ 2π × 200 MHz, γ ∼ 2π × 20 kHz, κ ∼ 2π × 50 kHz [50], ν ∼ 2π × 400 MHz, and δL = ΔL ∼ 2π × 1.8 GHz. With the above parameters, we obtain the generation time of the NOON state 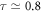 μs and the fidelity of the NOON state f ≃ 0.994.
μs and the fidelity of the NOON state f ≃ 0.994.
4. Conclusion
In conclusion, we have proposed a scheme for generating the many-atom NOON state in the dissipative cavity-QED systems. In our scheme, 2N atoms are separately trapped in two cavities which interact with each other through the photon-hopping. After the interaction time τ, the 2N atoms are driven into the desired NOON state by the collective atomic excitations. The whole procedure of generating the atomic NOON state only needs one-step, and the generation time τ does not increase with increasing the atom number N. The generation time τ only depends on the system parameters: the detunings, the coupling strengths, and the photon-hopping strength. While ensuring the validity of the approximations, decreasing the detuning δ and the photon-hopping strength ν can effectively shorten the generation time τ. We also investigate the effects of the dissipative environments on the state generation. Since the cavity modes are always in the vacuum state of photons in the whole procedure, our scheme is insensitive to cavity decay and can effectively resist cavity decay. In addition, during the whole generation process, the excited states of the four-level atoms are hardly excited due to the large detunings, and thus our scheme can also effectively suppress atomic spontaneous emission.
Acknowledgments
This work was supported by National Natural Science Foundation of China (NSFC) (11474077, and 11675046), Program for Innovation Research of Science in Harbin Institute of Technology (A201411, and A201412), the Fundamental Research Funds for the Central Universities (AUGA5710056414), Natural Science Foundation of Heilongjiang Province of China (A201303), and Postdoctoral Scientific Research Developmental Fund of Heilongjiang Province (LBH-Q15060).
: Appendix. The validity of the effective master equation
In the large detuning condition, we can adiabatically eliminate the atomic excited states and obtain the following effective master equation:
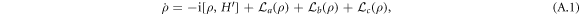
where
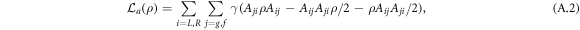
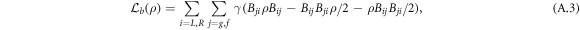

The effective atomic spontaneous emission jump operators are defined as follows:

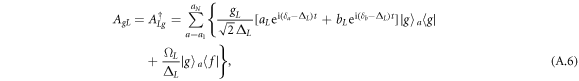
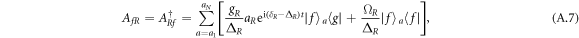
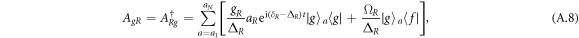
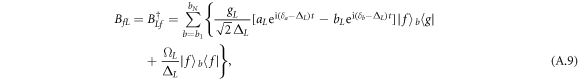


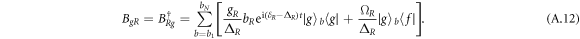
Now, we check the validity of effective master equation (12). The time evolution of the fidelity for two four-level atoms under the effective and the original master equations is plotted in figure A1, where the parameters are chosen as 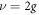 and
and 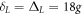 . It shows that the time evolution of the fidelity under the effective master equation agrees well with that under the original master equation, which exemplify the validity of the effective master equation (12). It is difficult to simulate the time evolution of the fidelity for four four-level atoms under the original master equation due to the large-dimension system. Thus, we use the effective master equation (12) to discuss the influence of dissipation in our paper.
. It shows that the time evolution of the fidelity under the effective master equation agrees well with that under the original master equation, which exemplify the validity of the effective master equation (12). It is difficult to simulate the time evolution of the fidelity for four four-level atoms under the original master equation due to the large-dimension system. Thus, we use the effective master equation (12) to discuss the influence of dissipation in our paper.
Figure A1. The time evolution of the fidelity for two four-level atoms under the effective and the original master equations with (a) the cavity decay rate 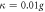 and (b) the atomic spontaneous emission rate
and (b) the atomic spontaneous emission rate 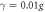 . Other common parameters:
. Other common parameters:  and
and 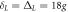 .
.
Download figure:
Standard image High-resolution image