Abstract
There has been growing interest in revealing exotic properties of chiral phonons since they were found in honeycomb AB lattice, and very recently they were experimentally verified in a tungsten diselenide monolayer (2018 Science 359 579). In this work, we manipulate phonon chirality through interface transmission via a one-dimensional atomic junction model by using the scattering boundary method. Due to the difference of phase change between two transverse directions induced by the anisotropy at interface coupling, the phonon polarization can be tuned between circular and linear in the high-frequency range. In a double-junction atomic model with an anisotropic center, we find that the phase change accumulates when the phonon transmits through the interface material thus the phonon can be tuned between different chirality in the medium frequency range. The phase change is found to linearly depend on the width of the interface material, while the transmission coefficient vibrates. To obtain the same value of the transmission coefficients along the two transverse directions and thus to keep the outgoing phonon circularly polarized, we can connect two interface materials with opposite anisotropy, where the phase-change difference for chirality tuning can be adjusted by the difference of widths of the two materials. Therefore, by using the atomic junction model, we find that the phonon chirality can be effectively tuned through interfaces, which is helpful for the manipulation and application of chiral phonons.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Chirality is a geometric property of an object which is not superposable to its mirror image; this property is well known for some molecules, ions and also for elementary particles such as neutrinos. In graphene, the electron chirality is defined by the pseudospin and it was found to induce exotic transport properties like unconventional Landau quantization and Klein tunneling [1, 2]. More generally, electrons display optical helicity in hexagonal lattices with broken inversion symmetry which opens the new field of valleytronics [3, 4]. The valley electron interband scattering involves a helical photoexcitation and photoluminescence; however, the intervalley electron scattering will involve bosonic collective excitations of phonons [5]. Given the fact that electrons have definite chirality at valleys, a natural question is whether the phonons involved are chiral. By applying an external magnetic field, through the spin–phonon interaction phonons can be distorted thus give rise to the phonon Hall effect [6–8] and phonon angular momentum [9]. In an asymmetric two-dimensional hexagonal lattice and without an applied external magnetic field, the intrinsic chirality of phonons was theoretically predicted [10]. The chiral phonon is comprised of unidirectional circular rotation and has a distinct energy level, which is not the superposition of linear modes in contrast to the circular polarization in non-chiral media [11, 12]. Very recently, chiral phonons were experimentally detected in monolayer tungsten diselenide via transient infrared spectroscopy [13], which were identified by the intervalley scattering of holes during the indirect infrared absorption. Chiral phonons are thus potentially important for the control of intervalley scattering [14], lattice-modulation-driven electronic phase transitions [15, 16] and topological states [17], as well as solid state quantum information applications [18]. The recent evidence of chiral phonons has attracted a wide attention also for the polarization properties of two-dimensional materials [19] and the valley transport in sonic crystals [20, 21].
On the one hand, non-degenerate chiral phonons can be excited by electronic intervalley scattering through an optical pump–probe technique [13]. On the other hand, in the process of helicity-resolved Raman scattering [12], phonons superposed by degenerate modes were excited to a defined chirality by using helical photons. Therefore, chiral phonons can be generally excited by optical helicity both in chiral (for non-degenerate phonon) or non-chiral (for degenerate phonon) media. The thermal transport or the phonon transport along one direction have been commonly simulated by atomic chain models, namely by the thermal diode [22], thermal transistor [23], thermal logic gates [24] and thermal memory [25], which are very attractive for investigating the emerging field of phononics [26]. For the interface thermal transport, atomic junctions through scattering boundary method have been regarded as an effective model for the sake of high accuracy due to the consideration on the atomic details in actual interface structures. This model was created by Lumpkin et al [27] to investigate the Kapitza resistance of a one-dimensional lattice, and it has been successfully applied to describe the mode-dependent energy transmission across nanotube junctions [28], magnon transport in spin chains [29], phonon interference effect [30], optimized thermal couplers [31–33], etc. These studies focused on the magnitude of the transmission coefficient which mainly affects the transport conductance.
In this paper, we study the manipulation on phonon chirality through interface transmission using the one-dimensional atomic junction model. For a single-junction model, the anisotropy at the interface coupling is found to induce a phase-change difference in the two transverse directions, which changes the phonon polarization from circular to linear. In a double-junction atomic model, we find that the phase change accumulates through an anisotropic interface material and thus it allows tuning phonon chirality in a specific frequency range. The phase change linearly depends on the width of the interface material, while the magnitude of the transmission coefficient vibrates in a small range. To achieve the chirality reversion and keep the phonon circularly polarized, we coupled two interface materials with opposite anisotropy to make the transmission coefficients along the two transverse directions be equal, while the phase-change difference for chirality tuning is achieved by adjusting the width difference of the two interface materials. The chirality tuning for phonon studied in this work could be applied to a three-dimensional heterostructure where we study chiral phonon transport along one dimension.
2. Model
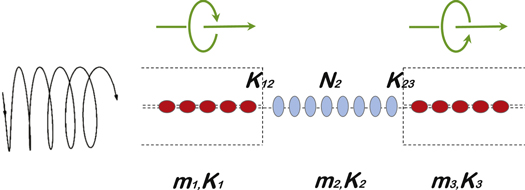
To study a chiral phonon transmission through an interface, we use a one-dimensional atomic junction model where the lattice vibration is three-dimensional. As shown in figure 1, the one-dimensional atomic chain consists of three parts: two semi-infinite parts and a central part, which are connected by the coupling constants K12 and K23. The left, center and right segments are harmonic chains with defined masses and spring constants m1, K1, m2, K2 and m3, K3. Since the vibration is three-dimensional, the spring constant are 3 × 3 matrices. Generally, the force constant matrix can be made diagonal [34], with elements of Klx, Kly and Klz in the lth part. Such assumption of diagonal force constant matrix has also been successfully applied to phonon Hall effect [7, 35], phonon angular momentum [9], and the finding of chiral phonon [10] which is consistent to real materials calculations. If we define the direction from left to right as the z axis, when a helical wave is transmitted, it is chiral in x–y plane perpendicular to the chain. In this work, we study how the interface affects the phonon chirality, thus two semi-infinite leads are set to be isotropic in the x–y plane (transverse directions), i.e., 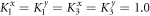 . Thus the phase difference keeps for x and y components of a chiral phonon transmitted along the leads while it changes after the chiral phonon transmitted through an anisotropic interface. Without loss of generality, we can use dimensionless units by setting m1 = m2 = m3 = 1.0. If there is no central region, the two semi-infinite leads are coupled directly by an interface coupling matrix K13.
. Thus the phase difference keeps for x and y components of a chiral phonon transmitted along the leads while it changes after the chiral phonon transmitted through an anisotropic interface. Without loss of generality, we can use dimensionless units by setting m1 = m2 = m3 = 1.0. If there is no central region, the two semi-infinite leads are coupled directly by an interface coupling matrix K13.
Figure 1. Schematic of the one-dimensional atomic chain model, a chiral phonon transmit through the atomic junction, where the phonon has circular polarization in the plane perpendicular to the atomic chain. The left (right) part is an isotropic semi-infinite chain with the same components of spring constant matrix along two transverse directions. The phonon with circular polarization in transverse plane corresponds to a helical polarization (as shown in the left), however, if the component along the longitudinal direction is zero, the transmission through the interface, makes the chiral phonon change the direction of circular polarization. The central part (N2) connects to the left and right parts by interface coupling contants K12 and K23. The masses (the spring constant matrices) for the left, center and right parts are m1(K1), m2(K2), and m3(K3), respectively. Here and after, we set m1 = m2 = m3 = 1.0, and 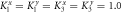 .
.
Download figure:
Standard image High-resolution imageSince we focus on the chirality manipulation by the interface, an incident chiral wave from left is assumed to have an amplitude of (1 i 0)T , which corresponds to a circularly-polarized transverse wave with no longitudinal component. The wave will be partially reflected and transmitted through the interface: the amplitude of the reflected and the transmitted waves can be written as r(1 i 0)T and t(1 i 0)T , respectively. Here both r and t are 3 × 3 matrices. Since all the force constants are diagonal 3 × 3 matrices, each component of the phonon will be transmitted individually, i.e., there is no interaction between the components. Therefore, the transmission and reflection coefficients can be written as diagonal matrices with the elements tα and rα (α = x, y, z). To solve the transmission coefficient for each component, we can reduce a problem of one-dimensional motion along an atomic chain. Using the scattering boundary method, the transmission of a wave from region i (with mass mi and spring constant ki) to j (with mass mj and spring constant kj) is given by [31]
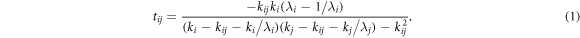
Here, kij denotes the coupling constant between regions i and j, 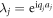 (qj is the wave vector, aj is the interatomic spacing ) satisfies the dispersion relation in the region j as
(qj is the wave vector, aj is the interatomic spacing ) satisfies the dispersion relation in the region j as  , we choose one of the roots satisfied by
, we choose one of the roots satisfied by 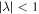 when ω is replaced by ω + iη where η is a small positive perturbation. With inputting the parameters along the αth direction
when ω is replaced by ω + iη where η is a small positive perturbation. With inputting the parameters along the αth direction 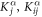 , with α = x, y, we can obtain the transmission coefficients
, with α = x, y, we can obtain the transmission coefficients 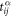 . Since we only consider the transverse wave, the components along zth direction Kjz and Kijz do not affect its transmission.
. Since we only consider the transverse wave, the components along zth direction Kjz and Kijz do not affect its transmission.
The transmission coefficient tij is a complex number, and in all previous studies, people only considered its magnitude; however its phase can change after the phonon transmits through the interface. Namely, if the interface is anisotropic, then it will induce a phase-change difference between x and y components. We set 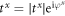 ,
,  , where φx and φy are the phase change of components x and y, respectively. Thus the phase-change difference
, where φx and φy are the phase change of components x and y, respectively. Thus the phase-change difference 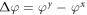 can tell us about the chirality change of the phonon. For an incident chiral phonon with circular polarization, if Δφ = (n + 1/2)π, where n is an integer, the outgoing phonon will be linearly polarized; if
can tell us about the chirality change of the phonon. For an incident chiral phonon with circular polarization, if Δφ = (n + 1/2)π, where n is an integer, the outgoing phonon will be linearly polarized; if 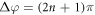 , the phonon will convert between left-handed and right-handed. The circular polarization will be kept only if
, the phonon will convert between left-handed and right-handed. The circular polarization will be kept only if 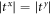 .
.
In the case of a double-junction model as shown in figure 1, there will be multiple reflections since the transmitted wave will be reflected and transmitted through the second boundary. Thus the total transmitted wave function can be given by a superposition of reflections and transmissions. Finally we obtain the transmission coefficient across the interface material (center region) as

where N2 denotes the number of atoms in the central region, and rij is calculated by 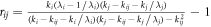 [31].
[31].
3. Results
3.1. Interface coupling
To investigate the chirality modification of phonon transmitted through an interface, we first look at the simple single-junction model where two semi-infinite atomic chains are coupled by an interface coupling. If the two semi-infinite chain are identical, then the interface coupling which is different from that of the leads can be interpreted as a defect, which will scatter the chiral phonons and decrease the conductivity. As shown in figure 2, we consider the transmission of chiral phonons through an anisotropic interface coupling 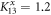 and
and 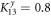 . Since K13x is larger an K13y is smaller than those of leads (
. Since K13x is larger an K13y is smaller than those of leads (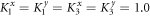 ), both the transmission coefficients (
), both the transmission coefficients (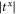 and
and 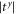 ) are smaller than 1 and decrease with increase of the frequency. Because of the anisotropy in the transverse directions, the phase-change along x and y directions are different, thus the phonon chirality will change. The phase-change difference is zero (2π has the same meaning with 0) at the long-wave limit
) are smaller than 1 and decrease with increase of the frequency. Because of the anisotropy in the transverse directions, the phase-change along x and y directions are different, thus the phonon chirality will change. The phase-change difference is zero (2π has the same meaning with 0) at the long-wave limit 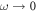 , where the defect at interface has no effect on the phonon transport since the wave length is far more larger than the defect, and thus the transmission coefficient is equal to 1. Because of the linear dependence of the frequency with the wave vector, when the frequency increases, the wave length decreases: when it becomes comparable with the defect then the transmission coefficient will decrease. At the same time, the anisotropic interface induces an increasing of phase-change difference, which can be observed in figure 2, where Δφ moves away from the value of 2π as the frequency increases.
, where the defect at interface has no effect on the phonon transport since the wave length is far more larger than the defect, and thus the transmission coefficient is equal to 1. Because of the linear dependence of the frequency with the wave vector, when the frequency increases, the wave length decreases: when it becomes comparable with the defect then the transmission coefficient will decrease. At the same time, the anisotropic interface induces an increasing of phase-change difference, which can be observed in figure 2, where Δφ moves away from the value of 2π as the frequency increases.
Figure 2. Transmission coefficient  (right scale) along two transverse directions and phase-change difference Δφ (left scale) between x and y directions versus frequency in single-junction chain with an anisotropic interface coupling components
(right scale) along two transverse directions and phase-change difference Δφ (left scale) between x and y directions versus frequency in single-junction chain with an anisotropic interface coupling components  ,
, 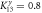 . The inset shows Δφ and ty as function of
. The inset shows Δφ and ty as function of  when
when 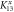 is fixed and for ω = 1.0. Here and after, the red solid and dashed lines correspond to the transmission (right scale) along x (tx) and y (ty) directions, respectively; and the black dash-dotted line corresponds to Δφ (left scale).
is fixed and for ω = 1.0. Here and after, the red solid and dashed lines correspond to the transmission (right scale) along x (tx) and y (ty) directions, respectively; and the black dash-dotted line corresponds to Δφ (left scale).
Download figure:
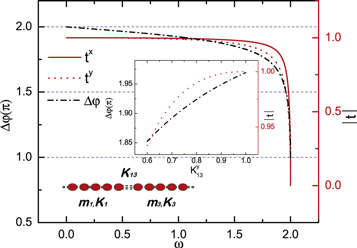
Standard image High-resolution imageAlthough the anisotropic interface can lead to phase-change difference between the x and y directions and then make the phonon chirality change, the large phase-change difference only occurs in the high-frequency range as shown in figure 2, where the transmission coefficient becomes small. If Δφ = 1.5π, the circularly polarized phonon changes to linear after it transmitted through the interface, and the transmission coefficient of one component decreases to about 0.6. To reverse the phonon chirality, the Δφ value has to be π in the high-frequency limit where the transmission coefficient becomes very small. For the medium frequency, the phase-change difference is smaller, so the anisotropy of the interface will induce a lower phase-change, as shown in the inset of figure 2 where the change of Δφ is less than 0.2π as K13y changes from 0.6 to 1.
Based on the results on the phonon chirality tuned by an anisotropic interface coupling, we can naturally extend the study to the double-junction interface model. Due to the phonon scattering at two interfaces, the phase-change difference accumulates after the phonon transmit through the two junctions. As shown in figure 3, the phase-change difference results to be larger compared to the single-junction. Both Δφ and 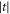 oscillate with the frequency because of the interference effect from the superposition of reflected and transmitted waves at the two interfaces. The transmission coefficient can be up to 1 for certain frequencies where the phonon has a constructive interference. In figure 3, the two interfaces are anisotropic while the other parts are isotropic, thus the phase-change difference comes only from the two interfaces which doubles the effect in the single-junction model. The large phase-change difference is still observed in the high-frequency range, as shown in figure 3, Δφ = 1.5π occurs at a frequency larger than 1.75 where the chiral phonon changes from circular polarization to linear. Δφ = π occurs at a frequencies larger than 1.95 where the two components of transmission coefficients have large difference, thus the circularly polarized phonon changes to an elliptically polarized phonon with an opposite chirality. Therefore, the anisotropic interface coupling can change the phonon chirality only in high-frequency range, while it is not easy to tune a phonon to opposite chirality and keep its circular polarization.
oscillate with the frequency because of the interference effect from the superposition of reflected and transmitted waves at the two interfaces. The transmission coefficient can be up to 1 for certain frequencies where the phonon has a constructive interference. In figure 3, the two interfaces are anisotropic while the other parts are isotropic, thus the phase-change difference comes only from the two interfaces which doubles the effect in the single-junction model. The large phase-change difference is still observed in the high-frequency range, as shown in figure 3, Δφ = 1.5π occurs at a frequency larger than 1.75 where the chiral phonon changes from circular polarization to linear. Δφ = π occurs at a frequencies larger than 1.95 where the two components of transmission coefficients have large difference, thus the circularly polarized phonon changes to an elliptically polarized phonon with an opposite chirality. Therefore, the anisotropic interface coupling can change the phonon chirality only in high-frequency range, while it is not easy to tune a phonon to opposite chirality and keep its circular polarization.
Figure 3. Transmission coefficient 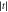 (right scale) and phase-change difference Δφ (left scale) in an atomic chain with three isotropic parts coupled by two anisotropic interface couplings,
(right scale) and phase-change difference Δφ (left scale) in an atomic chain with three isotropic parts coupled by two anisotropic interface couplings, 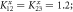
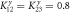 . The center part is isotropic with
. The center part is isotropic with 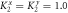 . The inset shows the zoom in large-frequency range.
. The inset shows the zoom in large-frequency range.
Download figure:
Standard image High-resolution image3.2. Interface material
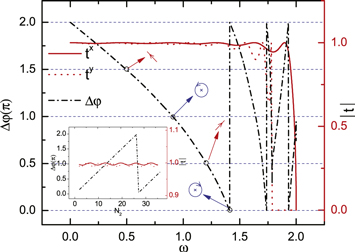
Going from the single-junction model to double-junction model, the phase-change difference accumulates due to the more interfaces, where the central part is isotropic thus no phase-change occurs. If we make the whole central part be an anisotropic material, the phase-change difference will accumulate so that the outgoing phonon could have a large phase-change difference. As shown in figure 4, we set the central part of the double-junction model with anisotropy of 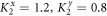 . With the increasing of the frequency, both
. With the increasing of the frequency, both  and
and 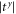 oscillate and decrease to zero in the high-frequency limit, they have different cutoff frequency due to different force constants. Due to the progressive accumulation of the phase-change difference, Δφ can take any value in the range of [0, 2π] in the medium frequency range. The Δφ value increases with enlarging frequency, however it oscillates since we keep it in a range [0, 2π]. In the frequency range below 1.25, as shown in figure 4, the transmission coefficients
oscillate and decrease to zero in the high-frequency limit, they have different cutoff frequency due to different force constants. Due to the progressive accumulation of the phase-change difference, Δφ can take any value in the range of [0, 2π] in the medium frequency range. The Δφ value increases with enlarging frequency, however it oscillates since we keep it in a range [0, 2π]. In the frequency range below 1.25, as shown in figure 4, the transmission coefficients 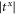 and
and 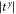 are approximately equal, then we can tune phonon between different polarizations. In the case of the incident phonon with right-handed circular polarization, the phonon passing through the interface material will display a right-handed circular polarization, linear polarization, left-handed circular polarization, and linear polarization, if Δφ = 0, 0.5π, π, 1.5π, respectively.
are approximately equal, then we can tune phonon between different polarizations. In the case of the incident phonon with right-handed circular polarization, the phonon passing through the interface material will display a right-handed circular polarization, linear polarization, left-handed circular polarization, and linear polarization, if Δφ = 0, 0.5π, π, 1.5π, respectively.
Figure 4. Transmission coefficient 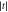 (right scale) and phase-change difference Δφ (left scale) for chiral phonons transmitted through an anisotropic interface material (the center part has a size of N2 = 8) with
(right scale) and phase-change difference Δφ (left scale) for chiral phonons transmitted through an anisotropic interface material (the center part has a size of N2 = 8) with 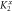 = 1.2,
= 1.2, 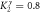 , while all other parts are isotropic,
, while all other parts are isotropic, 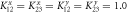 . In the case of an incident phonon with right-handed circular polarization we have drawn the schematics for the transmitted phonon with right-handed circular polarization, linear polarization, left-handed circular polarization, and linear polarization(Δφ = 0, 0.5π, π, 1.5π, respectively). The inset shows the transmission coefficient
. In the case of an incident phonon with right-handed circular polarization we have drawn the schematics for the transmitted phonon with right-handed circular polarization, linear polarization, left-handed circular polarization, and linear polarization(Δφ = 0, 0.5π, π, 1.5π, respectively). The inset shows the transmission coefficient 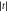 (right scale) and phase-change difference Δφ (left scale) versus the size of the central atomic part N2 with an anisotropic spring constant matrix, at a specific frequency of ω = 1.0.
(right scale) and phase-change difference Δφ (left scale) versus the size of the central atomic part N2 with an anisotropic spring constant matrix, at a specific frequency of ω = 1.0.
Download figure:
Standard image High-resolution imageWhen the phonons transmit along the interface material, due to the anisotropy in the transverse directions, then the phase-change for the two transverse directions are different; the difference accumulates as the phonon path increases, as shown in the inset of figure 4. As the size (N2) of the central part increases, the phase-change difference increases linearly and oscillates between 2π and 0. The transmission coefficients 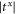 and
and 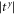 oscillate with the increasing of the phonon path because of the interference between the multiple reflections generated in the central material. In medium frequency range around ω = 1.0, when changing the size of the central part,
oscillate with the increasing of the phonon path because of the interference between the multiple reflections generated in the central material. In medium frequency range around ω = 1.0, when changing the size of the central part,  is almost equal to
is almost equal to 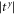 thus the phonon chirality can be reversed at specific size.
thus the phonon chirality can be reversed at specific size.
To reverse the phonon chirality while keeping a circular polarization, the amplitude along the x and y directions need to be the same, thus the transmission coefficients  and
and 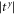 need to be equal. In the low and medium frequency range,
need to be equal. In the low and medium frequency range, 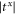 and
and 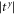 display small differences, however, we can adjust the force constant component K2x or K2y to the points where
display small differences, however, we can adjust the force constant component K2x or K2y to the points where  equals
equals  and Δφ = π. As shown in figure 5, in the frequency range [0, 1], at the crossing points (where
and Δφ = π. As shown in figure 5, in the frequency range [0, 1], at the crossing points (where  ,
, 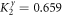 ,
, 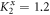 ,
, 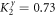 and
and  ,
, 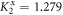 ) the phonon can be tuned between right and left circular polarization.
) the phonon can be tuned between right and left circular polarization.
Figure 5. Transmission coefficient 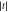 versus component
versus component 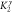 (a) (K2x (b)) for
(a) (K2x (b)) for  (
(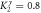 ) when the phase-change difference is Δφ = π, and the frequency is selected in the range of [0, 1].
) when the phase-change difference is Δφ = π, and the frequency is selected in the range of [0, 1].
Download figure:
Standard image High-resolution imageThe mismatch at the interface induces phonon scattering thus results in a resistance and makes the transmission coefficient be smaller than 1. Moreover it leads to the phase change between the outgoing and the incident phonons; the anisotropy between the transverse directions gives rise to a phase-change difference which accumulates and linearly depends on the phonon path. Therefore, it is possible to connect two interface materials with opposite anisotropy in series so that the transmission coefficients 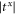 and
and 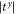 will be almost the same in a large range of frequency, as shown in figure 6. Compared to the transmission coefficients in figure 4 where
will be almost the same in a large range of frequency, as shown in figure 6. Compared to the transmission coefficients in figure 4 where 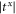 and
and 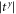 are almost equal only in the low-frequency range, in figure 6 we see that
are almost equal only in the low-frequency range, in figure 6 we see that 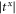 and
and 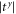 are almost the same in most of the frequency range. Since the two interface materials have different widths, the phase-change differences accumulated in each material does not cancel out which results in a total phase-change difference which increases with the frequency. If the two interface materials have the same width, the phase change is zero (0 or 2π), and its difference Δφ is linearly dependent on the size difference between the two interface materials, as shown in the inset of figure 6, where
are almost the same in most of the frequency range. Since the two interface materials have different widths, the phase-change differences accumulated in each material does not cancel out which results in a total phase-change difference which increases with the frequency. If the two interface materials have the same width, the phase change is zero (0 or 2π), and its difference Δφ is linearly dependent on the size difference between the two interface materials, as shown in the inset of figure 6, where 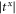 and
and 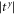 remain almost unchanged with a small oscillation near to 1. Therefore, by using two interface materials with opposite anisotropy and different widths, the phonon chirality can be well manipulated.
remain almost unchanged with a small oscillation near to 1. Therefore, by using two interface materials with opposite anisotropy and different widths, the phonon chirality can be well manipulated.
Figure 6. Transmission coefficient 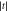 (right scale) and phase-change difference Δφ (left scale) for chiral phonons transmitted through two interface materials with opposite anisotropy together. Here, Na = 20, Nb = 30,
(right scale) and phase-change difference Δφ (left scale) for chiral phonons transmitted through two interface materials with opposite anisotropy together. Here, Na = 20, Nb = 30, 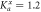 ,
, 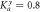 ,
, 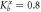 ,
,  . And all other parts are isotropic, with
. And all other parts are isotropic, with 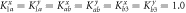 . The inset shows the phase difference Δφ as a function of size difference (Nb) for ω = 1.0 and ω = 1.5.
. The inset shows the phase difference Δφ as a function of size difference (Nb) for ω = 1.0 and ω = 1.5.
Download figure:
Standard image High-resolution image4. Conclusion
In this paper, we investigate the manipulation of the phonon chirality through the diffusion across an interface using a one-dimensional atomic junction model combined with the scattering boundary method. For the single-junction model, the anisotropy at interface coupling induces a phase change between the two transverse directions. Such phase-change difference can be as large as π/2 in the high-frequency range, where the phonon polarization can be tuned between circular and linear. Through a double-junction atomic model, we found that the phase change accumulates through an anisotropic interface material and thus make it possible to tune the phonon polarization between different chirality at a specific frequency. The phase change is linearly dependent on the width of the interface material, while the transmission coefficient vibrates in a small range.
The anisotropy in transverse directions gives rise to phase-change difference, however, it also makes the transmission coefficients be not equal, thus it is not easy to realize the conversion between left- and right-handed chiral phonons. If we can connect two interface materials with opposite anisotropy in series it is possible to eliminate the inequality between the two transmission coefficients, while the phase change for chirality tuning is satisfied by adjusting the difference of sizes of the two interface materials.
The one-dimensional atomic model proposed here can be regarded as a simple and effective model to study the tuning for phonon chirality by an anisotropic interface. The system can be a three-dimensional lattice, for example, an anisotropic layered material sandwiched by two parts (which are simplified as two semi-infinite atomic chains) of multi-layers of graphene or hexagonal boron nitride or transition-metal dichalcogenide. The incident phonons (only with transverse vibrations) with definite chirality can be vastly excited by photo-pumping technique, which then transport along the longitudinal direction. By controlling the anisotropy or width of the interface material the phonon chirality can be tuned effectively.
Acknowledgments
We acknowledge support from NSFC (Grant No. 11574154).