Abstract
The crystal electric field (CEF) scheme of YbNi4P2 is determined, based on experimental data from inelastic neutron scattering, heat capacity, susceptibility and NMR measurements. Despite the tetragonal crystal structure, 9 parameters are needed to describe the crystal field in YbNi4P2 due to the orthorhombic site symmetry of the Yb ion. A large basal plane anisotropy is detected by the local probe NMR. Our analysis yields CEF excitation energies of 8.5, 12.5 and roughly 30 meV and a ground state wave function that is dominated by the 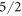 state. Furthermore, we present an analysis of the CEF scheme based on density functional theory calculations, which confirms the large basal plane anisotropy.
state. Furthermore, we present an analysis of the CEF scheme based on density functional theory calculations, which confirms the large basal plane anisotropy.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The heavy-fermion compound YbNi4P2 has recently attracted much interest because it represents one of the very few examples of ferromagnetic quantum criticality. The pure compound has a Curie temperature as low as 150 mK, which can be further tuned to zero temperature by As doping on the P site [1, 2]. Importantly, the transition stays second order, thus yielding a quantum critical point in the 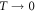 limit, contrary to theoretical predictions and experimental observations in other compounds that ferromagnetic transitions turn first order at low enough temperatures [3–5].
limit, contrary to theoretical predictions and experimental observations in other compounds that ferromagnetic transitions turn first order at low enough temperatures [3–5].
YbNi4P2 contains magnetic Yb3+ ions and shows Kondo characteristics with TK ≈ 8 K, while Ni is non-magnetic [1]. The crystal structure is tetragonal of ZrFe4Si2 type [6]. The magnetic properties are strongly anisotropic, the c-axis being the easy-axis in the paramagnetic phase [2]. However, in the ordered phase the spins lie within the ab-plane [2]. It has been suggested that the driving force for the hard-axis order is the maximisation of phase space for the transverse spin fluctuations [7].
For a better understanding of the magnetic properties of YbNi4P2, in particular the remarkable anisotropy, it is important to know the crystal electric field (CEF) scheme. While the crystal has tetragonal symmetry, the site symmetry of the Yb ions is only orthorhombic, leading to a complex CEF scheme with 9 parameters. Furthermore, the unit cell contains two Yb ions whose local crystal environment is rotated by 90° around the c-axis. Their CEF schemes are identical, but the local anisotropy in the ab-plane is averaged out in any macroscopic measurement due to their relative rotation by 90°.
The CEF excitations of YbNi4P2 have been studied by inelastic neutron scattering (INS), identifying two excitations at 8.5 and 12.5 meV [8]. In the present study, we combine these data with results from heat capacity, susceptibility and NMR measurements to perform a comprehensive analysis of the CEF scheme. To handle the complexity that results from the orthorhombic site symmetry, the programme package McPhase was used to fit the experimental data [9].
Furthermore, density functional theory (DFT) calculations were performed and the crystal field was evaluated based on the DFT-derived Wannier functions. The method, well tested for insulating rare earth compounds [10–12], has here been applied to a metallic compound. The DFT-derived crystal field analysis provides an independent verification of the McPhase fit.
2. Experimental and computational details
INS was measured at IN4 at ILL, Grenoble, on powder samples of YbNi4P2, as published previously [8]. Further data at lower energy transfer were obtained at ToFToF, FRM2 [13]. Heat capacity was measured on single crystals of YbNi4P2 and LuNi4P2 in a conventional PPMS by Quantum Design. The single-crystal growth of YbNi4P2 by Bridgman technique and the synthesis of polycrystalline LuNi4P2 are described in references [14] and [15]. The magnetic contribution to the heat capacity of YbNi4P2, Cmag, can be obtained from the difference C(YbNi4P2) − C(LuNi4P2), since the phonons of both compounds are expected to be very similar. The susceptibility data, measured on single crystals, have been published in reference [2], figure 1.
We performed 31P NMR on aligned powder, benefitting from the easy-axis anisotropy of YbNi4P2 at high temperatures. Finely powdered YbNi4P2 was mixed with Stycast 2850FT Black Epoxy and catalyst in a volume ratio of about 1:4, so that each individual grain has enough room to freely rotate in the external field. The mixture was filled into a small capsule which was quickly placed in a magnetic field of 8 T at room temperature. After solidification of the epoxy, NMR spectra were taken in a standard TecMag spectrometer at a frequency of 33 MHz, in the temperature range 2 K < T < 200 K and as a function of the capsule orientation. We found a clear orientation dependence of the spectra, which confirmed that the powder had been highly oriented along the easy c-direction: only one peak was observed for the NMR field parallel to the alignment field direction, but 2 maxima were observed when the NMR field was perpendicular to the alignment field direction.
McPhase simulations were done using the module 'so1ion', based on the programme 'cfield'. Here, the CEF is parametrised by the Stevens operator formalism [9, 16, 17], so that the Hamiltonian of one magnetic ion can be written as
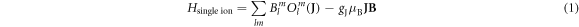
with the crystal field parameters 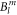 and the Stevens operators
and the Stevens operators 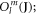 the last term accounts for the Zeeman effect in a magnetic field B. Throughout this paper we will be using the Stevens parameter convention (called B in McPhase [17]), following Hutchings' publication [16]; in this convention the crystal field parameters
the last term accounts for the Zeeman effect in a magnetic field B. Throughout this paper we will be using the Stevens parameter convention (called B in McPhase [17]), following Hutchings' publication [16]; in this convention the crystal field parameters 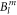 include the angular part of the wave function as well as the Stevens parameters. For the Yb ion in YbNi4P2, the relevant crystal field parameters are
include the angular part of the wave function as well as the Stevens parameters. For the Yb ion in YbNi4P2, the relevant crystal field parameters are 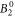 ,
, 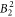 ,
, 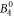 ,
, 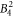 ,
, 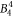 ,
, 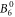 ,
, 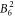 ,
, 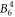 and
and 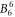 . Because the Hamiltonian (1) does not contain contributions of magnetic exchange interaction or Kondo effect, it cannot describe low-temperature data correctly. Thus, we have only used susceptibility data measured at T > 14 K.
. Because the Hamiltonian (1) does not contain contributions of magnetic exchange interaction or Kondo effect, it cannot describe low-temperature data correctly. Thus, we have only used susceptibility data measured at T > 14 K.
In the DFT calculations, we determined the band structure of YbNi4P2 using the WIEN2k package [18] with the exchange-correlation of the generalized-gradient approximation form [19]. Atomic sphere radii were 2.5, 2.36 and 1.88 a.u. for Yb, Ni and P, respectively. The number of basis functions amounted to ∼1190 (corresponding to RKmax = 7.0), the number of k points in the irreducible part of the Brillouin zone was 82. In the first step the Yb(4f) states were treated as core states, the division of other states between valence and core states followed standard WIEN2k prescription. The density of states (DOS) corresponds to a metal, in the vicinity of the Fermi energy the DOS is dominated by the Ni(3d) states.
No local or semilocal DFT method gives the correct position of R(4f) levels and we adjusted it by shifting the orbital potential using the hybridisation parameter Δ. In fluorides and oxides Δ may be estimated from E(fn−1LN+1) − E(fnLN) [12]. To find the positions of excited configurations of Yb in YbNi4P2 qualitatively, open core calculations for 4f12 and 4f14 electron configurations were carried out. The results show that the energy of Yb4+ is considerably higher than the energies of Yb3+ and Yb2+, which are almost degenerate, the energy of Yb2+ being lower by 0.34 eV. There is considerable uncertainty of order of eV in such an estimation [12]. As an Yb3+ state is found in experiment we conclude that Δ is positive with a small magnitude.
Next we continued by determining the Yb3+ crystal field parameters using Wannier functions. For this purpose, we performed a non-selfconsistent calculation that treats the Yb(4f) and Ni(3d) states as valence states. The electrons move in the selfconsistent potential obtained in the first step. The charge transfer energy is modified by means of the orbital potential, which is treated as an adjustable parameter. This calculation yields the 4f Bloch states, which are transformed into Wannier functions using wien2wannier [20] and Wannier90 [21] codes. Wannier90 provides the local Hamiltonian H4f, a 7 × 7 matrix, which is then expanded in spherical tensor operators. The expansion coefficients are the CEF parameters. Further details of the method are described in references [10–12]. At Δ < 4.76 eV, the Wannier functions loose their localised character and the calculation crashes. The dependence of the CEF parameters on Δ is shown in figure 1. Above Δ ≈ 10 eV, the dependence of the parameters on Δ is rather weak.
Figure 1. Dependence of the CEF parameters 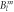 on the hybridisation parameter Δ, as deduced from DFT calculations.
on the hybridisation parameter Δ, as deduced from DFT calculations.
Download figure:
Standard image High-resolution imageThe calculations yield in total seven doublets, four of them corresponding to the spin–orbit ground state (J = 7/2) and three to the J = 5/2 state, which lie at much higher energy (E > 1 eV). Since the high-energy multiplet is not considered in the McPhase fit, it will be disregarded in the following.
3. Results and discussion
3.1. CEF transition energies
The Yb3+ ion has the electron configuration [Xe]4f13. For Yb, spin–orbit coupling is much stronger than CEF effects. This implies that the crystal fields acts on a state with total angular momentum J = 7/2, which is the ground state according to Hund's rules. This assumption is confirmed by the measured effective moment at high temperatures, 4.52 μB [1], which is very close to the theoretical value of 4.53 μB for an Yb3+ ion. The eight-fold multiplet of the J = 7/2 state is expected to split into four Kramer's doublets due to the orthorhombic crystalline environment.
Thus, in an INS experiment three transitions from the ground state should appear. However, only two transitions were detected in the range up to 60 meV, namely at 8.5 and 12.5 meV [8, 13], see also figure 2(b). The third transition seems to have a vanishing transition matrix element for neutron scattering.
Figure 2. (a) The magnetic heat capacity of YbNi4P2, derived from the difference C(YbNi4P2) − C(LuNi4P2) and fitted according to the formula from reference [22]. For details to the fits, see main text. (b) Neutron scattering intensity at Q = 1.7 ± 0.3 Å−1 (1.6 K). Till E = 6.3 meV, data have been measured at λ = 3 Å, while at higher energy transfers data have been measured at λ = 1.5 Å. The data sets have been joined by normalising the intensity to the elastic line, which has no Bragg peaks in this region. For the data set at 1.5 Å, phonons have been subtracted (see reference [8]). In this joined data set, the intensity of the quasi-elastic signal as well as the CEF transitions has been fitted, keeping their width and position fixed to the values given in references [13] and [8], respectively.
Download figure:
Standard image High-resolution imageTransitions between different CEF levels yield a Schottky anomaly in the magnetic heat capacity. Additionally, a contribution arising from the Kondo effect is expected at low temperatures. In the magnetic heat capacity of YbNi4P2, see figure 2(a), both features are clearly visible, the Kondo contribution being identified with the small hump at around 4 K and the Schottky anomaly with the broad maximum which peaks roughly at 50 K. We fit the data according to an approach suggested recently by Romero et al [22], which describes a 3-level (Ce3+) or 4-level (Yb3+) scheme with Kondo broadening of the ground state and the first excited state, respectively. All fit parameters, the energies E1, E2, E3, and Γ0 and Γ1, can in principle be obtained by neutron scattering measurements, Γ0 and Γ1 being the half-width at half maximum of the ground state and the first excited state, respectively. From references [8] and [13], we get E1 = 8.5 meV, E2 = 12.5 meV, Γ0 = 0.6 meV and Γ1 = 2.5 meV, leaving only E3 as a free fit parameter. This fit is shown by the blue line in figure 2(a) and yields E3 = 29.4 meV. In the temperature range around 5 K–30 K there is a significant discrepancy between the data and the fit. An alternative fit, with E2 = 8.5 meV, E3 = 12.5 meV, Γ0 = 0.6 meV and E1 < E2 and Γ1 as free parameters, gives a much poorer description of the data. A good fit can be obtained when all parameters are free (see red dotted line in figure 2(a)), yielding E1 = 6.5 meV, E2 = 14.0 meV, E3 = 27.9 meV, Γ0 = 1.1 meV and Γ1 = 1.2 meV.
A discrepancy of similar magnitude between crystal field levels obtained from neutron scattering data and heat capacity data has also been observed for other compounds, e.g. CePdAl [23] and CeCu2Ge2 [22, 24], independent of whether the approach by Romero et al [22] is used or a simple Schottky fit. In any case, the fits of the magnetic heat capacity of YbNi4P2 strongly suggest that there must be an excited CEF level at an energy significantly higher than the two observed by neutron scattering, i.e. roughly at 30 meV.
3.2. Details of the McPhase fit
Based on Hamiltonian (1), McPhase calculates the CEF transition energies, the corresponding neutron scattering intensities, and the susceptibility along three principal axes for any given set of 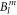 parameters. The three principal axes are defined by
parameters. The three principal axes are defined by 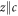 and x/y rotated by 45° with respect to the a- and b-axis. In a second step, these calculated single-ion properties can be compared to experimental data. In case of the transition energies and neutron scattering intensities, this comparison is straightforward. However, the measured susceptibility in the ab-plane corresponds to the average of the local basal plane susceptibilities, since the two Yb ions per unit cell have a crystal field which is rotated by 90°. Thus, only the average of the calculated local susceptibilities can be compared to the (macroscopic) susceptibility data.
and x/y rotated by 45° with respect to the a- and b-axis. In a second step, these calculated single-ion properties can be compared to experimental data. In case of the transition energies and neutron scattering intensities, this comparison is straightforward. However, the measured susceptibility in the ab-plane corresponds to the average of the local basal plane susceptibilities, since the two Yb ions per unit cell have a crystal field which is rotated by 90°. Thus, only the average of the calculated local susceptibilities can be compared to the (macroscopic) susceptibility data.
NMR, as a local probe, is one of the very few experimental methods which can provide insights into the local basal plane anisotropy in the case of an orthorhombic local symmetry in a globally tetragonal crystal structure. Fortunately, 31P with an abundance of 100% and a large gyromagnetic ratio is a very convenient NMR nucleus. There is only one crystallographic P position, but as in the case of Yb, the local symmetry of the P site is orthorhombic, with half of the P sites rotated by 90° around the c-axis. The basal plane main local axes are along [110] and [1–10], and thus parallel to the basal plane local main axes of Yb. As a result, one expects an basal plane anisotropic hyperfine field on the P site which is connected to the basal plane anisotropic 4f susceptibility at the Yb site. Thus, for a basal plane field away from the a or b direction, one expects an NMR resonance at two different fields, corresponding to the two P sites rotated by 90°. This leads to the two maxima we observed in the NMR spectra of the aligned powder for basal plane NMR field. Unfortunately, the relation between the 31P Knight shift and the anisotropic Yb susceptibility is complex, and we were not yet able to uniquely estimate the anisotropic susceptibilities from the NMR data. Presently new NMR measurements on single crystals are under way, and we expect that a much more reliable estimation of the basal plane anisotropy shall be possible based on these data. Therefore, we leave the details of the NMR analysis to a separate paper which will be concerned with the single-crystal NMR measurements. Here we shall only discuss the information relevant for the present CEF analysis.
The two maxima we observed in the NMR spectra for basal plane fields show very different temperature dependences of the Knight shift, plotted as 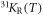 and 31KL(T) in figure 3. While 31KR follows a Curie–Weiss-like behaviour down to lowest temperature, similar to the Knight shift
and 31KL(T) in figure 3. While 31KR follows a Curie–Weiss-like behaviour down to lowest temperature, similar to the Knight shift 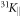 for a field along the easy c-axis, 31KL shows a Curie–Weiss-like behaviour only above 70 K, but levels out below 50 K. This remarkable difference in the temperature dependence of the two in-plane Knight shifts provides a direct and strong evidence for a significant in-plane anisotropy of the local susceptibility of Yb. Furthermore, the temperature independence of 31KL below 50 K indicates that one component of the in-plane local susceptibility of Yb is dominated by a T-independent Van Vleck contribution, while the Curie contribution is negligible. Accordingly, in order to account for the Curie–Weiss behaviour of 31KR at low temperature, the second in-plane susceptibility component of Yb has to present a sizable Curie contribution. Assuming that each line reflects the susceptibility along only one of the local basal plane main axes of Yb, the Yb susceptibilities χab,1 and χab,2 along the main in-plane axis can be estimated by simply scaling the two Knight shifts 31KR and 31KL (after subtracting the temperature independent orbital contribution of the Knight shifts). The scaling relies on the fact that the sum of both susceptibilities has to match the measured bulk susceptibility χab. The results of such a calculation are shown in figure 4(b). Since the underlying assumption is rather crude, these calculated susceptibilities have a large uncertainty. Nevertheless, on a qualitative level the NMR results provide guidance for an analysis of the CEF, and we use the estimated basal plane susceptibilities for a comparison with the susceptibilities calculated by McPhase.
for a field along the easy c-axis, 31KL shows a Curie–Weiss-like behaviour only above 70 K, but levels out below 50 K. This remarkable difference in the temperature dependence of the two in-plane Knight shifts provides a direct and strong evidence for a significant in-plane anisotropy of the local susceptibility of Yb. Furthermore, the temperature independence of 31KL below 50 K indicates that one component of the in-plane local susceptibility of Yb is dominated by a T-independent Van Vleck contribution, while the Curie contribution is negligible. Accordingly, in order to account for the Curie–Weiss behaviour of 31KR at low temperature, the second in-plane susceptibility component of Yb has to present a sizable Curie contribution. Assuming that each line reflects the susceptibility along only one of the local basal plane main axes of Yb, the Yb susceptibilities χab,1 and χab,2 along the main in-plane axis can be estimated by simply scaling the two Knight shifts 31KR and 31KL (after subtracting the temperature independent orbital contribution of the Knight shifts). The scaling relies on the fact that the sum of both susceptibilities has to match the measured bulk susceptibility χab. The results of such a calculation are shown in figure 4(b). Since the underlying assumption is rather crude, these calculated susceptibilities have a large uncertainty. Nevertheless, on a qualitative level the NMR results provide guidance for an analysis of the CEF, and we use the estimated basal plane susceptibilities for a comparison with the susceptibilities calculated by McPhase.
Figure 3. Temperature dependence of the Knight shifts 31KR and 31KL, the two peaks observed in the NMR spectra for field along the basal plane, and of the Knight shift 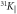 , corresponding to the single line observed for field along the c-axis.
, corresponding to the single line observed for field along the c-axis.
Download figure:
Standard image High-resolution imageFigure 4. (a) Comparison of the measured and fitted inverse susceptibility 1/χ(T). (b) Comparison of the measured and fitted susceptibility χ(T); for the c-axis macroscopic measurements have been used, while experimental data for the ab-plane are based on an NMR experiment. Note that all experimental data sets have been shifted to account for the Kondo effect, as described in the main text.
Download figure:
Standard image High-resolution imageIn the McPhase simulations, the difference δi between calculated and measured quantities is calculated for each set of  parameters. The overall agreement is quantified by a standard deviation s2,
parameters. The overall agreement is quantified by a standard deviation s2,
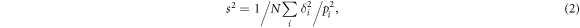
with the number of data points N and the weighting factor pi. The following experimental values are considered in the overall standard deviation: the transition energies 8.5 and 12.5 meV for the first and the second excited level; a vanishing neutron scattering cross section for the third excited level, which lies at higher energy than the other two; 20 data points each (40 K < T < 400 K) of the macroscopic inverse susceptibilities 1/χc and 1/χab; 20 data points each (14 K < T < 180 K) of χc, χab1 and χab2, taking χc again from the macroscopic measurement7 but χab1 and χab2 from the NMR data.
To cover a large 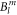 parameter space, we have performed a grid search that proceeds iteratively, such that regions of parameter space that have a very large standard deviation can be excluded in later levels. This allows a fine grid in interesting parameter regions while keeping the simulation time at a feasible level. In total we have calculated the standard deviation for 83 000 points in the 9-dimensional parameter space.
parameter space, we have performed a grid search that proceeds iteratively, such that regions of parameter space that have a very large standard deviation can be excluded in later levels. This allows a fine grid in interesting parameter regions while keeping the simulation time at a feasible level. In total we have calculated the standard deviation for 83 000 points in the 9-dimensional parameter space.
3.3. Results of the McPhase fit
Our first attempts to fit the set of experimental data showed little success, because the absolute values of 1/χ could not be reproduced in the McPhase calculations. A significant improvement could be achieved by assuming a deviation from Curie's law caused by the Kondo effect: it has been shown that this can be parametrised with an effective θ = 4.5 TK, describing the intersection of a high-temperature linear fit to the 1/χ-data with the T-axis [25]:
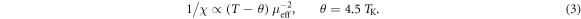
For YbNi4P2, θ = −26 K in polycrystalline average. Magnetic exchange interaction, which might also contribute to the deviation from Curie's law, is expected to have less influence than the Kondo effect due to the low ordering temperature. Thus, we have shifted all measured susceptibility data (also the NMR data) such that θ becomes zero, which corresponds to a shift of −10 mol cm−3 in 1/χ. This modified data set compares much better to the McPhase calculations, which do not take account of the Kondo effect. However, it is also clear that such a mean-field adjustment constitutes a rather coarse approximation.
The comparison of the Kondo-adjusted experimental data set with the fitted values of χ and 1/χ is shown in figure 4. The agreement of the McPhase model with data obtained from macroscopic susceptibility measurements, i.e. χc and χab (and their inverse), is satisfactory. The temperature dependence of χab1 and χab2, based on NMR data, is only qualitatively reproduced, while absolute values differ significantly especially at low temperature. However, as stated above, there is a large uncertainty in the absolute values of the anisotropic susceptibilities deduced from the NMR data, i.e. the accuracy of the experimental data is far lower than that of macroscopic susceptibility data.
The transition energies related to the fitted CEF parameters are E1 = 8.1 meV, E2 = 12.1 meV and E3 = 29.5 meV, with the neutron scattering cross section of the latter transition being close to zero. While the agreement of E1 and E2 with experimental data is enforced by the fit, it is encouraging that the third transition energy is calculated to be very similar to the value deduced from heat capacity data. The agreement of this level scheme with the heat capacity data is also shown in figure 2(a). It should be noted that the improvement of this fit compared to the one based on neutron results is mostly due to the fact that Γ0 and Γ1 are free in the fit, resulting in larger values than those observed by neutron scattering. This broadening improves the agreement at low temperatures. Furthermore, we can compare the neutron intensities of the non-forbidden transitions. We find an intensity ratio of 0.76:1:0.53 for the quasi-elastic signal, the first and the second excited level in the McPhase model. Experimentally, a ratio of 2.5:1:0.65 is found at Q = 1.7 Å−1 and T = 1.6 K (see figure 2(b)). Thus, the intensity ratio of E1 and E2 is well reproduced in the McPhase simulations, but the intensity of the quasi-elastic line is underestimated in comparison, possibly because experimental data at 1.6 K contain interactions that are not considered in the McPhase calculations.
In table 1, the fitted values of the 9 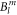 parameters are given, together with a confidence interval. This interval gives the range where the standard deviation changes by less than 10% (while keeping all other parameters constant) and such gives an idea of how well the parameter values can be established on the basis of our experimental data. The crystal field is strongly influenced by a large value of the
parameters are given, together with a confidence interval. This interval gives the range where the standard deviation changes by less than 10% (while keeping all other parameters constant) and such gives an idea of how well the parameter values can be established on the basis of our experimental data. The crystal field is strongly influenced by a large value of the 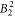 parameter, resulting in the significant basal plane anisotropy observed in the NMR data. Beside the
parameter, resulting in the significant basal plane anisotropy observed in the NMR data. Beside the 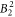 parameter, also the
parameter, also the 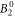 and the
and the 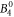 parameter can be determined with a rather small confidence interval. For all other parameters, we can only determine their sign and rough magnitude.
parameter can be determined with a rather small confidence interval. For all other parameters, we can only determine their sign and rough magnitude.
Table 1.
Crystal electric field parameters, as well as transition energies, of YbNi4P2, in meV. The lower and upper limit of the McPhase fitted CEF parameter are defined by a decrease of 10% in the standard deviation when changing this specific parameter, while leaving all other parameters at their optimum value. The lower two rows give results based on DFT calculations for Δ1 = 5.4 eV and Δ2 = 27.2 eV, respectively. CEF parameters follow the parameter convention called 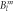 in McPhase [17] and reference [16]. Transition energies are additionally given as derived from inelastic neutron scattering (INS) and heat capacity data.
in McPhase [17] and reference [16]. Transition energies are additionally given as derived from inelastic neutron scattering (INS) and heat capacity data.
| [meV] |
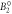
|
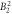
|
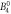
|
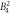
|
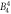
|
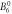
|
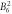
|
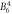
|
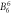
|
E1 | E2 | E3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower limit | −0.34 | −1.08 | 0.009 8 | 0.001 8 | 0.011 | 0.000 09 | −0.000 5 | 0.0 | 0.0 | |||
| McPhase fit |
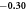
|
− 0. 99 | 0. 0106 | 0. 0071 | 0. 019 | 0. 00015 | 0. 0 | 0. 0012 | 0. 0011 | 8.1 | 12.1 | 29.5 |
| Upper limit | −0.26 | −0.89 | 0.011 4 | 0.013 4 | 0.029 | 0.000 21 | 0.000 6 | 0.002 4 | 0.002 1 | |||
| INS | 8.5 | 12.5 | − | |||||||||
| Heat cap. | 6.5 | 14.0 | 28.0 | |||||||||
| DFT, Δ1 | −0.23 | −1.04 | 0.005 0 | 0.034 1 | 0.034 | 0.000 05 | 0.001 0 | −0.001 4 | 0.000 4 | 2.8 | 6.7 | 27.0 |
| DFT, Δ2 | −0.18 | −0.98 | 0.003 3 | 0.023 2 | 0.025 | 0.000 03 | 0.000 5 | −0.000 8 | 0.000 2 | 3.7 | 6.2 | 23.8 |
The wave functions corresponding to the fitted 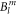 parameter set are:
parameter set are:
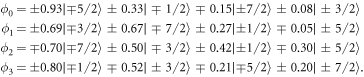
Since the 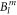 parameters are not determined with high accuracy, the values of the coefficients of the wave functions should only be seen as approximations to the true values. However, the fact that the ground state is dominated by the
parameters are not determined with high accuracy, the values of the coefficients of the wave functions should only be seen as approximations to the true values. However, the fact that the ground state is dominated by the 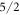 state and the third excited level by the
state and the third excited level by the 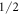 state is a robust result of our fit. It is a consequence of the requirement that the transition between these states is forbidden in neutron spectroscopy. The assumption that the ground state is dominated by the
state is a robust result of our fit. It is a consequence of the requirement that the transition between these states is forbidden in neutron spectroscopy. The assumption that the ground state is dominated by the  state is in good agreement with high-field magnetisation measurements [26].
state is in good agreement with high-field magnetisation measurements [26].
3.4. Comparison to DFT calculations
As a further tool to evaluate the CEF scheme of YbNi4P2, DFT calculations have been used. As discussed above, the DFT-derived crystal field parameters depend on the value of the hybridisation parameter Δ, which is only known approximately. We will constrain ourselves to the explicit discussion of two values: Δ = 5.4 eV, i.e. close to the lower cut-off edge, and Δ = 27.2 eV, i.e. in the parameter region where the dependence of the 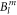 on Δ is weak (see figure 1). The crystal field parameter sets corresponding to these two values are also given in table 1 so that they can be compared to the McPhase fit. Even these two parameter sets do not differ strongly, so that the following discussing qualitatively applies for all parameter sets shown in figure 1.
on Δ is weak (see figure 1). The crystal field parameter sets corresponding to these two values are also given in table 1 so that they can be compared to the McPhase fit. Even these two parameter sets do not differ strongly, so that the following discussing qualitatively applies for all parameter sets shown in figure 1.
We note first of all that the agreement of the DFT-based 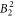 parameter with the one from the McPhase fit is very good (independent of the exact value of Δ). Thus, the calculations confirm the large basal plane anisotropy, which is experimentally seen in the NMR data.
parameter with the one from the McPhase fit is very good (independent of the exact value of Δ). Thus, the calculations confirm the large basal plane anisotropy, which is experimentally seen in the NMR data.
The 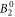 parameter, as well as the
parameter, as well as the  and the
and the 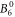 parameter, are smaller in the DFT-derived data sets than in the fit, with the discrepancy increasing with Δ. This implies a lower susceptibility along the c-axis compared to the fit. However, when comparing to experimental data, it can be seen that this apparent underestimation exists only with respect to the mean-field shifted data set; the actual measured susceptibility along c is rather well reproduced by the DFT-derived parameter sets (see figure 5). This reveals that the mean-field treatment, even though it improves the overall fit quality, also leads to distortions in the McPhase fitted parameter set.
parameter, are smaller in the DFT-derived data sets than in the fit, with the discrepancy increasing with Δ. This implies a lower susceptibility along the c-axis compared to the fit. However, when comparing to experimental data, it can be seen that this apparent underestimation exists only with respect to the mean-field shifted data set; the actual measured susceptibility along c is rather well reproduced by the DFT-derived parameter sets (see figure 5). This reveals that the mean-field treatment, even though it improves the overall fit quality, also leads to distortions in the McPhase fitted parameter set.
Figure 5. Comparison of the measured inverse susceptibility 1/χ(T) with the same quantity as derived from DFT calculations for Δ = 5.4 meV. Experimental data are shown in two ways: the solid lines give the data as measured, the dotted lines include the shift that accounts for the Kondo effect. The latter data sets are shown in figure 4(a).
Download figure:
Standard image High-resolution imageAs can also be seen in figure 5, the averaged susceptibility in the ab-plane is overestimated in the DFT calculations when compared to the actual measured data. Instead, a much better agreement is seen with the shifted data (and thus also the McPhase fit). This implies that the anisotropy between c-axis and ab-plane is underestimated by the DFT calculations.
Large discrepancies are seen when comparing the 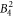 , the
, the 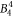 , the
, the  , the
, the 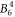 and the
and the  parameter derived from DFT calculations and the McPhase fit. Since the McPhase fit accuracy is poor for these parameters, the DFT-derived values are probably more reliable, although a quantification of the accuracy is difficult.
parameter derived from DFT calculations and the McPhase fit. Since the McPhase fit accuracy is poor for these parameters, the DFT-derived values are probably more reliable, although a quantification of the accuracy is difficult.
The DFT-based energy scheme is E1 = 2.8 meV (3.7 meV), E2 = 6.7 meV (6.2 meV) and E3 = 27.0 meV (23.8 meV) for Δ = 5.4 eV (27.2 eV). Thus, the calculations underestimate E1 and E2 compared to the neutron scattering data. However, the energy of the third level, not seen in neutron scattering, matches the values derived from both heat capacity data and from the McPhase fit. Furthermore, the cross section for neutron scattering for the highest transition is calculated to be close to zero.
The ground state wave functions belonging to the DFT-derived data sets are not as strongly dominated by the 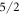 state as the one from the McPhase fit. Instead, the
state as the one from the McPhase fit. Instead, the 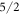 and the
and the 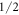 state contribute with similar coefficients, the magnitude of the
state contribute with similar coefficients, the magnitude of the 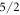 coefficient decreasing with increasing Δ.
coefficient decreasing with increasing Δ.
4. Summary
We have fitted experimental data from neutron scattering, susceptibility and NMR measurements using the programme package McPhase to determine the CEF parameters of YbNi4P2. We find that the ground state is dominated by the 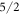 state. A large value of the
state. A large value of the 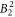 parameter, which is also confirmed by DFT calculations, results in a strong basal plane anisotropy. Experimentally, this is observed in the NMR data. The transition energies are 8.5 and 12.5 meV, as determined from neutron scattering, and roughly 30 meV, the latter being deduced from heat capacity measurements, from the McPhase fit and from the DFT calculations.
parameter, which is also confirmed by DFT calculations, results in a strong basal plane anisotropy. Experimentally, this is observed in the NMR data. The transition energies are 8.5 and 12.5 meV, as determined from neutron scattering, and roughly 30 meV, the latter being deduced from heat capacity measurements, from the McPhase fit and from the DFT calculations.
Acknowledgments
Work of PN was supported by the project 15-03777S of the Grant Agency of Czech Republic and work of ZH was partially funded by DFG Research Unit 960 'Quantum Phase Transitions'. KK and CK acknowledge support by the DFG via project KR3831/4-1 and CG support by the DFG via project GE602/4-1 Fermi-Nest. RS and H-HK are thankful to DFG for financial assistance through Grants No. SFB 1143 for the project C02.
Footnotes
- 7
Although this means fitting the same data twice, we consider this procedure sensible because it ensures equal weight of the c-axis and the ab-plane in the fit.








