Crossover of skyrmion and helical modulations in noncentrosymmetric ferromagnets

In magnetically ordered noncentrosymmetric crystals the chiral asymmetry of the exchange interaction induces specific Dzyaloshinskii–Moriya (DM) interactions [1]. In the energy functional of noncentrosymmetric ferromagnets, these interactions are described by energy contribution with antisymmetric terms linear in the first spatial derivatives of the magnetization M (r) (Lifshitz invariants) [1]

$$\begin{eqnarray}&&{{ \mathcal L }}_{{ij}}^{(k)}={M}_{i}\displaystyle \frac{\partial {M}_{j}}{\partial {x}_{k}}-{M}_{j}\displaystyle \frac{\partial {M}_{i}}{\partial {x}_{k}},\end{eqnarray} \tag{ 1 }$$

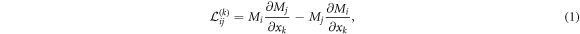
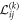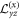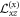where x_k are Cortesian components of the spatial variable r. Energy functionals ${{ \mathcal L }}_{{ij}}^{(k)}$ (1) favor spatial modulations of the magnetization propagating along the x_k axis and rotating in the (x_i, x_j) plane with a fixed rotation sense. For instance, the energy functionals ${{ \mathcal L }}_{{yz}}^{(x)}$ and ${{ \mathcal L }}_{{xz}}^{(x)}$ stabilize Bloch and Néel type modulations correspondingly (figures 1(a), (b)). The competition of the DM interaction with other magnetic forces stabilizes spatially modulated phases in a form of one-dimensional helices [1] or two-dimensional modulations composed of axisymmetric cells called skyrmion lattices [2, 3]. The magnetic-field-driven evolution of helical and skyrmionic states has been discovered and investigated in several groups of magnetic compounds with intrinsic and induced chirality. The former include noncentrosymmetric magnetically ordered crystals (e.g. cubic and uniaxial helimagnets [4, 5]) and the latter nanolayers of achiral ferromagnetic metals with surface/interface induced DM interactions (e.g. FePd/Ir(111) nanolayers [6]).

In ferromagnetic materials at a fixed temperature, the magnetization modulus 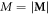$M=| {\bf{M}}|$ remains constant and is independent of the value of applied magnetic field. However, near the ordering temperature the longitudinal stiffness decreases and spatial longitudinal modulations of the magnetization modulus become a sizable effect (figure 1(c)). As a manifestation of this effect we recall the instability of rotational (Bloch and Néel) domains walls near the ordering temperatures of uniaxial ferromagnets, and the formation of domain walls with longitudinal modulations of the magnetization amplitude [7, 8].

For magnetic skyrmions the 'softening' of the magnetization modulus has dramatic consequences. Near the ordering temperature in applied magnetic fields, skyrmionic textures consist of complex combinations of rotational and longitudinal modulations (figures 1(d), (e)) [9–11]. It was also established that the coupling of rotational and longitudinal modes strongly influences the structure and magnetic properties of skyrmionic states and leads to the crossover of the inter-particle skyrmion–skyrmion interactions and a specific confinement effects of skyrmion lattices [9–11]. Earlier similar effects have been investigated in one-dimensional chiral modulations (helicoids) [12, 13]. In [10, 11] we have introduced a characteristic crossover temperature  T_cf ((T_C − T_cf)/T_C ≪1) separating the temperature interval below the Curie temperature (T < T_C) into two distinct regions. Over the broad temperature range from 0 to T_cf chiral modulated textures are composed of rotational modes (so called regular modulations). In the narrow temperature interval (T_cf < T < T_C), specific precursor modulations with a strong coupling between rotational and longitudinal modes determine the peculiar magnetic properties of chiral ferromagnets in this region.

Zoom In Zoom Out Reset image size

During the last years, the precursor states of noncentrosymmetric ferromagnets have been investigated experimentally and theoretically [14–17, 18–23]. Particularly, the recent observations in bulk cubic helimagnets MnSi [18] and FeGe [16–18] are consistent with the crossover effects of skyrmionic states theoretically described in [9–11] and earlier reported in a cubic helimagnet FeGe [10, 11].

In this paper we develop a consistent theory of skyrmion states near the ordering temperature and construct a magnetic phase diagram based on numerical calculations of the equilibrium skyrmionic states describing the crossover region between regular and precursor modulations. We discuss the results of [16, 18, 19] and the peculiarities of the precursor skyrmions in nanolayers of cubic and uniaxial chiral ferromagnets.

For investigations of the crossover phenomenon we consider the standard isotropic model for cubic noncentrosymmetric ferromagnets near the ordering temperature [10, 24]

$$\begin{eqnarray}&&W=A{(\mathrm{grad}{\bf{M}})}^{2}+D{\bf{M}}\cdot \mathrm{rot}{\bf{M}}-{\bf{M}}\cdot {\bf{H}}+{W}_{0}(M),\end{eqnarray} \tag{ 2 }$$

where A is the exchange stiffness, D is the Dzyaloshinskii constant, H is an applied magnetic field, W₀ collects short-range magnetic interactions dependent on the magnetization modulus 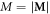$M=| {\bf{M}}|$. Near the ordering temperature W₀ can be written as [24]

$$\begin{eqnarray}&&{W}_{0}=\alpha (T-{T}_{0}){M}^{2}+{{bM}}^{4},\quad b\gt 0,\end{eqnarray} \tag{ 3 }$$

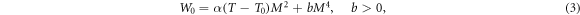
where T₀ is the ordering temperature of a ferromagnet with D = 0.

The functional (2) contains only the basic interactions essential to stabilize skyrmionic states in noncentrosymmetric ferromagnets. In particular, this includes the DM energy in the most symmetric isotropic form, and, thus, describes the most general properties of chiral modulations common for all noncentrosymmetric ferromagnets. In this paper, we omit some less important energy contributions such as magnetic anisotropy, stray-field energy, magneto-elastic coupling.

At zero field, model (2) describes the formation of one-dimensional twisting modulations (helices) (figure 1(a)) with period L_D below the Curie temperature, T_C where [11, 24]

$$\begin{eqnarray}&&{L}_{D}=\displaystyle \frac{4\pi A}{| D| },\quad {T}_{{\rm{C}}}={T}_{0}+{{\rm{\Delta }}}_{D}/4,\quad {T}_{{\rm{cf}}}={T}_{{\rm{C}}}-{{\rm{\Delta }}}_{D},\quad {{\rm{\Delta }}}_{D}=\displaystyle \frac{{D}^{2}}{2\alpha A}.\quad \end{eqnarray} \tag{ 4 }$$

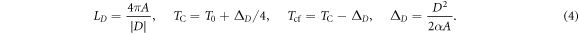
Exchange shift Δ_D (4) is a characteristic temperature related to the difference between the Curie temperature of a chiral ferromagnet (T_C) and T₀. We introduce here the crossover temperature T_cf separating the temperature intervals with repulsive (0 < T < T_cf) and attractive (T_cf < T < T_C) skyrmion–skyrmion interactions [9–11] The connection with the inter-skyrmion coupling crossover and the properties of skyrmion lattices will be discussed at the end of the paper.

By rescaling the spatial variable r = x/r₀ where r₀ = L_D/(4π) is related to the helix period L_D (4), the energy density functional (2) is reduced to the following form

$$\begin{eqnarray}&&{{\rm{\Phi }}}_{1}={({\bf{grad}}{\bf{m}})}^{2}-{\bf{m}}\cdot \mathrm{rot}{\bf{m}}-h({\bf{k}}\cdot {\bf{m}})+(t+1/4){m}^{2}+{m}^{4}.\end{eqnarray} \tag{ 5 }$$

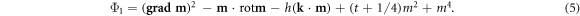
We introduce here the reduced temperature, magnetic field, and magnetization

$$\begin{eqnarray}&&t=(T-{T}_{{\rm{C}}})/{{\rm{\Delta }}}_{D},\quad {\bf{h}}={\bf{H}}/{H}_{0},\quad {\bf{m}}={\bf{M}}/{M}_{0},\end{eqnarray} \tag{ 6 }$$

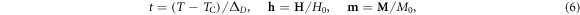
where H₀ = α Δ_D M₀, 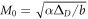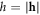${M}_{0}=\sqrt{\alpha {{\rm{\Delta }}}_{D}/b}$, $h=| {\bf{h}}|$, and k is a unity vector along the applied magnetic field.

Spatial variations of the magnetization modulus occurs only in the vicinity of the ordering temperature. Beyond this region at fixed temperatures, the modulus is equal to the saturated value, M = M_s (T) within the whole sample and independent of the applied magnetic field. For this case, the functional (5) can be replaced by the following reduced functional

$$\begin{eqnarray}&&{{\rm{\Phi }}}_{2}={({\bf{grad}}{\bf{n}})}^{2}-{\bf{n}}\cdot \mathrm{rot}{\bf{n}}-(H/{H}_{D})({\bf{k}}\cdot {\bf{n}}),\end{eqnarray} \tag{ 7 }$$

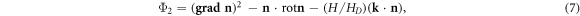
where H_D (T) = D²M_s (T)/(2A) is the saturation field [11, 25], n and 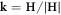${\bf{k}}={\bf{H}}/| {\bf{H}}|$ are unity vectors along the magnetization M the applied magnetic field H correspondingly.

Note that models (5) and (7) have different scales for applied magnetic fields. Rotational modulations within the model with a fixed modulus (7) are described by the reduced field H/H_D, and the equations for magnetic modulations with a 'soft' modulus include the reduced magnetic field H/H₀ (5).

We consider solutions for hexagonal skyrmion lattices which are homogeneous along the skyrmion axis (z-axis in this paper). This assumption is violated near the surfaces of cubic helimagnets where twisting modulations with the propagation along the z-axis arise [26]. However, these modulations are strongly localized near the surfaces (their penetration depth is estimated as 0.1L_D [26]) and are ignored in our work.

For the model with a soft magnetization modulus the equilibrium parameters for hexagonal skyrmion cells m (x, y) are derived by minimization of functional Φ₁ (5). This depends on three internal variables (components of the magnetization vector m) and two control parameters, the reduced magnetic field amplitude h and the 'effective' temperature t.

The solutions for the model with a fixed modulus n (x, y) i.e. well below the ordering temperature are derived by minimization of functional Φ₂ (7). Numerical solutions are obtained by using finite differences for gradient terms and adjustable grids to accommodate modulated states with periodic boundary conditions [10].

An important insight into the properties of skyrmion lattices is gained by calculations within the circular cell approximation [3, 27]. In this method the hexagonal cell is replaced by a circle of equal area transferring the boundary conditions at the cell edge from the hexagon to the circle. Following [3, 27] we use spherical coordinates for m (x, y) and cylindrical for the spatial variable (x):

$$\begin{eqnarray*}&&{\bf{m}}=m(\sin \theta \cos \psi ,\sin \theta \sin \psi ,\cos \theta ),\quad {\bf{x}}=(\rho \cos \varphi ,\rho \sin \varphi ,z)\end{eqnarray*}$$

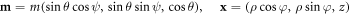
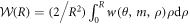and consider a 'lattice' composed of circular cells of radius R. After substitution of solutions ψ = φ + π/2 into (5) and integration with respect to φ the energy density per unit volume ${ \mathcal W }(R)$ for the lattice in the circular cell approximation is ${ \mathcal W }(R)=(2/{R}^{2}){\int }_{0}^{R}w(\theta ,m,\rho )\rho {\rm{d}}\rho$. The Euler equations for the functional 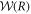${ \mathcal W }(R)$ with boundary conditions θ(0) = π, θ(R) = 0, m(R) = m_R describe the solutions for a Skyrmion cell and yield the energy density 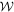${ \mathcal W }$ as a function of the control parameters t, h and the internal parameters m_R and R. The equilibrium profiles θ (t, h), m (t, h) are derived by the minimization of 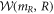${ \mathcal W }({m}_{R},R)$ with respect to m_R, R. A similar procedure is applied for calculations within the model with a fixed magnetization modulus [3].

Typical solutions for hexagonal lattices with a fixed magnetization modulus, i.e. well below the ordering temperature, are collected in figure 2 and for those in the precursor state are presented in figures 3–5. For the former a magnetic-field-driven evolution of the skyrmion lattice consists of two processes: an extension of the lattice period and a contraction of the skyrmion core [3] (figure 2). At the critical field H_s (T) = 0.801H_D (T) the skyrmion lattice transforms into the saturated state by an infinite extension of the lattice period [3]. Contrary to the common second-order transitions of Landau type, the lower symmetry phase (skyrmion lattice) does not disappear completely during the transition but remains in the high symmetry phase (saturated state) in a form of localized states (isolated skyrmions). De Gennes has designated these transitions as the nucleation type, and the common second-order transitions as the instability type [28]. The solutions for model (5) in the vicinity of the ordering temperature (t = −0.02) (figure 3) demonstrate a dominant role of longitudinal modulations. In this case the lattice periods practically do not change with increasing applied field and m(r) exhibits a profound spatial inhomogeneity and a strong field dependence (figure 3). Despite the strong transformation of their internal structures the skyrmion lattices preserve axisymmetric arrangement of the magnetization near the centres of the lattice cells (figures 3(a)–(d)). This remarkable property reflects the basic physical mechanism underlying the formation of skyrmion lattices. The local energetic advantage of skyrmion lattices over helicoids is due to a larger energy reduction in the 'double-twisted' skyrmion cell core compared to 'single-twisted' helical states [27]. This explains the unusual axial symmetry of the cell cores and their stability. An increasing magnetic field gradually suppresses the antiparallel magnetization in the cell core reducing the energetic advantage of the 'double-twist' and increases the overall energy of the condensed skyrmion lattice. At the critical field h_f, a first-order transition occurs into the saturated state. Above this field the skyrmion lattice still can exist as a metastable state until the magnetization modulus in the cell centre becomes zero (see the magnetization profile for h = 0.042 in figure 3(f)).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The calculated phase diagram (figure 4(a)) shows that the transition field h_s(t) between the skyrmion lattice and saturated state has three distinct sections separated by critical points h_s1 and h_s2.

• (i)  
  For h_s (t) > h_s1 the second-order transition of nucleation type occurs along the critical line h_s(t). At lower temperatures where spatial variations of m become negligible this critical line transforms into transition line h_s = 0.801H_D(T)/H₀.
• (ii)  
  For h_s1 > h_s(t) > h_s2 the skyrmion lattice transforms into the saturated state by the first-order process. In this case skyrmion lattices can exist as metastable state above the transition line. Figure 5(a) shows the potential profiles Φ (m_R) in the vicinity of the first-order transition. Magnetization profiles θ (ρ/L_D), m (ρ/L_D) in figures 5(b) and (c) demonstrate the evolution of solutions along the potential barrier.
• (iii)  
  Finally, in the vicinity of the ordering temperature (h_s2 > h_s(t) > 0 ) the second-order process of instability type occurs.

Near the ordering temperature helicoids also consist of coupled rotational and longitudinal modulations and exhibit a qualitatively similar evolution in the applied field [12–15]. The phase transition lines between the helicoid and saturated state have been calculated in [12]. In the phase diagram, they are indicated with light grey color (figures 4(a), (b)).

At lower temperatures (h_h(t) > h_h1) the applied field gradually unwinds the helicoid into a set of isolated domain walls (kinks) (the second-order transition of nucleation type). In the temperature interval h_h1 > h_h(t) > h_h2 the helicoid transforms into the saturated phase by the first-order process, and near the ordering temperature (h_h2 < h_h(t) < 0) the second-order transition of instability type occurs. Interestingly, the crossover of the inter-soliton coupling occurs on the same critical line as for skyrmions (8). Detailed calculations of helicoid states in the precursor state have been carried out by Shinozaki et al [15]. Note that h_h(t) line does not belong to the elements of the phase diagrams in figures 4(a), (b), and are plotted to compare the helicoid (h_h(t)) and skyrmion lattice (h_s(t)) transition fields.

Epilayers of cubic helimagnets with strong induced magnetic anisotropy of easy-plane type [29] and easy-plane noncentrosymmetric ferromagnets (e.g. a hexagonal helimagnet CrNb₃S₆ [5, 20, 21] provide an ideal setup for investigations of helicoid modulations in the regular and precursor regions. Chiral ferromagnets with easy-axis anisotropy and free-standing nanolayers of cubic helimagnets are characterized by extended stability areas for helicoids and skyrmion lattices [25, 30] and are convenient objects for investigations of the precursor modulated states.

In the phase diagram (figure 4(a)) we have plotted line 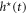${h}^{\star }(t)$ with turning point p (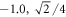$-1.0,\sqrt{2}/4$) and ending point u (−0.75, 0) described by the equation [9]

$$\begin{eqnarray}&&{h}^{\star }=\sqrt{2(1\pm \sqrt{t+1})}(t+5/4\pm \sqrt{t+1}),\quad t\lt -0.75.\end{eqnarray} \tag{ 8 }$$

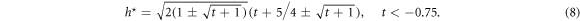
This line separates the areas with different types of the skyrmion–skyrmion and kink–kink coupling [9, 12]. Isolated skyrmions with rotational modes are always repulsive [31]. For skyrmions with longitudinal and rotational modes above a certain critical temperature the inter-particle potential gains an oscillatory character and imposes an attractive coupling between skyrmions [9–11]. Similar properties are exhibited by isolated chiral domain walls (kinks) [12]. In the phase diagram (figure 4(a)) the crossover fields of the phase transitions from the modulated (skyrmion lattice and helicoid) phases into the saturated states belong to the critical line 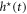${h}^{\star }(t)$ (8). This fact demonstrates that the character of inter-particle coupling between isolated skyrmions (kinks) determines the order of the phase transition from the skyrmion lattice (helicoid) into the saturated state. A skyrmion lattice composed of repulsive cores transforms into the saturated states by the second-order transition of the nucleation type (figure 2). A skyrmion lattice (helicoid) with attractive skyrmion cells transforms into the saturated state at finite period by the first-order process (figure 3). In other words, the crossover of the inter-soliton coupling triggers the crossover of the phase transition between the skyrmion lattice (helicoid) and saturated state. The first-order transition from the skyrmion lattice into the cone phase and the formation of skyrmion clusters observed in cubic helimagnet Cu₂OSeO₃ [32] are explained by the attractive inter-skyrmion potential in the cone phase [33].

The phase diagram of the solutions for skyrmion lattices and helicoids (figure 5(c)) surveys the soft modulus effects and crossover phenomena in the precursor states of cubic helimagnets. In bulk cubic helimagnets, however, the cone phase corresponds to the global minimum, and skyrmion lattices and helicoids are metastable [11]. Skyrmion lattices are stabilized only in the A-phase, a small pocket in the vicinity of the ordering temperature. A coexistence of twisted and longitudinal modulations observed in the A-phase [11, 34] is a manifestation of soft modulus effects in the skyrmion lattice phase. It was also established that in bulk MnSi, the skyrmion lattice in the A-phase is saturated by the first-order process [18] in accordance with the phase diagram in figure 5(c).

Similar crossover phenomena occur in type-II superconductors. This group of superconductors is usually characterized by the repulsive vortex–vortex potential and the nucleation type of the second-order transition between Abrikosov vortex lattice phase and superconducting phase. However, for compounds with small values of the Ginzburg–Landau parameters the inter-vortex coupling has an oscillatory character [35] which imposes the first-order transition between the vortex lattice and superconducting state [36].

In conclusion, the equilibrium states of skyrmion lattices in the precursor states of cubic helimagnets demonstrate the crossover from lower temperature twisting modulations (figure 2) to the precursor states with dominating longitudinal modes (figure 3). The calculated magnetic phase diagram shows in the precursor region skyrmion lattices transform into the saturated phase by first-order processes (figures 4, 5). These results are corroborated by the recent experimental findings [18, 19] and provide a theoretical basic for investigations of the precursor states in chiral ferromagnets.

The authors are grateful to J Campo, K Inoue, Y Kato, J Kishine, V Laliena, Y Masaki, M Mito, C Pappas, M Shinozaki, and Y Togawa for fruitful discussions and to J Loudon for critical reading of the manuscript. AOL thanks Ulrike Nitzsche for technical assistance. This work was funded by JSPS Core-to-Core Program, Advanced Research Networks (Japan) and JSPS Grant-in-Aid for Research Activity Start-up 17H06889.